Abstract
Background
Bioelectrical impedance vector analysis (BIVA) is a technique for the assessment of hydration and nutritional status, used in the clinical practice. Specific BIVA is an analytical variant, recently proposed for the Italian elderly population, that adjusts bioelectrical values for body geometry.
Objective
Evaluating the accuracy of specific BIVA in the adult U.S. population, compared to the ‘classic’ BIVA procedure, using DXA as the reference technique, in order to obtain an interpretative model of body composition.
Design
A cross-sectional sample of 1590 adult individuals (836 men and 754 women, 21–49 years old) derived from the NHANES 2003–2004 was considered. Classic and specific BIVA were applied. The sensitivity and specificity in recognizing individuals below the 5th and above the 95th percentiles of percent fat (FMDXA%) and extracellular/intracellular water (ECW/ICW) ratio were evaluated by receiver operating characteristic (ROC) curves. Classic and specific BIVA results were compared by a probit multiple-regression.
Results
Specific BIVA was significantly more accurate than classic BIVA in evaluating FMDXA% (ROC areas: 0.84–0.92 and 0.49–0.61 respectively; p = 0.002). The evaluation of ECW/ICW was accurate (ROC areas between 0.83 and 0.96) and similarly performed by the two procedures (p = 0.829). The accuracy of specific BIVA was similar in the two sexes (p = 0.144) and in FMDXA% and ECW/ICW (p = 0.869).
Conclusions
Specific BIVA showed to be an accurate technique. The tolerance ellipses of specific BIVA can be used for evaluating FM% and ECW/ICW in the U.S. adult population.
Introduction
The assessment of body composition, i.e. fat mass and fat free mass – according to the two-compartment model – and of hydration status, is essential in epidemiological studies or routine biomedical practice, particularly in the fields of nutritional research, geriatrics, and sports medicine.
However, the more accurate methodologies for the assessment of body composition (such as imaging techniques) and hydration status (isotope dilution as the gold standard) are procedurally complex, relatively invasive and expensive, therefore not suitable in routine medical practice or epidemiology.
Bioelectrical impedance analysis (BIA), and its variants multi-frequency BIA and bioimpedance spectroscopy (BIS), are easy and non-invasive methods for assessing body composition [1]. These methods are based on the analysis of bioelectrical impedance in the human body (particularly the resistive component) at the passage of an alternating electrical current of low intensity. In the conventional BIA approach, total body water (TBW) and fat-free mass (FFM) are estimated by means of regression equations, considering that the current flows proportionally to the quantity of body fluids, to which resistance (R) is inversely related. Even if equations generally take into account other influential variables, such as height, sex, and age, they can lead to substantial estimation errors when applied to individuals that differ from the sample used for validation, especially in clinical situations [2].
Bioelectrical impedance vector analysis (BIVA) [3] represents an interesting alternative method. By using an empirical approach and without referring to predictive equations or assumptions on body components, BIVA provides a semiquantitative evaluation of body cell mass and body water. BIVA considers both the components of bioelectrical impedance (R, and reactance, Xc, at 50 kHz and 800 µA), assuming that R correlates negatively with body fluids and Xc correlates positively with body cell mass, where cell membranes behave as capacitors. R and Xc, normalized for height, are compared with the tolerance ellipses of the reference population, where the major axis refers to hydration status and the minor axis to the body cell mass, thus allowing body composition evaluation.
Specific reference standards have been proposed for different populations, sex and age groups [4]–[9]. BIVA has been applied in different geographic contexts [10]–[13], in juvenile samples [10]–[17] as well as in the elderly [18]–[20], in athletes [21]–[25], and in many pathological conditions (see the reviews by Barbosa-Silva et al. [2] and by Norman et al. [26], and the more recent researches [27]–[33]. The clinical validation of BIVA showed a significant association of bioelectrical values with hydration [26], [34] and nutritional status [26].
However, the validation of BIVA in evaluating the relative amount of fat mass based on a gold standard technique is lacking. In effect, it is mainly based on the comparison with BMI [35], [36]. When compared to dual-energy X-ray absorptiometry (DXA) results in a sample of elderly Italian population, BIVA failed to recognize the differences of body composition [37]. On the contrary, a methodological variant of BIVA - specific BIVA - has proven to be effective in identifying the relative proportion of fat mass [37]. The new specific BIVA procedure is based on the simple assumption, inherent to the Ohm’s law, that body impedance is affected by cross-sectional area, besides than individual’s height.
The aim of this study is evaluating the accuracy of specific BIVA for the assessment of body composition in a large sample of the adult U.S. population, and performing a comparison with the ‘classic’ BIVA. Specific BIVA is proposed here as an accurate operational procedure to evaluate the relative amount of body fat mass (FM%) and of extracellular/intracellular water ratio (ECW/ICW) in the U.S. population.
Materials and Methods
The Sample
The sample under study is derived from the National Health and Nutrition Examination Survey (NHANES) 2003–2004 [38]. The data survey was approved by National Center for Health Statistics (NCHS) Research Ethics Review Board. The written informed consent was obtained as a first step of the NHANES procedure.
The NHANES open access data sets include interviews (demographic, socioeconomic, dietary, and health-related questions) and physical examinations (medical, dental, physiological measurements, laboratory tests results) from a stratified sample of the civilian non-institutionalized population of the U.S. The NHANES 2003–2004 is the most recent NHANES survey including both BIA and DXA data. Participants (10,122 individuals of all ages) are categorized into five ethnic groups: Mexican American; Other Hispanic; Non-Hispanic White; Non-Hispanic Black; Other Race - Including Multi-Racial. In order to better represent the whole variability and to increase the sample size, in this paper the five ethnic groups have been pooled. A similar approach was adopted for the production of NHANES growth charts, where the development of separate charts for various groups that constitute the U.S. population was considered not practical [39].
Selected variables included demographic information (age, sex), anthropometric data (weight, standing height, body mass index, arm – waist – maximal calf circumferences), impedentiometric variables (R and Xc at 50 kH, intracellular and extracellular fluid volume, according to BIS), and DXA measurements (total and percent fat, lean mass excluded bone mineral content of the four limbs). The skeletal muscle mass index (SMI, kg/m2) was calculated as the sum of the lean mass of the four limbs corrected for the height squared [40].
Case selection was made on the basis of the availability of measurements and of quality of data, as defined by NHANES comment codes [41], [42]. Bioelectrical variables were included only if showing an excellent fit (BIDFIT = 0) to the Cole model [42], [43].
A final sample of 1590 adult individuals (836 men and 754 women, 21–49 years old) was considered. The mean age was 34.2±8.6 years for men and 35.5±8.4 years for women.
The database is available at the Cagliari University institutional repository (http://veprints.unica.it/809/).
Measurements
The protocol used for the 2003–2004 National Health and Nutrition Examination Survey, including all procedures, policies, and standards, is detailed in manuals published on the CDC website (www.cdc.org), separately for anthropometric [41], and body composition (BIA and DXA) measurements [42]. All measurements were taken by trained health technicians, who were responsible for the maintenance and calibration of the equipment. Anthropometric variables were taken using a Toledo electronic weight scale, a Seca electronic stadiometer, and a steel measuring tape. The HYDRA ECF/ICF Bio-Impedance Spectrum Analyzer (Model 4200; Xitron Technologies, Inc, San Diego, California, USA) was used for bioelectrical measurements. Whole body DXA scans, for the estimation of body composition, were taken with a Hologic QDR-4500A fan-beam densitometer (Hologic, Inc., Bedford, Massachusetts).
Statistical Analysis
On the basis of resistance (R, Ohm) and reactance (Xc, Ohm) values, phase angle and impedance (Z, Ohm) were computed with the formula, respectively: arctan (Xc/R, degrees) and (R2+ Xc2)0.5. Descriptive univariate statistics (mean, standard deviation) were calculated for each indicator and each sex. Pearson correlation coefficients between bioelectrical and body composition values were calculated in sexes separated.
Bioelectrical Impedance Vector Analysis
BIVA [3] was conducted using bioelectrical measurements adjusted for the height (R/H, Ohm/m, Xc/H, Ohm/m), thus removing the conductor length effect. In BIVA procedure, R/H and Xc/H are plotted as a point on the probability graph (RXc graph), showing the 50%, 75%, and 95% tolerance ellipses of the reference population. Major and minor axis refer respectively to hydration status (dehydrated individuals tending towards the upper pole) and to cell mass, where the left side corresponds to a high cell mass (i.e. more soft tissue). On the left side, obese individuals shows shorter vector than athletic individuals but a similar phase angle. Similarly, on the right side, cachectic subjects have shorter vectors but similar phase angle than lean individuals.
Specific Bioelectrical Impedance Vector Analysis
The new approach of specific BIVA is detailed in Appendix S1 and Figure S1, and in Marini et al. [37]. The innovation with respect to classic BIVA is that bioelectrical values are standardized by cross-sections of the body, besides than by height. In fact, according to Ohm’s law, R is directly proportional to the conductor’s length (L) and inversely proportional to its cross-section (A), so that: R = ρ·L/A, where the resistivity (ρ = R·A/L), or specific resistance, is uninfluenced by size and shape.
In specific BIVA, R and Xc values were hence multiplied by a correction factor (A/L) in order to obtain an estimate of resistivity (or specific resistance, R sp), and reactivity (or specific reactance, Xc sp).
Area was estimated as: A = 0.45 arm area +0.10 waist area +0.45 calf area (m2). Arm, waist and calf area were estimated by the formula C2/4JI, where C (m) is the circumference of the respective segment; the multiplying coefficients were chosen considering the differential current flow through the human body [1], [44].
Length was estimated as: L = 1.1 H, where H is body height in meters and the coefficient 1.1 was determined on the basis of the anthropometric proportions of the human body [45].
Impedivity (Z sp) was calculated as (R sp 2+ Xc sp 2)0.5.
Phase angle values are unchanged with respect to classic BIVA.
In order to compare classic and specific BIVA, specific bioelectrical values were multiplied by a factor of 100. The BIVA software [46] was still used, with the expedient of not dividing for height in the BIVA-tolerance package, as this passage of calculation is automatically performed.
Validation of Specific BIVA
The sample distribution of the FMDXA% and ECW/ICW was divided into percentiles and the bioelectrical values of cases below the 5th were compared with those above the 95th percentile by means of confidence ellipses and by the Hotelling’s T2 test.
Classic and specific bioelectrical values of individuals with FMDXA% or ECW/ICW values below the 5th and above the 95th percentiles were projected on the RXc graph, in order to evaluate the classificatory performance of the BIVA procedures. In the case of classic BIVA, the areas of the RXc graph corresponding to different amounts of body fat mass (FM%) were defined on the basis of the literature [3]. In the other cases (specific BIVA, both FMDXA% and ECW/ICW; classic BIVA, ECW/ICW), the areas were defined on the basis of the empirical evidence.
The sensitivity (or true positive rate, e.g. the percentage of individuals above the 95th percentile of FMDXA% correctly identified as having such an high fat mass) and specificity (or true negative rate, e.g. the percentage of individuals who were correctly identified as not having such a high fat mass) of the classification were calculated for each sex and body composition indicator (5th and 95th percentile of FMDXA% and ECW/ICW), in classic and specific BIVA.
The accuracy of the classification realized with classic and specific BIVA was evaluated by means of receiver operating characteristic (ROC) curves. The ROC curve is a plot of the sensitivity versus the false positive rate (1-specificity) for a classifier system (in this case, classic or specific BIVA) as its discrimination threshold (in this case, 50th, 75th or 95th percentile) is varied. ROC curves can be summarized by the area under the curve, which can assume a value between 0 and 1; an area equal to 0.5 means the results are due to chance, and a larger area corresponds to a better classification [47]. The values of sensitivity and specificity are robust with respect to sample variability, because of the large sample size used to calculate the ellipses and hence the use of more sophisticated techniques to validate the classification error, such as the cross-validation technique, was considered unnecessary. The significance of the differences in the performance between classic and specific BIVA was evaluated by means of a probit multiple-regression [48] of their corresponding areas under the ROC curves. A successive regression analysis was performed in order to assess the possible different accuracy of specific BIVA in the assessment of FMDXA% and ECW/ICW, and in the classification of individuals in the 5th and 95th percentiles for both indexes. The minimum distance criteria [47] from the point of coordinates (1, 1), which corresponds to the point of perfect classification, was applied to identify the optimal cut-off for the classification of body composition.
In order to better describe the variability of the mean impedance vectors in the whole sample, according to body composition changes, the distribution of FM% and ECW/ICW was divided into deciles and the corresponding mean impedance vectors and confidence ellipses were projected on the specific tolerance ellipses.
Moreover, on the basis of the percentile distribution of SMI (<10th and >90th percentiles), individuals with different body muscular mass were selected: athletic (men: SMI >9.51 kg/m2; women: SMI >7.93 kg/m2) and lean individuals (men: SMI <7.39 kg/m2; women: SMI <5.66 kg/m2). In order to avoid confounding effects, the FMDXA% range of variability was limited to 20–24% in men and 32–36% in women. Bioelectrical vectors of the athletic and lean groups were projected on the specific tolerance ellipses and compared by means of the Hotelling’s T2 test.
NHANES data were downloaded in SAS transport file format by using the free SAS System Viewer release 8.2.1 (SAS Institute Inc). Subsequent analyses were performed using the free packages Open Office, R (http://www.R-project.org/) and BIVA softwares [46].
Results
Table 1 shows descriptive statistics of anthropometric, bioelectrical, and body composition variables in the sample subdivided by sex.
Table 1. Descriptive statistics in the sample subdivided by sex.
| Men | Women | |||
| mean | s.d. | mean | s.d. | |
| Anthropometric variables | ||||
| Height (cm) | 175.7 | 7.7 | 162.6 | 6.7 |
| Weight (kg) | 84.3 | 16.2 | 74.8 | 18.9 |
| BMI (kg/m2) | 27.3 | 4.8 | 28.3 | 7.0 |
| Calf circumference (cm) | 39.1 | 3.6 | 38.3 | 4.8 |
| Arm circumference (cm) | 33.8 | 4.0 | 32.0 | 5.3 |
| Waist circumference (cm) | 95.7 | 12.9 | 92.9 | 15.4 |
| Bioelectrical variables | ||||
| R (Ohm) | 463.5 | 61.0 | 559.3 | 79.1 |
| Xc (Ohm) | 60.2 | 8.2 | 62.6 | 8.8 |
| Phase (degrees) | 7.5 | 0.7 | 6.5 | 0.7 |
| R/H (Ohm/m) | 264.4 | 37.1 | 344.3 | 49.6 |
| Xc/H (Ohm/m) | 34.4 | 5.2 | 38.6 | 5.9 |
| Z/H (Ohm/m) | 264.5 | 37.1 | 344.4 | 49.6 |
| Rsp (Ohm · cm) | 402.4 | 62.9 | 492.0 | 95.9 |
| Xc sp (Ohm · cm) | 52.5 | 9.5 | 55.4 | 12.3 |
| Zsp (Ohm · cm) | 405.9 | 63.4 | 495.2 | 96.5 |
| r R/H-Xc/H | 0.741 (p≈0.00) | 0.741 (p≈0.00) | ||
| r Rsp-Xc sp | 0.839 (p≈0.00) | 0.875 (p≈0.00) | ||
| Body composition variables | ||||
| Extra cellular water (ECW) (L) | 19.2 | 3.0 | 14.7 | 2.6 |
| Intra cellular water (ICW) (L) | 18.8 | 3.9 | 18.8 | 4.0 |
| ECW/ICW | 0.7 | 0.1 | 0.8 | 0.1 |
| Total fat (DXA) (kg) | 23.0 | 8.3 | 29.7 | 11.3 |
| Percent fat (DXA) (FMDXA%) | 26.5 | 5.7 | 38.8 | 6.5 |
| SMI (DXA) (kg/m2) | 8.4 | 1.5 | 6.8 | 1.4 |
Legend: BMI: body mass index; H: height; R: resistance; Xc: reactance; Z: impedance; sp: specific; r: correlation; ECW: extracellular water; ICW: intracellular water; DXA dual X-ray absorptiometry; SMI: skeletal muscle mass index.
The results of the comparison between classic and specific BIVA are shown in Tables 2 and 3, and in Figure 1 and Figure 2 .
Table 2. Correlation between bioelectrical and body composition variables.
| Men | Women | |||||
| FM% | ECW/ICW | BMI | FM% | ECW/ICW | BMI | |
| R/H (Ohm/m) | −0.162** | 0.278** | −0.617** | −0.347** | 0.295** | −0.695** |
| Xc/H (Ohm/m) | −0.193** | −0.399** | −0.416** | −0.305** | −0.368** | −0.501** |
| Z/H (Ohm/m) | −0.162** | 0.277** | −0.617** | −0.347** | 0.295** | −0.695** |
| Phase (degrees) | −0.079* | −0.941** | 0.212** | 0.022 | −0.919** | 0.216** |
| Rsp (Ohm· cm) | 0.853** | −0.002 | 0.749** | 0.873** | −0.054 | 0.832** |
| Xcsp (Ohm · cm) | 0.678** | −0.514** | 0.750** | 0.765** | −0.484** | 0.824** |
| Zsp (Ohm · cm) | 0.852** | −0.011 | 0.751** | 0.873** | −0.060 | 0.834** |
Legend: * p<0.05; ** p<0.01;
R: resistance; Xc: reactance; Z: impedance; H: height; sp: specific; FM: fat mass; ECW: extracellular water; ICW: intracellular water; BMI: body mass index.
Table 3. Descriptive and comparative statistics between groups with different body composition: classic and specific bioelectrical values.
| Classic BIVA | ||||||||
| R/H | Xc/H | |||||||
| Percentile | Mean | s.d. | Mean | s.d. | T2 | p | D | |
| FM% | 95 th | 252.5 | 25.4 | 31.8 | 3.5 | 11.7 | 0.005 | 0.75 |
| (N = 42) | 5 th | 274.7 | 43.7 | 35.3 | 5.8 | |||
| ECW/ICW | 95 th | 294.8 | 48.6 | 30.0 | 5.4 | 450.0 | 0.000 | 4.66 |
| (N = 42) | 5 th | 248.5 | 28.0 | 38.1 | 4.7 | |||
| Specific BIVA | ||||||||
| Rsp | Xcsp | |||||||
| Percentile | Mean | s.d. | Mean | s.d. | T2 | p | D | |
| FM% | 95 th | 513.7 | 52.3 | 64.8 | 8.3 | 550.5 | 0.000 | 5.15 |
| (N = 42) | 5 th | 303.8 | 23.7 | 39.2 | 5.0 | |||
| ECW/ICW | 95 th | 382.9 | 82.9 | 39.6 | 10.8 | 840.9 | 0.000 | 6.29 |
| (N = 42) | 5 th | 391.6 | 51.6 | 59.9 | 7.7 | |||
Legend: T2: Hotelling’s test; p: p value; D: Mahalanobis distance. R: resistance; Xc: reactance; Z: impedance; H: height; sp: specific; FM: fat mass; ECW: extracellular water; ICW: intracellular water.
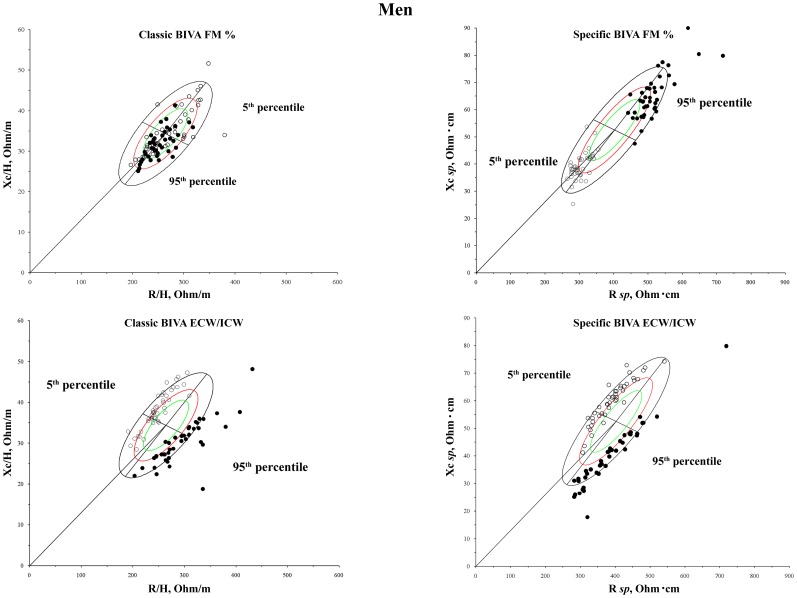
Figure 1. Distribution of bioelectrical vectors from individuals with different amounts of FMDXA% and ECW/ICW on the sex specific bivariate tolerance ellipses (men).
White dots: 5th percentile; black dots: 95th percentile.
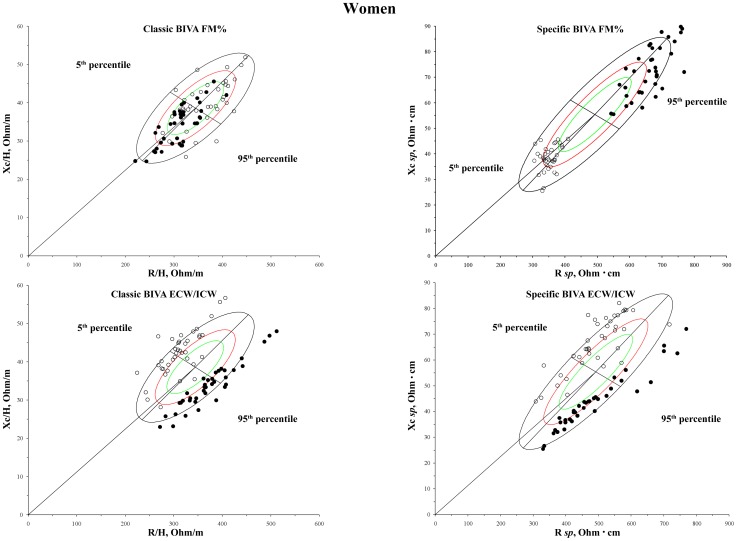
Figure 2. Distribution of bioelectrical vectors from individuals with different amounts of FMDXA% and ECW/ICW on the sex specific bivariate tolerance ellipses (women).
White dots: 5th percentile; black dots: 95th percentile.
Table 2 shows the correlation values between bioelectrical and body composition variables (FMDXA%, ECW/ICW, BMI). The correlation between FMDXA% and reactance and resistance was negative in the case of classic bioelectrical variables and positive in the case of specific bioelectrical variables. Although the correlation values proved highly significant in both cases, the association was much greater in the case of specific variables. The variables best correlated with the percentage of fat were resistivity and impedivity. The phase angle was negatively correlated with FMDXA% in men (p<0.05) but not in women. The correlations between bioelectrical variables and BMI showed a pattern analogous to that of the FMDXA%, with the exception of the phase angle, which was positively correlated with the BMI in both sexes. The ECW/ICW ratio showed the greatest (negative) correlation values with the phase angle. The correlation between ECW/ICW and reactance was negative with both procedures, but more pronounced in specific BIVA. The resistance was positively correlated with the ECW/ICW ratio in classic BIVA and non-correlated in specific BIVA.
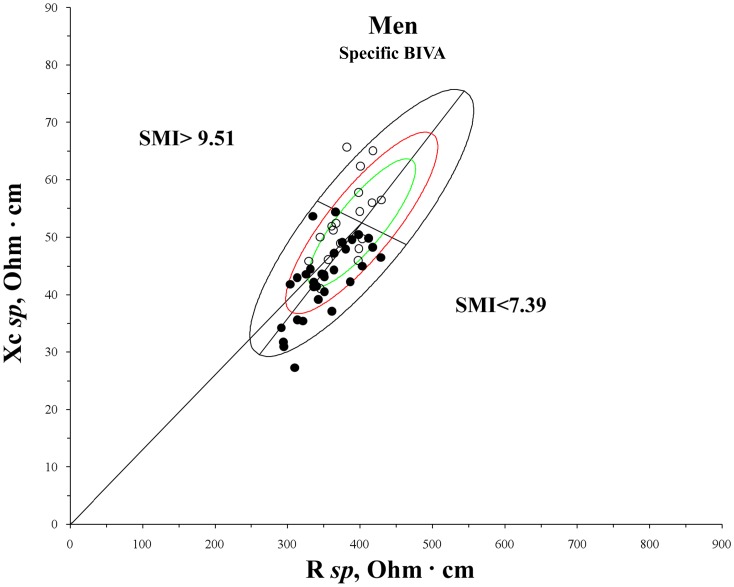
Table 3 shows the descriptive and comparative statistics between individuals below the 5th percentile and above the 95th percentile of FMDXA% and of ECW/ICW. The difference was significant in all the comparisons made. The distance between the groups was, however, always greater in the case of the specific BIVA, as showed by the Mahalanobis D values and by Figures 1 and 2. The distribution on the RXc graph of bioelectrical vectors from individuals with different amounts of fat mass was different in classic and specific BIVA (Figures 1 and 2): a tendency toward the central-right upper and central-left lower areas for 5th and 95th FMDXA% percentiles respectively, in the case of classic BIVA; same areas but opposite conditions in the case of specific BIVA. With respect to ECW/ICW, the distribution on the RXc graph is similar in classic and specific BIVA, but more concentrated in the specific case: vectors oriented towards left upper and right lower areas for 5th and 95th ECW/ICW percentiles respectively. Specific bioelectrical vectors of athletic individuals were located in the area corresponding to low ECW/ICW ratio, while those of lean ones in the area of high ECW/ICW ratio ( Figure 3 ); the difference between mean impedance vectors was significant in both sexes (men: T2 = 26.5, p<0.001; women: T2 = 32.3, p<0.001). Phase angle was positively correlated with skeletal muscle mass index (men: r = 0.35, p<0.01; women: r = 0.34, p<0.01).
Figure 3. Mean specific vectors of athletic and lean men plotted on the sex specific bivariate tolerance ellipse.
SMI = skeletal muscle mass index; white dots: SMI>9.51; black dots: SMI<7.39.
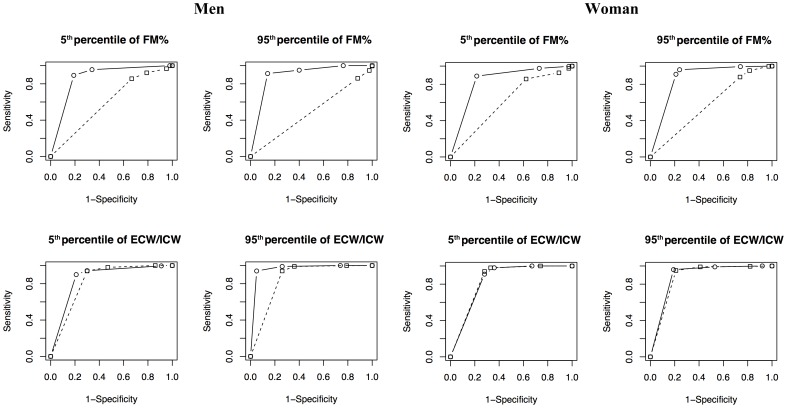
Figure 4 shows the ROC curves corresponding to the classification of individuals with different body composition obtained by classic and specific BIVA. As can be seen, the ROC area was almost always greater in the specific BIVA (ranging from 0.84 to 0.90 for FMDXA% and from 0.84 to 0.96 for ECW/ICW) than in the classic BIVA (ranging from 0.49 to 0.61 for FMDXA% and from 0.83 to 0.88 for ECW/ICW). The multiple-regression on the probit transformation of the areas showed that the specific BIVA was significantly more accurate than classic BIVA (p = 0.002) in evaluating FMDXA%, even considering the possible effect of sex, while the evaluation of ECW/ICW was similarly performed by the two techniques (p = 0.829). Moreover, with a separate probit multiple-regression, we showed that the accuracy of classification of specific BIVA was similar in the two sexes (p = 0.144), in ECW/ICW and FMDXA% (p = 0.869), but there was a slight evidence that it performs better in classifying the 95th with respect to the 5th percentile (p = 0.059). According to the minimum distance criterium, the cut-off showing the minimal distance from (1,1) was the 50% in all cases.
Figure 4. ROC curves showing the comparison between classic (dotted lines and squared symbols) and specific (continuous lines and dots) BIVA in the assessment of FMDXA% and ECW/ICW in the two sexes.
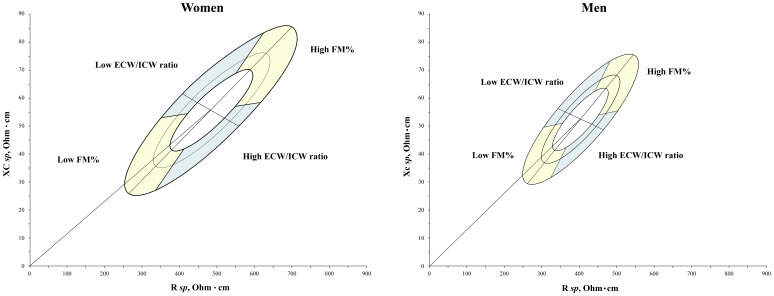
Figure 5 shows the 50th, 75th, and 95th specific BIVA tolerance ellipses of men and women with the interpretation of different regions in terms of body composition.
Figure 5. Specific tolerance ellipses with the interpretation of different regions in terms of body composition.
Left: women; right: men.
Figure 6 (women) and Table 4 (both sexes) show the mean bioelectrical characteristics of each decile of FM% and ECW/ICW distributions.
Figure 6. Mean vectors and confidence ellipses distribution of deciles of FM% and ECW/ICW ratio on the specific tolerance ellipses (women).
Left: FM% (higher deciles on the right); right: ECW/ICW (higher deciles on the bottom). Ellipses in red represent the 5° and 95° percentiles used for the validation.
Table 4. Bioelectrical characteristics of deciles of FM% and ECW/ICW ratio distributions.
| Men | Women | |||||||||||
| FM% | R sp | Xc sp | FM% | R sp | Xc sp | |||||||
| Decile FM% | Mean | s.d | Mean | s.d | Mean | s.d | Mean | s.d | Mean | s.d | Mean | s.d |
| 1st | 16.2 | 1.8 | 316.4 | 29.5 | 41.1 | 6.5 | 26.9 | 2.4 | 361.4 | 28.6 | 39.9 | 5.1 |
| 2nd | 20.4 | 0.9 | 342.7 | 33.9 | 45.0 | 7.1 | 31.9 | 0.9 | 399.3 | 32.5 | 44.9 | 5.9 |
| 3rd | 23.0 | 0.6 | 367.3 | 29.1 | 48.5 | 6.7 | 34.4 | 0.6 | 424.7 | 32.4 | 47.1 | 6.9 |
| 4th | 24.9 | 0.5 | 380.4 | 26.3 | 50.1 | 5.9 | 36.5 | 0.6 | 451.9 | 41.5 | 51.5 | 7.1 |
| 5th | 26.3 | 0.3 | 399.6 | 32.0 | 54.0 | 6.3 | 38.3 | 0.5 | 468.2 | 45.3 | 52.4 | 7.7 |
| 6th | 27.4 | 0.4 | 404.5 | 28.9 | 52.7 | 7.7 | 40.2 | 0.6 | 498.2 | 43.5 | 57.4 | 8.6 |
| 7th | 28.8 | 0.3 | 425.4 | 32.1 | 55.7 | 6.8 | 41.8 | 0.4 | 525.4 | 52.9 | 59.8 | 9.1 |
| 8th | 30.3 | 0.5 | 426.9 | 32.4 | 55.3 | 6.8 | 43.5 | 0.5 | 543.1 | 50.9 | 61.1 | 8.4 |
| 9th | 32.5 | 0.7 | 458.7 | 38.4 | 59.0 | 7.3 | 45.6 | 0.6 | 583.9 | 57.3 | 66.2 | 8.3 |
| 10th | 36.3 | 2.2 | 499.3 | 46.6 | 63.5 | 7.6 | 49.3 | 1.8 | 634.1 | 63.7 | 70.1 | 9.7 |
| ECW/ICW | R sp | Xc sp | ECW/ICW | R sp | Xc sp | |||||||
| Decile ECW/ICW | Mean | s.d | Mean | s.d | Mean | s.d | Mean | s.d | Mean | s.d | Mean | s.d |
| 1st | 0.6 | 0.03 | 398.2 | 52.9 | 60.0 | 7.8 | 0.7 | 0.03 | 493.7 | 93.3 | 64.8 | 12.2 |
| 2nd | 0.6 | 0.01 | 395.5 | 64.5 | 56.8 | 9.2 | 0.7 | 0.01 | 494.6 | 95.9 | 61.4 | 11.7 |
| 3rd | 0.6 | 0.01 | 412.3 | 54.7 | 57.4 | 7.7 | 0.7 | 0.01 | 517.7 | 105.3 | 62.5 | 12.8 |
| 4th | 0.7 | 0.01 | 393.9 | 59.8 | 53.6 | 7.9 | 0.8 | 0.01 | 482.7 | 91.4 | 56.5 | 10.9 |
| 5th | 0.7 | 0.01 | 391.7 | 60.4 | 51.8 | 8.0 | 0.8 | 0.01 | 501.9 | 95.9 | 57.1 | 10.9 |
| 6th | 0.7 | 0.01 | 400.5 | 60.6 | 51.6 | 7.7 | 0.8 | 0.01 | 492.2 | 97.0 | 54.6 | 10.9 |
| 7th | 0.7 | 0.00 | 419.2 | 69.2 | 52.4 | 8.8 | 0.8 | 0.01 | 493.4 | 87.0 | 53.2 | 9.4 |
| 8th | 0.7 | 0.01 | 413.8 | 60.7 | 50.7 | 7.6 | 0.9 | 0.01 | 477.1 | 88.6 | 49.8 | 9.1 |
| 9th | 0.8 | 0.01 | 411.6 | 66.1 | 48.7 | 8.0 | 0.9 | 0.01 | 482.7 | 85.1 | 49.0 | 9.0 |
| 10th | 0.9 | 0.08 | 388.8 | 72.7 | 42.0 | 9.3 | 1.0 | 0.05 | 490.2 | 112.0 | 45.9 | 10.9 |
Legend: R: resistance; Xc: reactance; sp: specific; FM: fat mass; ECW: extracellular water; ICW: intracellular water.
Discussion
Since its first introduction in 1994, BIVA [3] has shown to be a valid alternative to the conventional BIA methodology. The heuristic potential of the new semiquantitative approach, unaffected by errors due to the wrong application of equations or models, has been largely endorsed by the scientific community [4]–[34].
However, in spite of the BIVA validation for the ability to estimate hydration and nutritional status [26], its performance in estimating body composition, and particularly fat mass, has been poorly checked. Recently, Bronhara et al. [34] applied fuzzy linguistic models to improve and evaluate the diagnostic efficacy of BIVA in estimating seven body composition categories: normal, anasarca, obese, athletic, dehydration, lean, and cachetic. The Authors obtain a general good agreement between BIVA results and clinical diagnoses. However this result is mainly due to the correct diagnoses of hydration status, while the recognition of obese and athletic individuals was poorly checked either because of the low sample size and because of the apparent large classification error (see Table 2 in Bronhara et al. [34]). As a matter of fact, the validation of classic BIVA with respect to the classification of obese individuals is generally based on indirect indicators of body composition, such as the BMI [35], [36], while studies on athletic individuals are few and show a dishomogeneous bioelectrical pattern in different sports [21]–[25].
When compared with results from a gold standard for FM%, such as DXA, classic BIVA failed to distinguish individuals with different proportions of fat mass, as observed in a sample of elderly Italians [37]. The present analysis on the U.S. population showed consistent results. Even if classic BIVA recognized significant differences between bioelectrical values of groups below the 5th and above the 95th percentiles of FMDXA%, the vectors distribution from the two groups largely overlapped with the 50th percentile, i.e. the ‘normal region’ of the reference U.S. population. Such a pattern does not permit a correct classification, as indicated by the low area under the ROC curve, which corresponds to a slightly better than random classification.
It is worth noting that electro-physiological assumptions - according to which fat-free mass is characterized by a greater conductivity of electricity compared to the poorly hydrated adipose tissue [1] – do not justify the relative shortness of impedance vector of obese individuals with respect to athletic ones, expected by classic BIVA, unless considering their generally greater body size.
The adjustment of bioelectrical values performed with specific BIVA furnishes an estimate of the whole-body impedivity, which is independent from body size. As observed in previous researches [37], [49]–[51], specific bioelectrical values show a positive relation with the relative body fat content. When used with the same semiquantitative vectorial approach of classic BIVA, resistivity and reactivity behaved significantly better in the evaluation of body composition than the classic technique. Specific BIVA demonstrated a good performance, being able to recognize FM% differences both in elderly Italians [37] and in the U.S. population (present study). Individuals with different body composition states were located in distinct regions of the graph, thus allowing a good classification (as showed by the great areas under the ROC curves for FMDXA%, ranging from 0.84 to 0.90). The distance from a perfect classification could depend on the effect of the variables not included in the model. For example, the differences in body composition [52] or in bioelectrical characteristics [6] among the ethnic groups constituting the U.S. population can play a role. However, the high accuracy obtained in our results implicates only a little explanatory potential for the variable “ethnic group” and justify the interpretive approach adopted in this research in order to obtain a model useful for a large applicative use.
Even in the classification of the ECW/ICW ratio, specific BIVA shows a similarly good accuracy of classification (areas under ROC curves ranging from 0.84 to 0.96). However, in this case the difference with classic BIVA was not significant, as such procedure showed similar results (areas under ROC curves between 0.83 and 0.88). A high phase angle in patients with a low extracellular to intracellular water ratio, as assessed on the basis of NaBr isotope dilution, was already observed by other Authors [53]. The low ECW/ICW ratio can be related to high body cell mass [54], that is in turn related to high muscle mass [55]. In this study, bioelectrical values of athletic individuals effectively fell in the central part of the left area of the tolerance ellipse (low ECW/ICW ratio) and were significantly separated from lean ones, whose phase angle was lower and vector lengths higher (high ECW/ICW ratio) (Figure 3).
Specific BIVA has been validated considering the extreme percentiles of the FM% and ECW/ICW distributions. However this procedure has demonstrated to be sensitive also to the intermediate variations of body composition, as shown by the correlation analysis (Table 3) and by the regular migration trend of the bioelectrical impedance vector according to FM% and ECW/ICW deciles (Table 4 and Figure 6).
The validation of specific BIVA for its ability to evaluate the hydration status is out of the objectives of the present research, also because the use of classical BIVA for the state of hydration has been proven under various clinical conditions.
In conclusion, the present study demonstrates that the specific BIVA, recently used successfully in the elderly Italian population, is confirmed as an accurate technique in the analysis of a large sample from the U.S. adult population. The tolerance ellipses of specific BIVA allow the classification of FMDXA% and ECW/ICW in the two sexes and can be used as a reference for defining body composition.
Supporting Information
Schematic representation of human body proportions.
(TIF)
Description of specific bioelectrical impedance vector analysis: calculation of the correction factor.
(DOC)
Acknowledgments
The authors thank the Centers for Disease Control and Prevention (CDC), National Center for Health Statistics (NCHS) for use of the National Health and Nutrition Examination Survey Data - NHANES 2003–2004. Hyattsville, MD: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention (2012, http://www.cdc.gov/nchs/nhanes/nhanes2003-2004/nhanes03_04.htm). The authors thank A. Piccoli and G. Pastori (Department of Medical and Surgical Sciences, University of Padova, Italy) for providing the BIVA software, S. Piludu and dr. V. Succa (Department of Department of Environmental and Life Sciences, University of Cagliari, Italy) for the technical support.
Funding Statement
This research was financially supported by the University of Cagliari. ACR acknowledges financial support from “Regione Autonoma della Sardegna” through a research grant on fundings of the Project PO Sardegna FSE 2007–2013, L.R.7/2007 Promozione della ricerca scientifica e dell’innovazione tecnologica in Sardegna. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.National Institutes of Health Technology Assessment (1996) Bioelectrical impedance analysis in body composition measurement. National Institutes of Health Technology Assessment Conference Statement. Am J Clin Nutr 64 (3 Suppl): 524S–532S. [DOI] [PubMed]
- 2. Barbosa-Silva MC, Barros AJ (2005) Bioelectrical impedance analysis in clinical practice: a new perspective on its use beyond body composition equations. Curr Opin Clin Nutr Metab Care 8: 311–317. [DOI] [PubMed] [Google Scholar]
- 3. Piccoli A, Rossi B, Pillon L, Bucciante G (1994) A new method for monitoring body fluid variation by bioimpedance analysis: the RXc graph. Kidney Int 46: 534–539. [DOI] [PubMed] [Google Scholar]
- 4. Piccoli A, Nigrelli S, Caberlotto A, Bottazzo S, Rossi B, et al. (1995) Bivariate normal values of the bioelectrical impedance vector in adult and elderly populations. Am J Clin Nutr 61: 269–270. [DOI] [PubMed] [Google Scholar]
- 5. De Palo T, Messina G, Edefonti A, Perfumo F, Pisanello L, et al. (2000) Normal values of the bioelectrical impedance vector in childhood and puberty. Nutrition 16: 417–424. [DOI] [PubMed] [Google Scholar]
- 6. Piccoli A, Pillon L, Dumler F (2002) Impedance vector distribution by sex, race, body mass index, and age in the United States: standard reference intervals as bivariate Z scores. Nutrition 18: 153–167. [DOI] [PubMed] [Google Scholar]
- 7. Bosy-Westphal A, Danielzik S, Dörhöfer RP, Piccoli A, Müller MJ (2005) Patterns of bioelectrical impedance vector distribution by body mass index and age: implications for body-composition analysis. Am J Clin Nutr 82: 60–68. [DOI] [PubMed] [Google Scholar]
- 8. Espinosa-Cuevas Mde L, Rivas-Rodríguez L, González-Medina EC, Atilano-Carsi X, Miranda-Alatriste P, et al. (2007) Bioimpedance vector analysis for body composition in Mexican population. Rev Invest Clin 59: 15–24. [PubMed] [Google Scholar]
- 9. Margutti AV, Monteiro JP, Camelo JS Jr (2010) Reference distribution of the bioelectrical impedance vector in healthy term newborns. Br J Nutr 104: 1508–1513. [DOI] [PubMed] [Google Scholar]
- 10. Marini E, Maldonado-Contreras AL, Cabras S, Hidalgo G, Buffa R, et al. (2007) Helicobacter pylori and intestinal parasites are not detrimental to the nutritional status of Amerindians. Am J Trop Med Hyg 76: 534–540. [PubMed] [Google Scholar]
- 11. Buffa R, Baali A, Lahmam A, Amor H, Zouini M, et al. (2009) Assessment of nutritional status in the Amazigh children of Amizmiz (Azgour Valley, High Atlas and Morocco). J Trop Pediatr 55: 406–408. [DOI] [PubMed] [Google Scholar]
- 12. Barufaldi LA, Conde WL, Schuch I, Duncan BB, Castro TG (2011) Bioelectrical impedance values among indigenous children and adolescents in Rio Grande do Sul, Brazil. Rev Panam Salud Publica 30: 39–45. [PubMed] [Google Scholar]
- 13. Tanabe RF, de Azevedo ZM, Fonseca VM, Peixoto MV, dos Anjos LA, et al. (2012) Distribution of bioelectrical impedance vector values in multi-ethnic infants and pre-school children. Clin Nutr 31: 144–148. [DOI] [PubMed] [Google Scholar]
- 14. Buffa R, Floris G, Marini E (2002) Bioelectrical impedance vector in pre- and postmenarcheal females. Nutrition 18: 474–478. [DOI] [PubMed] [Google Scholar]
- 15. Savino F, Grasso G, Cresi F, Oggero R, Silvestro L (2003) Bioelectrical impedance vector distribution in the first year of life. Nutrition 19: 492–496. [DOI] [PubMed] [Google Scholar]
- 16. Guida B, Pietrobelli A, Trio R, Laccetti R, Falconi C, et al. (2008) Body mass index and bioelectrical vector distribution in 8-year-old children. Nutr Metab Cardiovasc Dis 18: 133–141. [DOI] [PubMed] [Google Scholar]
- 17. L’Abée C, Poorts-Borger PH, Gorter EH, Piccoli A, Stolk RP, et al. (2010) The bioelectrical impedance vector migration in healthy infants. Clin Nutr 29: 222–226. [DOI] [PubMed] [Google Scholar]
- 18. Buffa R, Floris G, Marini E (2003) Migration of the bioelectrical impedance vector in healthy elderly subjects. Nutrition 19: 917–921. [DOI] [PubMed] [Google Scholar]
- 19. Guida B, Laccetti R, Gerardi C, Trio R, Perrino NR, et al. (2007) Bioelectrical impedance analysis and age-related differences of body composition in the elderly. Nutr Metab Cardiovasc Dis 17: 175–180. [DOI] [PubMed] [Google Scholar]
- 20. Buffa R, Floris G, Lodde M, Cotza M, Marini E (2010) Nutritional status in the healthy longeval population from Sardinia (Italy). J Nutr Health Aging 14: 97–102. [DOI] [PubMed] [Google Scholar]
- 21. Piccoli A, Piazza P, Noventa D, Pillon L, Zaccaria M (1996) A new method for monitoring hydration at high altitude by bioimpedance analysis. Med Sci Sports Exerc 28: 1517–1522. [DOI] [PubMed] [Google Scholar]
- 22. Piccoli A, Pastori G, Codognotto M, Paoli A (2007) Equivalence of information from single frequency v. bioimpedance spectroscopy in bodybuilders. Br J Nutr 97: 182–192. [DOI] [PubMed] [Google Scholar]
- 23. Kim CH, Park JH, Kim H, Chung S, Park SH (2010) Modeling the human body shape in bioimpedance vector measurements. Conf Proc IEEE Eng Med Biol Soc 2010: 3872–3874. [DOI] [PubMed] [Google Scholar]
- 24. Gatterer H, Schenk K, Ferrari P, Faulhaber M, Schopp E, et al. (2011) Changes in hydration status of soccer players competing in the 2008 European Championship. J Sports Med Phys Fitness 51: 89–94. [PubMed] [Google Scholar]
- 25. Nescolarde L, Yanguas J, Medina D, Rodas G, Rosell-Ferrer J (2011) Assessment and follow-up of muscle injuries in athletes by bioimpedance: preliminary results. Conf Proc IEEE Eng Med Biol Soc 2011: 1137–1140. [DOI] [PubMed] [Google Scholar]
- 26. Norman K, Stobäus N, Pirlich M, Bosy-Westphal A (2012) Bioelectrical phase angle and impedance vector analysis - Clinical relevance and applicability of impedance parameters. Clin Nutr 31: 854–861. [DOI] [PubMed] [Google Scholar]
- 27. Walter-Kroker A, Kroker A, Mattiucci-Guehlke M, Glaab T (2011) A practical guide to bioelectrical impedance analysis using the example of chronic obstructive pulmonary disease. Nutr J 10: 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Castillo-Martínez L, Colín-Ramírez E, Orea-Tejeda A, González Islas DG, Rodríguez García WD, et al. (2012) Cachexia assessed by bioimpedance vector analysis as a prognostic indicator in chronic stable heart failure patients. Nutrition 28: 886–891. [DOI] [PubMed] [Google Scholar]
- 29. Haas V, Riedl A, Hofmann T, Nischan A, Burghardt R, et al. (2012) Bioimpedance and Bioimpedance Vector Analysis in patients with Anorexia Nervosa. Eur Eat Disord Rev Eur 20: 400–5. [DOI] [PubMed] [Google Scholar]
- 30. Kehayias JJ, Ribeiro SM, Skahan A, Itzkowitz L, Dallal G, et al. (2012) Water homeostasis, frailty and cognitive function in the nursing home. J Nutr Health Aging 16: 35–39. [DOI] [PubMed] [Google Scholar]
- 31. Saragat B, Buffa R, Mereu E, Succa V, Cabras S, et al. (2012) Nutritional and psychofunctional status in elderly patients with Alzheimer’s disease. J Nutr Health Aging 16: 231–236. [DOI] [PubMed] [Google Scholar]
- 32. Marini E, Buffa R, Saragat B, Coin A, Toffanello ED, et al. (2012) The potential of classic and specific bioelectrical impedance vector analysis for the assessment of sarcopenia and sarcopenic obesity. Clin Interv Aging 7: 585–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Buffa R, Saragat B, Succa V, Ruggiu R, Carboni L, et al. (2013) Elderly subjects with type 2 diabetes show altered tissue electrical properties. Nutrition 29: 132–137. [DOI] [PubMed] [Google Scholar]
- 34.Bronhara B, Piccoli A, Pereira JC (2012) Fuzzy linguistic model for bioelectrical impedance vector analysis. Clinical Nutrition doi:10.1016/j.clnu.2012.02.014. [DOI] [PubMed]
- 35. Guida B, De Nicola L, Pecoraro P, Trio R, Di Paola F, et al. (2001) Abnormalities of bioimpedance measures in overweight and obese hemodialyzed patients. Int J Obes Relat Metab Disord 25: 265–272. [DOI] [PubMed] [Google Scholar]
- 36. Piccoli A, Brunani A, Savia G, Pillon L, Favaro E, et al. (1998) Discriminating between body fat and fluid changes in the obese adult using bioimpedance vector analysis. Int J Obes Relat Metab Disord 22: 97–104. [DOI] [PubMed] [Google Scholar]
- 37.Marini E, Sergi G, Succa V, Saragat B, Sarti S, et al.. (2012) Efficacy of specific bioelectrical impedance vector analysis (BIVA) for assessing body composition in the elderly. The Journal of Nutrition, Health and Aging DOI: 10.1007/s12603-012-0411-7. [DOI] [PubMed]
- 38.Centers for Disease Control and Prevention (CDC) (2012) National Center for Health Statistics (NCHS). National Health and Nutrition Examination Survey Data. Hyattsville, MD: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention 2012: Available: http://www.cdc.gov/nchs/nhanes/nhanes2003-2004/nhanes03_04.htm. Accessed 2012 Feb 9.
- 39. Kuczmarski RJ, Ogden CL, Guo SS, Grummer-Strawn LM, Flegal KM, et al. (2000) 2000 CDC growth charts for the United States: Methods and development. National Center for Health Statistics. Vital Health Stat 11 (246): 1–190. [PubMed] [Google Scholar]
- 40. Baumgartner R, Koehler K, Gallagher D, Romero L, Heymsfield SB, et al. (1998) Epidemiology of sarcopenia among the elderly in New Mexico. Am J Epidemiol. 147: 755–763. [DOI] [PubMed] [Google Scholar]
- 41.NHANES (2004) Anthropometry procedures manual. Internet: Available: http://www.cdc.gov/nchs/data/nhanes/nhanes_03_04/BM.pdf. Accessed 2012 Feb 9.
- 42.NHANES (2004) Body composition procedures manual. Internet: Available: http://www.cdc.gov/nchs/data/nhanes/nhanes_03_04/BC.pdf. Accessed 2012 Feb 9.
- 43.Cole KS (1997) Membranes, Ions, and Impulses. Berkeley: University of California Press.
- 44. Bracco D, Thiébaud D, Chioléro RL, Landry M, Burckhardt P, et al. (1996) Segmental body composition assessed by bioelectrical impedance analysis and DEXA in humans. J Appl Physiol 81: 2580–2587. [DOI] [PubMed] [Google Scholar]
- 45.Marini E (1992) Il dimorfismo sessuale nella popolazione della Sardegna centro-meridionale. PhD Thesis, University of Cagliari.
- 46.Piccoli A, Pastori G (2002) BIVA software. Padua, Italy: Department of Medical and Surgical Sciences, University of Padua.
- 47.Krzanowski WJ, Hand DJ (2009) ROC Curves for Continuous Data. New York: Chapman & Hall/CRC.
- 48.Dobson AJ (2002) An introduction to generalized linear models. 2nd ed. Boca Raton: Chapman & Hall/CRC.
- 49. Chumlea WC, Baumgartner RN, Roche AF (1988) Specific resistivity used to estimate fat-free mass from segmental body measures of bioelectric impedance. Am J Clin Nutr 48: 7–15. [DOI] [PubMed] [Google Scholar]
- 50. Biggs J, Cha K, Horch K (2001) Electrical resistivity of the upper arm and leg yields good estimates of whole body fat. Physiol Meas 22: 365–376. [DOI] [PubMed] [Google Scholar]
- 51. Fuller NJ, Fewtrell MS, Dewit O, Elia M, Wells JC (2002) Segmental bioelectrical impedance analysis in children aged 8–12 y: 1. The assessment of whole-body composition. Int J Obes Relat Metab Disord 26: 684–691. [DOI] [PubMed] [Google Scholar]
- 52. Heo M, Faith MS, Pietrobelli A, Heymsfield SB (2012) Percentage of body fat cutoffs by sex, age, and race-ethnicity in the US adult population from NHANES 1999–2004. Am J Clin Nutr 95(3): 594–602. [DOI] [PubMed] [Google Scholar]
- 53. Chertow GM, Lowrie EG, Wilmore DW, Gonzalez J, Lew NL, et al. (1995) Nutritional assessment with bioelectrical impedance analysis in maintenance hemodialysis patients. J Am Soc Nephrol 6: 75–81. [DOI] [PubMed] [Google Scholar]
- 54. Siervo M, Faber P, Gibney ER, Lobley GE, Elia M, et al. (2010) Use of the cellular model of body composition to describe changes in body water compartments after total fasting, very low calorie diet and low calorie diet in obese men. Int J Obes (Lond). 34: 908–918. [DOI] [PubMed] [Google Scholar]
- 55. Dittmar M, Reber H (2001) New equations for estimating body cell mass from bioimpedance parallel models in healthy older Germans. Am J Physiol Endocrinol Metab 281(5): 1005–1014. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Schematic representation of human body proportions.
(TIF)
Description of specific bioelectrical impedance vector analysis: calculation of the correction factor.
(DOC)