Identifying high-risk areas for sporadic measles outbreaks: lessons from South Africa

Abstract

Objective

To develop a model for identifying areas at high risk for sporadic measles outbreaks based on an analysis of factors associated with a national outbreak in South Africa between 2009 and 2011.

Methods

Data on cases occurring before and during the national outbreak were obtained from the South African measles surveillance programme, and data on measles immunization and population size, from the District Health Information System. A Bayesian hierarchical Poisson model was used to investigate the association between the risk of measles in infants in a district and first-dose vaccination coverage, population density, background prevalence of human immunodeficiency virus (HIV) infection and expected failure of seroconversion. Model projections were used to identify emerging high-risk areas in 2012.

Findings

A clear spatial pattern of high-risk areas was noted, with many interconnected (i.e. neighbouring) areas. An increased risk of measles outbreak was significantly associated with both the preceding build-up of a susceptible population and population density. The risk was also elevated when more than 20% of infants in a populous area had missed a first vaccine dose. The model was able to identify areas at high risk of experiencing a measles outbreak in 2012 and where additional preventive measures could be undertaken.

Conclusion

The South African measles outbreak was associated with the build-up of a susceptible population (owing to poor vaccine coverage), high prevalence of HIV infection and high population density. The predictive model developed could be applied to other settings susceptible to sporadic outbreaks of measles and other vaccine-preventable diseases.

Introduction

Measles is highly contagious and the transmission intensity¹ of the measles virus exceeds that of most human pathogens.² Despite progress in controlling measles since 2000, the disease remains endemic in many countries and killed over 164 000 children worldwide in 2008.¹ Deaths also occur during outbreaks in areas where the disease is no longer endemic.³

Measles vaccination is highly effective, safe and relatively cost-effective⁴ and has interrupted measles transmission in most parts of the world,⁵ although high-risk areas remain in Africa and southern Asia. Immunization coverage is a key indicator for monitoring health sector performance and progress towards Millennium Development Goal 4 (i.e. reducing child mortality).⁶ Measles is difficult to control and eliminate and more than  90% of the population must be immune to interrupt transmission and prevent outbreaks.^7–11 Maintaining adequate vaccine coverage throughout countries is a global problem and, in 2010 and 2011, outbreaks occurred even in the developed world.⁴ Moreover, since the efficacy of the first vaccine dose is thought to be around 85%,^12,13 non-responders will add to the pool of susceptible children. In addition, achieving a high level of population immunity may be difficult in areas such as sub-Saharan Africa where the prevalence of human immunodeficiency virus (HIV) infection is high because infected children are less likely to respond to vaccination or maintain a protective antibody level or may acquire lower antibody levels from an HIV-positive (HIV+) mother.^14–16 Vaccination may need to be repeated more frequently in these areas.¹⁶

Since 1995, several African countries have launched initiatives to eliminate measles, as recommended by the World Health Organization (WHO).^17,18 These initiatives aim to: (i) achieve a coverage of  90% or more for the first vaccine dose; (ii) identify areas with low coverage and high-risk areas for “mop-up” immunization of children who missed vaccination; and (iii) enhance case-based measles surveillance with laboratory support.¹⁷

In South Africa, first and second measles vaccine doses have been given free of charge to children aged 9 and 18 months since April 2009 as part of the WHO Expanded Program on Immunization. At present, measles vaccination is mandatory and provided in the public sector, whereas combination vaccination against measles, mumps and rubella is available in the private sector at a cost. The South African National Department of Health introduced case-based measles surveillance in 1998 with laboratory support from the National Institute for Communicable Diseases.

A large outbreak of measles involving around 1700 cases occurred in South Africa between 2003 and 2005 following its introduction from Mozambique. More recently, there was an outbreak between 2009 and 2011, with over 18 000 cases recorded.⁴ The transient trough in cases following a large outbreak, which increases herd immunity, affords planners an opportunity to investigate the epidemic and refine prevention strategies.⁴ Spatial analysis has become an important epidemiological tool for detecting and predicting patterns of disease spread.¹⁹ In situations in which population-wide interventions are too expensive or are inefficient because they dilute available resources, the effectiveness of vaccination is increased by targeting high-risk areas, such as those implicated in measles transmission and those where vaccination coverage varies.^20,21

The objectives of this study were: (i) to investigate the pattern of measles spread in the South African outbreak between 2009 and 2011; (ii) to identify associations between the outbreak and population density, HIV prevalence and preceding lapses in measles vaccination; and (iii) to develop a model for identifying areas at a high risk for future large-scale sporadic outbreaks that can be used in prevention.

Methods

Administratively, South Africa is divided into 9 provinces and 52 districts, which include 6 metropolitan areas.³ Districts are further disaggregated into 248 local municipalities, with metropolitan areas being governed by metropolitan municipalities. Health service delivery is largely a municipal function.

We obtained data on individual cases observed between 2008 and 2011 from the measles surveillance programme at the National Department of Health and the National Institute for Communicable Diseases. Data on measles vaccination coverage among infants (i.e. children aged under 1 year), on the proportion of HIV+ infants aged under 2 months and on relevant denominators (e.g. the total number of infants in a given district, by year) were obtained from the District Health Information System. The main unit of analysis was the district.

We calculated the overall incidence of measles in each week between 2009 and 2011 to identify temporal peaks. In addition, we calculated the incidence in infants in each district by dividing the observed number of infant measles cases by the total infant population in the district. To identify districts in which the incidence was significantly above the average, either before or during the outbreak, we derived 95% confidence intervals (CIs) for each incidence proportion using the binomial distribution of the observed number of events.²² The incidence in a district was considered significantly above average in a particular year if the national incidence for that period was below the lower limit (i.e. α = 0.025) of the incidence proportion for the district.²³

Modelling the risk of measles

Standardized risk ratios (RR) were calculated for each district as the ratio of the observed to the expected number of infant measles cases in each district. The expected number of cases was the national measles incidence multiplied by the infant population of the district.

The most widely used strategy for tackling problems posed by small-area analysis is Bayesian hierarchical modelling.²⁴ The specific approach we adopted was developed by Besag, York and Molliè²⁵ and includes two random-effects terms (i.e. the convolution approach) that account for: (i) structured district contiguity and (ii) unstructured district heterogeneity. It is the most widely used spatial Poisson model and the basic kriging formulation, which includes no covariates, is as follows:

O_i ~ Poisson(E_iλ_i)

log(λ_i) = α  + ε_i + ω_i (1)

where O_i is the observed number of measles cases in district i, E_i is the expected number of cases, λ_i is the Poisson mean or expected value (and the variance), α is a constant, ε_i is the unstructured district heterogeneity random effect and ω_i is the conditional autoregressive spatial random effect accounting for district contiguity. Further details are provided in Appendix A (available at: http://www.fileswap.com/dl/fbTMr0X3gU/Appendix1.doc). This basic spatial model can also be extended to a space–time formulation: the full formulations involving Bayesian inference using Gibbs sampling (BUGS) are provided in Appendix B (available at: http://www.fileswap.com/dl/vEAvea1JcR/Appendix2.doc). If a large number of areas have excess or repeat zero counts, which is often the case with rare outcomes, then a zero-inflated Poisson approach must be used.^26–28

In anomaly detection, Bayesian exceedance probabilities were used to detect areas in which the risk was significantly increased.²⁹ We plotted model estimates on district maps that depicted smoothed estimates of the RR and the posterior probability that the RR was greater than 1. We used a more stringent version of Richardson’s criterion,²⁹ in which a district with a Bayesian exceedance probability (i.e. the probability that the RR would exceed 1) greater than 0.9 was deemed to be a high-risk area.

To investigate the influence of preceding lapses in vaccination, the prevalence of HIV infection among infants and vaccine failure on the observed risk of measles, we tested various determinants at the bivariate and multivariate level using the Bayesian approach described above with:

log(λ_i) = α + βX_i + ε_i + ω_i (2)

where X_i represents the vector of the associated covariates and β represents the corresponding regression coefficients. Factors found to be significant at the bivariate level (i.e. P < 0.2) were included in the multivariate model. Districts were divided into tertiles according to population density: low, medium and high density. All metropolitan areas were classified as high density but there were many high-density areas that were not metropolitan areas. We created a dummy variable with three categories to reflect this: low- to medium-population-density area, high-population-density nonmetropolitan area and high-population-density metropolitan area.

The formula below was developed to use data from the preceding year to estimate the size of the infant population susceptible to measles in each district, which is possibly the most important predictor of future high-risk areas. In this study, the proportion of infants who were not covered by vaccination in a given year was defined as the proportion that did not receive the first measles vaccine dose in that year.³⁰ The proportion that was not immunized was the combination of the proportion not covered by vaccination and the proportion that would fail to seroconvert following the first vaccine dose, taking into account the influence of HIV infection on the likelihood of seroconversion. A previous study showed that mortality in HIV-infected children without access to antiretroviral therapy can limit the effect of the HIV epidemic on increasing measles virus transmission.³¹ Consequently, we refined the formula by factoring in expected mortality rates among HIV-negative (HIV−) and HIV+ infants, with the proportion of HIV+ infants being defined as the proportion receiving antiretroviral therapy. The interaction between the proportion susceptible to measles and population density was also assessed.

The size of the infant population susceptible to measles in each district in year t (i.e. S_t) was derived using data from year t−1 for that district, by adding those not covered to those with vaccine failure among covered, as follows:

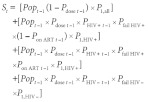(3)

where Pop_t−1 is the infant population of the district in year t−1, P_{dose t−1} is the proportion of infants who receive their first measles dose in year t−1, P_1,all is the proportion of all infants who survive to the age of 1 year, P_{HIV+ t−1} is the proportion of infants who are HIV+ in year t−1, P_{fail HIV+} is the proportion of HIV+ infants who fail to seroconvert after the first measles vaccine dose, P_{on ART t−1} is the proportion of HIV+ infants receiving antiretroviral therapy in year t−1, P_1,HIV+ is the proportion of HIV+ infants who survive to the age of 1 year, P_{HIV– t−1} is the proportion of infants who are HIV− in year t−1, P_{fail HIV–} is the proportion of HIV– infants who fail to seroconvert after the first vaccine dose and P_1,HIV– is the proportion of HIV– infants who survive to the age of 1 year.

The values of some of the parameters used in Equation 3 were based on data from the District Health Information System for 2006 to 2011.³² The proportion of infants who failed to seroconvert after the first vaccine dose was obtained from a recent meta-analysis³³: 64% (95% CI: 49–78%) of HIV+ infants seroconverted by 9 months after measles vaccination, compared with between 62 and 100% (weighted average: 87%) of those who were exposed to HIV but did not become infected and between 76 and 92% (weighted average: 85%) of those who were not exposed to HIV. Hence, P_{fail HIV+} was 0.36 (i.e. 1–0.64) and P_{fail HIV−} was 0.14 (i.e. [1–0.87] + [1–0.85] divided by 2). Values for the proportion of infants who survived to the age of 1 year were taken from a pooled analysis of data from sub-Saharan Africa, in which the estimate for P_1,HIV+ was 0.648 and, for P_1,HIV−, 0.951.³⁴ The value for P_1,all was derived from a weighted estimate of the proportion of infants who were HIV+ or HIV− and their respective expected survival proportions. The proportion of HIV+ infants receiving antiretroviral therapy was estimated to be 0.19 in 2008, 0.27 in 2009,  0.31 in 2010 and 0.40 in 2011.^35,36 The analysis was carried out using Stata (StataCorp. LP, College Station, United States of America) and WinBUGS (MRC Biostatistics Unit, Cambridge, United Kingdom of Great Britain and Northern Ireland). Risk maps were constructed in MapInfo Professional (Pitney Bowes Inc., Stamford, USA).

Results

Demographic data showed that, during the 2009 to 2011 measles outbreak, the incidence of the disease was highest among infants: 61 per 10 000 (95% CI: 59.3–62.4). The second highest incidence was in children aged 1 to 4 years: 7.3 cases per 10 000 (95% CI: 7.0–7.6). The incidence in children aged 10 to 14 years and in those aged 15 to 19 years was higher than in those aged 5 to 9 years. The baseline incidence among infants before and after the outbreak was 1.0 per 10 000 (95% CI: 0.9–1.3).

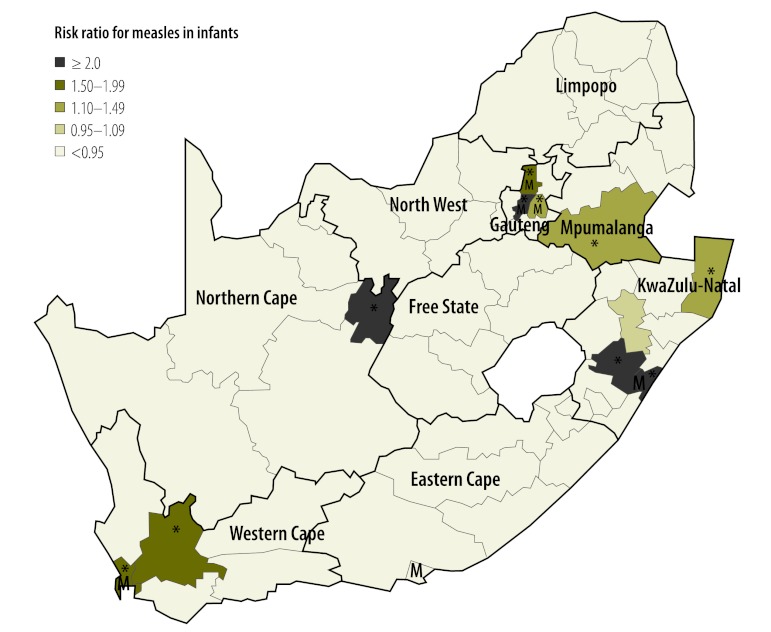
There were two peaks in measles incidence in infants during the outbreak: the smaller peak occurred in week 43 of 2009 and the slightly larger peak occurred approximately 20 weeks later, in week 10 of 2010 (Fig. 1). Spatial analysis identified districts in which the risk of measles was significantly increased over the course of the outbreak (Fig. 2 and Fig. 3). The distribution of disease incidence was distinctly nonrandom (Moran’s I global P < 0.001). Several neighbouring (i.e. connected) high-risk districts were observed: in Western Cape Province in the south-west of the country, in Gauteng and Mpumalanga Provinces in the north and in KwaZulu-Natal Province on the east coast (Fig. 2). In addition, the incidence was elevated in metropolitan areas. Fig. 3 shows the estimated incidence of measles in infants in all districts, the national baseline incidence in infants before the start of the outbreak and the national incidence during the outbreak. The two districts with the highest incidence were in Northern Cape and KwaZulu-Natal Provinces respectively, followed by the Johannesburg (Gauteng) and eThekwini (KwaZulu-Natal) metropolitan areas.

Fig. 1.

Incidence of measles in infants during an outbreak, South Africa, 2009–2011

Fig. 2.

Risk ratios for measles in infants in districts during an outbreak, South Africa, 2009–2011

Metropolitan areas are indicated by an M.

The * indicates districts in which the risk was significantly elevated as indicated by its Bayesian exceedance probability determined using a Bayesian convolution conditional autoregressive model.

Fig. 3.

Incidence of measles among infants in all districts during an outbreak, South Africa, 2009–2011

ECP, Eastern Cape Province; FSP, Free State Province; GAP, Gauteng Province; KZP, KwaZulu-Natal Province; LPP, Limpopo Province; MPP, Mpumalanga Province; NCP, Northern Cape Province; NWP, North West Province; WCP, Western Cape Province.

The length of the horizontal lines indicates the 95% confidence interval.

The grey dashed line indicates the baseline national incidence of around 1.0 per 10 000 before and after the outbreak.

The black dashed line indicates the national incidence of around 61 per 10 000 during the outbreak.

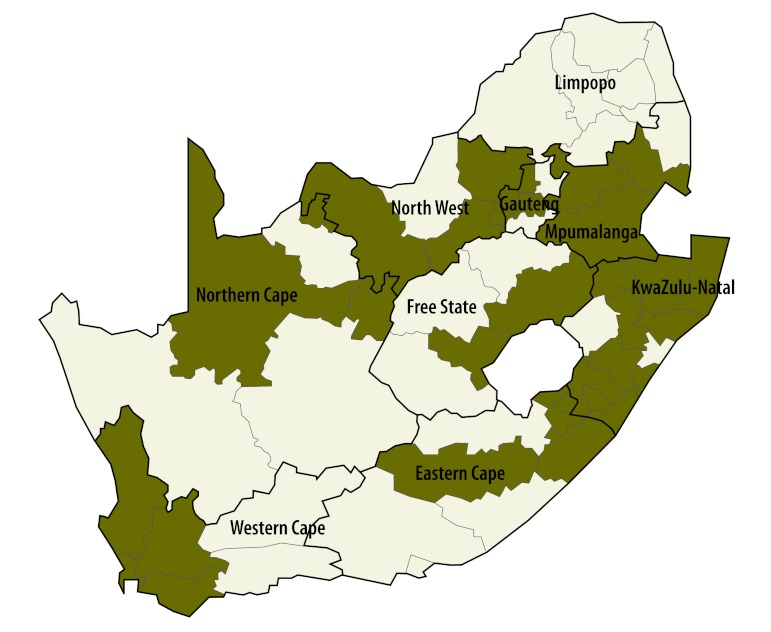
The first significant elevation in risk occurred in the Tshwane metropolitan area during weeks 35 and 36 of 2009, before the first peak in incidence. By week 37, the significant rise in risk had spread to the neighbouring metropolitan areas of Johannesburg and Ekuruleni. An analysis of the period leading up to the first peak suggested that the outbreak was concentrated in Gauteng province. Fig. 4 and Fig. 5 show the districts most affected by the outbreak at the two peaks in incidence. The districts with the highest incidence were similar at the two peaks, though the outbreak was more widespread at the first peak. There appeared to be no spread into surrounding districts.

Fig. 4.

Elevated risk of measles in infants in districts during the first outbreak peak,^a South Africa, 2009

The shaded districts are those in which the risk was significantly elevated as indicated by their Bayesian exceedance probabilities determined using a Bayesian convolution conditional autoregressive model.

^a The first outbreak peak occurred around week 43 in 2009.

Fig. 5.

Elevated risk of measles in infants in districts during the second outbreak peak,^a South Africa, 2010

The shaded districts are those in which the risk was significantly elevated as indicated by their Bayesian exceedance probabilities determined using a Bayesian convolution conditional autoregressive model.

^a The second outbreak peak occurred around week 10 in 2010.

Factors associated with measles outbreaks

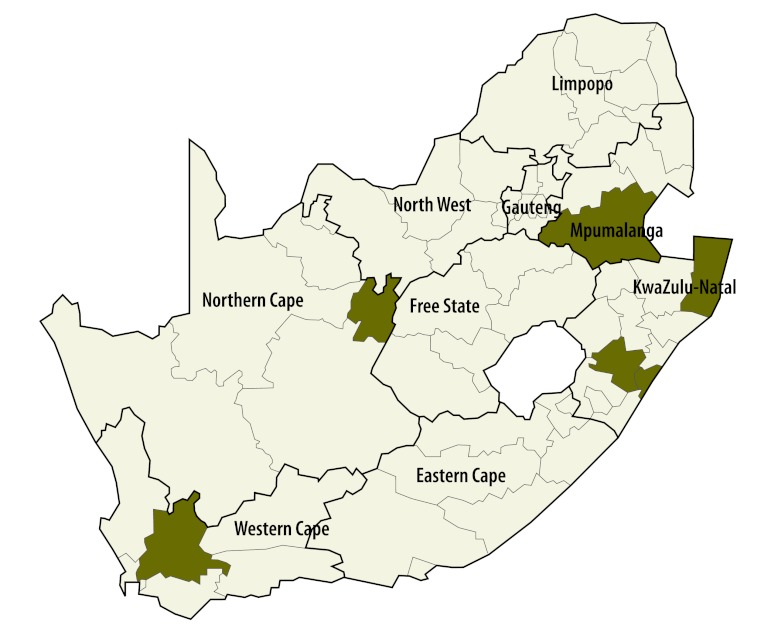
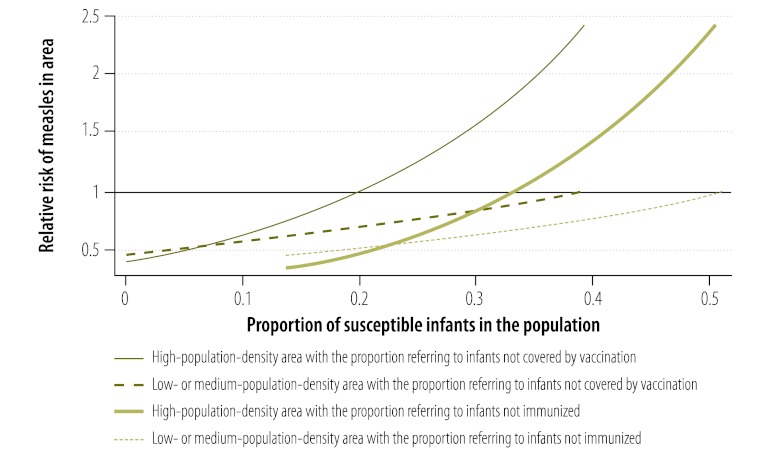
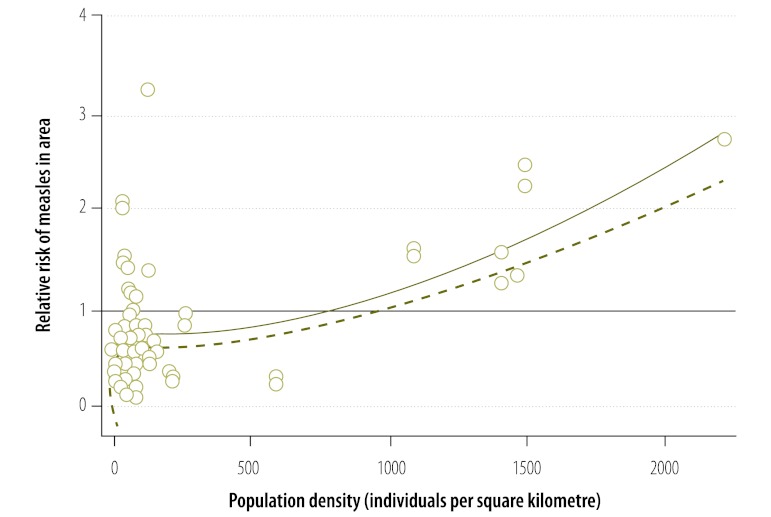
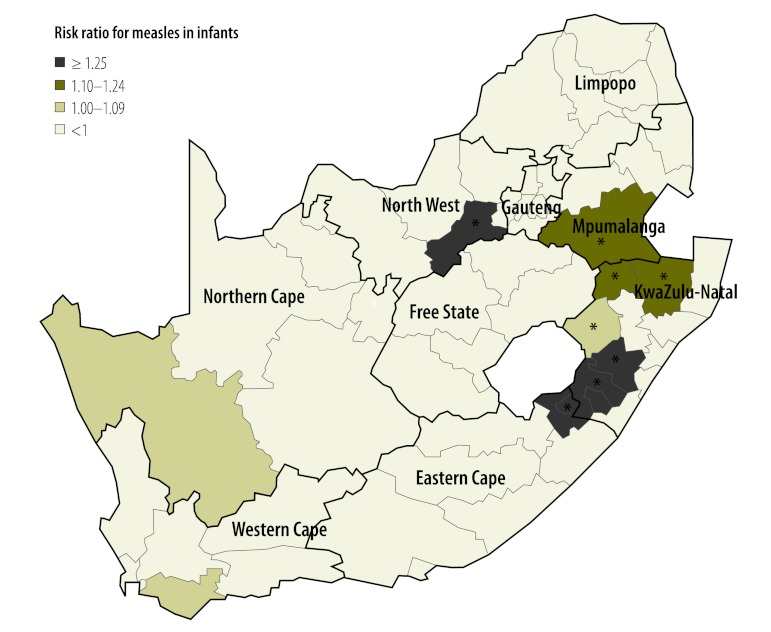
The average coverage of the first dose of measles vaccine in all districts was 88.1% (range: 85.4–90.7). Many districts repeatedly failed to meet the target of 90%: 56.9%, 49.0% and 64.5% of districts had coverage below this critical value in 2008, 2009 and 2010, respectively. The risk of measles in infants in a district showed a significant positive association with the proportion of unvaccinated infants and with the proportion of infants not immunized in the preceding year (Table 1). In addition, the risk of infection was increased in metropolitan districts, all of which had a high population density (P < 0.001). The model predicted that the critical cut-off proportion for coverage with the first vaccine dose is 0.2. Consequently, the risk would be elevated (i.e. RR > 1) in highly populated areas in which the percentage of susceptible infants exceeds 20% because of poor vaccination coverage in preceding years (Fig. 6). Bivariate interactions indicate that the threshold would be higher in less densely populated areas. Districts with a population density of more than 750 individuals per square kilometre also appear to be at an elevated risk (Fig. 7). Using data on the level of coverage of the first vaccine dose in districts in 2011, the model predicted that the high-risk areas in which the proportion of susceptible infants would exceed the critical cut-off level in 2012 lay mainly in KwaZulu-Natal (Fig. 8). Since these areas are highly connected (i.e. neighbouring), the outbreak could spread rapidly.

Table 1. Risk of measles in infants during an outbreak, South Africa, 2009–2011.

Parameter	Multivariate analysis (coverage)a			Multivariate analysis (immunization)b
	RRc (95% BCId)	RRe (95% CI)		RRc (95% BCId)	RRe (95% CI)
District parameter
Low- or medium-population-density nonmetropolitan area	1 (ref.)	NA		1 (ref.)	NA
High-population-density nonmetropolitan area	1.23 (0.64–2.43)	NA		1.24 (0.65–2.54)	NA
High-population-density metropolitan area	4.37 (2.27–8.56)	NA		4.42 (1.60–9.54)	NA
Proportion of infants not covered by vaccinationf in preceding yearg	7.84 (5.19–13.2)	NA		NA	NA
Proportion of infants not immunizedh in preceding yearg	NA	NA		12.88 (6.52–32.43)	NA
Interaction between infant population susceptible to measles and population densityi
Proportion of infants not covered by vaccinationf in the preceding year × high population density	NA	66.20 (40.49–108.25)		NA	NA
Proportion of infants not covered by vaccinationf in the preceding year × low or medium population density	NA	7.45 (4.72–11.77)		NA	NA
Proportion of infants not immunizedh in the preceding year × high population density	NA	NA		NA	89.35 (50.65–157.60)
Proportion of infants not immunizedh in the preceding year × low or medium population density	NA	NA		NA	8.89 (5.14–15.38)

BCI, Bayesian credibility interval; CI, confidence interval; NA, not applicable; RR, risk ratio.

^a The analysis considered infants aged under 1 year who were not covered by vaccination in the preceding year (i.e. they did not receive their first measles vaccine dose).

^b The analysis considered infants aged under 1 year who were not immunized in the preceding year (i.e. they were not covered by vaccination or failed to seroconvert following the first vaccine dose).

^c The multivariate association between parameters and the incidence of measles among infants was evaluated using a Bayesian Poisson conditional autoregressive convolution model.

^d The 95% Bayesian credibility interval is analogous to the conventional 95% confidence interval.

^e The multivariate association between parameters and the incidence of measles among infants was evaluated using a conventional Poisson approach.

^f The proportion of infants that did not receive the first measles vaccine dose.

^g The risk ratio is for a 1% increase, on a continuous scale, in the proportion of infants who were covered by vaccination or immunized.

^h The formula used to calculate this proportion is described in the methods.

ⁱ Since there was a strong, significant correlation between population density and metropolitan area (i.e. Spearman ρ = 0.64, P < 0.001), the interaction between metropolitan area and high population density was not included.

Fig. 6.

Predicted^a relative risk of measles in infants in a populated area, by proportion of susceptible infants^b

Infants were regarded as not covered by vaccination if they did not receive their first measles vaccine dose.

Infants were regarded as not immunized if either they were not covered by vaccination or they failed to seroconvert following the first vaccine dose.

^a Predicted by the model (see text).

^b Infants were susceptible to measles because of poor vaccination coverage in preceding years or because they failed to seroconvert.

Fig. 7.

Relative risk of measles in infants, by district population density, South Africa, 2009–2011

The circles indicate the observed relative risk and population density in individual districts.

The solid line represents the fitted association between the observed relative risk and population density and the dashed line represents the lower bound of the 95% confidence interval for the association.

Fig. 8.

Predicted^a high-risk areas for measles in infants in 2012, South Africa

The * indicates the districts in which the risk was significantly elevated.

^a Predicted by the model (see text) by taking into account the proportion of infants not covered by the first vaccine dose in 2011.

Discussion

The study showed that HIV infection, preceding lapses in vaccination and high population density were associated with an increased risk of measles outbreak and the predictive model we developed provides a means of identifying areas at high risk of a future outbreak or where herd immunity does not meet elimination criteria. In resource-limited settings, it is essential to focus on high-risk areas where vaccination coverage is poor and where the build-up of a susceptible population could fuel future outbreaks. Our model, which takes into account the influence of HIV infection, could be applied to other settings where sporadic measles outbreaks remain a problem and can be modified easily for application to other vaccine-preventable diseases.

Infants were the group at highest risk in the measles outbreak we examined. This is not surprising given that their immune systems are undeveloped. Although maternal measles antibodies generally protect infants in the first 6 months of life, studies suggest that the infants of mothers with vaccine-induced immunity and of HIV+ mothers receive significantly fewer antibodies.^37–39 In addition, HIV infection in infants in sub-Saharan Africa has been shown to reduce their ability to seroconvert following vaccination.³³ These factors have implications for herd immunity: the build-up of a susceptible population in an area with low vaccine coverage and a high prevalence of HIV infection could lead to a large measles outbreak. In areas where measles and HIV infection are prevalent,⁴⁰ both HIV-infected infants and infants exposed to HIV but not infected could benefit from earlier vaccination.³⁸

We found that, overall, national coverage with the first measles vaccine dose in South Africa was high, at around 88%, but was variable, with the coverage in many districts routinely falling well below 90%. A previous study in the country concluded that the heterogeneity in measles vaccine coverage challenges the goal of eliminating measles and that supplemental immunization activities have a negative effect on routine immunization coverage and health system functioning.^41,42 Areas with repeatedly low vaccine coverage should be targeted for improvement. It is also important to coordinate supplemental immunization activities between neighbouring countries during widespread outbreaks. It has been reported that the cases observed immediately following supplemental immunization tend to be due to immigration from nearby areas where it has not taken place.⁴³

Our findings suggest that both the build-up of a susceptible population due to poor vaccine coverage and high population density contributed to the South African outbreak. Similarly, the large measles outbreak in Sierra Leone during 2009 and 2010 was probably caused by the accumulation of susceptible individuals, largely due to nonvaccination.⁴⁴ The cumulative impact of nonvaccination is important and justifies using our predictive model to help identify and target areas with a large number of susceptible individuals. We observed that the measles outbreak in South Africa had a strong nonrandom spatial distribution with strong connectivity, as seen in other studies.^11,45 Previous studies also indicate that measles outbreaks generally persist through epidemic troughs when the community is above a critical size. Below this threshold, measles tends towards extinction during the troughs.^45,46 Our findings indicate that once the percentage of the population susceptible to measles in a densely populated district exceeds 20%, the risk of infection is increased. Districts with a smaller susceptible population appeared remarkably resilient to measles infiltration during the outbreak. Our observation that the risk of measles outbreak was significantly elevated in areas with a high population density and in metropolitan areas has also been reported in other settings.^11,45 The highly connected nature of these areas may have contributed to the persistence of the outbreak.

Study limitations include possible underreporting of measles cases, fragmentation of vaccination services, a change in measles vaccination schedule in 2009 and repeated changes in reporting forms during the past 5 years. Underreporting in particular districts may have affected the spatial pattern observed and weakened associations with key indicators. In addition, we cannot discount the possibility of ecological bias given that aggregated measles vaccination and HIV infection data were used.

Our study has important implications for the elimination of measles in South Africa and sub-Saharan Africa. Lapses in immunization, a high burden of HIV infection and the build-up of a susceptible population appear to be important for driving sporadic outbreaks, especially in populous areas. Supplemental immunization is by definition a catch-up strategy. It is also costly, may not be implemented quickly enough to limit outbreaks and has a negative effect on routine immunization services.^41,47 Identifying and targeting emerging high-risk areas in resource-limited settings where vaccine coverage is low or waning appears a more viable strategy for preventing outbreaks in sub-Saharan Africa than mass supplemental immunization. Improved vaccine coverage of small areas through highly targeted campaigns and by strengthening routine services are possible solutions.