Abstract
Background:
The ACCENT database, with individual patient data for 20 898 patients from 18 colon cancer clinical trials, was used to support Food and Drug Administration (FDA) approval of 3-year disease-free survival as a surrogate for 5-year overall survival. We hypothesised substantive differences in survival estimation with log-normal modelling rather than standard Kaplan–Meier or Cox approaches.
Methods:
Time to relapse, disease-free survival, and overall survival were estimated using Kaplan–Meier, Cox, and log-normal approaches for male subjects aged 60–65 years, with stage III colon cancer, treated with 5-fluorouracil-based chemotherapy regimens (with 5FU), or with surgery alone (without 5FU).
Results:
Absolute differences between Cox and log-normal estimates with (without) 5FU varied by end point. The log-normal model had 5.8 (6.3)% higher estimated 3-year time to relapse than the Cox model; 4.8 (5.1)% higher 3-year disease-free survival; and 3.2 (2.2)% higher 5-year overall survival. Model checking indicated greater data support for the log-normal than the Cox model, with Cox and Kaplan–Meier estimates being more similar. All three model types indicate consistent evidence of treatment benefit on both 3-year disease-free survival and 5-year overall survival; patients allocated to 5FU had 5.0–6.7% higher 3-year disease-free survival and 5.3–6.8% higher 5-year overall survival.
Conclusion:
Substantive absolute differences between estimates of 3-year disease-free survival and 5-year overall survival with log-normal and Cox models were large enough to be clinically relevant, and warrant further consideration.
Keywords: colon cancer, survival, log-normal, Cox, Kaplan–Meier, ACCENT database
The move towards personalised medicine involves assessing targeted agents in small patient groups, where survival may not be robustly estimated with standard methods. We demonstrate here a method for survival function estimation that may be more robust, with demonstrated differences from standard approaches.
Mismatch repair in colon cancer has been indicated as a predictive marker of benefit from standard adjuvant care, fluorouracil-based chemotherapy (Sargent et al, 2010). Patients with high level of microsatellite instability or defective mismatch repair had a favourable stage-adjusted prognosis, and did not benefit from fluorouracil-based therapy, while a significant benefit from fluorouracil therapy for tumours with microsatellite-stable or proficient mismatch repair has been demonstrated. In such a situation of differential response by biologic subtype (e.g. KRAS gene mutation and epidermal growth factor receptor inhibitors (Jonker et al, 2007; Karpetis et al, 2008; De Roock et al, 2010), or human epidermal growth factor receptor 2-positive status and trastuzumab immunotherapy), patient risk of relapse, or death pooled across different subgroups will differ in risk by follow-up time, which violates the usual Cox survival analysis assumption of proportional hazards. Specifically, the Cox model assumptions imply that all patients receive a consistent (and uniform) benefit of treatment over time. Tumour characterisation may in general be expected to impose non-proportional hazards for survival pooled across initially unidentified subgroup classifications. In some circumstances, this violation might either obscure the determination of a significant effect or falsely attribute a significant effect.
The large Adjuvant Colon Cancer End points (ACCENT) database with individual patient data for 20 898 patients enroled on 18 colon cancer clinical trials pre-dated the biologically targeted therapeutic approaches described above (Sargent et al, 2005, 2007). However, patients with tumours having the above identified mutations, or other as yet unidentified mutations, would have been included, and may have been differentially impacted by therapy; the tumour mismatch repair work utilised a subgroup of ACCENT trials where patients were allocated to fluorouracil-based therapy or surgery alone (Sargent et al, 2010). Pooled analyses with the ACCENT data showed that patients with stage II and III colon cancer exhibited stage-specific differences in risk of recurrence, or non-proportional hazards, during follow-up (Sargent et al, 2007, 2010). While proportional hazards is an assumption for the Cox model, it is not for the log-normal model. Further, the ACCENT data exhibited classical log-normal hazard shape for both stage II and III patients (see Figure 1 of previous work, Sargent et al, 2007). Thus, we hypothesised, based on recent breast cancer literature, that the ACCENT data would have substantive differences in survival estimates with log-normal survival modelling, rather than with the Cox model (Royston, 2001; Chapman et al, 2008).
The extended follow-up of patients in the large ACCENT database has been useful to characterise baseline survival experience. Pooled analyses with the ACCENT database led to the Food and Drug Administration (FDA) approval of 3-year disease-free survival as a surrogate end point for 5-year overall survival, so we emphasised here comparisons of survival estimates by therapeutic management for these end points and timepoints utilising the standard Kaplan–Meier estimation, Cox modelling and log-normal modelling.
Materials and methods
Analyses using the ACCENT database of 18 randomised phase III colon cancer adjuvant clinical trials were institutional review board approved; each trial was originally approved through appropriate local mechanisms (Sargent et al, 2005). The 43 treatment arms were collapsed here to examine survival for (1) combination chemotherapy with 5-fluorouracil (5FU) plus leucovorin, with or without levamisole (5FU+LV±LEV, referred to hereafter as 5FU), or (2) surgery alone (referred to as no 5FU therapy). All 20 898 randomly assigned patients were considered for inclusion in the analyses according to the intention-to-treat principle. The long-term follow-up practices of the trials differed, so to reduce the possibility of bias, follow-up for all patients was censored at 8 years from randomisation.
Therapeutic effect would standardly be reported with hazard ratios based on the full follow-up of patients. Patient experience at a particular timepoint would usually utilise absolute survival rates at that time obtained with the Kaplan–Meier method. The focus on 3- and 5-year rates leads to the common comparator for between model types for absolute survival rates, and absolute differences in survival rates by treatment.
End points
Three end points were utilised: time to relapse, to examine biologic relevance of therapy; and disease-free survival and overall survival, as 3-year disease-free survival was United States FDA approved as a surrogate for 5-year overall survival. Time to relapse was defined as the time from randomisation to the date of the first confirmed relapse; censoring was at longest follow-up or death without relapse. Disease-free survival was defined as the time from randomisation to the date of first disease recurrence, or for non-recurrence, death; censoring was at longest follow-up. Overall survival was defined as the time from randomisation to the date of death; censoring was at longest follow-up.
Patient Characterisation
Factors available for these analyses were sex (male, female), age (in years), stage (I–III), and treatment (5FU regimen, no 5FU), all of which had significant multivariate impact on outcome (P=0.005–<0.0001). Robust comparison with Kaplan–Meier results required a large subgroup of patients: we chose male subjects aged 60–65 years, with stage III primary colon cancer, treated with (1) 5FU, or (2) no 5FU: for time to relapse and disease-free survival, N=1540; for overall survival, N=1545.
Methods of estimating end points
Kaplan–Meier
Univariate estimation of efficacy is standard with the Kaplan–Meier method for specific subgroups of patients. Estimation is non-parametric based on a step function with adjustment at times of observed events. Kaplan–Meier plots were used for graphical depictions of patient experience. Patient data by follow-up time were used to obtain Kaplan–Meier estimates of each end point of interest at 3 and 5 years.
Cox (proportional hazards) model
Cox regression is standardly used to assess the effect of one or more factors through (log) relative risk of an event. For a factor, subgroups of patients are assumed to have proportional hazards, that is, that the differences in risks between factor-based subgroups do not differ by follow-up time (Appendix 1).
We examined the appropriateness of the assumption of proportional hazards using plots of the log of cumulative hazards against time; under the assumption of proportional hazards, there would be approximately constant differences between for instance treatments, or between stage II and III patients. Fit of the final Cox model was assessed with Cox–Snell residuals, based on the cumulative hazard for patient observation times, patient factor values, and estimated factor effects; a plot of Cox–Snell residuals against time would be expected to follow a straight line (Kalbfleisch and Prentice, 2002).
The Cox model is not typically used for survival function estimation, although it may be obtained for timepoints during the investigational period (Appendix 1). Cox survivor plots are based on semiparametric estimation, and like those with Kaplan–Meier, are step functions with adjustments at times of observed events. An important difference between the Cox and Kaplan–Meier models is that factors are rarely independent, and the Cox model permits estimation of joint effects on survival in the full group of patients. Further, it is more feasible to simultaneously ascertain survival for single patient values of multiple factors.
For comparability with the Kaplan–Meier model, we estimated survival with the Cox model for the same patients: male subjects aged 60–65 years, with stage III disease, who were treated with (1) 5FU, or (2) no 5FU therapy. Cox survivor plots were used for graphical depiction; the Cox survivor function was used for quantitative estimates of survival.
Log-normal
The log-normal model is a location-scale model (Appendix 2). Location-scale models may be more robust than the Cox model under model misspecification (He and Lawless, 2005), with specific characterisation an area of ongoing research. We examined support for the log-normal compared with common location-scale (or accelerated failure time) alternatives of an exponential, Weibull, or log-logistic. Observed patient event times and patient factor values are used to fit models; standardised residuals are the differences between the log of observed and log of expected patient event times, divided by estimated error. Residuals for disease-free survival are not centred around zero for any model type, likely indicating missing (biologic) prognostic factors such as those described earlier (Jonker et al, 2007; Karpetis et al, 2008; De Roock et al, 2010, Sargent et al, 2010). However, comparing the residuals obtained with available data, we found the range in size of residuals to be smaller with a log-normal model, particularly for events occurring in the first year: see Supplementary Figures 1–4 online for plots of standardised residuals for each model type. The focus for this work thus became the log-normal model. We further checked data support for assuming the log-normal model type by examining quantile–quantile (Q–Q) plots to compare quantiles of the empirical distribution of loge(t) for events with normal quantiles, for each event type; a straight line is expected. Standardised residual plots for disease-free survival indicated a much smaller range of residuals for the LN compared with common location-scale (or accelerated failure time) alternatives of an exponential, Weibull, or log-logistic. The focus for this work is thus the LN.
Log-normal modelling and estimation utilised the same patients as the Kaplan–Meier and Cox models. Like the Cox model, the standard log-normal formulation (Appendix 2) is a log-linear effect of factors, although the effect for log-normal is on log of (censored) survival time. Cox–Snell residuals were used to examine the fit of log-normal models, and are expected to follow a straight line. Log-normal Cox–Snell residuals were compared with those generated for the Cox model. Log-normal survivor plots, based on parametric estimation, were used for graphical depiction; the log-normal survivor function was used for quantitative estimates of survival.
Statistical Solutions BMDP 2009 with enhanced Enhanced Metafile (EMF) graphics was used for all survival analyses.
Results
Kaplan–Meier estimation for time to relapse was performed for 1540 patients, with 200 of 321 (62.3%) patients relapse-free on 5FU vs 676 of 1219 (55.5%) without 5FU-based therapy. Event counts for disease-free survival were 175 of 321 (54.5%) and 589 of 1219 (48.3%); for overall survival, 191 of 321 (59.5%) and 647 of 1224 (52.9%), for 5FU vs no 5FU, respectively.
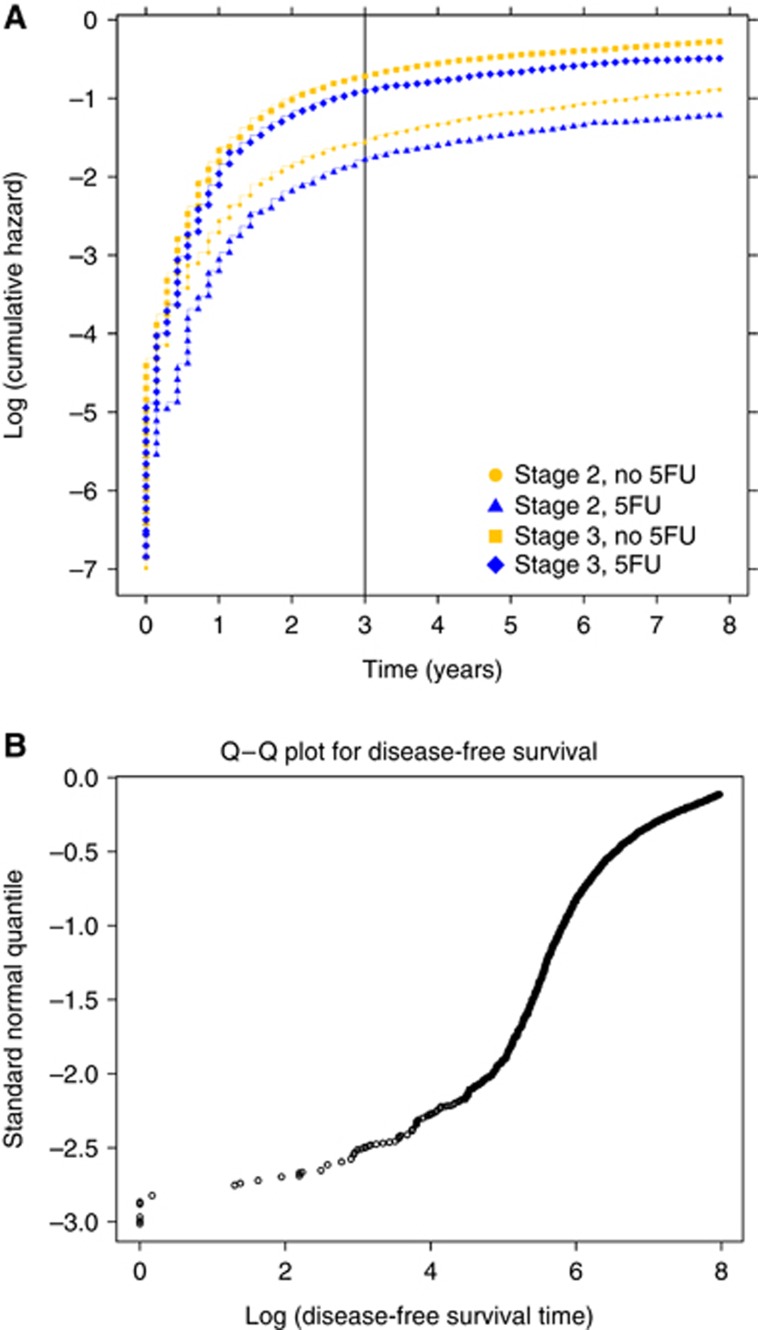
Disease-free survival at 3 years is the FDA-approved surrogate for 5-year overall survival. Figure 1A examines for disease-free survival the Cox model assumption of proportional hazards using a plot of cumulative hazards, stratified by stage and treatment. There is evidence of substantial non-proportionality of hazards both between patients with stage II and III disease and between those treated with and without 5FU in the first 15 months, where patients experienced the largest hazard of a disease-free survival event. Differences between stage and treatment groups are similar after 2 years. Meanwhile, the disease-free survival log-normal Q–Q plot (Figure 1B) indicates minor departures from a log-normal distribution (straight line) at short and long follow-up times.
Figure 1.
(A) Disease-free survival risk for male subjects aged 60–65 years by treatment and stage: plot depicts log of cumulative hazard by treatment, with or without 5FU, for stage II and III patients, to examine Cox model assumption of proportional hazards. (B) Disease-free survival quantile–quantile plot for male subjects: plot is a normal probability plot for log of disease-free survival event times, to examine the assumption that the logarithm of disease-free survival times has a normal distribution.
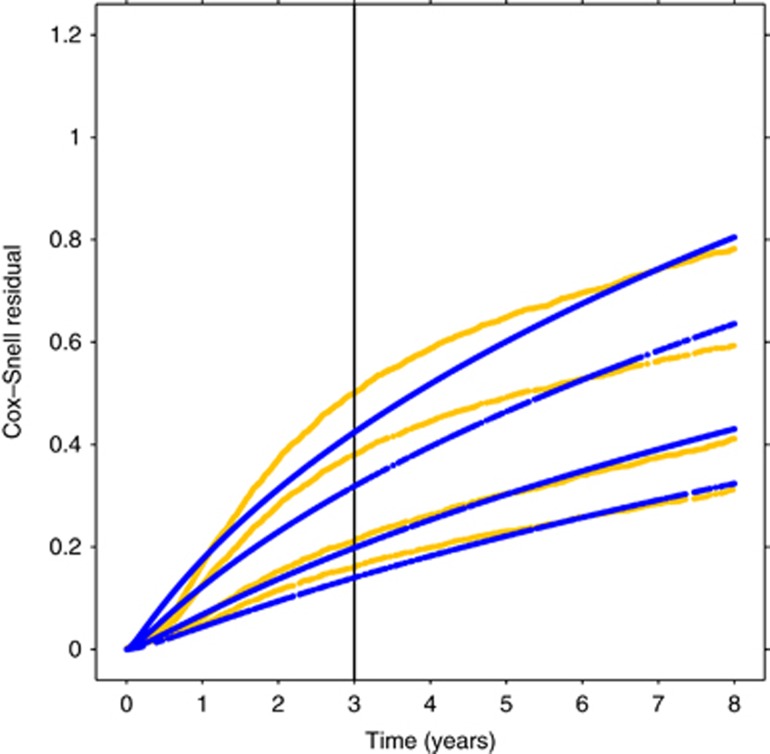
The experience of male subjects aged 60–65 years, with stage II and III disease, was used to fit disease-free survival Cox and log-normal models for each end point. The fit of each model is compared in Figure 2 with an overlay of Cox–Snell residuals by follow-up time. Patient differences between the fitted model and actual data were categorised by stage and treatment for both the Cox and log-normal models. Both model types exhibit systematic departures from a straight line for disease-free survival times less than a year; however, there is pronounced curvature of the Cox model residuals for stage III patients until after 3 years, indicative of lack of data support for the Cox model compared with log-normal model in the important 3-year time period where disease-free survival is generally considered.
Figure 2.
Disease-free survival Cox–Snell residuals by follow-up for male subjects aged 60–65 years by treatment and stage: plots of residuals examines fit of Cox model ((yellow online) lighter lines) and log-normal model ((blue online) darker lines) with factors treatment and stage; for each model (colour), top two lines are stage III with and without-5FU and bottom two lines are stage II with and without 5FU. An adequate fit is indicated with residuals having approximately straight lines.
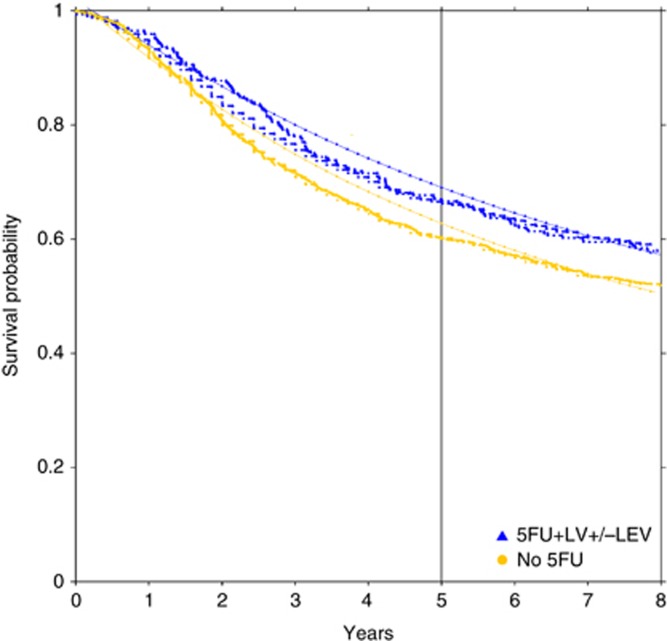
Direct comparisons of all three model types (Kaplan–Meier, Cox, and log-normal) are illustrated for male subjects aged 60–65 years with stage III disease, and who were, or were not, allocated to 5FU arm, with vertical lines at 3 years for time to relapse (Figure 3) and disease-free survival (Figure 4), and at 5 years for overall survival (Figure 5). In all instances, the estimated log-normal curves are higher than both the Kaplan–Meier and Cox estimates, whereas the Kaplan–Meier and Cox estimates are quite similar. Although the magnitude of survival estimates differed by model type, directionally, patients who received 5FU had better disease-free survival and overall survival than those who did not, regardless of model estimation method.
Figure 3.
Time-to-relapse survival probabilities for male subjects 60–65 years, stage III primary colon cancer treated with or without 5FU systemic therapy, with the vertical line indicating 3-year follow-up. Log-normal is identifiable by solid plot lines: log (time-to-relapse follow-up time)=2.0675+β × treatment+1.8919W, where β (s.e.; P-value) for treatment is 0.2902 (0.1386; P=0.04) and W∼N(0,1). For Cox model (dashed lines), β (s.e.; P-value) for treatment is −0.2054 (0.1005; P=0.04). Kaplan–Meier plot (dotted line) overlaps Cox (P=0.04).
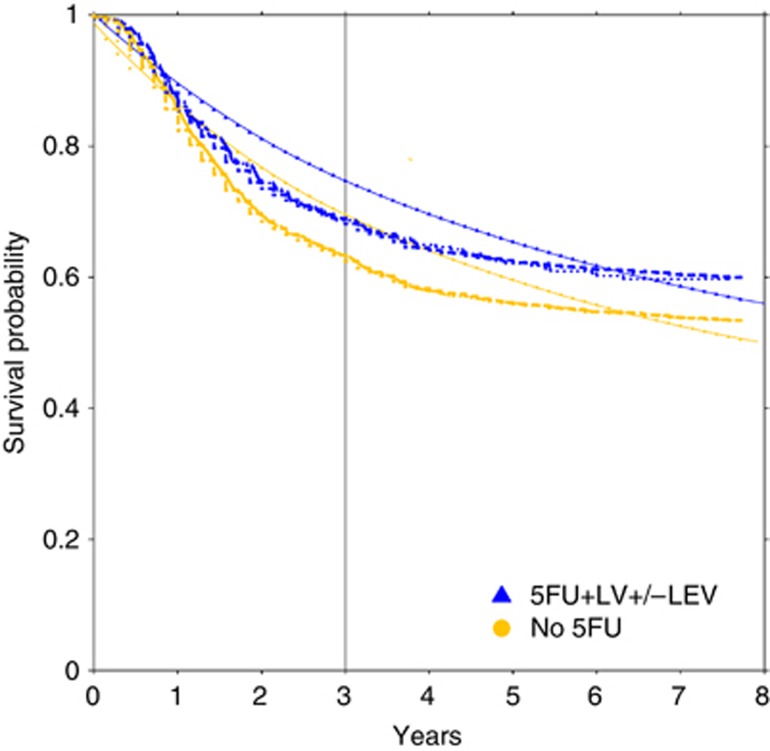
Figure 4.
Disase-free survival survival probabilities for male subjects aged 60–65 years, stage III primary colon cancer treated with or without 5FU systemic therapy, with the vertical line indicating 3-year follow-up. Log-normal is identifiable by solid plot lines: log (disease-free survival follow-up time)=1.8653+β × treatment+1.8919W, where β (s.e.; P-value) for treatment is 0.2599 (0.1274; P=0.04) and W∼N(0,1). For Cox model (dashed lines), β (s.e.; P-value) for treatment is −0.1845 (0.0919; P=0.04). Kaplan–Meier plots (dotted lines) is similar to Cox (P=0.04).
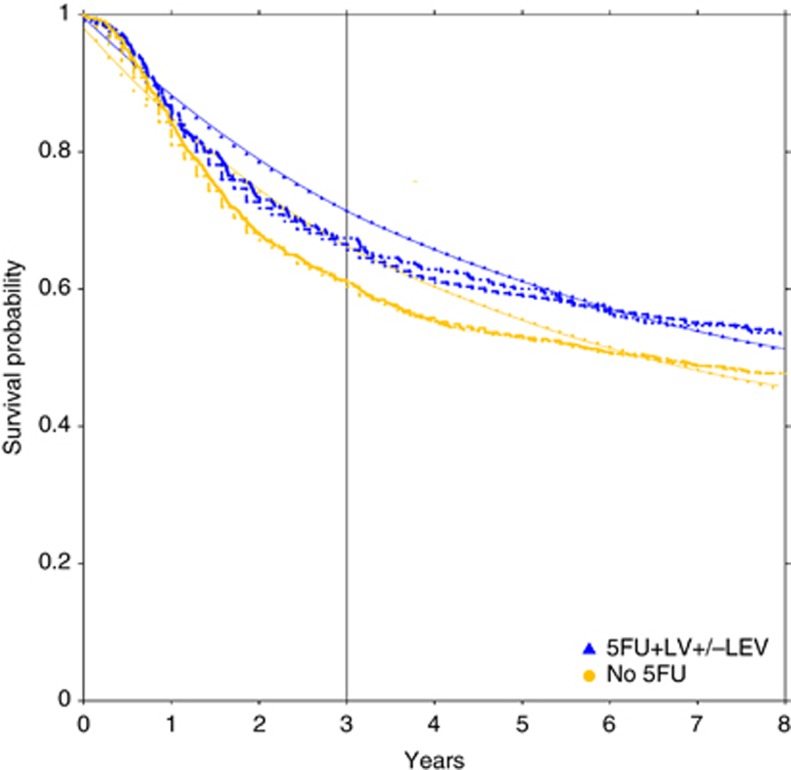
Figure 5.
Overall survival survival probabilities for male subjects aged 60–65 years, stage III primary colon cancer treated with or without 5FU systemic therapy, with the vertical line indicating 5-year follow-up. Log-normal is identifiable by solid plot lines: log (overall survival follow-up time)=2.0931+β × treatment+1.4833W, where β (s.e.; P-value) for treatment is 0.2548 (0.1069; P=0.02) and W∼N(0,1). For Cox model (dashed lines), β (s.e.; P-value) for treatment is −0.2116 (0.0971; P=0.03). Kaplan–Meier plots (dotted lines) overlaps Cox (P=0.02).
Table 1 summarises the comparisons of 3-year survival estimates for the Kaplan–Meier, Cox, and log-normal models for time to relapse and disease-free survival, and those for 5-year overall survival. Patients allocated to 5FU arm had significantly better 3-year time to relapse and disease-free survival (for both end oints, P=0.04 for three model types), and 5-year overall survival (P=0.02 for Kaplan–Meier and log-normal; P=0.03 for Cox). The 5FU arm had 5.0–6.7% higher 3-year estimated disease-free survival than the no 5FU arm, while the 5FU arm had 5.3–6.8% higher 5-year overall survival. Cox and Kaplan–Meier estimates were generally more similar than log-normal and Kaplan–Meier estimates: the range of differences of was −1.2% to 0.3% vs 2.0–6.3%, respectively. Absolute differences between log-normal and Cox estimates by therapy, at specific timepoints, varied by end point; the differences for 3-year time to relapse were: for 5FU, 5.8% and for no 5FU, 6.3% for 3-year disease-free survival, 4.8 and 5.1% and for 5-year overall survival, 3.2 and 2.2%.
Table 1. Comparison of 3-year time to relapse, disease-free survival with 5-year overall survival for Kaplan–Meier, Cox, log-normala.
| Males (60–65 years) | Stage III 5FU (%) | No 5FU (%) | Abs. diff. With 5FU (%) | P-valueb |
|---|---|---|---|---|
|
3-Year time to relapse | ||||
| Kaplan–Meier | 69.1 | 63.3 | 5.8 | 0.04 |
| Cox | 68.9 | 63.3 | 5.6 | 0.04 |
| Log-normal | 74.7 | 69.6 | 5.1 | 0.04 |
| Abs. diff. (Cox–Kaplan–Meier) | −0.2 | 0.0 | ||
| Abs. diff. (log-normal–Kaplan–Meier) | 5.6 | 6.3 | ||
| Abs. diff. (log-normal–Cox) |
5.8 |
6.3 |
|
|
|
3-Year disease-free survival | ||||
| Kaplan–Meier | 67.7 | 61.0 | 6.7 | 0.04 |
| Cox | 66.6 | 61.3 | 5.3 | 0.04 |
| Log-normal | 71.4 | 66.4 | 5.0 | 0.04 |
| Abs. diff. (Cox–Kaplan–Meier) | −1.1 | 0.3 | ||
| Abs. diff. (log-normal–Kaplan-Meier) | 3.7 | 5.4 | ||
| Abs. diff. (log-normal–Cox) |
4.8 |
5.1 |
|
|
|
5-Year overall survival | ||||
| Kaplan–Meier | 67.1 | 60.3 | 6.8 | 0.02 |
| Cox | 65.9 | 60.6 | 5.3 | 0.03 |
| Log-normal | 69.1 | 62.8 | 6.3 | 0.02 |
| Abs. diff. (Cox–Kaplan–Meier) | −1.2 | 0.3 | ||
| Abs. diff. (log-normal–Kaplan–Meier) | 2.0 | 2.5 | ||
| Abs. diff. (log-normal–Cox) | 3.2 | 2.2 | ||
Abbreviations: Abs. diff=absolute difference; 5FU=5-fluorouracil.
For male subjects 60–65 years, stage III primary colon cancer treated with or without 5FU systemic therapy.
P-value for Kaplan–Meier is from Wilcoxon (Peto–Prentice) test statistic, and for Cox and log-normal is from likelihood ratio criterion (∼χ2(1)).
Discussion
The move to personalised medicine requires robust estimation of experience in small subgroups of patients as it becomes increasingly possible to characterise specifically tumours. As tools like Adjuvant! Online for colon cancer (http://www.adjuvantonline.com/) move into clinical practice, it becomes important that modelling generates good estimates of patient risk for increasingly finer patient classifications. Here statistical models generated apparent differences in absolute patient risk that might influence decision-making.
The focus of this work was survival at specific timepoints relevant, in particular, to the 3-year disease-free survival as a surrogate for 5-year overall survival. Thus, our aim was to compare absolute differences in survival estimates. For this work, we needed to estimate and use the baseline hazards for the Cox model. We began this investigation with the hypothesis that the standard Cox assumption of proportional hazards, if inappropriate, might substantively affect estimation of survival. Previous work by the ACCENT group (Sargent et al, 2009) demonstrated that for the end point of disease-free survival, a time-varying treatment effect was present. In addition, we noted though that there was evidence of non-proportional hazards for the important clinical factor of stage, between stage II and III colon cancer patients (Sargent et al, 2007, 2010), both stage II and III patients exhibited classical log-normal-shaped patterns for recurrence risk. On the basis of these considerations, the ACCENT data provided a good vehicle for a case-study comparison of survival estimation obtained with the Kaplan–Meier, Cox, and log-normal approaches.
Survival estimation should be considered within a cohesive framework that incorporates both the Cox model and a variety of alternatives (Ciampi et al, 1989), or other more complex modelling (Royston and Parmar, 2002). In our data set, both stage II and III patients exhibited classical log-normal-shaped patterns for recurrence risk, so we restricted parametric examinations to the common model choices of exponential, Weibull, log-logistic, and log-normal. All four model types were inadequate at short follow-up up at a time period when unmeasured aggressive biologic factors may have been operative (Jonker et al, 2007; Karpetis et al, 2008; De Roock et al, 2010, Sargent et al, 2010); however, there was greatest support among these model options for the log-normal. On the basis of these considerations, the ACCENT data provided a good vehicle for a case-study comparison of survival estimation obtained with Kaplan–Meier, Cox, and log-normal approaches.
Boag (1949) proposed an early version of the log-normal model to estimate the proportion of (breast cancer) patients cured by cancer therapy. Pocock et al. (1982) demonstrated operative non-proportional hazards for breast cancer patients for the important factors of disease stage and menopausal status with long-term follow-up. Pooling of data from seven breast cancer ECOG trials (Saphner et al, 1996) showed similar-shaped hazard plots to those by stage within ACCENT (Sargent et al, 2007), with annual breast cancer hazard rates that reached a peak after several years of follow-up and decreasing thereafter (Sargent et al, 2007, 2009). Recent reports in the breast cancer literature indicate mounting evidence of potential for substantive differences in survival estimates when the data indicate that there are non-proportional hazards (Royston, 2001; Chapman et al, 2008). Royston (2001) found that prognosis for breast cancer patients differed by up to a year, depending on whether one utilised a Cox or log-normal assessment. He and Lawless (2005) examined the class of location-scale models, which includes the four parametric model types considered here (exponential, Weibull, log-logistic, and log-normal), and showed that they may be more robust than the Cox model when assumptions are incorrect such as they are for both the Cox and parametric models in the first year of follow-up. Location-scale models require ascertainment of a data-appropriate parametric function for the hazard rate; to estimate survival with a Cox model, it is necessary to (non-parametrically) estimate baseline hazard.
Kaplan–Meier plots require sufficiently large patient subgroups for stable survival estimation, while both the Cox and log-normal models may be fit and graphed with individual patient values; further, both the Cox and log-normal plots may be adjusted for the potentially confounding effects of other factors. Smooth estimation of survival with parametric log-normal survival analysis may be preferable to the step-wise discontinuities at event(s) exhibited by the Cox (Royston, 2001), or by the Kaplan–Meier approach. We showed here that substantive differences between fitted models, and the data indicated greater data support within the ACCENT database for the log-normal than the Cox model in the important first 3 years for the FDA-approved disease-free survival endpoint. Estimation in pooled, or meta-, analyses could be especially susceptible to conditions that will lead to differences in effects over time: changes arising from disease shift with earlier detection, or from therapeutic improvements. Such changes would lead to different patient cross-sections, who may be managed differently over a broad follow-up period (Sargent et al, 2005) and impose inherent differences in efficacy, or non-proportional hazards. The magnitude of effect of non-proportional hazards is largely unknown at this time.
Strategies exist to maintain the validity of the Cox model in the presence of non-proportional hazards. A traditional approach is to create separate time periods with stratification at time points, such that each period has proportional hazards; this approach would be problematic if multiple factors exhibit non-proportionality at different times. One can stratify by factor subgroups if, for instance, treatments have approximate proportionality within factor subgroups; there was evidence of non-proportionality indicated here for stage II and III patients. Alternatively, the Cox model formulation may be changed to have time-varying factors (Appendix 1); however, in most cases the study was powered and designed assuming proportionality, so in most cases the sample size will be inadequate to permit a good fit of time-varying factors (Grambsch and Therneau, 1994). These approaches, however, risk obscuring the statistical results from transparent clinical interpretation.
An advantage of the Cox model is that it does not require an underlying distributional assumption to assess factor effects, although it is necessary to estimate the baseline hazard for survival estimation. Parametric modelling requires an appropriate model. The log-normal model has been supported by breast cancer trial data (Chapman et al, 2008). In this colon cancer work, only minor departures were seen for disease-free and overall survivals in the tails of the distributions, which may have arisen from factors not available for modelling. One might hypothesise the existence of patients with aggressive tumour features (Jonker et al, 2007; Karapetis et al, 2008; De Roock et al, 2010; Sargent et al, 2010) not known to investigators, and thus not represented in the models to account for these differences.
All three model types indicate consistent evidence of improved 3-year disease-free survival and 5-year overall survival with 5FU over no 5FU therapy, with better 3-year time to relapse and disease-free survival (P=0.04), regardless of model type, and 5-year overall survival (P=0.02 for Kaplan–Meier and log-normal; P=0.03 for Cox). Further, all model types indicated the 5FU arm-treated patients having similar improvements over those with no 5FU arm. In particular, estimated 3-year disease-free survival was 5.0–6.7% higher, and 5-year overall survival was 5.3–6.8% higher with 5FU vs surgery alone control.
Cox and Kaplan–Meier estimates were generally more similar than log-normal and Kaplan–Meier, with differences between Cox and Kaplan–Meier varying from −1.2% to 0.3%, and log-normal and Kaplan–Meier, 2.0–6.3%. Absolute differences in estimable survival between the log-normal and Cox models varied substantively for 3-year time to relapse, 5.8 and 6.3% for 3-year disease-free survival, 4.8 and 5.1% and for 5-year overall survival, 3.2 and 2.2%.
Both the Cox and log-normal models permit finer multivariate specification in terms of patient characteristics (age in years, number of involved lymph nodes, tumour size in cm) than the Kaplan–Meier, which could be advantageous in smaller populations. Continued sequential partitioning of patients by tumour marker status, such as that arising from KRAS studies or tumour mismatch repair in colon cancer, challenges the traditional practice of large patient group counts based on patient characteristics, disease stage, or gross tumour descriptors.
We observed substantive differences between estimates of 3-year disease-free survival and 5-year overall survival with log-normal and Cox models, with greater data support for the log-normal fitted model in the first 3 years with the ACCENT database. The magnitude of differences in survival estimates with a log-normal vs a Cox model were large enough to be clinically relevant and warrant further consideration as we evaluate new therapies and prognostic/predictive factors. We are working to better understand the robustness of the Cox and log-normal statistical frameworks under misspecification, at anticipated levels of censoring for different cancer types.
Acknowledgments
This work was supported by a Canadian Cancer Society Research Institute grant to the NCIC Clinical Trials Group (CTG) for NCIC CTG Faculty; the ACCENT group is supported by the NCCTG grant from the National Cancer Institute at the National Institutes of Health (Grant CA25224); and N Hu was supported by a Canadian National Sciences and Engineering Research Council grant to K Ding and by Queen's University Department of Community Health and Epidemiology graduate student support.
Appendix 1
Cox model formulation
For the Cox model, it is assumed that the hazards for factor subgroups are proportional across follow-up, with h(t|z)=ho(t) exp(β′z). The hazard function, h(t|z), consists of an unspecified baseline hazard function, ho(t), and a multiplicative function of the covariates z. The Cox model is not typically used for estimation of survival, although such estimates may be obtained for timepoints during the investigational period by using the estimated baseline survival function So(t), estimated β, individual covariate data z, and the Cox survivor function, So(t|z): S(t|z)=So(t)exp(β′z). The Cox model formulation may be changed to have time-varying factors (h(t2 Z(t))=ho(t) exp (β′ z(t))).
Appendix 2
Log-normal model formulation
Log-normal regression is a location-scale model where Y, the logarithm of follow-up time, is a linear function of factors, z, Y=loge(t)=σ+β z+σW, and W is assumed to have a standard normal distribution. The log-normal survivor function is S(t)=1−Φ((loge(t)–(α+β z))/σ), where Φ is the standard normal distribution function.
Log-normal time to relapse and overall survival Q–Q plots (Supplementary Figures 5 and 6 online) also exhibited departures from a log-normal distribution in the tails of the distributions. Departures appeared minor for overall survival, and more moderate for time to relapse. In summary, the log-normal assumption appeared quite reasonable for disease-free and overall survivals, the two end points of interest from the perspective of surrogacy.
The authors declare no conflict interest.
Footnotes
Supplementary Information accompanies the paper on British Journal of Cancer website (http://www.nature.com/bjc)
This work is published under the standard license to publish agreement. After 12 months the work will become freely available and the license terms will switch to a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License.
Previous presentation: see reference Chapman J et al (2011).
Supplementary Material
References
- Adjuvant! Online for colon cancer Available at: http://www.uptodate.com/contents/adjuvant-therapy-for-resected-stage-iii-node-positive-colon-cancer Accessed 21 January 2013
- BMDP . Statistical Solutions. BMDP: Cork , Ireland; 2009. [Google Scholar]
- Boag JW. Maximum likelihood estimates of the proportion of patients cured by cancer therapy. J R Stat Soc Ser B. 1949;11 (1:15–53. [Google Scholar]
- Chapman JW, Meng D, Shepherd L, Parulekar W, Ingle JN, Muss HB, Palmer M, Yu C, Goss PE. Competing causes of death from a randomized trial of extended adjuvant endocrine therapy for breast cancer. J Natl Cancer Inst. 2008;100:252–260. doi: 10.1093/jnci/djn014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapman J, O'Callaghan C, Hu N, Ding K, Yothers G, Catalano P, Shi Q, Grey R, O'Connell M, Sargent D. Comparison of innovative estimation of efficacy to standard using the ACCENT database. J Clin Oncol. 2011;29 (15S, Part I of II:250s. [Google Scholar]
- Ciampi A, Chapman J, Hogg S, Thiffault J. GENCOV: a Fortran program that generates randomly censored survival data with covariates. Comput Methods Programs Biomed. 1989;29:51–57. doi: 10.1016/0169-2607(89)90090-4. [DOI] [PubMed] [Google Scholar]
- De Roock W, Jonker DJ, Di Nicolantonio F, Sartore-Bianchi A, Tu D, Siena S, Lamba S, Arena S, Frattini M, Piesssevaux H, Van Cutsem E, O'Callaghan CJ, Khambata-Ford S, Zalcberg JR, Simes J, Karapetis CS, Bardelli A, Tejpar S. Association of KRAS p.G13D mutation with outcome in patients with chemotherapy-refractory metastatic colorectal cancer treated with cetuximab. JAMA. 2010;304 (16:1812–1820. doi: 10.1001/jama.2010.1535. [DOI] [PubMed] [Google Scholar]
- Grambsch PM, Therneau TM. Proportional hazards tests and diagnostics based on weighted residuals. Biometrika. 1994;81:515–526. [Google Scholar]
- He W, Lawless JF. Bivariate location-scale models for regression analysis, with applications to lifetime data. J R Stat Soc Ser B. 2005;67:63–78. [Google Scholar]
- Jonker DJ, O'Callaghan CJ, Karapetis CS, Zalcberg JR, Tu D, Au H-J, Berry SR, Krahn M, Price T, Simes RJ, Tebbutt NC, van Hazel G, Wierzbicki R, Langer C, Moore MJ. Cetuximab for the treatment of colorectal cancer. N Engl J Med. 2007;357 (20:2040–2048. doi: 10.1056/NEJMoa071834. [DOI] [PubMed] [Google Scholar]
- Kalbfleisch JD, Prentice RL.2002The Statistical Analysis of Failure Time Data2nd edn.119–128.Wiley: Hoboken, NJ [Google Scholar]
- Karapetis CS, Khambata-Ford S, Jonker DJ, O'Callaghan CJ, Tu D, Tebbutt NC, Simes RJ, Chalchal H, Shapiro JD, Robitaille S, Price TJ, Shepherd L, Au H-J, Langer C, Moore MJ, Zalcberg JR. K-ras mutations and benefit from cetuximab in advanced colorectal cancer. N Engl J Med. 2008;359 (17:1757–1765. doi: 10.1056/NEJMoa0804385. [DOI] [PubMed] [Google Scholar]
- Pocock SJ, Gore SM, Kerr GR. Long term survival analysis: the curability of breast cancer. Stat Med. 1982;1:93–104. doi: 10.1002/sim.4780010202. [DOI] [PubMed] [Google Scholar]
- Royston P. The lognormal distribution as a model for survival time in cancer, with an emphasis on prognostic factors. Stat Neerl. 2001;55 (1:89–104. [Google Scholar]
- Royston P, Parmar MK. Flexible parametric proportional-hazards and proportional-odds models for censored survival data, with application to prognostic modeling an estimation of treatment effects. Stat Med. 2002;21:2175–2197. doi: 10.1002/sim.1203. [DOI] [PubMed] [Google Scholar]
- Saphner T, Tormey DC, Gray R. Annual hazard rates of recurrence for breast cancer after primary therapy. J Clin Oncol. 1996;14 (10:2738–2746. doi: 10.1200/JCO.1996.14.10.2738. [DOI] [PubMed] [Google Scholar]
- Sargent DJ, Wieand HS, Haller DG, Gray R, Benedetti JK, Buyse M, Labianca R, Seitz JF, O'Callaghan CJ, Francini G, Grothey A, O'Connell M, Catalano PJ, Blanke CD, Kerr D, Green E, Wolmark N, Andre T, Goldberg RM, De Gramont A. Disease-free survival versus overall survival as a primary end point for adjuvant colon cancer studies: individual patient data from 20 898 patients on 18 randomized trials. J Clin Oncol. 2005;23 (34:8664–8670. doi: 10.1200/JCO.2005.01.6071. [DOI] [PubMed] [Google Scholar]
- Sargent DJ, Patiyil S, Yothers G, Haller DG, Gray R, Benedetti J, Buyse M, Labianca R, Seitz JF, O'Callaghan CJ, Francini G, Grothey A, O'Connell M, Catalano PJ, Kerr D, Green E, Wieand HS, Goldberg RM, de Gramont A. End points for colon cancer adjuvant trials: observations and recommendations based on individual patient data from 20 898 patients enrolled onto 18 randomized trials from the ACCENT Group. J Clin Oncol. 2007;25 (29:4569–4574. doi: 10.1200/JCO.2006.10.4323. [DOI] [PubMed] [Google Scholar]
- Sargent D, Sobrero A, Grothey A, O'Connell MJ, Buyse M, Andre T, Zheng Y, Green E, Labianca R, O'Callaghan C, Seitz JF, Francini G, Haller D, Yothers G, Goldberg R, de Gramont A. Evidence for cure by adjuvant therapy in colon cancer: observations based on individual patient data from 20 898 patients on 18 randomized trials. J Clin Oncol. 2009;27:872–877. doi: 10.1200/JCO.2008.19.5362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargent DJ, Marsoni S, Monges G, Thibodeau SN, Labianca R, Hamilton SR, French AJ, Kabat B, Foster NR, Torri V, Ribic C, Grothey A, Moore M, Zaniboni A, Seitz J-F, Sinicrope F, Gallinger S. Defective mismatch repair as a predictive marker for lack of efficacy of fluorouracil-based adjuvant therapy in colon cancer. J Clin Oncol. 2010;28:3219–3226. doi: 10.1200/JCO.2009.27.1825. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.