Skip to main content
PMC home page
Taylor & Francis Open Select logoLink to Taylor & Francis Open Select
. 2012 Aug 21;4(1):12–20. doi: 10.1080/17588928.2012.716416

Resource allocation and prioritization in auditory working memory

S Kumar 1,3, S Joseph 2,✉, B Pearson 2, S Teki 1, Z V Fox 4,5, T D Griffiths 1,3, M Husain 2
PMCID: PMC3590753  PMID: 23486527

Abstract

A prevalent view of working memory (WM) considers it to be capacity-limited, fixed to a set number of items. However, recent shared resource models of WM have challenged this “quantized” account using measures of recall precision. Although this conceptual framework can account for several features of visual WM, it remains to be established whether it also applies to auditory WM.

We used a novel pitch-matching paradigm to probe participants’ memory of pure tones in sequences of varying length, and measured their precision of recall. Crucially, this provides an index of the variability of memory representation around its true value, rather than a binary “yes/no” recall measure typically used in change detection paradigms. We show that precision of auditory WM varies with both memory load and serial order. Moreover, auditory WM resources can be prioritized to cued items, improving precision of recall, but with a concomitant cost to other items, consistent with a resource model account.

Keywords: Working memory, Precision, Auditory perception, Resource model, Memory capacity, Pitch-matching

Traditionally, tests of auditory working memory (WM) such as those that measure span for digits, letters or words-often involve remembering sequences of items (Waugh & Norman, 1965). In these measures, performance is assessed in a categorical, binary fashion: On any given trial, an item is either remembered or not. The same also applies to change detection paradigms, which have been widely used to assess auditory WM (Deutsch, 1970; Jump & Ries, 2008; Lu, Williamson, & Kaufman, 1992; Starr & Pitt, 1997). On the basis of such measures, it has been suggested that auditory WM capacity is highly limited. Previous research suggested that the capacity limit of auditory WM is fixed and equal to two, or even fewer items (Fougnie & Marois, 2011; Saults & Cowan, 2007), compared to three-four items for visual WM (Luck & Vogel, 1997).

Although categorical change detection tasks can be used to assess WM in more informative ways than simply estimating fixed capacity limits (Bays & Husain, 2008; Rouder et al., 2008; Wilken & Ma, 2004), the problem with this approach to measuring WM is that detecting a change does not imply perfect recollection of an item; nor does detection failure necessarily mean total absence of memory. Instead of using a binary measure (recall/no recall), here we employ as our memory index a response method which operates in analogue fashion, over a continuous scale. By measuring the variability of recall around the true stimulus value, and using tone sequences of variable length, this technique allows us to estimate the precision of WM under different memory loads.

A similar approach for visual WM has revealed that the resolution with which items are represented is not fixed but changes with memory load and the fidelity with which each stored item is represented is not fixed, but can in fact vary, depending upon task demands (Anderson et al., 2011; Bays & Husain, 2008; Bays, Catalao, & Husain, 2009; Fougnie, Asplund, & Marois, 2010; Wilken & Ma, 2004). For example, if an item is pre-cued such that it is more likely to be probed, it is recalled with greater precision but with a cost in memory for other, uncued items (Bays & Husain, 2008; Gorgoraptis, Catalao, Bays, & Husain, 2011).

These findings have led some authors to propose that although WM is indeed highly limited, it is not fixed in capacity to holding a set number of items (Bays & Husain, 2008; Bays et al., 2009; Fougnie et al., 2010; Wilken & Ma, 2004). Instead, WM is better considered to be a resource that can be dynamically allocated to prioritized items (Bays & Husain, 2008; Gorgoraptis et al., 2011). This conception of WM has recently been shown to account for sequential as well as simultaneously presented visual stimuli, with the drop in precision with increasing memory load captured well by a power function (Gorgoraptis et al., 2011; Zokaei, Gorgoraptis, Bahrami, Bays, & Husain, 2011). But it remains unclear whether this new perspective on WM can generalize and be extended to domains other than vision.

Here we ask whether the resource framework applies also to auditory working memory for sequences of pure tones. Surprisingly, although there have been several studies of pitch WM (Clarke et al., 1998; Clement, Demnay, & Semal, 1999; Deutsch, 1970, 1972a, 1972b, 1974; Gosselin, Jolicoeur, & Peretz, 2009; Grimault et al., 2010; Jump & Ries, 2008; Linke, Vicente-Grabovetsky, & Cusack, 2011; Lu et al., 1992; Massaro, 1970; Mukari, Umat, & Othman, 2010; Pechmann & Mohr, 1992; Ries & DiGiovanni, 2007, 2009; Ruusuvirta, Wikgren, & Astikainen, 2008; Semal & Demany, 1991; Starr & Pitt, 1997; Wickelgren, 1969; Williamsom & Stewart, 2010), no previous investigation has used a pitch-matching task to test for the precision of recall as a function of memory load.

In the present study, participants listened to sequences of pure tones and were probed on their memory of one of the tones (indicated by its serial order position in the sequence). Importantly, their response was continuous rather than binary: They adjusted a tone to match its pitch as closely as possible to their memory of the probed tone. The precision of WM for pitch at each sequential position was calculated as the inverse of the standard deviation of response error. This pitch-matching paradigm provides a measure of the variability of a memory representation around its true value.

We examined how WM precision varies with memory load (number of tones in the sequence) and investigated sources of error in listeners’ responses using a probabilistic model that has been applied to visual WM (Bays et al., 2009; Fougnie et al., 2010; Gorgoraptis et al., 2011; Zhang & Luck, 2008; Zokaei et al., 2011). We then examined whether WM resources can be flexibly allocated to a prioritized tone by cuing its task relevance, just as for visual stimuli (Bays & Husain, 2008; Gorgoraptis et al., 2011). Our results show that measuring precision as an index provides new insights on how pitch information is represented in auditory WM.

METHODS

Participants

26 listeners with normal hearing and no musical training (16 female, mean age: 23.5 years, age range: 18–31) participated in this study after providing written informed consent to procedures approved by the local ethics committee. 11 volunteers took part in Experiment 1 and 15 took part in Experiment 2.

Stimuli and apparatus

Stimuli consisted of pure tones, logarithmically sampled at random from a range of 500–1000Hz. Auditory stimuli were created at a sampling rate of 44.1 kHz in Matlab 6.5 (Mathworks Inc.) and presented using Cogent (http://www.vislab.ucl.ac.uk). Sounds were delivered binaurally through headphones (Sennheiser HD 380 pro) in a soundproof testing room. The stimulus duration was 500ms with an ISI of 500ms. The beginning and end of each trial were indicated by text appearing onscreen. There was a minimum separation of two semitones between any two tones of the sequence. The probe tone was randomly selected from the same 500–1000Hz range, and participants could make a response in the range of 250–2000Hz by adjusting a dial (PowerMate, Griffin Technology).

Design and procedure

Experiment 1: Precision of pitch memory

On each trial, subjects listened to a sequence of variable length: One, two or four tones (Figure 1A). At the end of each sequence recall of one of the tones was probed, indicated by a number on the screen, e.g., 2 for second tone. A randomly selected probe tone was then played, whose pitch had to be adjusted to match the tone probed, using the dial. Subjects were required to perform the matching task within a maximum response window of 20s. Each subject completed six blocks of 48 trials each with equal number of trials for each memory load.

Figure 1.

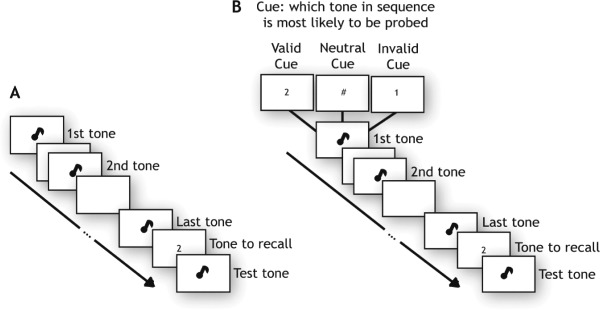
Figure 1.

Open in a new tab

Experimental paradigm.

Notes: (A) Sample sequence for Experiment 1: Subjects were presented with a sequence of tones (e.g., tone 1: 550Hz, tone 2: 710Hz,…, Last tone: 670Hz). The sequences comprised of one, two or four tones. After the test tone sequence, a number appeared on the screen, indicating the target. A randomly-chosen probe stimulus (e.g., 520Hz) was then played, which had to be adjusted to match the pitch of the target (here: Second tone with frequency of 710Hz). (B) Sample sequence for Experiment 2: Subjects were presented with a cue in the form of a number appearing on the screen, indicating which tone to prioritize. The test tone sequence was then played, consisting of three tones. Subsequently, a number appeared on the screen, indicating the target. A randomly-chosen probe stimulus was then played, which had to be adjusted to match the pitch of the target (here: Second tone).

Experiment 2: Effects of cueing on precision

To examine how WM precision varies when a tone in a sequence is made more task relevant, we used a variant of the previous experiment (Figure 1B). On each trial, before each sequence of three tones, a visual cue (presented for 2s) indicated the serial order position of the tone most likely to be probed. On 75% of trials, the cue was a number (62.5% valid, in which the cued tone was probed; 12.5%) invalid, in which one of the two uncued tones was probed). On 25% of trials, listeners saw a neutral cue (“#” sign) which indicated that all tones in the sequence were equally likely to be probed. All conditions were randomly interleaved and each subject completed six blocks of 48 trials.

DATA ANALYSIS

The deviation between the target tone frequency and the response made by the subject was calculated to obtain a measure of response error (∊, in semitones) on each trial as follows,

graphic file with name pcns4_12_ueq1.jpg

where fm is the measured or matched frequency (i.e., response given by the subject) and fa is the actual frequency.

Precision was calculated as the reciprocal of the standard deviation of response error (P = 1/σ), just as in visual experiments (e.g., Gorgoraptis et al., 2011). The precision was calculated separately for each subject, memory load, serial position (Experiment 1) and experimental condition (Experiment 2).

In order to describe the relation between precision, P, and number of items to be encoded, N, a power law of the form P ∝ NK, where K is a power law exponent, was fitted using maximum likelihood estimation. Each subject listened to varying numbers of tones in a sequence (memory loads) and each tone appeared at a different serial position (e.g., memory load 1 has serial position 1 and memory load 2 has serial positions 1 and 2 etc.). We fitted unadjusted and adjusted multilevel models to account for the fact that we had repeated measurements from individuals at different positions using different memory loads (Laird & Ware, 1982). Tests were performed in Stata 11.2 software (StataCorp LP, College Station, Texas) and all p-values < .05 were considered significant, using 2-tailed tests.

RESULTS

Effects of memory load on pitch-matching

The precision with which listeners performed the pitch-matching was assessed for different sequence lengths (memory loads; Figure 2A) and all serial positions within each sequence (Figure 2B). As the distribution of precision values across the group was positively skewed, a log transform was applied to precision values, which was then subjected to multilevel modeling (Laird & Ware, 1982). The results for the unadjusted analysis show that log-precision declined significantly with memory load (global p < .0001). The mean WM precision was 43% lower for two items compared to a single item (95% CI: 63%) to 23%). Thus there was a significant drop in precision even when the number of items to be maintained in WM was increased from one to two, i.e., below the capacity limit of two items assumed previously for auditory stimuli (Fougnie & Marois, 2011; Saults & Cowan, 2007). Precision was 73% lower for four items compared to one item (95% CI: 91% to 54%), demonstrating a further drop in memory resolution with the addition of more items.

Figure 2.

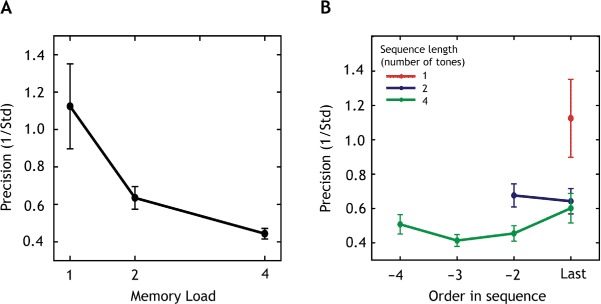
Figure 2.

Open in a new tab

Precision of recall varies with total memory load and serial order.

Notes: (A) Overall mean precision for every memory load. The plot shows how precision decreases with an increase in memory load (number of tones in the sequence). Errorbars represent one SEM. (B) Mean precision plotted against order in the sequence for different memory loads, denoted by different colors. Errorbars represent one SEM.

Secondly, there was an effect of serial position (a tone's order in a sequence) on precision of recall (global p < .0001): It was 35% lower for the first item in the sequence (95% CI: 58% to 12%) compared to trials on which the last item in the sequence was probed (Figure 2B), indicating a recency effect. Precision was 53% (95% CI: 76% to 30%) lower and 25% (95% CI: 43%) to 6%) lower for the third and second items in the sequence, respectively, compared to the last item. The unadjusted analysis shows that both factors, memory load and serial position, were significantly associated with precision.

We performed an adjusted analysis including both memory load and serial position in the model in order to assess the independent effects of both variables. In this model, the effect of memory load remained significant (p < .0001; decline in precision of 39%) for load 2 compared to load 1 (95% CI: 60% to –18%; decline in precision of 63% from load 1 to load 4 (95% CI: 85% to 42%). However, the effect of serial position on precision was no longer significant (p = .18). The interaction effect was marginally significant (p = .07), suggesting that within a given memory load serial position has an influence on precision. Importantly, pitch-matching performance was significantly better than chance for every combination of serial order and memory load (t(10) > 2.2, p < 0.05).

A power function (P α NK) was fitted to the scaled (with respect to the precision of trials with only one tone) precision values, an analysis previously used for visual experiments (Bays & Husain, 2008; Gorgoraptis et al., 2011). The function effectively quantifies the relation between the precision and the number of items (N) to be encoded. The value of K was estimated to be −0.53.

A probabilistic model to investigate the sources of error in pitch sequences

To examine sources of error contributing to performance, the distribution of responses was analyzed using a mixture model, as previously described for visual WM (Bays et al., 2009; Zhang & Luck, 2008). Here we use a model which assumes that errors in memory recall can be decomposed into two separate components: (1) Responses centered at the probed tone (target tone) and (2) random responses (guessing) unrelated to the target. The first component can be captured by a Gaussian distribution centered at the target frequency and we modeled the second component describing random guesses as a uniform distribution across the range of one octave. A third component explaining confusion errors was not added to the mixture model as no peak was found around the non-target frequencies in the raw error histograms. The model is described as:

graphic file with name pcns4_12_ueq2.jpg

where ∊ is the error computed as in equation presented in the data analysis section; N(0, σ) is the normal distribution with zero mean and standard deviation of σ; α is the probability of reporting the correct target value and (1 – α) is the proportion of all other responses, or random guessing in this model (Figure 3A). Maximum likelihood estimates (Myung, 2003) of the parameter α were obtained separately for each subject and memory load in Experiment 1 using an expectation-maximization algorithm (Figure 3B).

Figure 3.

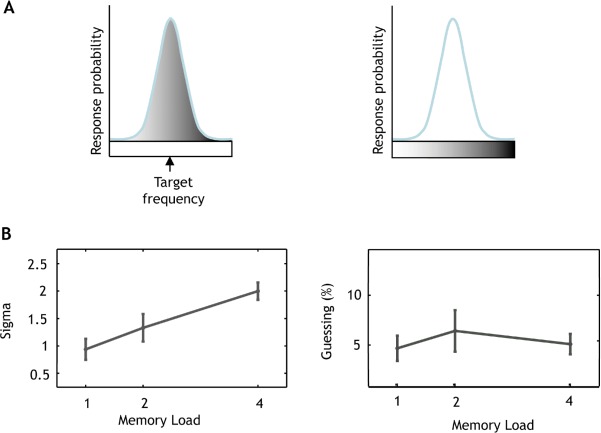
Figure 3.

Open in a new tab

Probabilistic modeling of response distribution.

Notes: (A) Error of subjects’ responses. Subject responses were decomposed into two components, illustrated by the shaded regions. The first component (left panel) captures responses directed at the target as a Gaussian normal distribution centered on the target frequency. The second component (right panel) captures random responses unrelated to any of the test tone frequencies as a uniform distribution. (B) Model components for each memory load. The variability of responses is expressed by the parameter sigma (σ) describing the standard deviation from the actual target frequency. Fitted precision increased with an increase in the number of tones in the sequence (left panel). The proportion of random responses (guessing percentage) is constant across memory loads (right panel), also showing that the proportion of responses directed at the target does not decrease with an increase in memory load. Errorbars represent one SEM.

As the number of tones in the sequence increased, responses centered on the target became increasingly variable, indicated by a significant increase in the standard deviation σ of their distribution across memory loads (global p > < .0001; increase in sigma of 39% from load 1 to load 2 (95% CI: 17% to 62%); increase in sigma of 106% from load 1 to load 4 (95% CI: 83% to 129%). But, importantly, there was no difference in the proportion of random responses (1 – α) across memory loads (global p = .59).

The decrease in precision with memory load was therefore not due simply to increased guessing, but increased variability of representation of the probed (target) pitch in memory.

Memory precision depends on task relevance

In contrast to Experiment 1 where all tones were equally likely to be probed and equally relevant to the task, we manipulated task relevance in Experiment 2: Subjects were informed which tone in the sequence was most likely to be probed by a visual cue prior to the onset of each pitch sequence (Figure 1B). This manipulation allowed us to study if the memory resource can be directed dynamically to a particular tone. A mixed effects multilevel analysis revealed a significant main effect of condition on precision (global p < .0001). Precision was 5% (95% CI: 1% to 9%) higher in the valid and 5% (95% CI: −9% to −1%) lower in the invalid condition with respect to baseline. Thus, there was a significant gain for the valid cue compared to baseline and a significant cost for the invalid cue compared to baseline.

We also investigated, whether the relative benefit of the cue is dependent on a tone's serial position (Figure 4B). The fractional difference in precision (P) between the valid or invalid target (PT) and baseline (PB) conditions for each serial position in the sequence was computed, as in Gorgoraptis et al. (2011):

graphic file with name pcns4_12_ueq3.jpg

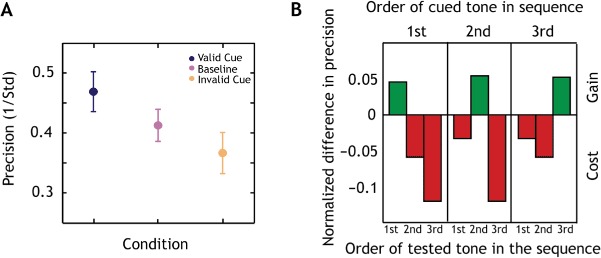
Figure 4.

Figure 4.

Open in a new tab

Prioritizing an item leads to better precision but at a cost for other items.

Notes: (A) Precision for cued tones (blue) was significantly higher than baseline (pink). In the baseline condition, where the memory resource was equally distributed across all tones in the sequence, precision was significantly higher than in the non-cued condition (orange), resulting in a significant cost for probing non-cued tones. Errorbars represent one SEM. (B) The fractional difference in precision between the trials of the cued condition and the baseline condition for each tone in the sequence. There was a gain in memory precision for the cued tones (green) and a cost for the uncued tones (red), which were both observed at all serial positions.

The relative gain (positive values in Figure 4B) was similar for the tones indicated by the valid cue at every serial position (t(14) < .31, p > .75). There was no significant difference between the relative cost (negative values) for the tones in the invalid condition at each serial position (t(14) < 1.2, p > .22). However, the relative gain was significantly different from the relative cost, when collapsing across serial positions (t(14) = 4.04, p < .001). Thus, with improved precision for a cued item there was a corresponding decrease in precision for uncued items.

GENERAL DISCUSSION

To investigate the fidelity of auditory WM representations for pitch of pure tones played in sequences, we analyzed the precision with which listeners matched the pitch of a target tone, rather than asking them whether a tone was higher/lower, or same/different from such a target. An influential model, developed on the basis of change detection measures, assumes that our working memory capacity is limited to a fixed number of items, which has been estimated in auditory change detection tasks to be two items or less (Fougnie & Marois, 2011; Saults & Cowan, 2007). Our results challenge this quantized account of WM and are better described by a shared resource model of WM.

The shared resource model predicts that the more items that are held in memory, the less precisely each item can be recalled, as has been shown for visual WM (Alvarez & Cavanagh, 2004; Bays & Husain, 2008; Bays et al., 2009; Gorgoraptis et al., 2011; Wilken & Ma, 2004; Zokaei et al., 2011). We demonstrated a clear decline in precision of WM as the number of tones in the sequence increased (Figure 2A), indicating that memory capacity is in fact highly limited. Importantly, however, even adding a single tone to a previous tone held in memory was sufficient to produce a significant drop in precision (Figure 2A).

Such a fall in WM precision cannot be explained on the basis of a fixed capacity model, which predicts optimal performance until the capacity limit is reached (Cowan, 2001; Fougnie & Marois, 2011; Luck & Vogel, 1997; Saults & Cowan, 2007). We also observed that the pitch-matching performance remained significantly above chance for the highest memory load of four items. This result cannot be explained by a fixed capacity account either, which predicts a sharp drop in performance when the fixed limit is exceeded. However, both results are consistent with a resource model in which a limited resource has to be shared between items held in WM (Bays & Husain, 2008).

The shared resource model proposes that memory representations are noisy and the amount of noise varies with information load. To measure this amount of representational “noise” for pitch memory, we used the method of adjustment in the form of a pitch-matching paradigm. Although previous attempts have been made to obtain a “continuous” response measure for pitch with the method of constant stimuli (MOS), (Ries & DiGiovanni, 2007, 2009), pitch matching by adjustment has several advantages over MOS. Instead of sampling tones from a predefined and therefore limited number of pitch values (frequencies), where the possible size of change between the test and probe stimulus defines potential stimulus properties, we aimed at obtaining a truly continuous response measure to allow precision to be better characterized.

Using the method of adjustment allowed us to sample from a wider range of stimuli than can be used with MOS, and allowed subjects to respond with any pitch within this range (and beyond). Pitch increments were sampled below the threshold for pitch discrimination. Consequently, a pitch adjustment of the probe tone can be made at any step along the continuum where a response is recorded. Measuring the pitch-matching performance using this method allows us to acquire very reliable estimates of the resolution of memory. Estimating the resolution with which information is stored, rather than assuming all-or-none storage, is crucial if we are to gain deeper insights into the mechanisms underlying WM.

A further methodological difference between the current study and previous work relates to the type of memory retrieval process tested. Pitch discrimination studies using change detection measures test for recognition memory, first introduced by Wickelgren (1969). Recognition memory can be considered to be a passive form of memory retrieval process (Cornoldi, Rigoni, Venneri, & Vecchi, 2000; Mohr & Linden, 2005). However, tasks other than change detection require the subject to reproduce or manipulate information held in WM. In our pitch-matching paradigm, subjects had to reproduce a tone from memory as accurately as possible. The memory retrieval process underpinning the reproduction of information may be different from simply recognizing whether information is present or absent.

In order to confirm that the increase in variability with memory load on this paradigm was not due to random guesses made by the subjects, we fitted a probabilistic mixture model to individual subjects’ data (Bays & Husain, 2008; Zhang & Luck, 2008). In this model, the variability due to random guesses was separated from the variability associated with noisy pitch representations in WM (responses to the target). The principles underlying the model (Figure 3) originated in several studies of visual WM (Bays et al., 2009; Fougnie et al., 2010; Gorgoraptis et al., 2011; Zhang & Luck, 2008; Zokaei et al., 2011). There was a significant increase in Gaussian variability in recall of the target tone frequency (described by the concentration parameter (σ) across memory loads, indicating that as the number of tones increases within a sequence, responses centered on the target become increasingly variable. Thus, as the amount of information held in auditory WM increases, the memory representation for each tone becomes noisier (expressed in a decrease in precision).

By contrast, the frequency of random responses was not different across memory loads, even for a number of items exceeded two (the supposed capacity limit for auditory WM). This finding is consistent with the principles of the resource model account applied previously to visual WM (Bays et al., 2009; Fougnie et al., 2010; Gorgoraptis et al., 2011; Wilken & Ma, 2004; Zokaei et al., 2011). In contrast, the fixed capacity model predicts that the addition of a further item above the maximum number of items that can be represented will produce an increase in random guesses. Our results did not show this.

Although the data was consistent with a resource model, our experiment was not designed to distinguish between different types of resource models, e.g., equal precision model and variable precision model (Mazyar et al., 2012; Van den Berg, Shin, Chou, George, & Ma, 2012). The equal precision model predicts that the resource is allocated evenly across all items, whereas the variable precision model predicts that the amount of resource an item receives varies randomly across items, trials and memory loads. Attempting to distinguish between these different types of resource models would be an important goal of future research.

Finally, WM performance depends on the ability to encode and maintain selected information most relevant to the task (Awh, Vogel, & Oh, 2006; McNab & Klingberg, 2007). Manipulating the factor of task relevance of different sequence positions by precueing, we found that precision was highest when the tone was most likely to be probed, relative to the neutral condition where each tone in the sequence was equally likely to be probed (Figure 4). Enhancing the priority of a particular tone in the sequence thereby resulted in a clear benefit in precision, but came at a cost in precision for other tones, which were less likely to be probed, analogous to results for visual WM (Bays & Husain, 2008; Gorgoraptis et al., 2011). These finding show working memory resources may be allocated flexibly according to priorities. Measuring the fidelity of auditory WM representations not only provides new insights into the dynamic nature of memory for pitch, but also shows unifying principles that exist across visual and auditory modalities.

REFERENCES

  1. Alvarez G. A., Cavanagh P. The capacity of visual short-term memory is set both by visual information load and by number of objects. Psychological Science. 2004;15:106–111. doi: 10.1111/j.0963-7214.2004.01502006.x. [DOI] [PubMed] [Google Scholar]
  2. Awh E. K., Vogel E. K., Oh S. H. Interactions between attention and working memory. Neuroscience. 2006;139:201–208. doi: 10.1016/j.neuroscience.2005.08.023. [DOI] [PubMed] [Google Scholar]
  3. Bays P. M., Catalao R. F. G., Husain M. The precision of visual working memory is set by allocation of a shared resource. Journal of Vision. 2009;9(7):1–11. doi: 10.1167/9.10.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bays P. M., Husain M. Dynamic shifts of limited working memory resources in human vision. Science. 2008;321:851–854. doi: 10.1126/science.1158023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Clarke S., Adriani M., Bellmann A. Distinct short-term memory systems for sound content and sound localization. Neuroreport. 1998;9(15):3433–3437. doi: 10.1097/00001756-199810260-00018. [DOI] [PubMed] [Google Scholar]
  6. Clément S., Demnay L., Semal C. Memory for pitch versus memory for loudness. The Journal of the Acoustical Society of America. 1999;106:2805–2811. doi: 10.1121/1.428106. [DOI] [PubMed] [Google Scholar]
  7. Cornoldi C, Rigoni E, Venneri A., Vecchi T. Passive and active processes in visuo-spatial memory: Double dissociation in developmental learning disabilities. Brain and Cognition. 2000;43:117–120. [PubMed] [Google Scholar]
  8. Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. The Behavioral and Brain Sciences. 2001;24:87–114. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
  9. Deutsch D. Tones and numbers: Specificity of interference in immediate memory. Science. 1970;168:1604–1605. doi: 10.1126/science.168.3939.1604. [DOI] [PubMed] [Google Scholar]
  10. Deutsch D. Effect of repetition of standard and comparison tones on recognition memory for pitch. Journal of Experimental Psychology. 1972a;93:156–162. doi: 10.1037/h0032496. [DOI] [PubMed] [Google Scholar]
  11. Deutsch D. Mapping of interactions in the pitch memory store. Science. 1972b;175:1020–1022. doi: 10.1126/science.175.4025.1020. [DOI] [PubMed] [Google Scholar]
  12. Deutsch D. Generality of interference by tonal stimuli in recognition memory: For pitch. Quarterly Journal of Experimental Psychology. 1974;26:229–234. doi: 10.1080/14640747408400408. [DOI] [PubMed] [Google Scholar]
  13. Fougnie D., Asplund C. L., Marois R. What are the units of storage in visual working memory? Journal of Vision. 2010;10(12):27, 1–17. doi: 10.1167/10.12.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fougnie D., Marois C. L. What limits working memory capacity? Evidence for modality-specific sources to the simultaneous storage of visual and auditory arrays. Journal of Experimental Psychology: Learning, Memory and Cognition. 2011;37:1329–1341. doi: 10.1037/a0024834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gorgoraptis N., Catalao R. F. G., Bays P. M., Husain M. Dynamic updating of working memory resources for visual objects. The Journal of Neuroscience. 2011;31:8502–8511. doi: 10.1523/JNEUROSCI.0208-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gosselin N., Jolicoeur P., Peretz I. Impaired memory for pitch in congenital amusia. Annals of the New York Academy of Sciences. 2009;1169:270–272. doi: 10.1111/j.1749-6632.2009.04762.x. [DOI] [PubMed] [Google Scholar]
  17. Grimault S., Lefebvre C, Vachon F., Peretz I., Zatorre R., Robitaille N., lolicoeur P. Load-dependent brain activity related to acoustic short-term memory for pitch. The Neurosciences and Music III: Disorders and Plasticity. 2010;1169:273–277. doi: 10.1111/j.1749-6632.2009.04844.x. [DOI] [PubMed] [Google Scholar]
  18. Jump R. L., Ries D. T. Effect of interaural level and phase cues on intervening interference in auditory working memory for loudness. Hearing Research. 2008;240:112–115. doi: 10.1016/j.heares.2008.04.004. [DOI] [PubMed] [Google Scholar]
  19. Laird N. M., Ware I. H. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
  20. Linke A. C, Vicente-Grabovetsky A., Cusack R. Stimulus-specific suppression preserves information in auditory short-term memory. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:12961–12966. doi: 10.1073/pnas.1102118108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lu Z. L., Williamson S. J., Kaufman L. Behavioral lifetime of human auditory sensory memory predicted by physiological measures. Science. 1992;258:1668–1670. doi: 10.1126/science.1455246. [DOI] [PubMed] [Google Scholar]
  22. Luck S. J., Vogel E. K. The capacity of visual working memory for features and conjunctions. Nature. 1997;390:219–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
  23. Massaro D. W. Retroactive interference in short-term recognition memory for pitch. Journal of Experimental Psychology. 1970;83:32–39. doi: 10.1037/h0028566. [DOI] [PubMed] [Google Scholar]
  24. Matlab. (6.5) [Computer software] Natick, MA: Mathworks Inc.; [Google Scholar]
  25. Mazyar H., Van den Berg R., Ma W. J. Does precision decrease with set size? Journal of Vision. 2012;12(10):1–16. doi: 10.1167/12.6.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. McNab F., Klingberg T. Prefrontal cortex and basal ganglia control access to working memory. Nature Neuroscience. 2008;11:103–107. doi: 10.1038/nn2024. [DOI] [PubMed] [Google Scholar]
  27. Mohr H. M., Linden D. E. J. Separation of the systems for color and spatial manipulation in working memory revealed by a dual-task procedure. Journal of Cognitive Neuroscience. 2005;17:355–366. doi: 10.1162/0898929053124929. [DOI] [PubMed] [Google Scholar]
  28. Mukari S. Z., Umat C, Othman N. I. Effects of age and working memory capacity on pitch pattern sequence test and dichotic listening. Audiology & Neuro-Otology. 2010;15:303–310. doi: 10.1159/000283007. [DOI] [PubMed] [Google Scholar]
  29. Myung I. J. Tutorial on maximum likelihood estimation. Journal of Mathematical Psychology. 2003;47:90–100. [Google Scholar]
  30. Pechmann T, Mohr G. Interference in memory for tonal pitch: Implications for a working-memory model. Memory & Cognition. 1992;20(3):314–320. doi: 10.3758/bf03199668. [DOI] [PubMed] [Google Scholar]
  31. Ries T D., DiGiovanni J. J. Release from interference in auditory working memory for pitch. Hearing Research. 2007;230:64–72. doi: 10.1016/j.heares.2007.04.003. [DOI] [PubMed] [Google Scholar]
  32. Ries T. D., DiGiovanni J. J. Effects of recurrent tonal information on auditory working memory for pitch. Hearing Research. 2009;255:14–21. doi: 10.1016/j.heares.2009.05.002. [DOI] [PubMed] [Google Scholar]
  33. Rouder J. N., Morey R. D., Cowan N., Zwilling C. E., Morey C. C, Pratte M. S. An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences. 2008;105:5975–5979. doi: 10.1073/pnas.0711295105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Ruusuvirta T, Wikgren J., Astikainen P. Proactive interference in a two-tone pitch-comparison task without additional interfering tones. Psychological Research. 2008;72:74–78. doi: 10.1007/s00426-006-0094-y. [DOI] [PubMed] [Google Scholar]
  35. Saults J. S., Cowan N. A central capacity limit to the simultaneous storage of visual and auditory arrays in working memory. Journal of Experimental Psychology General. 2007;136:663–684. doi: 10.1037/0096-3445.136.4.663. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Semal C, Demany L. Dissociation of pitch from timbre in auditory short-term memory. The Journal of the Acoustical Society of America. 1991;89:2404–2410. doi: 10.1121/1.400928. [DOI] [PubMed] [Google Scholar]
  37. Starr G. E., Pitt M. A. Interference effects in short-term memory for timbre. The Journal of the Acoustical Society of America. 1997;102:486–194. doi: 10.1121/1.419722. [DOI] [PubMed] [Google Scholar]
  38. Stata. (11.2) [Computer software] College Station, TX: StataCorp LP; [Google Scholar]
  39. Van den Berg R., Shin H., Chou W. C, George R., Ma W. J. Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences. 2012;109:8780–8785. doi: 10.1073/pnas.1117465109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Waugh N. C, Norman D. A. Primary memory. Psychological Review. 1965;72:89–104. doi: 10.1037/h0021797. [DOI] [PubMed] [Google Scholar]
  41. Wickelgren W. A. Auditory or articulatory coding in verbal short-term memory. Psychological Review. 1969;76:232–235. doi: 10.1037/h0027397. [DOI] [PubMed] [Google Scholar]
  42. Wilken P., Ma W. J. A detection theory account of change detection. Journal of Vision. 2004;4:1120–1135. doi: 10.1167/4.12.11. [DOI] [PubMed] [Google Scholar]
  43. Williamsom V J., Stewart L. Memory for pitch in congenital amusia: Beyond a fine-grained pitch discrimination problem. Memory. 2010;18:657–669. doi: 10.1080/09658211.2010.501339. [DOI] [PubMed] [Google Scholar]
  44. Zhang W., Luck S. J. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453:233–235. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zokaei N., Gorgoraptis N., Bahrami B., Bays P. M., Husain M. Precision of working memory for visual motion sequences and transparent motion surfaces. Journal of Vision. 2011;11(14):2, 1–18. doi: 10.1167/11.14.2. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Cognitive Neuroscience are provided here courtesy of Taylor & Francis

RESOURCES