The Spatiotemporal Program of Replication in the Genome of Lachancea kluyveri

Abstract

We generated a genome-wide replication profile in the genome of Lachancea kluyveri and assessed the relationship between replication and base composition. This species diverged from Saccharomyces cerevisiae before the ancestral whole genome duplication. The genome comprises eight chromosomes among which a chromosomal arm of 1 Mb has a G + C-content much higher than the rest of the genome. We identified 252 active replication origins in L. kluyveri and found considerable divergence in origin location with S. cerevisiae and with Lachancea waltii. Although some global features of S. cerevisiae replication are conserved: Centromeres replicate early, whereas telomeres replicate late, we found that replication origins both in L. kluyveri and L. waltii do not behave as evolutionary fragile sites. In L. kluyveri, replication timing along chromosomes alternates between regions of early and late activating origins, except for the 1 Mb GC-rich chromosomal arm. This chromosomal arm contains an origin consensus motif different from other chromosomes and is replicated early during S-phase. We showed that precocious replication results from the specific absence of late firing origins in this chromosomal arm. In addition, we found a correlation between GC-content and distance from replication origins as well as a lack of replication-associated compositional skew between leading and lagging strands specifically in this GC-rich chromosomal arm. These findings suggest that the unusual base composition in the genome of L. kluyveri could be linked to replication.

Introduction

The budding yeast Lachancea kluyveri (formerly designated as Saccharomyces kluyveri [Kurtzman 2003]), belongs to a clade of protoploid yeast species, that is, those that diverged from the S. cerevisiae lineage before the ancestral whole genome duplication (WGD) (Wolfe and Shields 1997; Souciet et al. 2009). The genome architecture is therefore different from that of S. cerevisiae with a set of 8 chromosomes (as opposed to 16), spanning 11.3 Mb (Génolevures Consortium et al. 2009). In addition, unlike Candida species, L. kluyveri undergoes complete sexual cycles. Cells from opposite mating types can mate and produce stable diploids. Lachancea kluyveri is a pure heterothallic species because it has lost the two silent cassettes, HML and HMR (Payen et al. 2009). Haploid cells are also stably propagated because of the lack the HO gene (Butler et al. 2004) and a-cells can be synchronized in the G1 phase of the cell cycle by treatment with alpha factor from S. cerevisiae. All these practical as well as fundamental characteristics make L. kluyveri a good model to study the biology of protoploid yeast genomes.

The most intriguing characteristic of the L. kluyveri genome is perhaps its unusual nucleotide composition. A region of 1 Mb, corresponding to the left arm of chromosome C (abbreviated here as Sakl0C-left) contains on average 53% G + C bases, whereas the rest of the genome averages 40% (Souciet et al. 2009). Regional variations in GC content along chromosomes have been reported in S. cerevisiae (Sharp and Lloyd 1993; Dujon 1996) with notably a negative correlation between chromosome length and GC content (Bradnam et al. 1999). However, the intensity of these variations and their span are far more limited than the large-scale compositional heterogeneity characterized in the L. kluyveri genome. Substantial GC-content variations were initially found in the genomes of mammals and birds and referred to as isochores (Bernardi et al. 1985). Isochores represent mosaics of alternating low- and high-GC content regions belonging to five compositional families, L1, L2, H1, H2, and H3, whose corresponding ranges of GC contents vary between an average of 39% for the L1 fraction up to 53% for the H3 family. These particular regions generally have a higher density of genes and a higher level of gene expression than the rest of the genome (see Bernardi 2007, for a review). By contrast, in L. kluyveri, the gene density in the GC-rich chromosomal arm is similar to that in the rest of the genome. The origin of this compositional heterogeneity is not understood. Phylogenetic analyses as well as synteny conservation studies have revealed that this chromosomal arm does not originate from horizontal transfer from a distantly related species (Payen et al. 2009). Two mutually exclusive hypotheses about its origin have been proposed: L. kluyveri could be a hybrid between a GC-rich (53%) and a GC-poor (40%) ancestor, both belonging to the Lachancea clade or the compositional heterogeneity of Sakl0C-left could result from specific mutational properties applying to this chromosomal arm.

In the human genome, GC-rich regions correspond to early-replicating segments and a transition from high- to low-GC content is evident for early- to late-replicating regions (Woodfine et al. 2004; Karnani et al. 2007). These early replicating segments have all the features of euchromatin: high gene density, high expression levels, and presence of activate chromatin marks. A positive correlation between early replication and gene transcription was also found in Drosophila cells (MacAlpine et al. 2004). Therefore, the factors that control the timing of replication could be functionally linked to the genetic composition and the chromatin environment of the DNA rather than to the nucleotide composition of the chromosome segments per se. The association between high GC-content and early timing of replication is probably an indirect consequence of the GC-biased nucleotide composition of isochores in the human genome. In L. kluyveri, the situation is different given that the high GC-content of Sakl0C-left is not associated with high gene density (Payen et al. 2009) or high expression level (Tsankov et al. 2010). Therefore, the genome of L. kluyveri offers a unique possibility to decipher the links between nucleotide composition and replication timing without these confounding factors.

Previous works already addressed the study of the replication program in L. kluyveri. A recent functional assay based on plasmid maintenance identified a set of 84 autonomously replicating sequences (ARS) in the genome of L. kluyveri (Liachko et al. 2011). Here, we provide a list of 252 chromosomally active replication origins and found a highly significant association between these origins and the set of previously published ARS. An initial survey of replication timing that was based on microarray experiments for two time points in late S-phase, suggested that the GC-rich chromosomal arm would be replicated late during S-phase (Payen et al. 2009). In this work, we describe the complete temporal program of replication in L. kluyveri and show that, contrarily to previous findings, this chromosomal arm is replicated early during S-phase. We show that the GC-rich chromosomal arm, Sakl0C-left has several unique replication properties not shared by the other chromosomes. We also provide evidence supporting the hypothesis that high GC-content in Sakl0C-left could result from a replication-associated mutational force that would specifically apply to this chromosomal arm.

Materials and Methods

Time-Course Experiments

For microarray experiments, haploid cells of L. kluyveri obtained by random sporulation from the CBS3082 strain (Payen et al. 2009) were grown to exponential phase in YPD medium (1% peptone, 1% Yeast extract, and 2% glucose) at 30 °C with shaking and arrested in G1 by treatment with alpha factor from S. cerevisiae at a final concentration of 7 µg/ml, for 2 h. G1-arrested cells were precipitated, washed with water, and re-suspended in proteinase K-containing YPD at a final concentration of 50 µg/ml. Cells were synchronously released into S-phase at 23 °C in YPD medium and one sample was taken every 5 min during 70 min. Alternatively, cells were released in YPD medium with hydroxyurea (HU) at a final concentration of 50 mM, grown at 23 °C and one sample was taken every 15 min, during 210 min.

For sequencing experiments, G1 cells were isolated from an asynchronous population by centrifugal elutriation (Beckman: JE-5.0 Elutriator Rotor and Avanti J-26 XP centrifuge). Centrifugal elutriation is a technique for the separation of cells by velocity sedimentation (Pretlow and Pretlow 1979). Asynchronous cells from an exponential culture in YPD were separated in different fractions. The fraction containing more than 95% of G1 cells was washed in phosphate-buffered saline and synchronously released into S-phase at 23 °C in YPD medium. One sample was taken every 10 min during 150 min.

Flow Cytometry Analysis

The progression through the cell cycle was followed by flow cytometry. Cells were fixed overnight in cold ethanol (70% final), washed, and re-suspended at 1.2 × 10⁷ cells/ml in sodium citrate (50 mM, pH 7). They were treated with RNAse A at a final concentration of 1 mg/ml, for 1 h. Cells were stained with propidium iodide at the final concentration of 40 µg/ml and analysed with FACSCalibur (BD Biosciences). Results were extracted with WinMDI (http://facs.scripps.edu, last accessed February 6, 2013). For each sample, the mean DNA content (N) was calculated as follow:

where G₁ and G₂ represents the percentage of cells in the population corresponding respectively to the two phases. N is therefore comprised between 1 and 2.

Microarrays Experiments

Genomic DNA was extracted using the genomic-tip 20/G isolation kit (Qiagen). Two micrograms of DNA from G1-arrested cells and samples was, respectively, labeled with Cy3 or Cy5 fluorescent dye (GE Healthcare – CyX-dCTP), using the Bioprime DNA labeling Kit (Invitrogen) and following the manufacturers’ protocol. 500 ng of G1 and sample-labeled DNA was competitively hybridized on 2×105k Agilent custom microarrays. Hybridization (40 h) and washing were performed using Agilent Oligonucleotide Array-Based CGH protocol. Microarrays were scanned using Axon 4000B scanner (5 µm resolution, PMT 700–500) and data were extracted with Genepix v6.0.1.00 software. All microarray data are available from the GEO database with the accession number GSE37244.

Generation of Replication Timing Profiles from Microarrays

Replication profiles were obtained by monitoring the change of DNA copy number from one to two during S-phase (Yabuki et al. 2002). Changes in DNA copy number were measured by calculating the intensity ratios between S-phase samples taken every 5 min and the G1-arrested cells. For each time point, the fluorescent signals for each probe (F635 and F532) were normalized using the median fluorescent signals of the corresponding microarray and scaled using the mean DNA content N for the corresponding time point. Scaled intensity ratios were calculated as follows:

where N_j is the mean DNA content calculated for time point j, F635_i,j, and F532_i,j are the fluorescent signals due respectively to the sample and the reference, measured for probe i at time point j and MeF635_j and MeF532_j are the medians of the fluorescent signal measured for the time point j. For each probe, processed ratios were calculated from the scaled ratios by adjusting the lowest and the highest ratio values between 1 and 2, respectively, using the following formula:

where is the scaled intensity ratio for probe i at time point j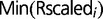, and and 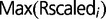are the minimum and maximum value, respectively, for all scaled intensity ratios for probe i. All processed ratios for the three replicate experiments are provided in supplementary table S0, Supplementary Material online, and deposited, along with raw microarray data, in the GEO database (accession number GSE37244).

T_rep were defined for each probe as the time where processed ratios equal 1.5. Replication timing profiles were obtained by plotting the T_rep as a function of the chromosome coordinates and by fitting a regression curve to the data (Loess) using a span of 30 kb. The final replication timing profile is defined, for each chromosome, as the mean of the three Loess curves calculated for the three independent time-course experiments. The coordinates of replication origins were defined as peaks in the replication timing profile where the sign of the slope switches from negative to positive values and is maintained on both side of the peak over at least 2 kb. The detection was performed separately on the three replicates and peaks were considered as origin when they were detected in at least two of the three experiments.

For the HU experiment, intensity ratios were normalized by chromosome with median values. For each time point, a Loess regression curve was calculated from these ratios as a function of chromosome coordinates, using a span of 30 kb. For two time points (T₀ = 0 min after release and T₃ = 45 min after release), a baseline calculated from local minima on a 30 kb sliding window was subtracted from the profiles. The noise threshold was defined by chromosome as the highest ratio value from T₀. All peaks from T₃ that exceed the noise threshold were considered as active origins in the presence of HU. All calculations were made using R basic statistical function and homemade R script (http://cran.r-project.org/, last accessed February 6, 2013).

Calculation of Mean Fraction of Replicated Probes, Discrete, and Normalized Slopes at Origins from Microarrays

The fraction of replicated probes at a given time point was estimated from data on the average DNA content x, as x – 1. Indeed, 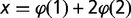, where 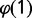is the fraction of probes with copy number equal to 1 and 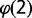is the fraction of probes with copy number equal to 2, which needs to be estimated. As 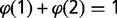, one has this result. This procedure yielded a fraction of replicated probes 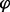(for each locus and time point), which was averaged over a sliding window of 10 kb. The initial discrete slope was defined as (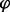_i (30 min) − 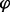_i (25 min))/5 min and plotted as a function of genome coordinate to perform origin detection under minimal interference. For the estimate of fork velocity, we measured the decay of the discrete slope with the distance d of a sliding window from an origin. To compare different origins, we divided the discrete slopes by their values at d = 0.

Noise Threshold

We used the statistics of negative slope data to establish the error threshold (as twice the standard deviation of negative-slope data, fig. 4). Negative slope corresponds to a decreasing average fraction of replicated probes between two consecutive time points in the microarray data, hence witnessing experimental errors in evaluating the copy number variation with time.

Fig. 4.—

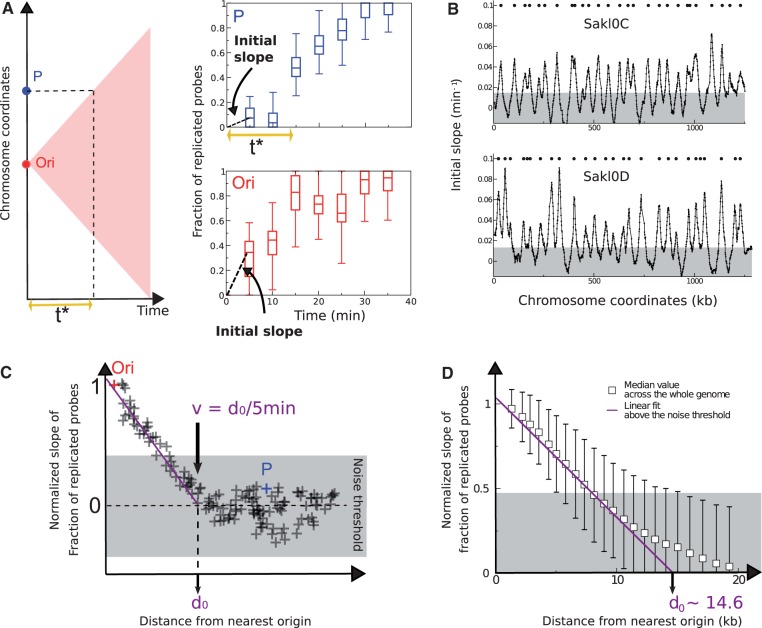
Inference of replication origins and fork velocity from the initial slope method. (A) Illustration of the replication delay t* in the first 5 min of the S-phase. In case the replication origin (Ori in red) initiates exactly at the start of the S phase (t = 0 min), the replication forks move in time following the edges of the pink triangle (left panel) and reach locus P at time t* ∼ 15 min (top right panel). Initial slope (estimated at t = 5 min) at locus P is smaller than the one at the Ori locus (compare top and bottom right panels). The box plots of the fraction of replicated probes versus time rise immediately at Ori (the data refer to the origin with coordinate 828,007 on chromosome Sakl0H), whereas they stay close to zero for the P locus (located at coordinate 858,544 bp on chromosome Sakl0H) for the two first time points (5 and 10 min). (B) Discrete slope plotted as a function of genome coordinates. Data are averaged on a sliding window of 10 with 1 kb step. The peaks correspond to origins and are a proxy for their firing rate (the unit of the y axis is an inverse time in minutes). The gray-shaded area is the noise threshold, estimated as twice the standard deviation of negative-slope data (see Materials and Methods). (C) Method of estimation of the maximum distance d₀ covered by replication forks in the first 5 min of the S-phase. The initial slope of the fraction of replicated probes decreases moving away from the origin (Ori). The distance where the slope becomes null (d₀=v/5 min) is obtained extrapolating linearly the trend above the noise threshold. The initial slope of this plot can be used to estimate fork velocity. At the point where the initial slopes drops to zero, the velocity is obtained dividing the distance from the origin (d₀) by the time taken by the replication front to reach that point (5 min in our case). (D) Evaluation of the fork velocity from genome-wide data. The genome-wide fork velocity is estimated from normalized discrete slope of the fraction of replicated probes as a function of time. The slope is divided by the slope at each origin and plotted as a function of distance from the origins, for all loci and origins. The distance d₀=v/5 min where the slope becomes null is obtained extrapolating linearly the trend above the noise threshold, which gives the estimate d₀ ∼ 14.6 kb and v ∼ 2.9 kb/min.

Deep Sequencing Experiments

Genomic DNAs from six samples covering S-phase (from 80 to 150 min) were extracted using the genomic-tip 20/G isolation kit (Qiagen). One microgram of DNA from each sample was sequenced using the Illumina technology (“GAIIx” device and “36 cycles Sequencing Kit v5” [FC-104-5001]). The six libraries were multiplexed before polymerase chain reaction amplification to avoid coverage heterogeneity between samples and sequenced in two channels producing 10 M reads (single-end) per sample. Fastq files were generated using CASAVA-1.8.2. Sequencing data are available from the SRA database (NCBI) under the accession number SRA059086. Sequence reads were mapped on the L. kluyveri CBS3082 reference genome (Souciet et al. 2009), using BWA 0.5.9, allowing no mismatch and no gap. Mapped reads were subsequently filtered to keep only unique match and high quality mapping scores (MAPQ > 37, i.e., base call accuracy > 99.98%).

Generation of Replication Timing Profiles from Sequencing Data

Changes in DNA copy number were measured by calculating the ratios of the number of reads between S-phase samples taken every 10 min and the first S-phase sample which correspond to G1-arrested cells. For each time point, the number of reads for every 500 bp window along the genome was calculated using the AMADEA Biopack platform developed by ISoft (http://www.isoft.fr/bio/biopack_en.htm, last accessed February 6, 2013). These ratios were processed as were processed the microarray intensity ratios (discussed earlier). All processed ratio from sequencing data are provided in supplementary table S1, Supplementary Material online. T_rep were defined for each 500 bp window as the time where processed ratios equal 1.5. Replication timing profiles were obtained by plotting the T_rep as a function of the chromosome coordinates and by fitting a Loess regression curve to the data, using a span of 60 kb.

Determination of the ARS Consensus Motifs

Sequences from the 84 ARS of L. kluyveri (Liachko et al. 2011) were filtered for full length and partial copies of LTRs (Long Terminal Repeats) using BLAST (E value < 0.001, match length > 25 nucleotides), for microsatellites using Tandem Repeat Finder v4.0.4 (Benson 1999) (match score, 2; mismatch penalty, 5; indel penalty, 5; match probability, 80/100; indel probability, 10/100; and minimal score, 20) and for coding sequences. This resulted in a list of 79 intergenic ARS sequences that was submitted to the Gibbs sampling motif finder GIMSAN (Ng and Keich 2008) with -oops mode (at least one occurrence per sequence) and Markov model of order 5 to identify ARS consensus motif (ACS) from 9 to 18 nucleotide long. Genome-wide intergenic sequences filtered for LTR were used as sequence background. Evaluation of the differences between two motif logos (http://weblogo.berkeley.edu/, last accessed February 6, 2013) was performed with Two Sample Logo (Vacic et al. 2006). Two motifs were considered to be similar if they were shifted at most by one position and if they differed in base composition at less than 10% of the positions (P value of difference ≤ 0.05). Perl scripts are provided on request.

GC-Content and Compositional Skews

All calculations were performed with the use of the AMADEA Biopack platform. To calculate compositional skews between the leading and the lagging strands, we selected a set of 207 replication origins corresponding to clear peaks flanked on both sides by clear valleys on the replication timing profile. Normalized positions along the 207 replicons were obtained by dividing the size of each replicon into 50 equal bins of 2%. The position of the origin (Ori) was set at 50% and the position of the flanking termination regions (Ter) were set at 0% and 100% in each replicon. For each 2% section, we pooled the data from all 207 replicons and compositional skews were calculated at third codon positions as S_GC3 = (G − C)/(G + C), S_TA3 = (T − A)/(T + A) and S₃ = S_GC3 + S_TA3.

Conservation of Origins and Association with Synteny Breakpoints

Pairs of genes between the genomes of L. kluyveri and S. cerevisiae were considered as orthologs if their products were reciprocal best-hits with at least 40% similarity in sequence and their sequences were less than 30% different in length as previously described (Drillon et al. 2011). Synteny blocks were defined as series of neighboring pairs of orthologs separated by less than three intervening orthologs. These blocks are then locally completed by adding neighboring syntenic homologs that are not reciprocal best hits (>30% similarity over 50% of the smallest protein). To look for origin conservation, we considered regions of 8 kb surrounding the mean origin positions because in L. kluyveri 95% of origins were mapped at less than 7,600 nucleotides between the 3 replicate experiments. To determine whether an origin in one genome was conserved in the other genome, we tested whether the origin-containing regions of 8 kb (4 kb on each side of the peak coordinates) in the first genome was conserved in synteny with the second genome and if an origin was also present in the corresponding region of conserved synteny in the second genome. For each of the three pairwise comparisons between the genomes of L. kluyveri, L. waltii and S. cerevisiae, origin conservation was sought in both possible directions (e.g., we tested the conservation of the L. kluyveri origins in the genome of S. cerevisiae and also the conservation of the S. cerevisiae origins in the genome of L. kluyveri) using the same parameters. The origins were defined as conserved only when they were found in both reciprocal comparisons in each pairwise combination between the three species. To test for possible association between replication origins and synteny breakpoints, we checked if at least one of the genes in the 8 kb region corresponded to an extremity of a synteny block between the two compared genomes. Perl scripts and AMADEA Biopack workflows are provided on request.

Results

The Replication Timing Profile of the L. kluyveri Genome

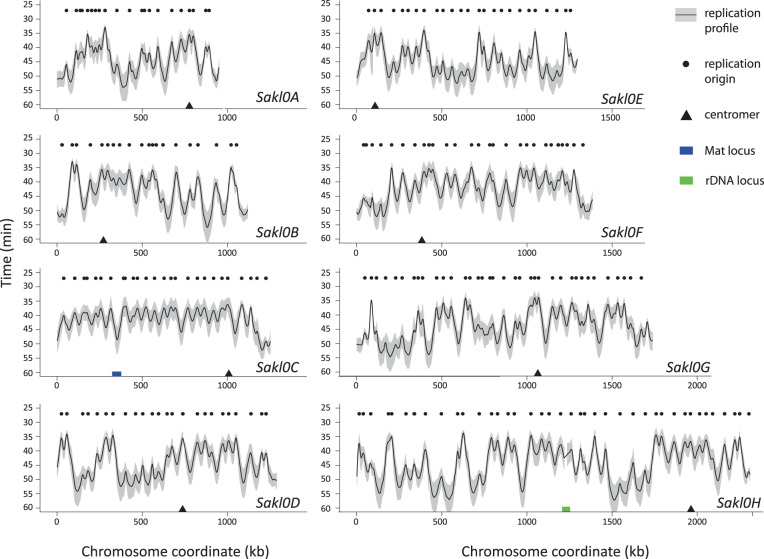
Replication timing profiles were generated for three independent biological replicates of the whole time-course. Timing profiles were obtained by monitoring the change of DNA copy number from one to two during S-phase as described in (Yabuki et al. 2002). Changes in DNA copy number were measured using microarrays by calculating the intensity ratios between S-phase samples taken every 5 min and the G1-arrested cells. For each time point, the fluorescent signals for each probe were normalized using the median fluorescent signals of the corresponding microarray and scaled using the mean DNA content estimated by flow cytometry for the corresponding time point (see Materials and Methods and supplementary fig. S0, Supplementary Material online). For each probe, processed ratios were calculated from the scaled ratios by adjusting the lowest and the highest ratio values between 1 and 2, respectively (see Materials and Methods). Plotting processed ratio as a function of chromosome coordinates allows visualizing replication dynamics for each chromosome (supplementary fig. S1, Supplementary Material online). For each probe, the calculation of the point in time when the sequence is replicated in half the population, termed T_rep (Raghuraman et al. 2001) was derived from processed ratio (see Materials and Methods). For the three replicate experiments, T_rep values were plotted as a function of chromosome coordinates and a regression curve was fitted to each data set (Loess using a span of 30 kb). Pairwise comparisons between these three fitted curves correlated very well for all chromosomes (Spearman correlation coefficients between 0.94 and 0.96, supplementary fig. S2, Supplementary Material online). To have a single reference measurement, fitted values (inferred from the Loess regression curve) were averaged for each position on the microarray. These average values were plotted as function of chromosome coordinates and the resulting curve corresponds to the replication timing profile presented in figure 1. Average replication times, noted Trep_avg in the rest of the manuscript, are deduced from this unique genome-wide replication timing curve.

Fig. 1.—

Replication timing profile of the Lachancea kluyveri genome. Black curves and grey intervals along all chromosomes represent mean replication times and standard deviation between three biological replicates, respectively. The black dots show the location of 220 replication origins detected as peaks on this replication profile. Chromosomes are drawn to scale.

We see that all eight centromeres replicate early in S-phase (on average between 34 min for the earliest [Sakl0G] and 39 min for the latest [Sakl0F]), whereas telomeres tend to replicate later in S-phase (on average between 44 min [Sakl0E-right] and 51 min [Sakl0A-left]), as in S. cerevisiae (Raghuraman et al. 2001), L. waltii (Di Rienzi et al. 2012), and C. albicans (Koren et al. 2010). The timing profile in figure 1 shows that for all chromosomes except Sakl0C-left, replication profiles alternate between large regions mostly replicated early and large regions mostly replicated late during S-phase as was already described in S. cerevisiae (McCune et al. 2008), although a thorough mathematical analysis of similar data sets concluded that there is no evidence for clustering of origins with similar activation time in S. cerevisiae (Yang et al. 2010).

Precocious Replication of the GC-Rich Chromosomal Arm during S-Phase

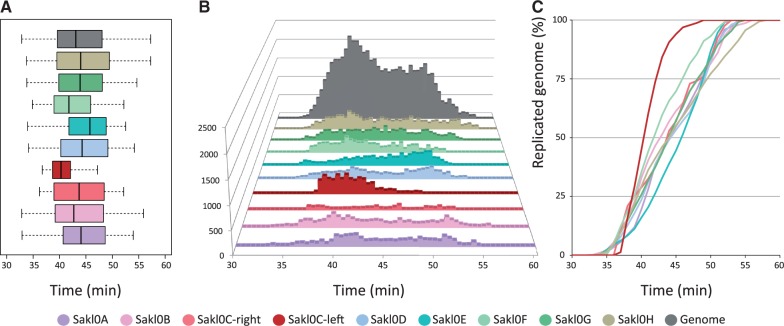
For Sakl0C-left, Trep_avg are distributed over a narrower range than for any other chromosomes suggesting that replication would be on average more homogeneous in the GC-rich chromosomal arm than in the rest of the genome (fig. 2A). No other region of 1 Mb in the genome presents such a narrow distribution of Trep_avg. At the genome scale, the distribution of Trep_avg is bimodal, with the two peaks approximately centered on 40 and 50 min (fig. 2B), indicating the presence of two regimes in the temporal program of replication in L. kluyveri. Interestingly, the equivalent distribution of replication times in S. cerevisiae is unimodal (based on the data published in Raghuraman et al. 2001). In L. kluyveri, all chromosomes (including Sakl0C-right), but Sakl0C-left, present a distribution covering the two regimes. Sakl0C-left presents a unimodal distribution with Trep_avg almost exclusively centered on the 40-min peak (fig. 2B). The few Trep_avg values that protrude onto the 50-min peak correspond to the region of the Mat locus located approximately at coordinates 350,000 on Sakl0C-left. This region corresponds to the latest replicating region on this chromosomal arm (fig. 1). Comparative replication kinetics between chromosomes reveals that replication of Sakl0C-left is completed significantly earlier than that of all the other chromosomes (fig. 2C). The same trend is already visible from primary data (supplementary fig. S1, Supplementary Material online).

Fig. 2.—

Distribution of Trep_avg values by chromosome (considering separately the left and right arms of chromosome Sakl0C). The same color code applies for the three subparts. (A) Box plot representation of the distribution of Trep_avg values chromosome by chromosome. The span of the box represents the interquartile range (50% of the data between the first and the third quartiles). The black bar within the box represents the median of the distribution and the whiskers show the span of data corresponding to 1.5 times the IQR. (B) Distribution of Trep_avg by chromosome and for the all genome. The y axis represents the number of probes that replicate at a given Trep_avg. (C) Replication kinetics showing the proportion of replicated chromosome as a function of time during S-phase. The y axis represents the cumulated number of Trep_avg values normalized at 100% for each chromosome.

This result contradicts a previous finding that suggested that the replication of Sakl0C-left would be completed later than for all the other chromosomes (Payen et al. 2009). However, this initial finding only relied on a single time-course experiment composed of only two time points in late S-phase. Here, we present a much more extensive data set composed of three independent complete time-course experiments, each composed of eight time points covering the whole kinetics of the S-phase. The initial interpretation of a replication delay for Sakl0C-left relied on a relative under-representation of Sakl0C-left probes on microarray. In our experiments, we found no evidence for such under-representation of Sakl0C-left. There is no straightforward explanation for this difference. However, the high G + C composition of this region may render Sakl0C-left as more sensitive to incomplete denaturation. A differential level of DNA denaturation between the S-phase and G1 samples before the labeling steps could have eventually resulted in a relative under-representation of Sakl0C-left probes on microarray

To conclusively show that Sakl0C-left is replicated before the majority of the genome, we undertook several additional analyses and experiments. First, to make sure that the apparent precocious replication of Sakl0C-left did not result from a bias linked to using Trep_avg as a proxy for the replication timing, we tested whether this trend was detectable directly from the microarray intensity ratios. Processed intensity ratios (see Materials and Methods) were gathered from the three replicate experiments and an overall mean was calculated for each probe of the microarray and for each time point. The resulting “mean fraction of replicated probes” 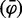was plotted chromosome by chromosome as a function of the time (fig. 3A and supplementary fig. S3, Supplementary Material online). From these plots, it can be seen in each of the three replicate experiments that Sakl0C-left replicates earlier than the other chromosomes, specifically in the time points between 40 and 50 min after cells were released into S phase. We built the table M_i,j(T ) whose elements are defined by the difference in the median fraction of replicated probes between chromosomes i and j at time T, normalized by the sum of their standard deviations.

Fig. 3.—

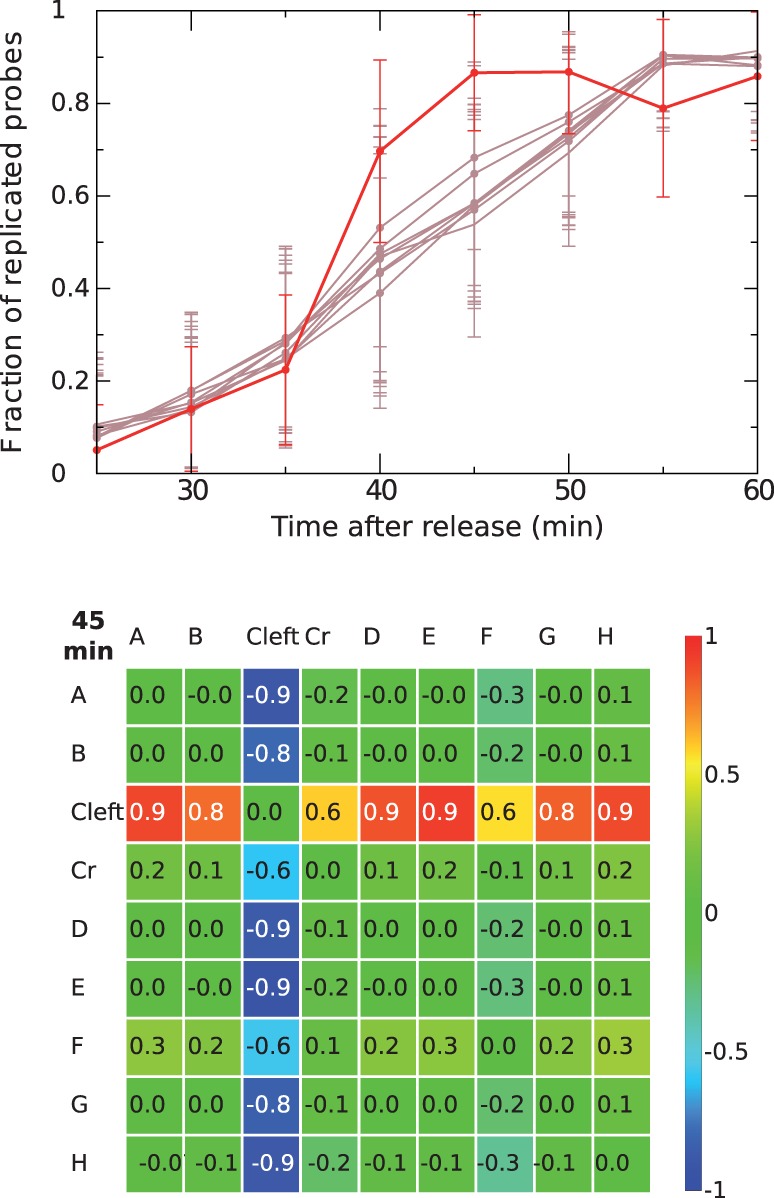
(Top) Fraction of replicated probes for the whole chromosome versus experimental time points in the S phase. The mean fraction of replicated probes 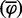corresponds to the mean processed intensity ratios from the three replicate experiments calculated for each probe of the microarray and for each time point Brown lines stand for all chromosomes except for Sakl0C-left, which is represented by the red line. Error bars are standard deviation (and not standard error, to show the wide scatter of data points). (Bottom) Heatmap representing the elements of M_ij(T) for T = 20 min elapsed (45 min in the experiment) in the S-phase (considering only Sakl0C-left instead of the whole chromosome Sakl0C). Numbers show the difference between the replicated fraction of chromosomes i and j at the time T, in units of standard deviations.

For every time sample, this gives a matrix that quantifies, in units of standard deviations, the differences in the overall replication kinetics from one chromosome to another. These values are graphically represented as heatmap tables (fig. 3B and supplementary fig. S3, Supplementary Material online). We can see that Sakl0C-left is the only chromosome that significantly differs from the others. The difference becomes greatest at T = 50 and is around 1σ (fig. 3B), which is fully consistent with the absence of late replication times in this chromosomal arm (discussed earlier). In conclusion, both Trep_avg and intensity ratios directly deriving from the microarray experiments indicate that the GC-rich chromosomal arm, Sakl0C-left is, on average, replicated early during S-phase and that in many cells within the population it would be fully replicated while the other chromosomes are still replicating.

We also decided to monitor the change in DNA copy number during S-phase by deep sequencing, which avoids all the hybridization steps of the microarray experiments. A new independent S-phase time-course experiment where cells were synchronized in G1 by centrifugal elutriation (instead of alpha factor treatment to additionally check that the replication kinetics was not influenced by the synchronization method) was performed. We sampled S-phase every 10 min for 6 time points, extracted DNA and generated an average of 10 million reads per sample using Illumina single read technology. Changes in DNA copy number were assessed by calculating the ratios between the number of reads for each time point relatively to the first time point of the kinetics (see Materials and Methods). These ratios were then processed as were processed the microarray intensity ratios to calculate T_rep values and generate a replication timing profile. For each chromosome, the sequencing-based replication profile strongly correlates with the microarray-based timing profile (Spearman correlation coefficients between 0.85 and 0.92, supplementary fig. S4, Supplementary Material online). In addition, the replication kinetics of Sakl0C-left is highly similar to the one derived from the microarray experiment. Quantification of the proportion of replicated chromosome as a function of time during S-phase confirmed the same trend as seen for microarray experiments showing that replication of Sakl0C-left is completed significantly earlier than for all the other chromosomes (supplementary fig. S5, Supplementary Material online).

In conclusion, we present strong evidence that, contrarily to the initial hypothesis, the GC-rich chromosomal arm of the L. kluyveri genome is, on average, replicated early during S-phase. This result relies on an extensive data set composed of 1) four independent replicates, each composed of six to eight time points, covering the whole kinetics of the S-phase, 2) two different analytical methods for quantifying changes in DNA copy number (i.e., Trep_avg and intensity ratios), 3) a combination of two different technologies to assess DNA copy number variations during S-phase (i.e., microarrays and deep sequencing), and 4) two different methods of cell synchronization (alpha factor treatment and elutriation).

Inference of Replication Origins

A whole genome replication profile provides the possibility to infer the position of the replication origins. We used two distinct methods to infer the number and the position of the origins in the genome of L. kluyveri. First, we directly identified peaks in replication timing profiles. Second, we determined the regions along the chromosomes where estimated rates of origin firing were the highest.

In the replication timing profile (fig. 1), one can safely assume that peaks correspond to the regions replicated the earliest, that is, replication origins, while valleys represent regions of fork termination. The precise positions of the peaks were defined as the points where the slopes of the fitted replication time curves switch sign (see Materials and Methods). Potential replication origins were defined as peaks in at least 2 of the 3 replicate experiments, separated by less than 15 kb. A total of 220 potential replication origins were detected (fig. 1 and supplementary table S2, Supplementary Material online).

We also predicted the position of origins independently of Trep_avg. This method relies on the existence of a lag time (t*) at the very beginning of S-phase, during which no replication is possible if a locus is not an origin. Therefore, when t ≤ t*, the slope of the curve corresponding to the “mean fraction of replicated probes” (discussed earlier) plotted as a function of the chromosomal coordinates is always close to zero, unless the chromosomal segment is a replication origin (fig. 4A). We inferred the position of the origins by estimating the initial discrete slope of the curve only using the first 2 time points of the kinetics (25 and 30 min after release), that is, relative to the first 5 min of the S-phase. Initial discrete slopes were estimated in 10 kb sliding windows for 1 kb steps (see Materials and Methods). This initial slope, which dimensionally is an inverse time, can be seen as a proxy for the overall firing rate, similarly to the (inverse) replication time but not subject to biases due to the interference of nearby origins. This method is similar to two approaches described previously (Alvino et al. 2007; Luo et al. 2010).

Plotting discrete slopes (or firing rates) as a function of the position along the chromosomes produces peaks corresponding to likely positions of replication origins (fig. 4B and supplementary fig. S6, Supplementary Material online). We identified 246 potential replication origins that include 214 out of the 220 origins detected on the replication timing profile (supplementary table S2, Supplementary Material online). Almost all late origins (49 out of 54, i.e., 91%) that fire in the population on average between t = 43 and t = 52 min after release from G1 (discussed later and supplementary table S2, Supplementary Material online) are readily detected at t = 30 min by the initial slope method. Moreover, an additional set of 32 origins that were overlooked by the replication timing profile method was detected by the initial slope method. This is due to two improvements brought by this method. First, nonefficient origins that fire only in a small proportion of the cells produce shoulders on the replication timing profiles instead of clear peaks. Nineteen out of the additional 32 origins detected by the initial slope method fall in this category. Second, as anticipated, the initial slope method disentangles the interference between replication forks coming from different origins. We call “interference” the fact that one origin can be passively replicated by a fork coming from a nearby origin. However, at the beginning of the S-phase during the lag time (when t ≤ t*), the fork from closest nearby origin cannot cause passive replication. During this “single origin” regime, it is possible to resolve some adjacent origins that appear as a single peak in the replication timing profile (supplementary fig. S7, Supplementary Material online). Eleven such origins were detected. The initial slope method allows detection of two additional origins that map very close to the telomeres (Sakl0B-right and Sakl0F-right) that appeared as half peaks on the replication timing profiles. By contrast, six (late firing) origins inferred from the replication timing profile escaped detection by the initial slope method as their slope falls below the noise threshold (supplementary fig. S7, Supplementary Material online, and see Materials and Methods). A further advantage of the initial slope method is that it allows evaluation of origin positions, and a proxy for their firing rate, with only two time points.

The combination of two detection methods produced a nonredundant list of 252 origins (supplementary table S2, Supplementary Material online). Individual locations were mapped between the three replicate experiments in less than 2.6 kb for 50% of the origins (both with the Trep_avg and the slope methods) and in less than 8 kb for 95% and 85% of them with the Trep_avg and the slope methods, respectively. To confirm that these peaks actually correspond well to replication origins, we compared the 252 peak regions with the published ARS data (Liachko et al. 2011). We found a highly significant association between ARS and peak coordinates as 54 out of 84 ARS (64%) were comprised within 8 kb intervals surrounding the position of the peaks (Binomial test, P value < 2.2E−16). On average, 21% of the peaks on the replication profiles correspond to an identified ARS (54 over 252, supplementary table S2, Supplementary Material online). No significant difference was found between the GC-rich chromosomal arm (8 ARS/22 peaks, 36%) and the rest of the genome (46 ARS/230 peaks, 20%; chi-square P value = 0.13).

With a complete set of 252 replication origins, there is an average density of about one origin every 45 kb in the genome. The number of origins per chromosome is not statistically different from random expectations, including in Sakl0C-left (Binomial test, P values of the differences comprised between 0.19 for Sakl0G and 0.53 for Sakl0C-left). In addition, the spatial distribution of origins along individual chromosomes, as measured by the distributions of the inter-origin distances between consecutive origins, show no statistical difference from one chromosome to another for each of the 36 pairwise comparisons (Wilcoxon test, P values > 0.001 (adjusted threshold to account for multiple testing, Bonferroni). Therefore, the precocious replication of the GC-rich chromosomal arm during S-phase is not due to a higher density of replication origins nor to a peculiar distribution of origin positions along the chromosome.

Fork Velocity in the Genome and across the Different Chromosomes

The analyses presented so far are compatible with a picture where origins are discrete genomic regions. As replication is initiated only at these discrete points, at a distance d away from one of the origins, there will be a delay time t* = d/v (where v is the speed of the fork) before replication occurs. The delay is due to the time it takes for the fork to reach a given locus from the nearest origin. This delay is visible as an effective change in the slope of the fraction of replicated probes plotted as a function of time from loci that are not replication origins (fig. 4A) and can be exploited to estimate the fork velocity v.

Data for the fraction of replicated probes are available at 5-min intervals. To estimate v, we considered the first two time points of the kinetics (25 and 30 min after release), and computed for all chromosomes the discrete slope as described above (fig. 4B). This quantity, related to the firing rate of the origins, decreases with increasing d and reaches zero at a distance d₀ from the origins, where d₀ = v/5 min (fig. 4C). Although this property holds for all origins, the slopes at the different origin positions (where d = 0) vary with individual origin firing rates. To compare different origins, we normalized the plot by the slope at d = 0. The resulting plot is shown in figure 4D. The normalized slope for all the origins decreases initially linearly, and slows down before reaching zero. As slope values close to zero are more affected by experimental noise than slope values close to 1 (as illustrated by the span of the error bars in fig. 4D), we extrapolate the linear behavior to estimate v, considering only data above an error threshold obtained as twice the standard deviation of negative-slope data (discussed earlier). This procedure yields an average velocity of 2.9 kb/min for the whole genome. The uncertainty of this measurement is rather large 20–25% (v ∼ 2.9 ± 0.8 kb/min). We speculate that the large spread in the empirical data is mainly due to experimental noise, such as incomplete synchronization between the cells, rather than to real variability of the fork speed as no significant difference between chromosomes could be found (supplementary fig. S8, Supplementary Material online).

Direct measurements of the movement of GINS complexes motion using microarrays indicate that in S. cerevisiae fork progression velocity is uniform throughout the genome, and close to v = 1.6 kb/min (Sekedat et al. 2010). This value is also confirmed by computational analyses of replication data similar to ours (de Moura et al. 2010; Yang et al. 2010). The difference between the measurement of GINS motion in S. cerevisiae (Sekedat et al. 2010) and our fork velocity estimation in L. kluyveri is probably not attributable to a difference in growth temperature because in both cases cell were grown at 30 °C before synchronization and subsequently released in fresh media at 25 °C (Sekedat et al. 2010) or at 23 °C (this work). Reanalyzing previous replication data sets in S. cerevisiae (Raghuraman et al. 2001; Yabuki et al. 2002) with our slope method described earlier yields values of 1.3 ± 0.6 kb/min, compatible with previous estimates. Therefore, our results on fork rate give consistent indications that the molecular replication speed could be higher for L. kluyveri than for S. cerevisiae.

An Absence of Late Firing Replication Origins in the GC-Rich Chromosomal Arm

We first looked at the distribution of the height of the 220 peaks on the Trep_avg replication timing profile. These values correspond to the time where 50% of the cells have replicated their origins either through active firing or through passive replication from forks originating from the firing of neighboring origins. This potential interference from nearby origins as well as the intrinsic statistical nature of origin firing explains why peak height does not truly represent origin firing times (de Moura et al. 2010). However, it gives some indications on the temporal regulation of origin firing. The distribution of peak heights shows a bimodal distribution with 123 “early” origins that are on average replicated between 33 and 40 min after release from the G1 phase, 54 “late” origins replicated on average between 43 and 52 min and 25 “intermediate” origins replicated on average between 41 and 42 min (fig. 5A). A bimodal distribution of peak-heights was also reported for S. cerevisiae (Yabuki et al. 2002). All origin peak-heights from Sakl0C-left fall into the “early” group (between 37 and 40 min [i.e., in the first 8 min of the S-phase]). All other chromosomes comprise both “early- and late-” replicating origins in variable proportions (fig. 5C). In addition, all origins from Sakl0C-left are on average replicated in a very narrow time interval of 4 min while the time interval required by all other chromosomes (including Sakl0C-right) to replicate their origins varies between 11 min for Sakl0A to 19 min for Sakl0B and Sakl0H. These observations suggest that Sakl0C-left origins would all fire early in S-phase.

Fig. 5.—

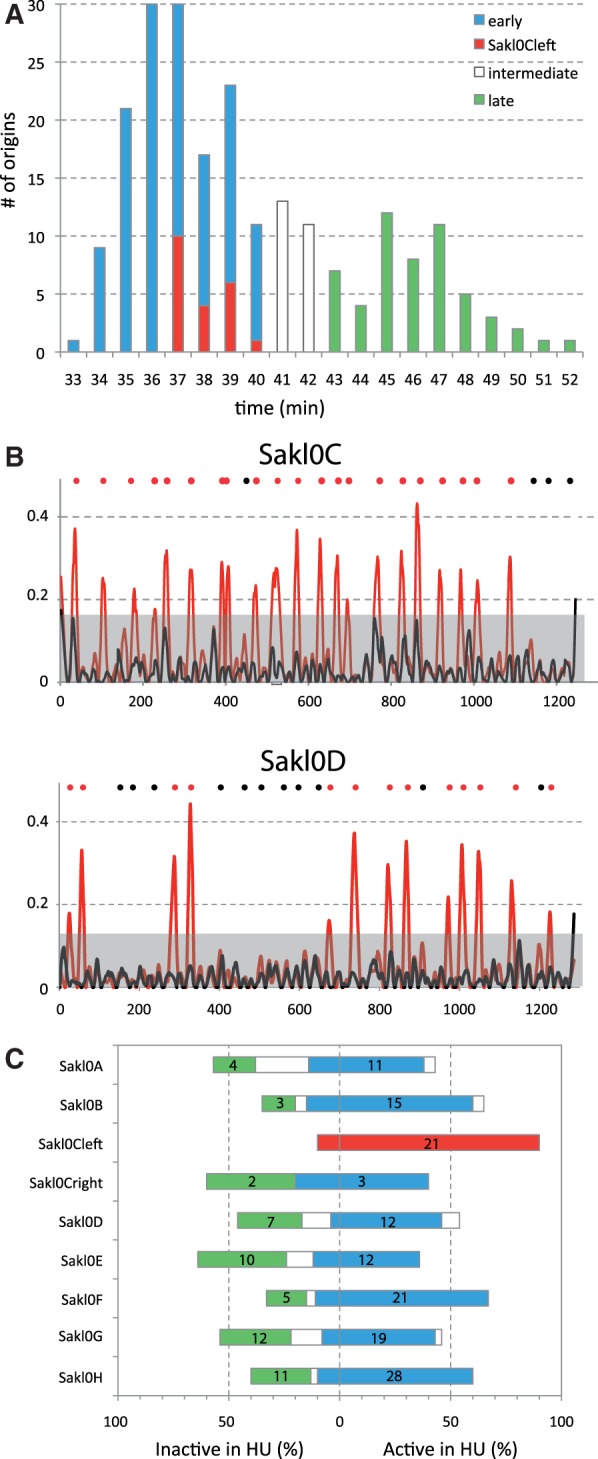
Distribution of origin peak-height. (A) Distribution of peak-heights for all 220 origins from the replication timing profile in figure 1. Three categories are defined “early” (blue bars), “intermediate” (white bars) and “late” (green bars) origins. Peak-heights show a bimodal distribution while origins from Sakl0C-left all correspond to “early” firing origin (in red). (B) Origin firing after release from G1 in the presence of HU for two chromosomes (SAKL0C and Sakl0D). Microarray normalized intensity ratios are presented for two time points (T₀ = 0 min [black] and T₃ = 45 min [red]). For each time point, a Loess regression curve was calculated, using a span of 30 kb. The noise threshold (grey background) was defined by chromosome as the highest ratio value in T₀. All peaks from T₃ that exceed the noise threshold were considered as active origins in the presence of HU. The positions of active and inactive origins are indicated by red and black dots, respectively. A similar representation for all chromosomes can be found in supplementary figure S9, Supplementary Material online. (C) Proportion of active origins in the presence of HU for each chromosome. The color code is identical to (A). All “late” origins and most of “intermediate” origins failed to activate in the presence of HU while most of the “early” origins fired (84%). Almost all origins from Sakl0C-left (90%) actively fired while the other chromosomes contain between 33% and 64% of inactive origins. The actual numbers of “early” and “late origins are indicated chromosome by chromosome.

To further confirm the early firing of Sakl0C-left origins, a time-course experiment where the cells were released in presence of HU was performed. In S. cerevisiae, HU inhibits the ribonucleotide reductase enzyme, which results in reducing the pool of nucleotides in the cell. On exposure to HU, S-phase progression takes place over an extended time frame and the activation of all origins is delayed (Alvino et al. 2007). We found here that in L. kluyveri, S-phase in HU also requires significantly longer time, given that 210 min after release, replication is still far from being completed. Forty-five minutes after release in the presence of HU, only 123 out of the 220 origins (56%) have actively fired (fig. 5B and supplementary fig. S9, Supplementary Material online). These origins correspond to 119 and 5 origins that belong to the “early” and “intermediate” peak-height distribution in figure 5A, respectively. By contrast, all the origins that belong to the “late” mode in the peak-height distribution are inactive in HU conditions (in green on fig. 5A and 5C) and only a small proportion of “early” origins (23/142), according to peak-height, are inactive 45 min after release in HU. These results show that despite peak-height from replication timing curves not being completely accurate, it can still provide valuable information in predicting origin activation time. The most striking point here is that a vast majority of origins from Sakl0C-left (19/21, 90%) actively fire 45 min after release in the presence of HU while for all the other chromosomes, only between 36% and 67% of origins actively fire (figs. 5B and 5C). On the basis of number of origins per chromosome and on the global proportion of active and inactive origins in the presence of HU in the genome, we calculated the expected number of active and inactive origins for each chromosome. The only significant difference between observed and expected numbers is found for Sakl0C-left (chi-square test with Yates correction, P value = 0.01). These results show that the precocious replication of the GC-rich chromosomal arm in the genome of L. kluyveri, directly results from the early firing of nearly all its replication origins.

A Specific ACS in the GC-Rich Chromosomal Arm

A functional assay based on plasmid maintenance has allowed identification of 84 ARS in the genome of L. kluyveri (Liachko et al. 2011). The authors identified a conserved DNA motif required for the ARS function. This ACS is 9–11 bp long and resembles to that of S. cerevisiae. The corresponding 84 sequences were filtered for all coding sequences, LTR sequences and microsatellites. This led to a set of 79 intergenic ARS that was submitted to the Gibbs sampling motif finder GIMSAN (Ng and Keich 2008). The most significant motif we identified corresponds to an 11 bp motif, very close to the ACS recently published (Liachko et al. 2011), the only small differences consisting on variable proportions of minority bases (fig. 6). This set of 79 sequences was further used to look for putative differences between ACS across different chromosomes. The eight subsets of ARS corresponding to individual chromosomes were subjected to the motif finder program. A significant motif could be identified from the subset of 12 ARS belonging to Sakl0C-left (P value = 0.016). However, significant motifs could not be found for any of the other chromosomes when analyzed individually although some of them comprised a number of ARS similar to that of Sakl0C-left (i.e., 11ARS in Sakl0F, 12ARS in Sakl0G or 13ARS in Sakl0H). This suggested that the specific consensus motif in Sakl0C-left would be more conserved than in other chromosomes. The Sakl0C-left motif presents a pattern globally similar to an ACS despite several clear differences. First, the best P value was obtained for a width of 12 bp instead of 11 bp and the corresponding motif was shifted by 2 bp to the left of the 11 bp published ACS (fig. 6). Second, the base composition of this motif was clearly different from the motif deriving from the other 67 ARS belonging to the other chromosomes (width of 11 bp motif, P value 2 × 10⁻⁶). Seven out of the 10 overlapping positions between the two motifs have significantly different base compositions with a clear enrichment in G + C bases for the Sakl0C-left motif (fig. 6).

Fig. 6.—

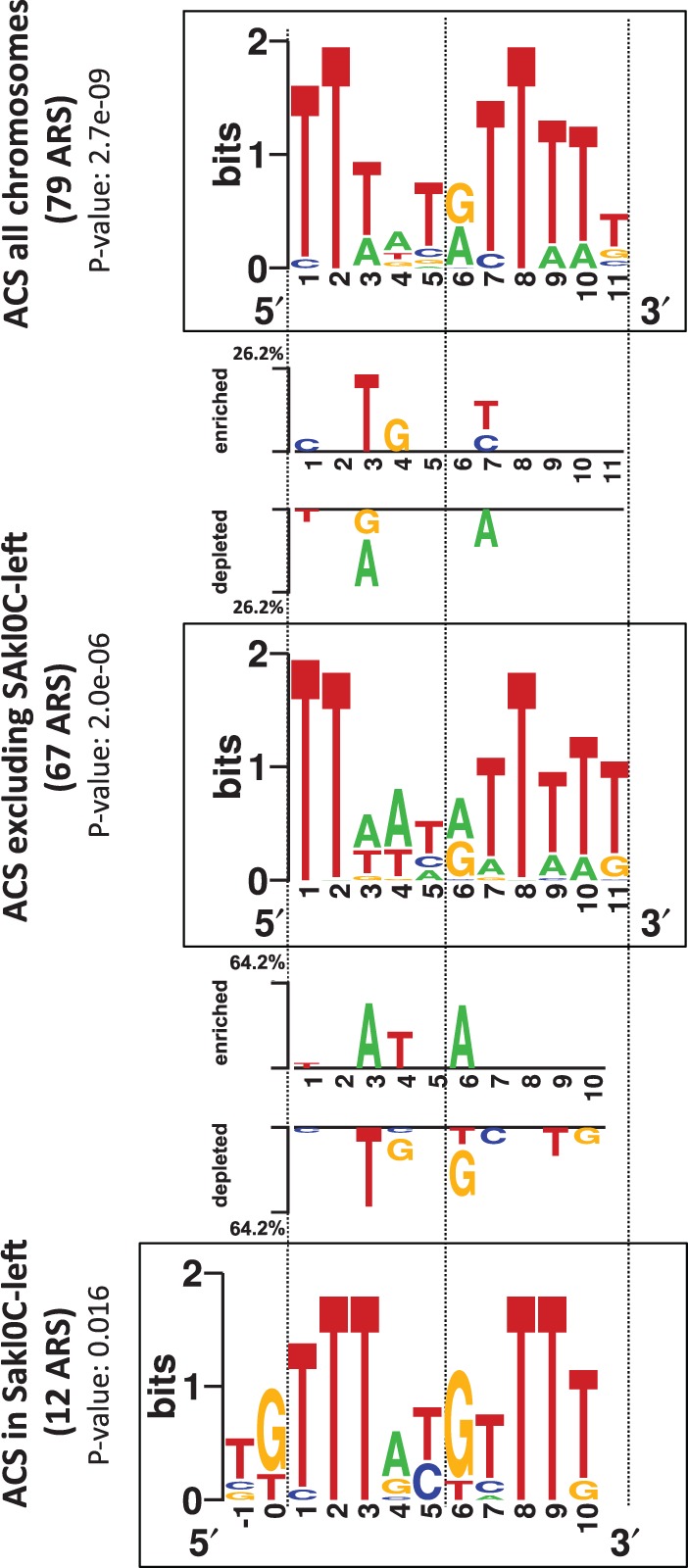
Identification of different ACS motifs in the genome of Lachancea kluyveri. The three squared logo sequences correspond to putative ACS motifs for all chromosomes (top), for all chromosomes excluding Sakl0C-left (middle), and for Sakl0C-left (bottom). The most significant motif for Sakl0C-left was obtained for a width of 12 bp instead of 11 bp for all other chromosomes and shifted by 2 bp to the 5'-end of the 11 bp motif. Significant base differences between “ACS of all chromosomes” (top) and “ACS excluding Sakl0C-left” (middle), and between “ACS excluding Sakl0C-left” (middle) and “ACS of Sakl0C-left” (bottom) are represented between the corresponding squared logos with the indication of the enriched or depleted bases at each position.

We checked whether this compositional difference could be simply due to a sample bias linked to the small number of sequences used for detection (only 12 ARS). We performed 1,000 random samplings of 12 sequences in the subset of 67 ARS from the other chromosomes and submitted each of the 1,000 samples to the motif finder program. In the resulting 1,000 motifs, only 5 were similar to the Sakl0C-left ACS (one motif was considered to be similar the Sakl0C-left motif if it was shifted at most by one position and if it significantly differed in base composition at less than 10% of the positions (P value of difference ≤0.05; supplementary fig. S10, Supplementary Material online), showing that the probability that the specific composition of the Sakl0C-left ACS result from a sample bias is very low (P = 0.005). In addition, we performed a Principal Coordinates Analysis to graphically represent chromosome by chromosome the relative clustering of the different motif sequences (supplementary fig. S11, Supplementary Material online). We showed that motif sequences from Sakl0C-left cluster in a region of the graph while motif sequences from other chromosomes are scattered, demonstrating that the motif sequences from Sakl0C-left are more similar to each others than the ones from the other chromosomes. Altogether, these results show that Sakl0C-left is the only chromosome in the genome that presents a specific base composition and higher sequence conservation of the ACS.

Finally, we tested whether early firing of replication origins in Sakl0C-left could be due to the particular base composition of its ACS. We found no evidence that Sakl0C-left ACS would be significantly closer to “early” ACS than to “late” ACS from the rest of the genome (supplementary fig. S12, Supplementary Material online).

A Specific Correlation between GC-Content and Distance to Replication Origin in the GC-Rich Chromosomal Arm

We showed here that Sakl0C-left has several unique replicative properties in addition to its unusual nucleotide composition (Souciet et al. 2009). We therefore looked at whether base composition (G + C content) varies with the replication profile. Variation in GC-content was calculated for all chromosomes and plotted as a function of the replication timing using 1 - and 4-min bins. No significant correlation was found between GC-content and replication timing for any chromosome. The absence of correlation could be due to the fact that all origins do not fire simultaneously and therefore two loci replicating at the same time could be located at very different distances from their respective active origins.

To test whether variation in GC-content might correlate with the physical distance covered by the replication forks rather than with replication timing, we plotted the GC-content as a function of the distance to replication origins within replicons for all chromosomes. We selected a subset of 207 replication origins that appear as clear peaks on the replication timing profile, flanked on both sides by clear valleys that correspond to termination regions. We considered up to 25 kb on each side of these origins when the distance between origin and termination regions were large enough (the average replicon size being 45 kb) and removed all regions located at more than 25 kb of the nearest origins. This data set represents 75% of the genome. We pooled all ori-ter regions by chromosome and calculated GC-content in 2.5 kb intervals for all chromosomes and for different types of sequences (all DNA, coding DNA, intergenic sequences, third codon positions, and 4-fold degenerated sites).

We found that Sakl0C-left was the only chromosome showing significant positive correlations between distance to replication origins and GC-content in all DNA bases (Rho = 0.93, P value = 1 × 10⁻⁴), all coding sequences (Rho = 0.88, P value = 2 × 10⁻³), third codon positions (Rho = 0.85, P value = 3 × 10⁻³), and 4-fold degenerated sites (Rho = 0.88, P value = 2 × 10⁻³, fig. 7 and supplementary fig. S13, Supplementary Material online, for the other chromosomes). The rate of GC-content increase with distance to origin was estimated from the slopes of the linear regression curves applied to the correlations. It corresponds to a GC-content increase of +0.11% of G+C bases per kb when considering all DNA bases in Sakl0Cleft. These rates are higher for more neutral positions such as third codon positions and 4-fold degenerated sites (+0.22% and +0.29% of GC bases per kb, respectively). Therefore, regions located at 25 kb away from replications origins in Sakl0C-left contain on average 5.5% and 7.25% more GC bases at third codon positions and 4-fold degenerated sites, respectively, than regions close to origins.

Fig. 7.—

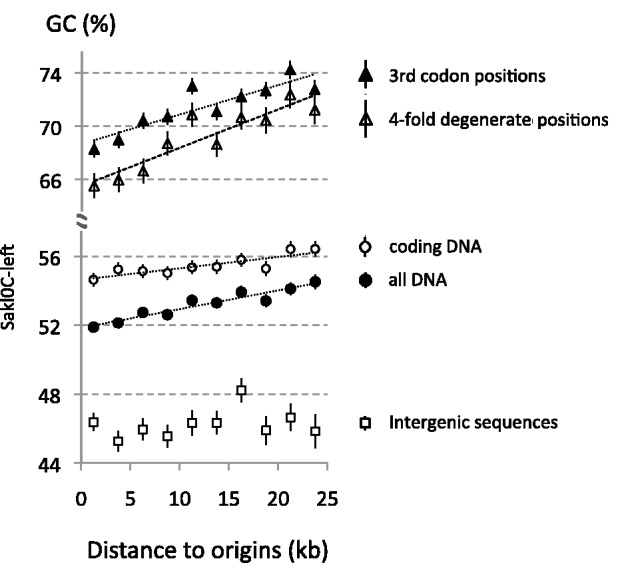
Variation of GC-content relatively to the distance from origins in Sakl0Cleft. Intervals between origin and termination regions from 20 replicons from this chromosomal arm were pooled by chromosome and GC-content was calculated in windows of 2.5 kb considering either all DNA bases, coding sequences, third codon positions, 4-fold degenerated sites, or intergenic sequences. Linear regression curves were plotted only for series showing statistically significant correlations (all DNA bases: Rho = 0.93, P value =1 × 10⁻⁴; all coding sequences: Rho = 0.88, P value =2 × 10⁻³; third codon positions: Rho = 0.85, P value =3 × 10⁻³; and 4-fold degenerated sites: Rho = 0.88, P value =2 × 10⁻³). Note that despite the absence of significant correlation in intergenic sequences in Sakl0C-left, the correlation measured by Rho values appears larger in “all DNA” than in “coding sequences.” This is due to a simple numerical effect because the correlation in intergenes does exist, even if it is not statistically significant, and contributes to the “all DNA” correlation.

For all the other chromosomes, most of the corresponding estimations show no significant correlations (supplementary fig. S13, Supplementary Material online). Few sporadic correlations (either positive or negative) were found to be statistically significant (supplementary fig. S13, Supplementary Material online) but the amplitude of these correlations were always very limited (for instance, +0.04% and −0.04% of GC variation per kb in Sakl0G and Sakl0E, respectively, for all DNA bases) and contrarily to what was observed in SAkl0C-left, no consistent slope increase could be found for more neutral positions (third codon positions and 4-fold degenerated sites) suggesting that these hectic correlations did not result from mutational forces.

No significant correlation was found in intergenic sequences for any chromosome (supplementary fig. S13, Supplementary Material online). This absence of correlation in intergenic sequences could result from selective constraints because these regions are short and are thought to contain many regulatory elements. Because significant correlations were only observed in coding sequences (and in all DNA) and also because mutational bias associated with transcription were previously observed in mammals (Green et al. 2003; Polak and Arndt 2008; Mugal et al. 2009), we checked that the observed GC-content increase along replicons in Sakl0C-left was not linked to transcription rather than to replication, We showed that coding sequences alternate in equivalent proportions with transcribed sequences along replicons (from ORI to Ter regions), excluding a transcriptional orientation bias in the data set (supplementary fig. S14A, Supplementary Material online). Using previously published expression data (Tsankov et al. 2010), we showed that the proportion of highly expressed genes does not change with the distance to replication origins, suggesting that the GC-content correlation is not linked to the expression level (supplementary fig. S14B, Supplementary Material online). Finally, we found no correlation between GC-content and the expression level (supplementary fig. S14C, Supplementary Material online), ruling out the possibility that the observed correlations would be linked to transcription.

In conclusion, it appears that a true correlation between GC-content and the distance covered by the replication forks only exist in Sakl0C-left. This correlation suggests that the high G+C composition of this chromosomal arm could be directly linked to replication.

A Specific Lack of Compositional Skew between Leading and Lagging Strands in the GC-Rich Chromosomal Arm

Replication is an intrinsically asymmetric process that could also lead to biased mutation rates between leading and lagging strands. In eukaryotes, the existence of such replication-associated mutational asymmetries has been established only for human (Chen et al. 2011) and for S. cerevisiae (Agier and Fischer 2012). It has been shown both in human and in S. cerevisiae that these asymmetries have resulted, after long evolutionary time, in compositional skews between the two DNA strands (i.e., G ≠ C and T ≠ A on one strand) (Chen et al. 2011; Agier and Fischer 2012; Marsolier-Kergoat 2012; Marsolier-Kergoat and Goldar 2012). Here, we examined the nucleotide composition between leading and lagging strands (i.e., between each side of replication origins), separately in each chromosome of L. kluyveri. We used the subset of 207 replication origins previously defined, considering this time the entire replicons, which comprise 5,038 open reading frames (ORFs) and represent 93% of the genome. The size of each of the 207 replicons was normalized into 50 bins of 2%. The position of each origin was set at 50% and the positions of the two flanking termination regions at 0% and 100%. The 207 normalized intervals were pooled and the GC, TA and total skews were calculated in each 2% section at third-codon positions of ORFs (see Materials and Methods). We found that the GC-rich chromosomal arm has no compositional skew between leading and lagging strands while for all other chromosomes, there is significant skew with S_GC3, S_TA3 and S₃ being positive on lagging and negative on leading strands, their sign switching at replication origins (chi-square test, all P values < 10⁻⁴, fig. 8). In all chromosomes except Sakl0C-left, lagging strands are enriched in G over C and in T over A bases, whereas leading strands are enriched in C and A bases. The global skew calculated on third codon positions for the whole genome, shows an average jump of approximately 8% around replication origins (fig. 8), similar to the replication-associated skew reported for both the human and S. cerevisiae genomes (Chen et al. 2011; Agier and Fischer 2012; Marsolier-Kergoat and Goldar 2012).

Fig. 8.—

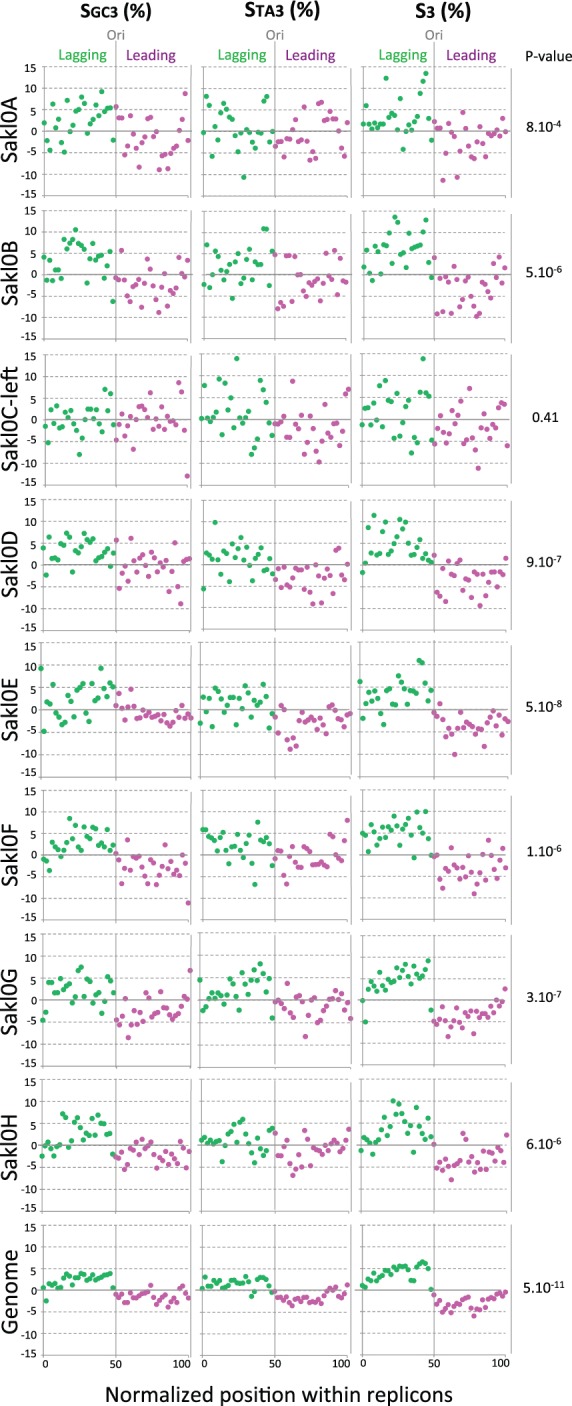
Compositional skews between leading and lagging strands by chromosome (considering only Sakl0C-left instead of the whole chromosome Sakl0C) and for the whole genome. Each of the 207 replicons was divided into 50 sections of 2%. The position of the origins (Ori) was set at 50% and the positions of the flanking termination regions (Ter) were set at 0% and 100% on the x axis. The 207 normalized replicons were pooled and S_GC3, S_TA3, and total skew S₃ were calculated on third codon positions using complementary bases for genes encoded on the bottom (Crick) strand. The values are indicated as percentages on the y axis. P values on the right indicate the probability that the observed distribution of S₃ values (chi-square) between leading and lagging strands for each chromosome and for the whole genome is random.

Replication Origins Are Poorly Conserved and Do Not Behave as Fragile Chromosomal Sites in Lachancea Genomes

We compared the relative conservation of our set of 252 origins in L. kluyveri with the sets of 275 and 194 replication origins in S. cerevisiae and in L. waltii, respectively (Alvino et al. 2007; Di Rienzi et al. 2012). To achieve this goal, we computed all synteny regions between the genome of L. kluyveri and the two other genomes and determined whether origin-containing regions of 8 kb (4 kb on each side of the peak coordinates) in one genome was conserved in synteny and if an origin was also present in the corresponding region of conserved synteny in each of the two other genomes.

We found that only 24% of the L. kluyveri origins (60/252) were conserved in the genome of S. cerevisiae (supplementary table S2, Supplementary Material online) and similarly 23% of the S. cerevisiae origins (63/275) were conserved in the genome of L. kluyveri. These two species share a similar number of replication origins (252 vs. 275, respectively) although S. cerevisiae underwent a WGD event in its lineage (Wolfe and Shields 1997), which resulted in the doubling of the replication origin number. We found that only a very small fraction of the origins have been retained as duplicates since the WGD event (only 3 out of the 63 (5%) conserved origins from L. kluyveri are still present in two copies in the genome of S. cerevisiae). These results are consistent with previous findings that origin location was poorly conserved between S. cerevisiae and K. lactis (5%, (Liachko et al. 2010) and between S. cerevisiae and L. waltii (28% or 21% after correction). We checked that our method produces similar estimations; we found 54 origins out the 194 in L. waltii that were conserved in the genome of S. cerevisiae (28%).

However, for more closely related species, such as those belonging to the Saccharomyces sensu stricto group, it was recently shown that the location of active origins was highly conserved (Muller and Nieduszynski 2012). Therefore, we estimated the fraction of conserved origins between the two related Lachancea species: L. kluyveri and L. waltii. Surprisingly, we found that the proportion of conserved origins was not significantly higher between these two species than between any of them and the more distantly related S. cerevisiae. We found that only 65 of the 252 L. kluyveri origins (26%) are conserved in the genome of L. waltii (supplementary table S2, Supplementary Material online) and similarly 65 of the 194 L. waltii origins (33%) are conserved in the genome of L. kluyveri, showing that replication origins are poorly conserved in the Lachancea clade. In addition, only 20 L. kluyveri origins are conserved both in S. cerevisiae and L. waltii, which is not significantly different from random expectation (65 × 60/252 = 15 origins expected to be conserved in both species, chi-squared P value = 0.5). Moreover, in all these comparisons, the proportion of origin conservation in Sakl0C-left was not statistically different from that in other chromosomes.

In S. cerevisiae, it has been previously reported that replication origins tend to colocalize with synteny breakpoints, suggesting that replication origins could correspond to evolutionary chromosomal fragile sites (Di Rienzi et al. 2009; Gordon et al. 2009). Association between synteny breakpoint and ARS position was also reported in the genome of K. lactis when compared with that of S. cerevisiae (Liachko et al. 2010). We also found a significant association between replication origins in the genome of S. cerevisiae and synteny breakpoints with the genome of L. kluyveri. Thus, 59% of origin-containing regions in S. cerevisiae colocalized with synteny breakpoints (162/275) while only 45% of regions of similar size but devoid of replication origin were associated with breakpoints (396/876, chi-squared P value = 1 × 10⁻⁴). However, we did not find any significant association between replication origins in L. kluyveri and synteny breakpoints with the genome of S. cerevisiae. The proportions of origin-containing and origin-devoid regions associated with at least one synteny breakpoint are similar in the L. kluyveri genome (76% [192/252] vs. 75% [659/876], respectively, chi-squared P value = 0.8). We performed the same analysis between the two Lachancea species. No association between replication origins and synteny breakpoints was found between L. kluyveri and L. waltii in either of the two possible directions (20% [50/252] of origin-containing and 17% [147/876] of origin-devoid regions in L. kluyveri were associated with at least one synteny breakpoint [P value = 0.3] and 23% [45/194] of origin-containing and 18% [154/858] of origin-devoid regions in L. waltii were associated with at least one synteny breakpoint [P value=0.1]). A similar lack of association between origins and breakpoints was also reported between the genomes of L. waltii and K. lactis (Di Rienzi et al. 2012). These results suggest that the association between replication origins and the presence of evolutionary breakpoints that is found in S. cerevisiae would not be a general rule governing yeast genome evolution.

Discussion

Here, we report the analysis of genome replication in L. kluyveri, a yeast species that diverged from the S. cerevisiae lineage before the ancestral WGD. The phylogenetic relatedness between these two species allowed us to determine the evolutionary conservation of several replication features. We identified a list of 252 active replication origins in L. kluyveri and found a considerable divergence in origin location with S. cerevisiae and L. waltii as only approximately 25% of active origins were conserved between the three genomes. An even smaller fraction, only 5% of the origins, has been retained in two copies in the present-day genome of S. cerevisiae since the WGD event. These results suggest that new active origins can emerge while others are lost during the course of evolution as previously reported (Di Rienzi et al. 2012). In addition, we found that contrary to S. cerevisiae and K. lactis (Di Rienzi et al. 2009; Gordon et al. 2009; Liachko et al. 2010), active replication origins in L. kluyveri and in L. waltii do not behave as evolutionary fragile sites. Large sets of replication origins and/or ARS are now available for 8 Saccharomycotina species, S. cerevisiae (Siow et al. 2012), S. paradoxus, S. arboricolus, S. bayanus (Muller and Nieduszynski 2012), Kluyveromyces lactis (Liachko et al. 2010), Candida albicans (Koren et al. 2010), L. waltii (Di Rienzi et al. 2012), and L. kluyveri (this work and Liachko et al. 2011) paving the road for comparative approaches aiming at understanding the evolution of replication program in eukaryotes.

Several global features of S. cerevisiae replication are conserved in the genome of L. kluyveri. Centromeres are among the earliest replicating regions while telomeres tend to replicate late, as it is also the case in L. waltii (Di Rienzi et al. 2012) and in C. albicans (at least for the centromeres [Koren et al. 2010]). We also confirmed the existence of a conserved motif (ACS) in L. kluyveri origins that resemble that of S. cerevisiae (Liachko et al. 2011). In addition, we showed that replication timing along chromosomes alternates between large regions of early and late activating origins as in S. cerevisiae (Raghuraman et al. 2001; Yabuki et al. 2002; Alvino et al. 2007; McCune et al. 2008). However, we found notable exceptions to the two latter features in a large region (1 Mb) of the L. kluyveri genome. The whole left arm of chromosome Sakl0C (abbreviated as Sakl0C-left) contains a specific ACS different from the one found in the other chromosomes and is completely devoid of late firing origins.

It is important to stress that the notion of early and late replication origin has intrinsic statistical nature because firing times come from an averaged replication profile deriving from a population-based microarray. We developed a method of origin detection based on the variations of microarray ratios restricted to the first 5 min after the beginning of S-phase. We showed that this method allows detection of almost all late origins in the first 5 min of S-phase (49 out of 54, i.e., 91%). The most trivial explanation for this could be that cells were not synchronized at 100% when they were released into S-phase (between 80% and 90% of the cells, supplementary fig. S0, Supplementary Material online) and that late origins detected at beginning of S-phase derived from the remaining 10% to 20% of nonsynchronized cells. Alternatively, it is possible that apparently late origins have already activated in the first 5 min of the S-phase in a significant proportion of the cells or that these origins would actually correspond to early origins used only by a small number of cells in the population. Thus, low efficiency origins could appear as late activating in population-based replication profiles although they would in reality activate early but only in a small proportion of the cells. This hypothesis would be compatible with a probabilistic model of replication that suggests that predetermined replication timing programs would be artifactually generated by population-based assays (Czajkowsky et al. 2008). However, DNA combing studies revealed the presence of late replicating regions repressed by checkpoint kinases (Tourriere et al. 2005), which argues against a fully probabilistic model of replication. Together, these findings support the view of a flexible pattern of origin firing between individual cells, as suggested from DNA fiber studies (Czajkowsky et al. 2008; Tuduri et al. 2010).

The lack of apparently late origins in Sakl0C-left results in a precocious replication of this particular chromosomal arm at the population level. Therefore, replication of Sakl0C-left would be completed in many cells within the population while the other chromosomes are still replicating. This finding contradicts previous results that suggested that the replication of Sakl0C-left would be delayed during S-phase (Payen et al. 2009). However, this hypothesis relied on a single microarray experiment corresponding to only two time points in late S-phase. Here, a much more extensive data set composed of four independent replicates of the whole kinetics of the S-phase and a combination of two different technologies to assess DNA copy number variations during S-phase (CGH and deep sequencing) clearly show that Sakl0C-left is precociously replicated during S-phase.

We showed that precocious replication of Sakl0C-left is mainly due to a visibly narrower distribution of average firing times and not to largely different origin density, origin spatial distribution or replication fork speed. In addition to these specific replication properties, this chromosomal arm has an unusual nucleotide composition with 53% of G + C bases while the rest of the genome averages 40% of G + C (Souciet et al. 2009). Therefore, we looked for a functional link between replication and higher GC-content in this region.

Although there is no direct link between GC-content and the DNA replication, numerous studies have reported a positive correlation between replication timing and the rate of base substitutions both in human (Wolfe et al. 1989; Gu and Li 1994; Watanabe et al. 2002; Stamatoyannopoulos et al. 2009; Chen et al. 2010) and in S. cerevisiae (Lang and Murray 2011; Agier and Fischer 2012). Moreover, several studies in S. cerevisiae have shown the existence of a mutational bias toward A:T base pairs (Lang and Murray 2008; Lynch et al. 2008; Nishant et al. 2010; Agier and Fischer 2012) probably resulting from cytosine de-amination and ultimately leading to an increased AT-content in the genome (Kreutzer and Essigmann 1998). It is generally accepted, at least in vertebrate genomes, that GC-biased gene conversion (BGC) during meiosis counter-balances this trend by favoring GC pairing over AT pairing during the repair of heteroduplexes (Duret and Galtier 2009). High resolution mapping of meiotic recombination events demonstrated the existence of BGC in S. cerevisiae (Mancera et al. 2008). However, the life cycle of wild yeasts is principally characterized by rapid clonal expansions. The proportion of sexual reproduction varies between lineages. Many lineages seem to be completely asexual while for those that undergo meiosis, mating mainly occurs between ascospores originating from the same tetrad (inbreeding). It was calculated that Saccharomyces species undergo one sexual cycle every 1,000 asexual divisions and that the proportion of outcrossing would be limited to once in every 50,000 to 100,000 asexual generations (Ruderfer et al. 2006; Tsai et al. 2008). This could explain why, contrary to vertebrate genomes, GC-content might not be fully driven by recombination in yeast (Marsolier-Kergoat and Yeramian 2009). However, the negative correlation that was reported between chromosome length and GC3-content in the genome of S. cerevisiae is fully consistent with the BGC hypothesis (Bradman 1999). This correlation was only visible at silent positions in ORFs but not when considering intergenic regions that are short and may contain many regulatory elements. We found a similar negative correlation between chromosome length and GC-content at third codon positions and 4-fold degenerated sites in L. kluyveri (not shown).

We also found a positive correlation between GC-content and distance covered by replication forks on the left arm of Sakl0C. We showed that this correlation is stronger at more neutral sites such as third codon positions or 4-fold degenerated sites, suggesting that the high GC-content in Sakl0C-left could result from a replication-associated mutational process rather than from a hybridization event between a GC-rich and a GC-poor strain. Additional experiments are needed to investigate the nature of this putative mutational process but a possible explanation to this observation would be that mutation rates would be specifically biased toward GC in this chromosomal arm and that this bias would be more pronounced near termination regions.

In addition, we found a specific absence of compositional skew between leading and lagging strands in Sakl0C-left. Compositional skews between leading and lagging strands result from the asymmetrical mutation rates applied for long evolutionary time on each side of the constitutively active replication origins. Therefore, the simplest hypothesis to explain the lack of compositional skew would be that most of the sequences in this chromosomal arm are replicated alternatively by the leading or the lagging strand depending on which neighboring origin is activated. This hypothesis would imply that passive origin replication in this chromosomal arm would be much more frequent than in other chromosomes, that is, the near complete set of origins used in a given S-phase would vary from cell to cell, whereas, in other chromosomes, the most efficient origins are used in the majority of the cells.

In addition, an intriguing question remains unanswered: Why are these phenomena only visible in this particular chromosomal arm? This arm contains the mating type locus (MAT, fig. 1). In the sister species, L. thermotolerans and L. waltii, the silent mating-type cassettes (HML and HMR) are located in subtelomeric regions of the chromosomal arm orthologous to Sakl0C-left (Butler et al. 2004; Fabre et al. 2005; Muller et al. 2007). These silent cassettes were lost in the genome of L. kluyveri (Payen et al. 2009). It is not perhaps entirely coincidental that the replication-associated GC-content increase was specifically found in the chromosomal arm that contains the MAT locus and that has lost of the silent cassettes. It is noteworthy that in S. cerevisiae, chromosome III is also atypical in base composition showing regional variations in GC3 composition much more pronounced that in any other chromosomes (Bradnam et al. 1999). This chromosome also contains the MAT locus and the two subtelomeric silent cassettes. Therefore it is possible that MAT-containing chromosomes could reveal some fundamental pattern of mutation that other chromosomes may never be able to reveal. This work provides the first evidence of a possible link between the evolution of the nucleotide composition in genomes and DNA replication.

Supplementary Material

Supplementary tables S0–S2 and figures S0–S14 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).