Evolution of Coding Microsatellites in Primate Genomes

Abstract

Microsatellites (SSRs) are highly susceptible to expansions and contractions. When located in a coding sequence, the insertion or the deletion of a single unit for a mono-, di-, tetra-, or penta(nucleotide)-SSR creates a frameshift. As a consequence, one would expect to find only very few of these SSRs in coding sequences because of their strong deleterious potential. Unexpectedly, genomes contain many coding SSRs of all types. Here, we report on a study of their evolution in a phylogenetic context using the genomes of four primates: human, chimpanzee, orangutan, and macaque. In a set of 5,015 orthologous genes unambiguously aligned among the four species, we show that, except for tri- and hexa-SSRs, for which insertions and deletions are frequently observed, SSRs in coding regions evolve mainly by substitutions. We show that the rate of substitution in all types of coding SSRs is typically two times higher than in the rest of coding sequences. Additionally, we observe that although numerous coding SSRs are created and lost by substitutions in the lineages, their numbers remain constant. This last observation suggests that the coding SSRs have reached equilibrium. We hypothesize that this equilibrium involves a combination of mutation, drift, and selection. We thus estimated the fitness cost of mono-SSRs and show that it increases with the number of units. We finally show that the cost of coding mono-SSRs greatly varies from function to function, suggesting that the strength of the selection that acts against them can be correlated to gene functions.

Introduction

An organism’s genome is filled with low-complexity repetitive sequences. One of the most frequently encountered low-complexity sequences are microsatellites, also known as simple sequence repeats (SSRs). An SSR is a tandemly repeated motif of which size ranges from 1 to 6 nucleotides. The most striking feature of an SSR is its very high mutation rate. It is well established that SSRs exhibit a very high expansion/contraction rate, mainly through replication errors caused by DNA polymerase strand slippage (Levinson and Gutman 1987; Schlotterer and Tautz 1992; Tautz 1994). A typical insertion/deletion (indel) event will add/remove one unit; however, changes of several units have also been observed (Henderson and Petes 1992). It has also been suggested that the substitution rate is increased in SSR sequences (Shankar et al. 2007; Pumpernik et al. 2008) as well as in their flanking regions (Siddle et al. 2011). In light of these previous results, SSRs can be regarded as mutational hot spots.

Whenever an SSR is included in a coding sequence, any insertion or deletion event alters the amino acid sequence. When the repeated unit is 3 (or 6) nt, an indel of a single unit adds/removes one (or two) amino acid(s). When the unit size is not a multiple of 3, an indel creates a frameshift that results typically in a premature STOP codon. In eukaryotes, the resulting messenger RNA is then degraded by the nonsense-mediated decay pathway (Ruiz-Echevarria et al. 1998), which prevents abnormal transcripts from being translated. A gene with a frameshift can be therefore assimilated to a recessive null allele for the gene. If this degradation step does not prevent translation, it can produce a negative dominant allele (Holbrook et al. 2004). This implies that SSRs are potentially harmful in coding sequences because of their high propensity to turn a wild-type allele into a null allele. Indeed, the probability that a gene containing an SSR is targeted by a nonsense mutation is several orders of magnitude higher than a gene without an SSR. The indel rate in an SSR ranges from 10⁻⁶ to 10⁻² per replication (Schlotterer 2000), whereas the average substitution rate is, in mammals, 10⁻¹⁰ per site per replication (Drake 1999). The nonsense substitution rate, for a gene size of 1 kb, can be approximated to 0.042 × 333 × 10⁻¹⁰ = 1.4 × 10⁻⁹ per replication (assuming symmetrical mutations, the average chance for codons to mutate in one step to a STOP codon is 0.042). Therefore, the presence of a single SSR in a coding sequence enhances, by several orders of magnitude, the probability of being targeted by a nonsense mutation.

Each SSR locus exhibits its own propensity of being targeted by an expansion or a contraction event. Several factors, including the species genome in which the locus is contained (Toth et al. 2000) and the composition of the repeated motif (Jurka and Pethiyagoda 1995), can greatly modulate the mutability of a given SSR. However, an excellent predictor of SSR mutability is the number of repeated units (Lai and Sun 2003; Kelkar et al. 2008; Leclercq et al. 2010). Indeed, it seems that the mutability increases exponentially with the number of repeated units (de Wachter 1981; Cox and Mirkin 1997; Metzgar et al. 2000). This suggests that there is an independent probability for each repeated unit to be targeted by an insertion or a deletion event.

We like to emphasize that coding SSRs not only carry a long-term impact on fitness but they also, and perhaps more importantly, have an impact on the fitness of the individual itself. Indeed, the coding SSR can be the target of an indel event in the germline (long-term cost) and also in the somatic cell lines (immediate cost). An example of such impact on individual fitness is found in their implication in tumor genesis (Zienolddiny et al. 1999; Vassileva et al. 2002; Yamada et al. 2002; Duval and Hamelin 2003). Furthermore, this instability also plays an important role during transcription, where an SSR locus will induce several abnormal transcripts with an altered number of units (Jacques and Kolakofsky 1991; Fabre et al. 2002). Last but not least, it has been shown that transcription enhances the genomic rate of insertion and deletion in SSRs (Lin et al. 2006).

Altogether, these observations suggest that SSRs instability is potentially very harmful in coding sequences when their unit size is not a multiple of 3. At least two previously described models provide expectations for the number of SSRs within a gene. The first model takes the frequency of each nucleotide into account and predicts the probability of finding an SSR of a given size in a gene (de Wachter 1981; Metzgar et al. 2000; Loire et al. 2009). Improvements that use frequencies of overlapping di- or tri-nucleotide frequencies can be obtained analytically (Robin et al. 2005) or by simulation (Loire E, unpublished results) and do not change the results. The second model assumes that the amino acid sequence is fixed and computes, for a given codon usage, the expected number of SSRs (Ackermann and Chao 2006). This second approach corrects for any over- or under-representation of tracts of lysine (that can be encoded by a poly-A), phenylalanine (poly-T), proline (poly-C), or glycine (poly-G). For example, contrary to what intuition suggests, tracts of prolines are commonly found in proteins (Rubin et al. 2000).

The results are quite clear, whatever the approach: sufficiently long SSRs that are not multiples of 3 (in our study, neither tri- nor hexa-SSRs) are fewer and/or smaller than expected in coding sequences (Metzgar et al. 2000; Ackermann and Chao 2006; Loire et al. 2009). This unambiguously shows that SSRs are globally avoided in coding sequences; this observation fits a model in which coding SSRs are associated with a negative selective coefficient. In addition, the analysis of SSRs in the human genome shows that these results can be extended to almost all functional categories (Loire et al. 2009) as defined by the Gene Ontology (GO) annotations (Ashburner et al. 2000).

In this study, we extend our previous results from the human genome (Loire et al. 2009) to a comparative genomics analysis that focuses on the dynamics of coding SSRs in four primate lineage genomes: human (Homo sapiens), chimpanzee (Pan troglodytes), orangutan (Pongo pygmaeus), and macaque (Macaca mulatta). Here, we tested whether the coding SSRs evolve like the rest of the coding sequences. We first show that SSR accumulate substitutions at a rate that is twice the basal rate of substitution in genes. We then show that, even though many coding SSRs appear and disappear through substitutions, the number of SSRs in coding sequences remains constant. This suggests that their abundance results from a balance between mutation, selection, and drift. Using two different models, we propose estimates for the selective cost of mono-SSRs and show that this cost increases with the number of units.

Materials and Methods

Dataset

The entire set of orthologs between human (H. sapiens), chimpanzee (P. troglodytes), orangutan (P. pygmaeus), and macaque (M. mulatta) were retrieved from the Homolens database (Penel et al. 2009). Primary alignments of codons were performed with PRANK (Loytynoja and Goldman 2005) and then visually inspected.

1469/5015 alignments contain one or more gaps larger than five codons (i.e., 15 nt). In 718/5015 alignments, there is a subsequence where one of the species differs greatly from the others on 20 or more nucleotides in a row. After visual inspection of these regions, we speculate that both large gaps and regions with an unrelated sequence in one species are typically cases where the exons are not the same in the different species. Although the study of coding SSR in alternatively spliced exons is interesting on its own (Haerty and Golding 2010), we focused our analysis on regions that have clear homology between the four species and therefore decided to exclude these regions from our analysis.

SSRs were detected using a size threshold above which their expansion/contraction rate becomes a major mutation force. Indeed, the expansion/contraction rate of an SSR locus will become significant only when the number of repeated units reaches a minimum. Based on the literature, we decided to set the minimum at 8 units for the mono-nucleotide SSRs (mono-SSRs); 5 units for the di-SSRs; 5 units for the tri-SSRs; and 4 units for the tetra-SSRs, penta-SSRs, and hexa-SSRs. An extensive discussion of these particular choices can be found in Loire et al. (2009) and will not be further addressed here. Only perfect SSRs are considered, since degenerate motifs show a dramatic decrease in the rate of insertion/deletion (Leclercq et al. 2010).

While detecting SSRs of a given unit size, repeated sequences that were themselves composed of SSR of smaller sizes were excluded. For example, (AA)_X, (CC)_X, (GG)_X, and (TT)_X are not included in di-SSRs and only count as mono-SSRs.

For SSRs whose unit sequence is two or more nucleotides, the total sequence of the reported SSR is the largest possible one, including overlapping repeated patterns. For example, the sequence TCACACACT hosts a di-SSR (that can be either CA or AC) of three repeated units that spans all the sequence highlighted in italic.

Ancestral sequences were reconstructed using CODEML (Yang 2007), with parameters set to seqtype = codons, NSsites = 0, and ncatG = 4. All ancestral sequences show a posterior probability above 0.8. Because gaps are considered as missing characters, we have not taken codons with deletion into account in our statistics using ancestral genomes.

dN is the number of nonsynonymous substitutions per nonsynonymous site and dS is the number of synonymous substitutions per synonymous site. Assuming a single dN/dS ratio for all branches but 10 classes of dN/dS for the codons within a gene, we estimated the dN/dS ratio of each codon of all alignments using CODEML (Yang 2007), with following parameters: seqtype = codons, NSsites = 5, and ncatG = 10.

The evolutionary distances between the species sequence were computed using an HKY model (Hasegawa et al. 1985) along with a gamma correction. Tree reconstruction was performed using TREE-PUZZLE (Schmidt et al. 2002) using concatenated sequences of SSRs loci or of the coding sequence regions devoid of SSRs.

We assessed the significance of the differences found among trees using a likelihood ratio test. We specifically tested the difference in branch length, as the topology and the model are identical for all tree reconstructions. To do so, we computed the likelihood of a tested tree on the data and compared it with the maximum likelihood tree. In the maximum likelihood tree, five extra parameters are optimized that correspond to the five branch lengths. In that respect, twice the log likelihood ratio is χ² distributed with five degrees of freedom.

Estimation of the Selection Coefficient

To estimate the selection coefficient associated with a coding SSR, we use a two-allele model (S and P), where S is the deleterious allele. The two models are depicted in figure 1. Although we analyzed a single genome, we assumed that at each SSR locus, there is an independent sampling from the population; therefore, the frequency of loci with an S allele within a genome is an estimator of the average frequency of S at each locus in the population. Each model makes a very different assumption regarding the unobserved states of the loci in the population.

Fig. 1.—

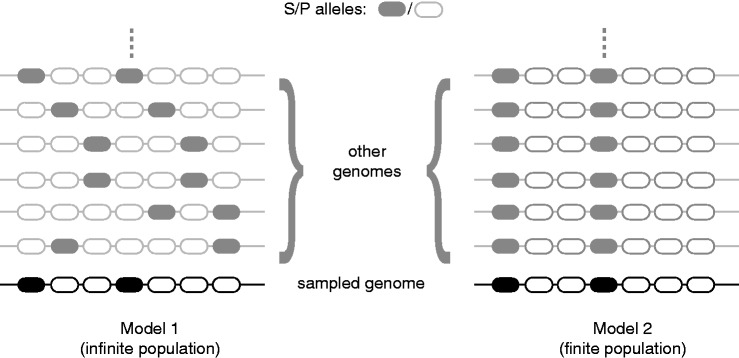
Two models to estimate the fitness cost of mono-SSRs. Schematic representation of two alternative models to estimate the selection coefficient associated with mono-SSRs. Both models assume that each locus evolves independently and has one of the two alleles S or P; the S allele is deleterious. In the first model, the population size is infinite, so that all loci are polymorphic in the population with the same frequency. In that case, the frequency of S for a given locus is estimated by the frequency of S among all loci of the same genome. In the second model, the population is sufficiently small so that polymorphic states are only transient and all loci are fixed for one of the two alleles. In this model, all genomes from the population are identical to the sampled genome.

Mono-X is defined as any motif composed of a single nucleotide repeated exactly X times. Proto-X is defined as a Mono-X motif that contains a single substitution anywhere along the repeat. These two motifs can then be viewed as two alleles of the same locus, each mutating onto the other by a single substitution. S_X represents the mono-X allele associated with a selective cost and P_X the paired proto-X alleles “neutralized” by its interruption. Following the work by Bulmer and co-worker (Bulmer 1991; Eyre-Walker and Bulmer 1995), we estimated the average selection coefficient associated with the S allele under two different models.

Model 1: Infinite Population Size

In the first model (fig. 1, left), the population size is infinite and all SSRs evolve identically but independently. This corresponds to a case where all S alleles have the same selection coefficient(s) and where free recombination occurs between loci. At each locus, the frequency p of the S allele is the same and consequently the expected fraction of loci in a single genome with an S allele equals to p. In this model, p is predicted by a mutation-selection equilibrium. If we define µ as the substitution rate per site, so a P allele mutates in an S allele at a rate cµ; conversely, an S allele mutates to a P allele at a rate dµ. Please note that “c” stands for creation (of the SSR) and “d” for disappearance. The fitness function is w_P/P = 1, w_P/S = 1 − hs, w_S/S = 1 − s. In the heterozygote fitness, h represents the degree of dominance of the S alleles. When h = 0, the S allele is completely recessive and when h = 1, it is completely dominant. Following standard derivations (Hartl and Clark 2006), the frequency after one generation of random mating is:

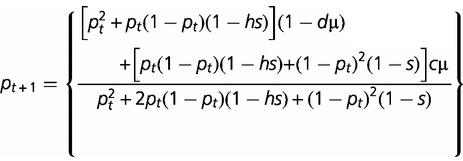At equilibrium (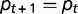), when 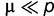, we have:

(1)

Model 2: Finite Population Size

In the second model (Bulmer 1991) (fig. 1, right), the population size, N, is finite and small enough so that any polymorphic state is only transient. At each locus, one of the two alleles is fixed; a fraction p of the loci is fixed for the S allele. When a new mutant is generated, it has a probability Ψ(α) to be fixed with α = 2N_es. Providing that the fitness function is, as in the previous model, w_P/P = 1, w_P/S = 1 − hs, w_S/S = 1 − s, the probability of fixation can be approximated by 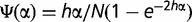, if h ≠ 0 (Rice 2004). The number of P allele loci that mutate to an S allele and become fixed is N(1 − p)cµΨ(−α). Reciprocally, the number of S allele loci that mutate to a P allele and become fixed is NpdµΨ(α). At equilibrium, these two numbers are equal, which leads to

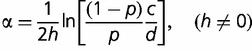(2)

and then s can be computed for a given population effective size, N_e:

Functional Analysis

Gene Ontology (GO) terms associated with human genes were downloaded from the Ensembl database (http://www.ensembl.org/index.html, last accessed January 28, 2013). We estimated that among all mono-8 (S₈ allele) and proto-8 (P₈ allele), the frequency of S alleles is p. Most genes of the human genome are annotated by one or several GO terms. Using the structure of the ontology, we collected for each gene all of the GO terms that are parents of the annotated term and added them to the gene annotation. Then, for each GO term, we tested whether the set of genes that are annotated by the GO term under consideration can be modeled as a random sample of genes. To test this, we computed the probability that, given the number of loci (loci with both P and S alleles) n in the set of genes, we observed at least this number of S alleles. The probability was computed using a cumulative binomial of parameters p and n. As in our previous study (Loire et al. 2009), we performed our tests level by level, to only compare equivalent terms. We define the level of a term as the number of nodes that exists between this term and the root of the graph (level 0). In the case of multiple paths, we kept the shortest one. For each level of the ontology, we performed only one test per term. To correct for multiple tests, we considered terms lying at the same level of the ontology to be independent and therefore can be corrected using the Bonferroni correction. However, we considered that tests between levels to be fully dependent, since they use the same annotations but with different accuracies.

Results

We analyzed the alignments of 5,015 orthologs from human, chimpanzee, orangutan, and macaque. In total, these alignments represent 8,201,087 sites after filtration (see Materials and Methods); a site is one column in the alignment: it is a homologous nucleotide, possibly containing a gap character (“-”). We define an SSR as a tandem exact repeat (no indel or substitution) containing a repeat unit from 1 to 6 bp in size. The union of all sites spanned by a homologous SSR in the different species defines an SSR locus. Because the mono-SSRs considered here are 8 nt or longer, a mono-SSR locus is a section of the alignment with eight sites or more. Accordingly, we found 571 mono-SSR loci, 227 di-SSR loci, 371 tri-SSR loci, 4 tetra-SSR loci, no penta-SSR loci, and 39 hexa-SSR loci. In total, these sums to 1,212 SSR loci, contained in 896 genes, which span 15,811 sites (∼0.2% of all sites).

Evolution of Coding SSRs among the Four Genomes

We split the sites of the alignments into three classes. The first class encompasses all tri- and hexa-SSR loci. We analyzed these SSRs on their own, because an insertion or a deletion of one unit does not alter the reading frame and is therefore more likely to be observed. The second class contains mono-, di-, and tetra-SSR loci. The last class gathers all the remaining coding sequences, devoid of SSRs. For each class, we counted the number of sites that contain at least one substitution or one gap.

Only Tri- and Hexa-SSR Evolve by Expansions and Contractions

Results (table 1 and supplementary table S1, Supplementary Material online) clearly show that for tri- and hexa-SSRs, there are more sites with gaps (indels) than sites with substitutions. However, for other SSRs and the rest of coding sequences, there are about 10 times fewer sites with gaps than with substitutions (P < 10⁻⁸ for any pairwise comparison using a χ² test). All gaps have a length that is a multiple of 3.

Table 1.

Substitutions and Insertions/Deletions

Sequence Type	Total Sites	Indels (% of Total)	Sites Without Indel	Substitutions (% of Sites)	Ts:Tva (% of Sites); Ratio
mono-, di-, tetra-, and penta-SSRs	7,312	130 (1.8%)	7,182	557 (7.7%)	340:206 (4.7%:2.9%); 1.7
tri- and hexa-SSRs	8,499	1,680 (19.8%)	6,819	373 (5.5%)	253:108 (3.7%:1.6%); 2.3
Rest of the coding sequence	8,185,286	31,720 (0.4%)	8,153,566	316,408 (3.9%)	235,381:76,618 (2.9%:0.9%); 3.1

NOTE.—Tri-SSRs and hexa-SSRs were analyzed independently from the other SSRs because insertion–deletion in these SSRs does not alter the reading frame. Both types of SSRs accumulate substitutions two times faster than the rest of the coding sequences.

^aThe numbers of transitions (Ts) and tranversions (Tv) were computed for di-allelic sites only (the tri-allelic sites being necessarily one transition and one transversion).

The length distribution of all coding SSRs has been shown to be very informative to estimate the relative importance of insertions/deletions and substitutions in SSRs (Kruglyak et al. 1998; Sibly et al. 2001; Sainudiin et al. 2004). In that respect, figure 2 shows that, except for very small counts (i.e., <5), the numbers of SSRs decreases geometrically with the number of repeated units for mono-, di-, tetra-, and penta-SSRs. On the contrary, the simple geometric model does not fit for tri- and hexa-SSRs. Tri-SSRs with five or more repeated units are more numerous than would be expected under a simple geometric model (the same holds for hexa-SSRs with four or more repeated units). The excellent fit of a geometric model for coding mono-, di-, tetra-, and penta-SSRs demonstrates that a single mutational rate can interrupt the SSR at each unit regardless of the number of units. This strongly suggests that insertions–deletions do not occur during the evolution of coding mono-, di-, tetra-, and penta-SSR. On the contrary, the overabundance of tri- and hexa-SSRs above some thresholds is very suggestive of expansion events that would create larger tri- and hexa-SSRs than substitutions would do.

Fig. 2.—

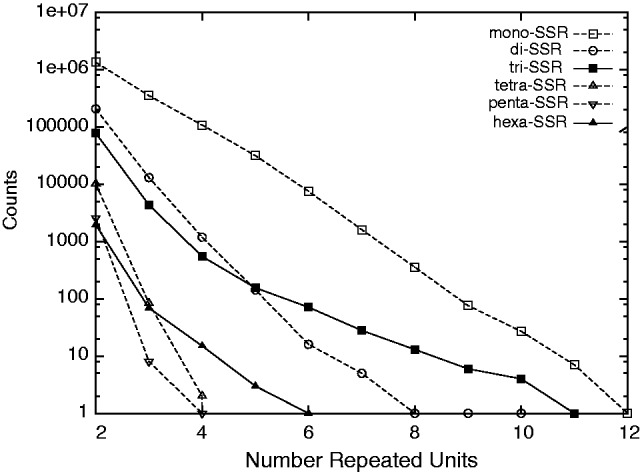
Length distribution of coding SSRs. In this semi-log scale, the numbers of SSRs in the 5,015 human genes decrease linearly with the number of units for mono-, di-, tetra-, and penta-SSRs (except when counts are very small, typically less than 5). On the contrary, although a linear decrease is observed for tri-SSRs with less than 6 units and hexa-SSR with less than 4 units, this trend does not fit for larger sizes. This shows that a simple geometric model fits the data except for tri- and hexa-SSRs, where at least a mix of two geometric variables is required.

Both analyses (i.e., table 1 and fig. 2) lead to the same conclusion: insertions and deletions are only observed for tri- or hexa-SSRs. Very likely, indel events also occur for other types of SSRs but are efficiently removed by purifying selection because of the strongly deleterious impact of frameshifts. Coding mono-, di-, tetra-, and penta-SSRs in coding regions mainly evolve by substitutions and not by insertions and deletions.

All Coding SSRs Evolve Faster Than the Rest of Coding Sequences

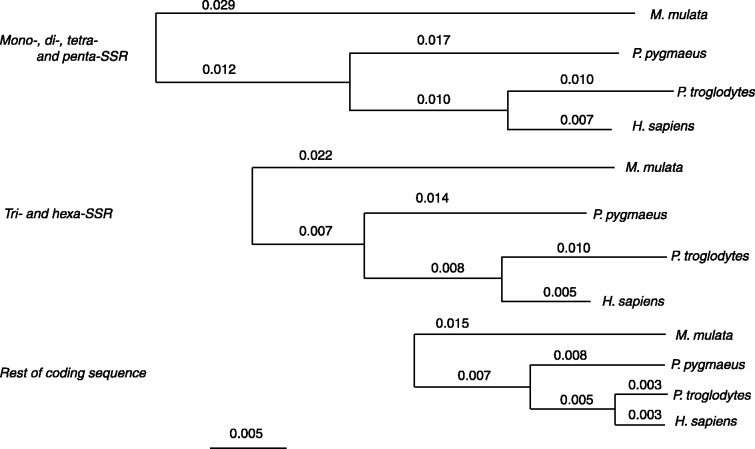
A distance tree, based on substitutions only, shows a highly concordant pattern among all lineages (fig. 3). It is clear that the substitution rate is about two times higher in coding SSRs than in the rest of the coding sequences in the four primate lineages analyzed in our study. The tree with the branch lengths for the rest of the coding sequence is very unlikely for the tri- and hex-SSR sequences (log-LR = 70; P ∼0) and even more unlikely for the mono- and tetra-SSR sequences (log-LR = 139; P ∼0).

Fig. 3.—

Genetic distance in SSRs among primate lineages. Distances were computed on three concatenated alignments; one of the coding mono-, di-, tetra-, and penta-SSRs, one of the coding tri- and hexa-SSRs, and one of the remaining coding sequences. Distances were computed using an HKY model and a Gamma Law and the tree was constructed by TREE-PUZZLE. The macaque genome is used as an outgroup and the root was placed arbitrarily on the branch leading to it. Branches length of coding SSRs exhibit a 2-fold increase when compared with rest of the coding sequences.

To gain insight regarding the cause for this accelerated rate, we computed the ratio of nonsynonymous to synonymous mutations rates in all codons. The number of genes where this ratio is higher within mono-, di-, tetra-, and penta-SSRs than in the rest of coding sequence is much smaller than its counterpart (198 vs. 418, P = 7 × 10⁻¹⁹ using a χ² test). The same applies to the ratio within tri- and hexa-SSRs when compared the rest of coding sequence (72 vs. 162, P = 4 × 10⁻⁹ using a χ² test). This suggests that the higher substitution rate is likely not a consequence of a higher fixation rate. We also counted independently the number of transitions and transversions. Table 1 (and supplementary table S1, Supplementary Material online) shows that, even though both rates are increased, the proportion of transversions is higher for coding SSRs (1.82 increases between the ratios of mono-, di-, and tetra SSR loci and the rest of coding sequence), suggesting a change in the mutation spectrum.

The Number of Coding SSRs Is Likely at Equilibrium

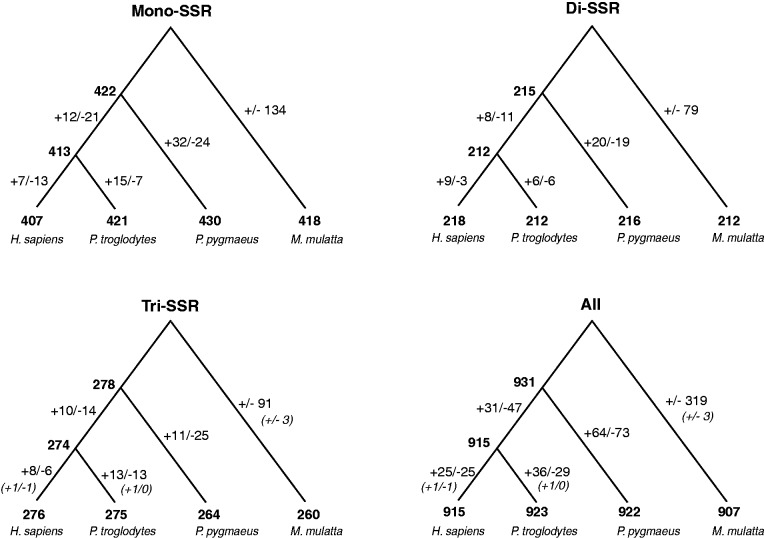
To test whether there was a tendency to lose or gain coding SSRs in the different primate lineages, we reconstructed the sequences of the human–chimpanzee ancestor as well as the human–chimpanzee–orangutan ancestor and detected all SSRs in these two ancestral genomes. In figure 4 (and supplementary table S2, Supplementary Material online), we report the number of coding SSRs loci in the alignment of the six genomes along with the number of gains and losses in each branch. Since the reconstruction of ancestral states for sites with gaps is problematic, we restricted the analysis to only sites with no indel in any species. The gains and losses were computed by comparing the state of each SSR locus in each genome (presence or absence of the SSR allele). Because the ancestral state of the root is unknown, we cannot distinguish gains and losses in the macaque lineage. Interestingly, for tri-SSRs, we observed few SSR fissions (i.e., one SSR giving rise to two) and SSR fusions; their totals are given in parentheses.

Fig. 4.—

Dynamics of SSRs among primate lineages. The evolution of SSR loci is represented on a cladogram of the four primate lineages. The numbers of loci are figured on nodes, while gains (+) and losses (−) are depicted on the branches. In parentheses (for tri-SSRs), the numbers of fusion (two SSRs merged in one) and fission (one SSR split in two) events are provided. We report counts for mono-, di-, and tri-SSRs as well as all pooled SSRs. Since the genome at the root cannot be reconstructed, gains and losses are undistinguishable in the macaque lineage. For all SSRs and all branches, the number of gains and losses are not significantly different (χ² tests).

Our results show that the numbers of SSRs are similar in all six genomes, regardless the type of SSRs. Because several gains and losses occurred for all types of SSRs, their number has likely reached equilibrium. Importantly, the numbers of gains do not differ significantly from the number of losses (using χ² tests) in mono-SSRs (66 vs. 65, NS), di-SSRs (43 vs. 39, NS), tri-SSRs (42 vs. 58, NS), or in all SSRs pooled together (156 vs. 174, NS)—numbers in the macaca lineage are not included here. When tested independently, no branch shows a significant difference between gains and losses when corrected for multiple tests (the largest difference is 15 vs. 21 in the P. pygmaeus branch for tri-SSRs; this difference leads to χ² = 5.44; P = 0.02, which is not significant when several branches are tested).

This observation is in good agreement with the hypothesis that SSRs have reached equilibrium, where gains of new SSRs are balanced with losses.

A Closer Look at the Evolution of Mono-SSRs

Mono-SSRs cannot have overlapping sequence motifs and therefore have a simple one-to-one correspondence between the number of repeated units and the length of the SSR. Other types of SSRs show more complex patterns that highly increases the complexity of models. We therefore chose to focus our subsequent analyses on mono-SSRs to estimate the selective cost of coding SSRs. We hypothesize that the selective cost of mono-SSRs is characteristic of all SSRs whose unit sizes are not multiple of 3 and that our results can be extended qualitatively to di-, tetra-, and penta-SSRs.

Mono-SSRs of 8 Units Are at Equilibrium

We first decided to focus more specifically on the mono-SSRs of exactly 8 units (mono-8), the smallest mono-SSRs that show a high propensity to mutate by slippage in noncoding regions. These sequences, along with the two nucleotides at their edges, are 10 bp long. Note that the two edges of an SSR of exactly X repeated units cannot be the same nucleotide as the SSR itself.

Complementarily, we also analyzed the related proto-SSR of size 8, which we define as sequences that can be turned into a mono-8 by a single mutation (they differ from mono-8 by only one nucleotide). Please note that we excluded all mono-SSRs of 9 or more units from these proto-8.

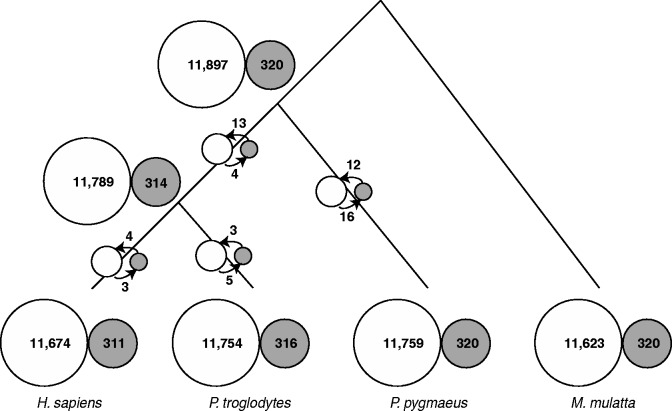
A mono-8 (hereafter an S₈ allele) and a proto-8 (hereafter a P₈ allele) are two alternative alleles for an SSR locus. Clearly, other alleles can be observed for an SSR locus, but our focus is only on S₈ and P₈ alleles. Because we assume that SSRs are at equilibrium, the existence of other states does not alter the following reasoning. The P₈ alleles are presumably neutral and the S₈ alleles are presumably negatively selected, because of their propensity to expand and contract (Metzgar et al. 2000; Ackermann and Chao 2006; Loire et al. 2009). The numbers of loci with an S₈ allele and with a P₈ allele are reported on the nodes of a cladogram (fig. 5). On the branches, we also report the number of mutations of S₈ into P₈ and vice versa. Note that these numbers alone do not explain the differences between the genomes, since other states are not reported here.

Fig. 5.—

Dynamics of S₈ and P₈ alleles among primate lineages. At each node, we report the number of S alleles (mono-SSRs of size 8) in the smaller dark circle and the number of P alleles (a sequence that can be turned into a mono-8 by a single substitution) in the larger clearer circle. On the branches, we report the number of mutations of S₈ into P₈ alleles as well as the reverse ones.

Again, we observe that the numbers of S₈ and P₈ alleles in all genomes are very similar even though S₈→P₈ and P₈→S₈ mutations are observed. We conclude from this that mono-8 and proto-8 have likely reached equilibrium in these lineages.

A Mutation-Only Model Does Not Fit the Data for Mono-SSRs of 7 Units or More

On average, there are 11,105.5 loci with a P₈ allele and 315.7 loci with an S₈ allele. This translates into an average frequency of the S allele of p = 0.026.

The frequency of S₈ alleles is variable among the four types of mono-SSRs of 8 units. Indeed, the average estimates of p are 0.04 (251.833 S₈ and 5996.5 P₈ alleles) for poly-A, 0.009 for poly-C (24.5 S₈ and 2667.8 P₈ alleles), 0.008 for poly-G (11.8 S₈ and 1527.8 P₈ alleles), and 0.017 (27.5 S₈ and 1555.5 P₈ alleles) for poly-T. This observation suggests that the selective cost of S₈ alleles depends on the composition of the SSR itself, with the poly-G and poly-C being more deleterious. It is noteworthy to mention that poly-C and ploy-G are less abundant in both coding and noncoding sequences (e.g., Loire et al. 2009), suggesting that other factors besides natural selection (e.g., alternative mutational mechanisms) could operate on coding SSRs.

In a mutation-only model, the frequency of S allele, p, simply results from the rates of creation and disappearance under the assumption of equilibrium. In this mutation-only model, we would expect the frequency of S to be µ_c / (µ_c + µ_d), where µ_c is the rate of creation and µ_d the rate of disappearance of S₈ alleles. Because creation and disappearance are both substitutions, they can be expressed as a function of µ. The average substitution rate per site for creation and disappearance of S₈ allele are µ_c = c × µ and µ_d = d × µ, respectively. Given this, the frequency of S is expected to be c/(c + d).

Assume a model with a single mutation rate (the JC model, for Jukes–Cantor). For a given P₈, we have to consider two cases. First, the interruption is located within the repeated pattern, and therefore only one substitution can create the S₈ allele (one site where only one of the three possible substitutions creates the SSR). Second, the P₈ interruption occurs at the edge (i.e., the P₈ is an S₇ allele), and therefore two mutations can create the S₈ allele, one at each edge (two sites for which only one of the three possible substitutions creates the SSR). If we define f₈ as the fraction of P₈ of the latter case (that is an S₇ allele), we can compute the creation rate as c = (1 − f₈) × 1/3 + f₈ × 2/3 = (1 + f₈)/3. We further assume f₈ to be 2/8, i.e., two of the eight sites are located at the edges. This translates into c = 5/12. As for the disappearance rate, d, any of the SSR nucleotides can be changed into any different nucleotide. We thus set d = 8 for the mutation of an S₈ allele to a P₈. Given this, we would expect, under the JC model, a frequency for the S₈ allele of 0.050.

We thus assume a second model with two mutation rates, one for transversion and one for transition (the K2p model, for Kimura 2 parameters). For the rate of creation, we must treat interrupting sites differently depending on whether there are transitions or transversions. Define κ as the ratio between of the rates of transition and transversion and λ the fraction of interrupting sites that are transitions. Given these, one can show that c = (1 + f₈)[λ × κ/(κ + 2) + (1 − λ)/(κ + 2)] and d = 8. With either κ = 1 (a unique mutation rate) or λ = 1/3 (the interrupting base is, on average, any of the three other nucleotides with equal chance), the expected ratio c/(c + d) is identical to the JC model. The expected frequency for the S₈ allele under the K2p model is larger than the one under the JC model when λ > 1/3 (with κ ≥ 1). Here, among the interrupting sites of P₈ loci, we observe a fraction λ = 0.47 of transitions; assuming κ = 6 (based on table 1; since there are two possible transversions for each transition, κ = 2 × Ts:Tv), this leads to an expected frequency for the S₈ allele of 0.061.

The ratio observed/expected for the frequency of S₈ alleles is 0.026/0.050 = 0.52 under the JC model and 0.026/0.061 = 0.42 under the K2p model. We hypothesize that this underrepresentation is caused by the selective advantage of the P₈ allele over the S₈ allele.

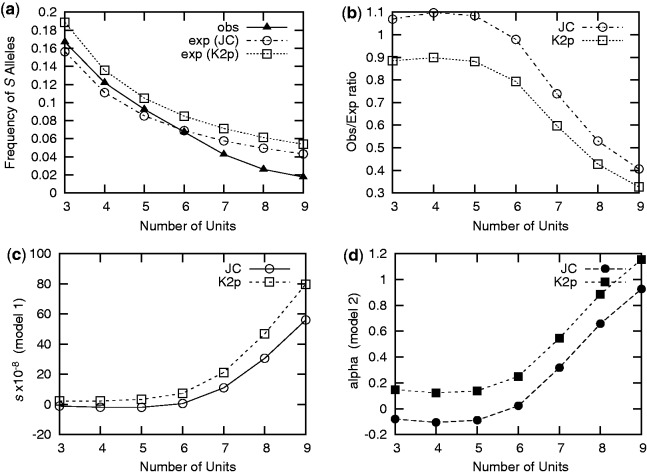
We then generalized this to other mono-SSRs and proto-SSRs of X repeated units. For a mono-X, we expect a frequency for the S_X allele of c/(c + d), where c = (1 + f_X)/3 for the JC model, c = (1 + f_X)[λ × κ/(κ + 2) + (1 − λ)/(κ + 2)] for the K2p model (setting λ = 0.47 and κ = 6) with f_X = 2/X and d = X for both models. For mono-SSRs of 3 to 9 units, we computed the observed and expected frequencies of S alleles as well as the ratio between observed and expected frequencies (fig. 6a and b; also see supplementary table S3, Supplementary Material online). We did not consider SSRs longer than 9 units in the analysis because their abundance was too low to have reliable estimates of observed frequencies (e.g., we observe only an average of 26.7 mono-10 in the alignments).

Fig. 6.—

Selective costs of mono-SSRs of various size. (a) In the top left panel, we report the observed and expected frequencies of S alleles for mono-SSRs of 3–9 units. (b) In the top right, we report the observed/expected ratio of frequencies for S alleles. (c and d) The bottom panel reports the estimated selective cost (either s or α) for two models introducing selection, for codominant alleles (h = 0.5). In the first model (c), only selection and mutation are modeled (infinite population), whereas in the second model (d), genetic drift is also considered (finite population).

From figure 6a and b we can conclude that, for small SSRs, the JC model slightly underestimates the frequencies whereas the K2p model slightly overestimates it. For SSRs with 7 units or more, both models largely overestimate the frequency of S₈ allele. The observed/expected ratio reaches 0.4 for mono-SSRs of 9 units (0.33 for the K2p model). Again, we interpret this difference as a consequence of the negative selection that acts against mono-SSRs longer than 6 units in the coding sequences. The negative impact is likely stronger for longer SSRs, as their propensity to contract and expand is higher. The observation that the frequencies of S alleles for poly-C/G are smaller than for the ones for poly A/T (see above for 8 nt) holds for other sizes, suggesting that poly-C/G are more deleterious than poly-A/T whatever their sizes (data not shown).

Estimation of the Selective Cost of Mono-SSRs

Since the mutation-only model cannot adequately predict the frequencies of long SSRs, we used the observed frequencies to estimate the fitness cost of mono-SSRs, focusing first on mono-8. We considered two alternative models where the S alleles are underrepresented because of their lower fitness value. Both creations and disappearances occur and selection acts against the S alleles. The expected frequency of the S alleles depends on the mutation rate and on the fitness function. Based on two alternative assumptions on the effective size, we used two alternative models to estimate the average fitness cost of the S alleles (fig. 1). In both models, there is the implicit assumption that the fitness cost associated with the S allele is equal at every loci.

In the first model (fig. 1, left), the population size is assumed to be infinite and all SSR loci evolve independently. In such a model, all loci are polymorphic and the frequency of the S alleles is equal at each locus. The expected frequency is given by the mutation-selection equilibrium. We used µ = 2 × 10⁻⁸ per generation, twice the average mutation rate in primates (Drake 1999). Results (table 2) show that, under those assumptions, the selection coefficient for the S₈ alleles range from 9 × 10⁻⁶ to ∼10⁻⁷, depending on the dominance of the S allele over the P allele and the mutational model (JC or K2p).

Table 2.

Estimation of the Fitness Cost of a Mono-SSR of 8 Units

	Model 1 (Selection and Mutation)	Model 2 (Selection, Mutation, and Drift)
h	s × 10−7	α	s × 10−7
0	58.2 (89.1)	—	—
0.1	12.6 (19.4)	3.3 (4.4)	1,645.7 (2,216.0)
0.5	3.1 (4.7)	0.7 (0.9)	329.1 (443.2)
1	1.6 (2.4)	0.3 (0.4)	164.6 (221.6)

Note.—In the first model (fig. 1, left), the population size is assumed to be infinite. In this case, drift is neglected and the selection coefficient s is computed using equation 1. In the second model (fig. 1, right), population size is finite and α = 2N_es is computed under equilibrium between selection, mutation, and drift using equation 2. Numbers in regular typeface are given assuming a JC mutational model; numbers in parentheses are computed assuming a K2p mutational model. The following values were used in the equations: c = (1 + 2/8)/3 for the JC model and c = (1 + 2/8)[0.47 × 6/(6 + 2) + (1 − 0.47)/(8 + 2)] for K2p model, d = 8, µ = 2 × 10⁻⁸, P = 0.026, N_e = 10⁴.

In the second model (fig. 1, right), the population size is assumed to be finite and the time in which a locus is polymorphic is negligible. All loci are fixed for either the S or the P allele. The proportion of loci that are fixed for the S alleles results from an equal number of fixation events of S and P alleles. The fixation probabilities are given by standard diffusion results, which are not available for the case of h ∼ 0. The estimated selective coefficients, for the S₈ alleles, range from α (=2N_es) ∼ 0.3 to α ∼ 4. No numerical value is available for h = 0. However, one could hypothesize that, in this second model, the increase in s between h = 0.1 and h = 0 is identical to the first model. This would result in a hypothetical largest value of α ∼ 20 for h = 0. This suggests that mono-8 have a moderate impact on fitness when compared with their counterpart (proto-8). If we assume that the human effective population size is N_e = 10,000 (Hill 1981), this translates into selection coefficients that are in the vicinity of 10⁻⁵ (table 2). This is about one hundred times larger than the selection coefficients estimated with the first model. Importantly, if we used N_e = 10⁵, the estimated effective population size for the human–chimpanzee ancestor (Takahata et al. 1995), the differences between both model would be approximately 10. Irrespective of the correct value for N_e, we would like to emphasize that estimations of α remain an order of magnitude below the value above which positive selection is strong enough to induce a selective sweep (see textbook, e.g., Rice 2004). In that regard, S alleles can be viewed as slightly deleterious alleles.

To assess the fitness impact of other mono-SSRs, we computed estimates of the selection coefficients for mono-SSRs of 3 to 9 units, using a fixed value h = 0.5. Results (fig. 6c and d) show that the selective cost of mono-SSRs increases with the number of units.

Fitness Cost of Mono-SSRs Varies from Function to Function

Although the average P can be computed for all mono-8/proto-8 loci, we wanted to test further if some functional groups (as defined by GO annotations) show more or less selective constraint than others. The frequency of the S₈ allele, computed among the 21,416 annotated human genes, is identical to the frequency we observe in our restricted set of 5,015 orthologous genes. Therefore, we tested for each functional category as defined by a GO term, whether the observed number of S₈ alleles is significantly above or below the expected number. These results are presented in supplementary table S4, Supplementary Material online. As one would expect, some functional groups of genes (development-related genes) show fewer S₈ alleles than expected, while others show a significant enrichment (genes involved in DNA maintenance, cell death, and lipid degradation). Thus, it is tempting to hypothesize that a reduction in S₈ alleles is a consequence of stronger purifying selection against the S alleles whereas enrichment suggest a relaxed purifying selection.

Discussion

In this study, we investigated the evolution of coding SSRs in a phylogenetic context. Our study revealed several previously unknown features of the evolutionary dynamics of coding SSRs in primate lineages, which could be extended to coding SSRs in genomes of other genera. Although SSRs represent only a small fraction of the genes (0.2% of the coding sites), they cannot be disregarded as far as mutability is concerned. Genes with such sequences are much more likely to generate null alleles or negative dominant alleles. Although the main focus of our study is on mono-, di-, tetra-, and penta-SSRs, we used tri- and hexa-SSRs mostly as controls.

We show that, except for tri- and hexa-SSRs, the evolution of SSRs in the primate lineages occurs mostly by substitution. This has to be interpreted as the deleterious effect of insertion/deletion events in a coding sequence. Whenever the length of an insertion or a deletion event is not a multiple of 3 (as it would be for tri- and hexa-SSRs), it generates a null allele for the gene (or in the worst case, a dominant negative allele). As a consequence, it is very likely that even though indels occur frequently, they are filtered out by selection. Inspection of polymorphisms among different populations may help to confirm this hypothesis and we leave it as a promising avenue for future work.

This study shows that coding SSRs are frequently created and lost in the course of evolution. Interestingly, their absolute numbers remain constant in the different primate lineages. This strongly supports the hypothesis that coding SSRs have reached equilibrium. It is, however, possible that the forces involved are weak and that only a larger dataset could unravel differences between the species. We can, however, safely assume that coding SSRs are likely close of being at equilibrium; otherwise major differences between species would be observed. Because of this “equilibrium” in the lineages, we can assume that the evolutionary forces involved are constant since the divergence of these genomes. We have then estimated the fitness costs associated with mono-SSRs of size varying from 3 to 9 (S alleles) when compared with their paired proto-SSR sequences (P alleles). We show that, for mono-SSRs of 7 units or more, the frequency of S alleles is smaller than expected by models of mutations only. In light of previous studies (Metzgar et al. 2000; Borstnik and Pumpernik 2002; Ackermann and Chao 2006; Loire et al. 2009), we conclude that this difference is very likely due to the purifying selection that acts against coding SSRs.

Interestingly, we observe, for mono-SSRs of 5 units or fewer, more S alleles than expected under the JC model and fewer S alleles than expected under the K2p model. Although the difference between observed and expected is not large for small mono-SSRs, we suspect that this is a consequence of the imperfect mutation models. The mutation pattern is very likely more complex (e.g., Amos 2010). This suggests that our mutation-only model slightly misestimates the expected frequency of S allele. In that regard, it seems difficult to simply generalize these mutational models to SSRs of larger motifs (e.g., di-SSRs), since their mutation rates will not be equal at all positions.

Using two alternate models, we estimated the selective cost of mono-SSRs when compared with the paired proto-SSRs for SSRs of 3 to 9 units. The first model (infinite population size) suggests that, even for SSRs of 9 units, the fitness cost of such an allele is very small (in the order of s = 10⁻⁷) unless it is completely recessive, whereas the second one (finite population) suggests that S alleles are slightly deleterious (the more recessive, the more deleterious). Because mono-SSRs are underrepresented in coding sequence and because primate populations are far from being infinitely large, we favor the hypothesis under which mono-SSR of 7 units or more are slightly deleterious (α = 2N_es is in the vicinity of [1,10]) when compared to the proto-SSR. The infinite population size model should be interpreted as giving a lower limit to the selective costs we infer. The fitness cost of S₈ alleles is similar to the one that acts on nonpreferred codons for codon usage in Drosophila melanogaster, which has been recently estimated to be α ∼ 1 (Zeng and Charlesworth 2010). The analysis of genomes from species of unrelated taxa with larger effective population size would help in characterizing the fitness cost of coding SSRs.

Importantly, in the both models, we observe that the longer the SSR, the higher the selective cost. We think that this correlation is a direct consequence of the mutability of the SSR. Indeed, their propensity to generate size variance (through insertions and deletions) increases exponentially with the number of units. As their chance of introducing a frameshift increases, we could hypothesize that the associated selective cost increases. We would like to emphasize that other factors likely also operate on coding SSRs and can modulate their frequencies in genes. This includes, for example, negative selection against SSR structure (regardless of their coding capacity) or mutational mechanisms that acts specifically against SSR (as it is suggested by the high substitution rate we report here).

The strength of selection that acts to remove mono-SSRs from coding sequences is very likely to vary from function to function and even from gene to gene. Many factors will influence the fitness cost of a mono-8. Some factors will be a consequence of the SSR structure itself [e.g., its composition (Jurka and Pethiyagoda 1995) or of its genomic environment (Li et al. 2002)]. Others will be related to the gene that hosts the SSR. The transcriptional activity of the gene is one obvious factor (Fabre et al. 2002); another one could be the functional class of the gene. To address this last point, we analyzed all functions defined by GO annotations that are annotated in the human genome. We show that, among all these functions, there are a set of functions, all of which are part of the developmental processes, which contain fewer proto-8 than expected. It is tempting to postulate that these genes are under strong purifying selection because early mutations in the somatic line may have a large impact. However, the analysis of the exact nature of the factors that explain the range of the selective cost is outside the scope of this study. We emphasize that the estimate of the selective coefficient we report here is only an average and that many factors will influence its value. The exact nature of the factors that are the most important on the fitness cost of coding SSRs remains to be elucidated.

One interesting aspect of the coding SSRs is their propensity to have both a long-term impact, through replication of the germline, and a short-term impact, because of the somatic line replications and the generations of abnormal transcripts. The long-term effect is difficult to fully characterize, because the SSR is only a pre-deleterious allele and its impact on fitness will be only moderate unless the deleterious frame-shifted allele is extremely likely to appear and is associated with a strong impact on fitness. The short-term effect, on the other hand, has a direct consequence on the fitness of the individual since it may alter the fitness of the individual itself. This is true if the SSR is located in a gene that is highly transcribed, since the energy loss due to abnormal transcriptions might be high enough to impact fitness. This is also true if the gene is essential before the reproductive age (e.g., genes implicated in development, as seen in supplementary table S4, Supplementary Material online). Most of the cancers that are caused by coding SSRs appear after the reproductive age and therefore only moderately impact the fitness of the individual.

One of the most unexpected results from this study is the accelerated substitution rate in coding SSRs when compared with the rest of the coding sequence. This accelerated substitution rate may be the consequence of either a higher mutation rate or a higher fixation rate. Because the ratio of nonsynonymous substitutions to synonymous ones is smaller in coding SSRs than in the rest of coding sequences and because the transitions to transversions ratio show a large difference (at most a 1.82 increase), we favor the first hypothesis as a major cause. Interestingly, the sites at the edges of mono-SSRs (we extracted 10 sites on each side) show a Ts:Tv ratio of 2.6 that is close to the one observed for the rest of coding sequence, discarding a potential local mutational bias. This would be in line with the observation that repetitive sequences show an accelerated evolution in noncoding regions as well (Pumpernik et al. 2008). Indeed, it is possible that SSRs are epigenetically modified (Libby et al. 2008), which would then change their intrinsic mutation rate. Interestingly, because the ratio of transversions to transitions is higher in coding SSRs, we suspect that the mutational mechanism is not only increased but also shifted in its spectrum. However, although the accelerated substitution rate is a robust observation, our explanation remains at this stage hypothetical. Only via a thorough analysis of noncoding SSRs could we strengthen our hypothesis.

Finally, the interplay of accelerated substitution rate on microsatellites and the weak selection toward disruption of harmful, repeated sequences highlight a neglected feature of gene evolution. Indeed, synonymous substitutions are silent in terms of protein evolution, but we show that a small fraction of them may be subject to DNA-stability-related selection when they interrupt coding microsatellites. This could slightly bias dN/dS ratio tests as well as population genetic studies and, as a result, deserves to be further evaluated in a systematic approach.

Supplementary Material

Supplementary tables S1–S4 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).