Antagonistic versus non-antagonistic models of balancing selection: Characterizing the relative timescales and hitchhiking effects of partial selective sweeps

Abstract

Antagonistically selected alleles -- those with opposing fitness effects between sexes, environments, or fitness components -- represent an important component of additive genetic variance in fitness-related traits, with stably balanced polymorphisms often hypothesized to contribute to observed quantitative genetic variation. Balancing selection hypotheses imply that intermediate-frequency alleles disproportionately contribute to genetic variance of life history traits and fitness. Such alleles may also associate with population genetic footprints of recent selection, including reduced genetic diversity and inflated linkage disequilibrium at linked, neutral sites. Here, we compare the evolutionary dynamics of different balancing selection models, and characterize the evolutionary timescale and hitchhiking effects of partial selective sweeps generated under antagonistic versus non-antagonistic (e.g., overdominant and frequency-dependent selection) processes. We show that that the evolutionary timescales of partial sweeps tend to be much longer, and hitchhiking effects are drastically weaker, under scenarios of antagonistic selection. These results predict an interesting mismatch between molecular population genetic and quantitative genetic patterns of variation. Balanced, antagonistically selected alleles are expected to contribute more to additive genetic variance for fitness than alleles maintained by classic, non-antagonistic mechanisms. Nevertheless, classical mechanisms of balancing selection are much more likely to generate strong population genetic signatures of recent balancing selection.

INTRODUCTION

Opposing selection between environments, between individual fitness components or life history stages, or between the sexes, can generate antagonistic selection at a population genetic scale (Prout 2000). Antagonistically selected alleles are those that improve fitness in some environmental contexts, while reducing fitness in others. Examples include antagonistic selection between spatially or temporally variable environments (Levene 1953; Felsenstein 1976; Hedrick et al. 1976; Hedrick 1986), between individual fitness components (i.e., “antagonistic pleiotropy”; Curtsinger et al. 1994), and between males and females (i.e., “sexual antagonism” or “intra-locus sexual conflict”; Rice and Chippindale 2001; Gavrilets and Rice 2006), with the latter receiving considerable recent attention and empirical support (Bonduriansky and Chenoweth 2009; Van Doorn 2009; Connallon et al. 2010). When individual alleles are subject to opposing selection, they can potentially evolve to intermediate population frequencies by way of balancing selection, and thereby disproportionately contribute additive genetic variation to fitness components (Charlesworth and Hughes 1999; Connallon and Clark 2012).

Although the empirical literature of antagonistic selection often emphasizes the potential contribution of balanced polymorphisms to fitness variance, theoretical population genetics has, in contrast, emphasized two restrictions relevant to hypotheses of balancing selection. First, a relatively small subset of the parameter space of antagonistic selection will generate balancing selection (Prout 2000; Hedrick 2007; Patten and Haig 2009), particularly when selection coefficients are small, as is generally expected for most mutations (Eyre-Walker and Keightley 2007). Second, even when parameter conditions for balancing selection are met, the effective strength of antagonistic selection (with selection scaled by the effective population size, N_e) may plausibly be too weak to maintain stable polymorphisms (Connallon and Clark 2012).

These restrictions do not negate the possibility of maintaining balanced polymorphisms by antagonistic selection. Indeed, if the effective population size is sufficiently large, and antagonism is sufficiently common throughout the genome so that some loci meet the requisite parameter conditions, then balanced polymorphisms are certainly possible. Nevertheless, there is a third factor that may additionally constrain evolution to a balanced polymorphism. Simulations by Livingstone (1992) demonstrate that, for some specific cases of antagonistic selection, evolutionary convergence to a balanced polymorphic state can be excruciatingly slow. In some of the examined cases, the approach to equilibrium requires tens of thousands of generations, despite moderately sized selection coefficients.

Slow evolutionary convergence rates, should these apply generally, have three broad implications for antagonistically selected loci and genetic variation. First, the slow approach to equilibrium places a lower limit on the age of alleles maintained as balanced polymorphisms. Alleles near equilibrium must be relatively old, which implies a striking degree of parameter constancy during long timescales of evolutionary convergence. Recent bouts of balancing selection may provide insufficient time for alleles to reach intermediate population frequencies. A second (and related) point is that populations may typically be far from evolutionary equilibrium at loci subject to antagonistic selection. Assumptions about the prevalence of equilibrium versus nonequilibrium population conditions should impact interpretations of the data on genetic variation, as well as the empirical predictions associated with models of antagonistic selection and variation. Lastly, the age and the rate of spread of selected alleles will impact patterns of heterozygosity and linkage disequilibrium (LD) at linked, neutrally evolving sites – the signals often used to identify genomic regions responding to recent selection (e.g., Sabeti et al. 2002; Nielsen 2005; Voight et al. 2006; Charlesworth 2006). Opportunities to detect candidate genome regions under short-term balancing selection are therefore contingent upon the rate at which selected alleles spread within a population.

There is currently no formal theory to describe the timescale to equilibrium for, or the hitchhiking effects associated with, alleles that are evolving under antagonistic balancing selection. Such an analysis may prove both useful and timely, particularly given the recent, compelling evidence for sexually antagonistic quantitative genetic variation in a variety of animal and plant systems (e.g., Chippindale et al. 2001; Fedorka and Mousseau 2004; Foerster et al. 2007; Brommer et al. 2007; Cox and Calsbeek 2010; Innocenti and Morrow 2010; Mokkonen et al. 2011; Delph et al. 2011; Lewis et al. 2011). Here, we provide a general analytical treatment of partial selective sweeps under antagonistic balancing selection. We first show that transit times of antagonistically selected alleles to equilibrium are expected to be extremely long, relative to the transit times of alleles evolving under non-antagonistic scenarios of balancing selection. We then consider the hitchhiking effects associated with different balancing selection scenarios, and show that antagonistic selection models are expected to leave weak signals of short-term balancing selection. These results have direct implications for the interpretation of population genomic data, and for opportunities to identify candidate loci evolving under short-term balancing selection.

MODEL AND RESULTS

Background and assumptions

Each model of balancing selection follows the evolutionary dynamics of a locus with two alleles: A₁ is the ancestral allele and A₂ is derived. Throughout the analysis, we characterize the trajectory of A₂ as it enters the population and spreads toward the equilibrium frequency. This approach facilitates assessment of the waiting time to equilibrium under each model, as well as the hitchhiking effects of the A₂ allele as it spreads within the population. We initially focus on autosomal inheritance, and explicitly contrast models of overdominant selection and antagonistic balancing selection (see Table 1). We later extend these results to models involving negative frequency-dependent selection and X-linked inheritance.

Table 1.

Relationship between genotype and fitness for overdominant and antagonistic selection models of balancing selection.

	A1A1	A1A2	A2A2
Overdominant selection	1 − s1	1	1 − s2
Antagonistic selection
Fitness context 1	1	1 − h1s1	1 − s1
Fitness context 2	1 − s2	1 − h2s2	1

Our general model of antagonistic selection involves two fitness contexts, which may be taken to represent: (1) distinct and equally abundant ecological niches encountered by individuals within a population (hereafter “niche antagonism”; this is the simplest version of Levene’s (1953) model; see Prout 2000); (2) distinct fitness components that jointly influence total fitness of individuals within a population (“antagonistic pleiotropy”); or (3) distinct sexes (male and female) that experience opposing selection for a pair of alleles at a single locus (“sexual antagonism”). Genotypic fitnesses for antagonistic selection and overdominance models are defined by two selection coefficients each (s₁, s₂), and for cases of antagonistic selection, dominance terms (h₁, h₂) specify the fitness of heterozygotes relative to homozygotes within each selection context.

To simplify the presentation, we focus on the results of several idealized, symmetrical dominance models, where h = h₁ = h₂ ≤ ½. As noted elsewhere (Prout 2000; Connallon and Clark 2012), the strictly additive case (h = ½) yields results that are typical of the more general case of “parallel dominance” (i.e., where A₁ is equally dominant to A₂ within both fitness contexts). Favorable reversals of dominance (i.e., within each fitness context, the “best” allele is always dominant to the “worst” allele; A₁ is dominant to A₂ in fitness context 1 and A₂ is dominant to A₁ in fitness context 2 of Table 1; h₁ < ½ and h₂ < ½) are well represented by the specific case, h = h₁ = h₂ < ½. We note that, while favorable dominance reversals are predicted to emerge under biologically plausible conditions (Gillespie 1978; Fry 2010; Connallon and Clark 2010), concrete empirical examples of such phenomena are currently lacking.

In modeling allele frequency trajectories under each model, we make two key assumptions:

1. Selection coefficients are small (0 < s_i, s_j ≪ 1). Given extensive evidence that the vast majority of mutations have small fitness effects (e.g., Eyre-Walker and Keightley 2007), the first assumption should generally be reasonable, in which case the analytically tractable approximations that we use below closely mimic exact allele frequency dynamics (Fig. S1). Violation of this assumption, does not, however, alter our conclusions about the relative times to equilibrium or hitchhiking effects of antagonistic versus non-antagonistic models (see Fig. S2). Several prior studies make use of similar approximations (e.g., Robertson 1962; Ewens and Thomson 1970; Connallon & Clark 2012; Mullon et al. 2012).

2. Balancing selection is strong compared to genetic drift. This assumption specifically applies when the expected allele frequency change per generation greatly exceeds the binomial sampling variance in a Wright-Fisher population with effective size N_e[i.e., when E(Δq) ≫ q(1 − q)/(2N_e), where q is the frequency of A₂, and E(Δq) is the expected change due to selection (see below)]. Under the balancing selection scenarios considered here, drift-dominated evolution will tend to decrease expected rates of allele frequency change within the population and will likewise dampen the effects of hitchhiking. Our results therefore define an upper limit for the rate of evolutionary convergence to equilibrium, or magnitude of hitchhiking.

The life cycle for each model includes, in order: birth, selection, and fertilization. Mating is random with respect to polymorphism at our locus of interest, and generations are discrete. Analytical results were tested against stochastic computer simulations using R (R Development Core Team 2012), and follow the frequency trajectories of successfully invading A₂ alleles or the linked loci that A₂ initially associates with when the allele is first introduced into the population. Individual runs were initiated with a single copy of A₂, and terminated when A₂ attained a specified fraction of the distance to equilibrium. Exact, deterministic recursions were used to calculate the expected allele or haplotype frequencies across single time steps, and multinomial sampling was used to mimic the effects of genetic drift in a Wright-Fisher population.

Allele frequency trajectories

Deterministic change

Under conditions stated above (and for now, ignoring the effects of genetic drift), allele frequency change across a single generation will be a function of population heterozygosity, equilibrium allele frequency of A₂ (q̂, which by definition of balancing selection must be between zero and one), and the combination of selection parameters (s₁, s₂, h) relevant to each model. For overdominant selection, allele frequency change is given by:

$$\mathrm{\Delta }q\approx 2\mathit{\text{sq}}(1-q)(\widehat{q}-q)$$ (1)

(Robertson 1962; Ewens and Thomson 1970), where s is the average of the two selection coefficients; s = (s₁ + s₂)/2. Antagonistic selection results differ between the specific scenarios of antagonistic pleiotropy and niche or sexual antagonism (see Appendix 1). Under antagonistic pleiotropy, allele frequency change is given by:

$$\mathrm{\Delta }q\approx 2s[1-h(2-\mathit{\text{sh}})]q(1-q)(\widehat{q}-q).$$ (2)

For antagonism between niches or between the sexes, allele frequency change is:

$$\mathrm{\Delta }q\approx s[1-2h(1-\mathit{\text{sh}})]q(1-q)(\widehat{q}-q).$$ (3)

The structure of eqs. (1–3) follows the same basic form: allele frequency change is the product of the distance to the equilibrium, (q̂ − q), one-half population heterozygosity, q(1 − q), and a model-specific function, f(s, h). Hereafter, let f(s, h) = 2s for the overdominant selection model, f(s, h) = 2s[1 − h(2 − sh)] for antagonistic pleiotropy, and f(s, h) = s[1 − 2h(1 − sh)] for niche and sexual antagonism models.

Finite population extension

We are interested in the frequency trajectories of alleles that successfully invade the population from low initial frequency (i.e., those avoiding stochastic loss immediately following their appearance within the population). Without conditioning on the eventual fate of an A₂ allele, its expected frequency change within a finite population is predicted by the deterministic result: E(Δq) = f(s, h)q(1 − q)(q̂ − q). The expected frequency change of an A₂ allele that successfully invades from low frequency, may be approximated as:

$$E(\mathrm{\Delta }q|\text{invading})\approx f(s,h)q(1-q)\left[\frac{\widehat{q}}{\text{tanh}[2\mathit{\text{Nf}}(s,h)\widehat{q}q]}-q\right],$$ (4)

where N is the population size and tanh(x) is the hyperbolic tangent function (see Appendix 2). Terms of tanh(x) evaluate to small values [tanh(x) ≪ 1], early during the invasion of A₂, and then rapidly approach unity. This inflates the early frequency increase of successful A₂ mutations.

Results in eq. (4) nicely parallel the evolutionary dynamics of sweeping, beneficial alleles (e.g., Maynard Smith 1971; Barton 1998; Betancourt et al. 2004; Ewens 2004, p. 170), which suggests a useful way to approximate conditional trajectories of partially sweeping alleles. Under strong selection relative to drift (i.e.: 2Nf(s, h) q̂ ≫ 1; see above), the early evolution of an invading A₂ allele should behave dynamically like a beneficial mutation with heterozygous selection coefficient f(s, h)q̂. Following the approach outlined in Betancourt et al. (2004; originally proposed by Maynard smith 1971) the spread of a successfully invading A₂ allele is well approximated using a deterministic model [eqs. (1–2)], and adjusting the initial frequency of A₂ to q₀ = 1/[4Nf(s, h)q̂]. This approach compares well to simulated data using the conditional trajectory in eq. (4), and exact, stochastic simulations (see below).

Transit time to equilibrium

The models presented above can be used to characterize the time required to approach a polymorphic equilibrium under different scenarios of balancing selection. Let q₀ be the initial frequency of A₂ (i.e., the finite population size adjusted value of q₀, presented above), and q_t be its frequency after T generations (the “transit time” for the A₂ allele). Because values of Δq are small, we can solve for T as:

$$T={\displaystyle \underset{q_0}{\overset{q}{\int }}\frac{\mathit{\text{dq}}}{f(s,h)q(1-q)(\widehat{q}-q)}=\frac{1}{f(s,h)\widehat{q}(1-\widehat{q})}\text{ln}\left[\frac{{(1-q_t)}^{\widehat{q}}{q}_t^{1-\widehat{q}}(\widehat{q}-q_0)}{{(1-q_0)}^{\widehat{q}}{q}_0^{1-\widehat{q}}(\widehat{q}-q_t)}\right]},$$ (5)

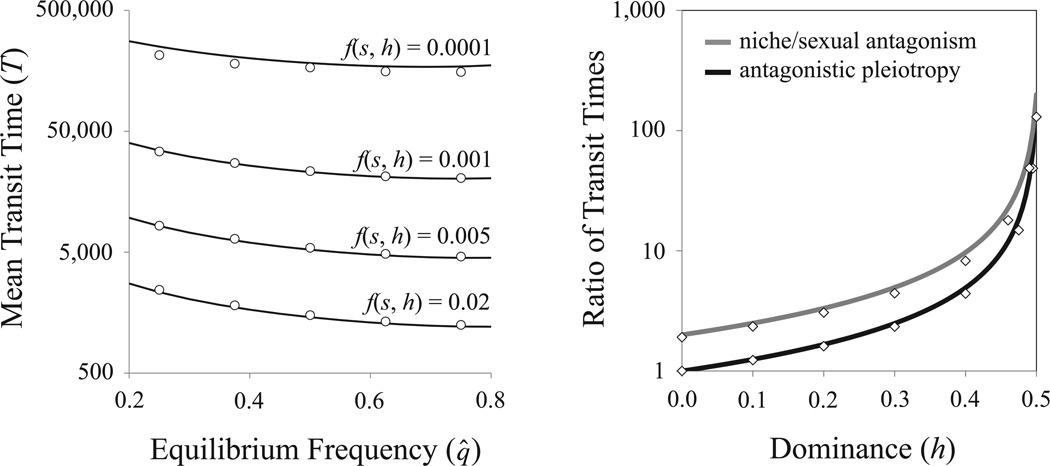
which parallels classical results describing the spread of a beneficial allele that will ultimately fix (see Haldane 1924; Crow and Kimura 1970, pp. 192–193; Charlesworth and Charlesworth 2010, p. 92). Eq. (5) compares very well with stochastic simulations in a Wright-Fisher population (Fig. 1, left panel, where we focus on the range of deterministic equilibria that is permissive for effective balancing selection, i.e.: 0.2 < q̂ < 0.8; see Robertson 1962; Hedrick 1999; Connallon and Clark 2012).

Figure 1.

Absolute and relative transit times under different balancing selection models. Solid lines represent the analytical approximations (the left panel uses eq. (5), and the right uses eq. (6a, b)); circles and diamonds give the average results from stochastic computer simulations of a Wright-Fisher population evolving under balancing selection and genetic drift. Additional parameters include N = 500,000 and (for the right panel) s = 0.02 and q̂ = 0.5. All results follow the time, in generations, for an allele to increase from a single mutant copy in the population, to within 95 percent of the deterministic equilibrium: q_t = 0.95q̂.

For fixed value of the mean selection coefficient (s = s₁/2 + s₂/2), we can directly contrast the different mechanisms of balancing selection. In the limit of infinite population size (N → ∞, leading to q₀ → 1/(2N)), the logarithmic term of eq. (5) will be the same under each model. The ratio of transit times under antagonistic selection relative to overdominance is approximated with:

$$R_T=\frac{1}{1-h(2-\mathit{\text{sh}})}$$ (6a)

and

$$R_T=\frac{2}{1-2h(1-\mathit{\text{sh}})},$$ (6b)

for cases of antagonistic pleiotropy and niche or sexual antagonism, respectively. Eqs. (6a, b) slightly overestimate the actual transit time ratio within a finite population, yet these approximations generally compare well with simulation results (Fig. 1, right panel). These approximations are also applicable to cases involving large selection coefficients (Fig. S2). The transit time is inflated over the entire parameter range for antagonistic selection, with T being severely inflated unless dominance reversals are extreme [under a complete dominance reversal (h = 0), T is similar between overdominant and antagonistic pleiotropy models; T is inflated by a factor of two for niche or sexual antagonism models]. In the absence of a dominance reversal (h = ½), transit times are inflated by a factor of ~4/s, which represents multiple orders of magnitude for small s.

There is a second way to interpret eq. (6a, b). For partial selective sweeps that take T generations to complete, the required strength of selection, s, must be larger under antagonistic versus non-antagonistic balancing selection. R_T represents the ratio of s (for the antagonistic relative to the overdominance models) that is required to render antagonistic and non-antagonistic models dynamically equivalent. For example, an overdominant selection model with mean selection coefficient s and an antagonistic selection model with mean selection coefficient sR_T, take approximately the same number of generations to equilibrate.

Hitchhiking effects at linked loci

The increase in frequency of an A₂ allele, from a single ancestral mutation to equilibrium, may be referred to as a “partial selective sweep” (Coop and Ralph 2012), with each sweep causing a hitchhiking effect at linked, neutral loci. Partial sweeps can potentially generate characteristic population genetic signatures of selection, including reduced neutral diversity, skewed site frequency spectra, and extended haplotypes and linkage disequilibrium associated with the invading allele (e.g., Maynard Smith and Haig 1974; Sabeti et al. 2002, 2006; Coop and Ralph 2012).

To characterize the severity of partial sweeps under different scenarios of balancing selection, we analyzed a simple, two-locus model with arbitrary linkage between a selected and a neutral locus. The A locus evolves under balancing selection, as described above. The B locus does not directly influence fitness, but may evolve by hitchhiking with alleles at the A locus. Let the probability of recombination between loci be r (per meiosis), q_A be the frequency of A₂, q_B be the frequency of a neutral variant B₂, and D be the degree of linkage disequilibrium between A₂ and B₂ [D = f(A₂B₂) − q_Aq_B, where f(A₂B₂) is the frequency of the A₂B₂ haplotype]. The deterministic dynamics of the two-locus system can be described, for any model of balancing selection, by the equations:

$$\begin{array}{l}\mathrm{\Delta }{q}_A\approx f(s,h)(\widehat{q}-q_A)q_A(1-q_A)\\ \mathrm{\Delta }{q}_B\approx f(s,h)(\widehat{q}-q_A)D\\ \mathrm{\Delta }D\approx D[f(s,h)(\widehat{q}-q_A)(1-2q_A)-r]\end{array}$$ (7)

(Appendix 3). As was the case for the single locus model (above), deterministic two-locus models can be used to characterize finite population phenomena, after the initial frequencies of derived alleles are adjusted to account for stochasticity during the initial phase of each sweep. Suppose that a single A₂ mutation is initially linked to a unique neutral background, B₂, such that the statistical association between A₂ and B₂ is initially perfect. Evolution of the A and B loci can be approximated using eq. (7), with initial linkage disequilibrium D₀ = q_A0(1 − q_A0), and “effective” starting allele frequency of q_A0 = 1/[4Nf(s, h)q̂].

Each A₂ allele that successfully invades the population will initially be associated with the random haplotype that it first appears on. Following Gillespie (2000; also see Betancourt et al. 2004), let B₂ represent alleles that are identical by descent (IBD) from an arbitrary position on the ancestral A₂-bearing haplotype. Assuming weak mutation at the locus, nearly every pair of B₂ alleles sampled from the population immediately following the sweep (at time t) will show no nucleotide differences, whereas the expected neutral diversity between pairs of B₁ alleles, or between B₁ and B₂ alleles, is simply the ancestral diversity at B before the sweep (π_before ≈ 4N_eu, where u is the neutral mutation rate at the B locus, and 4N_eu ≪ 1). Consequently, mean heterozygosity immediately following a sweep is π_after = [1 − q_B(t)²]π_before ≈ 4N_eu[1 − q_B(t)²], which represents a relative reduction of π_after/π_before = 1 − q_B(t)².

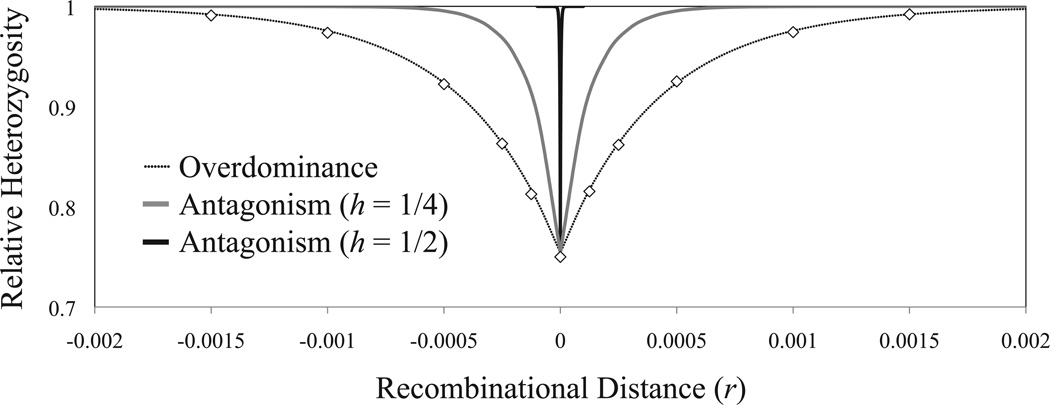
The reduction of heterozygosity from a partial selective sweep is plotted in Fig. 2. Parallel results for the temporary inflation of linkage disequilibrium are presented in Fig. S3. For a given recombinational distance between selected and neutral loci, the impact of each partial sweep will increase with the magnitude of the selection function, f(s, h). Hitchhiking effects are therefore much weaker under models of antagonistic selection. In the absence of dominance reversals, the hitchhiking effect of an antagonistically selected variant may be negligible, even for cases of very tight linkage. Dominance reversals increase the severity of hitchhiking effects, though these effects remain weak relative to cases of overdominant selection.

Figure 2.

Hitchhiking effects of partial selective sweeps. Analytical results (solid lines) comparing models of overdominance and niche or sexual antagonism were obtained by iterating eqs. (1), (3), and (7), with initial linkage disequilibrium (D₀) and “effective” starting allele frequencies (q_A0) as described in the main text. Mean neutral heterozygosity after the sweep, relative to before, is given by π_after/π_before = 1 − q_B(t)², as described in the main text, with parameters Ns² = 200, q̂ = 0.5, and s = 0.01. Diamonds represent the average values of 1 − [q_B(t)]², obtained from 20,000 replicate computer simulations with initial haplotype frequencies of [A₂B₂] = 1/(2N) and [A₁B₁] = 1 − 1/(2N), and conditional on the successful invasion of A₂.

Extensions and generalizations

The models presented above apply to cases of autosomal linkage, with each scenario of antagonistic balancing selection scaled relative to the classic model of overdominant selection. Similar results may also be obtained for scenarios of sex-linked inheritance and those that scale against negative frequency-dependence, which is an alternative model of non-antagonistic balancing selection.

Considerable theoretical attention has been directed towards sexually antagonistic polymorphism on the X (or Z) chromosome. When female-beneficial alleles are dominant to male-beneficial alleles (i.e., h < ½, within females), the X offers a broad parameter space for balancing selection (Rice 1984; Albert and Otto 2005; Patten and Haig 2009; Connallon and Clark 2012; Mullon et al. 2012; for s₁ and s₂ small, dominant male-beneficial alleles cannot be stably maintained and such cases may therefore be ignored; see Patten and Haig 2009). Focusing on the critical range of h < ½, the rate of change under X-linked sexual antagonism is approximated by Δq ≈ 2s₁(1 − 2h)q(1 − q)(q̂ − q)/3. For X-linked overdominant selection, the rate of change is Δq ≈ 4sq(1 − q)(q̂ − q)/3. Given a similar order of magnitude for the selection coefficients, the ratio of change for overdominant selection relative to sexual antagonism will be approximately ~2/(1 − 2h). This result is roughly the same as that obtained under autosomal inheritance with dominance reversals (i.e., eq. (6b) evaluated when 1 − 2h ≫ sh²). The main conclusion for the autosomal case is therefore robust: transit times are shorter, and hitchhiking effects more severe, for X-linked overdominant selection relative to sexually antagonistic balancing selection.

Negative frequency dependent selection may also be invoked as a balancing selection mechanism (e.g., Fitzpatrick et al. 2007) that does not require overdominance or antagonistic selection to maintain a stable polymorphism (nevertheless, composite models are certainly possible; e.g., Mokkonen et al. 2011). Although a wide variety of frequency-dependent scenarios are conceivable (e.g., Wright 1969, chapter 5; Golding 1992), we focus on the simple, two-allele case by Wright and Dobzhansky (1946), where relative fitness for the three genotypes is a linear function of the frequency of A₂, and the fitness of the heterozygote is intermediate to homozygote fitness (thus, we can exclude overdominant selection as a contributing force for maintaining variation). Genotypic fitnesses are: w(A₁A₁) = 1 − s₁ + s₂q, w(A₁A₂) = 1, and w(A₂A₂) = 1 + s₁ − s₂q, and s₁ and s₂ are assumed small, as before. Allele frequency change is Δq ≈ s₂q(1 − q)(q̂ − q), which scales linearly with the magnitude of the selection coefficient, as was also the case for the overdominance model (here, Δq is weighted by s₂, rather than 2s; see eq. (1)). Thus, contrasts between antagonistic and frequency-dependent models of balancing selection yield qualitatively similar results to contrasts between antagonism and overdominance.

CONCLUSION

Evolutionary theory predicts that antagonistically selected alleles may often reach intermediate population frequencies (Charlesworth and Hughes 1999; Connallon and Clark 2012), and are therefore likely to contribute heavily to observed additive genetic variation in fitness-related traits (Houle 1992; Pomiankowski and Moller 1995; Charlesworth and Hughes 1999). This theoretical conclusion is reinforced by recent, direct evidence for sexually antagonistic variation within a variety of plant and animal populations (e.g., Chippindale et al. 2001; Fedorka and Mousseau 2004; Foerster et al. 2007; Brommer et al. 2007; Cox and Calsbeek 2010; Innocenti and Morrow 2010; Mokkonen et al. 2011; Delph et al. 2011; Lewis et al. 2011). Non-antagonistic balancing selection, including overdominance and negative frequency-dependent selection, can also maintain alleles at intermediate population frequencies (e.g., Wright 1969), yet these evolutionary mechanisms are not expected to maintain additive genetic variation for fitness or its components (Charlesworth and Hughes 1999; Table S1).

The results presented here demonstrate that antagonistic and non-antagonistic mechanisms of balancing selection will differentially impact population genomic signatures of recent balancing selection, with weaker signatures under antagonism. Non-antagonistic processes induce partial selective sweeps that proceed faster, and generate stronger hitchhiking effects, than partial sweeps from antagonistic selection. Genome scans for extended, intermediate frequency haplotypes – a hallmark of short-term balancing selection (Charlesworth 2006; Andrés et al. 2009) – may therefore be well equipped to identify candidate loci evolving by overdominant selection (for discussion and a list of empirical examples, see Charlesworth 2006). Such scans are comparably less likely to identify candidate regions under antagonistic balancing selection. Recent theory similarly suggests that evidence of long-term balancing selection (which requires that alleles be old, i.e., stably maintained much longer than 2N_e generations; Charlesworth and Charlesworth 2010) should also be weak under scenarios of antagonistic selection (see Connallon and Clark 2012; Mullon et al. 2012).

APPENDIX 1. Allele frequency change under antagonistic balancing selection models

Antagonistic pleiotropy

With total fitness per genotype given by the product of the individual fitness components (Curtsinger et al. 1994; Prout 2000), and subject to the constraint h = h₁ = h₂ ≤ ½, the frequency change per generation is:

$$\mathrm{\Delta }q=\frac{[2s_1{s}_2{h}^2+(s_1+s_2)(1-2h)]q(1-q)(\widehat{q}-q)}{\overline{w}}\approx [2s_1{s}_2{h}^2+(s_1+s_2)(1-2h)]q(1-q)(\widehat{q}-q),$$ (S1)

where mean fitness is w̅ = q²(1 − s₁) + 2q(1 − q)(1 − hs₁)(1 − hs₂) + (1 − q)² (1 − s₂), and the final approximation obtained under weak selection (s₁, s₂ ≪ 1; see Connallon and Clark 2012). Letting s be the average of the two selection coefficients, s = (s₁ + s₂)/2, and 2δ = s₁ − s₂, we can modify eq. (S1) to be a function of the average of the selection coefficients:

$$\mathrm{\Delta }q\approx [2(s^2-{\delta }^2)h^2+2s(1-2h)]q(1-q)(\widehat{q}-q).$$ (S1a)

For the parameter range where terms of s² matter (i.e., in the limit, h → ½), terms of δ are, at most, on the order of s₁s₂. Consequently, terms of δ² always contribute negligibly to allele frequency change, which we can now approximate solely in terms of the average of the selection coefficients:

$$\mathrm{\Delta }q\approx 2s[1-h(2-\mathit{\text{sh}})]q(1-q)(\widehat{q}-q),$$ (S1b)

as in the main text.

Antagonistic selection between niches

Following Prout (2000), we assume that there are two niches that contribute equal numbers of individuals to the adult population. Mating is random among individuals from different niches. The frequency change per generation (again assuming that h = h₁ = h₂ ≤ ½) is the average of the allele frequency changes within each niche:

$$\mathrm{\Delta }q=\frac{q(1-q)}{2{\overline{w}}_1{\overline{w}}_2}[(s_2(1-h){\overline{w}}_1-s_{1}h{\overline{w}}_2)-q(1-2h)(s_2{\overline{w}}_1+s_1{\overline{w}}_2)],$$ (S2)

where w̅₁ = 1 − s₁q[2h + q(1 − 2h)] and w̅₂ = 1 − s₂(1 − q)[1 − q(1 − 2h)]. With weak selection and partial recessivity of the costly allele per niche (h < ½), the frequency change can be approximated to first order in the selection coefficients as Δq ≈ (s₁ + s₂)(1 − 2h)q(1 − q)(q̂ − q)/2 = s(1 − 2h)q(1 − q)(q̂ − q), where once again s = (s₁ + s₂)/2. As h nears ½, the frequency change is well approximated by the second order function: Δq ≈ s₁s₂q(1 − q)(q̂ − q)/2 = (s² − δ²)q(1 − q)(q̂ − q)/2 ≈ s²q(1 − q)(q̂ − q)/2. A useful approximation to account for the entire parameter range (from additive to recessive fitness costs) is Δq ≈ s[1 − 2h(1 − sh)]q(1 − q)(q̂ − q), which we use in the main text.

Sexually antagonistic selection

Let q_m be the frequency of A₂ in sperm, and q_f its frequency in eggs, among breeding adults (i.e., after selection). Arbitrarily letting A₂ be the male-beneficial allele (A₁ is female-beneficial), the allele frequency change under sexual antagonism is simply the average of the changes in males and females (respectively):

$$\begin{array}{l}\mathrm{\Delta }{q}_m=\frac{q_m{q}_f+\frac{1}{2}[q_f(1-q_m)+q_m(1-q_f)](1-s_{2}h)-q_m{\overline{w}}_m}{{\overline{w}}_m}\\ \mathrm{\Delta }{q}_f=\frac{q_m{q}_f(1-s_1)+\frac{1}{2}[q_f(1-q_m)+q_m(1-q_f)](1-s_{1}h)-q_f{\overline{w}}_f}{{\overline{w}}_f},\end{array}$$ (S3)

where w̅_f and w̅_m are equivalent to w̅₁ and w̅₂ from the niche antagonism model. Let q_m = q + ε and q_f = q − ε, where 2ε represents the allele frequency difference between male and female gametes. Substituting for q_m and q_f and ignoring terms of order ε² (see Nagylaki 1979; Charlesworth 1987; Charlesworth and Charlesworth 2010, p. 97), eq. (S3) simplifies to:

$$\begin{array}{l}\mathrm{\Delta }{q}_m\approx \frac{s_{2}q(1-q)[1-h-q(1-2h)]}{{\overline{w}}_m}-\epsilon \\ \mathrm{\Delta }{q}_f\approx \frac{s_{1}q(1-q)[h+q(1-2h)]}{{\overline{w}}_f}+\epsilon \end{array}$$

The net frequency change is then identical to that of the niche antagonism model:

$$\mathrm{\Delta }q=\frac{\mathrm{\Delta }{q}_m+\mathrm{\Delta }{q}_f}{2}\approx \frac{q(1-q)}{2{\overline{w}}_m{\overline{w}}_f}[(s_2(1-h){\overline{w}}_f-s_{1}h{\overline{w}}_m)-q(1-2h)(s_2{\overline{w}}_f+s_1{\overline{w}}_m)],$$ (S4)

Further approximations for the niche antagonism model (see above) similarly apply to cases of sexual antagonism.

APPENDIX 2. Conditional allele frequency trajectories in a finite population

Let the rate of frequency change under antagonistic balancing selection be described by the function Δq = f(s, h)q(1 − q)(q̂ − q), as described in the main text. An A₂ allele at low initial frequency will have two possible evolutionary fates. It may be lost due to drift, in which case, we are not concerned with it. Alternatively, it may escape stochastic loss, and if so (and assuming balancing selection is effectively strong, as described in the main text), the allele will evolve toward a balanced polymorphic equilibrium defined by the deterministic equilibrium, θ.

The probability that a single copy A₂ allele becomes successfully established within the population is approximated well by ~2f(s, h)q̂ (TC and AGC, unpublished data; Connallon and Clark 2010). The probability of establishment when there are initially k copies of the allele will be:

$$\pi (k)=1-{[1-2f(s,h)\widehat{q}]}^k\approx 1-\text{exp}[-4\mathit{\text{Nf}}(s,h)\widehat{q}q],$$ (S5)

where k = 2Nq, and N is the population size (for convenience, we assume this is the same as the effective population size: N_e ≈ N). Using eq. (S5), and the general approach of Ewens (2004; see p. 147), the expected frequency change of a successfully invading A₂ allele is given by:

$$E(\mathrm{\Delta }q|\text{establishment})\approx f(s,h)q(1-q)(\widehat{q}-q)+\frac{q(1-q)}{2N\pi (k)}·\frac{\partial \pi (k)}{\partial q},$$ (S6)

which ultimately leads to the result presented in eq. (4) of the main text.

APPENDIX 3. Two locus hitchhiking model

The A locus, under balancing selection, has two possible alleles: A₁ and A₂, at frequencies 1 − q_A and q_A, respectively. The B locus has two equally fit (i.e., neutral) alleles: B₁ and B₂, at frequencies 1 − q_B and q_B, respectively. Frequencies of the four possible haplotypes are: x₁ = [A₁B₁], x₂ = [A₁B₂], x₃ = [A₂B₁], and x₄ = [A₂B₂]. Linkage disequilibrium is defined as D = x₁x₄ − x₂x₃. Under weak selection, we can approximate the change in allele frequency as:

• Δq_A = Δx₃ + Δx₄ ≈ f(s, h)(q̂ − q_A)q_A(1 − q_A)

• Δq_B = Δx₂ + Δx₄ ≈ f(s, h)(q̂ − q_A)D

as presented in the main text. These follow from the generalized relationship between allele frequency change and covariance between fitness and genotype (e.g., Kruuk et al. 1999; Rice 2004). Allele frequency changes can be partitioned by haplotype, as follows:

• Δx₁ ≈ −f(s, h)x₁q_A(q̂ − q_A) − rD

• Δx₂ ≈ −f(s, h)x₂q_A(q̂ − q_A) + rD

• Δx₃ ≈ f(s, h)x₃(1 − q_A)(q̂ − q_A) + rD

• Δx₄ ≈ f(s, h)x₄(1 − q_A)(q̂ − q_A) − rD

and used to calculate the change in linkage disequilibrium, per generation:

• ΔD = (x₁ + Δx₁)(x₄ + Δx₄) − (x₂ + Δx₂)(x₃ + Δx₃) − D ≈ D[f(s, h)(q̂ − q_A)(1 − 2q_A) − r]

The approximation ignores terms of Δx_iΔx_j, which contribute negligibly to the final result.

This approach can also be extended to cases of X-linked inheritance. For an X-linked model with frequency change at the selected locus of Δq_A ≈ f(s, h)(q̂ − q_A)q_A(1 − q_A), prior results for the neutral locus remain applicable (i.e., it remains a function of D). The change in linkage disequilibrium under X-linked inheritance is modified to $\mathrm{\Delta }D\approx D[f(s,h)(\widehat{q}-q_A)(1-2q_A)-\frac{2}{3}r]$, with the two-thirds weighting reflecting the fact that recombination only occurs in females, and each X has a two-thirds probability of residing within a female.