Reconstructing Boolean Models of Signaling

Abstract

Since the first emergence of protein–protein interaction networks more than a decade ago, they have been viewed as static scaffolds of the signaling–regulatory events taking place in cells, and their analysis has been mainly confined to topological aspects. Recently, functional models of these networks have been suggested, ranging from Boolean to constraint-based methods. However, learning such models from large-scale data remains a formidable task, and most modeling approaches rely on extensive human curation. Here we provide a generic approach to learning Boolean models automatically from data. We apply our approach to growth and inflammatory signaling systems in humans and show how the learning phase can improve the fit of the model to experimental data, remove spurious interactions, and lead to better understanding of the system at hand.

1. Introduction

A fundamental question in biology is how a certain network of interacting genes and proteins gives rise to a specific cellular function. Most studies to date, particularly in the protein–protein interaction domain, aim to answer this question by analyzing a static topological description of the network. The most notable exception is the large-scale analysis of metabolic networks, which rely on constraint-based models that quantitatively describe the network's fluxes under a steady-state assumption. The advantage of the latter models is that they allow simulating the process of interest under different genetic and environmental perturbations. Recently, it was suggested that similar models could be applied to signaling networks. While metabolic-like models of signaling are only beginning to emerge (Klamt et al., 2006; Vardi et al., 2012), a large body of work exists on Boolean network modeling dating back to the 1960s and 70s (Kauffman, 1969).

Our focus here is on learning Boolean models from experimental data. In contrast to the rich literature on Boolean modeling frameworks, the learning and application of these frameworks to protein networks is very recent. Gat-Viks et al. (2006) developed a probabilistic framework for learning signaling models. Saez-Rodriguez et al. (2009) developed the CNO algorithm to optimize a Boolean model against experimental measurements on the involved proteins. Their algorithm is based on starting with an initial model and learning a compact representation of the model that fits the data well, using heuristic genetic algorithms. In a follow-up work, Mitsos et al. (2009) presented an integer linear programming (ILP) formulation of the problem that allows learning of a subset of the initial model interactions that will yield optimal fit to the observed data. Both modeling frameworks were applied to growth and inflammatory signaling systems in humans and were shown to agree well with available experimental data (Mitsos et al., 2009; Saez-Rodriguez et al., 2009, 2011; Ryll et al., 2011).

Despite their relative success, these previous learning algorithms had several shortcomings: (i) they relied on the availability of an annotation of activation/repression signs to the edges of the signaling network, thus limiting the search to logical functions that are monotone in an appropriate set of inputs; (ii) they relied on having an initial model in which each Boolean function is associated with a superset of the actual terms in some disjunctive normal form (DNF) representation of it; and (iii) in most cases heuristic rather than exact search algorithms were used. The only exception is the work of Mitsos et al. (2009), but their algorithm was demonstrated on a very simple model where the Boolean functions are typically assumed to have, at most, two inputs.

Here we suggest a novel algorithm for learning a Boolean model with two key advantages over previous work: (1) The algorithm allows learning general Boolean functions, with a particularly efficient learning scheme for symmetric threshold functions. Importantly, it can deal with unknown Boolean functions and does not necessarily need an annotation of edge signs. (2) The algorithm is guaranteed to find a maximum-fit solution, i.e., one that minimizes disagreements with experimental data. We apply our algorithm to learn Boolean models for two well-studied growth and inflammatory systems: epidermal growth factor receptor (EGFR) signaling and interleukin 1 (IL-1) signaling. We compare our learned models to state-of-the-art manual models for these systems. We show that our algorithm produces accurate reconstructions and can successfully pinpoint possible modifications to a model that will improve its fit to the experimental data.

2. Preliminaries

We assume we are given a directed acyclic signaling network G = (V, E) for the process in question. Such a network can either be gathered from the literature, as in the case of the EGFR and IL-1 systems described below, or learned from data using network reconstruction algorithms (Yeger-Lotem et al., 2009; Yosef et al., 2009). The network may or may not be signed with activation/repression effects on its edges. We treat each vertex (molecular species, including proteins and small molecules) in G as being in one of two states: active (1) or inactive (0). We further assume that the state of a vertex v is a Boolean function of the states of its direct predecessors in the network P(v). We denote this function by f (v). Given a Boolean model of some pathway of interest, where each function is described by some DNF representation of it, we adopt the terminology used in Samaga et al. (2009) and refer to each term in the given DNF representation of a function as a reaction.

If the given network is signed, we will assume that each of the “hidden” Boolean functions is monotone nondecreasing in an appropriately modified set of input variables. Specifically, given a vertex v and one of its predecessors 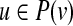, the function f (v) that determines the value of v is monotone non decreasing in u if the sign of (u, v) is +1, and, otherwise, f (v) is monotone non decreasing in 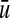– the negation of u.

The goal is to learn the Boolean logic of the network, i.e., the truth table of every Boolean function associated with a vertex of G. In order to learn the logic of the network, we are given a set of experiments, in each of which some subset of vertices is perturbed and the states of another subset of vertices are observed. Any suggested model gives rise to a state assignment to the nodes of G (under a steady state assumption). We will aim to derive a model that fits best (under a least-squares criterion) to the observed data. This maximum fit learning problem was shown to be NP-complete by Karlebach and Shamir (2012) and, hence, we tackle it via an integer programming–based approach.

3. Logic-Learning Via ILP

In this section, we present our algorithm for learning a Boolean model with no assumptions on the functions involved. Denote the number of nodes in the network by N = |V|. Let δ be the maximum in-degree of a node in G.

A Boolean model is specified by giving, for each noninput node v, a Boolean function f (v) on n(v) = |P(v)| inputs 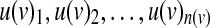specifying how the value of the node depends on its inputs. The function f (v) is specified by its truth table, a collection of 2^n(v) binary variables 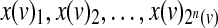, where x(v)_i denotes the value of v under the i-th input combination in lexicographic order.

Our goal is to find a Boolean model that minimizes the sum, over all experiments, of the number of experimental observations that differ from the predictions of the model. We formulate this as an integer programming problem. To do so, we derive integer linear constraints that determine the state a(v) of every node v, under some experimental condition (where the index of the condition is omitted for clarity), from the states of its input nodes under that condition, i.e., from 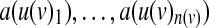. When v is one of the perturbed nodes, a(v) is fixed to its perturbed value. Otherwise, we derive its state using the following auxiliary constants and variables:

• 1. b(v, i, j)—a constant that is equal to the value of the j-th input variable in the input combination corresponding to the i-th row of the truth table of f (v). In other words, b(v, i, j) is the j-th bit of the number i – 1. The purpose of the constants b(v, i, j) is to select the correct row of the truth table.

• 2. y(v)_i—a variable that is 1 if and only if i is the row of the truth table that is selected by the inputs to node v and x(v)_i = 1.

The variables y(v)_i are determined by the following inequalities:

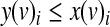(1)

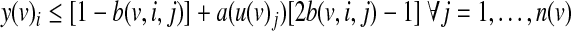(2)

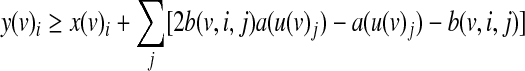(3)

The first constraint ensures that y(v)_i will evaluate to TRUE only if the truth value of the i-th row is TRUE. The second constraint ensures that y(v)_i will evaluate to TRUE only if the activity value of each input matches its designated value. Finally, the third constraint ensures that y(v)_i will evaluate to FALSE only if one of the previous constraints was not satisfied.

Finally, a(v) is 1 if and only if any of the y(v)_i is 1, as expressed by the following constraints:

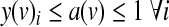(4)

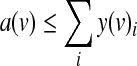(5)

In case the input network is signed and the monotonicity assumption holds, the ILP formulation can be made more efficient by noting that: (i) For any given row, no constraints are needed on the variables that should attain a value of 0; and (ii) the monotonicity requirements can be forced by appropriate inequality constraints on truth table variables: 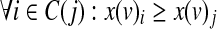, where C(j) is the set of at most n(v) indices whose binary representation has exactly one more ‘1’ than that of j.

The above constraints can be used to derive the state of all nodes given the input perturbed states. It remains to specify the objective of the ILP, which measures the agreement between the model-derived states and the experimental data at hand. We use a least-squares criterion, which becomes linear on binary variables (see, e.g., Mitsos et al., 2009). Formally, let O be the set of nodes whose output is experimentally observed. For a given condition, let e(v) denote the experimentally measured state of node 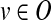. Then, the non constant contribution of this condition to the objective function is .

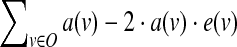The overall number of variables in the above ILP is O(N2^δ), and the same bound applies to the number of constraints. The overall size of the ILP is O(N2^2δ).

4. Symmetric Threshold Functions

In practice, for known signed models, most or all of the pertaining Boolean functions are of simple structure: single AND or OR gates or, more generally, symmetric threshold functions, where the function evaluates to TRUE if and only if sufficiently many of its activators (resp., repressors) are present (resp., absent). For example, in the EGFR system that we study below, 98 of its 112 nodes (87.5%) are associated with a single AND or OR gate. Similarly, in the IL-1 system all nodes whose gates are known (110 of 121) are associated with a single AND or OR gate.

Here we provide a more efficient formulation for symmetric threshold functions. The main improvement is obtained by representing each function using a single integer variable that ranges from 0 to the fan-in of the function plus one. Given a node v with incoming nodes 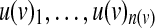, we let x(v) be the threshold variable representing its underlying Boolean function f (v). The activity status of v can be derived from the following set of constraints:

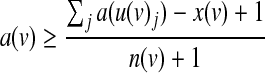(6)

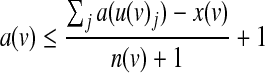(7)

Notably, a symmetric threshold function contains AND and OR as special cases, with x(v) equal to the fan-in in the case of an AND gate and x(v) = 1 in the case of an OR gate. Furthermore, a value of n(v) + 1 allows us to remove this function from consideration, as it will always evaluate to FALSE. This is advantageous when some of the given reactions may be redundant (see Section 6). In addition, this setting allows the discovery of redundant components of an OR gate. Last, a value of 0 allows setting the output of the function to 1 regardless of its inputs. This can be used to search for redundant components of an AND gate (see Section 6).

The overall number of variables in this special ILP is, at most, twice the number of molecular species (or nodes), and this is also the bound on the number of constraints. Thus, the overall size of the ILP is quadratic in the number of species and linear when the maximum fan-in is bounded.

5. Experimental Design

5.1. Learning read-once functions

There are interesting connections to be made between the reconstruction of Boolean models of signaling circuits and the branch of computational learning theory involving the identification of Boolean functions using queries (Angluin, 1988). In this theoretical framework one is given black-box access to a Boolean function of n variables known to be drawn from a specified class of functions. The input to a query is one of the 2ⁿ input combinations to the unknown function, and the output is the corresponding function value. The theory studies the worst-case number of queries required to identify a function in the given class.

The setting of the current article differs in several ways from the standard model of learning via queries. Most importantly, instead of black-box access to the unknown Boolean function we assume knowledge of the wiring diagram of the network being analyzed and of the possible Boolean functions that can be associated with the gates within it. Also, our networks may have multiple outputs rather than a single output, and there may be technological limitations on the input combinations that can be applied (i.e, on the feasible combinations of perturbations of the state of the network). Finally, it may be out of reach to determine the network exactly; instead, we seek a network model that has high agreement with the observed experimental outcomes.

Motivated by these differences, we concentrate on algorithms for learning an n-variable Boolean function realized by a network with a known wiring diagram but unknown gates. We allow arbitrary queries. We show that in the case of monotone read-once functions, knowing the wiring diagram gives a great advantage over black-box learning. A Boolean function is called monotone read-once if it is realized by a Boolean formula in which each connective is AND or OR and each input occurs exactly once. Such a formula can be represented as a tree of AND and OR gates, with the edges directed toward the root, such that each input variable occurs at exactly one leaf. We assume that the structure of the tree is given but the identities of the gates are unknown. We show how to identify the Boolean function with at most n queries (one query per gate), whereas Ω(n²) queries seem to be required in the black-box model (Angluin et al., 1993).

Our result follows from three observations:

• 1. We can set the Boolean value on any edge e of the tree to a Boolean value a by setting to a each input variable from which edge e is reachable.

• 2. Given any set of edges, no two of which are reachable from the same input variable, we can simultaneously set the values on those edges to any desired combination of values. This is done by applying the above construction simultaneously to each edge in the set.

• 3. Let g be a gate such that the types (AND or OR) of all gates on the path from g to the output are known. To find the type of g we can set to 0 one of the inputs to g, set to 1 all the other inputs to g, and cause the output of g to “propagate” to the final output by: (i) placing 1 on every edge that is not on the path from g to the output but is directed into an AND gate on the path; and (ii) placing 0 on every edge that is not on the path from g to the output but is directed into an OR gate on the path. Then g is an AND gate if the final output is 0, and an OR gate if the final output is 1.

Using these observations, we can work backward from the root to the leaves, determining the type of each gate with one query.

By an extension of this construction we can show the following. Let K be a class of nonconstant monotone nondecreasing Boolean functions learnable in the black-box query model with f (n) queries, where n is the number of inputs. Consider the class of Boolean functions representable by read-once tree networks with gates drawn from the class K. Given the wiring diagram of such a network, one can identify the gates and hence learn the Boolean function, with 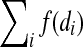queries, where i ranges over the gates in the network and d_i is the fan-in to the i-th gate. For example, given the wiring diagram of a read-once network of bounded fan-in symmetric threshold functions, the Boolean function represented by the network can be learned with O(n) queries.

5.2. An information-theoretic experimental design algorithm

Thus far we have assumed that the set of experiments to be applied to the network is externally specified. In this subsection, we present an algorithm for adaptively choosing experiments in order to efficiently acquire information about the Boolean circuit in question. Our algorithm draws inspiration from the field of genetic algorithms and is information-theoretic in nature. At a general step, we execute a feasible experiment whose outcome is least predictable according to an entropy measure, thus maximizing the information gain at each step. In selecting the next experiment we assume to be given a specification of the inputs and outputs of each experiment performed thus far, a population P of p high-scoring models relative to these experiments (where p is a parameter of the experimental design algorithm), and a set F of feasible experiments from which the next experiment will be drawn. We define a mutation of a model as any single change in the truth table of a gate that would alter the output of that gate under some past experiment.

The initial collection of N networks can be learned using the integer programming formulation of Section 3, while instructing the ILP solver to produce multiple optimal (or near-optimal) solution. A step of the algorithm consists of the following substeps:

• 1. Enlarge the population P by applying all possible mutations to its members.

• 2. Restrict the enlarged population P to the p models within it having the highest scores relative to the set of experiments performed so far; this entails simulating each circuit in the enlarged set under every past input.

• 3. Simulate each experiment in F on each of the p circuits to compute the output it would produce, and compute the entropy of the distribution of these outputs, assuming the uniform distribution over the p models in P.

• 4. Perform the candidate experiment of maximum entropy (i.e., the most informative candidate experiment).

6. Results

To test the ability of our ILP-based approach to provide an accurate logical model of a signaling system, we applied it to the well-studied EGFR and IL-1 signaling systems. These systems served as ideal test cases as their topologies and underlying logics have been extensively researched and large-scale models have been manually constructed for them (Samaga et al., 2009; Ryll et al., 2011). In the following, we describe our implementation, evaluation criteria, and the results we attained with respect to each of these systems.

6.1. Implementation and evaluation

We implemented the algorithm for learning symmetric threshold functions described in Section 4. To deal with the problem of multiple equally good solutions, we also implemented a variant of the algorithm in which a secondary objective is used to choose among the best performing solutions. In detail, the application of this variant is done as follows: (i) First, we run our algorithm to attain some optimal solution and record its value; (ii) then, we add a constraint to the ILP that restricts its solutions to those attaining the optimal value identified in the previous step; and (iii) last, we optimize the ILP with respect to the second objective. In the experiments reported below, we used as our main secondary objective the similarity (number of identical gates) of the output model to the original (manually curated) model.

In case a curated model is not available, Mitsos et al. (2009) propose using as a secondary objective a measure of the complexity of the resulting circuit—the number of reactions it contains (possibly weighted, out of an initial superset of reactions). A similar approach is taken by Saez-Rodriguez et al. (2009), who include this measure as part of their primary objective. Here we imitate these approaches and use as an alternative secondary objective (in addition to the curated model-based one) the number of nonconstant gates in the model.

The implementation was written in C using the CPLEX callable library version 12.1. All runs reported below were conducted on a single core of a Xeon 3.06 GHz server with 8 GB memory and were completed in a few seconds.

To evaluate our modeling framework, we applied it for the modeling of two signaling systems in humans: (i) EGFR, which regulates cellular growth, proliferation, differentiation, and motility; and (ii) IL-1, which is involved in coordinating the immune response upon bacterial infection and tissue injury. Both systems are well studied and detailed manual models exist for them. In particular, Samaga et al. (2009) have constructed a comprehensive Boolean model of the EGFR system that contains 112 molecular species and their associated Boolean functions; Ryll et al. (2011) have created a Boolean model of the IL-1 system with 121 molecular species. We retrieved both models from the CellNetAnalyzer repository (www.mpi-magdeburg.mpg.de/projects/cna/repository.html).

In order to learn logical models for these systems, we used data published by the above authors on the activity (phosphorylation) levels of certain proteins under different cellular conditions. Specifically, Samaga et al. (2009) measured within the EGFR system the activity levels of 11 proteins under 34 distinct conditions in Hep2G cells (Figure 8 in Samaga et al., 2009). Similarly, Ryll et al. (2011) measured within the IL-1 system the activity levels of nine proteins under 14 distinct conditions in primary hepatocytes (Figure 6 in Ryll et al., 2011). In both cases, the cells were stimulated with different ligands and treated with different inhibitors, thus simulating different conditions. Following Samaga et al. (2009) and Ryll et al. (2011), we focused our analysis on the measurements at the 30-min timepoint, representing the early response of each system. The reconstructed models were scored by their fit, according to a least-squares criterion, to the observed data.

6.2. The EGFR system

Our first and main test case is the well-studied EGFR system, whose model contains 112 nodes and 157 reactions (excluding input/output ones) with a maximum fan-in of 5. Experimental data for this system includes the activity levels of 11 proteins under 34 different perturbations. When testing the fit of the curated model of Samaga et al. (2009) to the observed experimental data, 278 out of 366 predictions (76%) matched the observed activities. In an effort to understand the erroneous cases, Samaga et al. have identified 12 gates for which the underlying logic was not clear (along with one more reaction that does not have an effect on the measured proteins and another reaction that happens at a later time; hence, both could be removed). In addition, they have suggested four modifications to existing gates that improve the fit of the model (along with three additional modifications that involve the introduction of new edges into the model and, hence, could not be captured by our ILP framework). Overall, there were 2³³ possible models to choose from when constraining the 16 gates in question to symmetric threshold functions. Full enumeration of these models was prohibitively expensive as each model had to be simulated in order to compare its fit to the experimental data.

We applied our algorithm to reconstruct these unknown logical functions, while aiming to maximize the fit to the experimental data. The program finished in less than a second producing a solution that matched 330 of the data points (90%). We then searched for a model with the same score (fit to data) that is closest to the original model. The reconstructed functions and their curated counterparts appear in Table 1. The proposed changes to the model and the respective reconstructions are summarized in Table 2.

Table 1.

Performance Evaluation of the Reconstruction Algorithm

Curated function	Reconstructed function
sos1_eps8_e3b1 OR vav2 → rac_cdc42	OR
mekk1 OR raf1 → mek12	OR
mkk3 OR mkk6 OR mkk4 → p38	OR
mekk1 OR mekk4 OR mlk3 → mkk4	OR
pak1 OR csrc → pak1crscd	OR
p90rsk OR mk2 → creb	OR
!akt AND !pak1 → bad	AND
!akt AND !p90rsk → gsk3	AND
jnk OR (erk12 AND p90rsk) → jnkerkp90rskd	MAJ
erk12 OR jnk → p70s6_1	OR
erbb11 AND eps8r → rntre	AND
dag AND ca → dagcad	AND

Reconstructed functions that match the curated ones appear in bold.

Table 2.

Performance Evaluation of the Reconstruction Algorithm with Respect to Proposed Modifications

Original function	Proposed modification	Reconstructed function
erb11 AND (pip3 OR pi34p2) → vav2	erb11 → vav2	erb11 → vav2
sos1_eps8_e3b1 → rac_cdc42	REMOVE	sos1_eps8_e3b1 → rac_cdc42
erb11 AND csrc → stat3	REMOVE	Remove
mk2 → hsp27	REMOVE	Remove

Reconstructions that match the suggested modification appear in bold.

An in-depth analysis of the reconstructed functions revealed that: (i) 11 of the 12 reconstructed functions matched the curated description, where an additional one was reconstructed as a majority function on three variables while its curated description was not a symmetric threshold function but was deemed “closest” to a majority one (line 9 in Table 1); and (ii) in three of the four proposed changes, the algorithm correctly predicted the suggested modification; the fourth modification was rejected by the algorithm. Quite strikingly, when testing the performance of the curated model with the suggested modifications, the same fit (330 of 366) was observed.

Next, we applied our algorithm with the alternative secondary criterion, minimizing the number of nonconstant gates in the resulting model. As the primary objective remained the same, the produced model had the same high fit to the data (330 of 366). However, the solution was markedly different with ten constant gates compared to three previously. This demonstrates the potentially vast space of equally good solutions (with respect to the primary criterion); thus, more experimental data is needed to choose between them.

6.3. IL-1 signaling

As a second test case, we applied our method to automatically learn the logic of the IL-1 circuit (Ryll et al., 2011). This circuit contains 121 nodes and 112 reactions (excluding input/output ones) with a maximum fan-in of 6. The logic of 11 of the reactions is not known, but this has no effect on the measured proteins under the available conditions (and assuming monotonicity). Overall, the model successfully explains 104 of the 118 experimental points (88%). In an attempt to improve this fit, Ryll et al. manually inspected the model and data and suggested the addition of seven reactions and the removal of one, albeit achieving only a slight increase in performance (89%).

Ryll et al. have classified the reactions in their model according to the literature support for them. The least reliable categories included those reactions that had evidence under different stimulations than IL-1/6. Hence, we thought to improve the fit of the model by learning the logic of these reactions (focusing on a subset of those that have at least two inputs) in addition to the 11 unknown ones. Overall, we applied our framework to learn the logic of 27 reactions, amounting to a search space of 2⁶⁰ models. Among the solutions obtained, we chose the one that is closest (in terms of the number of identical gates) to the original model. By modifying two reactions (removing one and changing another from AND to OR), the algorithm managed to find a solution with a slightly better fit to the data: 106 of the points agreed with the experimental measurements (90%). We note that these two modifications are not included in the set of modifications suggested by Ryll et al. (2011) and require further study. When running the algorithm with the alternative secondary objective, 21 of the 27 reactions were set to constant values, demonstrating yet again the potentially large size of the solution space given current data.

7. Conclusions

Transforming topological networks into working functional models of signaling is a fundamental problem with vast applications. Here we make a step toward achieving this goal by providing an algorithm to learn a Boolean model of a given signaling system automatically from data. We provide a general variant that is applicable to all Boolean functions and does not require knowledge on the activation/repression properties of the network's edges. In addition, we provide a specialized variant for learning symmetric threshold functions. Such functions are very common in known models. Our algorithms are based on reducing the learning problem to an integer linear program, which is solved to optimality in seconds on current systems. We demonstrate the power of our approach by applying it to two well-annotated signaling systems involved in growth and inflammatory response. The produced models allow completing information gaps, improving the fit to the experimental data, and pinpointing redundant reactions and components of reactions.

While our approach is generic, we focused our evaluation and experimentation on learning-constrained models in which the initial network is signed and the pertaining Boolean functions are assumed to be symmetric threshold functions. Further experimentation is needed to test the effectiveness of the full model and the accuracy of its predictions when relaxing these assumptions. In addition, it would be interesting to test the utility of our experimental design scheme in prioritizing current experiments and suggesting new ones.

Acknowledgments

Part of this work was done while RS was on sabbatical in ICSI, Berkeley. We thank Ron Shamir for fruitful discussions about this work. RS was supported by a research grant from the Israel Science Foundation (grant no. 241/11).

Disclosure Statement

The authors declare that no competing financial interests exist.