CNVeM: Copy Number Variation Detection Using Uncertainty of Read Mapping

Abstract

Copy number variations (CNVs) are widely known to be an important mediator for diseases and traits. The development of high-throughput sequencing (HTS) technologies has provided great opportunities to identify CNV regions in mammalian genomes. In a typical experiment, millions of short reads obtained from a genome of interest are mapped to a reference genome. The mapping information can be used to identify CNV regions. One important challenge in analyzing the mapping information is the large fraction of reads that can be mapped to multiple positions. Most existing methods either only consider reads that can be uniquely mapped to the reference genome or randomly place a read to one of its mapping positions. Therefore, these methods have low power to detect CNVs located within repeated sequences. In this study, we propose a probabilistic model, CNVeM, that utilizes the inherent uncertainty of read mapping. We use maximum likelihood to estimate locations and copy numbers of copied regions and implement an expectation-maximization (EM) algorithm. One important contribution of our model is that we can distinguish between regions in the reference genome that differ from each other by as little as 0.1%. As our model aims to predict the copy number of each nucleotide, we can predict the CNV boundaries with high resolution. We apply our method to simulated datasets and achieve higher accuracy compared to CNVnator. Moreover, we apply our method to real data from which we detected known CNVs. To our knowledge, this is the first attempt to predict CNVs at nucleotide resolution and to utilize uncertainty of read mapping.

1. Introduction

Genetic variation between individuals can range from single nucleotide differences to differences in large segments of DNA. Variations on the nucleotide level are referred to as single nucleotide polymorphisms (SNPs) and on the segment level as structural variations (SVs), including insertions, deletions, and copy number variations (CNVs). SVs and, in particular, CNVs, in which a large region of genome is deleted or duplicated, play an important role in the genetics of complex diseases and traits (Iafrate et al., 2004; Tuzun et al., 2005). Many recent studies have shown a correlation between CNVs and different genomic disorders, ranging from brain-related diseases [such as autism, schizophrenia, and idiopathic learning disability (Sebat et al., 2007)] to cancers [e.g., non-small cell lung cancer (Cappuzzo et al., 2005)].

Common methods to detect CNVs were, until recently, based on whole genome array comparative genome hybridization (ArrayCGH). In ArrayCGH, both a genome of interest (donor genome) and a reference genome are hybridized to a tiling array and the intensity ratio of the two genomes (donor/reference) provides an estimate of the copy number gain or loss (Redon et al., 2006; Carter, 2007; Chen et al., 2008). Although a powerful method to detect the presence of CNVs and estimate copy numbers, the ArrayCGH approach is unable to identify the boundaries of CNVs with high resolution.

The development of high-throughput sequencing (HTS) technologies provides great opportunities to detect CNV regions. With HTS technologies, whole genome shotgun sequencing of one or more individuals becomes possible. Methods to detect the CNVs from short reads generated by HTS technologies can be categorized by two main ideas. The first category of methods divides the genome into small windows, and the number of reads mapped to each specific window (read depth) is used as a proxy for the copy number of that window (Alkan et al., 2009; Chiang et al., 2009; Yoon et al., 2009; Sudmant et al., 2010; Simpson et al., 2010). Alkan et al. (2009) used a set of fixed regions, which are unique among all primates, as control windows and calculated the average read depth for those regions. Then they scaled the results to predict the copy number of other windows. Simpson et al. (2010) used the same idea of splitting the genome into windows while incorporating read depth and heterozygous SNPs information (in inbred mice) into a hidden Markov model (HMM). Adjacent windows with same copy number state are combined into one CNV region. Abyzov et al. (2011) developed a method for CNV discovery from statistical analysis of read depth. The method is based on the established mean-shift approach (Comaniciu and Meer, 2002), which is a popular method in computer vision. This approach is able to detect the presence of large CNVs and the copy numbers. However, the resolution of this approach is limited by the size of the windows, which is typically at least one kilobase.

In the second strategy, paired-end reads, where “paired-end” refers to the two ends of the same segment of a DNA molecule, are used to detect CNVs. A short gap appears between the two paired-end reads, and the distance of this gap is roughly fixed and known. The second class of approaches utilizes the discordant paired-end reads, which are the reads mapped to the reference genome in an unexpected way (Hormozdiari et al., 2009; He et al., 2010; Medvedev et al., 2010). Discordant reads may indicate the presence of CNVs. Read-depth information is then used to compute the copy number for each candidate CNV region (Alkan et al., 2009; Sudmant et al., 2010). Medvedev et al. (2010) introduced the idea of using both the read depth as well as the discordant reads to detect CNVs. This method first clusters the discordant reads to identify the CNVs' boundary, after which they build a “donor graph” representing the genome as segments of sequence connected by edges. Moreover, they use the maximum flow to estimate the most likely copy numbers for the donor genome. One limitation of this strategy is that it only detects CNVs in regions that are not repeat-rich. This may reduce the applicability of this method given the existence of many repeat-rich regions in the genome. Also, the CNVs may have complex structure. For example, if there exist multiple copies of CNVs in the reference genome, this method can not detect the variation within different copies.

Another important challenge for CNV detection lies in the uncertainty of read mapping. All of the mentioned methods use read-depth information. The read depth is obtained by mapping the short reads to the reference genome and then calculating number of reads within a region. However, a read can be mapped to multiple locations while the read originated from one specific locus in the donor genome. This mapping uncertainty can be due to short read length, sequencing errors, and the presence of repetitive regions. With few exceptions (He et al., 2011), most studies either consider all possible locations or randomly pick one mapping location, or even discard all such reads. These methods have difficulty in detecting CNVs with high accuracy, especially for CNVs in repeat-rich regions.

In this study, we show that handling the uncertainty of read mapping can help us in predicting the copy number of CNVs, especially in repeat-rich regions. We propose a probabilistic model, CNVeM, that utilizes the uncertainty of read mapping. We use maximum likelihood to estimate locations and copy number of copied regions and implement an expectation-maximization (EM) algorithm. One important contribution of our model is that we distinguish between similar copies of a region in the reference genome. We can predict exactly which copy of a region is duplicated or deleted utilizing the differences between copies and handling uncertainty of read mapping.

In our model, we predict the copy number for each nucleotide, and adjacent nucleotides with the same copy number are then combined to form a full CNV region. In this way, we can detect the boundaries precisely and are able to predict small CNVs. To our knowledge, this is the first attempt to detect CNVs at nucleotide resolution and to distinguish between similar sequences in the reference genome.

2. Methods

2.1. A motivating example

One important contribution of our method is that we distinguish between regions in the reference genome that differ from each other by a single nucleotide. Figure 1 illustrates an example. The reference genome has two nearly identical copies of a CNV region, represented as A and B. They only differ by one nucleotide as indicated in the figure, where the nucleotide is ‘C’ in region A and ‘T’ in region B. In the donor genome, region B is copied twice as B1 and B2. Reads 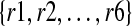are obtained from the donor genome as shown in the lower part of Figure 1 and then mapped to the reference genome as shown in the upper part of Figure 1. As shown in the figure, reads {r1, r3, r5} can be mapped to both region A and B in the reference. However, read {r2} can only be mapped to region A and reads {r4, r6} can only be mapped to region B. If we assign a read to one of multiple mapping positions randomly following the traditional strategy, we would determine the copy number of both region A and B to be 1.5. However, in CNVeM, we use the EM algorithm to find the optimal solution. In each iteration, we assign a read to different mapping positions according to the distribution of copy numbers of those positions and update the copy number of each position. Upon convergence, the EM algorithm assigns reads {r1, r3, r5} to region A with probability 1/3 and to region B with probability 2/3. We correctly predict the copy number of region A to be 1 and copy number of region B to be 2.

FIG. 1.

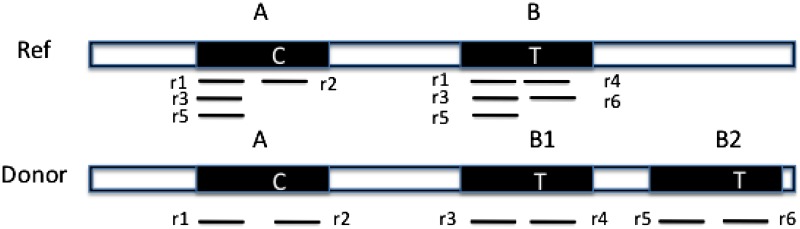
Similar copies of a copy number variations (CNV) region exist in the reference genome. “C” and “T” are the only different nucleotides between region A and B. Reads 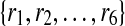are obtained from the donor genome as shown in the lower part of the figure. Furthermore, these reads can be mapped to the reference genome as shown in the upper part of the figure.

2.2. The generative model

We use short-read information from HTS technologies to detect copy number variants. Let 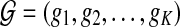be K continuous nucleotides in the reference genome, where g_i is the i^th nucleotide. We assign the copy number of each nucleotide in the reference genome to be 1. The donor genome is also composed of these nucleotides. However, large regions of the genome can be either deleted or duplicated and thus the copy number is changed. For each nucleotide g_i, we denote the copy number to be C_i in the donor genome. If C_i < 1, we call it a copy loss. If C_i > 1, we call it a copy gain. 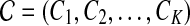can be interpreted as the copy number vector of the donor genome. For most nucleotides, the copy numbers are the same in the donor genome and in the reference genome. So one can assume that the length of donor genome is the same as the length of the reference genome, that is, 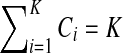. We define vector 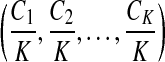to be the normalized copy number vector of the donor genome.

Using HTS technology, millions of short reads are sampled from the donor genome. We assume that a read r_j of length l is generated by randomly picking a position i from according to distribution 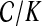and then copying l consecutive positions starting from position i. The copying process is error-prone, with known probability ε for a sequencing error rate at any position of the read. This process is repeated until we have a set of N reads 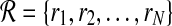. The objective is to infer 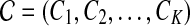from 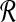. Since the reads are mapped to the reference genome, mapping information is utilized to infer CNVs.

In our model, each read r_j is sequenced starting from one position in the donor genome. As we assume that the donor genome is obtained from the reference genome by alternating the copy number of some regions, each position in the donor genome “originates” from a nucleotide in the reference genome. Consequently, each read originates from a position in the reference genome. If a region in the reference genome is duplicated in the donor genome, any read generated from the duplicated segments of the donor genome originates from a unique position in the reference genome. 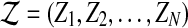is the origin for each read in the reference genome, where 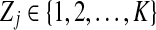. We then define the following likelihood model of all reads given copy number 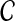and reference genome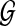

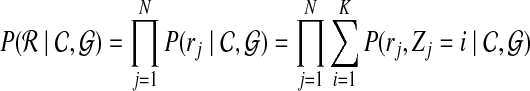(1)

where the first equality follows from the probability that read set 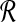is composed of independent probabilities of all the reads, and the second equality follows from the fact that the read probability is equal to the marginalization of read mapping uncertainty, that is, .

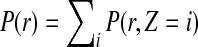The interpretation of the above probability definition 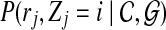is straightforward: the probability of j-th read originating from i-th position of the reference genome, given the copy numbers and reference genome. We can further expand this probability as follows

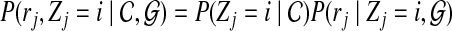(2)

where the equality follows from the fact that the read origin Z is independent of reference genome 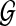and the sequence of read r is independent of copy number 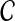. We define the first term 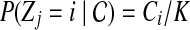to be the probability for read r_j originating from position i. For each position i and read r_j, we have a probability 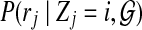, which stands for the probability of observing read sequence r_j given that the origin of read r_j is position i. We can write 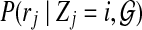as

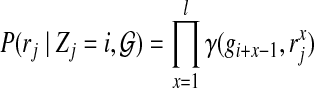and

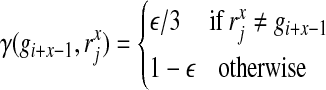where 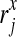stands for the x-th nucleotide of read r_j, and the l consecutive nucleotides starting from position i in the reference genome are 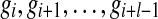. In practice, for each read r_j, the probability 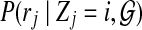will be close to zero for all but a few positions, which are reported by the mapping methods.

We also take the prior probability of the donor genome into consideration. As we assume the donor genome sequence can be obtained by either deleting or duplicating large regions of nucleotides from the reference genome, adjacent positions will have similar copy numbers in the donor genome. Then, in our probabilistic model, it is natural to assume that the copy number of the current nucleotide is only dependent on the previous nucleotide. We have .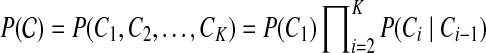

Using Bayes rule, we can get the posterior probability of 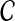given the read set 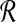and reference genome :

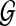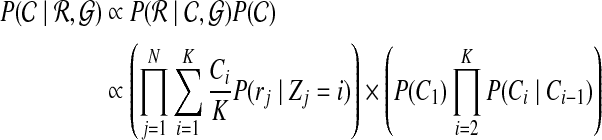(3)

2.3. Optimization

Maximizing the posterior of copy number in Equation (3) is equal to maximizing the following log probability with respect to :

In this section, we provide a more detailed description of our method. In order to make the above objective function simpler, we eliminate the constraint by introducing a penalty function 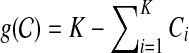, which prevents the 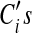from growing unbounded (the above objective function will have a higher value if the 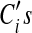grows larger). Incorporating the penalty function, our objective function now becomes

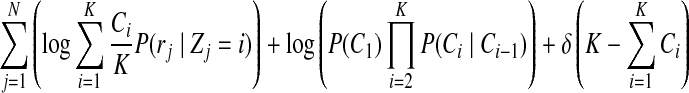(4)

where δ is a penalty function coefficient (we set 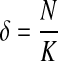in our experiments, from which we achieve best results). We optimize the objective function Equation (4) through an expectation-maximization (EM) algorithm. The algorithm iteratively applies the following two steps until convergence.

Expectation-step:

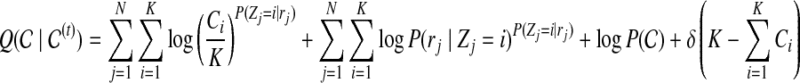Maximization-step:

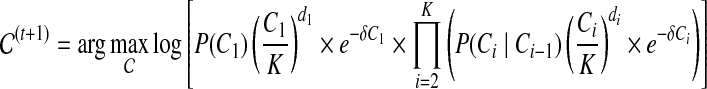(5)

where .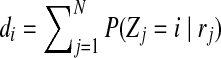

We solve the M-step using dynamic programming. Denote the objective function in the M-step to be

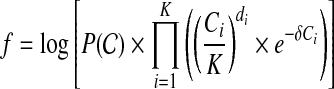(6)

Then we define f (k, x) to be the maximum function value for the first k positions when the copy number of kth position is C_k = x. Now we design the dynamic programming indicated in Equation (7).

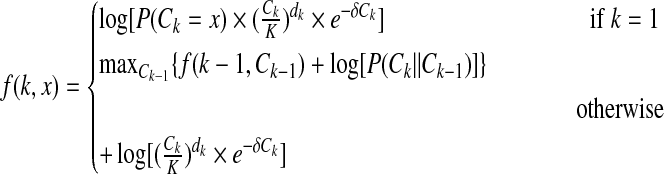(7)

We prove that the above dynamic programming returns the global optimal solution for the objective function in Equation (6).

Lemma 1

The objective function in Equation (6) is solved optimally using the dynamic programming mentioned in Equation (7).

Proof

For the sake of space, we describe the correctness of the dynamic programming in the Appendix.

The maximum value of the objective function in the M-step is then max_x f (K, x). Using a backtracking process, we find the vector 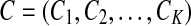that maximizes function f in the M-step. By iteratively running E-step and M-step, we achieve local optima.

2.4. Implementation

This optimization process requires an initial input of copy numbers. Different initial inputs will affect the convergence time. To achieve better performance, it is important to start with a “good” initial guess. In order to obtain a good initial input, we split the genome into nonoverlapping bins of 300 bp. All nucleotides within one bin share the same copy number. Using a similar model as in Equation (1), we get an initial guess of copy numbers by optimizing the objective function Equation (8).

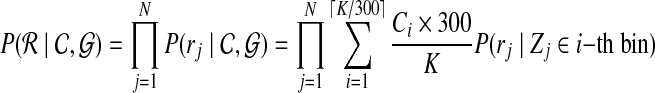(8)

where 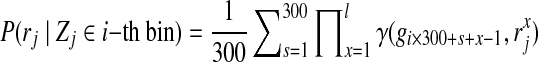. Similarly, we can optimize Equation (8) by the EM algorithm. As proved by Halperin and Hazan (2006), the likelihood of Equation (8) is concave. The EM algorithm will converge to global optimal solution, and it will be a good initial guess for the objective function in Equation (4).

After obtaining a solution using a standard EM algorithm, we conduct our extended EM algorithm introduced in Section 2.3. We summarize our method in Algorithm 1.

2.5. GC-bias correction

One of the shortcomings of the HTS technologies is the existence of different biases in the sequencing process. Some biases are due to the environment while others are due to chemical reactions (DNA amplifications, GC content). Studies show that both Sanger and HTS sequencing are bias toward high GC regions. GC-bias can influence the number of reads generated from a position, and thus the reads are no longer uniformly generated. There have been a number of articles (Alkan et al., 2009; Yoon et al., 2009; Sudmant et al., 2010; Abyzov et al., 2011) that deal with GC-bias in CNV calling. In this work, we adapted the idea mentioned by Abyzov et al. (2011) and Yoon et al. (2009) to correct for GC-bias. In Equation (5), d_i is the number of reads mapped to position i. We correct this bias by updating the definition of d_i to be 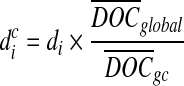, where 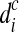is the corrected number of reads mapped to position i, d_i is the original number of reads mapped to position i, 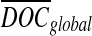is the average depth of coverage (DOC) over all positions, and 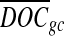is the average DOC over all positions in which the reads have the same GC content as in the reads mapped to position i.

Algorithm 1:

The complete algorithm of CNVeM

Input: Read mapping information, allowing reads map to multiple locations.

Output: Copy number variations compared to reference genome.

Initialization: Choose an initial configuration of copy numbers (0).

STAGE ONE:

Optimize the function in Equation (8) using a standard EM algorithm based on bins. We get an initial solution of copy numbers for each bin.

STAGE TWO:

2.1. Use the output from STAGE ONE as an initial guess.

2.2. For each read rj with , consider all mapping positions; calculate the posterior probability of each position according to the joint probability in Equation (2). Then map the read to multiple locations fractionally according to the posterior probability.

2.3. Calculate the total number of reads mapped to each position.

2.4. Update the copy numbers of all nucleotides using the dynamic programing in Equation (7).

2.5. Repeat Steps 2.3–2.4 until it converges.

3. Results

3.1. Simulation results

In order to assess our method, we carried out experiments on simulation datasets. We developed a simulation framework, in which a donor genome is obtained by altering the copy number of some regions in the reference genome.

3.1.1. Experiment on a simulated mouse chromosome

We first tested CNVeM on a simulated mouse genome. We obtained the masked reference chromosome 17 of Mus Musculus. After pruning all the N's, the length of the chromosome 17 reduced to 58 Mb. This can be used as the “template sequence.” We then duplicate segments of the sequence to generate a reference genome. The lengths of the duplicated segments are chosen from the range [1000, 10000]. We allow nucleotides to mutate with the probability of 1% in the duplication process. The copy numbers of these segments are then altered to generate the donor genome. The copy numbers are chosen from the set {0, 1, 2, 3, 4, 5}. In each experiment, we simulated 100 copy number variations between the reference genome and donor genome. To generate a read, we randomly picked a position from the donor genome and copied 36 consecutive bases starting from this position. The copying process is repeated until we have the desired coverage. All reads are then mapped to the reference genome using mrsFAST (Hach et al., 2010), allowing reads to map with two mismatches.

In addition to detecting the existence of copy number variants, CNVeM especially aims to distinguish which copy is duplicated or deleted in the donor genome, while others have the same number of copy occurrences compared to the reference genome. Simulations are performed using various depth of coverage settings. A CNV is considered to be detected correctly when it overlaps with the true CNV region, meanwhile the predicted copy numbers should be the same as the true copy numbers. The results are shown in the first row of Table 1.

Table 1.

The Results on the Simulated Mouse Chromosome 17 Under Different Sequencing Depth and Mutation Rates Between Duplicated Segments

Mutation rate between duplicated segments	Depth of coverage	No. of predicted CNVs	No. of correct CNVs	False discovery rate	False negative rate
1%	30X	102	100	2.0%	0
	15X	102	100	2.0%	0
	5X	105	100	4.8%	0
0.5%	30X	102	100	2.0%	0
	15X	105	100	4.8%	0
	5X	109	100	8.3%	0
0.1%	30X	101	97	4.0%	3.0%
	15X	107	98	8.4%	2.0%
	5X	116	96	17.2%	4.0%

No. of predicated CNVs are the number of regions CNVeM reports as CNVs. False discovery rate is the ratio between number of false positives and number of predicted CNVs, while false negative rate is the ratio between number of false negatives and number of true CNVs.

We also compared our reported CNVs to true CNVs by base pairs. The overlap is calculated by intersecting the coordinates of predicted CNVs with those of true CNVs. The results in the first row of Table 2 indicate high accuracy of CNVeM in predicting the break points.

Table 2.

Measuring the Accuracy of CNV Break Points by Base Pairs Under Different Sequencing Depth and Mutation Rates Between Duplicated Segments

Mutation rate between duplicated segments	Depth of coverage	Length of predicted CNVs (bp)	Length of overlap (bp)	False discovery rate	False negative rate
1% (504000 bp)	30X	506755	502183	0.9%	0.3%
	15X	506162	501291	1.0%	0.5%
	5X	507703	495074	1.8%	2.5%
0.5% (493000 bp)	30X	492271	488114	0.9%	1.0%
	15X	500460	488387	2.4%	0.9%
	5X	501139	483830	3.5%	1.9%
0.1% (492000 bp)	30X	469821	452120	3.8%	9.1%
	15X	465518	433495	6.9%	11.9%
	5X	462193	417340	9.7%	15.2%

False discovery rate is the ratio between length of false positive regions and total length of predicted CNVs, while false negative rate is the ratio between length of false negative regions and total length of true CNVs.

Furthermore, we simulated the duplicated segments under different mutation rates to assess the power of our method in locating the copy variation origin. All results are summarized in Table 1 and Table2. We see that both the mutation rate between duplicated segments and sequencing depth can affect the accuracy of our program. The smaller the mutation rate, the more similar the duplicated sequence, and the more difficult to distinguish which segment has copy number variation in the donor sequence. We have higher false discovery rate when the read depth is lower and the difference between duplicated copies is smaller, but we manage to recall almost all copy number variations.

The key observation in comparing the two tables (Table 1 and Table 2) is that the false negative rate in predicting the correct quantitive copy number is always lower than the false negative rate in calling the breakpoints of CNVs, moreover the false discovery rate of quantitative value for CNV is always higher than the false discovery rate in breakpoint calling. This illustrates that CNVeM is robust in detecting the existence of CNVs and determining the break points of CNVs. To achieve high sensitivity in CNV calling, CNVeM inevitably reports false positive regions. However, most of these false positive regions are short, and thus we have low false discovery rate in break points calling.

3.1.2. Comparing CNVeM with CNVnator on GC-biased data

In this section, we compare CNVeM with the CNVnator (Abyzov et al., 2011). Using a similar framework, we generated a reference genome and donor genome from chromosome 17 of Mus Musculus. We set the mutation rate between duplicated segments to be 0.1%. Reads are then simulated from the donor genome, allowing GC-bias (Yoon et al., 2009; Abyzov et al., 2011). In order to make the comparison fair for CNVnator, we used Bowtie (Langmead et al., 2009) to do the mapping with option ‘-best -M 1’. With this option, Bowtie returns the best mapping for each read, and in the case of tie, it will randomly pick one mapping location for a read. This step is due to the fact CNVnator assumes there exists one mapping location for each read. However, for CNVeM, we use mrsFAST (Hach et al., 2010) to return all possible mapping positions for each read. Figure 2 illustrates the intersection of CNVs found by CNVeM and CNVnator on the simulated dataset, where 100 CNVs are implanted to the donor genome. CNVeM finds 111 CNVs, which includes 98 of the true CNVs. This indicates that CNVeM has 13 false positives and 2 false negatives. However, CNVnator finds 250 CNV regions among which 91 regions are true CNVs. CNVnator fails to find 9 regions that are CNVs. Moreover, CNVnator reports 159 false positives. This results from the fact that CNVnator randomly places a read to one of its multiple mapping positions and thus affects the read-depth information, from which CNVnator determines the copy variation status. All the results indicate CNVeM has lower false discovery rate and false negative rate compared to CNVnator. We successfully locate the copy variation origins while CNVnator reports all possible CNV regions. Another disadvantage of CNVnator is that it can only determine the CNV to be a copy gain or copy loss, instead of recalling the exact quantitive copy number as in CNVeM.

FIG. 2.

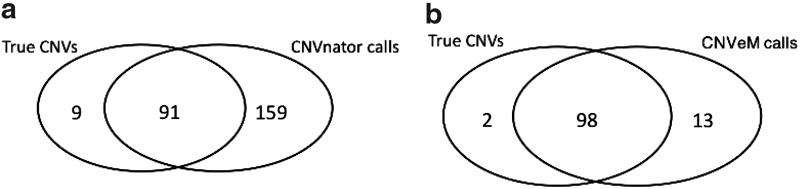
Intersection of two CNV detection results with true CNVs. (a) We illustrate the Venn diagram of the CNVnator calling with the true CNV regions. (b) We illustrate the intersection between the CNVeM calls and the true CNV regions. This figure indicates that we have less false positives and false negatives compared to the CNVnator.

3.1.3. Comparison between different strategies dealing with read mapping uncertainty

When handling reads that can be mapped to multiple positions, existing methods either discard those reads or randomly place the read to one of the multiple mapping positions. CNVeM considers all possible mapping positions, and a read can be placed to one of the positions with a probability. We compared the performance of these different strategies. Furthermore, we consider the popular strategy that divides the genome into bins. All nucleotides within one bin have the same copy number. We develop a method, “wind,” using the same EM framework as in Section 2.3 for the bin strategy.

We run these methods on the same simulated datasets. Following the same process as mentioned above, we generated the reference genome and donor genome from chromosome 17 of Mus Musculus, with mutation rate between duplicated segments set to be 0.1%, 0.5%, and 1%, respectively. Reads are simulated at 30X coverage. The results plotted in Figure 3 illustrate that CNVeM has the highest recall and precision at different mutation rates.

FIG. 3.

Comparison between several strategies dealing with read mapping uncertainty. The x-axis represents the mutation rate between duplicated segments. The shorthands CNVeM, wind, uniq, and rand represent the results from CNVeM; the results from wind, which divides the genome into bins; the results from only considering reads mapped to unique positions, and the results from placing a read to one of multiple mapping positions randomly, respectively.

3.1.4. Time and memory usage

When dealing with HTS technology, which generates tens of gigabytes of data per day, not only the accuracy of the method, but the memory and time usage, become important factors. The time and memory usage is estimated for the CNV calling process, we assume the mapping is done in a separate step. Our program takes 30 minutes to detect all the CNVs in the simulation dataset on masked chromosome 17 of the mouse genome, where we had 30X coverage (having around 50 million reads). All the experiments run on 64-bit AMD Opteron processor; furthermore, our program used 2 Gb of memory at the peak of usage. In order to run CNVeM on the whole-genome sequencing data, the memory usage increases linearly with the size of the genome.

3.1.5. Simulation on a whole mouse genome

To test the scalability of our program, we run CNVeM on a whole mouse genome simulation data. Using a similar framework as introduced in above sections, we generated a whole reference genome with 20 chromosomes, taking the genome (chr1-chr19, chrX) of the mouse strain C57BL/6NJ as the template. We implanted 100 CNVs to each chromosome, resulting in 2000 implanted CNVs. The mutation rate between duplicated segments in the reference genome is 1%. The donor genome is then sequenced at 15X depth of coverage. Among the 2188 CNV regions reported by CNVeM, 1956 regions have an overlap with the implanted CNVs, with the false discovery rate to be 10.6%, and false negative rate to be 2.2%. The results from whole-genome simulation consist with the results from single chromosome, where false positives are inevitably reported to achieve high sensitivity. Further investigation shows that most of the false positive regions are short. Another reason that leads to the false positives is the multiple mapping reads. The whole genome reference increases the proportion of multiple mapping reads compared to single chromosome reference, and thus increases the difficulty to precisely determine the origin of duplication events.

3.2. Results on real data

We used the data published by Sudbery et al. (2009), where chromosome 17 of mouse strain A/J is deeply sequenced using Illumina technology to test our method on real data. The data contains 112 million (56 million pair-end) reads, and the length of each read is 36 bp. This results in a 42X coverage. We aligned the reads to the masked chromosome 17 using mrsFAST (Hach et al., 2010), allowing up to two mismatches. Out of these 112 million reads, 39 million reads are mapped uniquely to the genome. However, 4 million reads are mapped to more than one position in the genome. We supply the mapping information of both uniquely and non-uniquely mapped reads to CNVeM and manage to detect 44 copy gain regions and 355 copy loss regions. Among those 44 copy gain regions, 28 regions have been reported by Sudbery et al. (2009), and 15 regions out of these 355 copy loss regions have been reported by Sudbery et al. (2009). We investigated those remaining 340 copy loss regions and found that these regions have a unique copy in the reference genome but have 0 depth of coverage from the mapping results. In Sudbery et al. (2009), these regions are referred to as potential “deletions.” Each of these remaining 340 copy loss regions have an overlap with at least one of the 416 deletions reported by Sudbery et al. (2009). Furthermore, we applied CNVnator on this real data and it managed to detect 42 copy gain regions and 264 copy loss regions. Comparing the CNVeM calls with those of CNVnator, we saw 26 copy gain regions overlap, and 86 copy loss regions were found by both methods.

4. Discussion

CNV regions have been shown to be correlated with many diseases ranging from cancers to learning disabilities (Cappuzzo et al., 2005; Sebat et al., 2007). Two main strategies exist to improve the CNV detection, either to improve the technology from which we gather data from individuals, or to design better algorithms. The shift from ArrayCGH to HTS is a great indication of improving the data gathering process, as current studies suggest that the use of HTS results in higher power in detecting CNV breakpoints and quantifying the true copy number for each region.

It has been shown previously that we can use both the depth of coverage and paired-end information to detect CNVs accurately (Medvedev et al., 2010). We illustrate that the correct usage of DOC improves the accuracy of CNV detection greatly. In this work, we present a probabilistic model for detecting CNVs based on an expectation-maximization (EM) method. Our method incorporates all possible mapping information in the CNV prediction. It not only has higher accuracy in detecting the CNVs but also can detect which of the paralog regions in the genome is copied or deleted. All previous methods fail to distinguish paralog regions as they either discard all multiple mapping reads (reads mapped to multiple positions) or randomly place a read to one of the mapping positions.

Another main contribution of this work is that we can predict the CNV breakpoints in base-pair resolution. Unlike previous methods, which define CNV for each bin (segment of fixed or variable length), our objective function is defined for each base-pair. In other words, we are predicting the CNV for each base-pair. This helps us detect the breakpoint of each CNV with high accuracy.

Although we mention that using DOC can improve the accuracy of CNV detection, we do not deny the fact that paired-end mapping has valuable information. Our future work is to incorporate paired-end reads information into our probabilistic model.

5. Appendix

Expectation-step:

Estimate the posterior probability of each read origin under the current estimate of ^(t):

(9)

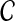We can then calculate the expected value of log objective function, with respect to the posterior probability of , under the current estimate of ^(t):

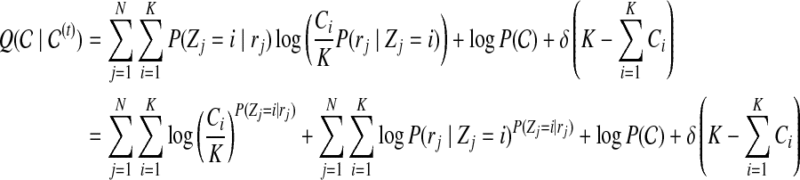(10)

Maximization-step:

Find the vector 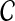^(t+1) that maximizes the above function:

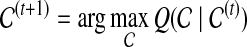(11)

In each iteration of the EM algorithm, both C^(t) and P(r_j|Z_j = i) are fixed values, so P(Z_j = i|r_j) is a fixed value within each iteration. Furthermore,

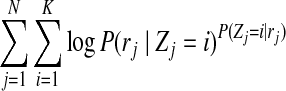is also a fixed value within one single iteration. Then, maximizing the above function reduces to finding

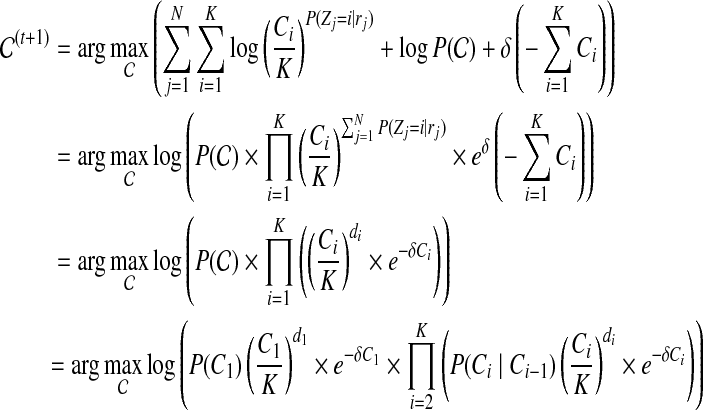(12)

where .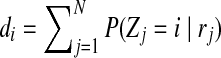

Lemma 2

The objective function in Equation (6) is solved optimally using the dynamic programming mentioned in Equation (7).

Proof

We recall 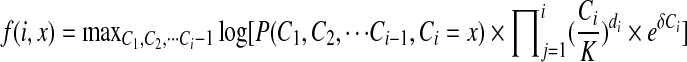where 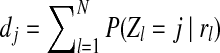. Moreover, f (i, x) is the maximum value of the copy number for the first i − 1 positions, and the copy number of position i is x (C_i = x). Using the above definition, we drive the f (i + 1, y).

 

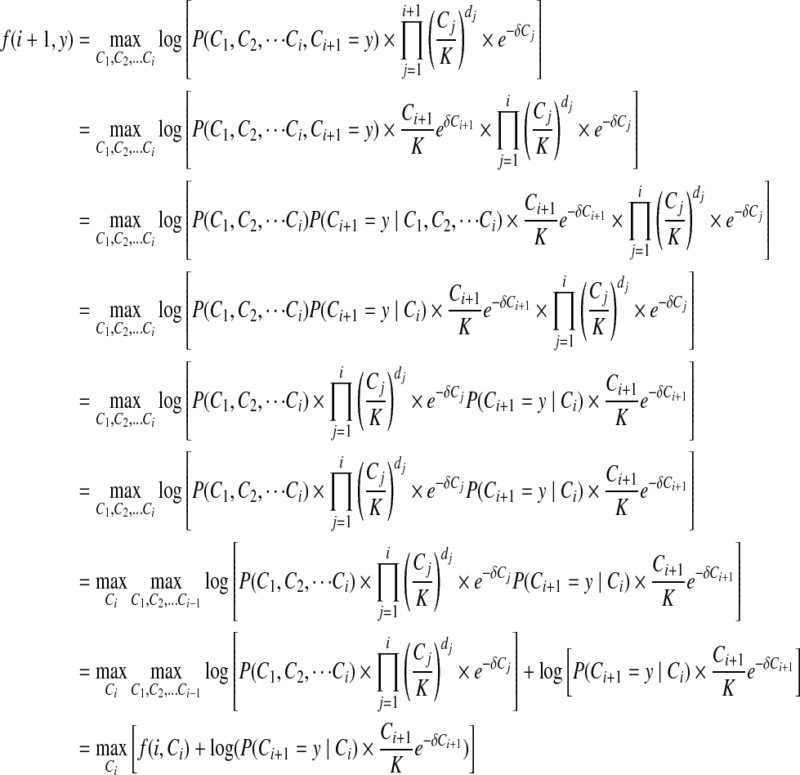Acknowledgments

Z.W., F.H., W.Y., and E.E. are supported by National Science Foundation grants 0513612, 0731455, 0729049, and 0916676, and NIH grants K25-HL080079 and U01-DA024417. This research was supported in part by the University of California, Los Angeles subcontract of contract N01-ES-45530 from the National Toxicology Program and National Institute of Environmental Health Sciences to Perlegen Sciences. E.H. is a faculty fellow of the Edmond J. Safra Bioinformatics program at Tel-Aviv University. E.H. was supported by the Israel Science Foundation grant 04514831.

Author Disclosure Statement

No competing financial interests exist.