Abstract
In this paper we utilize methods of hyperdimensional computing to mediate the identification of therapeutically useful connections for the purpose of literature-based discovery. Our approach, named Predication-based Semantic Indexing, is utilized to identify empirically sequences of relationships known as “discovery patterns”, such as “drug x INHIBITS substance y, substance y CAUSES disease z” that link pharmaceutical substances to diseases they are known to treat. These sequences are derived from semantic predications extracted from the biomedical literature by the SemRep system, and subsequently utilized to direct the search for known treatments for a held out set of diseases. Rapid and efficient inference is accomplished through the application of geometric operators in PSI space, allowing for both the derivation of discovery patterns from a large set of known TREATS relationships, and the application of these discovered patterns to constrain search for therapeutic relationships at scale. Our results include the rediscovery of discovery patterns that have been constructed manually by other authors in previous research, as well as the discovery of a set of previously unrecognized patterns. The application of these patterns to direct search through PSI space results in better recovery of therapeutic relationships than is accomplished with models based on distributional statistics alone. These results demonstrate the utility of efficient approximate inference in geometric space as a means to identify therapeutic relationships, suggesting a role of these methods in drug repurposing efforts. In addition, the results provide strong support for the utility of the discovery pattern approach pioneered by Hristovski and his colleagues.
Keywords: Distributional semantics, Literature-based discovery, Predication-based Semantic Indexing, Vector symbolic architectures
1. Introduction
This paper addresses the role of representation in the repurposing of pre-existing biomedical knowledge to identify novel therapeutic strategies. On account of the large number of possibly useful undiscovered connections between drugs and the diseases they treat, some work in literature-based discovery (LBD) has emphasized scalable methods based on the distributional statistics of terms or concepts in the literature. An advantage of many of these methods is the facility for efficient search to identify associations between terms and/or concepts that do not co-occur with one another in the literature, based on similarity between their vector representations, which are derived from their distributional statistics. However, as economic constraints limit the number of potential therapies that can be advanced for further testing, more stringent constraints based on the nature of the relationships between concepts are desirable. Recent work in LBD has introduced the notion of a discovery pattern [1–4], a pathway of logical connections between concepts that suggests a potentially therapeutic relationship. Up to this point, researchers have designed discovery patterns manually, by composing sequences of relationship types, such as “drug x INHIBITS substance y, substance y CAUSES disease z”, that suggest therapeutic potential. In addition, as these patterns are represented computationally as sequences of symbols, it is necessary to explore possible pathways in a stepwise manner, in contrast to the efficient search facilitated by the representation of terms or concepts in a vector space. In this paper we address these issues by representing both concepts and the relationships between them as vectors in hyperdimensional space, using the Predication-based Semantic Indexing (PSI) approach [5].
The paper proceeds as follows. First we discuss LBD research, with an emphasis on recent approaches that have been facilitated by advances in biomedical language processing, and introduce SemRep [6], the language processing system we have utilized for this research. We then introduce PSI [5], a representational approach we have developed that facilitates approximate inference across large volumes of knowledge extracted by SemRep, using a geometric approach. This background material is followed by a discussion of the mathematics underlying our approach, including our approach to inference in PSI space. We then proceed to a study, in which we identify discovery patterns from a set of known TREATS relationships, and an experiment in which we apply these “discovered” discovery patterns to a held out set of diseases. The aim of this experiment is to evaluate our hypothesis that directing search using the identified discovery patterns will improve the recovery of treatments for members of this held out disease set, when compared with a co-occurrence based approach. The results and implications of this empirical work are subsequently discussed.
2. Background
2.1. Literature-based discovery
The field of literature-based discovery traces its origins to a serendipitous discovery of a therapeutically useful [7] connection between fish oils and Raynaud’s disease by information scientist Don Swanson [8]. This discovery was made by finding points of intersection between two bodies of literature that were disconnected from one another with respect to authorship and readership. Swanson identified bridging concepts such as blood viscosity that could be used to connect Raynaud’s to concepts that had not occurred with it in the literature previously. This approach has been generalized and applied to a number of other problems (for recent reviews see [9–11]). The general idea is to use a bridging, or B concept, to link two other concepts, usually referred to as A and C, that have not co-occurred in the literature previously. This scheme allows for two modes of discovery, termed open and closed (5). Open discovery has two steps. Starting with a disease C, a set of intermediate B concepts is identified in literature related to this disease. The literature on these B (or “bridging”) concepts is then explored to seek out A concepts, potential treatments. In closed discovery, the starting point is the hypothesis, or observation, of a therapeutic relationship between treatment A and disease C (AC), and an explanation (AB, BC) for this observation or hypothesis is sought by exploring the literature for concepts related to both A and C. Swanson’s approach has also been incorporated into a number of automated systems that aim to promote discovery by encouraging scientists to search beyond the limits of their usual literature review (for example [12–16], and for a review see [17]).
Swanson’s initial work was motivated primarily by the increasingly disjointed nature of the scientific literature that is an inevitable consequence of increased specialization. As noted by Swanson [18], the rapid increase in the volume of the biomedical literature is accompanied by a combinatorial explosion in the number of implicit connections between entities described in this literature [19]. Consequently, a scalable alternative to stepwise exploration of every possible pathway from disease to discovery is desirable.
To this end, several LBD researchers have investigated the use of methods of distributional semantics [20] as a means to identify directly associations between terms or concepts that do not co-occur with one another in the biomedical literature [21–23]. Methods of distributional semantics learn measures of relatedness between terms or concepts from their distribution across large volumes of electronic text. With some distributional approaches, terms or concepts that occur in similar contexts will be strongly associated, even if they do not appear together directly. Therefore, search can proceed directly from A to C, without the need to explicitly identify a B concept. This, and the reduced-dimensional nature of the representations employed in distributional models, allow for efficient search for previously unrecognized meaningful relations. In our previous work we have shown that distributional approaches can be used to simulate historical literature-based discoveries, and predict terms that will co-occur with one another in the future from a time-delimited training set [23]. However, as they are based on occurrence in the context of similar surrounding words or concepts, the associations learned by these models tend to be general in nature. Given the vastness of the search space for possible discoveries, further representational richness is required to identify selectively candidates for discovery in which the nature of the relationships between concepts suggest a plausible therapeutic hypothesis. It is possible to extract this additional information from the biomedical literature using specialized natural language processing systems such as SemRep [6].
2.2. SemRep
SemRep is a symbolic natural language processing system that identifies semantic predications in biomedical text. For example, SemRep extracts “Acetylcholine STIMULATES Nitric Oxide” from the sentence “In humans, ACh evoked a dose-dependent increase of NO levels in exhaled air”. SemRep is linguistically based and intensively depends on structured biomedical domain knowledge in the Unified Medical Language System (UMLS SPECIALIST Lexicon, Metathesaurus, Semantic Network [24]). At the core of SemRep processing is a partial syntactic analysis in which simple noun phrases are enhanced with Metathesaurus concepts. Rules first link syntactic elements (such as verbs and nominalizations) to ontological predicates in the Semantic Network and then find syntactically allowable noun phrases to serve as arguments. A metarule relies on semantic classes associated with Metathesaurus concepts to ensure that constraints enforced by the Semantic Network are satisfied.
SemRep provides underspecified interpretation for a range of syntactic structures rather than detailed representation for a limited number of phenomena. Thirty core predications in clinical medicine, genetic etiology of disease, pharmacogenomics, and molecular biology are retrieved. Quantification, tense and modality, and predicates taking predicational arguments are not addressed. The application has been used to extract 23,751,028 predication tokens from 6,964,326 MEDLINE citations (with dates between 01/10/1999 and 03/31/2010). Several evaluations of SemRep are reported in the literature. For example, in [25] .73 precision and .55 recall (.63 f-score) resulted from a reference standard of 850 predications in 300 sentences randomly selected from MEDLINE citations. Kilicoglu et al. report .75 precision and .64 recall (.69 f-score) based on 569 predications annotated in 300 sentences from 239 MEDLINE citations [26]. Recent research in literature-based discovery [1–4] has exploited the additional information provided by specialized language processing systems such as SemRep by developing the idea of a discovery pattern.
2.3. Discovery patterns
Swanson’s description of his own approach presupposes the representation of the nature of the relationships that occur between concepts (emphasis added):
Suppose that one literature reports that, under certain circumstances, A causes B (e.g., drug A alters blood levels of hormone B). Such a causal statement is denoted by “AB.” Assume that a second literature reports a similar causal connection, BC (e.g., hormone B influences the course of disease (C). Presumably, then, anyone aware of the two premises AB and BC would notice that A might influence C (denoted “AC”)
– Swanson 1990
However, approaches based on co-occurrence alone do not offer the representational richness required to populate a syllogistic construction of this nature. In recognition of the limitations of co-occurrence based approaches, Hristovski and his colleagues introduced the notion of a “discovery pattern”, a set of predications (object-relation-object triplets) that might suggest plausible therapeutic hypotheses [1–4]. The extraction of predications from the biomedical literature is accomplished through the application of natural language processing technology, specifically the SemRep [6] and MedLEE [27] systems for biomedical language processing.
As an example of a discovery pattern, consider the “may_disrupt” pattern, as defined by Ahlers and her colleagues [4]:
Substance X <inhibits> Substance Y;
Substance Y <causes|predisposes|associated_with> Pathology Z;
Substance X <may_disrupt> Pathology Z
This pattern is represented using the following set of relationship types (or predicates) extracted by SemRep: {INHIBITS, CAUSES, PREDISPOSES, ASSOCIATED_WITH}, with the aim to identify explanatory hypotheses for the observation that schizophrenic patients, who are often treated with anti-psychotic agents, have lower incidences of cancer than the general population [4]. Other discovery patterns have been used to simulate Swanson’s original discovery [1], and to suggest therapeutic hypotheses for Parkinson’s disease by combining predications derived from the literature with others derived from DNA micro-array results [3]. Up to this point, researchers, based on their domain knowledge and their interpretation of what might construe a meaningful explanatory pathway, have constructed discovery patterns manually, and applied them by traversing the network of concepts and relations on a node-by-node basis.
Consider the “may_disrupt” pattern from the perspective of a researcher searching for a novel treatment for a particular pathology. Exhaustive exploration of all possible therapies for this pathology according to this pattern requires retrieving all concepts that occur as the subjects of a CAUSES, ASSOCIATED WITH or PREDISPOSES relationship with it, or any variant forms of interest (for example, Ahlers and her colleagues took any concept of the UMLS type “neop” or neoplastic process as their set of “Z” pathologies). Subsequently, any concept occurring as the subject of an INHIBITS relationship with any of these retrieved concepts must be explored. Therefore, the size of the search space in this case is the product of the number of concepts describing the disease in question, all of which must be explored to seek relevant predicates, multiplied by the number of unique predications involving any of these concepts and the predicates CAUSES, ASSOCIATED_WITH or PREDISPOSES, multiplied in turn by the number of the subjects of these predications that occur in predications with the predicate INHIBITS. As anticipated by Swanson, a combinatorial explosion in the size of this search space would occur if more than one bridging term were considered.
In practice, Ahlers and her colleagues took a closed discovery approach, enabling them to triangulate from starting points including both neoplastic processes and a number of selected antipsychotic agents. The number of predications in the search space was also limited to those extracted from related PubMed queries, as was the case in other LBD work in which discovery patterns were utilized [1,2]. However, as anticipated by Swanson, the ever-increasing numbers of logical connections between biomedical concepts limit the computational tractability of exhaustive search across the breadth of the biomedical literature for the purpose of either open or closed discovery.
2.4. Predication-based Semantic Indexing
The extent to which inference can be accomplished is constrained by the way in which knowledge is represented. A common strategy for re-use of the biomedical literature is to draw associations between concepts (or terms) occurring in similar contexts [21–23]. This leads to a measure of general relatedness that is convenient to derive, but limited in its specificity. Another strategy involves representation of concepts, and the relations between them, as symbols [1,2]. This allows search to be directed precisely, but requires node-by-node exploration of the network of concepts and relations. Our approach, which is based on the hyperdimensional computing paradigm [28], combines the strengths of both of these strategies. Both concepts and the relationships between them are represented as vectors in hyperdimensional space. Inference occurs as a function of the geometry of this space, mediated by reversible vector transformations. This approach, which we have named Predication-based Semantic Indexing [5] (PSI), integrates algebraic and geometric models of intelligence to support scalable search [29] and efficient inference [30] across large volumes of computable knowledge, providing a computationally tractable means to generate therapeutic hypotheses.
2.5. Mathematical structure and methods
2.5.1. Vector symbolic architectures
PSI adopts the Random Indexing approach as described in [23], in which a semantic vector for a concept is generated by superposing randomly constructed elemental vectors representing the contexts in which this concept occurs. These vectors may be binary, real or complex in nature. However, regardless of this representational choice, it is important that elemental vectors be constructed such that they are unlikely to be similar to one another. This constraint is important, as it ensures that an elemental vector provides a unique signature for the entity it is encoding, so that this entity can be correctly re-identified despite any distortions of the original elemental vector that may occur during the learning process. Vectors utilized in this approach are of high dimensionality (in the thousands or tens of thousands), and the combination of this high dimensionality and the construction of dissimilar elemental vectors makes the representation robust.
Semantic vectors can be thought of as containers for knowledge encoded by elemental vectors. Throughout this paper we will write E(X) and S(X) for the elemental and semantic vectors associated with the concept X. In addition, we introduce elemental vectors for relations, such that E(R) denotes the elemental vector for the relation R. As many relations are directional, we will use RINV to denote the inverse of R, such that A R B (e.g. thalidomide TREATS multiple myeloma) and B RINV A (e.g. multiple myeloma “TREATSINV” = “IS TREATED BY” thalidomide) carry the same meaning, though they may be encoded by different vector representations.
To encode relations, PSI utilizes the hyperdimensional computing paradigm [28] exemplified by the models of Kanerva [31] and others [32–34] that are collectively known as Vector Symbolic Architectures (VSAs) [33]. VSAs are descendants of Smolensky’s tensor-product based connectionist approach [35] to encoding symbolic knowledge and nested compositional structure. Relations are encoded in these models using reversible vector transformations, a process referred to as binding.
Binding is a multiplication-like operator through which two vectors are combined to form a third vector C that is maximally dissimilar from either of its component vectors, A and B. We will use the symbol “⊗” for binding, and the symbol “⊘” for the inverse of binding throughout this paper. It is important that this operator be invertible, in order to facilitate the recovery (or release) of information encoded into a bound product. Consequently, if C = A ⊗ B, then A ⊘ C = A ⊘ (A ⊗ B) = B. Under some circumstances this ⊗ recovery will be approximate, but the robust nature of the underlying hyperdimensional vector representation ensures that A ⊘ C will be sufficiently similar to B that the original vector for B can be recognized as the best matching candidate for A ⊘ C in the original set of concepts.
Note that binding is implemented differently in different VSAs, and that the symbol “⊗” should not be identified with the tensor product. For example, Plate’s Holographic Reduced Representations use circular convolution of real or complex vectors [32], while Kanerva’s Binary Spatter Code (BSC) [31], which we utilize in our experiments, uses bitwise exclusive or (XOR) and binary vectors. In this case, the binding operator is its own inverse (⊗ and ⊘ are the same operator, namely XOR), but we will nonetheless ⊗ use different symbols to represent these operators to maintain consistency with VSAs in general. In addition to being invertible, the binding operators used in VSAs all produce a bound product of the same dimensionality as the component vectors from which it was derived. This distinguishes VSAs from earlier models using tensor products, which resulted in a bound product with the dimensionality of its components vectors squared. Of note, using bitwise XOR to implement binding for binary vectors implies that in this case, binding commutes: A ⊗ B = B ⊗ A.
Bundling is an addition-like operator, through which superposition of vectors is achieved. Unlike binding, bundling produces a vector that is maximally similar to the component vectors from which it was derived. One example of a bundling operator is the use of vector addition and subsequent normalization. Another is the majority rule used in the BSC, where each dimension of the vector resulting from the superposition is assigned either “1” or “0” in accordance with the most popular value in this dimension in the component vectors, with ties broken at random. We will use the symbol “+” to denote bundling, and the computer science “+=” for “bundle the left hand side with the right hand side, and assign the outcome to the symbol on the left hand side”. So, for example S(A) + = E(B) denotes the addition of the elemental vector for B to the semantic vector representing A, a common operation in training.
2.5.2. Predication-based Semantic Indexing
PSI combines the binding and bundling operators to encode predications during the training process. For example, the predication “thalidomide INHIBITS cyclooxygenase 2” is encoded by the following sequence of steps:
Similarly, the predication “cyclooxygenase 2 ASSOCIATED WITH multiple myeloma is encoded as follows:
Note that in the case of ASSOCIATED_WITH, we have not used an inverse, as this relationship is not directional. In practice, statistical weighting and frequency thresholds are used to limit the influence of uninformative predications, as will be discussed further in the methods section. The net result is a hyperdimensional vector space, with dimensionality predetermined by the size of the pre-assigned elemental vectors. A vector that captures, albeit approximately, the predications this concept has occurred in, represents each concept.
2.5.3. Statistical properties of hyperdimensional binary space
While we have presented the operations underlying our approach such that they will be compatible with VSAs in general, for the research described in this paper we utilized Kanerva’s Binary Spatter Code[31] (BSC). The BSC uses hyperdimensional (e.g. dimensionality ≥ 10,000) binary vectors as a representation for concepts and relations (or variables). Elemental vectors are randomly generated such that every dimension in the vector has an equal probability of being one or zero, and there are an equal number of ones and zeros in each vector. As noted by Kanerva [36], this leads to some useful statistical properties.
As there is a 50% probability of a one or zero occurring in each dimension, the mean Hamming distance between any two randomly constructed vectors will be a half of the dimensionality of the vectors. For example, in a 10,000 dimensional space we would anticipate elemental vectors being 5000 bits apart from one another on average. In hyperdimensional binary space, this distance is referred to as the indifference distance, and two points at this distance from one another are considered to be orthogonal to one another [36]. Secondly, the standard deviation of this distribution of Hamming distances is a half of the square root of the dimensionality of the vectors. To continue our example, we would anticipate a standard deviation of 50 in a 10,000-dimensional space. A consequence of this distribution is that an elemental vector has a high probability of being far apart from every other elemental vector. This sparseness of the space confers robustness, as it implies that it is possible to distort an elemental vector considerably, while retaining confidence that it will be closer to its original form than to any other elemental vector in the space.
2.5.4. Inference in PSI space
2.5.4.1. Inferring predicate pathways
PSI provides the means to facilitate two sorts of inference. Firstly, it is possible to infer from two semantic vectors the dual-predicate pathway through which they are connected. Consider the following steps that occurred during the training process:
As both S(thalidomide) and S(multiple_myeloma) now contain E(cox_2) (cyclooxygenase 2 is abbreviated as cox_2), applying the inverse of the binding operator, ⊘, will result in this common concept cancelling out, such that:
The resulting vector will be a noisy approximation of the elemental vectors concerned, but in hyperdimensional space it is highly probable that this approximation will be significantly closer to these elemental vectors than to any other vector in the space [28]. In some cases, the resulting predicate pathway provides a plausible explanatory hypothesis. For example, it is plausible that thalidomide’s therapeutic effect in multiple myeloma may be related to inhibition of cox-2. As further examples, in one of the PSI spaces utilized for our experiments, the three closest bound pairs of predicate vectors to the vector produced by this operation are shown in Table 1.
Table 1.
Inferring the connections between multiple myeloma and thalidomide. 1-HD = 1-(normalized Hamming distance); SD > random = number of Standard Deviations above mean (1-HD) between random vectors.
| Paired predicate | 1-HD | SD > random |
|---|---|---|
| ASSOCIATED_WITH; COEXISTS_WITH | 0.5158 | 5.653 |
| INHIBITS; ASSOCIATED_WITH | 0.5154 | 5.510 |
| INTERACTS_WITH; ASSOCIATED_WITH | 0.5123 | 4.401 |
Note that the relatedness between these pathways and the vector S(thalidomide)⊘S(multiple_myeloma was significantly higher than that of the next-nearest neighboring) vector, which was only 3.31 SD above the mean anticipated between random vectors.
2.5.4.2. Generalizing to new diseases
As we have shown previously [30], an inferred predicate pathway can be applied to other semantic vectors to direct search across predicate paths of interest. For example, either the vector representing E(INHIBITS ⊘ E(ASSOCIATED_WITH) or the approximation of this vector inferred from S(thalidomide) ⊘ S(multiple_myeloma), can be used to direct search through PSI space for concepts that relate to some other concept in the same manner as the first two concepts were related to one another. For example, consider the following composite cue vectors:
Either of these composite cue vectors can be used to direct search toward semantic vectors representing concepts that relate to malignant mesothelioma in the same manner that thalidomide is related to multiple myeloma, effectively solving the proportional analogy problem “what is to malignant mesothelioma as thalidomide is to multiple myeloma?” When the second approach is used, accuracy depends on the contribution that the relevant predicate pathways make to the vector representations of the component semantic vectors, which are likely to also encode other, unrelated, predicate-argument pairs.
These approaches provide the means to implement discovery patterns at scale, as novel relationships between A and C concepts are identified directly, without the need to explicitly traverse bridging B concepts. In the section that follows, we present an evaluation of the utility of this approach as a means to identify therapeutic relationships. We do so using the sequence of inference procedures we have just described: first we infer explanatory pathways from pharmaceutical agents to diseases they are known to treat, and then we generalize to another held out set of diseases, to attempt to identify pharmaceutical agents that treat them.
3. Evaluation
3.1. Overview
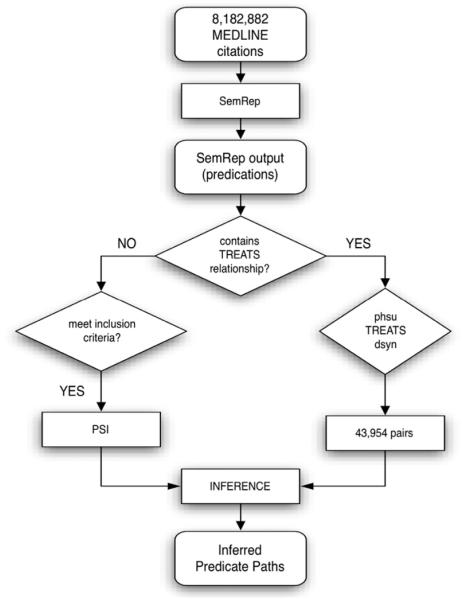
Fig. 1 provides an overview of the research described in this paper. To evaluate the ability of our methods to support discovery, we conduct a study (Fig. 1, left, described in Section 3.2) followed by an experiment (Fig. 1, right, described in Section 3.3). In the first of these, we generate a PSI space (PSI space 1) without encoding any TREATS relationships, and infer the most strongly associated dual-predicate path between all pharmaceutical substances (UMLS semantic type “phsu”) and diseases or syndromes (UMLS semantic type “dsyn”) that occur together in a TREATS relationship (n = 48,204) in the SemRep database. In the second, we utilize the 5-to-10 most popular inferred paths to direct search through predication space. This search occurs in the context of a PSI space (PSI space 2) in which no direct relationships of any kind between pharmaceutical substances and neoplastic processes (UMLS semantic type “neop”) are encoded. We evaluate the extent to which the discovered discovery patterns can be used to “rediscover” TREATS relationships involving pharmaceutical substances and neoplastic processes in the SemRep database, and compare this to the performance of a distributional approach, Reflective Random Indexing [23], that derives an estimate of the relatedness between concepts from their distributional statistics in a corpus of documents.
Fig. 1.
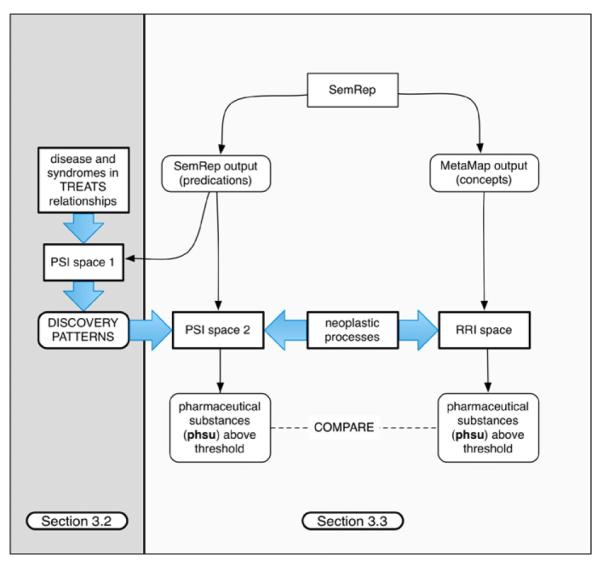
Overview of the Evaluation.
Our hypothesis is that directed search using the discovery patterns identified during the initial study (using PSI) will be more productive than search using general association between concepts, without considering the nature of the relationships concerned (using RRI).
3.2. Generating explanatory hypotheses
In this study, we infer the most popular dual-predicate paths between diseases or syndromes and pharmaceutical substances that occur together in TREATS relationships in the SemRep database (n = 48,204). The study is conducted in the context of a PSI space that is ignorant of all TREATS relations so as to eliminate the possibility of indirect treats relationships being inferred from direct treats relationships (for example, it may be inferred that one drug that has been compared with another that is known to treat diabetes, would also treat diabetes).
3.2.1. Methods
An overview of the study is presented in Fig. 2. The predications extracted by SemRep from a set of 8,182,882 MEDLINE citations dated between 1999 and 2011 (n = 21,720,623) were divided into TREATS predications (n = 1,592,143), and other predications (n = 20,128,480). The TREATS pairs were kept aside, and from these a set of unique predications of the form “phsu TREATS dsyn” where phsu represents the UMLS semantic type “pharmaceutical substance”, and dsyn represents the UMLS semantic type “disease or syndrome” were extracted (n = 48,204). All other predications of the permitted predicate types, defined by the set {ASSOCIATED_WITH; COEXISTS_WITH; AFFECTS; AUGMENTS; CAUSES; DISRUPTS; INHIBITS; INTERACTS_WITH; PREDISPOSES; STIMULATES} were used to generate a PSI space. All concepts occurring 100,000 times or more were excluded from the space, to eliminate frequently occurring concepts that carry little information content. Only those dsyn-phsu pairs in which both elements were represented in the PSI space were retained (n = 43,954).
Fig. 2.
Generation of explanatory hypotheses.
Training occurred as follows. Every concept Cn was assigned a semantic vector S(Cn). Every concept Cn was also assigned an elemental vector E(Cn). Elemental vectors for this study were 32,000-dimensional binary vectors, with 16,000 1s and 16,000 0s distributed at random across the vector. To maintain consistency across experiments, we seeded our random number generator with a hash function derived from the name of the concept-to-be-represented, as described in [37]. Therefore, the “random” vectors in this case are in fact deterministic, so the incidental overlap between vectors was consistent across experiments. Each predicate, Pm, is also assigned an elemental vector, E(Pm). For each unique predication that a given concept Ca occurred in, training for this concept occurred as follows:
where Cb and Pc are the other concept and the predicate in the predication respectively, and lw and gw are local and global weighting metrics respectively, defined as follows:
Consequently the weight of the contribution of a predicate-argument pair is equal to the log of one plus the frequency with which this predication occurs, multiplied by the sum of inverse document frequencies (idf) of the concept and the relation concerned. These statistical weighting metrics were utilized to enhance the influence of infrequently occurring concepts and relations. As we were generating semantic vector representations for both concepts, the complementary encoding also occurred:
In this instance we have used the inverse of the predicate Pc, PcINV, to encode the direction of the relationship concerned. However, in some cases, such as the predicate “COEXISTS_WITH”, the relationship is not directed, and so a single predicate vector is used (Pc = PcINV). Once training was complete, a search space of possible dual-predicate paths was constructed by combining the elemental vectors for each permitted predicate type (n = 17, when allowing for inverse relations with some predicate types) using the following procedure:
For each predicate p1 For every other predicate p2 S(predicate path) = E(p1) ⊘ E(p2)
Once this search space of predicate paths was constructed, inference was performed by generating a composite cue vector from the semantic vectors of each of the 43,954 phsu–dsyn pairs. This was accomplished using the following procedure:
This search was performed for all of the phsu–dsyn pairs, and in each case the most strongly associated dual-predicate pathway was retained. Each of the possible pathways was ranked according to the number of times it was most strongly associated with an example. Inference is computationally efficient (scaling at a rate linear to the number of predicate pathways, or quadratic to the number of permitted predicates). In our experiments, the 43,954 example pairs were processed in around 5 min.
3.2.2. Results and discussion
The results of this study are shown in Table 2, which shows the number of times each of the 10 most popular predicate-pathways were most strongly associated with one of the 43,954 example pairs. In addition, an illustrative example of each of the predicate pathways is provided. Examples were selected on the basis of our ability to interpret them, and represent one possible application of the predication pathway concerned only. In some cases, such as when the “COEXISTS_WITH” predicate is involved, patterns are quite flexible, as this predicate is extracted from sentences with a broad range of meanings, including statements that drugs were used together in combination, descriptions of commonly comorbid conditions and structural similarity between entities. In each instance, we retrieved a bridging or “B” term from the SemRep database. Having identified the concepts and predicates involved, this can be accomplished efficiently by triangulating the search.
Table 2.
Ten most popular predicate pathways. Pathways labeled “MD” generalize a component, or are a component, of the “may_disrupt” (MD) discovery pattern.
| Predicate path | Pairs | Example and Comment |
|---|---|---|
| COEXISTS_WITH ASSOCIATED_WITH MD |
7954 |
Heparin,_low-molecular-weight COEXISTS_WITH thrombin ASSOCIATED_WITH antiphospholipid syndrome. COEXISTS_WITH here indicates changes in thrombin in the presence of low molecular-weight heparin. As such, this pattern can is a generalization of MD |
| INTERACTS_WITH ASSOCIATED_WITH MD |
6053 |
Pegvisomant INTERACTS_WITH somatotropin ASSOCIATED_WITH acromegaly
This pattern generalizes the “INHIBITS:ASSOCIATED_WITH” component of the “may_disrupt” discovery pattern. Elevated somatotropin (or growth hormone) is a defining characteristic of acromegaly, so drugs interacting with it may be plausible treatments |
| CAUSES COEXISTS_WITH | 2339 |
Dopaminergic_agents CAUSES dyskinetic_syndrome COEXISTS_WITH parkinsonian_disorders. This pattern relates drug to disease via a side effect. This can occur as an epiphenomenon (many patients are treated these drugs, so we see these side effects in them), or on account of superfluous effects on pathophysiologically relevant systems |
| INHIBITS ASSOCIATED_WITH MD |
2338 |
Crestor INHIBITS ldl_cholesterol_lipoproteins ASSOCIATED_WITH hypercholesterolemia,_familial. This plausible pathway is part of the MD discovery pattern, and reveals the lipoprotein that crestor targets in treatment of hypercholesterolemia |
| STIMULATESASSOCIATED_WITH MD |
1146 |
Isobutyramide STIMULATES gamma-globin ASSOCIATED_WITH beta_thalassemia. Isobutyramide has been shown to reduce transfusion requirements in patients with beta-thalassemia, and its activation of gamma-globin transcription provides a plausible explanatory hypothesis for this observation, as levels of this globin are reduced in beta-thalassemia |
| INTERACTS_WITH CAUSES MD |
1001 |
Finasteride INTERACTS_WITH testosterone CAUSES prostatic_hypertrophy. This pattern is a generalization of the MD pattern, and here correctly suggests that finasteride’s therapeutic effect in prostatic hypertrophy is due to interaction with testosterone |
| PREDISPOSES COEXISTS_WITH | 750 |
Proton pump inhibitors PREDISPOSES malignant neoplasm of stomach COEXISTS_WITH hiatal hernia. This instance of this pattern links proton pump inhibitors (PPIs) to a premalignant condition of the esophagus via the link between extended use of these drugs and an increased predisposition toward stomach cancer |
| INTERACTS_WITH PREDISPOSES MD |
653 |
Pravastatin INTERACTS_WITH plasminogen activator inhibitor 1 PREDISPOSES coronary heart disease. This pattern links drugs affecting genes to diseases predisposed to by those genes |
| INTERACTS_WITH COEXISTS_WITH |
650 |
Emollients INTERACTS_WITH psoriasis COEXISTS_WITH eczema. In this instance, a treatment is linked to a disease via it’s therapeutic effect on a commonly comorbid disease |
| COEXISTS_WITH AUGMENTS | 560 |
Vardenafil COEXISTS_WITH cyclic_gmp AUGMENTS erectile dysfunction. In this case COEXISTS_WITH was extracted from a sentence indicating structural similarity between vardenafil and cyclic_gmp, and AUGMENTS here indicates improvement |
Five of the “discovered” discovery patterns can be interpreted as generalizations of the may_disrupt pattern designed by Ahlers and her colleagues. In most cases, generalization occurs by relaxing the constraint that the predicate linking the pharmaceutical substance to the bridging concept must be “INHIBITS”, allowing “INTERACTS_WITH” and “STIMULATES” as alternatives. In addition four of the other discovery patterns involve the predicate “COEXISTS_WITH”. In some cases, these involve linking a drug to a disease via a side effect of this drug. While this may be a reasonable thing to do in the case that these side effects are produced by an excessive action on the same pathway involved in the therapeutic effects concerned, at times this inference may indicate that many patients on the drug experience side effects of the drug. This latter case is unlikely to lead to discovery. However, in general, the most popular predicate pathways are readily interpretable, and their application for the purpose of literature-based discovery seems intuitive.
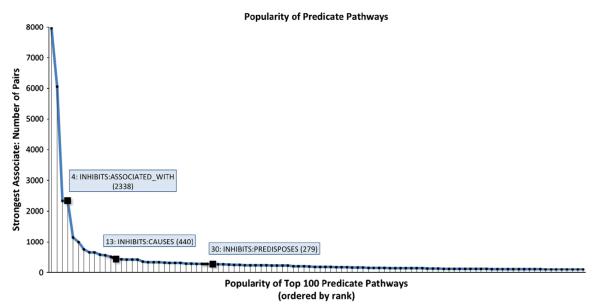
Fig. 3 provides an overview of the popularity of the 100 most popular pathways. As is evident from the graph, a relatively small number of the 272 possible dual-predicate pathways are most strongly associated with most of the TREATS relationships in our data set. As it is probable that TREATS relationships occur for which no dual-predicate pathway exists that leads from the pharmaceutical substance to the disease or syndrome concerned, we should not assume that an accurate mapping was obtained in all cases. The most strongly associated predicate path in such cases would be an artifact of random overlap between random vectors. However, random overlap alone would result in an equal distribution of popularity across dual-predicate pathways, while it is clear from the figure that certain pathways are strongly associated with far greater frequency than others. As illustrated on the figure, amongst the thirty most popular pathways are the pathways “drug x INHIBITS substance y; substance y ASSOCIATED with disease Z”; “drug x INHIBITS substance y; substance y CAUSES disease z” and “drug x INHIBITS substance y”; “substance y PREDISPOSES disease z”. These are the predicate pathways that make up that “may_disrupt” discovery pattern designed by Ahlers and her colleagues [4].
Fig. 3.
Popularity of dual-predicate pathways.
In the experiment that follows we attempt to apply the 10 most popular predicate pathways to the problem of identifying agents that treat cancers of various sorts.
3.3. Generalizing explanatory hypotheses
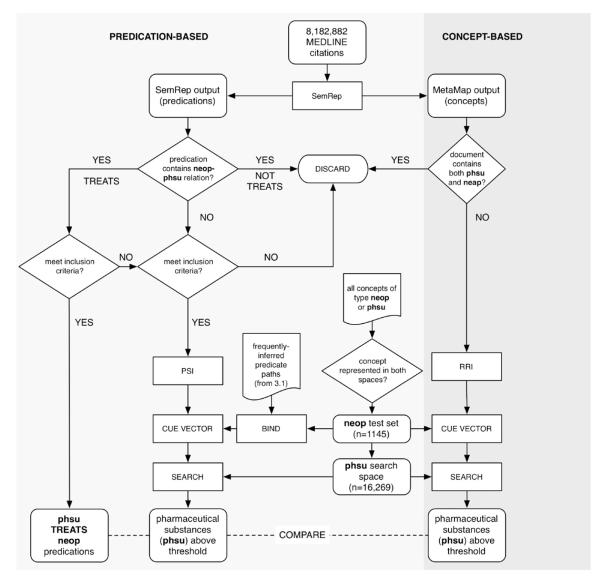
In this experiment we evaluate the extent to which the discovery patterns identified during our previous study can mediate the identification of “TREATS” relations between pharmaceutical substances (UMLS type “phsu”) and neoplastic processes (UMLS type “neop”). In order to accomplish this we created a PSI space ignorant of any direct relations between concepts of these semantic types. We then constructed a test set of neoplastic processes, and used the “discovered” discovery patterns to guide search through these spaces using two different approaches that will be described in the sections that follow. To provide a baseline, in addition to comparing PSI-based models to random selection of pharmaceutical agents, we created a space capturing general relatedness between concepts from the same set of titles and abstracts using Reflective Random Indexing (RRI), a technique that we have used effectively to simulate aspects of literature-based discovery in previous research [23], [15].
3.3.1. Methods
3.3.1.1. Model construction and test set
Fig. 4 provides an overview of the methods and experimental design. A PSI space with the same parameters as those employed in the previous study was created from SemRep predications that met the following constraints:
Does not involve a pharmaceutical substance (UMLS type “phsu”) and a neoplastic process (UMLS type “neop”).
Both concepts involved have a global frequency <100,000
Predicate is part of the set {ASSOCIATED_WITH; COEXISTS_WITH; AFFECTS; AUGMENTS; CAUSES; DISRUPTS; INHIBITS; INTERACTS_WITH; PREDISPOSES; STIMULATES}.
Fig. 4.
Experimental design.
3.3.1.2. Reflective random indexing
Reflective Random Indexing is an iterative approach that is able to derive meaningful indirect associations between terms or concepts from their distributional statistics, without the scalability constraints imposed by computationally demanding alternatives [23]. One RRI space was created from all documents in the set of citations (titles and abstracts) from which the predication database was derived (n = 8,182,882) that did not include both a “phsu” and a “neop” concept. Another, which we will refer to as RRI_ALL, was derived from all documents in this set without this constraint. Both were derived from the MetaMap [38] output for these documents, which consists of the unique concepts extracted by MetaMap from the citation text. This output is embedded within the output of the SemRep system, which draws on these concepts to extract predications. Consequently, the RRI model had access to the collocated concepts from which the predication database was derived, as well as those concepts extracted by MetaMap that were not a part of predications extracted by SemRep. Documents that contained a UMLS concept of both the semantic type “phsu” and the semantic type “neop” were excluded, to ensure that the RRI model, like the PSI model, is ignorant of any direct connections between concepts falling into this category.
To ensure that differences observed occur on account of the introduction of typed relations in PSI, we used a binary vector implementation of RRI. Each represented concept was assigned two binary vectors, an elemental vector and a semantic vector, each of 32,000 dimensions. As was the case with our PSI implementation, elemental vectors were constructed by randomly assigning 1s and 0s such that there was approximately a 0.5 probability of each occurring in any given dimension, and the random number generator was seeded deterministically as described previously to ensure that incidental overlap between elemental vectors was consistent across models. Elemental vectors were superposed using the majority rule to obtain semantic vectors, with training occurring in the following sequence of steps:
In order to ensure fair comparison between the two models, a test set was constructed. This included all of the concepts categorized as neoplastic processes (UMLS semantic type “neop”) that were represented in both models, which would require the concept concerned meeting the global frequency threshold of <100,000 in both spaces, and occurring in a predication that met the constraints of the PSI space detailed in the prior paragraph. In addition, only neoplastic processes that occurred in at least one TREATS relationship with a pharmaceutical substance represented in both spaces were included. The resulting test set consisted of 1,145 UMLS concepts categorized as neoplastic processes. Similarly, the set of pharmaceutical substances in which treatments were sought was constrained to concepts represented in both models, resulting in a set of 16,269 pharmaceutical substances in which to attempt to rediscover TREATS relationships extracted by SemRep from the biomedical literature. We also retained the randomly constructed elemental vectors used to generate the RRI space, to approximate the random selection of pharmaceutical substances as an additional control.
3.3.1.3. Approach to search across pathways
In addition to comparing PSI and RRI, we compared two different approaches to searching across the predicate pathways identified in the study, using either the five or the 10 most popular predicate pathways. In the first of these, which we will denote “MAX”, pharmaceutical substances are scored according to the strongest association to the disease in question across any single pathway. So, for example, if we were considering only the pathways “INHIBITS:ASSOCIATED_WITH” and “INHIBITS:CAUSES”, the score of a pharmaceutical substance (phsu) for a neoplastic process in question (neop) would be:
where SIM = 1-normalized Hamming Distance.
That is to say, the score is the maximum score across any of the predicate pathways. A disadvantage of this approach is that it considers individual predicate pathways only (although these may involve a number of different middle terms). However, one might anticipate a pharmaceutical substance being meaningfully connected to a disease that it treats through multiple predicate pathways. Therefore, rather than considering the maximum similarity, it would seem pertinent to consider a measure of similarity that considers the set of popular predicate pathways as a whole. We use for this purpose an approximation of the span of vectors, described as the quantum disjunction operator by Birkhoff and von Neumann [39], and applied to information retrieval by Widdows and Peters [40]. This operator measures the proportion of a vector that can be projected onto a subspace derived from a set of component vectors. The continuous implementation of this operator is applied as follows:
1. An orthonormal subspace is constructed from the individual vectors using the Gram-Schmidt orthogonalization procedure [41]. That is to say, each vector in the set is rendered orthogonal to every other vector in the set, such that no information is represented redundantly, and each vector is normalized to unit length.
The individual vector v is projected into this subspace, to generate .
The cosine metric is used to calculate the similarity between the vector v, and , it’s projection in the subspace.
This procedure can be interpreted as measuring the proportion of the vector v that can be represented in the subspace, and will return a value of close to one if v is either similar to any individual vector from which the subspace was derived, or partially similar to several of the vectors from which this space was derived. For our research, as our underlying representation is a hyperdimensional binary vector rather than a real or complex vector, we developed a binary approximation of the quantum disjunction operator we have just described [42].
The intuition underlying this operator is that maximal dissimilarity between a pair of vectors in the binary space will result in a Hamming distance of half of the dimensionality of the vectors concerned. Therefore, the extent to which the Hamming distance between two vectors is less than d/2 is analogous to the proportion of one vector that could be projected onto another in continuous (real or complex) vector space. We utilize a binary approximation of the Gram–Schmidt procedure, through which binary vectors are rendered mutually orthogonal (i.e. Hamming distance = d/2) by introducing or eliminating identical dimensions at random. We then calculate the similarity between an individual binary vector and the set of (mutually orthogonal) vectors representing the popular predicate pathways to a neoplastic process (neop) by taking the sum of 2 × (0.5 – the normalized Hamming distance) between the vector representing the pharmaceutical substance (phsu) and each of these pathway vectors. So our approximation of the subspace-based metric, which we will denote SUB, considering only the pathways “INHIBITS:ASSOCIATED_WITH” and “INHIBITS:CAUSES”, would be calculated as follows:
where HD = the normalized Hamming Distance.
For each of the 1145 neoplastic processes, the PSI representations of the 16,269 pharmaceutical substances were searched using both of these approaches, with either the 5 or the 10-most popular predicate pathways identified during our previous studies. In addition, the RRI representations of the pharmaceutical substances were searched using the RRI representation of the neoplastic process concerned as a cue. Finally, elemental vectors for the pharmaceutical substances were searched using the elemental vectors of the neoplastic processes as cues. This last step simulates random selection of drugs for each disease, allowing for associations introduced by incidental overlap between elemental vectors.
In all cases, the experiment was repeated at different statistical thresholds, which were defined in terms of the mean and standard deviation of the anticipated Hamming distance between randomly constructed elemental vectors. The thresholds used varied some from model to model, as they were adjusted such that models were compared according to the number of TREATS relationships “rediscovered” when comparable quantities of pharmaceutical substances were suggested.
3.3.2. Results and discussion
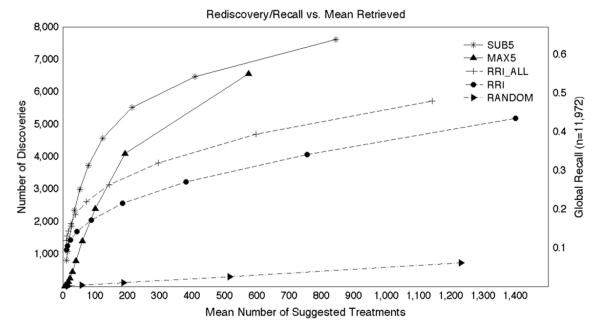
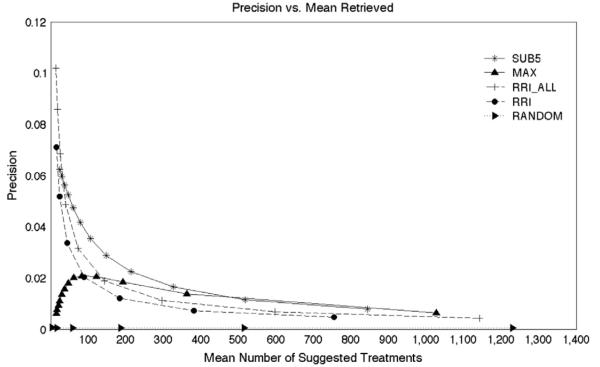
The results of this experiment are shown in Fig. 5, which plots the number of rediscovered treatments (left axis) and proportion of the total TREATS relationships rediscovered (or recall, right axis) for each model against mean number of pharmaceutical substances retrieved at different statistical thresholds.
Fig. 5.
Overall rediscovery/recall. The y axes show the total number of rediscovered treatments for all test cases (left) and the global recall (right). The x axis shows the mean number of treatments suggested per test case.
The random model does not “rediscover” many therapeutic relationships unless a large number of pharmaceutical agents are retrieved. In contrast, the RRI-based model, here denoted “RRI” is far more productive, recovering around two thousand TREATS relationships with a recall of around 0.17 at frequency thresholds that return approximately 100 pharmaceutical substances on average. The results for two RRI-based models are shown. In the first, documents that included both a pharmaceutical substance (“phsu”) and a neoplastic process (“neop”) were excluded from the training process, as described previously. The second model, RRI_ALL differs from the RRI model in that the entire corpus was utilized, including those citations from which the test set was derived. The results for SUB10 (not pictured) were close to, but below those obtained with SUB5, which was the most productive of all the models tested, recovering around 4500 TREATS relationships with a recall of around 0.37 at a frequency threshold returning approximately 100 pharmaceutical substances on average. Interestingly, the SUB models also outperformed RRI_ALL across all but the most stringent thresholds. That is to say, the SUB models showed an advantage over RRI trained on the entire set of documents processed by SemRep, including those containing the statements from which the TREATS relationships in the test set were derived. This was not the case with the MAX models with more stringent thresholds, which serves as further evidence of the benefit of the subspace-based approach. The MAX models, based on the single most strongly associated predicate pathway, generally outperform the RRI model, except at the most stringent statistical thresholds. A small advantage over the MAX10 model (not pictured) occurs when only the five most popular predicate pathways are utilized (MAX5, pictured). The SUB models perform best of all, recovering thousands of TREATS relationships even at the most stringent statistical thresholds utilized. The model generally performs best when the five most popular predicate paths are utilized (SUB5), except at most stringent thresholds where using the 10 most popular predicate paths appears to confer a slight advantage. With respect to precision (Fig. 6), the subspace-based approaches again outperformed RRI-based and MAX approaches at most frequency thresholds, although RRI_ALL and RRI had highest precision at the most stringent thresholds, where the MAX models performed relatively poorly. At the point at which one hundred treatments on average are retrieved, the precision of the SUB5 model is around 0.038, suggesting that we might anticipate rediscovering approximately four known treatments per one hundred drugs retrieved. This number of agents is of interest as it could feasibly be tested against cancer cell lines using contemporary high-throughput screening methods, and the successful repurposing of four therapeutically active compounds in a hundred would be an excellent result.
Fig. 6.
Overall precision. The y axis shows the precision and the x axis shows the mean number of treatments suggested per test case.
When interpreting these results one should bear in mind: (a) the fact that a drug does not occur in a TREATS relationship with a particular condition in the SemRep database does not preclude its being a plausible treatment; (b) a few TREATS relationship may be SemRep errors; and (c) some TREATS relationships may refer to activity against cell lines or animal models relevant to a particular cancer rather than proven therapeutic activity in the context of a clinical trial. Nonetheless, evaluations have shown that around 75% of the predications extracted by SemRep are accurate so the results show that the incorporation of discovery patterns enhances the recovery of drugs with possible therapeutic activity against the cancers concerned.
The results presented above report the overall recall and precision across the entire test set. The use of a global statistical threshold allows for each model to suggest a different number of treatments for each cancer, based on the strength of association between this cancer type and each of the pharmaceutical substances in the search space. As the number of TREATS relationships for each cancer in the set varies considerably (mean = 10.46, std = 24.12, min = 1, max = 289, median = 3), there is an advantage for methods that retrieve results selectively where treatments are likely to occur, as would be expected from the predication-based approaches in which treatments that are linked across one of the predicate pathways would be more strongly associated. In order to evaluate this hypothesis, we calculated the average precision for each model for each cancer in the test set. The Average Precision (AP) [43] is a widely used summary statistic in information retrieval, and measures the precision at each point at which each correct result is retrieved. This can be calculated by adding the precision at the point of each discovery (which is equal to the known TREATS relations (rediscoveries) retrieved over the number results retrieved) as follows:
Consequently the average precision provides a summary of the performance related to a particular cancer across all of the relevant TREATS relationships in the test set. The correlation between the average precision for each method and the number of TREATS relationships available for discovery is shown in Table 3. As anticipated, the performance of the PSI-based methods is better correlated with the number of treatments available for discovery than that of the RRI-based methods.
Table 3.
Pearson’s correlation between AP and existing TREATS relationships.
| SUB5 | SUB10 | MAX5 | MAX10 | RRI | RRI_ALL | RAND | |
|---|---|---|---|---|---|---|---|
| r | 0.5114 | 0.5085 | 0.4994 | 0.5602 | −0.0352 | −0.0423 | 0.1807 |
The number of treatments available for discovery for a particular cancer is strongly correlated (Pearson’s r = 0.8473) with the number of unique predications involving this cancer in the predication database. So PSI-based methods perform better where more knowledge is available, which is not surprising.
Table 4 shows the mean and median rank of recovered treatments for each model across all of the 11,972 treatments available for discovery. Higher ranks (i.e. lower numbers) are preferable. For example a rank of one would indicate that a treatment was the first result retrieved. Therefore, with higher average rediscovery rank as a metric, the rank order of the performance of the models is SUB5 > SUB10 > MAX5 > MAX10 > RRI_ALL > RRI > RAND. All differences in average rank are statistically significant as measured by the paired t test (for the mean) and Wilcoxon’s signed rank test (for the median). As shown in the last two rows of the table, which give the percentage of all discoveries ranked in the top 100 and top 1000 results, the rank distributions for models other than RAND are skewed to the right, with around 20% of the rediscoveries by the SUB models ranked in the top 100.
Table 4.
Summary statistics for discovery rank. All differences in median rank are significant as measured by Wilcoxon’s signed rank test. All differences in mean rank are significant as measured by paired t test. Boldface indicates best performance.
| SUB5 | SUB10 | MAX5 | MAX10 | RRI | RRI_ALL | RAND | |
|---|---|---|---|---|---|---|---|
| Mean | 2559.5 | 2647.4 | 2828.3 | 2897.4 | 4305 | 3497 | 10162.5 |
| Median | 742 | 915.5 | 1021.5 | 1078 | 2866 | 1838 | 10108.5 |
| Rank ≤100 | 20.5% | 19.5% | 11.1% | 10.8% | 14.4% | 19.7% | 0.48% |
| Rank ≤1000 | 55% | 51.34% | 49.6% | 48.6% | 31.9% | 40.7% | 4.9% |
The enhanced performance of the SUB5 model is also evident when weighting the results for each cancer in the test set equally, although the picture is more nuanced. Table 5 shows the Mean and Median AP for each method, along with a rank ordering for each measure. Note that the means and medians give different rank orderings for the methods. This discrepancy between mean and median AP can be explained by the presence of a relatively small number of outliers in the RRI results with AP > 0.5. On account of these outliers, the median AP gives a more robust measure of overall performance than the mean AP.
Table 5.
Mean and median average precision scores. Boldface indicates best performance.
| SUB5 | SUB10 | MAX5 | MAX10 | RRI | RRI_ALL | RAND | |
|---|---|---|---|---|---|---|---|
| Mean AP | 0.0255 | 0.0247 | 0.0115 | 0.0108 | 0.0845 | 0.1097 | 0.0012 |
| Rank | 3 | 4 | 5 | 6 | 2 | 1 | 7 |
| Median AP | 0.0027 | 0.0021 | 0.0023 | 0.0021 | 0.0022 | 0.0086 | 0.0003 |
| Rank | 2 | 4 | 3 | 4 | 6 | 1 | 7 |
Table 6 compares summary statistics for AP across all methods evaluated. Each cell in the table compares the proportion of the 1145 neoplastic processes for which the method in the row had a greater AP than the method in the column. In addition, the table indicates cases in which the mean and/or median AP for the method in the row was significantly higher than that of the method in the column. So, for example, the cell [SUB5, MAX5] shows that SUB5 had a higher AP than MAX5 around 70% of the cases, that the difference between their median AP (SUB5 = 0.0027 > MAX5 = 0.0023) is significant as measured by the Wilcoxon signed rank test, and that the difference between their mean AP (SUB5 = 0.0255 > MAX5 = 0.0115) is significant as measured by paired t test. In contrast, the cell [MAX5, SUB5] shows that MAX5 had a higher AP in the remaining ±30% of cases. In general the tests using medians favor the SUB5 model, although this advantage is less pronounced than when considering the results from a per-discovery perspective. It does not outperform RRI-ALL in this respect, but that model enjoys access to information withheld from the other models.
Table 6.
Comparison of Average Precision (AP) scores. Proportion of Cases in which AP for Row Method was Greater than Column Method t+ indicates a significantly greater row mean than column mean by paired t test w+ indicates a significantly greater row median than column median by Wilcoxon’s signed rank test. Boldface indicates a greater proportion of row cases than column cases had greater AP.
| SUB5 | SUB 10 | MAX5 | MAX10 | RRI | RRL_ALL | RANDOM | |
|---|---|---|---|---|---|---|---|
| SUB5 |
|
0.5319 w+ | 0.6961 w+, t+ | 0.6996 w+ t+ | 0.5057 w+ | 0.3886 | 0.8480 w+, t+ |
| SUB 10 | 0.4664 |
|
0.6498 t+ | 0.6699 t+ | 0.5074 | 0.3808 | 0.8524 w+, t+ |
| MAX5 | 0.3022 | 0.3502 |
|
0.7817 w+, t+ | 0.4376 w+ | 0.3179 | 0.8437 w+, t+ |
| MAX10 | 0.2996 | 0.3293 | 0.2017 |
|
0.4245 | 0.3092 | 0.8463 w+, t+ |
| RRI | 0.4943 t+ | 0.4917 w+, t+ | 0.5624 t+ | 0.5747 w+, t+ |
|
0.2419 | 0.8725 w+, t+ |
| RRL_ALL | 0.6105 w+, t+ | 0.6183 w+, t+ | 0.6821 w+, t+ | 0.6908 w+, t+ | 0.7354 w+, t+ |
|
0.9188 w+, t+ |
| RANDOM | 0.1520 | 0.1476 | 0.1563 | 0.1537 | 0.1275 | 0.0812 |
|
In summary, PSI-based models, in particular the SUB models, recover more total TREATS relationships at all but the most stringent statistical thresholds applied. This corresponds to lower average retrieval rank across all treatments available for discovery in the test set, with statistically significant differences in performance by this metric across models such that SUB5 > SUB10 > MAX5 > MAX10 > RRI_ALL > RRI > RAND. Analysis of average precision on a per-disease basis reveals that the performance of PSI-based methods is correlated with the number of TREATS relationships available for discovery, which is in turn correlated with the amount of knowledge related to this disease in the predication database. So the advantage in performance when weighting each disease equally is less pronounced than when considering the results from a per-discovery perspective.
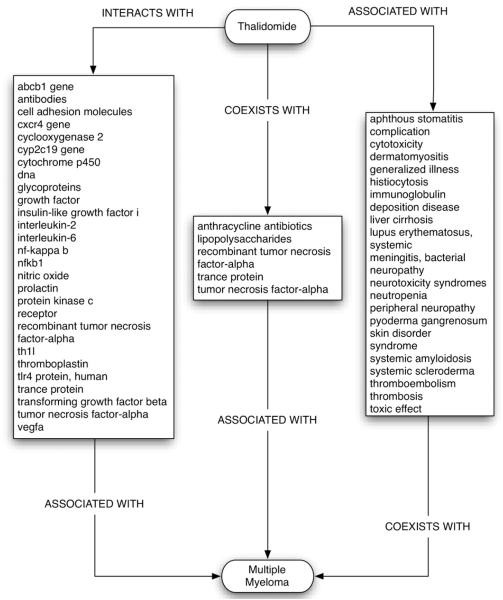
The performance of the SUB models suggests that effective therapeutic agents tend to be connected to diseases they treat across more than one predicate pathway. This supports recent criticism of targeted drug discovery efforts as being inappropriately unidimensional [44]. To illustrate the encoded connections that underlie this finding, we reconstruct the pathways between multiple myeloma and thalidomide, which account for this therapeutic relationship (an oft-cited example of successful drug repurposing) being “rediscovered” consistently, even at the most stringent statistical thresholds applied to the SUB models (it is the 14th-ranked recommendation in the SUB10 model, and 38th-ranked recommendation in the SUB5 model). The pathways were reconstructed by searching the original predication index for middle terms that relate to both thalidomide and multiple myeloma in accordance with the constraints imposed by the two most popular predicate pathways from the original study, ASSOCIATED_WITH:COEXISTS_WITH and INTERACTS_WITH:ASSOCIATED_WITH. As the binding operator in our implementation commutes and is its own inverse, middle terms that reverse the order of the relationships concerned, in this case COEXISTS_WITH:ASSOCIATED_WITH, would also contribute toward similarity to the cue vector, and consequently have also been included. Only middle terms that were encoded in the PSI space were retrieved, and middle terms of UMLS semantic type “phsu”1 or “neop” were excluded, as predications linking these to multiple myeloma and thalidomide respectively would not have been encoded on account of the constraints placed during generation of the space.
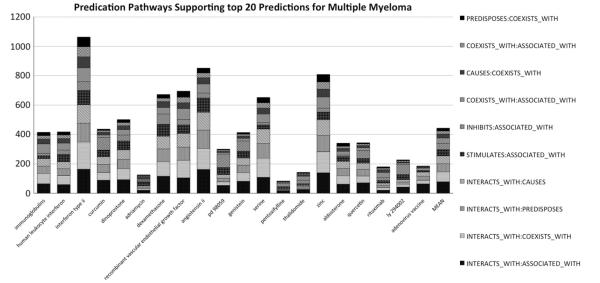
The pathways illustrated in Fig. 7 include biological entities that interact with thalidomide and are associated with multiple myeloma, and relationships between thalidomide and related diseases, such as consequences of the overproduction of immunoglobulins, that occur in multiple myeloma. While uninformative high-level concepts such as “complication” and “dna” are included in the diagram for completeness, these would have had less influence on the relevant vector representations on account of the use of global weighting statistics. Together, these two most popular predicate pathways account for 54 of the 143 unique predication pathways (all predicate + middle term combinations within the constraints of the 10 most popular pathways) that were encoded linking thalidomide with multiple myeloma during the process of model construction. With the SUB10 model, the number of unique predication pathways relating multiple myeloma to its top 20 ranked pharmaceutical substances was consistently on the order of 100, with a mean of 442.75 and a median of 413.5. These statistics are summarized in Fig. 8 and support the proposal that the PSI approach provides a computationally efficient way of searching across large networks of interconnected biological entities, as these networks are encoded into hyperdimensional vector representations that can be compared to one another without the need to consider their components individually.
Fig. 7.
Predicate pathways and bridging terms linking thalidomide to multiple myeloma considering the two most popular pathways only.
Fig. 8.
Predication pathways supporting the top twenty ranked results for multiple myeloma (SUB10 model).
The figure shows the top 20 results in rank order from left to right, as well as the mean number of predication pathways in each category. In all cases, 100 or more unique predication pathways support the prediction, and in one case this number exceeds 1000. The figure also shows the breakdown of these unique predicate pathways in accordance with the popular predicate pathway involved. Of interest, in this case the highest ranking results are generally connected across all 10 of the popular predicate pathways we identified in our study, albeit with different distributions. The four most popular predicate pathways in these results all permitted predications of the form “drug x INTERACTS WITH biological entity y”.
While similar numbers of predication pathways were found to support several other predictions we examined, it was not always the case that the entire spectrum of popular predicate paths was represented. In addition, less frequently occurring concepts that were highly ranked were linked to the disease in question by fewer predication pathways. At times a pharmaceutical substance that occurred infrequently in the database would obtain a high ranking on account of a substantial proportion of the predications it occurs in in the database being connected to the disease in question in accordance with the popular predicate pathways. This is what we would anticipate, given that the tallying of the voting record across superposition operations ensures that the relative contribution of predications encoded into a semantic vector is of greater importance than the absolute number of predications processed. However, as our inspection of our results suggests that this may lead to erroneous high ranking for agents about which little knowledge is available, it seems likely that the addition of a minimum frequency threshold could improve results.
This evaluation compares the ability of these models to recover known TREATS relationships. However, it is also probable that during the course of the evaluation the system recovers hitherto unknown therapeutic relationships. Therefore, we evaluated a small set of our experimental results to determine the plausibility of a set of highly ranked results, only some of which occurred in known TREATS relationships. Author PD, who is a pharmacologist with expertise in cancer-related drug discovery, conducted an independent evaluation of the twenty top-ranked results produced by the SUB10 model. All of the results with the exception of the amino acid “serine” and the biomarker “zinc” were found to have citations that would justify their potential as treatments of either multiple myeloma, or problems such as hypogammaglobulinemia that afflict patients with multiple myeloma. A summary of this review with selected references is included in Table 7.
Table 7.
Summary of Plausibility of Top 20 Results with Selected References.
| Recommendation | Interpretation |
|---|---|
| Immunoglobulins | Intravenous immunoglobulins have been evaluated as prophylactic therapy in hypogammaglobulinemic patients with lymphoproliferative disorders such as multiple myeloma [45] |
| Human leukocyte interferon | Human leukocyte interferon has been shown to have in vitro effects and multiple myeloma cell lines [46] and has been proposed as a therapeutic alternative in patients that do not tolerate therapy with other interferons |
| Interferon type ii | This interferon, also known as interferon gamma, is known to produce Beta cell activating factor, an important cell survival factor expressed by haematopoeitic cells [47] |
| Curcumina | Curcumin analogs have been shown to suppress the growth of multiple myeloma cells in vitro [48] |
| Dinoprostone | The cyclic AMP (cAMP) pathway, which is stimulated by dinoprostone (also known as prostaglandin E2) has been identified as a possible therapeutic target for multiple myeloma, as elevated cAMP kills multiple myeloma cells in vitro [49] |
| Adriamycin | Adriamycin (doxorubicin) is a component of standard treatment regimes for multiple myeloma (e.g. [50]) |
| Dexamethasonea | Dexamethasone has been evaluated as maintenance therapy for multiple myeloma [51] |
| Recombinant vascular endothelial growth factora |
Vascular endothelial growth factor is targeted by the anti-neoplastic agent Bevacizumab, which has been shown to inhibit the growth of multiple myeloma cells [52] |
| Angiotensin ii | Inhibition of angiotensin ii has been shown to augment the anti-tumor activity of other drugs in hepatocellular carcinoma. Mechanisms of action appears to include inhibition of angiogenesis, and down-regulation vascular endothelial growth factor [53]. |
| pd_98059 | pd_98059 is a MAP kinase inhibitor, and the MAP kinase pathway has been identified as a new therapeutic target for multiple myeloma [54] |
| Genistein | Genistein has been shown to inhibit the growth of multiple myeloma cells in vitro [55] |
| Serine | We were unable to identify a potential therapeutic role for this amino acid |
| Pentoxifylline | Pentoxifylline (Trental) has been shown to inhibit leukemic and lymphoma cells in vitro [56] |
| Thalidomidea | Thalidomide has been shown to be effective in clinical trials against advanced multiple myeloma [57] |
| Zinc | Zinc-alpha-2-glycoprotein is a biomarker that predicts responsiveness to thalidomide-based therapy in multiple myeloma [58] |
| Aldosterone | Suppression of aldosterone has been shown to suppress the growth of hepatocellular carcinoma. The mechanism is related to the inhibition of angiogenesis, which is an important therapeutic mechanism in multiple myeloma [57] |
| Quercetin | Quercetin has been shown to induce multiple myeloma cell death at high doses [59] |
| Rituximaba | Rituximab has been used to treat Acquired factor VIII inhibitor, a rare disorder that occurs in multiple myeloma patients [60] |
| ly294002 | Ly294002 is an inhibitor of phosphoinositide 3-kinases (PI3ks). These kinases have been shown to be important for proliferation of multiple myeloma cell lines[61] |
| Adenovirus vaccine | Adenoviral-mediated gene transfer has been shown to cause growth suppression and cytotoxicity of multiple myeloma cells in vitro [62] |
Occurrence in a TREATS relationship with multiple myeloma.
4. Implications
In the research presented in this paper, we have used an approach based on the hyperdimensional computing paradigm[28], in which both concepts and the relations between them are represented as vectors in hyperdimensional space. This approach is used to implement efficient inference across tens of millions of assertions, using geometric operators. In our experiments, conducted on a Linux workstation with 24G of RAM, inferring the most strongly connected dual-predicate path took around 800 μs per search, and searching across the 16,269 pharmaceutical substances took around 80 ms per search. When examined further, highly ranked results were often linked to the disease in question by hundreds of unique predication pathways, which would need to be explored independently with conventional methods. The subspace approach, which rewards those pharmaceutical agents connected to the disease in question across multiple predicate pathways, was found to enhance the recovery of TREATS relationships.
PSI’s successful recovery of large numbers of TREATS relationships suggests the utility of such geometrically supported approaches as the means to support efficient inference at scale. The use of VSAs to accomplish reasoning that would traditionally be attempted using symbolic approaches is not in and itself novel. In fact, the enhancement of connectionist models of cognition to enable computation of this sort was one of the original motivations for the development of VSAs [33]. However, while this family of representational approaches has been adopted by the cognitive science community as a means to simulate individual cognition (see for example [63–65]), their utility as means to support approximate inference at scale has not been widely explored. Therefore, from our perspective perhaps the most important implication of this research is that of the untapped potential of representational approaches that combine the strengths of geometric and symbolic approaches as a means to support computational intelligence at scale. In order to encourage the further development of these approaches, we have released an implementation of PSI [66] as a part of the open source semantic vectors package [67,68].
With respect to literature-based discovery, our findings provide strong support for the utility of the discovery pattern approach, pioneered by Hristovski and his colleagues [2], as a means to constrain the search space for new therapeutic approaches. On a size-able test set, search across predicate pathways outperformed search based on co-occurrence alone in what to the best of our knowledge is the first large-scale comparative evaluation of discovery pattern based vs. co-occurrence based approaches. These evaluations were enabled by the computational convenience afforded by the PSI approach. In addition, PSI provides the means to “discover” discovery patterns, by inferring these from known TREATS relationships. This provides an alternative to the manual generation of discovery patterns, a process that requires both domain expertise and detailed knowledge of the predications extracted by SemRep.
Ultimately, our goal is to develop tools that can enhance the cognitive capacity of biomedical scientists by enabling them to draw upon knowledge extracted from beyond the bounds of their usual literature review in order to generate novel therapeutic hypotheses. This represents a deliberate move on our part away from the goal of fully automated knowledge discovery, and toward the notion of a dynamic and interactive discovery system in which the user is free to refine the predictions made by a system in an exploratory iterative process. Developments along these lines include Wilkowski’s discovery browsing approach [69], and the EpiphaNet system for biomedical knowledge discovery [15]. The methods developed in this research provide the means to support efficient yet highly customizable searches across large volumes of extracted biomedical knowledge, and therefore are likely to be useful as the means to facilitate dynamic and interactive exploration of knowledge extracted from the breadth of the biomedical literature.
In addition, our approach has implications for the repurposing of existing drugs to identify new therapeutic approaches for inadequately treated diseases. The rapidly escalating cost of new drug development coupled with the prolonged delay in bringing new drugs to clinical application, limits the availability of new therapies for many devastating diseases. One of the most efficient strategies for addressing this problem is the “repurposing” of existing drugs for novel therapeutic applications. There are currently approximately 4000 drugs approved for use in humans and an additional 5000 investigational drugs registered for human use but not approved by regulatory agencies. These drugs represent a rich reservoir of potential therapeutics because much of the pharmacologic and toxicologic information necessary for their clinical use has already been acquired. Brute force screening of all possible combinations of approved drugs or investigational agents is logistically impossible and needlessly inefficient. Knowledge applicable to the selection of agents, and combinations of agents, is accessible in large biomedical literature databases, and other repositories. While efforts have been undertaken to integrate this knowledge, and present it in computable form, exhaustive exploration of this knowledge is not currently feasible. In the research presented in this paper, we utilize the techniques of hyperdimensional computing to mediate approximate reasoning across large volumes of biomedical knowledge in a scalable and efficient manner. The improved recovery of TREATS relationships achieved by this method, and the plausibility of the results we have evaluated to date, suggest that this approach may provide the means to leverage existing biomedical knowledge to support future drug repositioning efforts.
5. Limitations and future work
In this paper, we document an evaluation of the ability of different distributional models to recover TREATS relationships extracted by SemRep from the biomedical literature, in order to simulate discovery. Manual evaluation of a small number of our results suggests that in many instances, predicted relationships were plausible despite their not being extracted by SemRep previously. However, even in the cases where these relationships are new to SemRep, they are not necessarily new to science. Without further evaluation to establish their novelty, we would not argue that these results necessarily constitute anything more than simulated discoveries. Our results also highlight a number of challenges that must be addressed if we are to realize the translational potential of these methods. Our knowledge base currently includes individual drug-treatment relations, though we know that drug combinations best treat many illnesses. Further investigation of the nature of the TREATS relationships extracted by SemRep reveals that the system currently does not distinguish between effective treatments and agents that are active against a cell line in in vitro experiments, so the recovered TREATS relations do not necessarily represent treatments that have advanced to clinical trials. Our knowledge base does not include knowledge gleaned from high throughput experiments, which has been shown to be of value for drug repositioning [44]. Also, our models account for dual predicate pathways only. While this was a necessary step, VSAs support encoding of nested relationships, to perform inference over longer pathways [33]. In future work, we will address these challenges by enhancing the breadth and granularity of the knowledge utilized and developing models that accommodate the interactions between multiple agents. In addition, we will explore the utility of real and complex vectors as alternative representations to support inference in PSI.
6. Conclusion
In the research presented in this paper, we leveraged efficient inference mediated by hyperdimensional representations for two purposes. Firstly, we inferred previously unknown discovery patterns, pathways of predicates from a drug to a treated disease, from a large number of example pairs. Secondly, we utilized these inferred patterns to guide the search through PSI space for treatments for neoplastic processes. When compared to a co-occurrence based approach, discovery pattern based models were better able to recover a held-out set of “TREATS” relations for these neoplastic processes. This advantage was further emphasized when rewarding drugs that were connected to the neoplasms in question across several of the discovered discovery patterns. These results demonstrate the utility of geometric representational approaches as a means to draw inferences from large volumes of knowledge efficiently. In addition, they provide strong support for the value of discovery patterns as a means to support literature-based discovery.
| RRI step one: generate document vectors |
| For each document: |
| For each concept in document: |
| S(document)+ = E(concept) × lw × gw |
| where: |
| lw = log(1 + frequency of concept in document) |
| gw = entropy(concept) |
| cfij = frequency of concept i in document j |
| gfi = frequency of concept i in corpus |
| For each semantic document vector: |
| Normalize (majority rule) |
| RRI step two: generate semantic concept vectors |
| For each concept: |
| For each document concept occurs: |
| S(concept)+ = S(document) |
| For each semantic concept vector: |
| Normalize (majority rule) |
Acknowledgments
This research was supported by the US National Library of Medicine Grant (R21LM010826), Encoding Semantic Knowledge in Vector Space for Biomedical Information Retrieval and the Intramural Research Program of the National Institutes of Health, National Library of Medicine.
References
- [1].Hristovski D, Friedman C, Rindflesch T, Peterlin B. Literature-based knowledge discovery using natural language processing. In: Bruza P, Weeber M, editors. Literature based discovery. Springer; Berlin (Heidelberg): 2008. pp. 133–52. [Google Scholar]
- [2].Hristovski D, Friedman C, Rindflesch TC, Peterlin B. Exploiting semantic relations for literature-based discovery. AMIA annu symp proc; 2006. pp. 349–53. [PMC free article] [PubMed] [Google Scholar]
- [3].Hristovski D, Kastrin A, Peterlin B, Rindflesch T. Combining semantic relations and DNA microarray data for novel hypotheses generation. Linking literature, information, and knowledge for biology. 2010:53–61. [Google Scholar]
- [4].Ahlers CB, Hristovski D, Kilicoglu H, Rindflesch TC. Using the literature-based discovery paradigm to investigate drug mechanisms. AMIA annu symp proc; 2007. pp. 6–10. [PMC free article] [PubMed] [Google Scholar]
- [5].Cohen T, Schvaneveldt R, Rindflesch T. Predication-based Semantic indexing: permutations as a means to encode predications in semantic space. AMIA annu symp proc; 2009. pp. 114–8. [PMC free article] [PubMed] [Google Scholar]
- [6].Rindflesch TC, Fiszman M. The interaction of domain knowledge and linguistic structure in natural language processing: interpreting hypernymic propositions in biomedical text. J Biomed Inform. 2003;36:462–77. doi: 10.1016/j.jbi.2003.11.003. [DOI] [PubMed] [Google Scholar]
- [7].DiGiacomo RA, Kremer JM, Shah DM. Fish-oil dietary supplementation in patients with Raynaud’s phenomenon: a double-blind, controlled, prospective study. Am J Med. 1989;86:158–64. doi: 10.1016/0002-9343(89)90261-1. [DOI] [PubMed] [Google Scholar]
- [8].Swanson DR. Fish oil, Raynaud’s syndrome, and undiscovered public knowledge. Perspect Biol Med. 1986;30:7–18. doi: 10.1353/pbm.1986.0087. [DOI] [PubMed] [Google Scholar]
- [9].Ganiz M, Pottenger WM, Janneck CD. Recent advances in literature based discovery. Lehigh University, CSE Department; 2005. technical, report, LU-CSE-05-027. [Google Scholar]
- [10].Bekhuis T. Conceptual biology, hypothesis discovery, and text mining: Swanson’s legacy. Biomed Dig Librar. 2006;3:2. doi: 10.1186/1742-5581-3-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Sehgal AK, Qiu XY, Srinivasan P. Analyzing LBD methods using a general framework. In: Bruza P, Weeber M, editors. Literature based discovery. Springer-Verlag; Berlin (Heidelberg): 2008. pp. 75–100. [Google Scholar]
- [12].Pratt W, Yetisgen-Yildiz M. LitLinker: capturing connections across the biomedical literature. Proceedings of the 2nd international conference on knowledge capture; New York (NY, USA). ACM; 2003. pp. 105–12. [Google Scholar]
- [13].Hristovski D, Peterlin B, Mitchell J, Humphrey S. Using literature-based discovery to identify disease candidate genes. Int J Med Inform. 2005;74:289–98. doi: 10.1016/j.ijmedinf.2004.04.024. [DOI] [PubMed] [Google Scholar]
- [14].Swanson DR, Smalheiser NR. An interactive system for finding complementary literatures: a stimulus to scientific discovery. Artif Intell. 1997;91:183–203. [Google Scholar]
- [15].Cohen T, Whitfield GK, Schvaneveldt RW, Mukund K, Rindflesch T. EpiphaNet: an interactive tool to support biomedical discoveries. J Biomed Discov Collab. 2010;5:21–49. [PMC free article] [PubMed] [Google Scholar]
- [16].Smalheiser NR, Torvik VI, Bischoff-Grethe A, Burhans LB, Gabriel M, Homayouni R, et al. Collaborative development of the Arrowsmith two node search interface designed for laboratory investigators. J Biomed Discov Collab. 2006;1 doi: 10.1186/1747-5333-1-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Weeber M, Kors JA, Mons B. Online tools to support literature-based discovery in the life sciences. Brief Bioinform. 2005;6:277–86. doi: 10.1093/bib/6.3.277. [DOI] [PubMed] [Google Scholar]
- [18].Swanson DR. Medical literature as a potential source of new knowledge. Bull Med Libr Assoc. 1990;78:29. [PMC free article] [PubMed] [Google Scholar]
- [19].Wren JD, Bekeredjian R, Stewart JA, Shohet RV, Garner HR. Knowledge discovery by automated identification and ranking of implicit relationships. Bioinformatics. 2004;20:389. doi: 10.1093/bioinformatics/btg421. [DOI] [PubMed] [Google Scholar]
- [20].Cohen T, Widdows D. Empirical distributional semantics: methods and biomedical applications. J Biomed Inform. 2009;42:390–405. doi: 10.1016/j.jbi.2009.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Gordon MD, Dumais S. Using latent semantic indexing for literature based discovery. J Am Soc Inform Sci. 1998;49:674–85. [Google Scholar]
- [22].Cole RJ, Bruza PD. A bare bones approach to literature-based discovery: an analysis of the Raynaud’s/Fish-oil and migraine-magnesium discoveries in semantic space. In: Hoffman A, Motoda H, Scheffer T, editors. Lecture notes in artificial intelligence; Discovery science, 8th international conference, DS 2005; Singapore. October 8–11; Springer; 2005. pp. 84–98. [Google Scholar]
- [23].Cohen T, Schvaneveldt R, Widdows D. Reflective random indexing and indirect inference: a scalable method for discovery of implicit connections. J Biomed Inform. 2010;43:240–56. doi: 10.1016/j.jbi.2009.09.003. [DOI] [PubMed] [Google Scholar]
- [24].Bodenreider O. The unified medical language system (UMLS): integrating biomedical terminology. Nucleic Acids Res. 2004;32:D267. doi: 10.1093/nar/gkh061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Ahlers CB, Fiszman M, Demner-Fushman D, Lang F, Rindflesch TC. Extracting semantic predications from MEDLINE citations for pharmacogenomics. Pac Symp Biocomput. 2007;2006:209–20. [PubMed] [Google Scholar]
- [26].Kilicoglu H, Fiszman M, Rosemblat G, Marimpietri S, Rindflesch TC. Arguments of nominals in semantic interpretation of biomedical text. Proceedings of the 2010 workshop on biomedical natural language processing.2010. pp. 46–54. [Google Scholar]
- [27].Friedman C. A broad-coverage natural language processing system. Proc AMIA Symp; 2000. pp. 270–4. [PMC free article] [PubMed] [Google Scholar]
- [28].Kanerva P. Hyperdimensional computing: an introduction to computing in distributed representation with high-dimensional random vectors. Cogn Comput. 2009;1:139–59. [Google Scholar]
- [29].Cohen T, Widdows D, Schvaneveldt RW, Rindflesch TC. Logical leaps and quantum connectives: forging paths through predication space. AAAI-Fall 2010 symposium on quantum informatics for cognitive, social, and semantic processes; November 2010.pp. 11–3. [Google Scholar]
- [30].Cohen Trevor, Widdows Dominic, Schvaneveldt Roger, Rindflesch Thomas. Finding Schizophrenia’s Prozac: emergent relational similarity in predication space. QI’11, Proceedings of the 5th international symposium on quantum interactions; Aberdeen, Scotland. Berlin (Heidelberg). Springer-Verlag; 2011. [Google Scholar]
- [31].Kanerva P. Binary spatter-coding of ordered K-tuples. Artif Neural Networks—ICANN. 1996;96:869–73. [Google Scholar]
- [32].Plate TA. Holographic reduced representation: distributed representation for cognitive structures. CSLI Publications; 2003. [Google Scholar]
- [33].Gayler RW. Vector symbolic architectures answer Jackendoff’s challenges for cognitive neuroscience. In: Slezak Peter., editor. ICCS/ASCS international conference on cognitive science; Sydney, Australia. University of New South Wales; 2004. pp. 133–8. [Google Scholar]
- [34].Pollack JB. Recursive distributed representations. Artif Intell. 1990;46:77–105. [Google Scholar]
- [35].Smolensky P. Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artif Intell. 1990;46:159–216. [Google Scholar]
- [36].Kanerva P. Sparse distributed memory. The MIT Press; Cambridge (Massachusetts): 1988. [Google Scholar]
- [37].Wahle M, Widdows D, Herskovic J, Bernstam E, Cohen T. Deterministic binary vectors for efficient automated indexing of MEDLINE/PubMed abstracts. To appear in: Proc AMIA Symp; 2012. [PMC free article] [PubMed] [Google Scholar]
- [38].Aronson AR, Lang F-M. An overview of MetaMap: historical perspective and recent advances. J Am Med Inform Assoc. 2010;17:229–36. doi: 10.1136/jamia.2009.002733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Birkhoff G, von Neumann J. The logic of quantum mechanics. Ann Math. 1936;37:823–43. [Google Scholar]
- [40].Widdows D, Peters S. Mathematics of language. Vol. 8. Bloomington, Indiana: Jun, 2003. Word vectors and quantum logic experiments with negation and disjunction. [Google Scholar]
- [41].Golub GH, van Loan CF. Matrix computations (Johns Hopkins studies in mathematical sciences) 3rd ed The Johns Hopkins University Press; 1996. [Google Scholar]
- [42].Cohen T, Widdows D, DeVine L, Schvaneveldt R, Rindflesch T. Many paths lead to discovery: analogical retrieval of cancer therapies. To appear in: Proceedings of the 6th annual quantum interaction symposium; Paris, France. 2012. [Google Scholar]
- [43].Manning CD, Raghavan P, Schtze H. Introduction to information retrieval. Cambridge University Press; New York (NY, USA): 2008. [Google Scholar]
- [44].Dudley JT, Schadt E, Sirota M, Butte AJ, Ashley E, et al. Drug discovery in a multidimensional world: systems, patterns, and networks. J Cardiovasc Transl Res. 2010;3:438–47. doi: 10.1007/s12265-010-9214-6. [DOI] [PubMed] [Google Scholar]
- [45].Raanani P, Gafter-Gvili A, Paul M, Ben-Bassat I, Leibovici L, Shpilberg O. Immunoglobulin prophylaxis in chronic lymphocytic leukemia and multiple myeloma: systematic review and meta-analysis. Leuk Lymphoma. 2009;50:764–72. doi: 10.1080/10428190902856824. [DOI] [PubMed] [Google Scholar]
- [46].Plesnicar A, Vidmar G, Stabuc B, Kores Plesnicar B. Effects of native human leukocyte interferon-alpha and recombinant human interferon-alpha on P3-X63-Ag8.653 mouse myeloma cell growth. J Int Med Res. 2009;37:1570–6. doi: 10.1177/147323000903700535. [DOI] [PubMed] [Google Scholar]
- [47].Shen X, Zhang X, Xu G, Ju S. BAFF-R gene induced by IFN-c in multiple myeloma cells is related to NF-κB signals. Cell Biochem Funct. 2011;29:513–20. doi: 10.1002/cbf.1780. [DOI] [PubMed] [Google Scholar]
- [48].Kudo C, Yamakoshi H, Sato A, Ohori H, Ishioka C, Iwabuchi Y, et al. Novel curcumin analogs, GO-Y030 and GO-Y078, are multi-targeted agents with enhanced abilities for multiple myeloma. Anticancer Res. 2011;31:3719–26. [PubMed] [Google Scholar]
- [49].Follin-Arbelet V, Hofgaard PO, Hauglin H, Naderi S, Sundan A, Blomhoff R, et al. Cyclic AMP induces apoptosis in multiple myeloma cells and inhibits tumor development in a mouse myeloma model. BMC Cancer. 2011;11:301. doi: 10.1186/1471-2407-11-301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Larocca A, Palumbo A. Evolving paradigms in the treatment of newly diagnosed multiple myeloma. J Natl Compr Canc Netw. 2011;9:1186–96. doi: 10.6004/jnccn.2011.0096. [DOI] [PubMed] [Google Scholar]
- [51].Alexanian R, Weber D, Dimopoulos M, Delasalle K, Smith TL. Randomized trial of alpha-interferon or dexamethasone as maintenance treatment for multiple myeloma. Am J Hematol. 2000;65:204–9. doi: 10.1002/1096-8652(200011)65:3<204::aid-ajh5>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- [52].Attar-Schneider O, Drucker L, Zismanov V, Tartakover-Matalon S, Rashid G, Lishner M. Bevacizumab attenuates major signaling cascades and eIF4E translation initiation factor in multiple myeloma cells. Lab Invest. 2012;92:178–90. doi: 10.1038/labinvest.2011.162. [DOI] [PubMed] [Google Scholar]
- [53].Yoshiji H, Noguchi R, Ikenaka Y, Kaji K, Aihara Y, Fukui H. Impact of renin-angiotensin system in hepatocellular carcinoma. Curr Cancer Drug Targets. 2011;11:431–41. doi: 10.2174/156800911795538084. [DOI] [PubMed] [Google Scholar]
- [54].Mahindra A, Cirstea D, Raje N. Novel therapeutic targets for multiple myeloma. Future Oncol. 2010;6:407–18. doi: 10.2217/fon.10.2. [DOI] [PubMed] [Google Scholar]
- [55].Li W, Frame LT, Hoo KA, Li Y, D’Cunha N, Cobos E. Genistein inhibited proliferation and induced apoptosis in acute lymphoblastic leukemia, lymphoma and multiple myeloma cells in vitro. Leuk Lymphoma. 2011;52:2380–90. doi: 10.3109/10428194.2011.598251. [DOI] [PubMed] [Google Scholar]
- [56].Biddle W, Ambrus CM, Gastpar H, Ambrus JL. Antineoplastic effect of the xanthine derivative Trental. J Med. 1984;15:355–66. [PubMed] [Google Scholar]
- [57].Singhal S, Mehta J, Desikan R, Ayers D, Roberson P, Eddlemon P, et al. Antitumor activity of thalidomide in refractory multiple myeloma. N Engl J Med. 1999;341:1565–71. doi: 10.1056/NEJM199911183412102. [DOI] [PubMed] [Google Scholar]
- [58].Rajpal R, Dowling P, Meiller J, Clarke C, Murphy WG, O’Connor R, et al. A novel panel of protein biomarkers for predicting response to thalidomide-based therapy in newly diagnosed multiple myeloma patients. Proteomics. 2011;11:1391–402. doi: 10.1002/pmic.201000471. [DOI] [PubMed] [Google Scholar]
- [59].Liu F-T, Agrawal SG, Movasaghi Z, Wyatt PB, Rehman IU, Gribben JG, et al. Dietary flavonoids inhibit the anticancer effects of the proteasome inhibitor bortezomib. Blood. 2008;112:3835–46. doi: 10.1182/blood-2008-04-150227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Muzaffar J, Katragadda L, Haider S, Javed A, Anaissie E, Usmani S. Rituximab and intravenous immunoglobulin (IVIG) for the management of acquired factor VIII inhibitor in multiple myeloma: case report and review of literature. Int J Hematol. 2012;95:102–6. doi: 10.1007/s12185-011-0968-7. [DOI] [PubMed] [Google Scholar]
- [61].Gangavarapu KJ, Olbertz JL, Bhushan A, Lai JCK, Daniels CK. Apoptotic resistance exhibited by dexamethasone-resistant murine 7TD1 cells is controlled independently of interleukin-6 triggered signaling. Apoptosis. 2008;13:1394–400. doi: 10.1007/s10495-008-0265-y. [DOI] [PubMed] [Google Scholar]
- [62].Ren S-P, Wu C-T, Huang W-R, Lu Z-Z, Jia X-X, Wang L, et al. Adenoviral-mediated transfer of human wild-type p53, GM-CSF and B7-1 genes results in growth suppression and autologous anti-tumor cytotoxicity of multiple myeloma cells in vitro. Cancer Immunol Immunother. 2006;55:375–85. doi: 10.1007/s00262-005-0011-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Gayler RW, Wales R. Connections, binding, unification, and analogical promiscuity. In: Holyoak K, Gentner D, Kokinov B, editors. Advances in analogy research: integration of theory and data from the cognitive, computational, and neural sciences (Proc. Analogy ’98 workshop, Sofia) New Bulgarian University; Sofia: 1998. pp. 181–190. [Google Scholar]
- [64].Eliasmith C, Thagard P. Integrating structure and meaning: a distributed model of analogical mapping. Cogn Sci. 2001;25:245–86. [Google Scholar]
- [65].Plate TA. Analogy retrieval and processing with distributed vector representations. Expert Syst. 2000;17:29–40. [Google Scholar]
- [66].Widdows D, Cohen T, DeVine L. Real, complex and binary semantic vectors. To appear in: Proceedings of the 6th annual Quantum Interaction symposium; Paris, France. 2012. [Google Scholar]
- [67].Widdows D, Cohen T. The semantic vectors package: new algorithms and public tools for distributional semantics. IEEE fourth international conference on semantic COMPUTING (ICSC), n.d..2010. pp. 9–15. [Google Scholar]
- [68].Widdows D, Ferraro K. Semantic vectors: a scalable open source package and online technology management application. Sixth international conference on language resources and evaluation (LREC 2008).2008. [Google Scholar]
- [69].Wilkowski B, Fiszman M, Miller CM, Hristovski D, Arabandi S, Rosemblat G, et al. Graph-based methods for discovery browsing with semantic predications. AMIA Annu Symp Proc. 2011;2011:1514–23. [PMC free article] [PubMed] [Google Scholar]