Quantified Choice of RMSEAs for Evaluation and Power Analysis of Small Differences between Structural Equation Models

Abstract

MacCallum, Browne, and Cai (2006) proposed a new framework for evaluation and power analysis of small differences between nested structural equation models (SEMs). In their framework, the null and alternative hypotheses for testing a small difference in fit and its related power analyses were defined by some chosen root-mean-square error of approximation (RMSEA) pairs. In this article, we develop a new method that quantifies those chosen RMSEA pairs and allows a quantitative comparison of them. Our method proposes the use of single RMSEA values to replace the choice of RMSEA pairs for model comparison and power analysis, thus avoiding the differential meaning of the chosen RMSEA pairs inherent in the approach of MacCallum et al. (2006). With this choice, the conventional cutoff values in model overall evaluation can directly be transferred and applied to the evaluation and power analysis of model differences.

Comparison of nested structural equation models (SEMs) was traditionally based on the null hypothesis that competing models have the same fit in population. By far, the classical normal theory-based likelihood ratio (NTLR) test (e.g., Jöreskog, 1971; Steiger, Shapiro, & Browne, 1985) is the most common method used for testing this null hypothesis. Unquestionably, the power of the NTLR test to detect any difference in fit between competing models should be an important issue for this null hypothesis testing.

Despite the popularity of this approach, MacCallum, Browne, and Cai (2006) suggested that the traditional null hypothesis that competing models have the same fit in population is always false and will be rejected by the NTLR test in practice when the sample size (N = n + 1) is large enough. Instead, they advocated that a null hypothesis of testing some small difference in fit between nested models should replace the traditional one for comparison of SEMs. Under this new null hypothesis, the restricted model can be selected if the NTLR test doesn't detect a large enough difference in fit between two nested models. Similarly, for this type of null hypothesis testing, the power of the NTLR test to detect a large enough difference in fit between two nested models should be an important issue, too.

MacCallum et al. (2006) proposed a unified approach to such model comparison and power analysis. In their approach, the null and alternative hypotheses needed for model comparison and power analysis are defined by pairs of root-mean-square error of approximation (RMSEA; Browne & Cudeck, 1993; Steiger & Lind 1980) values chosen for competing models. Under these newly defined hypotheses, the power of the NTLR test and the comparison of models by the NTLR test can be investigated.

In this article, we first review this new approach to model comparison and power analysis. Then we propose a new method to quantify the RMSEA pairs chosen for the model comparison and the power analyses in MacCallum et al. (2006). By this new method, the choice of single RMSEA values is suggested to replace the choice of RMSEA pairs to define the null and alternative hypotheses needed for model comparison and power analysis. Our new method is then compared with the choices of RMSEA pairs by MacCallum et al. (2006) and applied to some empirical examples in the literature, followed by a discussion at the end of the article.

An Approach to Model Comparison and Power Analysis

Let us assume for the moment that the model is estimated by the normal theory-based maximum likelihood (ML) discrepancy function, which is defined as

$$F_{ML}=log|\widehat{\sum }|-log|S|+\text{t}r(S{\widehat{\sum }}^{-1})-q,$$

where S is the sample covariance matrix, Σ̂ is the covariance matrix implied by the model, and q is the number of observed variables. Let two models M₁ and M₂ have degrees of freedom ν₁ and ν₂ respectively and M₂ be nested in M₁. Let F̂₁ and F̂₂, respectively, be the minimized F_ML values of M₁ and M₂ in sample. Let F₁ and F₂ be the corresponding population values of F̂₁ and F̂₂ respectively. Suppose for the moment that the data are normal, and two nested models are not badly specified and satisfy the so-called population drift assumptions (see Steiger et al., 1985, for detail). The well-known NTLR statistic T_ML = nF̂₂ − nF̂₁ will asymptotically follow the noncentral ${\chi }_{{\nu }_2-{\nu }_1,n{F}_2-n{F}_1}^2$ distribution with degrees of freedom ν₂ − ν₁ and noncentrality parameter nF₂ − nF₁.

In SEM, analysis of statistical power of T_ML to reject H₀ : F₂ − F₁ = 0, the null hypothesis of no difference in fit between nested models, is a traditional issue. For this power analysis, because the value of F₂ − F₁ is generally unknown, we need an alternative hypothesis H₁ : F₂ − F₁ = δ, where δ is a positive chosen value. Then T_ML will have an approximate central ${\chi }_{{\nu }_2-{\nu }_1}^2$ distribution with degrees of freedom ν₂ − ν₁ under H₀ and an approximate noncentral ${\chi }_{{\nu }_2-{\nu }_1,n\delta }^2$ distribution with degrees of freedom ν₂ − ν₁ and noncentrality parameter nδ under H₁. Let us use α = .05. The critical value for T_ML to reject H₀ will be the 95 percent quantile of the central ${\chi }_{{\nu }_2-{\nu }_1}^2$ distribution. Let us denote this critical value by ${\chi }_{{\nu }_2-{\nu }_1,.95}^2$. The approximate power of T_ML to reject H₀ under H₁ is the probability of T_ML greater than ${\chi }_{{\nu }_2-{\nu }_1,.95}^2$ under H₁. For this power analysis, given ν₂ − ν₁, n, and α, the distribution of T_ML and the critical value ${\chi }_{{\nu }_2-{\nu }_1,.95}^2$ are fixed under H₀. However, a value must be chosen for δ to define the noncentral ${\chi }_{{\nu }_2-{\nu }_1,n\delta }^2$ distributions of T_ML under H₁.

MacCallum et al. (2006) defined the value of δ as follows. Let r₁ and r₂ denote the population RMSEAs of M₁ and M₂ respectively and be defined as $r_1=\sqrt{F_1/{\nu }_1}$ and $r_2=\sqrt{F_2/{\nu }_2}$. Then F₂ − F₁ can be expressed as

$$F_2-F_1={\nu }_2{r}_2^2-{\nu }_1{r}_1^2.$$ (1)

Mimicking the expression of F₂ − F₁ in (1), MacCallum et al. (2006) defined

$$\delta ={\nu }_2{r}_{2\delta }^2-{\nu }_1{r}_{1\delta }^2,$$ (2)

where r_1δ and r_2δ are some RMSEA values chosen for M₁ and M₂, respectively, to define δ in H₁ for the power analysis.

MacCallum et al. (2006) stated that H₀ : F₂ − F₁ = 0 is too restrictive and always would be false in practice. As an alternative, they advocated the good enough principle (Serlin & Lapsley, 1985) for model comparison, and proposed a new null hypothesis of the form

$$H_0:F_2-F_1\le {\delta }_{\ast },$$ (3)

where δ_* is some chosen small positive value. They argued that this null hypothesis of small difference in fit between nested models is more realistic than the null hypothesis of no difference in fit between nested models for SEM model comparison in practice. Under this null hypothesis, M₂ can be selected as long as the difference in fit between M₁ and M₂ is small enough. Under this null hypothesis, the critical value for T_ML to reject H₀ now becomes the 95 percent quantile of the noncentral ${\chi }_{{\nu }_2-{\nu }_1,n{\delta }_{\ast }}^2$ distribution and can be denoted by ${\chi }_{{\nu }_2-{\nu }_1,.95,n{\delta }_{\ast }}^2$. If T_ML is greater than ${\chi }_{{\nu }_2-{\nu }_1,.95,n{\delta }_{\ast }}^2$, M₁ would be preferred. Otherwise, M₂ would be preferred. MacCallum et al. (2006) defined

$${\delta }_{\ast }={\nu }_2{r}_{2{\delta }_{\ast }}^2-{\nu }_1{r}_{1{\delta }_{\ast }}^2,$$ (4)

where r_1δ* and r_2δ* are some RMSEA values chosen for M₁ and M₂, respectively, to determine the value of δ_*.

As with the power of rejecting H₀ : F₂ − F₁ = 0, the statistical power of T_ML to reject H₀ : F₂ − F₁ ≤ δ_* should be an important issue for testing the null hypothesis H₀ : F₂ − F₁ ≤ δ_*. Notice that the power of T_ML in this context no longer refers to the probability of detecting any difference in fit between competing models as in traditional power analysis. Instead, it now becomes the probability of detecting a large enough difference in fit between models.

For this type of power analysis, an alternative hypothesis H₁ : F₂ − F₁ = δ_** is needed. Under this alternative hypothesis, T_ML has an approximate noncentral ${\chi }_{{\nu }_2-{\nu }_1,n{\delta }_{\ast \ast }}^2$ distribution. The approximate power of T_ML to reject H₀ : F₂ − F₁ ≤ δ_* is the probability of T_ML greater than ${\chi }_{{\nu }_2-{\nu }_1,.95,n{\delta }_{\ast }}^2$ under the alternative hypothesis. MacCallum et al. (2006) again defined δ_** in terms of a RMSEA pair as

$${\delta }_{\ast \ast }={\nu }_2{r}_{2{\delta }_{\ast \ast }}^2-{\nu }_1{r}_{1{\delta }_{\ast \ast }}^2,$$ (5)

where r_1δ** and r_2δ** are some RMSEA values chosen for M₁ and M₂, respectively, to determine δ_**. Notice that δ_** here must be greater than δ_* for this type of power analysis.

A New Method for the Choice of RMSEAs

From the description above, it is clear that the choice of RMSEA pairs, such as (r_1δ, r_2δ) in (2), (r_1δ*, r_2δ*) in (4), and (r_1δ**, r_2δ**) in (5), is crucial to the power analyses and model comparison methodology proposed in MacCallum et al. (2006). In this article, we propose a way to quantify those RMSEA pairs chosen for model comparison and power analysis and suggest a new method to replace the choice of RMSEA pairs to define δ, δ_* or δ_** across models and conditions.

We use δ_C to represent the chosen value for δ, δ_* or δ_**, and use (r_1C, r_2C) to represent the chosen values for the defining RMSEA pairs in (2), (4), and (5). Then the equations in (2), (4), and (5) can be expressed in a general equation, that is,

$${\delta }_C={\nu }_2{r}_{2C}^2-{\nu }_1{r}_{1C}^2.$$ (6)

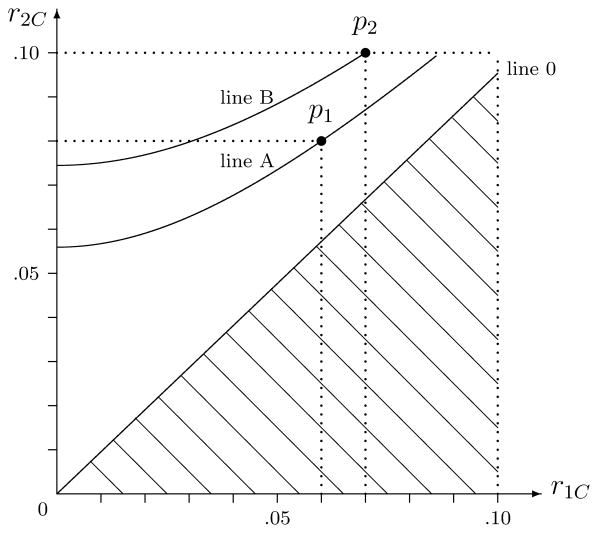
We use Figure 1 to illustrate our idea. Let us assume for moment that ν₁ = 20 and ν₂ = 22. Let the horizontal and vertical axes in Figure 1 represent r_1C and r_2C respectively. Then in Figure 1 the area of any reasonable (r_1C, r_2C) pair to define δ, δ_* or δ_** should be above Line 0, where Line 0 is the line $r_{2C}=\sqrt{{\nu }_1/{\nu }_2}\cdot r_{1C}$ with δ_C = 0. This is because the minimum value of F₂ − F₁ is zero and δ_C defined by (r_1C, r_2C) must be greater than zero. In addition, Line 0 clearly should be lower than the diagonal line since M₂ is assumed to be nested in M₁ and $\sqrt{{\nu }_1/{\nu }_2}<1$.

Figure 1.

The equi-discrepancy lines with ν₁ = 20 and ν₂ = 22

Let p₁ denote the point (r_1C, r_2C) = (.06,.08) in Figure 1 and be our choice of RMSEA pair, for example for (r_1δ**, r_2δ**). There should exist one line, Line A in Figure 1, which consists of a series of points (r_1C′, r_2C′) in Figure 1 and satisfying the following equality

$${\delta }_C={\nu }_2{r}_{2C}^2-{\nu }_1{r}_{1C}^2={\nu }_2{r}_{2C^{\prime }}^2-{\nu }_1{r}_{1C^{\prime }}^2.$$ (7)

Similarly, when the point p₂ = (.07,.10) is chosen for (r_1δ**, r_2δ**), Line B exists in Figure 1 by (7). In fact, to any RMSEA pair chosen for such as (r_1δ, r_2δ) in (2), (r_1δ*, r_2δ*) in (4), and (r_1δ**, r_2δ**) in (5), there will always exist a line in the figure consisting of infinitely many RMSEA pairs satisfying (7). Let us call this line the equi-discrepancy line because all RMSEA pairs on this line have the same value of δ_C and represent the same degree of discrepancy between two nested models.

It is not hard to see that Line 0 is also a line satisfying (7), where all RMSEA pairs represent the same zero discrepancy between nested models. Suppose that the points on Line 0 are chosen as (r_1C, r_2C) for model comparison. The null hypothesis of no difference in fit between nested models can be redefined as $H_0:F_2-F_1={\nu }_2{r}_2^2-{\nu }_1{r}_1^2={\nu }_2{r}_{2C}^2-{\nu }_1{r}_{1C}^2=0$ and can be interpreted as a null hypothesis of whether the true RMSEA pair (r₁, r₂) is on Line 0 or not. In addition, combining the identity $F_2-F_1={\nu }_2{r}_2^2-{\nu }_1{r}_1^2$ in (1) with (3) and (4), we obtain a null hypothesis equivalent to (3), that is,

$$H_0:{\nu }_2{r}_2^2-{\nu }_1{r}_1^2\le {\delta }_{\ast }={\nu }_2{r}_{2{\delta }_{\ast }}^2-{\nu }_1{r}_{1{\delta }_{\ast }}^2.$$ (8)

By (8), testing the null hypothesis of small difference in fit between nested models can be interpreted as testing if the true RMSEA pair (r₁, r₂), which we don't know exactly, is inside the area between the equi-discrepancy line defined by the chosen RMSEA pair (r_1δ*, r_2δ*) and Line 0 or not. When the chosen RMSEA pair (r_1δ*, r_2δ*) represents a higher equi-discrepancy line, the area of testing is larger, δ_* is larger, and a greater discrepancy is allowed between nested models. In contrast, when (r_1δ*, r_2δ*) represents a lower line, the area of testing is smaller, δ_* is smaller and less discrepancy is allowed.

This is also the case for power analysis. When the chosen RMSEA pair (r_1C, r_2C) for defining δ or δ_** in the alternative hypothesis represents a higher equi-discrepancy line, T_ML will have more power of rejection given n, ν₂ − ν₁, α and a fixed null hypothesis. Otherwise, it will have less power of rejection.

Furthermore, no matter whether a RMSEA pair is chosen for model comparison or power analysis, its corresponding equi-discrepancy line in Figure 1 by (7) will cross the vertical axis and have a point $(r_{1C_0^{\prime }},r_{2C_0^{\prime }})$ for which $r_{1C_0^{\prime }}=0$. In Figure 1, for example, $(r_{1C_0^{\prime }},r_{2C_0^{\prime }})=(0,.056)$ for Line A, and $(r_{1C_0^{\prime }},r_{2C_0^{\prime }})=(0,.074)$ for Line B, illustrate this phenomenon. Combining $(r_{1C_0^{\prime }},r_{2C_0^{\prime }})$ with (6) and (7), we obtain

$${\delta }_C={\nu }_2{r}_{2C}^2-{\nu }_1{r}_{1C}^2={\nu }_2{r}_{2C_0^{\prime }}^2.$$ (9)

By (9), any discrepancy defined by a chosen RMSEA pair (r_1C, r_2C) for model comparison or power analysis is equivalent to a discrepancy between the saturated model and a close-fitting model with degrees of freedom ν₂ and true $\text{R}\mathit{\text{MSEA}}=r_{2C_0^{\prime }}$. For example, p₁ on Line A can be considered to represent an overall discrepancy of a model with degrees of freedom 22 and true RMSEA=.056 against the saturated model, while for p₂ on Line B, this close-fitting model has degrees of freedom 22 and a true RMSEA=.074. By (9), we translate the choice of (r_1C, r_2C) for model comparison and power analysis into an equivalent choice of $r_{2C_0^{\prime }}$ for a close-fitting reference model with degrees of freedom ν₂.

Given this equivalence, we can be free from a two-dimensional choice of (r_1C, r_2C) and instead define δ, δ_* or δ_** for model comparison and power analysis based on the choice of $r_{2C_0^{\prime }}$. By definition, RMSEA indicates discrepancy per degree of freedom. Choosing $r_{2C_0^{\prime }}$ to define δ, δ_* or δ_** would retain the same meaning for δ, δ_* or δ_** in spite of the change of ν₁ or ν₂. Specifically, even though the value of δ, δ_* or δ_** and the shape of the corresponding equi-discrepancy line may change with ν₁ or ν₂ by (7) and (9), the δ, δ_* or δ_** defined by a specific $r_{2C_0^{\prime }}$ means the same average discrepancy over degrees of freedom across studies.

In contrast, this is not the case when a two-dimensional choice of (r_1C, r_2C) is used for defining δ, δ_* or δ_**. For example, MacCallum et al. (2006) selected r_1δ* = .05 and r_2δ* = .06 for δ_* in (3) to test small difference between models for two published empirical studies: Joireman, Anderson, and Strathman (2003) and Dunkley, Zuroff, and Blankstein (2003). In Joireman et al. (2003), ν₁ = 10 and ν₂ = 12. By (9), with r_1δ* = .05 and r_2δ* = .06, the corresponding $r_{2C_0^{\prime }}=\sqrt{(12\times {.06}^2-10\times {.05}^2)/12}=.039$. In Dunkley et al. (2003), ν₁ = 337 and ν₂ = 338. With r_1δ* = .05 and r_2δ* = .06, $r_{2C_0^{\prime }}=\sqrt{(338\times {.06}^2-337\times {.05}^2)/338}=.033$ correspondingly. By our method, we find that the values of δ_* defined by r_1δ* = .05 and r_2δ* = .06 as in MacCallum et al. (2006) vary in terms of $r_{2C_0^{\prime }}$ and hence have different meaning across these two studies. The same phenomenon could happen to δ or δ_** when a constant RMSEA pair (r_1C, r_2C) is selected for the power analyses across studies.

In addition to eliminating this differential meaning of RMSEA pairs inherent in the approach of MacCallum et al. (2006), the choice of $r_{2C_0^{\prime }}$ also allows us to utilize the RMSEA cutoff criteria, established in SEM for a close-fitted reference model, for our model comparison and power analyses. It is well-known that RMSEAs equal to .056 or .074 may represent discrepancies between some mildly misspecified models and the corresponding saturated models. Thus, p₁ and p₂ by their corresponding $r_{2C_0^{\prime }}$ equal to .056 and .074 respectively can be considered to allow too much discrepancy to define δ_* in (3) for small difference evaluation. In SEM, .05 is the widely used RMSEA cutoff value for model close fit (e.g., Browne & Cudeck, 1993). It can be used as $r_{2C_0^{\prime }}$ to define δ_* for model comparison.

MacCallum, Browne, and Sugawara (1996) used $r_{2C_0^{\prime }}=.05$ to define the alternative hypothesis and estimated the power, or the minimum N, of the likelihood ratio test to reject the exact fit of SEM models with degrees of freedom ν₂. In this article, by (9) and the equi-discrepancy lines above, we demonstrated the connection between choices of $r_{2C_0^{\prime }}$ for model overall evaluation and for model comparison. This connection also bridges our power analysis with MacCallum et al. (1996). By the same rationale, we could use $r_{2C_0^{\prime }}=.05$ to define δ in the alternative hypothesis and then estimate the power, or the minimum N, of T_ML to reject the null hypothesis of no difference in fit between nested models.

Moreover, with δ_* defined by such as $r_{2C_0^{\prime }}=.05$ in the null hypothesis, the $r_{2C_0^{\prime }}$ for defining δ_** in the alternative hypothesis should be greater than .05. With such choice of $r_{2C_0^{\prime }}$, the corresponding δ_** may represent some degree of discrepancy between a mildly misspecified model and the saturated model. MacCallum et al. (1996) used $r_{2C_0^{\prime }}=.08$ for the alternative hypothesis and estimated the power of the likelihood ratio test to reject model close fit. Similarly, we could use $r_{2C_0^{\prime }}=.08$ to define δ_** and then estimate the power of T_ML to reject the null hypothesis of a small difference in fit between nested models.

Of course, we need to emphasize here that the cutoff values above borrowed from the model overall evaluation are merely guidelines. We have no intention to insist any constant RMSEA value for all situations. For example, some other values less than .05 such as .033 or .039 mentioned above can be selected as $r_{2C_0^{\prime }}$ for model comparison too. MacCallum et al. (2006) provided a good discussion on how these cutoff criteria for model overall evaluation may not consistently yield valid conclusions in practice. In total, the choices of $r_{2C_0^{\prime }}$ for model difference evaluation and power analysis still depend upon the scrutiny of investigators for their particular application. However, no matter what values they choose, our method is still valid and there would be no contradiction between their choices and our method.

Another interesting point we should mention here is that the interval between Line 0 and any other equi-discrepancy line always shrinks as r_1C increases as in Figure 1. Substantively, this means that under the same tolerable discrepancy for two nested models, the model comparison as in (8) allows more restriction or parsimony (larger r₂ − r₁) when the general model contains less misspecification (smaller r₁), or equivalently, less restriction (smaller r₂ − r₁) when the general model becomes less trustable (larger r₁). Although we do not know the values of r₁ and r₂, the model comparison as in (8) automatically sets a corresponding standard for r₁ and r₂ by the equi-discrepancy lines.

Relevant Developments

The equi-discrepancy line above is defined by a series of infinite equivalent alternatives to an arbitrary pair of RMSEA values. In fact, the equivalence of infinitely many RMSEA pairs is not a completely new idea. MacCallum, Lee, and Browne (2010) used a series of infinite alternatives to an arbitrary RMSEA pair to define their isopower contour. For any RMSEA pair on the isopower contour, the power of the likelihood ratio statistic to reject model overall fit (either exact or close fit) remains the same. The isopower contours in their Figures 9 and 10 look similar to our equi-discrepancy lines in Figure 1.

However, we need to point out that the equivalence of their infinite alternatives is defined by a power calculation which requires (among other things) a choice of discrepancy function, a test statistic, the distribution of the test statistic under the null hypothesis, the distribution of the test statistic under the alternative hypothesis, sample size N, and a choice of α. Each point on the isopower contour represents the power of a statistic for model overall evaluation. On the other hand, the equivalence of our infinite alternatives requires none of these and is defined by (7) only. The points on our equi-discrepancy lines do not yield a plot for the power of a test statistic without further information.¹ Although coming from different directions, the idea of the equivalence of infinitely many RMSEA pairs is shared by the two studies and may be applicable to other SEM contexts beyond these studies in the future.

Comparison and Application to Issues in SEM

Our new method quantifies the RMSEA pairs chosen for the model comparison and the power analyses proposed by MacCallum et al. (2006) and allows discrepancies defined by different RMSEA pairs to be compared with each other quantitatively in a common metric. By our method, the choice of a single $r_{2C_0^{\prime }}$ is suggested to replace the choice of a RMSEA pair (r_1C, r_2C) for the model comparison and the power analyses proposed by MacCallum et al. (2006). In this section, we reexamine the RMSEA pair choices for the examples in MacCallum et al. (2006) using our method and apply our choice of $r_{2C_0^{\prime }}$ to issues in SEM.

Quantification of the RMSEA pair choices

MacCallum et al. (2006) suggested to use a large set of pairs of r_1C and r_2C in a reasonable range to define δ or δ_** for power analysis. For example, in their Table 1 and Table 2, given ν₁ = 20 and ν₂ = 22, MacCallum et al. (2006) selected r_1δ from .03 to .09 and r_2δ from .04 to .10 to define δ in the alternative hypothesis and estimated the power, or minimum N, of T_ML to reject the null hypothesis of no difference in fit between nested models. We apply our method to compare those choices and use (9) to calculate the $r_{2C_0^{\prime }}$ values for the pairs of r_1δ and r_2δ selected by MacCallum et al. (2006) in their tables. The R code used for the calculation is given in the Appendix and the calculated values are presented in our Table 1.

Table 1.

The $r_{2C_0^{\prime }}$ for the selected pairs of r_1C and r_2C with ν₁ = 20 and ν₂ = 22.

	r1C
r2C	.03	.04	.05	.06	.07	.08	.09
.04	.028
.05	.041	.032
.06	.053	.046	.036
.07	.064	.059	.051	.040
.08	.075	.070	.064	.056	.044
.09	.085	.082	.076	.069	.060	.048
.10	.096	.092	.088	.082	.074	.065	.051

In our Table 1, eight pairs of r_1δ and r_2δ have $r_{2C_0^{\prime }}$ values less than .05, while all other twenty pairs have $r_{2C_0^{\prime }}$ values greater than .05. By our method, we would say that for this power analysis eight pairs of r_1δ and r_2δ suggested by MacCallum et al. (2006) may represent a discrepancy between a close-fitting model and the saturated model while all other twenty pairs may represent a larger discrepancy. Furthermore, in our Table 1, with the same ν₁ and ν₂, the RMSEA pairs at the higher end of the RMSEA scale such as (.08,.10) have larger $r_{2C_0^{\prime }}$ values and represent larger discrepancies than the pairs at the lower end of the RMSEA scale with the same difference of r_1δ and r_2δ such as (.03,.05) or (.04,.06). This phenomenon in turn accounts for the increasing statistical power in detecting model difference or the decreasing minimum N required for the same power along the diagonal bands of Table 1 and Table 2 in MacCallum et al. (2006).

The choice of $r_{2C_0^{\prime }}$ for issues in SEM

The choice of $r_{2C_0^{\prime }}$ was recommended in this article to replace the choice of RMSEA pairs to define δ, δ_* and δ_** for model comparison and power analysis. MacCallum et al. (2006) selected r_1δ = 0.4 and r_2δ = .06 to define δ in the alternative hypothesis H₁ : F₂ − F₁ = δ and conduct power analysis for two published empirical studies (Manne & Glassman, 2000; Sadler & Woody, 2003). In Sadler and Woody (2003), ν₁ = 24 and ν₂ = 27. In Manne and Glassman (2000), ν₁ = 19 and ν₂ = 26. Suppose that we choose a single value $r_{2C_0^{\prime }}=.05$ to define δ for power analysis. By (9), $\delta ={\nu }_2{r}_{2C_0^{\prime }}^2=27\times {.05}^2=.0675$ for Sadler and Woody (2003) and $\delta ={\nu }_2{r}_{2C_0^{\prime }}^2=26\times {.05}^2=.065$ for Manne and Glassman (2000). Given these δ s, we can calculate the power of T_ML to reject H₀ : F₂ − F₁ = 0 in each study. As mentioned before, T_ML would have an approximate central ${\chi }_{{\nu }_2-{\nu }_1}^2$ distribution under H₀ : F₂ − F₁ = 0 and have an approximate noncentral ${\chi }_{{\nu }_2-{\nu }_1,n\delta }^2$ distribution under H₁ : F₂ − F₁ = δ. With α = .05, this power is the probability of T_ML to exceed the critical value ${\chi }_{{\nu }_2-{\nu }_1,.95}^2$ under H₁ : F₂ − F₁ = δ. In Sadler and Woody (2003), ν₂ − ν₁= 3 and N = 112. Given α = .05, the power is .62. In Manne and Glassman (2000), ν₂ − ν₁= 7 and N = 191. Given α = .05, the power is .73. The steps of power calculation for the two studies are coded in R and given in the Appendix.

Both Sadler and Woody (2003) and Manne and Glassman (2000) failed to detect a significant difference between their nested models by T_ML. As a result, both studies selected the restricted models after comparison. Given the power analyses above, the nonsignificance of T_ML in both studies, as mentioned by MacCallum et al. (2006), may partially be due to the moderate power of rejection in both studies. Given this possibility, we decided to calculate the minimum N to achieve a .80 power of rejection. With α = .05, this minimum N is the minimum sample size that the probability of T_ML to exceed ${\chi }_{{\nu }_2-{\nu }_1,.95}^2$ under H₁ : F₂ − F₁ = δ is equal to or greater than .80. In Sadler and Woody (2003), given ν₂ − ν₁= 3 and δ defined by $r_{2C_0^{\prime }}=.05$ above, we find that this minimum N is 163. In Manne and Glassman (2000), given ν₂ − ν₁= 7 and δ defined by $r_{2C_0^{\prime }}=.05$ above, we find that this minimum N is 222. The steps for the calculation of minimum N s are coded in R and given in the Appendix. As in MacCallum et al. (2006), our minimum N s calculated here suggest that more additional subjects are needed for T_ML in both studies to reach a rejection power of .80.

We demonstrated before that when the δ_* in H₀ : F₂ − F₁ ≤ δ_* is defined by r_1δ* = .05 and r_2δ* = .06 as in MacCallum et al. (2006), the corresponding $r_{2C_0^{\prime }}$ would be equal to .039 for Joireman et al. (2003) and be equal to .033 for Dunkley et al. (2003). Now we instead select a single value, for example $r_{2C_0^{\prime }}=.033$, to define δ_*. By (9), ${\delta }_{\ast }={\nu }_2{r}_{2C_0^{\prime }}^2=12\times {.033}^2=.013$ for Joireman et al. (2003). With ν₂ − ν₁= 2, α = .05 and N = 154, the critical value for rejecting H₀ : F₂ − F₁ ≤ δ_* is ${\chi }_{{\nu }_2-{\nu }_1,.95,n{\delta }_{\ast }}^2=10.84$. The observed value of T_ML = 19.13 yields a significant level of p < .05, indicating rejection of the null hypothesis of small difference in fit for this study. For Dunkley et al. (2003), δ_* = 338×.033² = .368 by (9). With ν₂ − ν₁= 1, α = .05 and N = 163, the critical value is ${\chi }_{{\nu }_2-{\nu }_1,.95,n{\delta }_{\ast }}^2=87.74$. The observed value of T_ML =3.84 yields a nonsignificant level of p >.99, suggesting that the null hypothesis of small difference in fit is acceptable. The steps for the calculation of critical and p -values are coded in R and given in the Appendix.

Both Joireman et al. (2003) and Dunkley et al. (2003) observed the significance of T_ML when they compared a general model with a more parsimonious and interpretable model under the traditional approach. As a result, Joireman et al. (2003) selected the general model while Dunkley et al. (2003) selected the parsimonious one despite the significance of T_ML. Like the traditional one, our model comparison under the null hypothesis of small difference in fit supports the choice of the general model for Joireman et al. (2003). However, for Dunkley et al. (2003), it is different from the traditional approach and supports the parsimonious model, the choice of the authors in their article.

For our model comparisons above, a related issue is the power of T_ML to reject the null hypothesis of small difference in fit. In their example with ν₁= 20 and ν₂= 22, MacCallum et al. (2006) selected r_1δ** = .05 and r_2δ** = .08 to define δ_** in the alternative hypothesis H₁ : F₂ − F₁ = δ_**. From our Table 1, we find the corresponding $r_{2C_0^{\prime }}=.064$. As a result, we set $r_{2C_0^{\prime }}=.064$ to define δ_** for our power analysis. By (9), ${\delta }_{\ast \ast }={\nu }_2{r}_{2C_0^{\prime }}^2=12\times {.064}^2=.0492$ for Joireman et al. (2003) and ${\delta }_{\ast \ast }={\nu }_2{r}_{2C_0^{\prime }}^2=338\times {.064}^2=1.3844$ for Dunkley et al. (2003). Given these δ_** s and the δ_* s defined by $r_{2C_0^{\prime }}=.033$ above, we can calculate the power of T_ML to reject H₀ : F₂ − F₁ ≤ δ_* in the two studies. In this case, T_ML would have an approximate noncentral ${\chi }_{{\nu }_2-{\nu }_1,n{\delta }_{\ast }}^2$ distribution under H₀: F₂ − F₁ ≤ δ_** and have an approximate noncentral ${\chi }_{{\nu }_2-{\nu }_1,n{\delta }_{\ast \ast }}^2$ distribution under H₁ : F₂ − F₁ = δ_**. With α = .05, this power is the probability of T_ML to exceed the critical value ${\chi }_{{\nu }_2-{\nu }_1,.95,n{\delta }_{\ast }}^2$ under H₁ : F₂ − F₁ = δ_**. Our steps of power calculation for the two studies are coded in R and given in the Appendix. Our calculation shows that the power of rejection is .35 for Joireman et al. (2003) and is 1 for Dunkley et al. (2003). Notice that the degrees of freedom of competing models in Dunkley et al. (2003) are high. This may explain the higher power in their study with the same $r_{2C_0^{\prime }}$. The $r_{2C_0^{\prime }}$ value may be adjusted downward given the high degrees of freedom of their models (see p. 32 of MacCallum et al., 2006).

Our power analysis results above strengthen the selection of the general model for Joireman et al. (2003) and the restricted model for Dunkley et al. (2003). In Joireman et al. (2003), the observed T_ML is significant even though the power for this study is just .35. In contrast, the observed T_ML in Dunkley et al. (2003) is nonsignificant even though the power is 1. Given the low power in Joireman et al. (2003), we calculate the minimum N for T_ML to reach a .80 power of rejection in this study. The steps for this calculation are coded in R and given in the Appendix. Our calculation shows that this minimum N is 555. Some additional subjects are needed for this study to gain a desirable power.

Discussion and Recommendations

In this article, we followed the footsteps of MacCallum, Browne, and Cai (2006) and developed a new method for conducting model comparison and power analysis consistent with the approach of MacCallum et al. (2006). In this development, we defined an equi-discrepancy line by equation (7). Our equi-discrepancy line reminds investigators that there always exists a series of infinite alternatives to their chosen RMSEA pair to equivalently define the null or alternative hypothesis for model comparison and power analysis as in MacCallum et al. (2006). With these infinite alternatives, testing no or a small difference between nested models can be graphically translated or understood as testing whether the true RMSEA pair of nested models falls on Line 0 or the region below the equi-discrepancy line in Figure 1.

Among these infinite alternatives, we also identified a unique RMSEA pair that is at the cross of the equi-discrepancy line and the vertical axis in Figure 1. With this unique RMSEA pair, any chosen RMSEA pair can be quantified into the RMSEA value of a reference SEM model. Consequently, for investigators, their choices of RMSEA pairs for model comparison and power analysis can be compared quantitatively. This comparison as in our Table 1 also provides a reminder to investigators that the RMSEA pairs at the different parts of the RMSEA scale, for example, (.03,.05) vs. (.08,.10) in our Table 1, would represent different discrepancies for model comparison and have different implications for power analysis even though they have the same difference of RMSEA values.

More importantly, given this quantification, the choice of RMSEA pairs in MacCallum et al. (2006) now is recommended to be replaced by the choice of a single RMSEA value instead. For model comparison and power analysis following MacCallum et al. (2006), this choice of single RMSEA value can eliminate the differential meaning of the RMSEA pairs inherent in the original approach of MacCallum et al. (2006). This choice also bridges the two branches of SEM model evaluation, model overall evaluation and model difference evaluation, and makes possible for the criteria established for model overall evaluation to be transferred and applied to the issues of SEM model difference evaluation and power analyses.

As a result, in our new procedure illustrated in the examples above, we propose to first choose some reasonable RMSEA values to define the null and alternative hypothesis for model comparison and power analysis as per MacCallum et al. (2006). These choices could be made based on some established criteria for model overall evaluation (e.g., Browne & Cudeck, 1993; MacCallum et al., 1996) or some other values upon the scrutiny of investigators. Once these defining RMSEA values are chosen, model comparison and power analysis as in MacCallum et al. (2006) can be conducted under the corresponding null and alternative hypotheses as illustrated in our examples above.

Of course, as a followup to MacCallum et al. (2006), our proposed method for model comparison and power analysis would inevitably inherit many issues encountered by MacCallum et al. (2006). These issues include assumptions such as T_ML to be central or non-central chi-square distributed, estimation methods other than the ML discrepancy function, limitations of RMSEA cutoff criteria for practical use, different approaches to model comparison (e.g., Satorra & Saris, 1985), etc. For all these issues, please refer to MacCallum et al. (2006) for a thorough discussion in the context of the general framework. In addition, in multisample SEM studies, due to constraints across groups, Steiger (1998) proposed a modification of the definition of RMSEA. That is, $r_1=\sqrt{G}\sqrt{F_1/{\nu }_1}$ and $r_2=\sqrt{G}\sqrt{F_2/{\nu }_2}$ for M₁ and M₂ respectively, where G is the number of groups. Under this definition, by dividing the right side of (2), (4), (5) or (6) by G, our proposed method could be still valid to define the value of δ_C for model comparison and power analysis in MacCallum et al. (2006). Of course, RMSEA in this case doesn't have the interpretation as discrepancy per degree of freedom as pointed out by MacCallum et al. (2006).

MacCallum et al. (2006) pointed out that their framework can be generalized into some fit indices other than RMSEA. Correspondingly, our developments are also applicable to those fit indices. For example, let γ_1C and γ_2C denote the values of Steiger's (1989) γ chosen for M₁ and M₂ respectively. Then δ_C can be defined as δ_C = (p/2) · (1/γ_2C − 1/γ_1C) (see Kim, 2005). Similarly, let Mc_1C and Mc_2C denote the values of McDonald's (1989) fit index chosen for M₁ and M₂ respectively. Then δ_C can be defined as δ_C = −2log(Mc_2C) + 2log(Mc_1C) (see Kim, 2005). Following the same logic for RMSEAs in (7) and (9), we obtain

$${\delta }_C=\frac{p}{2}\left(\frac{1}{{\gamma }_{2C}}-\frac{1}{{\gamma }_{1C}}\right)=\frac{p}{2}\left(\frac{1}{{\gamma }_{2C^{\prime }}}-\frac{1}{{\gamma }_{1C^{\prime }}}\right)=\frac{p}{2}\left(\frac{1}{{\gamma }_{2C_0^{\prime }}}-1\right)$$

and

$${\delta }_C=-2\text{l}og({Mc}_{2C})+2\text{l}og({Mc}_{1C})=-2\text{l}og({Mc}_{2C^{\prime }})+2\text{l}og({Mc}_{1C^{\prime }})=-2\text{l}og({Mc}_{2C_0^{\prime }})$$

where γ_1C and γ_2C′ constitute infinite alternatives to γ_1C and γ_2C, Mc_1C′ and Mc_2C′ constitute infinite alternatives to Mc_1C and Mc_2C, and ${\gamma }_{2C_0^{\prime }}$ and $\text{M}{c}_{2C_0^{\prime }}$ are the corresponding values of Steiger's γ and McDonald's fit index for the reference model. Again, by these infinite alternatives, different equi-discrepancy lines can be drawn. By these equations, the choice of ${\gamma }_{2C_0^{\prime }}$ and $\text{M}{c}_{2C_0^{\prime }}$ can replace the choice of pairs of Steiger's γ and McDonald's fit index to define δ, δ_* and δ_** in the null and alternative hypotheses for model comparison and power analysis. Similarly, some conventional cutoff values of these fit indices (e.g., Hu & Bentler, 1999) can be used for the choice of ${\gamma }_{2C_0^{\prime }}$ or $\text{M}{c}_{2C_0^{\prime }}$ for model comparison and power analysis.

Appendix

1. The R code to calculate the $r_{2C_0^{\prime }}$ values for the pairs of r_1δ and r_2δ selected by MacCallum, Browne, and Cai (2006) in their Table 1 and Table 2:

   dfM1<-20 # degrees of freedom of M1

   dfM2<-22 # degrees of freedom of M2

   r1<-seq(.03,.09,.01) # RMSEA choice for M1

   r2<-r1+.01 # RMSEA choice for M2

   Fn<-matrix(0,length(r2),length(r1))

   for (i in 1:length(r2)) {

   for (j in 1:i) {

   Fn[i,j]<-sqrt((r2[i]ˆ2*dfM2-r1[j]ˆ2*dfM1)/dfM2)

   }

   }

   print(Fn,digits=2)

2. The R code to calculate the power of T_ML to reject H₀ : F₂ − F₁ = δ for Sadler and Woody (2003):

   n<-111 # (Sample size-1)

   dfM1<-24 # degrees of freedom of M1

   dfM2<-27 # degrees of freedom of M2

   delta<-dfM2*.05ˆ2 # define delta in the alternative hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1) # Critical value under the null hypothesis

   power<-1-pchisq(cv,df=dfM2-dfM1,ncp=n*delta)

   print(power,digits=2)

   For Manne and Glassman (2000):

   n<-190 # (Sample size-1)

   dfM1<-19 # degrees of freedom of M1

   dfM2<-26 # degrees of freedom of M2

   delta<-dfM2*.05ˆ2 # define delta in the alternative hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1) # Critical value under the null hypothesis

   power<-1-pchisq(cv,df=dfM2-dfM1,ncp=n*delta)

   print(power,digits=2)

3. The R code to calculate the minimum N for T_ML to achieve the .80 power of rejecting H₀ : F₂ − F₁ = 0 in Sadler and Woody (2003):

   dfM1<-24 # degrees of freedom of M1

   dfM2<-27 # degrees of freedom of M2

   delta<-dfM2*.05ˆ2 # define delta in the alternative hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1) # Critical value under the null hypothesis

   for (n in 1:100000) {

   power<-1-pchisq(cv,df=dfM2-dfM1,ncp=n*delta)

   if (power>=.80) break # reach the desirable power

   }

   N<-n+1

   print(N)

   For Manne and Glassman (2000):

   dfM1<-19 # degrees of freedom of M1

   dfM2<-26 # degrees of freedom of M2

   delta<-dfM2*.05ˆ2 # define delta in the alternative hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1) # Critical value under the null hypothesis

   for (n in 1:100000) {

   power<-1-pchisq(cv,df=dfM2-dfM1,ncp=n*delta)

   if (power>=.80) break # reach the desirable power

   }

   N<-n+1

   print(N)

4. The R code to calculate the p -value for T_ML to reject H₀ : F₂ − F₁ ≤ δ_* in Joireman, Anderson, and Strathman (2003):

   Tml<-19.13 # the observed value of the likelihood ratio test

   n<-153 # (Sample size-1)

   dfM1<-10 # degrees of freedom of M1

   dfM2<-12 # degrees of freedom of M2

   delta<-dfM2*.033ˆ2 # define delta* in the null hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1,n*delta) # Critical value under H0

   pvalue<-1-pchisq(Tml,df=dfM2-dfM1,ncp=n*delta)

   print(cv,digits=4)

   print(pvalue,digits=2)

   For Dunkley, Zuroff, and Blankstein (2003):

   Tml<-3.84 # the observed value of the likelihood ratio test

   n<-162 # (Sample size-1)

   dfM1<-337 # degrees of freedom of M1

   dfM2<-338 # degrees of freedom of M2

   delta<-dfM2*.033ˆ2 # define delta* in the null hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1,n*delta) # Critical value under H0

   pvalue<-1-pchisq(Tml,df=dfM2-dfM1,ncp=n*delta)

   print(cv,digits=4)

   print(pvalue,digits=2)

5. The R code to calculate the power of T_ML to reject H₀ : F₂ − F₁ ≤ δ_* for Joireman et al. (2003):

   n<-153 # (Sample size-1)

   dfM1<-10 # degrees of freedom of M1

   dfM2<-12 # degrees of freedom of M2

   delta1<-dfM2*.033ˆ2 # define delta* in the null hypothesis

   delta2<-dfM2*.064ˆ2 # define delta** in the alternative hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1,n*delta1) # Critical value under H0

   power<-1-pchisq(cv,df=dfM2-dfM1,ncp=n*delta2)

   print(power,digits=2)

   For Dunkley et al. (2003):

   n<-162 # (Sample size-1)

   dfM1<-337 # degrees of freedom of M1

   dfM2<-338 # degrees of freedom of M2

   delta1<-dfM2*.033ˆ2 # define delta* in the null hypothesis

   delta2<-dfM2*.064ˆ2 # define delta** in the alternative hypothesis

   alpha<-.05

   cv<-qchisq(1-alpha,df=dfM2-dfM1,n*delta1) # Critical value under H0

   power<-1-pchisq(cv,df=dfM2-dfM1,ncp=n*delta2)

   print(power,digits=2)

6. The R code to calculate the minimum N for T_ML to achieve the .80 power of rejecting H₀ : F₂ − F₁ ≤ δ_* in Joireman et al. (2003):

   dfM1<-10 # degrees of freedom of M1

   dfM2<-12 # degrees of freedom of M2

   delta1<-dfM2*.033ˆ2 # define delta* in the alternative hypothesis

   delta2<-dfM2*.064ˆ2 # define delta** in the alternative hypothesis

   alpha<-.05

   for (n in 1:100000) {

   cv<-qchisq(1-alpha,df=dfM2-dfM1,ncp=n*delta1) # Critical value under H0

   power<-1-pchisq(cv,df=dfM2-dfM1,ncp=n*delta2)

   if (power>=.80) break # reach the desirable power

   }

   N<-n+1

   print(N)

7. The difference between the isopower contour of MacCallum, Lee and Browne (2010) and our equi-discrepancy line:

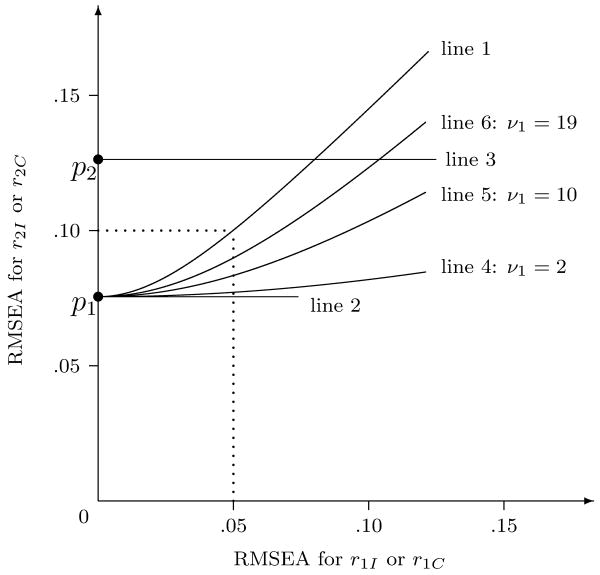
   The purpose of the description below is to help researchers distinguish those two concepts in the two studies and facilitate the application of both of them. As a result, the first difference we want to point out is that the context of the isopower contour of MacCallum et al. (2010) is model overall evaluation (exact or close fit). Instead, our equi-discrepancy line applies to comparison of any pair of nested SEM models. For further illustration, we consider a special situation where the less restricted model M₁ is a saturated model with ν₁= 0, F₁ = 0 and r₁ = 0, and the more restricted one M₂ is a model with degrees of freedom, for example, ν₂ = 20 as assumed in Figure 9 of MacCallum et al. (2010)². Notice that the isopower contour and the equi-discrepancy line are now discussed in the same context of overall evaluation of M₂.

   Let (r_1I, r_2I) be a pair of RMSEA values to define the null hypothesis H₀ : r₂ ≤ r_iI and its alternative one H₁ : r₂ = r_2I for overall evaluation of M₂ as in MacCallum et al. (2010). With a choice of α and sample size N, the central or noncentral χ² distribution of T_ML under H₀ and H₁ can be determined and the power of T_ML to reject H₀ under H₁ can be calculated. MacCallum et al. (2010) argued that T_ML can reach the same rejection power when H₀ and H₁ are defined by another RMSEA pair among an infinite number of isopower alternatives to (r_1I, r_2I). Let α = .05, N = 200, r_1I =.05 and r_2I = .10 as in Figure 9 of MacCallum et al. (2010). Then we calculated some of those isopower alternatives and replicated the isopower contour in their Figure 9 as Line 1 in our Figure 2³. The rejection power of T_ML under any set of H₀ and H₁ defined by the points on Line 1 would be the same as .84.

   For model comparison and power analysis by our method, r_1C and r_2C are selected for M₁ and M₂ respectively to define δ in H₁ : F₂ − F₁ = δ, or δ_* in H₀ : F₂ − F₁ ≤ δ_*, or δ_** in H₁ : F₂ − F₁ = δ_**. According to MacCallum et al. (2006), r_1C and r_2C should be some reasonable RMSEA values representing the misspecification of two nested models. When M₁ is assumed to be a saturated model with ν₁= 0, F₁ = 0 and r₁ = 0, the only reasonable choice of RMSEA value for r_1C (and its alternative r_1C′) should be zero. Correspondingly, r_2C and its alternative r_2C′ should be the same by the definition of the equi-discrepancy line in (7). Consequently, in the context of overall evaluation of M₂ as in MacCallum et al. (2010), our equi-discrepancy line is no longer a line and reduces to a point on the vertical axis in Figure 2. For example, when .076 or .126 is selected for r_2C, our equi-discrepancy line reduces to the point p₁ or p₂ in Figure 2, respectively.

   In fact, even when r_1C or r_1C′ is not limited to zero and can be any value greater than zero, r_2C and r_2C′ should still be the same to satisfy (7) because M₁ is a saturated model and ν₁= 0 at this time. For example, when ν₁= 0, ν₂= 20, and the point p₁ = (.00,.076) is selected as (r_1C, r_2C), r_1C′ should always be .076 by (7) in spite of the value of r_1C′. As a result, the equi-discrepancy line in this case would be Line 2 in Figure 2, which is a straight line parallel to the horizontal axis. Similarly, when the point (.08,.126) is selected as (r_1C, r_2C), the equi-discrepancy line would be Line 3 in Figure 2, which crosses the vertical axis at p₂.

   Furthermore, in spite of the value of (r_1C, r_2C) or (r_1C′, r_2C′) on the equi-discrepancy line, equation (7) now would reduce to ${\delta }_C={\nu }_2{r}_{2C}^2$ because ν₁= 0 and (r_1C, r_2C′). Given F₁ = 0 now, substituting this δ_C into the null and alternative hypotheses, H₁ : F₂ − F₁ = δ could reduce to H₁ : r₂ = r_2C, H₀ : F₂ − F₁ ≤ δ_* could reduce to H₀ : r₂ ≤ r_2C, and H₁ : F₂ − F₁ = δ_** could reduce to H₁ : r₂ = r_2C. Obviously, in the context of model overall evaluation, the points (r_1C, r_2C) and (r_1C′, r_2C′) on an equi-discrepancy line (if this line exists) equivalently define either r_iI of H₀ : r₂ ≤ r_iI or r_2I of H₁ : r₂ = r_2I in MacCallum et al. (2010), instead of both.

   Finally, when ν₁ becomes some positive values rather than zero and M₁ is no longer a saturated model, the isopower contour of MacCallum et al. (2010) doesn't apply while our equi-discrepancy line still exists. We plotted the equi-discrepancy line when ν₁ is equal to 2, 10 and 19, as Line 4, Line 5 and Line 6 in Figure 2, respectively. The equi-discrepancy lines now become some curves similar to the isopower contour of MacCallum et al. (2010). However, they can not coincide with each other because the isopower contour does not exist in this situation. In addition, notice that the points on an equi-discrepancy line can equivalently define the null or alternative hypothesis for model comparison and its related power analysis. However, unlike the points on the isopower contours, they do not represent a plot of power for any test statistic without further information.

Figure 2.

The equi-discrepancy line vs. the isopower contour with ν₂ = 20