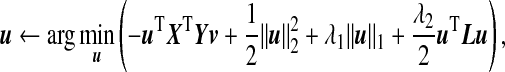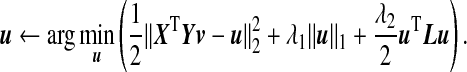Abstract
Motivated by studying the association between nutrient intake and human gut microbiome composition, we developed a method for structure-constrained sparse canonical correlation analysis (ssCCA) in a high-dimensional setting. ssCCA takes into account the phylogenetic relationships among bacteria, which provides important prior knowledge on evolutionary relationships among bacterial taxa. Our ssCCA formulation utilizes a phylogenetic structure-constrained penalty function to impose certain smoothness on the linear coefficients according to the phylogenetic relationships among the taxa. An efficient coordinate descent algorithm is developed for optimization. A human gut microbiome data set is used to illustrate this method. Both simulations and real data applications show that ssCCA performs better than the standard sparse CCA in identifying meaningful variables when there are structures in the data.
Keywords: Dimension reduction, Graph, Phylogenetic tree, Regularization, Variable selection
1. Introduction
A microbiome is a collection of micro-organisms (mostly bacteria) in a certain environment such as the human gut. The development of next generation sequencing methods such as 454 pyrosequencing and Solexa sequencing enables researchers to study the microbiome composition by directly sequencing the environmental DNAs. A commonly used sequencing strategy is to sequence a variable region of the 16S ribosomal RNA (rRNA) gene in the bacterial genome, and this variable region can be used for taxonomic classification by comparing it with existing 16S rRNA gene databases. Such 16S data can eventually produce a taxonomic profile for each sample, that is, the abundance for all the identified taxa. However, bacterial taxa are not independent of one another and are related evolutionarily by a phylogenetic tree. Taxa that are phylogenetically close usually behave similarly or have similar biological functions. Such phylogenetic tree information has been effectively utilized in the commonly used UniFrac distance between two microbiome samples (Lozupone and Knight, 2005). In an attempt to visualize the human gut microbiomes from different samples, Purdom (2011) proposed a phylogenetic tree-based principle component analysis (PCA) on the 16S data set. This phylogenetic PCA was shown to separate the environmental samples in a biologically more sensible way than the standard PCA.
In this paper, we consider another commonly used dimension-reduction method, canonical correlation analysis (CCA), that can be used to relate the bacteria taxa with environmental covariates when the number of covariates is large. Our motivating example is a data set generated from a human gut microbiome study at the University of Pennsylvania, where we aim to associate nutrient intake to the bacterial composition in the human gut (see Section6 for details). We have both the nutrient intake data and the bacterial abundance data measured on 99 individuals and are interested in selecting the bacterial taxa and nutrients that are most closely correlated. CCA aims to identify the linear combinations of two sets of variables that are maximally correlated with each other and provides an important tool to summarize the overall dependency structures between the two sets of variables. It has been applied to linking two sets of high-dimensional genomic data measured on the same set of samples(Parkhomenko and others, 2009).
The standard CCA, however, does not perform variable selection and hence usually lacks biological interpretability, especially when the dimension of variables is high. When the number of variables exceeds the number of observations, CCA cannot be applied directly due to singularity of the covariance matrix. To overcome these two major limitations, various types of sparse CCA (sCCA) have been proposed and developed and applied to genomic data analysis (Parkhomenko and others, 2009; Witten and others, 2009). In sCCA, a sparsity penalty function such as the l1 penalty is often imposed on the linear coefficients in order to explain the correlation between two data sets using the least number of variables. The sparsity constraint in sCCA not only makes the computation feasible but also increases the biological interpretability of the selected variables.
Available approaches to sCCA do not, however, exploit the prior structure information among the variables. In many applications, there exists some structure among the set of variables in the CCA analysis. These structures can be simple group structures such as gene sets or graphical structures such as gene networks in genomic studies. By including this prior structure information of the data, one can gain better biological insight from the analysis. This has been clearly demonstrated in sparse regression analysis(Li and Li, 2008).
In this paper, we utilize the phylogenetic tree structure of the data from human microbiome studies in CCA analysis. The phylogenetic information from the bacterial taxa could guide us to select relevant taxa in the context of CCA by inducing a tendency to select closely related taxa together, since these taxa are very likely to be associated with the covariates in a similar fashion. We propose to develop a structure-constrained sCCA (ssCCA), where we impose an additional structure-constrained penalty function based on the phylogenetic tree structure. The ssCCA extends the sCCA formulation of Witten and others (2009) by imposing a smoothness penalty for the loading coefficients of the taxa based on their closeness on the phylogenetic tree. We also develop an efficient coordinate descent algorithm to implement ssCCA. Our simulations that mimic real microbiome data demonstrate that ssCCA can result in much better performance in selecting bacteria that are associated with other environmental variables. Our analysis of the microbiome and nutrient data has concluded that fat-related nutrients are closely related to human gut microbiome composition, a conclusion that agrees with a previous analysis of the data set(Wu and others, 2011).
The rest of the paper is organized as follows. The data structure from 16S microbiome and the concept of phylogenetic tree-structured data are presented in Section2. A brief review of CCA and the formulation of ssCCA is given in Section3. Details of the coordinate descent algorithm are presented in Section4. Results from simulation studies to evaluate our method are given in Section5. An application to a real human microbiome study to associate nutrient intake with bacterial abundance is presented in Section6. Finally, a brief discussion of the methods and results is presented in Section7.
2. 16S microbiome data processing, phylogenetic tree and Laplacian matrix
Typical gut microbiome study involves the collection of fecal samples, isolating all bacterial DNA and then sequencing it using next generation sequencing machines such as the 454 genome sequencer. Since each bacterial cell is assumed to have the same number of copies of this gene, the basic step of a 16S microbiome study is to count different versions of the sequences, and then to identify to which bacteria the versions correspond; in this way, the types and abundance of different bacteria in a sample are determined. After preprocessing of the raw sequences, the 16S sequences are either mapped to an existing phylogenetic tree in a taxonomy-dependent way (Matsen and others, 2010) or clustered into operational taxonomic units (OTUs) at a certain similarity level in a taxonomic-independent way (Caporaso and others, 2010). At the 97% similarity level, these OTUs are used to approximate the biological species.
The method proposed in this paper is mainly applied to OTU-based 16S data where each of the N 16S sequences belongs to one of p OTUs. Each OTU is characterized by a representative DNA sequence and can be assigned a taxonomic lineage by comparison to a known bacterial 16S rRNA database (Wang and others, 2007). Most species-level OTUs are in extremely low abundance with a large proportion of OTUs being simply singletons, possibly due to a sequencing error. We can further aggregate the OTUs from the same genus to form genus-level OTUs and perform analysis at the genus level, which is more robust to sequencing error and can reduce the number of variables significantly. A distance between any two OTUs can be computed using the OTU representative sequences based on an evolution model such as the Jukes–Cantor, Kimura, and Felsenstein model, and a phylogenetic tree for the OTUs can be built based on these distances(Felsenstein, 2003).
Let x=(x1,x2,…,xp)T represent the vector of the relative abundance of p OTUs obtained from the 16S sequencing, where each OTU is a leaf node of a phylogenetic tree of all the OTUs. We first construct an adjacency matrix using a pairwise distance matrix between any two OTUs. With the given phylogenetic tree, we can use the patristic distance, which is the sum of the branch lengths linking the two OTUs. The distance is usually normalized to the scale of [0,1], with 0 for identity and 1 for complete difference. Denote by djk the distance between OTU j and OTU k. We then form a p×p adjacency matrix A with the diagonal elements of 1 and the jkth element between OTUs j and k defined as ajk=ϕ(djk), where ϕ is some decreasing function. Several possible functions are 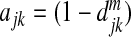 ,
, 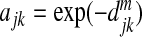 , or
, or 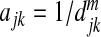 , where the power m>0 determines how much weight one puts on closely related OTUs. In this paper, we define the adjacent matrix as
, where the power m>0 determines how much weight one puts on closely related OTUs. In this paper, we define the adjacent matrix as
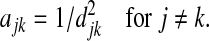 |
(2.1) |
By taking the square of djk, large edge weight is given to closely related OTUs and meanwhile, the edge weights for distantly related OTUs are made small. As shown later, this adjacent matrix is only used in the definition of the smoothness penalty. The choice of the adjacent matrix definition should not greatly affect the variable selection results.
The phylogenetic tree is a special case of general undirected graphs, and the adjacency matrix is related to the Laplacian matrix associated with the graph. For a given adjacency matrix A, define D=diag(d1,d2,…,dp), where 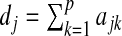 . The associated Laplacian matrix is defined as L=D−A (Chung, 1997). The Laplacian matrix L is associated with a labeled weighted graph
. The associated Laplacian matrix is defined as L=D−A (Chung, 1997). The Laplacian matrix L is associated with a labeled weighted graph 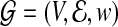 with vertex set V =1,…,p and edge set
with vertex set V =1,…,p and edge set 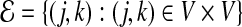 . Here ajk is the weight of edge (j,k) and dj is the degree of vertex j. For a given vector u, it is easy to show that
. Here ajk is the weight of edge (j,k) and dj is the degree of vertex j. For a given vector u, it is easy to show that
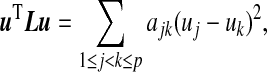 |
(2.2) |
which measures the smoothness of the vector u with respect to the labeled weighted graph 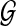 . Based on this interpretation, Li and Li (2008) proposed a smoothness penalty of the form uTLu in high-dimensional regression settings. The structure constraint displays a local smoothing effect by encouraging the variables that are linked on the prior graphical structure to have similar coefficients. In the next section, we extend sCCA to include this smoothness penalty to further encourage some smoothness of the coefficients in linear projections.
. Based on this interpretation, Li and Li (2008) proposed a smoothness penalty of the form uTLu in high-dimensional regression settings. The structure constraint displays a local smoothing effect by encouraging the variables that are linked on the prior graphical structure to have similar coefficients. In the next section, we extend sCCA to include this smoothness penalty to further encourage some smoothness of the coefficients in linear projections.
3. Structure-constrained sparse canonical correlation analysis
We consider the CCA between two random vectors x=(x1,x2,…,xp)T and y=(y1,y2,…,yq)T, where vector x contains an abundance of p OTUs on a given phylogenetic tree and y is the q-dimensional vector of the environmental covariates. Suppose that we have collected n i.i.d. samples of x and y, denoted by X and Y, respectively. Assume both are column-standardized to have mean 0 and variance 1. Let A be the adjacency matrix defined in the previous section based on the phylogenetic tree structure and L be the corresponding Laplacian matrix.
CCA aims to find two projection directions 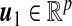 and
and 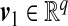 so that
so that
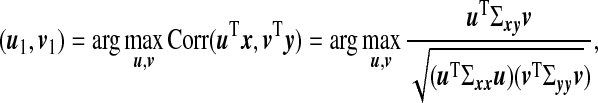 |
where Σxx,Σyy, and Σxy are covariance and cross-covariance matrices. This maximization is equivalent to
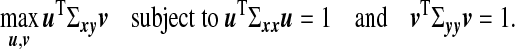 |
(3.1) |
Here u1,v1 are called the first pair of canonical vectors, while the new variables η1=u1Tx,ξ1=v1Ty are called the first pair of canonical variables or latent variables and ρ1=Corr(η1,ξ1) is referred to as the first canonical correlation. When data are available, one estimates u1 and v1 by replacing Σxy,Σxx, and Σyy by the observed sample cross-covariance and covariance matrices XTY, XTX, and YTY, respectively.
When the dimensions p and q are high, regularization is required in order to obtain a unique solution to the optimization problem (3.1). Given the tuning parameters c1>0,c2>0,c3>0, we propose the following ssCCA criterion that extends the sCCA of Witten and others (2009):
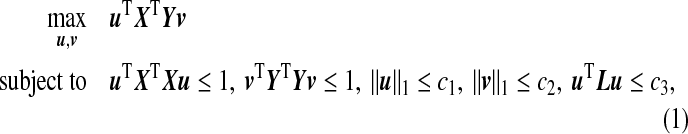 |
(3.2) |
where 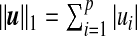 and
and 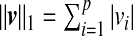 are sparsity l1 penalty functions. Different from the sCCA formulation, we impose another structure constraint on the coefficient vector u through the quadratic Laplacian quantity defined in (2.2), uTLu≤c3. This constraint encourages smoothness of the estimated coefficients of the OTUs that are closely related on the phylogenetic tree. A smaller value of the tuning parameter c3 results in a smoother estimate of the coefficient vector u over the phylogenetic tree.
are sparsity l1 penalty functions. Different from the sCCA formulation, we impose another structure constraint on the coefficient vector u through the quadratic Laplacian quantity defined in (2.2), uTLu≤c3. This constraint encourages smoothness of the estimated coefficients of the OTUs that are closely related on the phylogenetic tree. A smaller value of the tuning parameter c3 results in a smoother estimate of the coefficient vector u over the phylogenetic tree.
It has been shown that in other high-dimensional problems, treating the covariance matrix as diagonal can yield good results (Tibshirani and others, 2003; Witten and others, 2009). For this reason, rather than using (3.2) as our ssCCA criterion, following the same strategy adopted by many of the existing sCCA algorithms (Parkhomenko and others, 2009; Witten and others, 2009), we substitute in the identity matrix I for XTX and YTY in the ssCCA formulation (3.2), which gives the ssCCA formulation that we use in this paper:
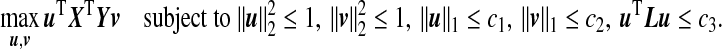 |
(3.3) |
4. Coordinate descent algorithm for the ssCCA
4.1. Algorithm to obtain the first ssCCA factor
To facilitate computation, we write constraints on u in Lagrangian form and the ssCCA criterion (3.3) becomes:
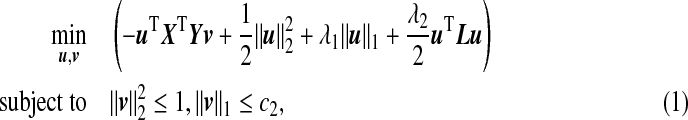 |
(4.1) |
where λ1≥0,λ2≥0, and c2>0 are tuning parameters. Note that when λ2=0, ssCCA is reduced to sCCA. Since the Laplacian penalty function (λ2/2)uTLu is convex in u, the criterion (4.1) remains biconvex in u and v, such that we can still use an iterative method to solve this optimization problem.
Algorithm to obtain the first ssCCA factor
Initialize v as the first right singular vector with unity l2 norm from the singular value decomposition of XTY.
- Iterate until convergence:
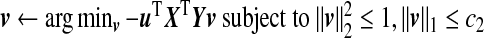 , which is given by
, which is given by
where S(.,.) is the soft-thresholding function, i.e.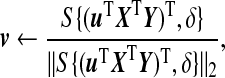
and δ=0 if this results in ||v||1≤c2; otherwise, δ is chosen so that ||v||1=c2. The choice of δ can be determined using a binary search (Witten and others, 2009).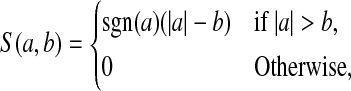
Let L=UΓUT and S=UΓ1/2. Then step 2(a) can be converted into a simple Lasso problem as in Li and Li (2008):
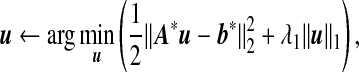 |
where
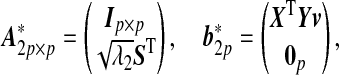 |
Ip×p is a p×p identity matrix, and 0p is a p-dimensional vector of 0’s. Note that no intercept is included in this Lasso problem and a coordinate descent algorithm can be implemented to obtain the solution at a given λ1(Friedman and others, 2007).
Though the objective function is biconvex, i.e. is convex in either u or v, it is not convex in (uT,vT)T, so the coordinate descent algorithm does not necessarily converge to the global optimum; however, by using the first right singular vector of the covariance matrix as the initial starting point, it does converge to a stationary point (Tseng and Yun, 2009) and interpretable solutions.
4.2. Choosing tuning parameters
The tuning parameters λ=(λ1,λ2,c2) control the model complexity and have to be tuned. We use an M-fold two-stage cross-validation (CV) method to choose λ. First, we divide all the samples into M disjoint subgroups, also known as folds, and denote the index of samples in the mth fold by Im for m=1,…,M. The M-fold cross-validated function is defined as
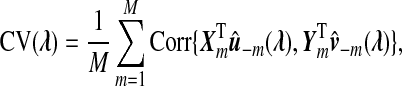 |
(4.2) |
where Corr(.,.) is the correlation function and 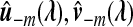 is the estimate of u,v based on the samples
is the estimate of u,v based on the samples 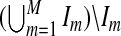 with λ as the tuning parameter. It is well known that CV can perform poorly in tuning parameter selection for problems involving l1 penalties due to biases in parameter estimates (Meinshausen and Bühlmann, 2006). To reduce the shrinkage problem, we reestimate the non-zero coefficients without penalization by performing singular value decomposition on the training data set excluding the variables with zero coefficients in the penalized procedure. Specifically, for a given tuning parameter λ, we recalculate the loading coefficients using the variables that are selected by ssCCA and use these coefficients in the CV score (4.2). This avoids bias of the estimates due to penalization. We then choose λ*=argmaxλCV(λ) as the best tuning parameters. From our simulations, we observe that the two-stage CV procedure almost always performs better than standard CV without reestimating the parameters.
with λ as the tuning parameter. It is well known that CV can perform poorly in tuning parameter selection for problems involving l1 penalties due to biases in parameter estimates (Meinshausen and Bühlmann, 2006). To reduce the shrinkage problem, we reestimate the non-zero coefficients without penalization by performing singular value decomposition on the training data set excluding the variables with zero coefficients in the penalized procedure. Specifically, for a given tuning parameter λ, we recalculate the loading coefficients using the variables that are selected by ssCCA and use these coefficients in the CV score (4.2). This avoids bias of the estimates due to penalization. We then choose λ*=argmaxλCV(λ) as the best tuning parameters. From our simulations, we observe that the two-stage CV procedure almost always performs better than standard CV without reestimating the parameters.
5. Simulation studies
We present Monte Carlo simulations to evaluate ssCCA in identifying the relevant variables that explain the correlation between two multivariate vectors. The solution of sCCA is obtained by setting λ2=0 in ssCCA. The simulations are carried out to mimic an association study between nutrient intake and genus-level OTU abundance that is presented in Section6. Since the phylogenetic tree implies distances between the OTUs, we simulate the distance matrix directly. Specifically, since OTUs are often clustered on the phylogenetic tree, we generate random OTU clusters of size 1–15, where the OTU cluster members are sequentially indexed. If two OTUs are from the same cluster (e.g. from the same taxonomic rank family), their distance is drawn from a uniform distribution on (0.1,0.2); if two OTUs are from different clusters, then their distance is drawn from a uniform distribution on (0.2,1). We then construct the adjacency matrix A using the method (2.1) based on the distances.
5.1. Simulation based on a latent variable model
We use a latent variable model to generate the data matrices X and Y where the dependency between these two sets of variables is induced by a latent random variable ζ and the variances in x,y can be explained in part by ζ. We assume x=ζwx+ϵx and y=ζwy+ϵy, where 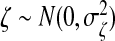 , ϵx,ϵy are random noise vectors that follow
, ϵx,ϵy are random noise vectors that follow 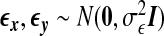 , and
, and 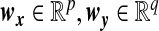 are column vectors of preset weights. The σϵ/σζ ratio controls the overall association strength between x and y, with a small value indicating strong association. The coefficients wx and wy control the relative contributions of individual variables to the overall association. We assume that only the first px=10 elements of wx and the first qy=10 elements of wy are non-zero and take the values of (0.1,…,0.1) and (0.08,0.084,0.089,…,0.12), respectively. In addition, we let wi and wj be identical or similar if xi and xj are from the same cluster of the phylogenetic leaf nodes. We consider the scenarios where we have one relevant cluster of size 10, two relevant clusters of size 5 and 5, and three relevant clusters of size 3, 4, and 4. The highest correlation between linear combinations of x and y is given by Parkhomenko and others (2009):
are column vectors of preset weights. The σϵ/σζ ratio controls the overall association strength between x and y, with a small value indicating strong association. The coefficients wx and wy control the relative contributions of individual variables to the overall association. We assume that only the first px=10 elements of wx and the first qy=10 elements of wy are non-zero and take the values of (0.1,…,0.1) and (0.08,0.084,0.089,…,0.12), respectively. In addition, we let wi and wj be identical or similar if xi and xj are from the same cluster of the phylogenetic leaf nodes. We consider the scenarios where we have one relevant cluster of size 10, two relevant clusters of size 5 and 5, and three relevant clusters of size 3, 4, and 4. The highest correlation between linear combinations of x and y is given by Parkhomenko and others (2009):
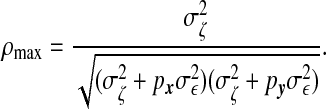 |
(5.1) |
We fix 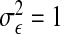 and vary
and vary 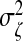 to control the strength of the canonical correlation. When σζ=5, ρmax=0.7.
to control the strength of the canonical correlation. When σζ=5, ρmax=0.7.
5.2. Evaluation of the selection performance
We evaluate the performance of our methods in terms of selecting the relevant variables that lead to correlation between random vectors x and y by considering models with various combinations of the parameters. For each simulated data set, we use 5-fold two-stage CV to select the tuning parameter values and then compute the true positive rate (TPR), false positive rate (FPR), and Matthew’s correlation coefficient (MCC) to measure the selection performance for both x and y. These three measures are defined as
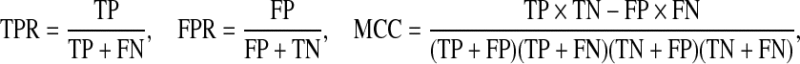 |
where TP, FP, TN, and FN are true positives, false positives, true negatives, and false negatives, respectively. For each model, we generate the observed data set X and Y 100 times and summarize the TPR, FPR, and MCC as averages over 100 runs. Results from 10-fold two-stage CV are very similar and are omitted here.
We also compare the performance of different methods using the receiver operating characteristic (ROC) curve (FPR against TPR) for identifying the relevant taxa OTUs by varying the tuning parameters. Specifically, the three tuning parameters are searched over a 10×10×10 grid for a total of 1000 tuning parameter combinations. For each combination, we obtain the FPR and the TPR, which represents one point in the ROC plot. The ROC curve is then obtained by joining these points for each run. We then average the ROC curves over 100 runs to produce an average ROC curve.
5.3. Comparison of ssCCA and sCCA under one latent variable model
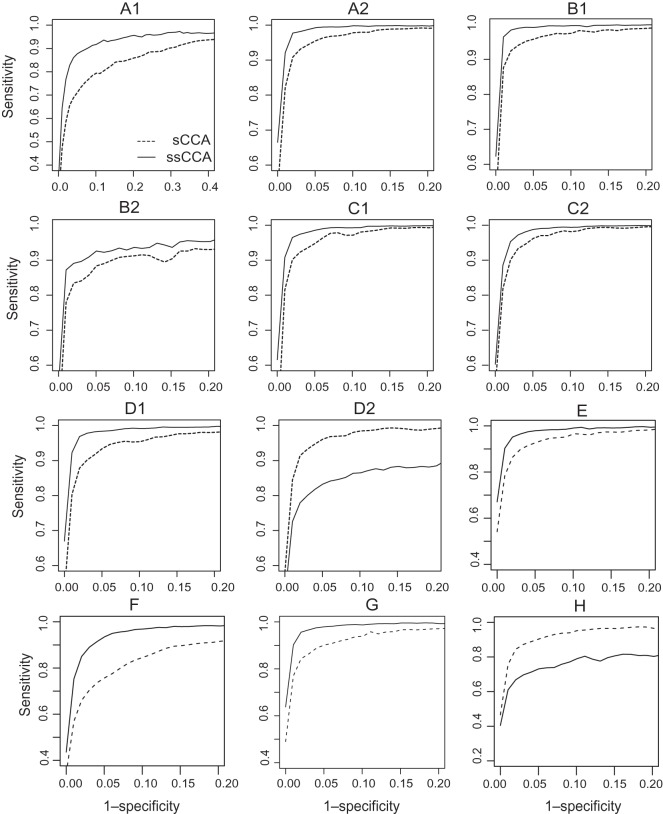
We consider models with various combinations of the parameters (labeled A1–D2), including the number of relevant OTU clusters, the signal strength as measured by 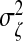 and the dimensions p and q and present the results in Table1 and Figure1. We observe that the advantage of ssCCA over sCCA is more obvious under weak association (Model A1). As the signal becomes stronger, the performance of sCCA becomes closer to ssCCA (Model A2). This agrees with our intuition: the advantage of ssCCA lies in borrowing information from closely related OTUs and, when the association is weak, pooling information across closely related OTUs can improve the OTU selection. Another interesting observation is that better selection of OTUs can lead to better selection of nutrients, which is best shown in the weak association case by obtaining a higher MCC. We also observe that as the dimension increases, both ssCCA and sCCA become less efficient in selecting relevant OTUs and nutrients (Models B1 and B2). However, ssCCA performs consistently better than sCCA in all dimensions considered. Finally, as the cluster size decreases, we do not see a significant deterioration of the selection performance of ssCCA (Models C1 and C2). ssCCA still performs better than sCCA. As long as the cluster contains more than one OTU, using structure information always improves variable selection.
and the dimensions p and q and present the results in Table1 and Figure1. We observe that the advantage of ssCCA over sCCA is more obvious under weak association (Model A1). As the signal becomes stronger, the performance of sCCA becomes closer to ssCCA (Model A2). This agrees with our intuition: the advantage of ssCCA lies in borrowing information from closely related OTUs and, when the association is weak, pooling information across closely related OTUs can improve the OTU selection. Another interesting observation is that better selection of OTUs can lead to better selection of nutrients, which is best shown in the weak association case by obtaining a higher MCC. We also observe that as the dimension increases, both ssCCA and sCCA become less efficient in selecting relevant OTUs and nutrients (Models B1 and B2). However, ssCCA performs consistently better than sCCA in all dimensions considered. Finally, as the cluster size decreases, we do not see a significant deterioration of the selection performance of ssCCA (Models C1 and C2). ssCCA still performs better than sCCA. As long as the cluster contains more than one OTU, using structure information always improves variable selection.
Table 1.
Simulation results to evaluate ssCCA under models of different association signals, dimension sizes, cluster sizes, model misspecification, and complexity
| Selection of x variables |
Selection of y variables |
|||||
|---|---|---|---|---|---|---|
| Method | TPR-x | FPR-x | MCC-x | TPR-y | FPR-y | MCC-y |
| A1: one cluster, σζ=4,p,q=100 | ||||||
| ssCCA | 0.91 (0.20) | 0.07 (0.10) | 0.76 (0.22) | 0.78 (0.22) | 0.12 (0.12) | 0.58 (0.18) |
| sCCA | 0.70 (0.31) | 0.09 (0.12) | 0.56 (0.22) | 0.75 (0.24) | 0.12 (0.12) | 0.54 (0.21) |
| A2: one cluster, σζ=5,p,q=100 | ||||||
| ssCCA | 0.96 (0.10) | 0.03 (0.08) | 0.89 (0.16) | 0.87 (0.17) | 0.05 (0.09) | 0.78 (0.16) |
| sCCA | 0.89 (0.17) | 0.05 (0.08) | 0.79 (0.17) | 0.87 (0.16) | 0.05 (0.09) | 0.77 (0.17) |
| B1: one cluster, σζ=5,p,q=200 | ||||||
| ssCCA | 0.98 (0.08) | 0.05 (0.11) | 0.87 (0.19) | 0.87 (0.16) | 0.07 (0.11) | 0.75 (0.18) |
| sCCA | 0.89 (0.17) | 0.09 (0.15) | 0.74 (0.22) | 0.87 (0.16) | 0.08 (0.11) | 0.72 (0.20) |
| B2: one cluster, σζ=5,p,q=400 | ||||||
| ssCCA | 0.89 (0.30) | 0.06 (0.11) | 0.74 (0.33) | 0.81 (0.28) | 0.12 (0.13) | 0.60 (0.30) |
| sCCA | 0.77 (0.32) | 0.09 (0.23) | 0.66 (0.32) | 0.78 (0.31) | 0.11 (0.12) | 0.57 (0.32) |
| C1: two clusters, σζ=5,p,q=100 | ||||||
| ssCCA | 0.93 (0.14) | 0.03 (0.07) | 0.88 (0.15) | 0.83 (0.16) | 0.05 (0.09) | 0.76 (0.16) |
| sCCA | 0.87 (0.16) | 0.05 (0.08) | 0.78 (0.16) | 0.85 (0.16) | 0.06 (0.10) | 0.76 (0.17) |
| C2: three clusters, σζ=5,p,q=100 | ||||||
| ssCCA | 0.94 (0.11) | 0.03 (0.07) | 0.88 (0.15) | 0.88 (0.15) | 0.07 (0.11) | 0.75 (0.18) |
| sCCA | 0.89 (0.16) | 0.05 (0.10) | 0.80 (0.18) | 0.88 (0.16) | 0.07 (0.10) | 0.76 (0.18) |
| D1: one cluster, σζ=5,p,q=100, variable coefficients of the same signs | ||||||
| ssCCA | 0.95 (0.11) | 0.02 (0.05) | 0.90 (0.13) | 0.86 (0.19) | 0.06 (0.10) | 0.76 (0.17) |
| sCCA | 0.87 (0.15) | 0.04 (0.08) | 0.79 (0.15) | 0.88 (0.16) | 0.07 (0.10) | 0.75 (0.18) |
| D2: one cluster, σζ=5,p,q=100, variable coefficient of opposite signs | ||||||
| ssCCA | 0.89 (0.14) | 0.05 (0.09) | 0.81 (0.17) | 0.89 (0.15) | 0.08 (0.11) | 0.75 (0.20) |
| sCCA | 0.90 (0.15) | 0.04 (0.09) | 0.82 (0.17) | 0.90 (0.14) | 0.07 (0.11) | 0.76 (0.19) |
| E: correlated noise, one cluster, σζ=5,p,q=100 | ||||||
| ssCCA | 0.92 (0.18) | 0.04 (0.07) | 0.84 (0.19) | 0.78 (0.21) | 0.05 (0.08) | 0.72 (0.17) |
| sCCA | 0.85 (0.20) | 0.05 (0.10) | 0.77 (0.18) | 0.82 (0.21) | 0.06 (0.10) | 0.73 (0.18) |
| F: count data, one cluster, σζ=5,p,q=100 | ||||||
| ssCCA | 0.92 (0.16) | 0.04 (0.11) | 0.84 (0.17) | 0.72 (0.26) | 0.06 (0.14) | 0.71 (0.20) |
| sCCA | 0.72 (0.22) | 0.09 (0.15) | 0.62 (0.18) | 0.80 (0.24) | 0.08 (0.16) | 0.75 (0.23) |
| G: two directions, one cluster, σζ=5,p,q=100 | ||||||
| ssCCA | 0.95 (0.13) | 0.03 (0.08) | 0.87 (0.17) | 0.85 (0.17) | 0.05 (0.09) | 0.76 (0.16) |
| sCCA | 0.85 (0.19) | 0.07 (0.10) | 0.73 (0.17) | 0.82 (0.19) | 0.06 (0.09) | 0.72 (0.16) |
| H: two directions, two clusters, model misspecification, σζ=5,p,q=100 | ||||||
| ssCCA | 0.83 (0.20) | 0.05 (0.09) | 0.74 (0.19) | 0.88 (0.19) | 0.11 (0.13) | 0.67 (0.20) |
| sCCA | 0.87 (0.18) | 0.06 (0.10) | 0.76 (0.18) | 0.89 (0.17) | 0.10 (0.13) | 0.69 (0.20) |
Five-fold two-stage CV is used to select the tuning parameters. As a comparison, results from sCCA are also presented. Each column represents a measure of selection performance for OTU (x) or nutrient (y). TPR, true positive rate; FPR, false positive rate; MCC, Matthew’s correlation coefficient. The results are averaged over 100 replications with SD indicated in the parenthesis.
Fig. 1.
ROC curves for selecting the OTUs using the ssCCA and sCCA for Models A1–H. The corresponding model parameters are given in Table1.
Since the smoothness penalty encourages the variables that are close on the phylogenetic tree to have similar linear projection coefficients, we evaluate the sensitivity of ssCCA when this assumption does not hold. We investigate the performance of ssCCA when data contradict with our smoothness assumption. We consider the model where the first 10 elements of wx have different coefficients but with the same signs, and take values that are equally spaced on [0.08,0.12] (Model D1). The performance of ssCCA is still much better than sCCA. Model D2 considers the scenario when the first five and the second five elements of wx are 0.1s and −0.1s, respectively, where the coefficients are different and have different signs. This scenario violates our model assumption that closely linked OTUs have similar coefficients. The structure-constrained penalty now has an adverse effect. This is clearly seen in the ROC plot (Figure1(D2)). However, when the CV procedure is applied to select the tuning parameters and the corresponding OTUs and nutrients, the performance of ssCCA and sCCA is very similar (Table1). This is because if the prior structure information is not useful, CV procedure tends to select λ2=0, which reduces ssCCA to sCCA. Therefore, the selection performance of ssCCA should be at least as good as sCCA, but ssCCA performs better when the prior assumption holds.
5.4. Comparison of ssCCA and sCCA under complex models
We compare the performance of ssCCA and sCCA under several complex models and also present the results in Table1 and Figure1. Under Model E, we consider the scenario when the noises are correlated with correlation 0.4|i−j| for ϵiand ϵj for both x and y, where the OTU cluster members have sequential index numbers. The performances of ssCCA and sCCA are both slightly worse when compared with Model A2 when the noises are independent; ssCCA still outperforms sCCA.
We then consider Model F where we simulate count data with zeros. Specifically, we first generate the data matrix X as previously. We then convert it into a proportion matrix P and generate the counts based on P. For the jth column Xj, we first map the column values into the range of 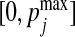 by a linear transformation
by a linear transformation 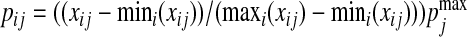 , where
, where 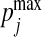 is sampled from [0.01,0.1], so the maximum OTU abundance can vary by 10-fold. Rows of P are further scaled to sum up to 1. Given the OTU proportions for each sample, we generate counts using a Dirichlet-multinomial model with a total count of 1000 and an overdispersion of 0.01. Since we introduce extra variation by simulating counts, we increase the first 10 components of wx to 0.4 to achieve a moderate association (ρ1∼0.7). Under this parameter setting, the data matrix contains about 20% 0’s. To apply ssCCA and sCCA, we convert the simulated count matrix into a proportion matrix. Table1(F) and Figure1(F) again show that ssCCA outperforms sCCA in selecting the relevant variables.
is sampled from [0.01,0.1], so the maximum OTU abundance can vary by 10-fold. Rows of P are further scaled to sum up to 1. Given the OTU proportions for each sample, we generate counts using a Dirichlet-multinomial model with a total count of 1000 and an overdispersion of 0.01. Since we introduce extra variation by simulating counts, we increase the first 10 components of wx to 0.4 to achieve a moderate association (ρ1∼0.7). Under this parameter setting, the data matrix contains about 20% 0’s. To apply ssCCA and sCCA, we convert the simulated count matrix into a proportion matrix. Table1(F) and Figure1(F) again show that ssCCA outperforms sCCA in selecting the relevant variables.
Finally, we consider two models where two orthogonal directions induce the correlation between two sets of random vectors. We assume 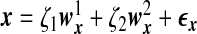 and
and 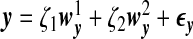 , where under Model G, the two directions are given by
, where under Model G, the two directions are given by
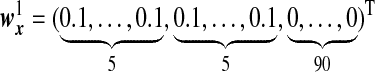 |
and
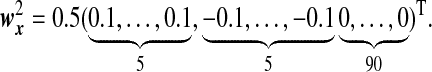 |
We assume that 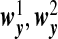 are the same as
are the same as 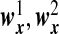 , and the OTUs from the same cluster have the same coefficients on the first direction. Under Model H, we consider model misspecification where the two directions are given by
, and the OTUs from the same cluster have the same coefficients on the first direction. Under Model H, we consider model misspecification where the two directions are given by
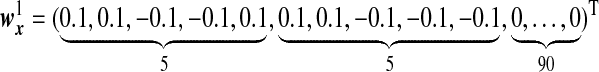 |
and
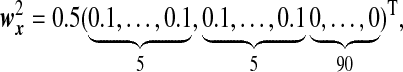 |
and 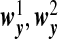 are the same as
are the same as 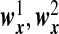 . OTUs from the same cluster have coefficients of different signs on the first direction. Under Model H, ssCCA has higher true positive and lower false positive rates and higher area under the ROC curve (Table1(G) and Figure1(G)). Under the model misspecification (Model H), the performances of ssCCA and sCCA are comparable.
. OTUs from the same cluster have coefficients of different signs on the first direction. Under Model H, ssCCA has higher true positive and lower false positive rates and higher area under the ROC curve (Table1(G) and Figure1(G)). Under the model misspecification (Model H), the performances of ssCCA and sCCA are comparable.
6. Application to gut microbiome data analysis
We apply ssCCA to a microbiome study on association between the nutrient intake and bacterial abundance in the human gut conducted at the University of Pennsylvania. The human gut is inhabited by trillions of bacterial cells, and some bacterial species have a profound influence on human health and disease. One goal of the study is to investigate the relationship between diet and microbiome composition and to identify a short list of potential nutrients and their associated bacteria in the human gut. For this study, both gut microbiome 16S data and nutrient intake data were available for 99 healthy subjects. Fecal samples were obtained from these 99 subjects and bacterial DNA was extracted using a standard protocol. After multiplexed 454 pyrosequencing, about 900 000 high quality, partial (∼370 bp) 16S rRNA gene sequences were generated. These sequences were analyzed using the Qiime pipeline (Caporaso and others, 2010), where the sequences were clustered at 97% sequence identity into OTUs and assigned a taxonomic identity by comparing to the Ribosomal Database Project reference 16S rRNA database (Wang and others, 2007). We consolidated these species-level OTUs into 119 genera (genus-level OTUs) and used the representative sequence from the most abundant species-level OTU as the genus level representative sequence for distance calculation and for construction of the phylogenetic tree. In our analysis, we further excluded the uncommon genera that occurred in less than 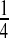 of the samples; so we only considered p=40 relatively common genera (Figure2). These 99 subjects also completed a carefully designed food frequency questionnaire (FFQ). Based on the FFQ, the daily intake for q=214 nutrients were calculated for each subject by nutritionists. Because nutrient intake is clearly dependent on the overall energy consumption, we regressed the nutrient intake on the total energy consumption and took residuals as the normalized nutrient intake. Our final data set can be summarized as the OTU abundance matrix X99×40 and the nutrient intake matrix Y99×214. Since the sampling depths are very different for different samples, we normalize the counts into proportions and standardize the columns to have mean 0 and variance1.
of the samples; so we only considered p=40 relatively common genera (Figure2). These 99 subjects also completed a carefully designed food frequency questionnaire (FFQ). Based on the FFQ, the daily intake for q=214 nutrients were calculated for each subject by nutritionists. Because nutrient intake is clearly dependent on the overall energy consumption, we regressed the nutrient intake on the total energy consumption and took residuals as the normalized nutrient intake. Our final data set can be summarized as the OTU abundance matrix X99×40 and the nutrient intake matrix Y99×214. Since the sampling depths are very different for different samples, we normalize the counts into proportions and standardize the columns to have mean 0 and variance1.
Fig. 2.
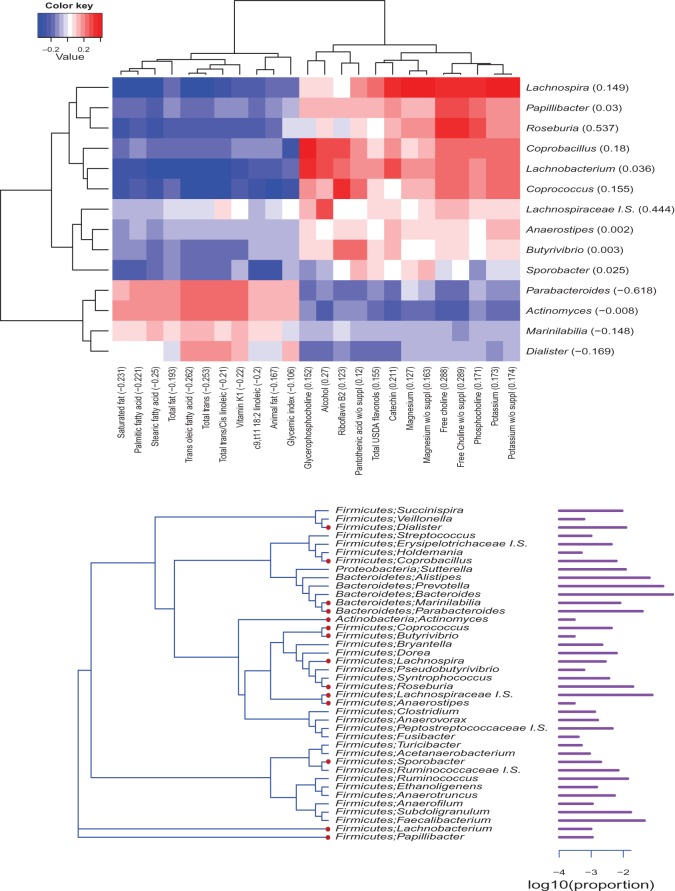
Analysis of gut microbiome data. Top: heatmap that shows the correlations between the selected genera and nutrients. The number in parenthesis of each variable is the estimated loading coefficient. Red and blue colors indicate positive and negative correlations, respectively. Bottom: Phylogenetic tree of the 40 genera used in the analysis. The genera selected by ssCCA are marked with red circles. The bars on the right side indicate the average relative abundances of these genera on log 10 scale.
The goal of our analysis is to investigate the overall association between gut bacteria abundance and nutrient intake. We used the method presented in (2.1) to construct the adjacency matrix A, and the distances between any two OTUs were calculated using the “K80” model (R “ape” package, “dist.dna” function). Five-fold two-stage CV was performed to search the optimal tuning parameters on a grid of 20×20×20, and the range of the tuning parameters was set to explore all possible models: from the most dense to the most sparse model. We applied ssCCA to the data set and identified 24 nutrients and 14 genera whose linear combinations gave a cross-validated correlation of 0.42 between gut bacterial abundance and nutrients. Figure2 shows the heatmap of pairwise correlations between these selected nutrients and OTUs, where the estimated loading coefficients are given in parentheses. The signs of the estimated loading coefficients correspond very well to the pairwise correlations. The nutrients related to fats are clustered together, while the other nutrients show association in the opposite direction.
The selected microbiome-associated nutrients are biologically interpretable. More than half of the selected nutrients are related to fat. It has been experimentally shown that fats can change the gut microbiome composition independent of obesity in a mouse study (Hildebrandt and others, 2009). There are also four selected nutrients related to choline, and it was found by a recent human microbiome study that the composition of the gastrointestinal microbiome changed with the choline levels of diets (Spencer and others, 2011). The selected nutrients are also consistent with the candidate nutrients we identified using a distance-based testing procedure (Wu and others, 2011). This procedure utilized the overall UniFrac distances (Lozupone and Knight, 2005) between microbiomes of any two subjects computed using both the OTU abundances and the phylogenetic relationship among them. Twenty out of 24 nutrients selected by ssCCA were in the nutrients selected by the distance-based individual testing method at the false discovery rate of 25%.
The pattern of selected OTUs is also interesting. The selected OTUs are marked with red circles in the phylogenetic tree of Figure2. We see that the closely related OTUs tend to be selected together; for example, the genus Parabacteroides and Marinilabilia, Butyrivibrio and Coprococcus, and Anaerostipes and Lachnospiraceae Incertae Sedis are all close relatives on the tree. ssCCA tends to select closely related OTUs together by making the coefficients of neighbors similar through imposing a phylogenetic tree-constrained smoothness penalty. This feature of ssCCA can also be viewed as borrowing information from nearby OTUs; that is, if several neighbors all exhibit similar weak association, ssCCA amplifies the signal strength and selects them together. On the other hand, if some OTU exhibits low-level association but all its neighbors show the opposite evidence, ssCCA will not select that OTU.
By a comparison, an sCCA that does not account for the phylogenetic relationship among the OTUs selects only one OTU, the FirmucuteLachnospira, which was also selected by ssCCA, but a total of 122 nutrients. The interpretation of the result is not as clear as that from ssCCA. The resulting combinations gave a cross-validated correlation of 0.39, smaller than that obtained from ssCCA.
7. Conclusion and discussion
We have extended the sCCA to incorporate the graphical structure among the variables in CCA. When the number of variables exceeds the number of samples, using prior structure information to guide variable selection is important. The prior knowledge could lead to a solution that is biologically more interpretable. The structured sCCA utilizes the phylogenetic information to select the bacterial OTUs that are associated with covariates. The power of the ssCCA method has been demonstrated in the simulation studies, and its performance is unanimously better than sCCA in all the simulated scenarios when there are structures in the data. Even when the prior information is not completely accurate, our method still performs comparably to sCCA due to selection of the tuning parameter by CV.
One limitation of the ssCCA formulation is that it assumes a linear relationship among the variables, which may not always hold for OTU compositional/abundance data. Our analysis of the gut microbiome data did not indicate too much deviation from the linearity between OTU abundance and nutrient intake. One interesting future research direction is to develop structure-constrained non-linear measures of association and sparse non-linear CCA.
Funding
This research was supported by the National Institutes of Health (CA127334, GM097505, and DK083981).
Acknowledgments
We thank two reviewers for their helpful comments. Conflict of Interest: None declared.
References
- Caporaso J. G., Kuczynski J., Stombaugh J., Bittinger K., Bushman F. D., Costello E. K., Fierer N., Peña A. G., Goodrich J. K., Gordon J. I. Qiime allows analysis of high-throughput community sequencing data. Nature Methods. 2010;7:335–336. doi: 10.1038/nmeth.f.303. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung F. R. K. Spectral Graph Theory. Volume 92. Providence, RI: American Mathematical Society; 1997. [Google Scholar]
- Felsenstein J. Inferring Phylogenies. Sunderland, Massachusetts: Sinauer Associates; 2003. [Google Scholar]
- Friedman J., Hastie T., Hofling H., Tibshirani R. Pathwise coordinate optimization. Annals of Applied Statistics. 2007;1:302–332. [Google Scholar]
- Hildebrandt M. A., Hoffmann C., Sherrill-Mix S. A., Keilbaugh S. A., Hamady M., Chen Y. Y., Knight R., Ahima R. S., Bushman F., Wu G. D. High-fat diet determines the composition of the murine gut microbiome independently of obesity. Gastroenterology. 2009;137:1716–1724. doi: 10.1053/j.gastro.2009.08.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C., Li H. Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics. 2008;24:1175–1182. doi: 10.1093/bioinformatics/btn081. [DOI] [PubMed] [Google Scholar]
- Lozupone C., Knight R. Unifrac: a new phylogenetic method for comparing microbial communities. Applied and Environmental Microbiology. 2005;71:8228. doi: 10.1128/AEM.71.12.8228-8235.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsen F., Kodner R., Armbrust E. V. pplacer: linear time maximum-likelihood and bayesian phylogenetic placement of sequences onto a fixed reference tree. BMC Bioinformatics. 2010;11:538. doi: 10.1186/1471-2105-11-538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N., Bühlmann P. High-dimensional graphs and variable selection with the lasso. Annals of Statistics. 2006;34:1436–1462. [Google Scholar]
- Parkhomenko E., Tritchler D., Beyene J. Sparse canonical correlation analysis with application to genomic data integration. Statistical Applications in Genetics and Molecular Biology. 2009;8:1. doi: 10.2202/1544-6115.1406. [DOI] [PubMed] [Google Scholar]
- Purdom E. Analysis of a data matrix and a graph: metagenomic data and the phylogenetic tree. Annals of Applied Statistics. 2011;5:2326–2358. [Google Scholar]
- Spencer M. D., Hamp T. J., Reid R. W., Fischer L. M., Zeisel S. H., Fodor A. A. Association between composition of the human gastrointestinal microbiome and development of fatty liver with choline deficiency. Gastroenterology. 2011;140:976–986. doi: 10.1053/j.gastro.2010.11.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R., Hastie T., Narasimhan B., Chu G. Class prediction by nearest shrunken centroids, with applications to dna microarrays. Statistical Science. 2003;18:104–117. [Google Scholar]
- Tseng P., Yun S. A coordinate gradient descent method for nonsmooth separable minimization. Mathematical Programming Series B. 2009;117:387–423. [Google Scholar]
- Wang Q., Garrity G. M., Tiedje J. M., Cole J. R. Naive bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Applied and Environmental Microbiology. 2007;73:5261. doi: 10.1128/AEM.00062-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten D. M., Tibshirani R., Hastie T. A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics. 2009;10:515–534. doi: 10.1093/biostatistics/kxp008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu G. D., Chen J., Hoffmann C., Bittinger K., Chen Y. Y., Keilbaugh S. A., Bewtra M., Knights D., Walters W., Knights R. Linking long-term dietary patterns with gut microbial enterotypes. Science. 2011;334:105–108. doi: 10.1126/science.1208344. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]