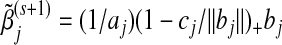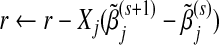Incorporating group correlations in genome-wide association studies using smoothed group Lasso

Abstract

In genome-wide association studies, penalization is an important approach for identifying genetic markers associated with disease. Motivated by the fact that there exists natural grouping structure in single nucleotide polymorphisms and, more importantly, such groups are correlated, we propose a new penalization method for group variable selection which can properly accommodate the correlation between adjacent groups. This method is based on a combination of the group Lasso penalty and a quadratic penalty on the difference of regression coefficients of adjacent groups. The new method is referred to as smoothed group Lasso (SGL). It encourages group sparsity and smoothes regression coefficients for adjacent groups. Canonical correlations are applied to the weights between groups in the quadratic difference penalty. We first derive a GCD algorithm for computing the solution path with linear regression model. The SGL method is further extended to logistic regression for binary response. With the assistance of the majorize–minimization algorithm, the SGL penalized logistic regression turns out to be an iteratively penalized least-square problem. We also suggest conducting principal component analysis to reduce the dimensionality within groups. Simulation studies are used to evaluate the finite sample performance. Comparison with group Lasso shows that SGL is more effective in selecting true positives. Two datasets are analyzed using the SGL method.

1. Introduction

In genome-wide association studies (GWASs), hundreds of thousands of single nucleotide polymorphisms (SNPs) are genotyped for a large number of individuals, typically ranging from several hundred to several thousand. Even though several multi-SNP methods have been developed, many or even the majority of analyses conducted nowadays are still single SNP-based. Single-SNP approaches may not be appropriate when we investigate a complex polygenic trait, since they fail to take into account the accumulated and/or joint effects of multiple genetic markers on the trait. In contrast, multivariate analysis, which describes the joint effects of multiple SNPs in a single model, may be more appropriate.

In GWAS, it is expected that only a subset of SNPs are associated with the response variables. Thus, to analyze SNP data in a multivariate setting, variable selection is needed along with regularized estimation. Penalization methods have been adopted for such a purpose. SNPs are naturally ordered along the genome with respect to their physical positions. They can be highly correlated due to tight linkage and linkage disequilibrium (LD). Therefore, it is sensible to group SNPs based on their physical locations and correlation patterns among them. Commonly adopted penalization approaches, such as Lasso, smoothly clipped absolute deviation (SCAD) , and minimax concave penalization (MCP)(Tibshirani, 1996; Fan and Li, 2001; Zhang, 2010), assume interchangeable effects and cannot effectively accommodate grouping structure. The group versions of Lasso, SCAD, and MCP have been developed to analyze data with grouping structure(Yuan and Lin, 2006; Wang and others, 2007; Huang and others, 2011b).

In addition to the grouping structure, there is also possible strong correlation among adjacent groups. For the first dataset described in Section5, we find that even after grouping SNPs based on their physical locations and correlations, there still exist strong correlations among groups (see supplementary material available at Biostatistics online, Figure3, Appendix). Similar correlation has been noted in the literature. Broët and Richardson (2006) proposed a spatially correlated mixture model to incorporate dependence between genomic sequences. Gottardo and others (2008) proposed a Bayesian hierarchical model to take into account the spatial dependence between probes. Huang and others (2011a) showed that a sparse Laplacian shrinkage estimator has superior estimation and selection properties. This approach can accommodate the correlation among covariates but not the grouping structure.

In this article, our goal is to identify markers associated with response variables, while properly accommodating the high-dimensionality, grouping structure , and correlation between groups of GWAS data. The proposed approach is referred to as smoothed group Lasso (SGL). Its penalty is the sum of the group Lasso penalty and the quadratic penalty on the difference of regression coefficients of adjacent groups. It is expected that the group Lasso penalty promotes sparsity and can select groups of SNPs associated with responses. The second penalty, the quadratic difference penalty, takes into account the natural ordering of groups and accommodates the correlation between adjacent groups. Here, the correlations between groups are measured with canonical correlations. We derive a group coordinate descent (GCD) algorithm for computing the SGL estimator. Beyond developing the new penalty, we also investigate several related practical problems. The first is an extension of the proposed approach to incorporate negative log-likelihood as a loss function for case–control studies. In practical data analysis, high correlations within groups lead to high colinearity among variables, which can have adverse effects on selection and estimation. We propose applying principal component analysis (PCA) within each group to reduce dimensionality and colinearity. In addition, we adopt a modified multi-split method to evaluate the statistical significance of selected groups.

The rest of the article is organized as follows. In Section2, we introduce the SGL penalty and develop a GCD algorithm for quadratic loss functions. Tuning parameter selection is also discussed. In Section3, we investigate several related practical issues, including accommodating case–control data, reducing dimensionality within groups using PCA , and evaluating the significance level. Simulation studies are conducted in Section4. We analyze two case–control studies in Section5. The article concludes with a discussion in Section6.

2. Smoothed group LASSO

2.1. Data and model setting

We first consider quadratic loss functions, which naturally arise from linear regression with continuous responses. Extension to binary trait with logistic regression is discussed in Section3.

Suppose that the data consist of n subjects. Let y_i be the continuous response variable for subject i. The genotype at an SNP is scored as 0, 1, or 2 depending on the number of copies of a reference allele in a subject. The SNPs are divided into J groups, each with size d_j,j=1,…,J, according to their physical locations and correlation patterns. Our approach for grouping SNPs is discussed in Section5. Let x_ij be the d_j×1 covariates vector corresponding to the jth group of SNPs for the ith subject. Denote β_j by the d_j×1 vector of regression coefficients for x_ij. It measures the effects of predictors in the jth group. Let β=(β₁′,…,β_J′)′. Assume the linear regression model where β₀ is the intercept and ϵ_i is the random error. With centered response variables and standardized covariates, we have β₀=0. Consider the quadratic loss function

where Y =(y₁,…,y_n)^′, X_j is an n×d_j matrix corresponding to the jth group, and ||·|| denotes the l₂ norm.

2.2. Penalized estimation

The goals of SGL are 2-fold. The first is to select groups of SNPs associated with response. The second is to smooth regression coefficients between adjacent groups with strong correlations. To achieve the first goal, we use the group Lasso penalty

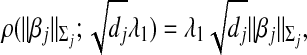(2.1)

where 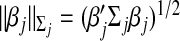, is the empirical covariance matrix for the jth group, and λ₁>0 is a data-dependent tuning parameter. In(2.1), the rescaling factor ensures that small groups are not overwhelmed by large groups in selection. The group Lasso penalty has been investigated in multiple studies. See, for example, Kim and others (2006) and Meier and others (2008).

To achieve the second goal, we propose a new penalty that can incorporate correlations between adjacent groups. Specifically, consider

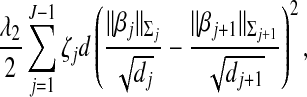where λ₂ is a data-dependent tuning parameter, the weight ζ_j is a measure of correlation between the jth and (j+1)th groups, and 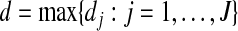is the largest group size. Here d is used to scale the squared difference of the two norms so that λ₂ can be on the same scale as λ₁. In this study, we set ζ_j as the canonical correlation between the two groups. More details on this measure are provided in Appendix. This penalty has been motivated by the following considerations. When ζ_j=0, the two groups are unrelated, and there should be no relationship between the regression coefficients. Hence the penalty reduces to zero. When ζ_j gets larger, the two groups are more highly correlated and hence the corresponding regression coefficients should be “more similar”. A penalty on the difference of norms may shrink the difference. Note that we only penalize the difference between adjacent groups. Such groups are physically next to each other and hence are more likely to have similar regression coefficients if they are highly correlated. In addition, our empirical investigation shows that groups far away from each other tend to have ζ∼0. Introducing a large number of penalties with ζ∼0 may increase the computational cost and reduce stability. Even though it is possible to extend the proposed penalty and consider all pairs of groups, we focus on the adjacent pairs because of the above considerations.

In summary, the SGL penalty function is

Given a loss function ℓ(β), the SGL estimate 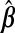is defined as the minimizer of

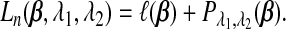2.3. GCD algorithm

The GCD algorithm is a natural extension of the coordinate descent algorithm(Wu and Lange, 2007; Friedman and others, 2010). It optimizes a target function with respect to a single group parameter at a time and iteratively cycles through all group parameters until convergence. It is particularly suitable for problems such as the current one which has a simple closed-form solution for a single group but lacks one for multiple groups.

First, for each group, we orthogonalize the design matrix so that the empirical covariance matrix is equal to identity. We can write 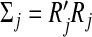for a d_j×d_j upper triangular matrix R_j with positive diagonal entries via the Cholesky decomposition. Let 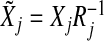and b_j=R_jβ_j. With the transformation, the objective function is

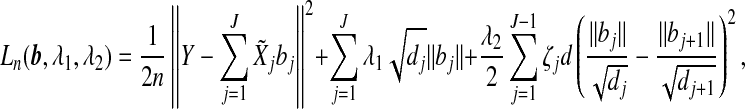where b=(b₁′,…,b_J′)′. Note that 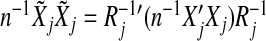. Thus using the ||·||_Σj norm amounts to standardizing the design matrices. Therefore, without loss of generality, we assume that X_j’s are orthonormalized with .

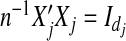Given the group parameter vectors β_k (k≠j) fixed at their current estimates 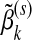, we seek to minimize the objective function L_n(β,λ₁,λ₂) with respect to the jth group parameter β_j. Here only the terms involving β_j in L_n(β,λ₁,λ₂) matter. Some algebraic derivations show that this problem is equivalent to minimizing R(β_j), defined as

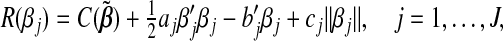(2.2)

where

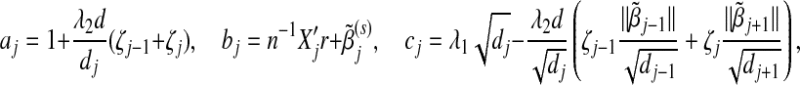and 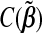is a constant free of β_j. It can be shown that the minimizer of R(β_j) in(2.2) is

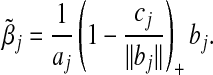(2.3)

This explicit solution facilitates the implementation of the GCD algorithm described below.

Let 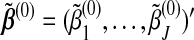be the initial value. A convenient choice for the initial value is zero (component-wise). With fixed λ₁ and λ₂, the GCD algorithm proceeds as follows:

1. set s=0. Initialize the vector of residuals ;

2. for j=1,…,J,

   • (a) calculate a_j,b_j and c_j in expression(2.2);
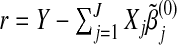   • (b) update using expression(2.3);
   • (a) [(c)] update ;

3. update ;

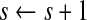4. repeat Steps 2 and 3 until convergence.

Of note, in the above algorithm, we take the convention that ζ₀=ζ_J=0.

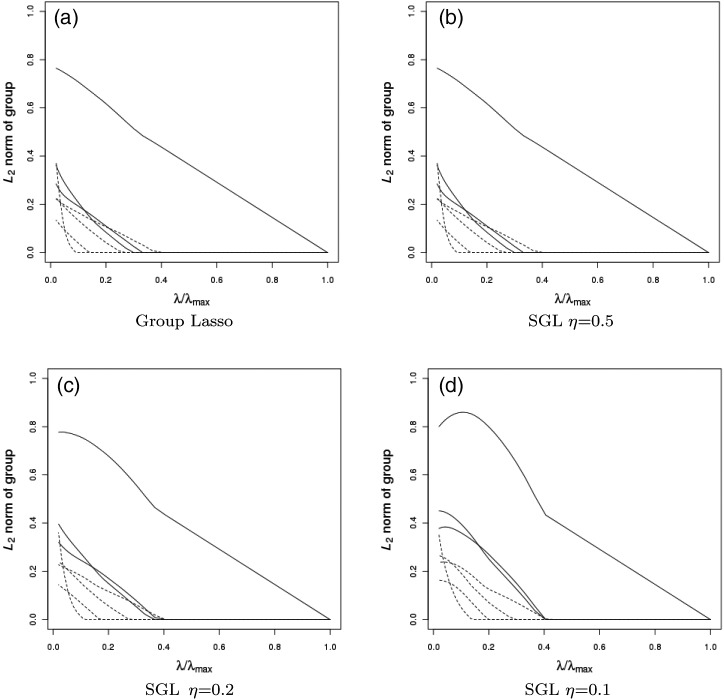
In Step2b, the SGL takes a form similar to a group soft-thresholding operator for the Lasso. The difference lies in the support of c_j. With group Lasso, 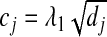and is always positive. With SGL, c_j can be negative or positive depending on the choice of λ₂ and the weight ζ. Under the simplified scenario with only one group, the group Lasso and SGL estimates are the same. With multiple groups, consider , for example, the jth group. If its adjacent groups are selected with non-zero regression coefficients, then c_j−1 and c_j+1 from adjacent groups get smaller. Group j is then more likely to be selected. The solution path for a simulated dataset with correlation structure the same as Example 1 is provided in Figure1 for group Lasso and SGL with η=0.1, η=0.2 and η=0.5, where η=λ₁/(λ₁+λ₂).

Fig. 1.

Solution path for a simulated dataset with correlation structure the same as Example 1 for (a) group Lasso, and SGL with (b) η=0.5, (c) η=0.2, and (d) η=0.1, where η=λ₁/λ and λ=λ₁+λ₂. Solid lines are paths of non-zero groups and dashed lines are paths of irrelevant groups.

Convergence of this algorithm follows from (Tseng, 2001, Theorem4.1(c)). The objective function of SGL can be written as 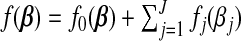where

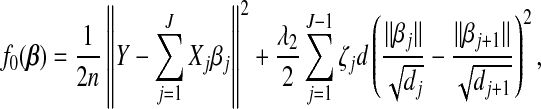and . Since f is regular in the sense of Tseng (2001) and 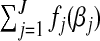is separable (group-wise), the GCD solutions converge to a coordinate-wise minimum point of f, which is also a stationary point.

2.4. Selection of tuning parameters

Various methods can be applied for tuning selection, including akaike information criterion, bayesian information criterion, cross-validation and generalized cross-validation. However, they are all based upon the prediction error. In GWASs, disease markers may not be in the set of SNP markers, resulting in a non-true model for SNP data. Hence, the methods mentioned above may be inappropriate in GWASs.

We adopt the approach proposed in Wu and others (2009), which sets a predetermined number of selected SNPs based on the unique nature of a GWAS. We implement a similar approach to search for the tuning parameter that yields a predetermined number of selected SNPs. For this purpose, λ₁ and λ₂ are reparameterized as τ=λ₁+λ₂ and η=λ₁/τ. The value of η is fixed beforehand. We use a bisection approach to find the τ value such that r(τ), the number of selected markers, is equal to s. Let 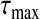be the smallest value for which all estimated coefficients are 0. From the update steps2a and2b, 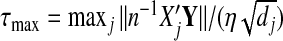. We select ϵ (usually =0.01 in numerical studies) and let 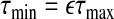. Initially, we set 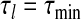and 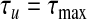. If r(τ_u)<s<r(τ_l), then we employ bisection. This involves testing the midpoint 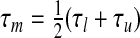. If r(τ_m)<s, replace τ_u by τ_m. If r(τ_m)>s, replace τ_l by τ_m. If r(τ_m)=s, the calculation is terminated. In either of the first two cases, we bisect again and continue the loop until r(τ_m)=s.

3. Practical considerations

3.1. Accommodating case–control data with logistic regression

Consider a case–control study with n subjects. For the ith subject, let y_i∈{0,1} denote the response variable and 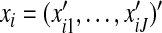. The logistic regression model assumes that 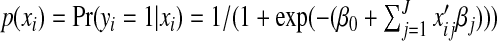. The SGL estimate is defined as

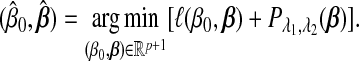(3.1)

The negative log-likelihood function in expression(3.1) is

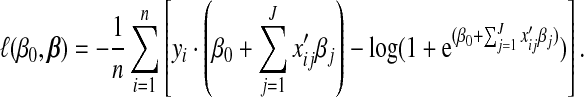(3.2)

When implementing the GCD algorithm, there is no simple, closed-form solution for penalized estimation with a single group. To tackle this problem, we propose using an majorize–minimization (MM) approach(Ortega and Rheinboldt, 2000). Note that negative log-likelihood(3.2) is a convex function. With the MM approach, we majorize the negative log-likelihood by

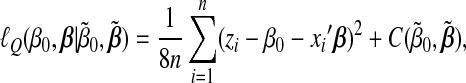where

are evaluated at the current estimate 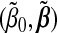, and the last term is free of (β₀,β).

With fixed (λ₁,λ₂), our computational algorithm consists of a sequence of nested loops:

Outer loop: Update the majorized quadratic function l_Q using the current estimates .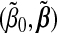

Inner loop: Run the GCD algorithm developed for the penalized least-squares problem and solve for argmin.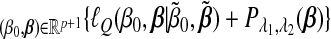

In the penalized group least-squares problem(Section2.3), we do not estimate β₀. In logistic regression, we can estimate it after estimating all other β_js for each majorized function as 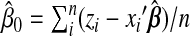. In addition, τ_max is not explicitly defined as in linear models. We evaluate the quadratic approximation for the negative log-likelihood at all coefficients β_j,j=1,…,J, equal to zero. Then τ_max can be calculated in a similar way.

3.2. Reducing within-group colinearity and dimensionality

Because SNPs are densely located in many regions, there may exist high correlations within a group of SNPs due to high linkage disequilibrium. This may cause an instability problem in Cholesky decomposition when some eigenvalues of the correlation matrices are too small. In our group selection, we are more interested in the group effects as opposed to specific covariates within groups. To reduce the dimensionality within groups and to tackle the colinearity problem, when there is evidence of a lack of stability, we first conduct PCA within groups. Specifically, we choose the number of PCs such that 90% of the total variation is explained. Then PCs, as opposed to the original covariates, are used for downstream analysis. Our empirical study suggests that this simple step may ensure that the smallest eigenvalues of the covariance matrices are not too small and that the Cholesky decomposition is stable.

3.3. Significance level for selected SNPs

With penalization methods, the “importance” of a covariate is determined by whether its regression coefficient is non-zero. In GWAS, the p-value may also be of interest.

We adopt a multi-split method that was first proposed by Meinshausen and others (2009). With linear regression, we use the F-test for each group to evaluate whether there are elements in this group with significant effects. With logistic regression, we use the likelihood ratio statistic. This procedure will put us in a position to produce p-values at the group level. It is simulation-based and automatically adjusts for multiple comparisons.

The multi-split method proceeds as follows: (1) Randomly split data into two disjoint sets of equal size: D_in and D_out. In case–control studies, we split the samples in a way that maintains the case–control ratio; (2) Fit data in D_in with SGL. Denote the set of selected groups by S . (3) Compute 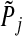, the p-value for group j, as follows: (a) if group j is in set S, set 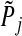equal to the p-value from the F-test in the regular linear regression where group j is the only group. In case–control studies, the likelihood ratio test is evaluated at this step. (b) if group j is not in set S, set 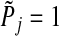. (4) Define the adjusted p-value as 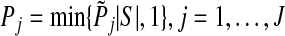, where |S| is the size of set S. This procedure is repeated B times for each group. Let 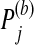denote the adjusted p-value for group j in the bth iteration. For π∈(0,1), let q_π be the π-quartile of 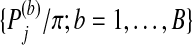. Define 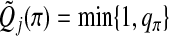. Meinshausen and others (2009) showed that 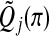is an asymptotically correct p-value, adjusted for multiplicity. They also proposed an adaptive version that selects a suitable value of quartile based on data

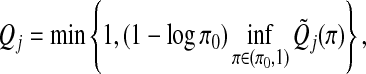where π₀ is chosen to be 0.05. It is shown that Q_j,j=1,…,J, can be used for both family-wise error rate and false discovery rate (FDR) control.

4. Simulation study

We conduct simulation to better gauge the performance of SGL. For comparison, we also consider group Lasso, which has a statistical framework closest to that of SGL. Four simulation examples are considered. The first three are linear models with normal residuals. The fourth one has binary responses. SNPs in the first two models are generated with a two-stage procedure (Wu and others, 2009). First, we draw the predictor vector x_i from a p-dimensional multivariate normal distribution. Then, with the assumption that SNPs have equal allele frequencies, the genotype of the ith SNP is set to be 0, 1, or 2 according to whether x_ij<−c,−c<x_ij<c, or x_ij>c. The cutoff point −c is the first quartile of a standard normal distribution. For the third and fourth examples, the genotype data are excerpted from a rheumatoid arthritis (RA) study (Section5). In all examples, we set n=400 and p=5000.

Example 1 —

There are 1253 groups for 5000 SNPs. For phenotypic irrelevant groups i and j, cov(x_i,x_j)=0.6^|i−j| and cov(x_i,x_i)=1. For phenotypic relevant groups k and l, cov(x_k,x_l)=0.8 if k and l are in the same group, cov(x_k,x_l)=0.6 if k and l are not in the same group, and cov(x_k,x_k)=1. There are no correlations between irrelevant and relevant groups. The size for all irrelevant groups is 4. The non-zero groups have regression coefficients as follows: β₂₅=β₂₈=(0.1,0.1,0.1,0.1)^′, β₂₆=1, β₂₇=(−1,1,−1)^′, β₁₀₀₂=−β₁₀₀₆=(0.2,0.2,0.2,0.2)^′, β₁₀₀₃=−0.8, β₁₀₀₄= (−0.8,−0.8)^′, and β₁₀₀₅=−0.8. The response variable Y is generated from a linear regression model with N(0,1.5²) residuals.

Example 2 —

We use the same regression coefficients and grouping structure as with Example1. An auto-regressive correlation structure is adopted. For SNP i and j, cov(x_i,x_j)=0.7^|i−j|.

Example 3 —

To make the LD structure as realistic as possible, genotypes are obtained from the RA study provided by the Genetic Analysis Workshop (GAW) 16. For individual i, its phenotype y_i is generated from a linear regression model. The regression coefficients have elements all equal to zero except that and . SNPs are grouped if the value of absolute lag-1 autocorrelation is larger than a certain value, which is 0.2 in Examples3 and4. The number of groups is 1432.

Example 4 —

The genotype data and regression coefficients are the same as with Example3. The linear predictors are generated in the same way as with Example3. The binary response variables are generated from Bernoulli distributions with .

We analyze Examples1–4 using SGL and group Lasso. PCA is used to reduce within-group colinearity. We are aware of other group selection methods. We focus on comparison with group Lasso because of its similarity with SGL, which may help us better understand the effects of the smooth penalty. Summary statistics based on 100 replicates are shown in Table1. Simulation suggests that SGL is computationally affordable, with analysis of one replicate taking about 5 min on a desktop PC. For each replicate in all four examples, we prefix the number of selected groups equal to 15 and use the method described in Section2.4 for tuning parameter selection. With a total of 9 true positive (TP) groups, selecting 15 groups can ensure that a large number of TPs are selected. As shown in Table1, we have experimented with different η values and found that η=0.3 is an appropriate choice with linear regression and η=0.1 is appropriate with logistic regression. Note that, when η=1, SGL becomes group Lasso. To assess robustness, we assign wrong block sizes in all four examples. In Examples1 and2, the correct block sizes for (β₂₅,…,β₂₈,β₁₀₀₂,…,β₁₀₀₆) are (4, 1, 3, 4, 4, 1, 2, 1, 4), with the incorrect assignment being (3, 2, 4, 3, 2, 3, 3, 2, 2). In Examples3 and 4, the correct block sizes for (β₇₀₅,…,β₇₀₇,β₇₀₉,…,β₇₁₄) are (4, 6, 2, 4, 3, 1, 3, 2, 6), with the incorrect assignment being (5, 5, 3, 3, 2, 2, 2, 4, 5). Result under incorrect group assignment is presented in Table3. (see supplementary material available at Biostatistics online, Appendix). In addition, we also evaluate performance with s=10, under both correct and incorrect group assignments. Results are presented in Tables 4 and 5 (see supplementary material available at Biostatistics online, Appendix), respectively.

Table 1.

Mean (standard deviation) of TP number of groups, FDR, and false negative rate (FNR) for simulated data, s=15. Note that the optimal η for linear models (Examples 1–3) is 0.3 and the optimal η for the logistic regression model (Example4) is 0.1. When η=1, SGL becomes group Lasso.

	Example1			Example2
η	TP	FDR	FNR	TP	FDR	FNR
0.1	8.96 (0.20)	0.40 (0.01)	0.004 (0.02)	8.66 (0.52)	0.42 (0.03)	0.04 (0.06)
0.2	8.68 (0.51)	0.42 (0.03)	0.04 (0.06)	8.44 (0.54)	0.44 (0.04)	0.06 (0.06)
0.3	8.30 (0.54)	0.45 (0.04)	0.08 (0.06)	7.98 (0.59)	0.47 (0.04)	0.11 (0.07)
0.4	7.86 (0.73)	0.48 (0.05)	0.13 (0.08)	7.86 (0.64)	0.48 (0.04)	0.13 (0.07)
0.5	7.54 (0.68)	0.50 (0.05)	0.16 (0.08)	7.58 (0.64)	0.49 (0.04)	0.16 (0.07)
0.6	7.48 (0.61)	0.50 (0.04)	0.17 (0.07)	7.54 (0.65)	0.50 (0.04)	0.16 (0.07)
0.7	7.02 (0.87)	0.53 (0.06)	0.22 (0.10)	7.32 (0.82)	0.51 (0.05)	0.19 (0.09)
0.8	7.08 (0.70)	0.53 (0.05)	0.21 (0.08)	7.22 (0.65)	0.52 (0.04)	0.20 (0.07)
0.9	6.60 (0.78)	0.56 (0.05)	0.27 (0.09)	6.98 (0.80)	0.53 (0.05)	0.22 (0.09)
1	6.28 (0.64)	0.58 (0.04)	0.30 (0.07)	6.68 (0.89)	0.55 (0.06)	0.26 (0.10)
	Example3			Example4
0.1	7.94 (0.89)	0.47 (0.06)	0.12 (0.10)	6.28 (1.44)	0.58 (0.10)	0.30 (0.16)
0.2	7.74 (0.92)	0.48 (0.06)	0.14 (0.10)	5.82 (1.21)	0.61 (0.08)	0.35 (0.13)
0.3	7.32 (0.84)	0.51 (0.06)	0.19 (0.09)	5.46 (1.28)	0.64 (0.09)	0.39 (0.14)
0.4	7.30 (0.76)	0.51 (0.05)	0.19 (0.08)	5.50 (1.34)	0.63 (0.09)	0.39 (0.15)
0.5	7.22 (0.76)	0.52 (0.05)	0.20 (0.08)	5.24 (1.12)	0.65 (0.07)	0.42 (0.12)
0.6	7.02 (0.80)	0.53 (0.05)	0.22 (0.09)	4.98 (1.17)	0.67 (0.08)	0.45 (0.13)
0.7	6.82 (0.80)	0.55 (0.05)	0.24 (0.09)	4.34 (1.21)	0.71 (0.08)	0.52 (0.13)
0.8	6.28 (0.86)	0.58 (0.06)	0.30 (0.10)	4.06 (1.04)	0.73 (0.07)	0.55 (0.12)
0.9	5.76 (0.77)	0.62 (0.05)	0.36 (0.09)	3.60 (0.97)	0.76 (0.06)	0.60 (0.11)
1	4.80 (0.78)	0.68 (0.05)	0.47 (0.09)	2.46 (1.03)	0.84 (0.07)	0.73 (0.11)

Table1 suggests that SGL is capable of selecting the majority of TPs. We do observe a few false positives, which is reasonable considering the extremely high dimensionality and noisy nature of data. Under all simulated scenarios, SGL outperforms group Lasso by identifying more TPs and/or less false positives. We also conduct receiver operating characteristics (ROC) analysis by varying the number of selected groups, and compare SGL with different η values, group LASSO and single-SNP analysis. Results are presented in Figures4–7 (see supplementary material available at Biostatistics online, Appendix). It is easy to see that SGL outperforms alternatives with ROC curves dominatingly “higher”. The ROC plots also suggest choosing η=0.3 for examples 1–3 and η=0.1 for example 4. Comparing with Table 1, Table3 (see supplementary material available at Biostatistics online, Appendix) shows that the incorrect assignment of block sizes does not have much effect on performance, although the number of TPs decreases. Table4 (see supplementary material available at Biostatistics online, Appendix) shows that with a smaller s, the number of TPs decreases as expected since the number of groups selected decreases. Table5 (see supplementary material available at Biostatistics online, Appendix) shows that, with incorrect block sizes, the performance is still similar to that with correct block sizes (see supplementary material available at Biostatistics online, Table4, Appendix). For a representative dataset simulated under Example3 with correct block sizes and s=15, we show the selected group norms and their corresponding p-values (see supplementary material available at Biostatistics online, Table6, Appendix). We see that SGL under linear regression selects a more clustered set of groups. Furthermore, SGL selects more groups that are TP and some of their p-values are significant. Note that SGL selects true groups 706, 712, and 714 which are significant, while group Lasso does not.

5. Data analysis

5.1. Analysis of RA data

RA is a long-term condition that leads to inflammation of the joints and surrounding tissues. It is a complex human disorder with a prevalence ranging from around 0.8% in Caucasians to 10% in some native American groups(Amos and others, 2009). There are solid evidences that multiple genetic risk factors contribute to the risk of RA. Genetic risk factors underlying RA have been mapped to the HLA region on 6p21(Newton and others, 2004) and other regions.

The GAW 16 data are from the North American Rheumatoid Arthritis Consortium . This was the initial batch of whole genome association data after removing duplicated and contaminated samples. SNP genotype data were generated using an Illumina 550k platform and available for 868 cases and 1194 controls. After quality control and removing SNPs with low minor allele frequencies, there are 31 670 SNP measurements on chromosome 6.

In Figure3 (see supplementary material available at Biostatistics online, Appendix), we provide the plot of ζ values. It is easy to see that some correlations are very high. Note that there are more groups having ζs smaller than 0.6, since the SNPs are grouped if the absolute lag-1 autocorrelations are larger than 0.6. The proportion of ζ_j>0.6 for 100 non-overlapping groups is also plotted (see supplementary material available at Biostatistics online, Figure3, Appendix).

With SNP data, one possible way of grouping SNPs is based on the distance to the closest genes. However, overlapping of genes happens frequently with SNP data. Thus, sometimes it can be difficult to identify to which group an SNP belongs. Here we use an alternative way to group SNPs. The lag-1 Pearson’s correlation coefficients are first calculated for all SNPs. Then we group SNPs using lag-1 correlations: if two adjacent SNPs have absolute correlation larger than 0.6, we put them in the same group. We choose the threshold to be 0.6 as it leads to a reasonable number of groups, neither too large nor too small. Different from simulation studies, we do not know the number of true groups beforehand. We choose the predetermined number of selected groups equal to 100. This choice has been motivated by several considerations. Figure2(a) and (b) suggests that 100 should be sufficient to catch the important groups. On the other hand, it is not too large so that there should not be many false positives. From simulation studies, we choose η=0.1 for data analysis. The value of the tuning parameter for SGL with η=0.1 is 1.783, whereas the value of the tuning parameter for group Lasso is 0.138. As described in Section3.2, we apply PCA to reduce the dimensionality within groups. Therefore, a direct plot of point estimates cannot be produced. We use the group norms to plot against their original positions. The plots for SGL and group Lasso are provided in Figure2(a) and (b), respectively. For comparison, we also conduct single-SNP analysis. Results are provided in Figure2. The information for SNPs selected by SGL is given in Table7 (see supplementary material available at Biostatistics online, Appendix). SGL identifies 127 SNPs in 40 genes, and 8 of them are HLA genes. Group Lasso identifies 106 SNPs in 82 genes, and 5 of them are HLA genes. Single-SNP analysis identifies 326 SNPs in 85 genes, and 12 of them are HLA genes. Information for SNPs selected by SGL but not single-SNP analysis is presented in Table8 (see supplementary material available at Biostatistics online, Appendix). The numbers of overlapping SNPs selected using SGL, group Lasso, and single-SNP analysis for these data are presented in the first part of Table2. We note that the overlapping SNPs between SGL and single-SNP analysis is much more than the ones between group Lasso and single-SNP analysis, implying indirectly that SGL is superior to group Lasso under high correlation settings. To evaluate the influence of threshold-forming groups, we choose the threshold to be 0.2 to analyze the same data. The plots can be found in Figure8 (see supplementary material available at Biostatistics online, Appendix) in which we can find similar trends to those in Figure2.

Fig. 2.

Plots of ||β|| for SGL and group Lasso with threshold = 0.6 to form groups, and |β| for single-SNP logistic regression for RA data. In(a) and(b), the smaller dots are estimates with insignificant p-values, and the larger dots stand for estimates with significant p-values.

Table 2.

The Number of SNPs and genes identified, and overlap of SNPs among the three methods for RA data and GAW 17 data

	RA data				GAW 17 data
			Overlap†				Overlap†
Method	# of SNPs	# of Genes	G‡	S§	# of SNPs	# of Genes	G‡	S§
SGL	127	40	39	106	12	10	6	3
Group Lasso	106	82		33	12	10		3
single-SNP analysis	326	85			16	8

From Figures2 and 8 (see supplementary material available at Biostatistics online, Appendix), we see that single-SNP analysis produces estimates with much lower signal to noise ratio. Group Lasso and SGL are capable of conducting screening and yielding much sparser estimates. Compared with group Lasso, group estimates from SGL are more clustered in the HLA region that has been found to be associated with RA. Moreover, there are more significant groups (larger dots) identified by SGL in the HLA region. It is consistent with the results from simulation.

5.2. GAW 17 data

The GAW 17 data(Almasy and others, 2011) consist of 24 487 SNP markers throughout the genome for 697 individuals. Genotype data are real sequence data from the 1000 Genomes Project. We analyze unrelated individual data with quantitative trait Q1 in replicate 1. All SNPs are included in analysis. We coded the seven population groups as dummy variables. The quantitative trait Q1 is first regressed on gender, age, smoking status, SC and group dummy variables in order to remove their confounding effects. This procedure helps adjust for population stratification. Then, the residuals from this regression are used as response.

Since there are only 24 487 SNPs throughout the genome, the correlations among those SNPs are weak. Thus, we choose the threshold to be 0.01 or 0.05 as it leads to a reasonable number of groups. The selected SNPs by SGL with η=0.3 are shown in Table9 (see supplementary material available at Biostatistics online, Appendix). Since all SNPs are rare variants, we are unable to evaluate their significance via multi-split. We see that SNPs C13S522, C13S523, and C13S524 are associated with phenotype. Only three true SNPs are selected because all SNPs for these data have minor allele frequencies less than 0.05. For GAW 17 data, SGL and group Lasso identify the same number of phenotype-associated SNPs. The numbers of overlapping SNPs selected using SGL, group Lasso, and single-SNP analysis for these data are presented in the second part of Table2. We see that there are six overlapped SNPs between SGL and group Lasso. The number of overlapped SNPs selected by SGL and single-SNP analysis is three, which is the same as that between group Lasso and single-SNP analysis.

6. Discussion

Penalization provides an effective way of analyzing the joint effects of multiple SNPs in GWAS. Because of the natural ordering of SNPs on the genome and possible high linkage disequilibrium among tightly linked SNPs, SNP data can be highly correlated and hence have the grouping structure. In addition, adjacent groups can still be highly correlated, which may give rise to similar association with the phenotype of interest. Existing penalized marker selection methods do not effectively accommodate all the aforementioned properties of SNP data. In this article, we propose a new penalized marker selection approach. It uses the group Lasso penalty for group marker selection and a new penalty to smooth the regression coefficients between adjacent groups. We also investigate several related issues, including computation, within-group dimension reduction, and evaluation of significance. Our numerical studies show that the proposed approach has satisfactory performance.

In individual marker and group selections, it has been shown that some penalties can outperform Lasso-based penalties. It is possible to extend the proposed approach, for example, by replacing group Lasso with group MCP or group SCAD. Such an extension may incur high computational cost and will not be pursued. There are multiple ways of defining the difference between groups and hence smoothing. The proposed way is computationally simple and intuitively reasonable. The proposed approach can accommodate more subtle structure in SNPs. As a consequence, it inevitably demands new structure and tunings. For example, there may be multiple ways of constructing groups. We are aware of “more automatic” approaches, for example, the hierarchical clustering plus Gap approach. However, such methods may rely on assumptions that SNP data clearly violate; and some methods cannot fully accommodate the spatial adjacency of SNPs on chromosome. The adopted tuning parameter selection approach has been developed in published studies. Our literature review suggests that there is a lack of consensus on tuning parameter selection with high-dimensional SNP data. A comprehensive investigation on tuning parameter selection is beyond the scope of the current paper. In our study, we use a predetermined number of groups to be selected. Usually, this number can be determined based on prior knowledge, limitation of resources for downstream analysis, and possible trial and error. We note that the proposed SGL can be easily coupled with other tuning parameter selection approaches such as cross-validation. In this paper, we focus on the development of the new methodology. Further work is needed to investigate the theoretical properties of the SGL method.

Funding

The rheumatoid arthritis data for Genetic Analysis Workshop (GAW) 16 and GAW 17 data are supported by NIH grant R01-GM031575. This study has been supported by awards CA120988, CA165923, and CA142774 from NIH.

Supplementary Material

Supplementary material is available at http://biostatistics.oxfordjournals.org.