Abstract
Individuals differ not only in their background characteristics, but also in how they respond to a particular treatment, intervention, or stimulation. In particular, treatment effects may vary systematically by the propensity for treatment. In this paper, we discuss a practical approach to studying heterogeneous treatment effects as a function of the treatment propensity, under the same assumption commonly underlying regression analysis: ignorability. We describe one parametric method and two non-parametric methods for estimating interactions between treatment and the propensity for treatment. For the first method, we begin by estimating propensity scores for the probability of treatment given a set of observed covariates for each unit and construct balanced propensity score strata; we then estimate propensity score stratum-specific average treatment effects and evaluate a trend across them. For the second method, we match control units to treated units based on the propensity score and transform the data into treatment-control comparisons at the most elementary level at which such comparisons can be constructed; we then estimate treatment effects as a function of the propensity score by fitting a non-parametric model as a smoothing device. For the third method, we first estimate non-parametric regressions of the outcome variable as a function of the propensity score separately for treated units and for control units and then take the difference between the two non-parametric regressions. We illustrate the application of these methods with an empirical example of the effects of college attendance on womens fertility.
Keywords: causal effects, treatment effects, heterogeneity, propensity scores, matching
1 Introduction
A feature common to all social phenomena is variability across units of analysis (Xie 2007). The development of statistical methods to better understand and accommodate such variability has been a major methodological achievement of modern quantitative social science. Individuals differ not only in their background characteristics, but also in how they respond to a particular treatment, intervention, or stimulation. A long-standing common practice in quantitative sociology has been the examination of variation in effects through interactions terms, although the meaning of “main effects” in the presence of effect heterogeneity has not always been well understood (Elwert and Winship 2010). For causal inference with observational data under the assumption of ignorability, the only interaction consequential for selection bias is between the treatment of interest and the propensity of selection into treatment (Heckman, Urzua, and Vytlacil 2006; Xie 2011). This interaction also yields substantively important results for social research and policy. In this paper, we are concerned with the estimation of this interaction and refer to it as “heterogeneous treatment effects.” Although the importance of heterogeneous treatment effects, so defined, has been widely recognized in the causal inference literature, they are seldom studied empirically in quantitative sociological research. We suspect that lack of accessible statistical methods is one reason why heterogeneous treatment effects are not routinely assessed and reported. In this paper, we describe a straightforward approach, with observational data, to exploring and estimating heterogeneous treatment effects as a function of the treatment propensity.
Heterogeneity in treatment effects has important implications for social and behavioral research and for social policy (e.g., Bjorklund and Moffitt 1987; Blundell, Dearden, and Sianesi 2005; Brand and Xie 2010; Heckman, Urzua, and Vytlacil 2006; Manski 2007; Xie 2011). On the one hand, if a treatment is costly and difficult to administer and, as a result, is available only to those subjects who are likely to benefit most from it, increasing the pool of subjects receiving the treatment may reduce its average effectiveness. On the other hand, if individuals with current access to a treatment are not the individuals likely to benefit most from the treatment, increasing the availability of the treatment may increase the average effect among the treatment recipients. If policy makers understand patterns of treatment effect heterogeneity, they can more effectively assign different treatments to individuals so as to balance competing objectives, such as reducing cost, maximizing average outcomes, and reducing variance in outcomes within a given population (Manski 2007). The study of treatment effect heterogeneity can also yield important insights about how scarce social resources are distributed in an unequal society.
We propose an approach with three methods to studying treatment effect heterogeneity that builds on a common framework for estimating causal effects. The first method has been applied in several recent empirical applications (Brand 2010; Brand and Davis 2011; Brand and Xie 2010; Tsai and Xie 2008; Xie and Wu 2005). In this paper, we focus on estimating issues of this previously applied method. The second and third methods are non-parametric counterparts to the first method. Our discussion proceeds as follows. In section 2, we discuss population heterogeneity, selection into treatments, causal inference, and the sociological significance of studying heterogeneous treatment effects. In section 3, we present our approach to studying treatment effect heterogeneity. In section 4, we present an empirical example in which we demonstrate the methods. In section 5, we discuss the benefits and limitations of this approach and conclude the paper.
2 Background and Significance
2.1 Causal Inference in the Population Sciences
Population sciences, including economics, demography, epidemiology, psychology, and sociology, all treat individual-level variation as a main object of scientific inquiry, rather than a mere nuisance or measurement error (Angrist and Krueger 1999; Ansari and Jedidi 2000; Bauer and Curran 2003; Greenland and Poole 1988; Heckman 2001, 2005; Heckman and Robb 1985; Lubke and Muthén 2005; Manski 2007; Moffitt 1996; Rothman and Greenland 1998; Winship and Morgan 1999; Xie 2007). The recognition of inherent individual-level heterogeneity has important consequences for research designs in the social sciences. Because individuals differ from one another and differ in their response to treatments, results can vary widely depending on population composition. The large methodological literature on causal inference recognizes the importance of and consequently allows for population heterogeneity (Heckman 2005; Holland 1986; Manski 1995; Rubin 1974; Winship and Morgan 1999).
Suppose that a population, U, is being studied. Let Y denote an outcome variable of interest (with its realized value being y). Let us define treatment as an externally induced intervention that can, at least in principle, be given to or withheld from a unit under study. For simplicity, we consider only dichotomous treatments and use D to denote the treatment status (with its realized value being d), with D=1 if a member is treated and D=0 if a member is not treated. Let subscript i represent the ith member in U. We further denote as the ith member’s potential outcome if treated (i.e., when di=1), and as the ith member’s potential outcome if untreated (i.e., when di=0). For a population science, we can only compute quantities of interest that reveal treatment effects at the group level. For example, we may compare the average difference between a randomly selected set of members in U that were treated to another randomly selected set of members that were untreated. If treatment assignment is random, the comparison of the treated and untreated groups yields an estimate of a quantity called the Average Treatment Effect (ATE):
| (1) |
While ATE is defined for the whole population, the researcher may wish to focus and define a treatment effect for a well-defined subpopulation. For example, Treatment Effect of the Treated (TT) refers to the average difference by treatment status among those individuals who are actually treated:
| (2) |
Analogously, Treatment Effect of the Untreated (TUT) refers to the average difference by treatment status among those individuals who are not treated:
| (3) |
If treatment effects are homogeneous across all units in a population, the three quantities are identical. Differences in these three quantities of interest, ATE, TT, and TUT, indicate treatment effect heterogeneity.
Because all statistical quantities of interest can be computed only at the group level, the researcher necessarily “ignores” within-group individual-level heterogeneity within the context of a given study, although we know individual-level variation must exist (Xie 2007). This is always true despite various efforts to allow for or to recover some degree of heterogeneity through statistical approaches, such as regression models with interactions between treatment indicators and contextual or individual level variables, as commonly practiced in multilevel models (Raudenbush and Bryk 2002; Vermunt 2003), Bayesian analysis (Gelman et al. 2004), growth-curve analysis (Muthén and Muthén 2000), meta-analysis (Hedges 1982), the latent class model (D’Unger et al. 1998; Heckman and Singer 1984; Vermunt 2002), and Rasch models (Duncan, Stenbeck, and Brody 1988; Rasch 1966). Notably, Heckman and his associates have extensively discussed heterogeneous treatment effects, what they call “essential heterogeneity,” in a class of models relying on instrumental variables (Carneiro, Heckman, and Vytlacil forthcoming; Heckman, Urzua, and Vytlacil 2006).1 Earlier, we stated that there is a practical need to overlook within-group individual-level heterogeneity in a research setting. Although many researchers are ready to assume within-group homogeneity, we consider any analysis essentially “marginal” in the sense that we obtain results that are group-level averages over unobserved factors. That is, the real challenge in a research setting is not to establish absolute homogeneity across units of analysis, which is impossible, but to realize that in order to focus on differences across subpopulations to answer questions of research interest, we temporarily overlook individual-level heterogeneity within subpopulations defined by observable characteristics by aggregating over heterogeneous units of analysis within subpopulations thus defined.2 Different analytic specifications are essentially different ways to define such subpopulations.
2.2 Pre-Treatment and Treatment Effect Heterogeneity
We have established the need to conduct group-level comparisons, where groups are essentially comparable except for their treatment status, for causal inference. However, due to population heterogeneity, there is no guarantee that the group that actually receives the treatment is comparable, in observed and particularly in unobserved contextual and individual characteristics, to the group that does not receive the treatment. Individuals may self-select into treatment based on their anticipated monetary and nonmonetary benefits and costs of treatment. To see this, let us partition the total population U into the subpopulation of the treated U1 (for which D=1) and the subpopulation of the untreated U0 (for which D=0). We can thus decompose the expectation for the two counterfactual outcomes as follows:
| (4) |
and
| (5) |
What we observe from data are: E(Y1|D = 1), E(Y0|D = 0), P(D = 1), and P(D = 0). A concern with selection bias is due to the possibility that:
| (6) |
and
| (7) |
To see how selection into treatment may cause biases on treatment effect estimates, let us now use the following abbreviated notations:
p = the proportion treated (i.e., the proportion of cases for which D=1),
q = the proportion untreated (i.e., the proportion of cases for which D=0),
,
,
,
.
Using the iterative expectation rule, we can decompose ATE as follows:
| (8) |
where, as previously defined in equations (2) and (3), TT is the average Treatment Effect of the Treated, and TUT is the average Treatment Effect of the Untreated.
Note that the simple comparison estimator from observed data is . If we use this naive estimator for ATE, we see two sources of bias from equation (8):
The average difference between the two groups in outcomes if neither group receives the treatment: . We call this the “pre-treatment heterogeneity bias.”
The difference in the average treatment effect between the two groups, (TT – TUT), weighted by the proportion untreated q. The weight of q results from our choice to define pre-treatment heterogeneity bias for the untreated state. We call this the “treatment-effect heterogeneity bias.”
Consider two concrete examples representing the two different sources of selection bias. First, pre-school children from poor families are selected into Head Start programs and thus would compare unfavorably to other children who do not attend Head Start programs without an adequate control for family socioeconomic resources (Xie 2000). Second, economic theory predicts that attainment of college education may be selective because it attracts persons who gain more from college than persons who do not attend college (Willis and Rosen 1979). While the first example illustrates the importance of controlling for pre-treatment heterogeneity bias that may be represented by “covariates” or “fixed effects,” the second example underscores treatment-effect heterogeneity bias – sorting on the treatment effects – that cannot be “controlled for” by covariates or fixed-effects.3
2.3 Conditioning on Observed Covariates and the Propensity Score
In general, with data from observational studies, subjects are sorted into treatment or control groups for a number of reasons, some of which may be unknowable to the researcher. Only covariates that meet the condition of affecting both the treatment assignment and the outcome confound the observed relationship between treatment and outcome (Rubin 1997). It is hoped that through control of the relevant covariates the treatment will be independent of potential outcomes. This conditional independence assumption is called “ignorability,” “unconfoundedness” or “selection on observables.” Let X denote a vector of observed covariates. The ignorability assumption states:
| (9) |
Because we can never be sure after inclusion of which covariates equation (9) would hold true, the ignorability condition is always held as an assumption, indeed an unverifiable assumption. Substantive knowledge about the subject matter needs to be brought in before a researcher can entertain the ignorability assumption. Measurement of theoretically meaningful confounders makes ignorability tentatively plausible, but not necessarily true. Pearl (2009) provides conditions for including relevant covariates as appropriate controls. Results for causal inference under the ignorability assumption thus should always be interpreted provisionally and cautiously and assessed through sensitivity or auxiliary analyses (Brand 2010; Brand and Davis 2011; Brand and Xie 2010; Cornfield et al. 1959; DiPrete and Gangl 2004; Harding 2003; Rosenbaum 2002; Tsai and Xie 2008; Xie and Wu 2005).
Conditioning on X can be difficult in applied research due to the “curse of dimensionality.” However, Rosenbaum and Rubin (1983,1984) show that, when the ignorability assumption holds true, it is sufficient to condition on the propensity score as a function of X (propensity score theorem). Thus, equation (9) is changed to
| (10) |
where P(D = 1|X) is the propensity score, the probability of treatment that summarizes all the relevant information in covariates X. The literature on propensity score matching recognizes the utility of the propensity score as a solution to data sparseness in a finite sample (Morgan and Harding 2006).
3 An Approach for Estimating Heterogeneous Treatment Effects under Ignorability
3.1 The Rationale
We propose a simple and straightforward approach to estimate heterogeneous treatment effects under the ignorability assumption. We have established the central role of the estimated propensity score as a means of summarizing all the relevant information between the set of observed covariates that affect treatment and outcome. Here we argue that if we are theoretically concerned with causality and selection bias, then the only consequential interaction is between the treatment status and the propensity for treatment. Moreover, analyzing the pattern of treatment effects as a function of the propensity score offers insights as to the implications of the distribution of social resources, policy interventions, and events across the population. Our approach therefore augments existing approaches to studying treatment effect heterogeneity, such as comparisons between the TT and TUT (see for example, Brand and Halaby 2006 and Morgan 2001) or weighted regressions to recover subpopulation treatment effects (Morgan and Todd 2008).
Why can we eliminate the two types of heterogeneity bias when controlling for the propensity score if the ignorability assumption is true? Recall from equation (10) that, under the ignorability assumption, conditional on the propensity score, treatment status is independent of the two potential outcomes under alternative treatment conditions. In other words, given a level of the propensity score, there is no bias under ignorability. Given our earlier discussion that bias can manifest in two types (subsection 2.2), this is tantamount to two “no-bias” conditions:
-
(1)There is no pre-treatment heterogeneity bias conditional on p(X). In reference to equation (10), this means
(11) -
(3)There is no treatment-effect heterogeneity bias conditional on p(X). In reference to equation (10), this means
Given (11) and (12), it is easy to show that(12) (13)
Hence, the proposed approach places a large emphasis on the propensity score, as it plays a crucial role in both pre-treatment heterogeneity and treatment-effect heterogeneity, as shown in equations (11) and (12). Both types of heterogeneity bias, i.e., systematic differences between the treatment group (D = 1) and the control group (D = 0) for causal inference, are captured by the propensity score. That is to say, the researcher should pay attention only to the interaction between the treatment indicator and the propensity score, as far as a selection bias is concerned.
It is obvious that not all types of treatment effect heterogeneity can be studied with this approach. The propensity score theorem does not imply that treatment effects are homogeneous at the individual level given the propensity score. To appreciate this point, suppose that there is a covariate G that affects the treatment effect size. Let X denote all covariates, including G. For illustration, let us assume that G takes on two possible values, g1 and g2. We assume ignorability to hold true. The earlier statement that G affects the treatment effect size means:
| (14) |
This is commonly understood as indicating an interaction effect between treatment and covariate G. This interaction effect, however, has no direct bearing on selection bias for causal inference, net of the propensity score, if ignorability holds true. By iterative expectation, we can express the two sides of Equation (12) as weighted sums over G as follows:
| (15) |
where d = 0,1 and wd,p = P(G = g1|D = d, p(X)). Since
| (16) |
due to the ignorability assumption and
| (17) |
as a result of the balancing property of the propensity score (Rosenbaum and Rubin 1983), all terms in equation (15) stay unchanged when we vary D = 0,1. Hence, equation (12) holds even if treatment effects vary by G for a given propensity score.
3.2 Estimation of the Propensity Score
Thus far, we have discussed the propensity score as if it is known. In reality, of course, it is unknown and needs to be estimated. For estimating the propensity score we use a probit model.4 All pre-treatment covariates that are unevenly distributed between the treatment group and the control group could potentially contribute to selection biases; they can all be included as predictors of the propensity model. How good the covariates are as predictors of the propensity score is a substantive question. There is a large literature on the estimation and use of the propensity score (see Morgan and Harding 2006; Gangl 2010 for recent reviews). Sometimes, we do not observe both treated and untreated cases in regions of the propensity score. When there are such regions of no “common support,” the researcher can either impose a structure to essentially impute data for propensity score estimation there or, to be safe, give up inferences for such regions.
We now assume that we have obtained good estimated individual-level propensity scores . These estimated propensity scores are used to balance the distribution in covariates between the treatment and control groups. Once balanced, we can examine heterogeneous treatment effects as a function of the propensity score. Below, we discuss three different estimation methods based on estimated propensity scores: the stratification-multilevel method, the matching-smoothing method, and the smoothing-differencing method.
3.3 The Stratification-Multilevel Method (SM)
The first method we discuss is what we call the stratification-multilevel (SM) method of estimating heterogeneous treatment effects. It consists of the following concrete steps:
Estimate propensity scores for all units for the probability of treatment given a set of observed covariates, P(d=1|X), using probit or logit regression models, as discussed in subsection 3.2.
Construct balanced propensity score strata (or ranges of the propensity score) where there are no significant differences in the average values of covariates and the propensity score between the treatment and control groups.5 This practice ignores heterogeneity within a stratum. As we discussed earlier, some grouping is necessary when computing statistical quantities representing causal effects. While units within a stratum are not homogenous aside from treatment status, they are more so than the data before stratification. It is hoped that the stratification by the propensity score is an effective way to remove most biases between the treated and untreated groups (Rosenbaum and Rubin 1984).
Estimate propensity score stratum-specific treatment effects within strata. We can do this either by drawing a direct comparison in the outcome variable between the treatment group and the control group within strata, shown in equation (13), or by applying a regression model within strata to further adjust for any remaining covariate imbalance within strata. Results by strata, or level-1 estimates, are obtained from this step of the analysis. Because we do not constrain the comparison of the treatment group and the control group across strata in any way, data analysis at this stage is non-parametric across strata.
Evaluate a trend across the strata using variance-weighted least squares regression of the strata-specific treatment effects, obtained in step (3), on strata rank at level-2. This step departs from the conventional use of propensity scores in constructing strata, where the emphasis is usually on removing biases due to covariate imbalances simply by averaging the estimated treatment effects across strata (Dehejia and Wahba. 1999; Rosenbaum and Rubin 1984). Instead, the main research objective we emphasize is to look for a systematic pattern of heterogeneous treatment effects across strata. For simplicity and to preserve statistical power, we mainly suggest modeling the heterogeneity pattern as a linear function across strata ranks. A linearity specification would force the data to tell us whether the treatment effect is either a positive or a negative function of the propensity. This strategy has proved useful in empirical research (Brand 2010; Brand and Davis 2011; Brand and Xie 2010; Tsai and Xie 2008; Xie and Wu 2005). Of course, with more complicated research goals and richer data, the researcher is free to specify different parametric functions at level 2 for the heterogeneity in treatment effects across propensity-score strata, as in ordinary multi-level models (Raudenbush and Bryk 1986, 2002).
The SM approach offers useful and easily interpretable estimates of strata-specific treatment effects and the unit change in estimates as we move between strata. However, SM has two notable shortcomings. First, the researcher is forced to divide the full range of the propensity score into a limited number of strata within which we assume neither pre-treatment nor treatment effect heterogeneity bias. That is, we impose a form of within-group homogeneity so that treated and untreated observations are considered interchangeable within strata. Second, across the strata, we impose a higher-level regression to detect a pattern of treatment heterogeneity. Given the limited number of observations, i.e., strata, for this secondary analysis, a strong functional form, such as the linear form, is often used. To overcome these shortcomings, we introduce more flexible methods below.
3.4 The Matching-Smoothing Method (MS)
The second method, which we call the matching-smoothing (MS) method of estimating heterogeneous treatment effects, overcomes the assumption of homogeneity within strata in the SM method. The researcher using this method can retain individual-level information before making cross-individual comparisons to detect heterogeneous treatment effects. In a way, however, the method can be thought of as the limiting case of SM, with the strata being individual treatment-control comparisons at the most elementary level at which such comparisons can be constructed.
A typical approach to matching is to first define treated (or untreated) units as the target group to be matched and then select appropriate untreated (or treated) units as matches based on closeness in propensity scores. One convenience of this approach is that the researcher can easily obtain TT (or TUT) by aggregating differences over all matches between treated units and untreated units. For simplicity, we focus on the treatment group and find a matched control case for each treated case to illustrate the method. The method consists of the following concrete steps:
Estimate the propensity scores for all units, as discussed in subsection 3.2 and step (1) of subsection 3.3.
Match treated units to control units with a matching algorithm. We will discuss matching options below. The basic idea is to find a control unit (or units) that is a good match for each treated unit based on estimated propensity scores. Again, for simplicity, the discussions in (2)-(4) presume one-to-one matching. With one-to-one matching, the data are paired, with each pair consisting of a treated unit and an untreated unit with (almost) the same propensity score. When one-to-multiple matching is used instead, the comparison is made to the group mean of multiple matched controls rather than to just a single matched control.
Plot the observed difference in a pair between a treated unit and an untreated unit against a continuous representation of the propensity score. While we cannot treat the difference between only two observations in a pair as a true “estimate,” it is the building block for the next step of the analysis. In other words, we transform the data so that the differences in pairs between treated units and their matched untreated units constitute the observed data subject to further modeling.
Apply a nonparametric model such as local polynomial regression (Fan and Gijbels 1996) or lowess smoothing (Cleveland 1979) to the matched differences to yield a pattern of treatment effect heterogeneity. That is, we will obtain, typically in a graphic form, a non-parametric smoothed curve for the trend in matched differences as a function of the propensity score. The researcher can then interpret the curve to answer substantive research questions.
Algorithmically, matching estimators differ according to the number of matched control units and how multiple matched control units are weighted if more than one control unit is matched to each treated unit (Abadie and Imbens 2009; Morgan and Harding 2006). In one-to-one matching, we match to the nearest neighbor, that is, the control unit that is closest to the treated unit in its estimated propensity score. One can either use replacement or no replacement of controls to match to treated units. We recommend using replacement to ensure matching availability. The original motivation of matching is to change the observed distribution of the control cases to that of the treatment cases to estimate treatment effects for the treated. As such, many observed units may be discarded in matching procedures. Alternative algorithms include (1) one-to-multiple matching, where we match to k nearest neighbors and assign a weight of 1/k to each, and (2) kernel matching, where a kernel function is used to derive a weighted average from the control units in the local neighborhood around the propensity score of the treated unit. Various variants and alternatives have been proposed in the literature, but there is no clear consensus as to which matching estimator performs best in each application (Morgan and Harding 2006). We compare nearest neighbor matching with 1 and 5 controls to kernel matching.
While we focus on a matching estimator for TT, we could instead match treated units to control units to construct an estimate of TUT. These different estimators require different assumptions, as described in the large literature on matching (Morgan and Harding 2006). As we discussed around equation (13), the ignorability assumption states that there is no bias resulting from using the naive estimator for estimating the treatment effect conditional on the propensity score. This also means that TT and TUT are the same conditional on the propensity score. As a result, the distinction between choosing treated units or untreated units as the target group is of minor consequence for the MS method. Note that the choice of the target group is however consequential for unconditional TT and TUT because the choice dictates the weights over which conditional treatment effects are aggregated over the range of the propensity score. That is, in theory, the MS provides the same pattern for heterogeneous treatment effects as a function of the propensity score, no matter whether treated units or untreated units are taken as the target group for matching. In practice, results of the two approaches often differ due to data limitations, typically at the tails of the propensity score distribution.
3.5 The Smoothing-Differencing Method (SD)6
The third method, which we call the smoothing-differencing (SD) method of estimating heterogeneous treatment effects, is closely related to the second method as it also uncovers the heterogeneity pattern as a non-parametric function of the propensity score. The steps of the method are:
Estimate the propensity scores for all units, as discussed in subsection 3.2 and step (1) of subsection 3.3.
For each group (the control group and the treatment group) fit separate nonparametric regressions of the dependent variable on the propensity score. This is the smoothing step of the method. For example, we may use local polynomial regression with suitable bandwidth parameters for this step (Fan and Gijbels 1996).
To obtain the pattern of treatment effect heterogeneity as a function of the propensity score, take the difference in the non-parametric regression line between the treated and the untreated at different levels of the propensity score (e.g., using a grid of values over the common support).
Recall that in the MS method we first match the untreated to the treated to obtain observation-level differences and then smooth the differences. We conceptually reverse the procedure in the SD method by applying the smoothing step first among the treated and among the untreated and then comparing the two groups. The results of the two procedures should be comparable, although both procedures have specific advantages. The main advantage of the MS method is that it allows the researcher to look at observation-level differences between a treated unit and an untreated unit (or units). Such close examination of raw data may be helpful to the researcher. The SD method has two advantages. First, if we consider matching a modeling device, the MS method (as well as the SM method) involves two modeling processes. In contrast, the SD method requires only a single-modeling procedure, in the smoothing step; the second step, the differencing step, is a mathematical operation that does not require any statistical modeling. For this reason, the SD method is simpler and requires fewer modeling decisions. Second, because this procedure requires only single-step modeling, the computation of confidence intervals for the treatment effects by the propensity score is much easier for the SD method than for the SM method.7
4 Empirical Example
To demonstrate the three methods, we draw on Brand and Davis’s (2011) study in analyzing the effects of college attendance on women’s fertility. We replicate one segment of their original analysis with our first estimator (SM) and then demonstrate our second and third estimators (MS and SD). In the subsections that follow, we (1) describe our data; (2) report results for our propensity score model; (3) present results for effects of college attendance on women’s fertility under an assumption of treatment effect homogeneity; and (4) discuss results for heterogeneous college effects using SM, MS, and SD.
4.1 Data Description
We use panel data from the National Longitudinal Survey of Youth 1979 (NLSY), a nationally representative sample of 12,686 respondents who were 14-22 years old when they were first interviewed in 1979. NLSY respondents were interviewed annually through 1994 and are currently interviewed on a biennial basis. We use data gathered from 1979 through 2006. We restrict our sample to women (n = 6,283) who were 14-17 years old at the baseline survey in 1979 (n = 2,736), who had completed at least the 12th grade when they were 19 years old (n = 2,090), who did not have missing data on college attainment (n = 2,013) or fertility in the 2006 survey (n = 1,512). We set these sample restrictions so that all measures we use are pre-college, particularly ability, and to compare college-educated women with women who completed at least a high school education.8 The women we lose due to missing data and attrition tend to be from more disadvantaged family backgrounds and levels of achievement than those women we retain.
Our treated group is comprised of women who completed at least the first year of college by age 19, and our control group is comprised of women who completed high school but did not attend college by age 19. Of those women who attend college by age 19, roughly half complete college by age 23 and two-thirds complete by their early 40s. About 40% of non-college attendees attend college later, although less than 14% complete college. Non-college attendees who attend college at some future point represent a distinct treatment group who are on average more disadvantaged than timely college attendees (Rosenbaum, Deli-Amen, and Person 2006). We do not restrict the control group to women who never attend college; we follow Brand and Xie (2007) in this regard and collapse all future paths when assessing the treatment at a particular time. That is, we focus on whether or not a college education occurs at a particular time and remain agnostic about future educational acquisition.
Appendix A provides descriptive statistics for the precollege covariates we use to construct propensity score strata. These measures figure prominently in economic and sociological studies of educational and occupational attainment, and their measurement is straightforward. The likelihood of attending college varies by race and ethnicity, social origins, ability,9 academic achievement, and pre-college fertility in expected directions. Blacks, Hispanics, teenage mothers, and women with disadvantaged social backgrounds and low levels of academic achievement and ability are less likely to go to college than white women, women who are not teen mothers, and women with advantaged social backgrounds and high levels of academic achievement and ability.
4.2 Propensity Score Estimation
The first step in our analysis is to estimate propensity scores for each woman in the sample for the probability of timely college attendance given a set of observed covariates using a probit regression model. Alternative specifications of this model, including interactions and higher order terms (in addition to mother’s education), yield substantively similar results, so we chose the more parsimonious model. Table 1 provides results for the propensity model, which support the literature on the determinants of college attendance.
Table 1. Propensity Score Probit Regression: Model Predicting College Attendance (N=1,512).
| Black | −0.133 (0.116) |
| Hispanic | 0.054 (0.158) |
| Mother’s education | −0.137 † (0.080) |
| Mother’s education2 | 0.009 ** (0.003) |
| Father’s education | 0.038 * (0.018) |
| Parent’s inc. (1979 $1,000s) | −0.257 (0.448) |
| Intact family | 0.042 (0.112) |
| Number of siblings | −0.041 † (0.024) |
| U.S. born | 0.351 (0.258) |
| Rural residence | −0.156 (0.110) |
| Southern residence | 0.283 ** (0.099) |
| Catholic | −0.017 (0.108) |
| Jewish | 0.283 (0.462) |
| Mental ability | 0.640 *** (0.079) |
| College-preparatory | 0.369 *** (0.098) |
| Parents’ encouragement | 0.454 *** (0.119) |
| Friends’ plans | 0.058 * (0.023) |
| Child by age 18 | −1.238 *** (0.243) |
| Non-missing on covariates | 0.004 (0.098) |
| Constant | −2.430 *** (0.610) |
| Wald χ2 | 298.98 |
| P > χ2 | 0.000 |
Notes: Numbers in parentheses are standard errors.
Dependent variable is college attendance by age 19 (1) versus high school completion but no college attendance by age 19 (0).
p<.10
p<.05
p<.01
p< .001 (two-tailed tests)
4.3 Homogenous Effect Estimates
Before turning to our heterogeneous effect estimates, we estimate the effect of education on women’s fertility under an (unrealistic) assumption of college effect homogeneity. We evaluate the average effect of college attendance by age 19 on number of children by age 41 using a Poisson regression model controlling for the estimated propensity score.10 Our estimator takes the following form:
| (18) |
where μi is the conditional expected number of children for the ith observation; di indicates whether or not a woman attends college; and pi represents the propensity for college attendance. We report the estimated average effects in Table 2. The results from Model 1, the zero-order relationship, suggest a 16% reduction in the number of children for college-educated women relative to less-educated women. Controlling for the propensity for college attendance in Model 2, or factors that might lead to pre-treatment heterogeneity bias, we find a 10% reduction in the number of children women bear by age 41 associated with college attendance. However, these average effects, whether or not we control for factors that predispose women to attend college, conceal underlying systematic heterogeneity in the effects of college attendance shaped by the population composition of college goers. To this heterogeneity issue we now turn.
Table 2. Homogenous Effects of College Attendance on Fertility (N=1,512).
| Poisson Regression | Model 1 | Model 2 |
|---|---|---|
| College Attendance | −0.171 ** (0.049) |
−0.107 † (0.057) |
| Incidence rate ratio | 0.843 | 0.899 |
| Propensity Score | --- | −0.221 * (0.108) |
| Incidence rate ratio | 0.802 | |
| Constant | 0.647 *** (0.024) |
0.696 *** (0.034) |
| Wald χ2 | 12.10 | 15.59 |
| P > χ2 | 0.001 | 0.000 |
Notes: Numbers in parentheses are standard errors.
Dependent variable is number of children by age 41. Propensity scores were generated by a probit regression model of college attendance by age 19 on the set of pre-college covariates.
p<.10
p<.05
p<.01
p<.001 (two-tailed tests)
4.4 Heterogeneous Effect Estimates using the SM Method
To estimate heterogeneous treatment effects with the stratification-multilevel method (SM), we first group respondents into propensity score strata such that average values of the propensity score and each covariate do not significantly differ between college and non-college women (p<.001) (Becker and Ichino 2002). The frequency distributions for college and non-college women run in opposite directions: for college-educated women the frequency count increases with the propensity score whereas for non-college-educated women the count decreases, as shown in Table 3. There is, however, overlap within each stratum (i.e., for each propensity score stratum there are both college and non-college educated women).
Table 3. Covariate Means by Propensity Score Strata and College Attendance (N= 1,512).
| Stratum 1 [0.0-0.1) |
Stratum 2 [0.1-0.2) |
Stratum 3 [0.2-0.3) |
Stratum 4 [0.3-0.4) |
Stratum 5 [0.4-0.6] |
Stratum 6 [0.6-1.0] |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||||||||||
| Variables |
E(X)| d=0 |
E(X)| d=1 |
B |
E(X)| d=0 |
E(X)| d=1 |
B |
E(X)| d=0 |
E(X)| d=1 |
B |
E(X)| d=0 |
E(X)| d=1 |
B |
E(X)| d=0 |
E(X)| d=1 |
B |
E(X)| d=0 |
E(X)| d=1 |
B |
| Black | 0.02 | 0.07 | 0.35 | 0.14 | 0.21 | 0.19 | 0.14 | 0.17 | 0.07 | 0.19 | 0.11 | 0.23 | 0.07 | 0.10 | 0.12 | 0.10 | 0.06 | 0.14 |
| Hispanic | 0.07 | 0.35 | 0.72 | 0.05 | 0.05 | 0.01 | 0.04 | 0.05 | 0.03 | 0.05 | 0.04 | 0.05 | 0.05 | 0.02 | 0.15 | 0.06 | 0.02 | 0.21 |
| Mother’s edu. | 10.35 | 9.97 | 0.13 | 11.19 | 11.73 | 0.29 | 11.49 | 11.17 | 0.17 | 12.15 | 12.29 | 0.08 | 12.58 | 12.57 | 0.00 | 14.07 | 14.47 | 0.17 |
| Mother’s edu.2 | 111.8 | 112.0 | 0.00 | 128.4 | 141.3 | 0.31 | 134.7 | 129.5 | 0.14 | 151.3 | 153.3 | 0.05 | 162.7 | 160.9 | 0.04 | 203.5 | 214.8 | 0.18 |
| Father’s edu. | 9.89 | 9.83 | 0.02 | 11.18 | 10.92 | 0.10 | 11.74 | 11.89 | 0.05 | 12.37 | 12.93 | 0.20 | 12.81 | 13.17 | 0.13 | 15.37 | 15.38 | 0.00 |
| Parents’ inc/1000 | 0.18 | 0.16 | 0.27 | 0.20 | 0.17 | 0.39 | 0.20 | 0.20 | 0.02 | 0.20 | 0.21 | 0.06 | 0.23 | 0.26 | 0.21 | 0.29 | 0.32 | 0.22 |
| Intact family | 0.70 | 0.77 | 0.16 | 0.73 | 0.69 | 0.09 | 0.77 | 0.76 | 0.03 | 0.71 | 0.57 | 0.29 | 0.81 | 0.89 | 0.22 | 0.79 | 0.85 | 0.14 |
| Num. of siblings | 3.96 | 3.68 | 0.13 | 3.32 | 3.50 | 0.08 | 3.08 | 2.85 | 0.11 | 2.53 | 2.86 | 0.19 | 2.71 | 2.42 | 0.20 | 2.22 | 2.34 | 0.09 |
| U.S. born | 0.96 | 0.74 | 0.62 | 0.97 | 0.96 | 0.01 | 0.95 | 0.98 | 0.16 | 0.98 | 0.98 | 0.02 | 0.93 | 0.98 | 0.25 | 0.98 | 0.97 | 0.04 |
| Rural res. | 0.25 | 0.02 | 0.68 | 0.23 | 0.33 | 0.21 | 0.26 | 0.20 | 0.14 | 0.28 | 0.20 | 0.20 | 0.19 | 0.22 | 0.06 | 0.15 | 0.16 | 0.03 |
| Southern res. | 0.31 | 0.28 | 0.05 | 0.26 | 0.36 | 0.21 | 0.30 | 0.16 | 0.35 | 0.36 | 0.50 | 0.29 | 0.41 | 0.38 | 0.07 | 0.40 | 0.35 | 0.11 |
| Catholic | 0.28 | 0.40 | 0.24 | 0.31 | 0.46 | 0.32 | 0.34 | 0.39 | 0.10 | 0.33 | 0.24 | 0.21 | 0.37 | 0.37 | 0.01 | 0.40 | 0.32 | 0.17 |
| Jewish | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.04 | 0.27 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.17 | 0.04 | 0.05 | 0.05 |
| Mental ability | −0.34 | −0.47 | 0.26 | −0.03 | 0.03 | 0.15 | 0.28 | 0.24 | 0.12 | 0.34 | 0.33 | 0.02 | 0.59 | 0.67 | 0.20 | 0.98 | 1.05 | 0.14 |
| College-prep. | 0.06 | 0.03 | 0.16 | 0.16 | 0.13 | 0.10 | 0.21 | 0.31 | 0.23 | 0.47 | 0.33 | 0.29 | 0.58 | 0.61 | 0.07 | 0.73 | 0.77 | 0.11 |
| Parents’ enc. | 0.45 | 0.58 | 0.26 | 0.67 | 0.65 | 0.05 | 0.82 | 0.82 | 0.00 | 0.82 | 0.83 | 0.02 | 0.92 | 0.91 | 0.06 | 0.96 | 0.96 | 0.04 |
| Friends’ plans | 12.77 | 13.75 | 0.58 | 13.80 | 13.88 | 0.04 | 14.24 | 14.75 | 0.28 | 14.67 | 14.68 | 0.01 | 15.04 | 14.90 | 0.08 | 16.17 | 15.88 | 0.20 |
| Child by age 18 | 0.23 | 0.11 | 0.32 | 0.02 | 0.01 | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.10 | 0.00 | 0.00 | 0.03 |
| Non-missing | 0.65 | 0.62 | 0.06 | 0.66 | 0.87 | 0.50 | 0.76 | 0.61 | 0.32 | 0.70 | 0.73 | 0.07 | 0.80 | 0.76 | 0.09 | 0.78 | 0.71 | 0.14 |
| Propensity score | 0.05 | 0.06 | 0.40 | 0.15 | 0.16 | 0.51 | 0.25 | 0.26 | 0.38 | 0.34 | 0.35 | 0.17 | 0.48 | 0.50 | 0.39 | 0.72 | 0.74 | 0.19 |
| Sample Size | 419 | 21 | 225 | 56 | 151 | 40 | 92 | 57 | 112 | 118 | 73 | 148 | ||||||
Notes: E(X)|d=0 indicates the mean of X for women who did not attend college by age 19 but completed high school, and E(X)|d=1 indicates the mean of X for women who attended college by age 19.
Two issues may emerge when studying effect heterogeneity with SM. First, there may not be a sufficient number of treated and control cases within each stratum to estimate level-1 effects. The number of treated cases in the lowest propensity score stratum and the number of control cases in the highest propensity score stratum, the "against the odds" units, pose the most likely problem. There is a tension between achieving balance in the covariate distribution and stability in the estimated effects. We suggest at least 20 treated and 20 control cases within each stratum. For our empirical example, we did not have a sufficient number of non-college goers in the final stratum (i.e., initially we had 15), and therefore collapsed the final two strata and adjusted for the estimated propensity score in the level-1 stratum 6 regression. Second, some covariates may not balance within some strata. We suggest trying different specifications of the propensity score, such as adding interactions and quadratic terms, to achieve balance. But if there is no reasonable adjustment that renders all strata balanced, the analyst may adjust for the unbalanced covariate(s) in the level-1 models. Our indicator of Hispanic ethnicity was not balanced in stratum 1 for the college attendance model, even after various alternative model specifications, and was thus added as a covariate in our level-1 stratum 1 model.
Table 3 provides covariate means by propensity score strata and college attendance. These statistics demonstrate the characteristics of a typical woman within each stratum. For the kth covariate in the jth stratum, we estimate the standardized mean covariate difference to quantify the bias between the treatment and the control groups (DiPrete and Gangl 2004; Morgan and Winship 2007):
| (19) |
where is the sample mean and is the sample variance of the kth covariate in the jth stratum for the treated and control groups as indexed by D=(1,0). The standardized difference is clearly larger in some strata than in others for some covariates. For several characteristics, including race, nativity, rural residence, friend’s plans, and teenage fertility, bias between college and non-college goers’ is largest in stratum 1 for our empirical example; we consider this differential bias when we interpret our results.
We next report results of estimating heterogeneous treatment effects with the SM. We first present the results after stratification only, i.e., level-1 propensity score stratum-specific college effects on number of children using Poisson regression models:
| (20) |
where all the terms are defined above. Subjects indexed by i are nested in propensity score strata indexed by j. Separate Poisson regression models are estimated for each propensity score stratum as indicated by the subscript j. Intercepts and slopes are estimated freely within propensity score strata.
To detect patterns in treatment effects across propensity-score strata, we take the estimated stratum-specific slopes as observations in a level-2 model. For simplicity, we summarize the pattern in heterogeneous treatment effects across propensity-score strata with the following linear model:
| (21) |
where level-1 slopes (δj) are regressed on propensity score rank indexed by j, δ0 represents the level-2 intercept (i.e., the predicted value of the effect of college for the lowest propensity women), and ϕ represents the level-2 slope (i.e., the change in the effect of college on fertility with each one-unit change to a higher propensity score stratum). Normality of ηj is assumed for inference. We use variance-weighted least squares to estimate equation (21), and thus do not assume homogeneity of variances across the δ’s. Variances across the δ’s come from two sources: sampling variation (due to different sample sizes by group) and true population variance (heteroskedasticity). When we account for varying precision of level-1 slopes estimated within strata due to sampling variation, the level-2 slope estimate is more efficient. Heteroskedasticity in this case is substantively significant, as it suggests that the uncertainty of treatment effects may vary across groups (Raudenbush and Bryk 2002).
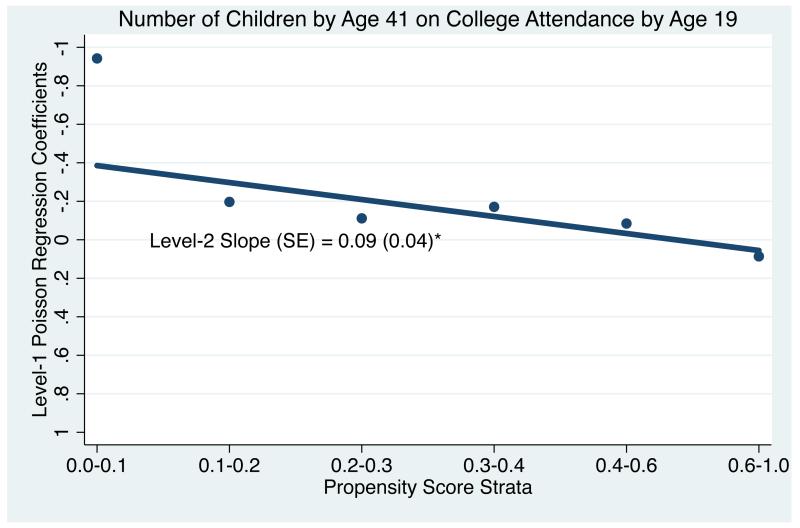
Table 4 and Figure 1 report our multilevel model results for heterogeneous effects of college on fertility. To facilitate implementation of our method, we use the newly developed Stata module --hte-- (Jann, Brand, and Xie 2010).11 The level-2 slope indicates a significant decline in the fertility-decreasing effect of college attendance, a difference of 0.09 for each unit change in propensity score rank. Level-1 estimates range from a 61% decrease in the number of children for women with the lowest propensity to attend college (stratum 1) to an 18% decrease in stratum 2, to a 9% increase in the number of children for women with the highest propensity to attend college (stratum 6). Figure 1 summarizes the results in Table 4. “Dots” in Figure 1 represent point estimates of level-1 slopes, stratum-specific Poisson regression effects of college on number of children by age 41. The linear plot in the figure is the level-2 variance-weighted least squares slope. We reverse the y-axis to emphasize the fertility-decreasing effect of college.
Table 4. Heterogeneous Effects of College Attendance on Fertility (SM; N = 1,512).
| Level-1 Slopes | |
| Poisson Regression | |
| P-Score Stratum 1 | −0.942 ** |
| [0.0-0.1) | (0.348) |
| Incidence rate ratio | 0.390 |
| P-Score Stratum 2 | −0.197 |
| [0.1-0.2) | (0.144) |
| Incidence rate ratio | 0.822 |
| P-Score Stratum 3 | −0.111 |
| [0.2-0.3) | (0.154) |
| Incidence rate ratio | 0.895 |
| P-Score Stratum 4 | −0.171 |
| [0.3-0.4) | (0.140) |
| Incidence rate ratio | 0.843 |
| P-Score Stratum 5 | −0.084 |
| [0.4-0.6] | (0.117) |
| Incidence rate ratio | 0.919 |
| P-Score Stratum 6 | 0.086 |
| [0.6-1.0] | (0.126) |
| Incidence rate ratio | 1.090 |
| Level-2 Slope | 0.088 * |
| Variance Weighted Least Squares | (0.040) |
Notes: Numbers in parentheses are standard errors.
Dependent variable is number of children by age 41. Propensity scores were generated by a probit regression model of college attendance by age 19 on the set of pre-college covariates. Propensity score strata were balanced such that mean values of covariates did not significantly differ between college and non-college goers.
p <. 05
p<.01 (two-tailed tests)
Figure 1.
College Effects on Fertility (SM)
A few additional issues about the SM approach should be noted. First, as shown in Table 4, few of the level-1 estimated effects are significant, despite the significant level-2 slope. This is primarily due to the small sample sizes within strata. Second, there may be differential bias in observed and unobserved factors influencing the treatment and the outcome across propensity score strata. If the bias is greater in stratum 1 than in stratum 6, for example, what can we say about the estimated trend in effects? Perhaps the researcher should resort to sensitivity tests to gauge the susceptibility of the level-2 slope to the presence of stratum-specific omitted variable bias. This issue requires future research.
Finally, Figure 1 depicts the close correspondence between the level-1 college effects on fertility and the level-2 linear regression line. Although this example demonstrates a linear trend in effects of college, linearity is unlikely to hold in most applications [see, for example, Brand (2010) and Brand and Xie (2010)]. In an actual research setting, linearity should be taken as the first-order approximation of a trend. If an analyst has a larger sample size and more strata, and finds evidence of non-linearity, he or she might fit a quadratic or cubed model in level-2. However, in practice, the researcher would have difficulty identifying higher-order terms with the SM approach because typically only a few strata are formed so that only a limited number of δ’s are estimated in the stratification step. It is precisely the need for detecting potential non-linearity that motivates our second and third, non-parametric methods.
4.5 Heterogeneous Effect Estimates using the MS and SD Methods
To estimate heterogeneous treatment effects with the matching-smoothing (MS) method or smoothing-differencing (SD) method, we begin once again by estimating the propensity for treatment. For MS, the second step is to match treated and control units by the estimated propensity scores and generate differences between treated and control units. As we discussed earlier in subsection 3.4, there are several options for matching treated and control units. We choose three options for illustration and compare the results from these options: (1) nearest neighbor matching with 1 control; (2) nearest neighbor matching with 5 controls; and (3) kernel matching (Leuven and Sianesi 2003).12 For the main substantive results, we plot the matched differences between treated and control units along a propensity score x-axis and fit a smoothed curve. Since the main objective of using the MS method is to be non-parametric with respect to the pattern of the heterogeneous treatment effects over the range of the propensity score, the researcher would want to use a flexible modeling device to fit the data. In our example, we use local polynomial regression of degree 1 (i.e. local linear regression), employing the Epanechnikov kernel function with a half-width of 0.2.
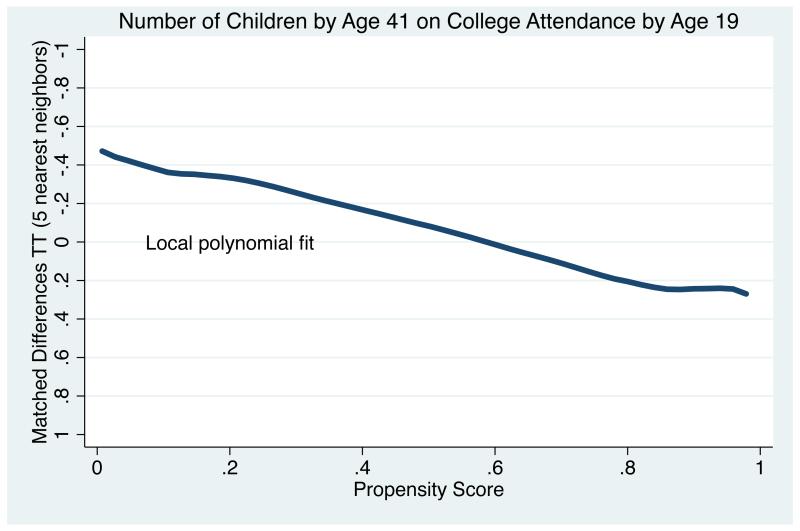
Figure 2 depicts the estimated results for the treatment group with nearest neighbor matching with 5 controls.13 The curve for the treatment effect as a function of the propensity score in Figure 2 can be interpreted as a non-parametric regression for the individually matched differences given in Appendix C. In other words, the “raw” data for the second step of smoothing analysis (Figure 2) are differences of matched comparisons in the first step (Appendix C).14
Figure 2.
College Effects on Fertility (MS)
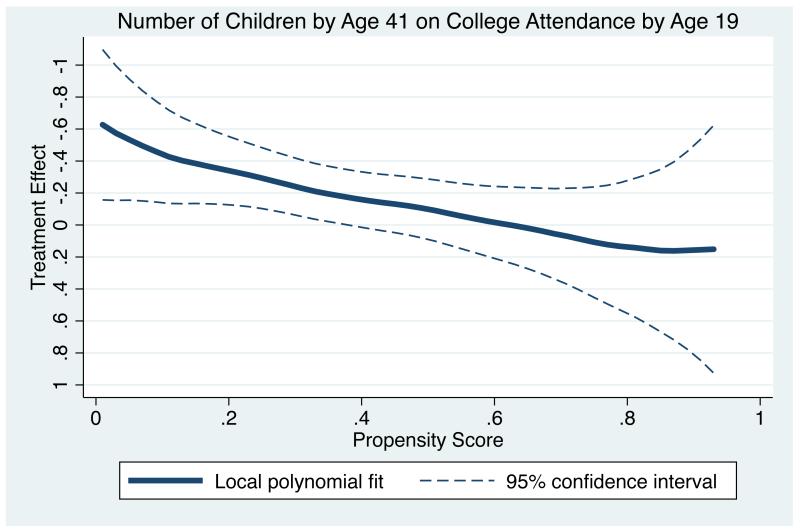
For the smoothing-differencing (SD) method, the first step is to fit two separate non-parametric regression models for the outcome variable on the propensity score, one for the treatment group and one for the control group. Again we use local polynomial regression as a smoothing device (degree 1, Epanechnikov kernel, bandwidth 0.2). The difference between the group-specific regressions gives an estimate of the heterogeneous treatment effects. Figure 3 displays the resulting curve, evaluated over the common support of the propensity score. The 95% confidence interval (using a pilot bandwidth of 0.3 for variance estimation) is included in this plot. Overall, the pattern of the heterogeneous treatment effects in Figure 3 is similar to the one observed using the MS method in Figure 2. Furthermore, changing the bandwidth does not substantially alter the picture; affected are mostly the regions at the boundaries, where statistical precision is low (not shown).
Figure 3.
College Effects on Fertility (SD)
Figures 2 and 3 differ from Figure 1 in that the x-axis is now a continuous representation of the propensity score rather than discrete strata, and the y-axis now depicts differences in the expected number of children rather than Poisson regression coefficients. Moreover, we now have a fully non-parametric depiction of treatment effect heterogeneity, rather than the imposition of a functional form on effect heterogeneity. In our empirical example, it appears that linearity is a reasonable functional form. Hence, the substantive conclusion from using either the SM or the MS/SD method is the same. That is, we still observe a progressively smaller fertility-decreasing effect of college attendance as women’s propensity for college increases. While the data analyzed for this empirical example are well suited to SM because the trend in effects appears linear, there are surely scenarios in which MS or SD can be shown to be advantageous over SM, and vice-versa.
In summary, the example shows that, while women who attended college have lower fertility than similar women who did not attend college, the college effect is the largest for women least likely to attend college and attenuates as we consider women from backgrounds more predictive of college attendance. We offer two alternative interpretations for the results. The first interpretation is that the causal effect of college declines with the propensity of college attendance. Educated women from disadvantaged social backgrounds utilize college for economic gain and consequently limit fertility, while less-educated women from disadvantaged backgrounds have particularly poor labor market prospects and deem motherhood their means to personal fulfillment (Brand and Davis 2011). Such factors would generate, as we observe, a large fertility differential by college education for women from disadvantaged backgrounds. By contrast, college-educated women from advantaged social backgrounds are more likely to have financial and social resources that translate into domestic assistance and childcare, making it possible to have children without the same apprehensions faced by college-educated women from disadvantaged backgrounds, leading to smaller effects of college on fertility. An alternative explanation involves differential selection bias by the propensity for college. For example, women who attend college may be selectively less interested in having children overall, and this selectivity bias is particularly important for women with low propensities of college attendance according to their observed attributes. At higher levels of the propensity, the selectivity affecting both college attendance and fertility may play a smaller role, as such women, if they go to college, are driven more by factors other than this unobserved selectivity.
5 Discussion and Conclusion
Heterogeneous treatment effects, i.e. effects that vary by the probability of selection into treatment, are seldom studied in empirical sociological applications. Researchers are often concerned with key covariates that are believed to be of primary importance, such as gender and race, and often test interaction effects between treatment and these covariates in their analyses. However, studying variation in effects by the treatment probability yields important advantages. For questions of whether there are potential selection biases, i.e., systematic differences between the treatment group and the control group, the interaction between the propensity score and the treatment indicator is the only interaction that should concern the researcher -- a fact already recognized in econometrics (Heckman and Robb 1985; Heckman, Urzua, and Vytlacil 2006) and quantitative sociology (Morgan and Winship 2007; Xie 2011). The propensity score summarizes all relevant information in covariates X, providing a useful solution to data sparseness (Rosenbaum and Rubin 1983,1984). If heterogeneity in treatment effects is such that the treatment effect size is correlated with the propensity score, average treatment effects for units at the margin, units being treated, and units not being treated all change when selection criteria for receiving treatment change (Xie 2011). This is true even when the proportion receiving treatment simply increases or decreases, as in situations when the pool of treatment expands due to either eligibility criteria becoming lower or incentives becoming higher. By revealing how effects differ among subpopulations defined according to their selection into treatment, we can contribute to sociological knowledge about the mechanisms through which treatments affect individuals’ opportunity structures and enable policy makers to make informed decisions to benefit targeted populations.
In this paper, we discuss a practical approach to studying heterogeneous treatment effects, under the same assumption commonly underlying regression analysis: ignorability. We describe three methods within this general approach. For the first method (SM), we begin by estimating propensity scores for the probability of treatment given a set of observed covariates for each unit and construct balanced propensity score strata; we then estimate propensity score stratum-specific average treatment effects and evaluate a trend across the strata-specific treatment effects. For the second method (MS), we match control units to treated units based on the propensity score and transform the data into treatment-control comparisons at the crudest level possible; we then estimate treatment effects as a function of the propensity score by fitting a non-parametric model as a smoothing device. For the third method (SD), we first estimate non-parametric regressions of the outcome variable as a function of the propensity score separately for treated units and for control units and then take the difference between the two non-parametric regressions.
There are tradeoffs between the three methods. The first method (SM) generates stratum-specific estimates that aid the interpretation of treatment effects across strata, which can be compared to population regression estimates under an assumption of homogeneity. This method also provides an estimate of the across-stratum slope, indicating whether or not effect heterogeneity is roughly increasing or decreasing across propensity-score strata. The second and third methods (MS and SD) do not share these advantages, but overcome a major disadvantage specific to SM, i.e., they do not assume a global functional form on the heterogeneity in treatment effects. They allow for heterogeneous treatment effects as a continuous function of the propensity score rather than imposing homogeneity within strata with a sufficient number of observations. We suggest using these methods concurrently.
A few comments are in order as to the benefits of the general approach of focusing on observable heterogeneity in treatment effects. First, while the ignorability assumption is unlikely to be true for most sociological applications, its plausibility depends on how selective the treatment is and how rich the observed covariates are, and is thus a substantive issue in actual research rather than a methodological question that can be debated in general. Second, we assume ignorability only so as to see how much we can learn from the data. Without this assumption, strong parametric assumptions are needed about unobservable variables (Heckman 1978; Willis and Rosen 1979). Third, we can always revisit the assumption of ignorability after the analyses are conducted (Harding 2003; Rosenbaum 2002; Xie and Wu 2005). Indeed, one of the advantages of our approach relative to comparisons between the TT and the TUT is the heightened recognition of potential violations of the ignorability assumption across the distribution of the propensity score. For example, Xie and Wu (2005) interpret a negative selection pattern detected under the ignorability assumption in terms of differential selectivity into treatment status. That is, the ignorability assumption may yield empirical patterns of heterogeneous treatment as a function of covariates, but the empirical results are subject to different interpretations, including those involving selection mechanisms due to unobserved variables. Xie and Wu’s (2005) interpretation of observed heterogeneous treatment effects in terms of unobserved selectivity shows that ignorability is not entirely incompatible with the common notation of selection bias. Indeed, treatment effect heterogeneity we observe may have resulted from unobserved heterogeneity by selection into treatment. Our approach facilitates investigation of heterogeneity bias across the observed likelihood of treatment. Our work on heterogeneous treatment effects therefore complements a large literature that capitalizes on unobserved variables and identification strategies through parametric assumptions and instrumental variables (Heckman 1978; Heckman, LaLonde, and Smith 1999; Heckman, Urzua, and Vytlacil 2006; Willis and Rosen 1979).
Finally, while the kind of heterogeneity in treatment effects we discuss is potentially observable in empirical research using regression analyses without any additional assumptions, it does not mean that it is actually observed or reported in empirical research. That is, while treatment effect heterogeneity under ignorability has long been recognized and accepted, few researchers actually examine patterns of treatment effect heterogeneity by propensity for treatment. We suspect that lack of ready-to-use statistical methods is a reason why heterogeneous treatment effects are not routinely checked and reported. In this paper, we discussed methods that can be used to detect this important interaction pattern, under the same assumption that underlies most of the empirical analyses currently practiced in sociology, no matter whether they are interested in homogeneous effects or interaction effects. That is, while we maintain the ignorability assumption, we relax the strict homogeneity assumption.
Of course, a study of heterogeneous effects using methods discussed in this paper does not solve the main methodological challenge facing empirical researchers: selection on unobservables. Thus, the methods we proposed in this paper are limited, only because they use the same information and presume the same assumption as conventional methods. However, without any additional assumption or additional data, the new methods yield new information of potential importance that is often overlooked in empirical research. Given that no more new data or assumptions are required for the methods being proposed here, continuing the practice of ignoring this kind of information seems unwarranted. Thus, we recommend that researchers use the methods we have proposed here in their empirical work, if not to test theoretically derived hypotheses about heterogeneous treatment effects, then merely as a new way to explore and better understand their empirical data.
Acknowledgments
Financial support for this research was provided by the National Institutes of Health, Grant 1 R21 NR010856-01 and by the Population Studies Center at the University of Michigan and the California Center for Population Research at UCLA, which receive core support from the National Institute of Child Health and Human Development, Grants R24HD041028 and R24 HD041022. A version of this paper was presented at the 2010 Stata Users meeting in Germany. We are grateful to Xiang Zhou and three anonymous reviewers from Sociological Methodology for comments and suggestions on earlier drafts of the paper. We thank Dwight Davis for data analysis that facilitated the empirical example used herein, and Cindy Glovinsky and Jingwei Hu for assistance. The ideas expressed herein are those of the authors.
AUTHOR BIOGRAPHY PAGE
YU XIE
Yu Xie is Otis Dudley Duncan Distinguished University Professor of Sociology and Statistics at the University of Michigan. He is also a Research Professor at the Population Studies Center and Survey Research Center of the Institute for Social Research, and a Faculty Associate at the Center for Chinese Studies. His main areas of interest are social stratification, demography, statistical methods, Chinese studies, and sociology of science. His recently published works include Women in Science: Career Processes and Outcomes (Harvard University Press 2003) with Kimberlee Shauman, Marriage and Cohabitation (University of Chicago Press 2007) with Arland Thornton and William Axinn, Statistical Methods for Categorical Data Analysis (Second edition, Emerald 2008), and Is American Science in Decline? (Harvard University Press 2012) with Alexandra Killewald.
JENNIE E. BRAND
Jennie E. Brand is Associate Professor of Sociology at the University of California – Los Angeles and Associate Director of the California Center for Population Research. Her research focuses on the relationship between social background, educational attainment, job conditions, and socioeconomic attainment and well-being over the life course. This substantive focus accompanies a methodological focus on causal inference and the application and innovation of statistical models for panel data. Current research projects include evaluation of heterogeneity in the effects of education on socioeconomic outcomes and the social consequences of job displacement.
BEN JANN
Ben Jann is Professor of Sociology at the University of Bern, Switzerland. His research interests include social-science methodology, statistics, social stratification and labor market sociology. Recent publications include a paper on the Randomized Response Technique in Sociological Methods & Research (with Elisabeth Coutts) and a paper on asking sensitive questions using the Crosswise Model in Public Opinion Quarterly (with Julia Jerke and Ivar Krumpal).
Appendix A. Descriptive Statistics of Pre-College Covariates and Fertility by College Attendance, NLSY Women (N=1,512)
| No College Attendance by Age 19 |
College Attendance by Age 19 |
|||
|---|---|---|---|---|
| Variables | Mean | Std. Dev. | Mean | Std. Dev. |
| Race | ||||
| Black (0-1) | 0.149 | 0.356 | 0.100 | 0.301 |
| Hispanic (0-1) | 0.055 | 0.228 | 0.035 | 0.185 |
| Family background | ||||
| Mother’s education (years) | 11.403 | 2.286 | 13.050 | 2.429 |
| Father’s education (years) | 11.424 | 3.095 | 13.636 | 3.246 |
| Parents’ income (1979 dollars) | 20434 | 11626 | 26077 | 13144 |
| Intact family age 14 (0-1) | 0.737 | 0.440 | 0.800 | 0.401 |
| Number of siblings | 3.285 | 2.195 | 2.610 | 1.686 |
| U.S. born (0-1) | 0.960 | 0.197 | 0.971 | 0.167 |
| Rural residence, age 14 (0-1) | 0.235 | 0.423 | 0.197 | 0.397 |
| Southern residence, age 14 (0-1) | 0.321 | 0.466 | 0.360 | 0.476 |
| Catholic (0-1) | 0.322 | 0.467 | 0.345 | 0.476 |
| Jewish (0-1) | 0.005 | 0.071 | 0.025 | 0.156 |
| Ability and academics | ||||
| Mental ability* | 0.089 | 0.616 | 0.660 | 0.563 |
| College-prep. (0-1) | 0.252 | 0.423 | 0.559 | 0.492 |
| Social-psychological | ||||
| Parents’ enc. college (0-1) | 0.679 | 0.457 | 0.881 | 0.322 |
| Friends’ plans (years schooling) | 13.904 | 2.060 | 15.133 | 1.900 |
| Fertility history | ||||
| Had a child by age 18 (0-1) | 0.084 | 0.276 | 0.004 | 0.063 |
| Fertility | ||||
| Number of children age 41 | 1.909 | 1.301 | 1.610 | 1.246 |
| Sample Size | 1072 | 440 | ||
| Weighted Sample Prop. | 0.68 | 0.32 | ||
Notes: Ability is measured with a scale of standardized residuals of the ASVAB. All statistics are weighted by a NLSY panel weight.
Appendix B. Matching Estimates of Effects of College Attendance on Fertility (N = 1,512)
| TT | TUT† | |
|---|---|---|
| Nearest neighbor matching, 1 control | −0.136 (0.115) |
−0.319 * (0.170) |
| Nearest neighbor matching, 5 controls | −0.100 (0.097) |
−0.427 ** (0.159) |
| Kernel matching | −0.097 (0.090) |
−0.395 ** (0.153) |
Notes: Numbers in parentheses are standard errors.
Dependent variable is number of children by age 41. Treatment is college attendance by age 19. Propensity scores were generated by a probit regression model of college attendance on the set of pre-college covariates. The unmatched difference is −0.361 with a standard error of 0.074.
Bootstrapped sandard errors based upon 50 replications.
p<.10
p<.01 (two-tailed tests)
Appendix C. College Effects on Fertility (MS)
Footnotes
There are actually two large literatures of using instrumental variables (IV) to identify heterogeneous treatment effects. In one literature, a binary IV is used to identify a “local average treatment effect” (LATE) (Angrist, Imbens, and Rubin 1996; Angrist and Pischke 2009). In another literature, Heckman and his associates (Heckman, Urzua, and Vytlacil 2006; Heckman and Vytlacil 1999, 2001, 2005) have developed a method of estimating marginal treatment effect (MTE) with continuous and perhaps multiple IVs. For an application of the MTE approach in sociology, see Tsai and Xie (2011).
See similar comments in Angrist and Krueger (1999), Elwert and Winship (2010), Morgan and Winship (2007), and Xie (2007, 2011).
Note that the commonly used fixed-effects estimator for observational studies eliminates only (time-invariant) pre-treatment heterogeneity bias, but not treatment-effect heterogeneity bias, because the fixed effects estimator only eliminates pre-treatment (i.e., fixed) differences between the treated and untreated groups (Angrist and Krueger 1999).
Of course, we can also estimate the propensity score with a logit model. Differences between the two models are usually minor (Powers and Xie 2008, p.44).
The researcher would need to specify a level of significance for testing the differences. As expected, the lower the level, the more stringent the test (i.e., the more likely that some covariates do not satisfy it and remain unbalanced). Alternative algorithms to determine propensity score balance are also possible, such as minimizing the standardized bias for each covariate and the propensity score (Imai, King, and Stuart 2008).
We thank Xiang Zhou and an anonymous reviewer for suggesting this method to us. The method has also been applied in previous work by one of the authors (Fritschi and Jann 2009).
We provide confidence intervals for the SD method in the companion Stata module.
We impute missing values for our set of pre-treatment covariates based on all other covariates. Most variables have 1-2% missing values. Only two variables are missing for more than 5% of the sample: parents’ income (355 cases) and high school college-preparatory program (135 cases).
In 1980, 94% of the NLSY respondents were administered the Armed Services Vocational Aptitude Battery (ASVAB), ten intelligence tests measuring knowledge and skill in areas such as mathematics and language. We residualize separately by race and ethnicity each of the ASVAB tests on age at the time of the test, standardize the residuals to mean zero and variance one, and construct a scale of the standardized residuals (α = .92) with a mean of zero, a standard deviation of 0.75, and a range of −3 to 3 (Cawley et al. 1997).
We use a Poisson rather than a negative binomial model because we did not find evidence of overdispersion (i.e., the variance of the outcome is not greater than the mean of the outcome).
In Stata, type “ssc install hte.”
Appendix B provides matching estimates of TT and TUT using these alternative algorithms. Estimates suggest heterogeneity in treatment effects, as we observe substantially greater negative effects for the TUT than for the TT, irrespective of which matching algorithm we use, although none of the estimates reflect statistically significant differences. A greater effect for a randomly selected non-college attendee relative to a randomly selected college attendee would support the results from Figure 1, i.e., that the fertility-decreasing effects of college are larger for women with a low propensity than for women with a high propensity for college attendance.
In results not shown, we observe a moderately steeper slope using nearest neighbor matching with 5 controls than with kernel matching and we observe a larger effect for women with a low likelihood of college attendance when we apply the method to the untreated rather than to the treated. This is due to the increased data mass at the lower end of the propensity score, which makes the smoothing more adaptive in this region.
The y-axis is wider in Appendix C than in Figure 2 in order to fit all the data points.
Contributor Information
Yu Xie, University of Michigan.
Jennie E. Brand, University of California – Los Angeles
Ben Jann, University of Bern, Switzerland.
References
- Abadie Alberto, Guido Imbens. “Matching on the Estimated Propensity Score”. Unpublished manuscript. 2009 [Google Scholar]
- Angrist Joshua D., Imbens Guido W., Rubin Donald B. “Identification of Causal Effects Using Instrumental Variables.”. Journal of the American Statistical Association. 1996;91(434):444–455. [Google Scholar]
- Angrist Joshua D., Krueger Alan B. “Empirical Strategies in Labor Economics.”. In: Ashenfelter O, Card D, editors. Handbook of Labor Economics. 3A. Elsevier; Amsterdam: 1999. pp. 1277–1366. [Google Scholar]
- Angrist Joshua D., Jörn-Steffen Pischke. Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press; Princeton, NJ: 2009. [Google Scholar]
- Ansari Asim, Jedidi Kamel. “Bayesian Factor Analysis for Multilevel Binary Observations.”. Psychometrika. 2000;65:475–496. [Google Scholar]
- Bauer Daniel J., Curran Patrick J. “Distributional Assumptions of Growth Mixture Models: Implications for Overextraction of Latent Trajectory Classes.”. Psychological Methods. 2003;8:338–363. doi: 10.1037/1082-989X.8.3.338. [DOI] [PubMed] [Google Scholar]
- Becker Sascha, Ichino Andrea. “Estimation of Average Treatment Effects Based on Propensity Scores”. Stata Journal. 2002;2:358–377. [Google Scholar]
- Bjorklund Anders, Moffitt Robert. “The Estimation of Wage Gains and Welfare Gains in Self-Selection Models”. The Review of Economics and Statistics. 1987;69:42–49. [Google Scholar]
- Blundell Richard, Dearden Lorraine, Sianesi Barbara. “Evaluating the Effect of Education on Earnings: Models, Methods, and Results from the National Child Development Survey”. Journal of the Royal Statistical Society: Series A. 2005;168:473–512. [Google Scholar]
- Brand Jennie E. “Civic Returns to Higher Education: A Note on Heterogeneous Effects”. Social Forces. 2010;89(2):417–433. doi: 10.1353/sof.2010.0095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brand Jennie E., Davis Dwight. “The Impact of College Education on Fertility: Evidence for Heterogeneous Effects”. Demography. 2011;48(3):863–887. doi: 10.1007/s13524-011-0034-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brand Jennie E., Halaby Charles N. “Regression and Matching Estimates of the Effects of Elite College Attendance on Educational and Career Achievement”. Social Science Research. 2006;35:749–770. [Google Scholar]
- Brand Jennie E., Xie Yu. “Identification and Estimation of Causal Effects with Time-Varying Treatments and Time-Varying Outcomes”. Sociological Methodology. 2007;37:393–434. [Google Scholar]
- Brand Jennie E., Xie Yu. “Who Benefits Most from College? Evidence for Negative Selection in Heterogeneous Economic Returns to Higher Education”. American Sociological Review. 2010;75(2):273–302. doi: 10.1177/0003122410363567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carneiro Pedro, Heckman James J., Vytlacil Edward. “Estimating Marginal Returns to Education”. American Economic Review. doi: 10.1257/aer.101.6.2754. Forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cawley John, Conneely Karen, Heckman James, Vytlacil Edward. “Cognitive Ability, Wages, and Meritocracy.”. In: Devlin B, Fienberg SE, Resnick D, Roeder K, editors. Intelligence, Genes, and Success: Scientists Respond to the Bell Curve. Springer; New York: 1997. pp. 179–192. [Google Scholar]
- Cleveland William S. “Robust Locally Weighted Regression and Smoothing Scatterplots”. Journal of the American Statistical Association. 1979;74:829–836. [Google Scholar]
- Cochran WG. “Observational Studies.”. In: Bancroft TA, editor. Statistical Papers in Honor of George Snedecor. Iowa State University Press; Ames, IA: 1972. pp. 77–90. [Google Scholar]
- Cornfield Jerome, William J, Haenszel W, Hammond EC, Lilienfeld Abraham M., Shimkin Michael B., Wynder Ernst L. “Smoking and Lung Cancer: Recent Evidence and a Discussion of Some Questions”. Journal of the National Cancer Institute. 1959;22:173–203. [PubMed] [Google Scholar]
- Dehejia Rajeev H., Wahba Sadek. “Causal Effects in Nonexperimental Studies: Reevaluating the Evaluation of Training Programs”. Journal of American Statistical Association. 1999;94:1053–1062. [Google Scholar]
- DiPrete Thomas, Gangl Markus. “Assessing Bias in the Estimation of Causal Effects: Rosenbaum Bounds on Matching Estimators and Instrumental Variables Estimation with Imperfect Instruments”. Sociological Methodology. 2004;34:271–310. [Google Scholar]
- Duncan Otis Dudley. Notes on Social Measurement, Historical and Critical. Russell Sage Foundation; New York: 1984. [Google Scholar]
- Duncan Otis Dudley, Stenbeck Magnus, Brody Charles. “Discovering Heterogeneity: Continuous versus Discrete Latent Variables”. American Journal of Sociology. 1988;93:1305–1321. [Google Scholar]
- D’Unger AV, Land Kenneth C., McCall Patricia L., Nagin Daniel S. “How Many Latent Classes of Delinquent/criminal Careers? Results from Mixed Poisson Regression Analyses”. American Journal of Sociology. 1998;103:1593–1630. [Google Scholar]
- Elwert Felix, Winship Christopher. “Effect Heterogeneity and Bias in Main-Effects-Only Regression Models.”. In: Dechter R, Geffner H, Halpern JY, editors. Heuristics, Probability and Causality. A Tribute to Judea Pearl. College Publications; 2010. pp. 327–336. [Google Scholar]
- Fan Jianqing, Gijbels Irène. Chapman & Hall; London: 1996. Local Polynomial Modelling and Its Applications. [Google Scholar]
- Frangakis Constantine E., Rubin Donald B. “Principal Stratification in Causal Inference.”. Biometrics. 2002;58(1):21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritschi Tobias, Jann Ben. Zum Einfluss vorschulischer Kinderbetreuung auf den Bildungsweg und den erwarteten Erfolg am Arbeitsmarkt [The influence of preschool childcare on educational outcomes and expected labor market success] Empirische Pädagogik. 2009;23:500–520. [Google Scholar]
- Gangl Markus. “Causal Inference in Sociological Research.”. Annual Review of Sociology. 2010;36:21–47. [Google Scholar]
- Gelman Andrew, Carlin John B., Stern Hal S., Rubin Donald B. Bayesian Data Analysis. second edition Chapman & Hall/CRC; Boca Raton, FL: 2004. [Google Scholar]
- Greenland Sander S., Poole Charles. “Invariants and Noninvariants in the Concept of Interdependent Effects.”. Scandinavian Journal of Work, Environment & Health. 1988;14:125–129. doi: 10.5271/sjweh.1945. [DOI] [PubMed] [Google Scholar]
- Harding David J. “Counterfactual Models of Neighborhood Effects: The Effect of Neighborhood Poverty on Dropping out and Teenage Pregnancy.”. American Journal of Sociology. 2003;109(3):676–719. [Google Scholar]
- Heckman James J. “Dummy Endogenous Variables in a Simultaneous Equation System.”. Econometrica. 1978;46(4):931–959. [Google Scholar]
- Heckman James J. “Micro Data, Heterogeneity, and the Evaluation of Public Policy: Nobel Lecture.”. Journal of Political Economy. 2001;109:673–748. [Google Scholar]
- Heckman James J. “The Scientific Model of Causality.”. Sociological Methodology. 2005;35:1–97. [Google Scholar]
- Heckman James J., LaLonde Robert, Smith Jeffrey. “The Economics and Econometrics of Active Labor Market Programs.”. In: Ashenfelter A, Card D, editors. Handbook of Labor Economics. Vol. 3. Elsevier Science; New York: 1999. pp. 1865–2097. [Google Scholar]
- Heckman James J., Robb Richard. “Alternative Methods for Evaluating the Impact of Interventions.”. In: Heckman J, Singer B, editors. Longitudinal Analysis of Labor Market Data. Cambridge University Press; Cambridge: 1985. pp. 156–245. [Google Scholar]
- Heckman James J., Singer B. “A Method for Minimizing the Impact of Distributional Assumptions in Econometric Models for Duration Data.”. Econometrica. 1984;52:271–320. [Google Scholar]
- Heckman James J., Urzua Sergio, Vytlacil Edward. “Understanding Instrumental Variables in Models with Essential Heterogeneity.”. The Review of Economics and Statistics. 2006;88:389–432. [Google Scholar]
- Heckman James J., Vytlacil Edward J. “Local Instrumental Variables and Latent Variable Models for Identifying and Bounding Treatment Effects.”. Proceedings of the National Academy of Sciences of the United States of America. 1999;96:4730–734. doi: 10.1073/pnas.96.8.4730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J., Vytlacil Edward J. “Policy-Relevant Treatment Effects.”. American Economic Review. 2001;92:107–111. [Google Scholar]
- Heckman James J., Vytlacil Edward J. “Structural Equations, Treatment Effects, and Econometric Policy Evaluation.”. Econometrica. 2005;73:669–738. [Google Scholar]
- Hedges Larry V. “Fitting Categorical Models to Effect Sizes from a Series of Experiments.”. Journal of Education Statistics. 1982;7:119–137. [Google Scholar]
- Holland Paul W. “Statistics and Causal Inference” (with discussion) Journal of American Statistical Association. 1986;81:945–960. [Google Scholar]
- Imai Kosuke, King Gary, Stuart Elizabeth A. “Misunderstandings between Experimentalists and Observationalists about Causal Inference.”. Journal of the Royal Statistical Society. 2008;171(2):481–502. [Google Scholar]
- Imbens Guido W. “Nonparametric Estimation of Average Treatment Effects under Exogeneity: A Review.”. The Review of Economics and Statistics. 2004;86:4–29. [Google Scholar]
- Imbens Guido W., Angrist Joshua. “Identification and Estimation of Local Average Treatment Effects.”. Econometrica. 1994;62:467–475. [Google Scholar]
- Jann Ben, Brand Jennie E., Xie Yu. “hte : Stata module to perform heterogeneous treatment effect analysis.”. Stata: ssc install hte. 2010 http://econpapers.repec.org/software/bocbocode/s457129.htm.
- Leuven Edwin, Sianesi Barbara. “psmatch2 : Stata module to perform full Mahalanobis and propensity score matching, common support graphing, and covariate imbalance testing.”. Stata: ssc install psmatch2. 2003 http://econpapers.repec.org/software/bocbocode/s432001.htm.
- Lubke Gitta H., Muthén Bengt. “Investigating Population Heterogeneity with Factor Mixture Models.”. Psychological Methods. 2005;10:21–39. doi: 10.1037/1082-989X.10.1.21. [DOI] [PubMed] [Google Scholar]
- Manski Charles. Identification Problems in the Social Sciences. Harvard University Press; Boston, MA: 1995. [Google Scholar]
- Manski Charles. Identification for Prediction and Decision. Harvard University Press; Cambridge: 2007. [Google Scholar]
- Mayr Ernst. The Growth of Biological Thought: Diversity, Evolution, and Inheritance. Harvard University Press; Cambridge, MA: 1982. [Google Scholar]
- Mayr Ernst. “The Philosophical Foundations of Darwinism.”. Proceedings of the American Philosophical Society. 2001;145(4):488–495. [PubMed] [Google Scholar]
- Moffitt Robert. “Identification of Causal Effects Using Instrumental Variables: Comment.”. Journal of the American Statistical Association. 1996;91:462–465. [Google Scholar]
- Morgan Stephen. “Counterfactuals, Causal Effect Heterogeneity, and the Catholic School Effect on Learning.”. Sociology of Education. 2001;74:341–74. [Google Scholar]
- Morgan Stephen L., Todd Jennifer J. “A Diagnostic Routine for the Detection of Consequential Heterogeneity of Causal Effects.”. Sociological Methodology. 2008;38:231–81. [Google Scholar]
- Morgan Stephen, Harding David. “Matching Estimators of Causal Effects: Prospects and Pitfalls in Theory and Practice.”. Sociological Methods and Research. 2006;35(1):3–60. [Google Scholar]
- Morgan Stephen, Winship Christopher. Counterfactuals and Causal Inference: Methods and Principles for Social Research. Cambridge University Press; Cambridge, UK: 2007. [Google Scholar]
- Muthén Bengt, Muthén Linda K. “Integrating Person-centered and Variable-centered Analyses: Growth Mixture Modeling with Latent Trajectory Classes. ”. Alcoholism:Clinical and Experimental Research. 2000;24(6):882–891. [PubMed] [Google Scholar]
- Pearl Judea. Causality: Models, Reasoning, and Inference. Second Edition Cambridge University Press; New York: 2009. [Google Scholar]
- Powers Daniel, Xie Yu. Statistical Methods for Categorical Data Analysis. 2nd Edition Academic Press; 2008. [Google Scholar]
- Rasch Georg. “An Individualistic Approach to Item Analysis.”. In: Lazarsfeld PF, Henry NW, editors. Readings in Mathematical Social Science. Science Research Associates, Inc; Chicago: 1966. pp. 89–107. [Google Scholar]
- Raudenbush Stephen, Bryk Anthony S. “A Hierarchical Model for Studying School Effects.”. Sociology of Education. 1986;59(1):1–17. [Google Scholar]
- Raudenbush Stephen W., Bryk Anthony S. Hierarchical Linear Models: Applications and Data Analysis Methods. Sage; Newbury Park, CA: 2002. [Google Scholar]
- Rosenbaum James E., Deli-Amen Regina, Person Ann E. After Admission: From College Access to College Success. Russell Sage Foundation; New York: 2006. [Google Scholar]
- Rosenbaum Paul R. Observational Studies. Springer; New York: 2002. [Google Scholar]
- Rosenbaum Paul R., Rubin Donald B. “The Central Role of the Propensity Score in Observational Studies for Causal Effects.”. Biometrika. 1983;70:41–55. [Google Scholar]
- Rosenbaum Paul R., Rubin Donald B. “Reducing Bias in Observational Studies Using Subclassification on the Propensity Score.”. Journal of the American Statistical Association. 1984;79:516–524. [Google Scholar]
- Rothman Kenneth J., Greenland Sander., editors. Modern Epidemiology. 2nd Edition Lippincott-Raven Publishers; Philadelphia, PA: 1998. [Google Scholar]
- Rubin Donald B. “Matching to Remove Bias in Observational Studies.”. Biometrics. 1973a;29:159–183. [Google Scholar]
- Rubin Donald B. “The Use of Matched Sampling and Regression Adjustment to Remove Bias in Observational Studies.”. Biometrics. 1973b;29:185–203. [Google Scholar]
- Rubin Donald B. “Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies.”. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Rubin Donald B. “Estimating Causal Effects from Large Data Sets Using Propensity Scores.”. Annals of Internal Medicine. 1997;5(127):757–763. doi: 10.7326/0003-4819-127-8_part_2-199710151-00064. 8 Pt 2. [DOI] [PubMed] [Google Scholar]
- Sobel Michael E. “Causal Inference in the Social Sciences.”. Journal of the American Statistical Association. 2000;95:647–651. [Google Scholar]
- Tsai Shu-Ling, Xie Yu. “Changes in Earnings Returns to Higher Education in Taiwan since the 1990s.”. Population Review. 2008;47:1–20. [Google Scholar]
- Tsai Shu-Ling, Xie Yu. “Heterogeneity in Returns to College Education: Selection Bias in Contemporary Taiwan.”. Social Science Research. 2011;40:796–810. doi: 10.1016/j.ssresearch.2010.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vermunt Jeroen K. “Comments on Latent Class Analysis of Complex Sample Survey Data: Application to Dietary Data.”. Journal of the American Statistical Association. 2002;97(459):736–737. [Google Scholar]
- Vermunt Jeroen K. “Multilevel Latent Class Models.”. Sociological Methodology. 2003;33(1):213–239. [Google Scholar]
- Willis Robert J., Rosen Sherwin. “Education and Self-Selection.”. Journal of Political Economy. 1979;87:S7–36. [Google Scholar]
- Winship Christopher, Morgan Stephen L. “The Estimation of Causal Effects from Observational Data.”. Annual Review of Sociology. 1999;25:659–706. [Google Scholar]
- Xie Yu. “Assessment of the Long-Term Benefits of Head Start.”. In: Oden S, Schweinhart LJ, Weikart DP, editors. Into Adulthood: A Study of the Effects of Head Start. High/Scope Press; Ypsilanti, MI: 2000. pp. 139–167. [Google Scholar]
- Xie Yu. “Otis Dudley Duncan’s Legacy: the Demographic Approach to Quantitative Reasoning in Social Science.”. Research in Social Stratification and Mobility. 2007;25:141–156. [Google Scholar]
- Xie Yu, Xiaogang Wu. “Market Premium, Social Process, and Statisticism.”. American Sociological Review. 2005;70:865–870. [Google Scholar]
- Xie Yu. PSC Research Report. Population Studies Center; University of Michigan: 2011. “Population Heterogeneity and Causal Inference.”; pp. 11–731. [Google Scholar]