A Critical Assessment of Information-guided Protein–Protein Docking Predictions

Abstract

The structures of protein complexes are increasingly predicted via protein–protein docking (PPD) using ambiguous interaction data to help guide the docking. These data often are incomplete and contain errors and therefore could lead to incorrect docking predictions. In this study, we performed a series of PPD simulations to examine the effects of incompletely and incorrectly assigned interface residues on the success rate of PPD predictions. The results for a widely used PPD benchmark dataset obtained using a new interface information-driven PPD (IPPD) method developed in this work showed that the success rate for an acceptable top-ranked model varied, depending on the information content used, from as high as 95% when contact relationships (though not contact distances) were known for all residues to 78% when only the interface/non-interface state of the residues was known. However, the success rates decreased rapidly to ∼40% when the interface/non-interface state of 20% of the residues was assigned incorrectly, and to less than 5% for a 40% incorrect assignment. Comparisons with results obtained by re-ranking a global search and with those reported for other data-guided PPD methods showed that, in general, IPPD performed better than re-ranking when the information used was more complete and more accurate, but worse when it was not, and that when using bioinformatics-predicted information on interface residues, IPPD and other data-guided PPD methods performed poorly, at a level similar to simulations with a 40% incorrect assignment. These results provide guidelines for using information about interface residues to improve PPD predictions and reveal a bottleneck for such improvement imposed by the low accuracy of current bioinformatic interface residue predictions.

Proteins work in close association with other proteins to mediate the intricate functions of a cell. The atomic resolution of the structure of a protein complex can therefore help one understand a protein's function in detail. Protein–protein docking (PPD),¹ a computational approach that complements experimental structure determinations, has attracted increasing research interest (1, 2), in part because it remains challenging to determine most structures of protein complexes via experimental techniques (3).

To improve the performance of PPD predictions, experimentally derived data (e.g. distances) and information (e.g. the identity of interface residues) have been used either as a filter allowing less plausible docking solutions to be disregarded (4–9) or as a constraint to guide the docking process (10, 11). Various types of data and information have been used to aid PPD (12); these range from distances between, or the relative orientation of, the two interacting proteins to simple identification of the amino acid residues directly involved in the binding of the two proteins (13). Despite considerable success, the caveat for all these data-guided PPD predictions is that the data or information used must be correct in order to avoid spurious results caused by misguiding (12). It is therefore pertinent and important to evaluate the effects of errors in the incorporated data or information on the quality of PPD solutions.

We have recently shown that the use of just a few distance constraints can improve the success rates of PPD such that they rival, or are even better than, those of a global search ranked using a sophisticated energy function, and that errors in the distance data significantly decrease the success rates of prediction (11). However, because distance data for interacting proteins are usually hard to obtain, other types of data or information, even if “ambiguous” (10), are increasingly used in PPD predictions (12, 14). In this study, we investigated the effects of incompletely and incorrectly assigned interface/non-interface residues, a major source of the so-called ambiguous data, on information-guided PPD predictions.

As illustrated in Fig. 1, the information content of interface/non-interface residues can be rich enough to reveal the identity of every pair of residues in contact, but not their contact distances, or so poor as to reveal the interface/non-interface state of these residues but not their pairing relationship, for one or both of the two interacting proteins. To determine how these different levels of residue information content can help PPD predictions and the extent to which the use of incorrectly assigned residues degrades prediction success rates, we have developed a new interface information-driven PPD method (IPPD) and carried out a series of PPD simulations on a well-tested benchmark dataset. The results showed that when the information content was rich, excellent predictions (success rates for producing an acceptable top-ranked model > 70%) could be made via IPPD or by re-ranking a global search's solutions using the same interface information, and that, encouragingly, the success of predictions remained respectable (top-ranked success rates > 15%) when the content was poor. However, when enough of the interface residues were incorrectly assigned, as would be the case when using interface residues predicted by a state-of-the-art bioinformatics method such as CPORT (15), few models ranked first by IPPD or other PPD methods, including HADDOCK (10), a popular ambiguous data-driven PPD method, came close to being acceptable. These results suggest that we can greatly increase the power of PPD predictions for practical applications only if the accuracy of current bioinformatics methods for predicting the interface residues of protein complexes can be significantly improved.

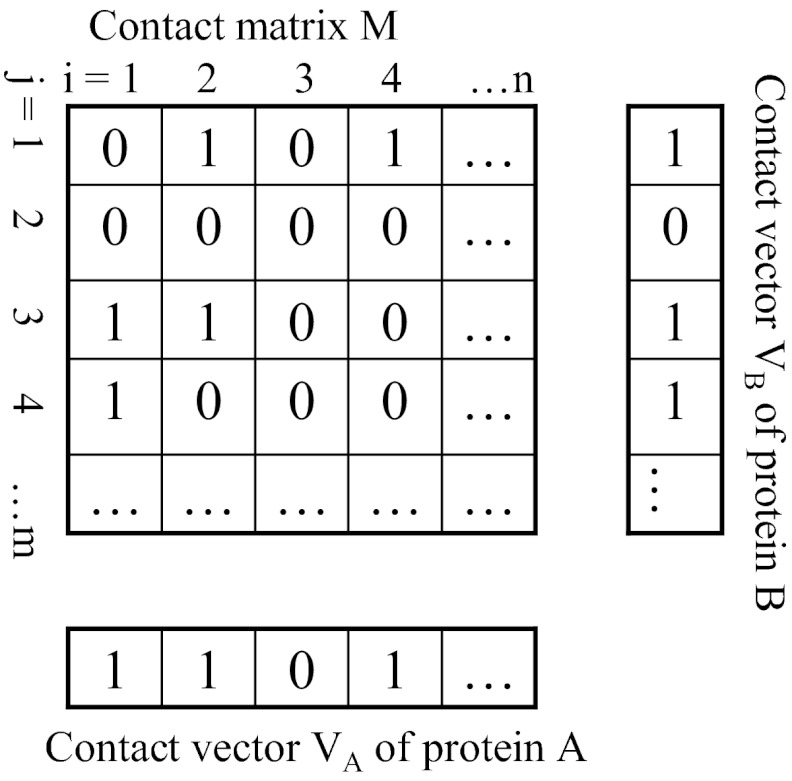
Fig. 1.

Contact matrix of two interacting proteins, A and B, and the contact vectors of their residues. In the contact matrix, M_ij = 1 or 0, respectively, denotes contact or a lack of contact between residue i in protein A and residue j in protein B. In the contact vectors, V_Ai = 1 or 0, respectively, when residue Ai has, or does not have, at least one contact with any residue of protein B.

EXPERIMENTAL PROCEDURES

The steps and parameters used to develop IPPD and perform docking simulations and evaluations closely followed those we reported for a previous study of distance-constrained docking (DPPD) (11). The main differences were the type of data used as constraints (i.e. residue information in IPPD versus distance in DPPD), the expansion of the benchmark dataset of bound/unbound complex structures from 84 (PPD benchmark 2.0 (16)) in the previous study to 124 (PPD benchmark 3.0 (17)) in the present study, and, for re-ranking, the use of a more updated set of ZDOCK's global search (the top 54,000 solutions using a 6° rotational sampling produced by ZDOCK 3.0 (18) instead of ZDOCK 2.0 (19)). These ZDOCK solutions, along with the benchmark structures, were downloaded from the ZDOCK website. As in DPPD (11), ZDOCK re-ranking was included not only to provide a comparison for the performance of IPPD but also to assess the effect of using varying levels of residue information content with respect to both completeness and correctness on different PPD approaches. As before, the interface root mean square deviation (IRMSD) on interface residues, as defined in CAPRI meetings (12, 20–22), was used to determine docking success rates.

The IPPD Method

Like DPPD (11), IPPD finds the best docking solution using the Snyman–Fatti multi-start global minimization algorithm with dynamic search trajectories (23). As described below, the difference between the methods is that in IPPD, an energy function penalizing violations to designated residue information (interface/non-interface state and/or residue pairing relationship) is used instead of one penalizing violations to specific distances, as in DPPD.

Let m and n be, respectively, the number of residues in the receptor (the larger protein in the complex) A = (A₁, …, A_m) and in the ligand (the smaller protein) B = (B₁, …, B_n). The effective energy function used by IPPD to discriminate between different docking solutions is

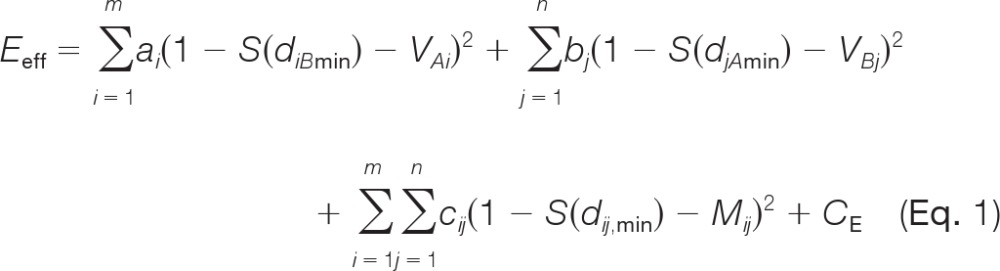where C_E is a clash term used to prevent the overlapping of atoms, as defined previously (11); as in the previous DPPD study (11), this was ignored in ZDOCK re-ranking because atom clashes have already been taken into account in ZDOCK (18, 19). a_i (or b_j) is either 1 or 0, depending on whether or not residue A_i (or B_j) is involved in the calculation; c_ij is 1 or 0, depending on whether or not pairing relationships are used; contact vector element V_Ai for protein A (or V_Bj for protein B) is either 1 or 0, depending on whether residue A_i (or B_j) is designated as an interface residue or a non-interface residue; contact matrix element M_ij is 1 if pairing between residue A_i and residue B_j is designated to occur and 0 if it is not (Fig. 1); d_iBmin (or d_jAmin) is the minimum distance between any heavy (i.e. non-hydrogen) atom of residue A_i (or B_j) and every heavy atom of protein B (or A); and d_ij,min is the shortest distance between heavy atoms in residue A_i and residue B_j that form a pair. To provide constraints from experimentally determined complex structures, a surface residue with a non-zero accessible surface area, as calculated by the Surface program (24), was classed as an interface residue if it had at least one heavy atom within 5 Å of any heavy atom in the other protein in the bound complex and as a non-interface residue if it did not. Finally, S(x) is the s-shaped (sigmoidal) function derived from Bohr et al. (25),

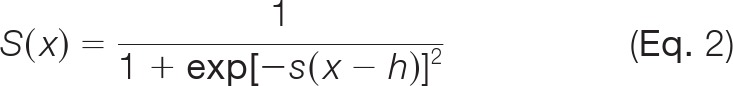where h is the distance threshold used to define interface residues, and the constant s is the slope of the tangent of the function S(x) at x = h (see supplemental Fig. S1). The values in the contact vector are binary (1 or 0; Fig. 1), which confers limited differential states for the energy function to be optimized easily. The purpose of the S(x) function is to transform binary values to a range of real values to allow a better performance of optimization (25). In this work, h was set as 5.0 Å, and s as 0.5, as these values seemed to yield the best performance in preliminary tests.

In essence, the effective energy function works as follows: for a docking pose generated during the docking process, if the computed state of a residue as an interface/non-interface residue or of a pair of residues in terms of meeting the defined pairing relationship is in agreement with the designation (constraint), the result is a contribution of a value between 0 and 0.5 to the energy function, and if not (i.e. a violation of the constraint), it is a value between 0.5 and 1.0, with the exact value of the contribution depending on the magnitude of the shortest distance (see supplemental Fig. S1).

As one might expect, optimization was harder for IPPD than for DPPD because the former is constrained to the much more ambiguous residue information data. For example, in simulations using unbound structures, only 26% of IPPD runs reached the 0.99 confidence level of Bayesian statistics, compared with ∼90% of DPPD runs (11). Those that did not reach the desired high confidence level usually exhausted the optimization limit of 5000 iterations. However, raising the number of optimization iterations to twice this limit did not produce a better, or even a distinctive, docking solution for all the complexes tested (data not shown), indicating that the failure to find a successful docking solution for the unsuccessfully predicted cases was not a result of the use of insufficient optimization iterations.

Graphic Processing Unit Computation

The very large number of distance computations required in order to compute the energy using Equation 1 would result in a very high cost in terms of computing time. To decrease the computational burden, we implemented the docking simulations on a general purpose graphic processing unit, a type of parallel computing architecture in which many processing units execute the same instruction on different data elements (26) that is particularly suitable for calculating atomic coordinates and distances, as in this study. Graphic processing unit computing has been applied to a number of bioinformatics studies in recent years, including sequence alignment (27, 28), systems biology studies of interaction network analysis (29), and structural bioinformatics studies that require the use of desolvation estimates (30) and molecular dynamics simulations (31). In general, compared with state-of-the-art conventional processors, 10 to 30 times more acceleration can be achieved with a graphic processing unit, depending on the type of algorithm executed. In some favorable situations, 300 times more acceleration in sequence alignment (28) and 700 times more acceleration in molecular dynamics simulations (31) have been reported. In our study, the average time for an IPPD run of unbound structures using two contact vectors (Fig. 1) was 2550 s on a Xeon E5620 central processing unit (2.4 GHz) machine with a C2050 graphic processing unit card (448 cores and 144 GB/s memory bandwidth), which is about 30 times faster than using a central processing unit only. The time required varied significantly depending on the size of the protein complex.

RESULTS

Performance of IPPD and ZDOCK Re-ranking Using Different Levels of Information Content

We examined the performance of IPPD and that of a re-ranking of ZDOCK's global search using Equation 1, with three levels of information content derived from the contact matrix in Fig. 1. Because experimentally determined bound complex structures were used to derive the matrix, the information used to constrain/re-rank the docking was without errors, but it was still ambiguous because the residue–residue pairing relationships (for contact vectors) and the specific distances between residues in the contact matrix were unknown.

The results, shown in Table I, indicate that when the information about the contact matrix was correct and complete, (a) all of the 124 benchmark experimental complex structures could be reproduced with precision (IRMSD < 2.5 Å) even without any distance data, (b) almost all of these complexes could be successfully predicted when only the contact vectors were known (i.e. a residue was either at the interface or not, but its contact partners were unknown), and (c) about one-third of the predictions were still good even if only one vector (i.e. information on one, but not both, of the two interacting proteins) was available.

Table I. Top-ranked success rates of IPPD and ZDOCK re-ranking using different levels of information for the 124-complex benchmark dataset.

	Bound structuresa		Unbound structuresb
	IPPD		IPPD		ZDOCK re-rankingc
Criterion (IRMSD)	<2.5 Å	<4.0 Å	<2.5 Å	<4.0 Å	<2.5 Å	<4.0 Å
Full contact matrix	100%	100%	86%	95%	69%	85%
Two contact vectors	98%	99%	64%	78%	56%	73%
One contact vectord	34%	35%	9%	15%	22%	25%

^a ZDOCK solutions for bound structures not available.

^b The best possible success rates for unbound structures (obtained by superimposing them on the bound structures using only interface residues) were 88% for IRMSD < 2.5 Å and 97% for IRMSD < 4.0 Å.

^c The best possible (i.e. top 54,000) success rates for ZDOCK were 78% for IRMSD < 2.5 Å and 94% for IRMSD < 4.0 Å.

^d The top-ranked success rates were for 248 cases, because each complex in the 124-complex benchmark dataset was tested twice, using the contact vector for either the receptor or the ligand.

As might be expected, the performance degraded when unbound structures were used for docking. The degree of degradation depended on information content, being slight (5% to 14%) with use of the full matrix but significant (20–30%) with the use of only vectors. Degradation was largely a consequence of docking not accounting for binding-induced conformational changes, but it also, in small part, was a result of constraining the unbound structures to data derived from bound complexes (11).

Table I also shows that, as in our distance-constraint PPD study (11), re-ranking ZDOCK with the same constraints used in IPPD yielded similar top-ranked (top1) success rates. The main difference between IPPD and ZDOCK re-ranking was that ZDOCK re-ranking had a somewhat worse performance than IPPD when the constraints were abundant, but a better one than IPPD when the constraints were few.

Comparison with Other Methods

In a comparison with three other methods that reported benchmark results using information similar to that of contact vectors, IPPD was superior to all three on identical test structures, with the top1 success rates being 80% versus 36% using 3D-Garden (32) and 53% using HADDOCK (10), and 50% versus 25% using CFTDOCK2 (33) (Table II); the set of structures used by CFTDOCK2 contained a larger percentage of “medium” and “difficult” structures, making them harder to predict.

Table II. Number of top-ranked (top1) docking models produced by 3D-Garden, HADDOCK, CFTDOCK2, and IPPD according to CARPI evaluation criteria.

CAPRI criteriaa	45 complexesb			52 complexesc
	3D-Gardend	HADDOCKe	IPPDf	CFTDOCK2g	IPPDf
High	0	3	7	0	0
Medium	6	14	21	3	12
Acceptable	10	6	8	10	14
Incorrect	29	20	9	39	26
Top1 success rate	16/45 (36%)	23/43 (53%)	36/45 (80%)	13/52 (25%)	26/52 (50%)

^a In these criteria, in addition to IRMSD, ligand RMSD (L_rms) and the fraction of the correctly identified residue-residue contacts (f_nat) are considered (20).

^b Test cases used in 3D-Garden (32).

^c All these are new complexes included in PPD benchmark 4.0 (44). They contain 33 (64%) “rigid body,” 11 (21%) “medium,” and 8 (15%) “difficult” cases; in comparison, PPD benchmark 3.0 (6) contains 88 (71%) rigid body, 19 (15%) medium, and 17 (14%) difficult cases.

^d As reported in Ref. 32.

^e The same interface and non-interface residues used in IPPD were respectively assigned as active and passive residues to run HADDOCK on its server. The server failed to output prediction results for two cases; for those with prediction results, the best structure from the best cluster of each case was selected as the top1 model. When passive residues were assigned by default (residues within 6.5 Å of active residues), the top1 success rate was 52% (22/42), because of an additional case without a prediction result.

^f Contact vectors of both receptor and ligand (see Fig. 1) were used.

^g Based on models kindly provided by Dr. W. Huang, author of CFTDOCK2. The 25% success rate obtained is consistent with those (∼16% to 27%, varying depending on the parameters used) reported in Ref. 33, obtained using only the criterion of IRMSD < 4 Å.

It should be noted that each of these PPD methods is unique in its methodology, and largely because of this the interface data used in these comparisons were not identical. In 3D-Garden, docking solutions were generated by superimposing triangulated facets, a simplified representation of the protein surface, at the interface, and interface information was restricted to a 100-Ų circular patch centered on a point of close contact between two interacting proteins (32), whereas in IPPD, a complete set of specific interface residues (see “Experimental Procedures”) was used that generally covered an irregular shape of contact area of a much larger size (800 to 3370 Ų for these benchmark complexes (16)). The use of a larger interface by IPPD does not completely explain its better success rate in these predictions, however, because increasing the patch size to more than a few hundred square angstroms could lead to compromise of 3D-Garden's ability to identify acceptable models (32). In the comparison with HADDOCK, identical sets of interface and non-interface residues were used, with the former assigned as active residues and the latter as passive residues per HADDOCK's instruction (34). However, in HADDOCK, passive residues are needed to provide distance data to help bring active residues of the interacting proteins into close contact, but, unlike in IPPD, there is not an explicit term in the energy function to penalize models that place passive residues at the interface. Perhaps as a result, using all non-interface residues or just those within 6.5 Å of active residues as passive residues produced almost the same success rate for HADDOCK (see Table II, footnote e). CFTDOCK2 is essentially a ZDOCK re-ranked by a scoring function similar to that of HADDOCK that uses a smaller set of active residues (contact < 4.5 Å, as opposed to the default 6.5 Å used by HADDOCK) (33). Compared to the success rate (73%) of ZDOCK re-ranked by Equation 1 (Table I), and adjusting for the use of harder-to-predict test cases as mentioned above, the comparatively low success rate of CFTDOCK2 again suggests an advantage of explicitly including the contribution of non-interface residues in the energy function. The role of non-interface residues in IPPD is discussed more later.

Performance of IPPD and ZDOCK Re-ranking Using Incomplete and Inaccurate Information

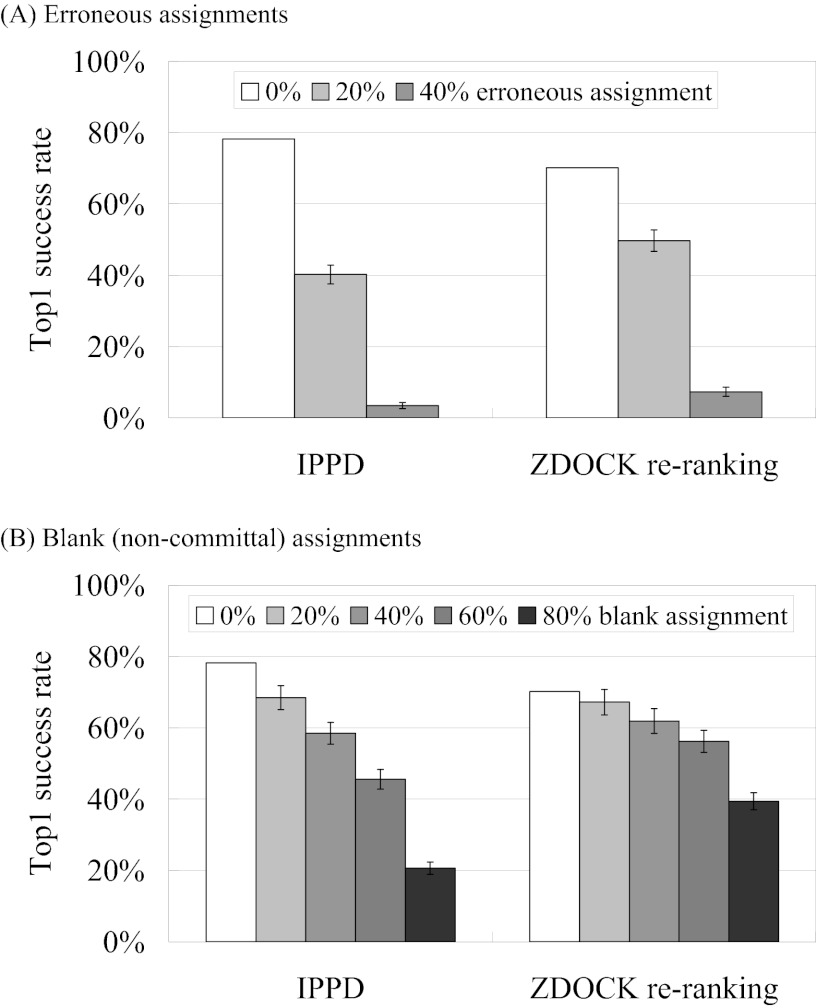
Without knowledge of the complex structure, the contact matrix of Fig. 1 is, at best, partially known, and the correctness of the “known” information is usually uncertain. We therefore carried out a series of IPPD and ZDOCK re-ranking simulations on unbound structures to examine the effects of such uncertainties and errors. The results, presented in Fig. 2, show that, on average, the top1 success rates of IPPD decreased from 78% (for IRMSD < 4 Å; Table I) to 40% when 20% of the residues were incorrectly assigned, providing wrong information for the constraints (i.e. interface residues assigned as non-interface residues and vice versa, or, equivalently, 1 assigned as 0 and 0 as 1 in the contact vectors in Fig. 1); these assignment changes were made randomly and uniformly on both interface and non-interface residues. The success rates decreased further to only 3% on average when 40% of the residues were erroneously assigned (Fig. 2A). In contrast, as shown in Fig. 2B, nearly 60% of the 124 benchmark complexes were successfully predicted when these 40% of residues were not included in the calculation of the effective energy (Equation 1); that is, they were given a blank (i.e. non-committal), as opposed to incorrect, assignment in the contact vectors. Furthermore, a good 20% of top1 success rates could still be achieved using information for just 20% of the residues if they were all assigned correctly (or 80% of the residues were given a blank assignment). The results for ZDOCK re-ranking showed a similar trend, but the decrease in success rates was less marked, suggesting that a global search followed by filtering has a better tolerance for incomplete and inaccurate information than direct data-driven PPD.

Fig. 2.

Top1 success rates of IPPD and ZDOCK re-ranking for the 124 benchmark complexes at a specific percentage of (A) erroneously assigned or (B) blank-assigned interface and non-interface residues. The success rate for each complex was the percentage of 100 independent runs that produced the lowest effective energy solution within 4.0 Å IRMSD of its experimentally determined native state. The 100 independent docking/re-ranking runs for each complex were all subject to the same docking conditions, but the specific set of designated interface and non-interface residues differed from one run to another, owing to random and independent sampling. Dockings were performed on unbound structures. The error bars are the standard error of the mean.

Using CPORT-predicted Interface Residues

In practical PPD predictions, interface residues (and thus non-interface residues) are usually predicted using bioinformatics tools. For example, the success rates of HADDOCK obtained when using only the identity of interface residues predicted by CPORT for 59 of the 124 benchmark complexes have recently been reported (15). In Fig. 3, we compare the results of IPPD and ZDOCK re-ranking with those reported for HADDOCK and for PI-LZerD-2, a method that employs multiple cycles of structure clustering to guide the sampling of docking solutions (35), using CPORT-predicted interface residues for all four methods. The results show that all four PPD methods performed similarly, with ZDOCK re-ranking giving somewhat worse success rates for models outside the top 100 than other methods when evaluated by an IRMSD < 4 Å (Fig. 3B), and PI-LZerD-2 giving somewhat better results than other methods for models within the top 100, especially when a more stringent IRMSD (<2.5 Å) was used (Fig. 3A). In comparison, ZRANK, which does not incorporate CPORT predictions and, instead, employs a sophisticated physical-chemistry-based energy function to sample and rank docking solutions (36), was somewhat better than all four PPD/CPORT methods, especially when the more stringent IRMSD was used (Fig. 3A). However, the top1 success rates were very low (<10%) for all these methods. On average, for the 59 complexes tested, the percentages of incorrectly assigned interface and non-interface residues were 47% and 18%, respectively, for the CPORT predictions, so the low top1 success rates are consistent with those for the simulations using a high percentage of incorrectly assigned residues presented in Fig. 2.

Fig. 3.

Performance of four docking predictions using CPORT-predicted residue information (interface or non-interface). Success rates are shown for the criteria of (A) IRMSD < 2.5 Å and (B) IRMSD < 4.0 Å as a function of the number of ranked models used. The dataset tested contained 59 unbound complexes (mostly enzymes), which were taken from PPD benchmark 2.0 (16). To get the best performance, 87.5% of ambiguous interaction restraints were omitted in HADDOCK/CPORT (15), and 50% of interface and non-interface residues were omitted in IPPD/CPORT. No data were omitted in the ZDOCK re-ranking/CPORT results, and the omission of up to 60% of CPORT's predictions gave similar results (data not shown). Data were downloaded from websites or taken from the indicated reference: CPORT and HADDOCK/CPORT (15), ZRANK (36), and PI-LZerD/CPORT (see Figs. 10C and 10D of Ref. 35).

DISCUSSION

The poor accuracy of current ab initio PPD predictions, which usually involve a grid-based global search of docking solutions, means that they usually fail to place an acceptable model (IRMSD < 4 Å) at the top of the solution list. Data-guided PPD methods have become popular in attempts to overcome this problem. Multiple types of experimental and computational data have been used to predict protein complex structures with success (3, 14, 37). In general, these data are transformed into spatial restraints to guide docking. The transformation of some types of the data, such as distances from cross-linking experiments, is straightforward, whereas that for other types of data, such as information about interface residues or the shape and symmetry of the complex, is not, and restraints resulting from the latter types of data are often referred to as “ambiguous” (13, 37). Ambiguous or not, they all work to restrict the docking space or reduce the degree of freedom (DOF) of the system, which is six (three translational plus three rotational) for docking two rigid bodies (38). Depending on the uncertainties of their measurements and on how they might be used as spatial restraints, different types of data might have different levels of effectiveness in reducing the DOF, and on different aspects of the DOF, too. For example, whereas in ideal situations one distance can reduce the complexity of PPD by one DOF (11), for symmetric interface, at least one rotational DOF cannot be removed using only interface information (39), and information about symmetry can reduce the DOF of a Cn complex from six to four (40). By integrating diverse data, an approach such as that of the Integrative Modeling Platform for macromolecular assembly modeling (41) can resolve much of the ambiguity by harnessing the complementary complex-determining abilities conferred by different types of data. In this study, we devised an effective energy function (Equation 1) to allow information about interface and non-interface residues to be used to make PPD predictions; such types of constraints on the state of information's “presence” or “absence,” analogous to “1” and “0” in the contact matrix (Fig. 1), should be extendable to some other types of data in order for IPPD to include them, as well as for IPPD to be integrated into other approaches.

The so-called ambiguous data are usually incomplete and contain errors, but their effects on PPD predictions have not been rigorously studied. Although many different types of ambiguous data can be utilized, in this study, we focused on a residue's interface information (i.e. whether or not it is an interface residue), because it is a type of information that can be readily obtained from bioinformatics predictions or inferred from mutagenesis experiments, and it therefore has the potential to be widely used.

As demonstrated above, almost all of the bound complex structures tested could be reproduced with good quality (IRMSD < 2.5 Å) if every residue's interface information was known, even if their pairing residues on the other protein and the distances between them were not (Table I). This is at odds with the PI-LZerD-2 results, in which, with clustering, only 20% of bound complexes could be successfully predicted by the top1 model, compared with nearly 100% without clustering (see Fig. 5A of Ref. 35). This suggests that although the clustering of docking solutions might improve PPD performance when the quality of the constraints is not good (Fig. 3), it cannot, for some unknown reason, take full advantage of accurate information. The 5% to 15% drop in the top1 success rates of IPPD when going from bound to unbound structures, which increases with less information content (Table I), was primarily due to binding-induced conformational changes, which are not accounted for by IPPD, an approach based on rigid-body framework, like most other PPD methods (11). Nevertheless, using accurate information for only 20% of all residues, a 20% top1 success rate for producing an acceptable model (IRMSD < 4 Å) could be achieved by IPPD (40% by ZDOCK re-ranking) for unbound docking (Fig. 2B), which is much better than the 8.5% of ZRANK (Fig. 3B), a sophisticated non-data-guided PPD method (36).

On average, for the benchmark structures tested, 20% of all residues amount to 5 interface and 43 non-interface residues per complex. One main difference between our method and other ambiguous data-guided methods, such as HADDOCK, is that in our method, all residues, interface or not, are utilized and treated equally in the effective energy function (Equation 1), and the inclusion of the contributions from non-interface residues significantly improved the success rates, especially for IPPD relative to ZDOCK re-ranking (supplemental Fig. S2). This might have an advantage in that, in general, there are more non-interface residues than interface residues, and therefore more information can be utilized, although it still needs to be correct in order to be helpful.

Our results suggest that the main problem in obtaining a good top1 model for data-guided PPD is the errors in the residue information used. Consequently, we cannot yet expect satisfactory PPD results when using a bioinformatics tool such as CPORT (or others, as none of them are significantly better (42)) to predict the interface residues (and thus the non-interface residues) for use in PPD, because the error rates of these interface predictions are still high (about 30% specificity at 50% sensitivity on average (42)). Indeed, for optimal performance, 87.5% of ambiguous interaction restraints were omitted from the calculations in the HADDOCK/CPORT study (15), and 50% of the data for interface and non-interface residues was omitted in our IPPD/CPORT study (Fig. 3). By not using some of the CPORT predictions, which is equivalent to converting some of the erroneous assignments to non-committal assignments, the sensitivity of IPPD to data errors can be mitigated. No explanation for the omission in the HADDOCK/CPORT study was given, but it could be for a similar reason. In contrast, using all of the CPORT-predicted residues did not significantly affect the performance of ZDOCK re-ranking (Fig. 3), again demonstrating that a global search/filtering method generally has a higher tolerance of data errors. These results suggest that, when in doubt, a non-committal blank assignment is better than a guess if confidence in the interface/non-interface assignment is low. It remains to be determined whether a method for assigning confidence levels on predicted interface/non-interface residues can be developed, as in secondary structure predictions (43), and whether this will significantly increase the success rates of PPD, as suggested by the results of this study.