DNA Looping in Prokaryotes: Experimental and Theoretical Approaches

Abstract

Transcriptional regulation is at the heart of biological functions such as adaptation to a changing environment or to new carbon sources. One of the mechanisms which has been found to modulate transcription, either positively (activation) or negatively (repression), involves the formation of DNA loops. A DNA loop occurs when a protein or a complex of proteins simultaneously binds to two different sites on DNA with looping out of the intervening DNA. This simple mechanism is central to the regulation of several operons in the genome of the bacterium Escherichia coli, like the lac operon, one of the paradigms of genetic regulation. The aim of this review is to gather and discuss concepts and ideas from experimental biology and theoretical physics concerning DNA looping in genetic regulation. We first describe experimental techniques designed to show the formation of a DNA loop. We then present the benefits that can or could be derived from a mechanism involving DNA looping. Some of these are already experimentally proven, but others are theoretical predictions and merit experimental investigation. Then, we try to identify other genetic systems that could be regulated by a DNA looping mechanism in the genome of Escherichia coli. We found many operons that, according to our set of criteria, have a good chance to be regulated with a DNA loop. Finally, we discuss the proposition recently made by both biologists and physicists that this mechanism could also act at the genomic scale and play a crucial role in the spatial organization of genomes.

INTRODUCTION

Different levels of DNA organization exist within bacterial chromosomes. In the case of Escherichia coli, the genome has been shown to be organized, on the largest scale, in four individual macrodomains (Ter, Ori, Right, and Left) and two less-structured regions (1) that have a precise localization within the cell throughout the cell cycle and are associated with specific binding proteins (2). Large-scale DNA loops have been visualized by nucleoid-spreading techniques and are thought to be stabilized by membrane and/or RNA components (3, 4). Then, at the scale of 10 kb, there are topological domains formed by supercoiled structures (5, 6) whose barriers are not placed stably at fixed sites but instead are randomly distributed (7). These intermediate loops can be stabilized with nucleoid-associated proteins like H-NS (8). Finally, there are smaller loops of a few hundred base pairs made by specific transcription factors that have a direct impact on transcription. Although loops of different sizes can have functional consequences for genomic organization and genetic regulation, it is the last category that we focus on in this review.

A first hint that a transcription factor can bind simultaneously to two sites derived from the work of Kania and Müller-Hill in 1977 (9). However, the first experimental demonstration and clear proposal for the existence of a DNA loop affecting gene regulation was in 1984, by the team of Robert Schleif (10), working on the regulatory region of the ara operon. Since then, this phenomenon has been found to play a role in the regulation of several other operons in Escherichia coli. Several historical reviews published in the beginning of the 1990s describe and compare these different cases of DNA loop formation and start to consider the energetics of loop formation (11, 12, 13). Regulatory mechanisms involving DNA looping have also been found in eukaryotes. These often involve more-sophisticated models requiring long-range interactions, like “enhancers” or “insulators” (14) forming higher-order chromatin structures.

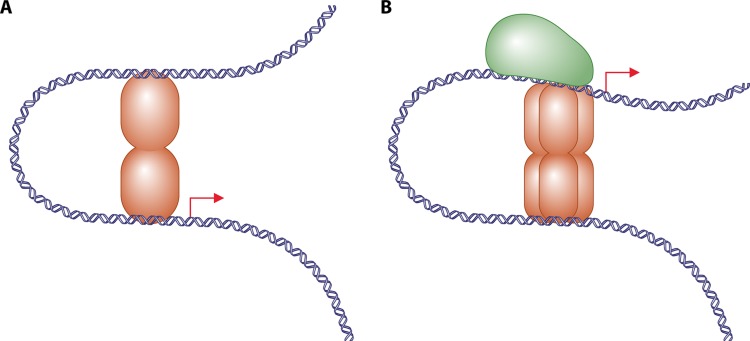
A DNA loop is formed when a protein or a complex of proteins simultaneously binds to two different sites on DNA. Depending on the location of the proteins relative to the transcriptional start site, the formation of the DNA loop can be responsible for transcriptional repression or for transcriptional activation. Examples of both have been documented experimentally, but the phenomenon of transcriptional repression has been better studied at the theoretical level (15, 16, 17). Figure 1 presents the two simple schemes of how a DNA loop can be at the origin of transcriptional repression or activation. In Fig. 1A, a bivalent transcription factor binds simultaneously to two binding sites, creating a loop, generally of the order of a hundred base pairs. The activity of RNA polymerase is blocked, and there is no expression of the operon. Inhibition of transcription can be either at the level of polymerase binding, e.g., due to competition between repressor and polymerase for overlapping binding sites, or at later stages, because RNA polymerase can be trapped in the loop or not be able to recruit an activator (e.g., cyclic AMP receptor protein [CRP]) (11). Repression requiring DNA looping has been experimentally shown in several operons in Escherichia coli; the best-studied examples are ara (10), lac (18, 19), gal (20, 21), deo (22, 23), and nag (24, 25).

Fig 1.

The two main mechanisms of DNA looping in transcriptional regulation are depicted. (A) A DNA loop can be responsible for transcriptional repression. A bivalent transcription factor binds simultaneously to two binding sites and blocks access to the RNA polymerase (e.g., the regulation of the lac operon, the best studied in E. coli). (B) A DNA loop can be responsible for transcriptional activation. Transcription factors bind away from the site of fixation of RNA polymerase (normally of σ⁵⁴ type) and help the recruitment of RNA polymerase and formation of an open complex (in E. coli, the glnALG operon is regulated by this mechanism).

DNA looping can also be at the origin of transcriptional activation. The activation of the expression of the glnALG operon of Escherichia coli by NtrC, which is sometimes called a bacterial “enhancer,” is one of the best-studied cases of this type of system (26). Several binding sites for the transcription factor are placed upstream of the promoter site. RNA polymerase, which in all cases studied is of the σ⁵⁴ type, binds only weakly to the promoter and is unable to form an open complex. Supplementary proteins can facilitate the binding of RNA polymerase and are absolutely required to melt the DNA at the transcription start site. These proteins are called EBPs, for “enhancer binding proteins.” Interestingly, these proteins act at a distance from the promoter site, but generally on the order of about a hundred base pairs, and can function independently of the orientation of the binding site. It is the latter characteristic that recalls the enhancers of eukaryote genomes (27). In their inactive state, the prokaryotic enhancer proteins are usually dimers that bind to pairs of tandem sites in the enhancer elements. Upon encountering inducing conditions, they oligomerize into hexameric or heptameric ATPase-active rings that use the energy of ATP hydrolysis to physically remodel the otherwise stable “closed” complex formed by RNA polymerase with σ⁵⁴ at its promoters. ATP hydrolysis changes the conformation of the EBP from ATP bound to ADP bound and alters its contact with σ⁵⁴. This overcomes the blockage to open complex formation, resulting in separation of the double-stranded DNA and binding of the template strand in the active site of the polymerase, producing a strong transcriptional activation of the operon (28, 29). In the genome of Escherichia coli, there exist several operons that have been shown to be regulated by a similar mechanism, including fdhF, glnH, hypA, prpB, etc. (28, 30). Examples are known in other species (31).

Since the early years of the 21st century, transcription factor-DNA interactions and the phenomenon of DNA looping have become a subject of analysis and research by theoretical physicists (15, 17, 32, 33, 34). DNA looping is seen as a thermodynamic system, and the formalism of statistical physics allows, for example, calculation of the probabilities of a molecule being in one of the different accessible states, i.e., looped or not-looped states (16, 35, 36, 37). This approach brought new ideas and made predictions concerning DNA loops that are interesting to compare with the experimental results.

In this review, we will start by describing various experimental techniques that can be relevant for the detection and justification of the presence of a DNA loop inside a regulatory region. In the second section, we will present the advantages that a mechanism involving DNA looping could bring to gene regulation systems. Several of these properties are predictions derived from recent theoretical work. In the third section, we attempt to identify other operons that could be regulated by such a mechanism. We will focus on the model organism Escherichia coli and make use of some bioinformatics tools to look for new loops that we compare to those in the existing literature.

EXPERIMENTAL TECHNIQUES TO SHOW DNA LOOPING

Several different techniques have been used to demonstrate the existence of a DNA loop. Some of them are classical molecular biology, whereas others involve electron microscopy. The various techniques give information on different aspects of the DNA looping phenomenon, i.e., its impact on gene expression and, also, its thermodynamics. Interestingly, we will see that gene expression and the thermodynamics of the system are connected.

Requirement of two operator sites acting synergistically.

One of the simplest experiments routinely employed to show DNA looping is to mutate one or other of the binding sites and see an effect on the transcriptional regulation, for example, by quantifying the activity of a reporter gene. If the loss of one binding site is equivalent to the loss of both binding sites, it means that the two sites act with “cooperativity.” Regulation does not have to be 100% dependent on the two sites for them to be cooperative; e.g., at lac, binding to O1 and either O2 or O3 is cooperative but there is still some repression by the single O1 site (18, 19). The two sites must act synergistically and not additively. For example, a mutation that inactivates one of the two binding sites for GalR suppresses the repression at the galP2 promoter of the gal operon (38). It should be noted that cooperativity is a necessary but not sufficient condition for the existence of a DNA loop. It is not possible to completely exclude the possibility that other mechanisms responsible for the observed cooperativity could exist (for example, propagation of a physical constraint along the DNA). Therefore, other experiments are necessary to prove that the observed cooperativity is effectively due to a mechanism of DNA looping.

DNase I footprinting.

Another classic technique is DNase I footprinting, because it shows precisely where a regulatory protein can bind on a DNA sequence. Complementing the previous technique, it can confirm the existence of two sites and, under certain circumstances, can show the cooperative binding to the two sites, e.g., if the loss of one operator reduces the affinity of the repressor for the other site (25). Moreover, in the case of certain small DNA loops, it has been noticed by several workers that a pattern of hypersensitive DNase I cleavages every 10 to 11 bp, (with some protection of the intervening DNA) appears between the two binding sites implicated in the DNA loop (24, 39), as shown originally for phage λ repressor (40). The bending that is required to form a small DNA loop compresses the grooves on the face of the DNA on the inside of the loop and makes the grooves on the outside of the loop wider. Because DNase I cuts in the minor groove and its activity is highly sensitive to the width of the minor groove (41), looped regions are readily identified by the formation of hypersensitive cleavages separated by about one turn of a B-form DNA helix. Thus, this technique can bring convincing evidence in favor of DNA looping in a regulatory region. (It should be noted that this technique is carried out on a population of DNA fragments, so there is still the possibility that partial protection could come from different fragments.)

Requirement for the two binding sites to be in phase.

For the formation of DNA loops, and particularly for small loops of about 100 bp, it is necessary that the two binding sites are in phase on the double-helix to allow the interaction. DNA has natural torsional rigidity and develops a resistive torque when it is twisted. Torsional stiffness thus affects the cyclization of DNA, and it can be measured by single-molecule experiments (42). If the two sites are on opposite sides of the double helix, torsional energy is required to twist the DNA so that the operators are available to be simultaneously bound by the oligomeric protein. The torsional energy amounts to 4 kcal/mol to twist by one half turn a linear DNA molecule of 200 bp in vitro (43). It is comparable to the binding affinities between a transcription factor (TF) and its binding site that are between 5 and 15 kcal/mol (44, 45). So when two binding sites are dephased by adding 5 to 6 bp (i.e., half a turn of a double helix), a loss of regulation can be expected. This is the method used by the team of Robert Schleif to demonstrate DNA looping in the regulatory region of the ara operon (10). Repression was impaired in cases in which half-integral turns of the DNA helix were introduced, but repression was nearly normal for the insertions of +11 and +31 bp. It can also be noted that the sequence of the intervening DNA is not completely neutral. In the case of NagC repression of the divergent nagE-nagB genes, the CRP binding site introduces an intrinsic bend in the interoperator DNA. Displacing the CRP binding site by half a turn derepresses the expression of both genes, even though the interoperator distance is not altered (46).

Band shift experiments.

Electrophoretic mobility shift analysis (band shift) can help to indicate the formation of a DNA loop inside a region. The migration of DNA-protein complexes in a polyacrylamide gel depends upon molecular mass, charge, and shape. It is generally used to determine the affinity of a protein for a specific DNA sequence and can be used to calculate a value of the dissociation constant of a protein for a binding sequence. Complexes forming a DNA loop migrate more slowly than the same components in a complex on a linear DNA molecule, i.e., without a DNA loop (19). Therefore, this technique could detect the formation of DNA looping, but as the migration of a protein-DNA complex in a gel depends upon many variables, it is important to be able to compare the same components in a linear and looped conformation. Oehler et al. (19) observed, in a single lane, two shifted bands, one corresponding to two dimers of LacI binding independently and one to a tetramer of LacI binding and forming a loop. The latter band was only observed with LacI, which was capable of forming tetramers, which is a strong argument in favor of its identification as a looped complex. It should be noticed that the position of migration of a looped complex varies considerably with the sequence of the DNA, as observed in reference 47.

Requirement for oligomeric regulators.

To be capable of forming a DNA loop, the regulatory protein must form oligomers with two independent DNA-binding domains. For the majority of standard helix-turn-helix-containing prokaryotic regulators binding to palindromic sequences, this implies the formation of a tetramer. Two methods have been employed to demonstrate the necessity of an oligomeric repressor for regulation.

In the case of the gal operon, the two GalR operators, which were suspected to be at the origin of a DNA loop, were replaced by LacI binding sites. Then, repression of the system in the presence of LacI was compared to that with GalR. Comparable repression in the two cases implied loop formation. This interpretation was confirmed by the use of a mutated form of LacI that is incapable of forming tetramers but that exhibits the same DNA binding properties. In this case, the gal operon was derepressed, showing that a DNA loop was very likely formed in the case of GalR (21). This method works well for related proteins with similar affinities for DNA and whose sites do not interfere with RNA polymerase binding but could be complicated if the operator covers the promoter and its affinity for DNA is not similar to that of LacI for its sites. A more general method is to create mutations within the oligomerization domain of the regulatory protein (48). This method was first applied (by chance) to the lac operon, where a frameshift mutation in LacI produced a protein missing the C-terminal oligomerization domain. This protein repressed much less well than the wild-type protein that is capable of forming tetramers (19).

It should also be noted that, in some cases, a repressor can require an auxiliary protein to stabilize a DNA loop. This is the case for GalR. The laboratory of Sankar Adhya demonstrated that the Gal repressor can only form a loop at the gal operon when the nucleoid-associated protein HU is bound to a specific site near the apex of the loop. The resulting nucleoprotein complex, called a “repressosome,” was shown to carry an antiparallel loop (49, 50).

Plasmid concatenation.

An original method was devised by the team of Kustu to support the model of DNA loop formation responsible for the transcriptional activation in the glnALG operon (51). They showed that the consequence of DNA looping was an increase in the local concentration of the transcriptional activator near the promoter. The transcription of glnA requires NtrC (nitrogen regulatory protein C) to bind upstream of the glnA promoter. Their method consisted of forming concatemers of two plasmids, one carrying the enhancer binding sites that bind NtrC regulatory protein and the other one carrying the glnA promoter. The 3-dimensional (3-D) interaction of NtrC with the RNA promoter-polymerase complex by DNA looping was shown by the comparison of the quantity of transcripts synthesized in the case where the plasmids were concatenated and in the case where they were not. For certain concentrations of the regulatory proteins, the system with concatenated plasmids showed a greater production of glnA transcripts. This experiment demonstrated that one function of DNA loop formation is to enhance the local concentration of the activator in the vicinity of the promoter. To our knowledge, this method has not been applied to loops responsible for transcriptional repression, but it might still work for this type of regulation.

Electron microscopy.

A direct proof of DNA loop formation is the observation of DNA loops between bound proteins by electron microscopy. In 1986, Griffith et al. (52) took pictures of the DNA loop formed by λ repressor binding to operator sites separated by an integral number of turns of the DNA helix. DNA loops of different sizes have been seen with LacI on lac DNA (39). In 1990, striking double loops of octomeric DeoR on native deo DNA were observed (22). To be convincing, several control experiments are needed, as well as rigorous statistics. Indeed, DNA loops can form with a certain probability but without any biological significance (13).

Tethered particle motion.

A more recent technique is tethered particle motion (TPM) (53), which uses concepts from statistical physics and gives information on a single molecule. A DNA molecule is attached by one of its extremities to a glass plate. The second extremity, to which a ball is attached (for example, a microball of polystyrene with a diameter of 0.2 μm), is free to move. The Brownian motion of the ball is then followed by microscopy over a certain time period. If the DNA molecule is in a looped state, the motion of the ball is modified: its motions are more restricted and its statistical properties (as measured by the amplitude of the fluctuations) have changed. An advantage of this technique is that it can distinguish between different configurations of loops (54). It can also give information concerning the duration of the looped and nonlooped states (55). In concept and in the type of information it can bring, this technique is much more oriented to the thermodynamics of the loop than to effects on gene regulation. This technique has been used to study the antiparallel loops formed by GalR in the repressosome (56).

Atomic force microscopy.

Atomic force microscopy (AFM) allows the visualization of the surface topography of a sample. It is based on the physical interactions (as measured by the repulsion of electronic clouds) between the sample surface and a mechanical probe. Lyubchenko et al. (57) analyzed samples of supercoiled minicircles containing the regulatory region of gal. They saw asymmetric structures that correspond to the formation of a loop between the two operator sites with GalR in the presence of HU. This technique also requires careful controls to distinguish protein-bound loops from those formed on plectonemic superhelical DNA. AFM was also used to study the regulatory region of melR (58), using a linear DNA fragment, and seemed to exclude loop formation in this case.

In this section, we have described several experimental methods to show the presence of a DNA loop inside a regulatory region. It is important to keep in mind that it is necessary to combine several methods to validate the physical interaction and demonstrate a role in gene regulation in vivo.

ADVANTAGES OBTAINED VIA DNA LOOPING

Several of the conceivable benefits to the cell from employing the formation of a DNA loop have been described and tested experimentally. Theoretical physics suggests additional advantages that need to be tested, although there are hints to be found in the literature that they do apply in vivo.

High local concentration.

The major advantage that is gained by the formation of a DNA loop is that it produces a high local concentration at the right place (13, 51, 59, 60, 61). The same level of repression could be achieved by higher cellular levels of the transcription factors, but this runs the risk of allowing nonspecific binding to similar but unrelated sites. The DNA loop permits specific binding at a lower concentration than achieved by a single site. If we take the example of the lac operon, the two auxiliary operators will help to increase the concentration of Lac repressor around the principal binding site. Intuitively, the loop keeps the Lac repressor trapped in the vicinity of the principal binding site. In general, transcription factors are only synthesized in small amounts (for example, about 10 LacI tetramers per E. coli cell [59]), so it is necessary to find strategies to keep regulatory proteins at the correct place. The advantage offered by a DNA loop is already experimentally proven, as well as theoretically understood. Müller-Hill and colleagues showed that inactivation of one auxiliary binding site produced a significant loss in repression (18, 19). This effect of local concentration is no longer visible if the concentration of LacI repressors is increased, which shows that the formation of a DNA loop is equivalent to an increase in the concentration of regulatory proteins. The effect has now been quantified using the formalism of statistical physics. Vilar and Leibler (17) calculated that adding an auxiliary binding site is equivalent to increasing the effective concentration of repressors per cell, in agreement with the experimental data. This important concept is related to the chelate effect, which explains local concentration effects on enzymatic and intramolecular reactions (61, 62).

Attenuation of fluctuations.

It is now well accepted that gene regulation has a stochastic component that can have a crucial impact on many biological processes (63, 64). For example, transcription can be observed to occur in “bursts” within individual cells (65). One of the sources of noise is the discrete and small number of molecules that are involved in the regulation of individual genes. Physicists and biologists have proposed that during the course of evolution, mechanisms developed to attenuate these fluctuations (66, 67). DNA looping has been proposed to have such a property. Vilar and colleagues (17, 68), using stochastic simulations (Gillespie algorithm [69]), showed that DNA looping attenuates the temporal fluctuations during gene expression compared to the fluctuations in a system with a single operator. This interesting result is at the moment a numerical prediction and has not been investigated in vivo. Looping allows a fast switching between active and inactive states because the repressor can be quickly recaptured by the main operator and thus maintain a greater repression level for a given level of repressor. If the switching rate is very slow, as in the case of binding to and release from a single operator, there are long periods of time in which mRNA is produced constantly or not at all, which generates larger fluctuations in the expression level.

Another argument in favor of a role of DNA looping in stabilizing a system is that the formation of the loop could prevent the access and the binding of other transcription factors that could interfere with the regulation process. As stated by Michèle Amouyal (70), “loops might insulate a gene and its expression from the genomic environment.”

Lower variability inside a clonal population.

Another theoretical prediction from the work of Vilar and Leibler (17) is that DNA looping can generate a lower variability inside a clonal population. Indeed, they compared the equations for the repression level of a system with a single operator and one with two operators forming a DNA loop. They showed that the system with the DNA loop produced a more homogeneous population of gene expression. This difference is due to the fact that in the looping case, the repression level is a nonlinear function of the number of repressors, which decreases the sensitivity of the repression level to variations in the number of repressors. To our knowledge, no work has been undertaken to test this prediction experimentally. However, we think it would be technically possible by means of time-lapse microscopy techniques, as described in reference 71, or with flow cytometry techniques, as described in reference 72. These experiments could measure the fluorescence distribution of a reporter gene (like gfp) regulated by a single operator or by two operators that can interact by DNA looping and see if the fluorescence distribution of the looping system is narrower than in the case of DNA looping. (The operators would have to be chosen so that the average expression levels from the two systems are similar.)

Faster search of a target location.

It has recently been proposed that the mechanism of DNA looping could accelerate the search by a transcription factor for its target location (73). Indeed, in its search for its target, the transcription factor is proposed to first diffuse in 3 dimensions and then undergo a 1-dimensional (1-D) diffusion along the DNA molecule (sliding). The actual distance that can be covered during the 1-D diffusion is still under debate. Elegant experiments with the restriction enzyme BbvCI show that this distance is 50 bp in vitro (74), and a similar distance has been measured for the Lac repressor in vivo (75). So if two binding sites are separated by more than this distance, they can be considered independent and DNA looping will facilitate the transfer of the protein from the auxiliary binding site to the principal binding site, which is responsible for the regulation. So auxiliary operators can be seen as “waymarks” for the searching protein, allowing transfer between sites separated by distances greater than the 1-D diffusion limit.

Bistability.

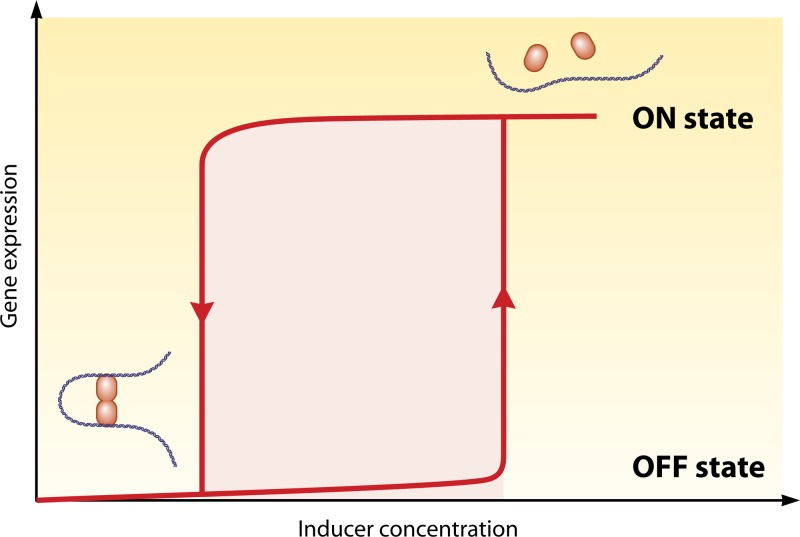
The phenomenon of “bistability” is another concept first described by theoretical physics that has now found its place in experimental biology (76). A bistable system can be in two different stable states at a given level of a stimulus, depending upon its history. As illustrated in Figure 2, in the bistability area (in pink in the figure), the system can correspond to either the ON or the OFF state depending on its initial condition (e.g., the presence or absence of an inducer in a preculture). Such a system will not respond gradually according to the intensity of a stimulus but will have an all or none response (77). Since the expression level depends upon its previous state, this kind of system is often linked to the notion of memory (77, 78). It has been proposed that bistable systems are at the origin of the decision for cell differentiation (79).

Fig 2.

The mechanism of DNA looping could generate the phenomenon of “bistability.” The nonlinear response associated with the cooperativity of DNA looping, as well as a positive feedback in the regulation of the system, can generate bistability. Bistable systems can be in one state or another depending on their history, which can have consequences for the biology of the system. The pink area indicates the concentrations of inducer where the gene can be either repressed or expressed depending upon its initial condition (with low inducer or high inducer concentration).

We would like to suggest that DNA looping could contribute to the formation of a bistable state. Two conditions are necessary to generate bistability: the presence of strong nonlinearities and a positive feedback in the regulatory network (80). The cooperativity produced by DNA looping generates a nonlinearity in the response of the system, so it can facilitate the appearance of bistability. Indeed, for the lac operon, the cooperativity introduced by the DNA loop (17, 81) is responsible for the sigmoidicity of the induction curve of the response (82). Bistability was experimentally shown in early work on the lac operon (83) (but the term bistability was not used) and, more recently, by Ozbudak et al. (82), looking at the expression of a lac-gfp reporter in individual cells. However, the link between the appearance of bistability and the presence of multiple operators with the formation of a DNA loop has not been directly addressed, to our knowledge. Using the same experimental techniques, it would be interesting to verify whether bistability is observed when one or both of the two auxiliary sites is inactivated or if the dimeric LacI protein is used. Although bistability could arise from other phenomena, (e.g., active transport [82]) and has been observed in bacterial systems where nonlinearities arise from positive autoregulation not invoking DNA loop formation (84), it might be worth looking for multiple operators capable of forming a loop in other systems exhibiting bistability. It is also worth noting that DNA looping systems generally present much larger response factors than non-DNA looping systems. Such systems allow a cell to rapidly pass from a genetic state with low gene expression to a genetic state with very high gene expression. For example, wild-type lac operon expression increases by a factor of 1,300 after treatment with the inducer, whereas the construct with just a single O1 operator increases just 18-fold (19). DNA looping appears to be a very practical method of producing a rapid and large-scale biological switch, e.g., when a bacterium has to respond to an environmental signal such as a new carbon source. This is the reason why this type of regulation is widely used in synthetic biology constructs (85).

Robustness to binding site mutations.

Morelli et al. (86) used forward flux sampling simulations to analyze the contribution that DNA looping makes to the stability of the bacteriophage lambda (λ) lysogenic state and its resistance to the effects of mutations in the λ repressor operator sites. In their stochastic simulations, they changed the affinities of the λ repressor binding sites to represent a mutation and found that the global functionality of the system (i.e., its ability to change from the lysogenic to the lytic phase) was unaltered when the loop was present. Their results suggest that DNA looping is crucial for stability and provides a mechanism to minimize the effects of operator site mutations. This property of robustness has been experimentally observed in the λ phage system, by examining the effect of mutations interchanging the OR1 and OR3 operators on the lysogenic/lytic switch (87). Despite large effects on the relative binding of Cro and CI, they found that the phage was still capable of lysogeny and regulated lytic development. A plausible explanation of this robustness is that the cooperativity present in the DNA looping mechanism allows it to compensate when binding sites become less efficient. The analysis by Morelli et al. (86) also showed that DNA looping is necessary for the bistability observed in the bacteriophage λ switch.

ARE THERE OTHER SYSTEMS USING DNA LOOPING TO REGULATE GENE EXPRESSION IN ESCHERICHIA COLI?

It seems surprising that few examples of gene regulation involving DNA looping have been reported in the literature. In E. coli, only six operons have been experimentally investigated and conclusively shown to be regulated by a mechanism involving a DNA loop (ara, lac, gal, deo, nag, and ptsG), which represents only a small proportion of the regulatory regions. As a first approach to look for more systems potentially regulated by DNA looping, we examined the database RegulonDB (88) for gene regulatory regions that could have the requisite characteristics to form a DNA loop. (We realize that not all the transcription factor [TF] binding sites listed in RegulonDB are experimentally demonstrated, but some have been inferred on the basis of sequence analysis. The data set is, however, an unbiased starting point to look for the possible existence of more looping systems.) Using bioinformatics tools, we selected, from among the 600 regulatory regions present in the database (RegulonDB “TF binding sites” file 2011), the ones that have two binding sites separated by a distance of about 90 bp for the same regulator. This distance is the minimum observed in naturally occurring DNA loops, although smaller loops have been shown to function in artificial lac constructs (89). Ninety base pairs is distinctly shorter than the persistence length for DNA, which is about 150 bp for naked DNA (90), as usually measured in vitro by cyclization assays (91, 92). To make smaller loops, the curvature energy of the DNA becomes too great and the formation of the loop is not favorable. However, intrinsic curvature in the intervening DNA and/or the presence of additional DNA-bending proteins like CRP or integration host factor (IHF) can facilitate DNA loop formation (46). Garcia et al. (91) have argued that the cellular environment, which means a supercoiled genome and a high concentration of other specific, as well as nucleoid-associated, DNA binding proteins, favors the formation of smaller DNA loops in vivo. Moreover, Wiggins et al. (93) showed, by AFM, that spontaneous large-angle bends in short DNA fragments were many times more prevalent than expected from classical models of polymers. In addition, the configuration and flexibility of the protein affects its ability to form a loop (94). More precisely, a protein that can exist in a V-shaped structure (as proposed for LacI [95]) will facilitate the formation of a DNA loop with either a parallel or antiparallel configuration (94).

In our bioinformatics survey, we have considered only the simplest case and have looked for those regions with two or more binding sites for the same repressor, obtaining many candidates that are listed in Table 1. We have not looked for examples of loops involving heterologous proteins, (e.g., between σ⁵⁴ RNA polymerase and an EBP [28, 30]). Finally, we have only considered binding sites for a gene-specific regulator; that is to say, we eliminated regions with multiple binding sites for the global transcriptional regulators, i.e., CRP, integration host factor (IHF), FNR, Fis, ArcA, Lrp, and H-NS (118). Indeed, we looked for configurations similar to that of the lac operon, involving a specific regulator. We found 48 regions that, according to these criteria, are good candidates for the detection of a DNA loop. We then compared them to the existing literature (Table 1). Only 6 have been convincingly shown to be regulated by loops (Table 1, indicated in boldface). For 16, there are indications in the literature that a loop is involved. Most of the others have not been studied at the molecular level. It is also striking to note that 14 of these systems are part of divergent promoter systems, so the total number of operons potentially regulated by loops is 61; however, in some cases, only one of the genes has been studied, e.g., exuT-exuC, where only exuT is regulated by ExuR, or fadL-yfcZ, where the OmpR sites regulate fadL. The possibility of coordinate regulation of both directions in this and other cases should be considered. Divergent promoters can provide an economical target for gene regulation via a DNA loop involving two operator sites.

Table 1.

Genes or operons in Escherichia coli known or predicted to be regulated with a DNA loop responsible for transcriptional repression^a

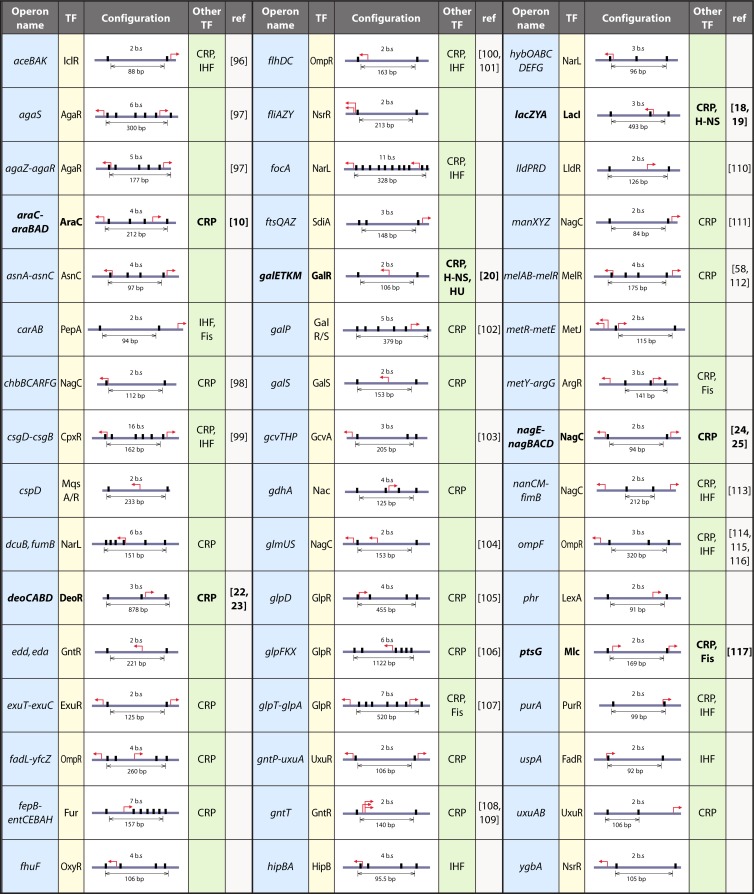
^aData under the column heads are as follows. TF, transcription factor forming or predicted to form the DNA loop. Configuration, configuration of the binding sites responsible for DNA loop formation: the black boxes show the positions of the repressor binding sites relative to the transcription start site, indicated by a bent arrow, and the total number of binding sites (bs) and the distance between the first and last sites are indicated. Other TF, includes other transcription factors (CRP, H-NS, IHF, Fis, or HU) binding in the regulatory region that could have an impact on DNA loop formation. ref, reference(s) to the literature that validate or suggest regulation involving a DNA loop mechanism for this operon or give evidence against looping. Boldface indicates those operons where the loop has been clearly demonstrated.

CONCLUSION AND PERSPECTIVES

DNA looping mechanisms are now well characterized in the regulatory regions of several bacterial operons, either for transcriptional activation or repression. Although this mechanism seems to offer advantages for genetic regulation, relatively few examples have been experimentally investigated. We forecast that loops will be found in other operons of Escherichia coli and hope this review will encourage researchers to investigate potential DNA loops in their systems. We think an exhaustive experimental search for such loops (as predicted in Table 1) would be interesting in a well-studied genome like that of Escherichia coli. Indeed, cooperative binding of transcription factors has been shown for several operons; e.g., see reference 99. If DNA looping is not the cause of this cooperativity, then it means that some other mechanism involving long-range interactions might be discovered.

Looping at the genome scale?

Several biologists and physicists proposed that DNA looping could occur on a genomic scale (16, 119, 120, 121). Bivalent proteins could bind to sites belonging to different genes of a regulon (which could be distant on a 1-D representation of the genome but very close in 3 dimensions). This hypothesis is present in the theoretical work of Buchler et al. (119). The geometrical confinement of the E. coli genome implies that regulatory proteins (the same or different) bound to two different regulatory regions can interact and regulate expression. They point out, however, that excessive “cross talk” between regulatory regions could have negative consequences on gene regulation (119). Coregulation of distal genes is the basis of the solenoidal model of the genome imagined by Képès (121). This author proposed that genes regulated by the same transcription factor are placed periodically on the DNA molecule, thus allowing transcription factors to act on several operons located at one locus inside the cell. Other evidence from analysis of transcriptome data also suggested a correlation in the pattern of expression from distant loci (122). The advantages offered by DNA looping can apply at the genome scale and could help optimize transcriptional regulation (121). At this scale, entropy is the major contributor to the energy required for the formation of macro-DNA loops, and specific mechanisms must come into play to overcome the entropy cost (16). On the other hand, it has been proposed that entropy can be the motor of macroloop formation (123, 124). Indeed, taking into account the size of macromolecules like RNA polymerases and of the crowded nature of the intracellular environment, the global entropy of the system can be minimized by bringing together these large molecules. This forces the grouping of transcription factors, RNA polymerases, and regulated genes into discrete loci, so-called “transcription factories” (125, 126). Computational modeling even suggests that the physical structure of the chromosome is a direct result of regulatory interactions by transcription factors (127). Moreover, the fluorescent probe localization experiments of Wiggins et al. (128) suggest that classical models for DNA being a “wormlike” random coil might not apply to the bacterial genome but that intranucleoid interactions organize the E. coli chromosome into a nucleoid filament precisely positioned within the cell.

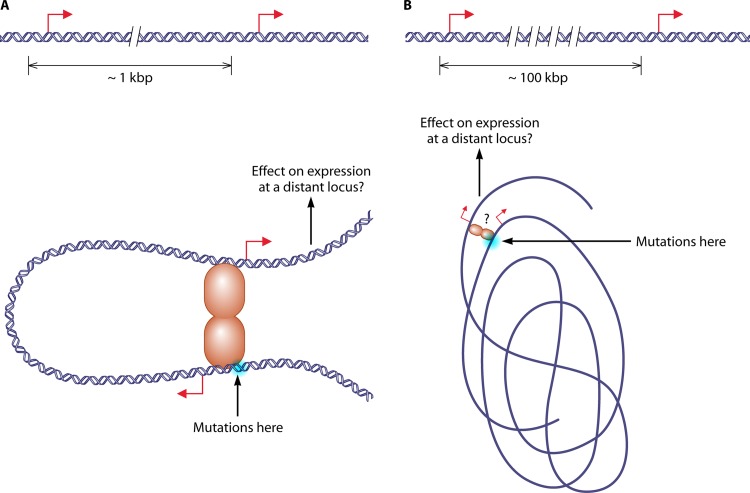
As illustrated in Figure 3, if loops form between regulatory regions of distally located genes, mutations or deletions in binding sites placed elsewhere in the genome could affect the expression of a distally located gene. Classical molecular biology techniques could be used to test this interesting hypothesis. The development of new biochemical techniques to visualize the 3-D conformation of the eukaryotic genome, like capturing chromosome conformation (3C) (129, 130, 131) and circularized chromosome conformation capture (4C), carbon-copy chromosome conformation capture (5C), and high-throughput 3C (Hi-C), etc. (132, 133, 134), as well as the genetic approach based on site-specific recombination developed in reference 1, offers potential ways to validate the existence of such “long-range” interactions inside a bacterial genome. A very recent 3C study in E. coli has demonstrated the existence of long-range interactions between specific DNA binding sites for the GalR repressor in stationary-phase cells (135). This is the first demonstration of a transcription factor organizing the chromosome structure in space at the bacterial genome scale. We believe other examples will be found in the next few years in other bacterial genomes.

Fig 3.

The mechanism of DNA looping could apply to the regulatory regions of two different genes so that binding to distant sites becomes cooperative (16, 121). We can imagine that cooperativity can occur between the regulatory regions of two genes that are relatively close on the genome (separation of the order of 1 kb [120]) (A) or between two genes that are far away in a 1-D representation of the genome (separation of the order of 100 kb) but near in a 3-D one (B). If these kinds of interactions exist, inactivation of binding sites adjacent to one gene would also affect the expression of other genes via the mechanism of DNA looping.

The mechanism of DNA looping is one example where we can see how the thermodynamic properties of macromolecules can have a direct impact on gene regulation. Thus, viewing biological systems as thermodynamic systems, coupled with experimental investigation, produces original ideas and information. Finally, we can say that DNA looping is an interesting phenomenon in transcriptional regulation since it represents one of the first examples of “gene regulation in the third dimension” (136). Understanding the phenomenon of DNA looping and its biological and physical implications will bring new insight to our understanding of other biological phenomena, like the 3-D organization of genomes, in prokaryotes and eukaryotes.