Interpreting genomic data via entropic dissection

Abstract

Since the emergence of high-throughput genome sequencing platforms and more recently the next-generation platforms, the genome databases are growing at an astronomical rate. Tremendous efforts have been invested in recent years in understanding intriguing complexities beneath the vast ocean of genomic data. This is apparent in the spurt of computational methods for interpreting these data in the past few years. Genomic data interpretation is notoriously difficult, partly owing to the inherent heterogeneities appearing at different scales. Methods developed to interpret these data often suffer from their inability to adequately measure the underlying heterogeneities and thus lead to confounding results. Here, we present an information entropy-based approach that unravels the distinctive patterns underlying genomic data efficiently and thus is applicable in addressing a variety of biological problems. We show the robustness and consistency of the proposed methodology in addressing three different biological problems of significance—identification of alien DNAs in bacterial genomes, detection of structural variants in cancer cell lines and alignment-free genome comparison.

INTRODUCTION

Never before have the boundaries of disciplines appeared to have been so effaced than in this era of ‘omics’, which has created unprecedented opportunities to unravel the mysteries of life by decoding the wealth of information obscured beneath assemblies of molecules that epitomize a life. The advent of the era of genomics, proteomics, transcriptomics or metabolomics has transformed the science of life, the transformation being triggered by recent advances in sequencing technologies. The vast amount of genomic data generated from high-throughput sequencing platforms has necessitated the development of efficient computational methods to decode the biological information underlying these data. However, interpreting genomic data is notoriously difficult because of their inherent complexities imparted by evolutionary factors such as mutations, insertions, deletions, duplications, gene transfers, etc.

One approach to interpret a yet uncharacterized genome sequence is to move a window along the sequence and study the local properties of the region within the window (e.g. G+C content of DNA sequence). This is one of the most popular and frequently invoked approaches to study sequence characteristics, owing to its simplicity and the ease in its implementation. However, the scan window methods are sensitive to window size—smaller windows increase stochastic variations, whereas larger windows diminish resolution. Moreover, precise detection of locations of transition from one property to another is not possible within this framework. Probabilistic approaches to interpreting genomic data gained momentum in early 1990s with the adaptation and improvisation of methodologies such as hidden Markov models (HMMs) (1–3). The probabilistic methods were readily adapted to solving a host of biological problems (4–7). Unlike frequently invoked heuristic approaches, the HMMs have a strong theoretical underpinning and are often used to search for optimal partitioning of a sequence (or sequence data set) into classes with distinctive properties. HMMs, however, require to specify the model structure a priori (e.g. the model order or number of distinct classes). Further, HMMs often require a reliable set of training data for learning the values of the model parameters, which may not be available a priori.

A more flexible optimal partitioning is possible using Bayesian methodology, which allows to draw inferences on all unknown quantities of interest on the basis of posterior distributions of these quantities (8,9). Inferences on ‘change points’ delineating compositionally different regions within a genome sequence could be made feasible by the development of efficient sampling techniques, namely, the Markov Chain Monte Carlo (MCMC) methods (10–14). Variants of Bayesian methods included those that obtain the posterior distribution of change point at each sequence position using dynamic programing algorithms and then obtain the optimal partition of the data by maximizing a score function over all possible partitions (9,15). Unlike HMMs, these methods treat each partition independently, characterized by its own set of statistical parameters. However, in reality, the number of distinct classes is often much smaller than the number of all partitions. Further, these methods generate numerous short sequence segments of doubtful biological significance. Further advances allowed characterizing all partitions by fewer feature or data types, which, however, have to be assigned a priori (16,17). Combined approaches, integrating both HMM and Bayesian techniques, were also developed to exploit the complementary strengths of both methods (18). A salient feature of this methodology is to treat the model structure, namely, the model order and number of feature types, also as unknown parameters in the model and infer their values from the posterior distributions obtained via an MCMC technique. Though theoretically appealing, the combined method is computationally demanding and cannot be applied to genome sequences of length >60 kb. When applied to bacteriophage lambda genome (size ∼50 kb), the optimal partitioning recovered the strand identity by generating segments with genes in the same direction of transcription; beyond this, the usefulness of this method has not yet been demonstrated.

Interpreting genomic data at the intrusive levels of complexities is the objective of recursive segmentation methods (19–23). Starting with the entire sequence data, the complexity is decomposed successively by performing a binary segmentation recursively until none of the segments or regions can be divided further, thus outputting regions that are homogeneous within but heterogeneous between, according to a certain criterion. This recursive procedure can be accomplished within a hypothesis-testing framework (21) or a model-selection framework (24). Although this is not driven by the premise to generate optimal partitioning of the data, the flexibility to examine data complexity at different scales makes this approach particularly attractive. The partitions were indeed shown to correlate with known biological features such as isochores, CpG islands or the origin and terminus of replication (23). The recursive segmentation methods belong to the class of change-point methods, designed to detect abrupt transitions in sequence properties but not directly the functional or structural features within the sequence data (25,26). Subsequent studies aimed to group the segments into fewer numbers of distinct classes; however, the biological significance of the data decomposition was not clearly demonstrated (27).

A survey of the methods developed in the past two decades for interpreting genomic data through segmentation illustrates their achievements, as well as pitfalls, in decoding the information underlying the molecular data. The recursive segmentation methods, designed to detect the change points in a given genomic sequence, have come a long way since it was first introduced to measure long-range fractal correlations in DNA sequences (19). Significant advances in the field include the generalization of the segmentation method in the framework of Markov chain model to account for short-range correlations within DNA sequences (28,29). Although this improved the sensitivity in detecting the change points, it did not address the issue of identifying distinct sequence types within a sequence of interest. The resulting compositionally homogeneous sequence segments are considered independent entities, which may not be true. In reality, many of these sequence segments may share similarities with other non-neighboring segments. Therefore, the number of sequence types could in fact be much less than the number of sequence segments. The issue of identifying different sequence or data types representing distinct sources lies at the core of genomic data deconstruction problems that go beyond the goal of detecting the change points alone, currently the focus of most segmentation methods. A meaningful interpretation of genomic data is feasible only within an integrated framework for change point detection, as well as source identification, the former through segmentation and the latter through classification.

Although sustained efforts to develop more robust and sensitive segmentation methods are ongoing, now, the focus is shifting to developing integrated methodologies for data deconstruction through segmentation and classification simultaneously without prior assumptions about the data. Although a number of such methods have appeared in past few years (16–18,30,31), a comprehensive assessment of their strengths and weaknesses is yet to be accomplished. Additionally, as a consequence, a general and widely applicable methodology for genomic data decomposition, and their interpretation, has remained elusive. Through this work, we have attempted to bridge this gap by assessing the current state-of-the-art methodologies on a test platform of artificial, as well as genuine, genomic data, and also by developing a novel approach to deciphering the organizational structures underlying genomic data. This is, to the best of our knowledge, the first comprehensive assessment of ‘segmentation and classification’ methods for deciphering genomic data heterogeneities.

We posit that the recursive segmentation performed at a rather relaxed stringency will allow precise localization of the change points, and a non-hierarchical agglomerative clustering procedure will allow removal of numerous undesirable splits created as a consequence of threshold relaxation. We further hypothesize that the clustering procedure will aid not just in robust detection of change points but also in deconstruction of the inherent heterogeneity by identifying non-contiguous homogeneous fragments that share similar properties. To test this hypothesis, we invoked recursive segmentation procedure to iteratively dissect the complex data heterogeneities through Shannon information entropy function and followed this up with a two-step agglomerative clustering procedure to reconstruct the organizational structure underlying the data. Our proposed approach addressed the problems associated with both the segmentation methods for detecting the change points and the segmentation-classification methods for detecting not just the change points but also different feature types underlying the data. One of the major bottlenecks of the recursive segmentation approach is often the difficulty in establishing a threshold that can result in precise detection of change points with fewer false positives. Relaxing the threshold may help in precise delineation, yet this may also generate many false positives. On the other hand, a stringent threshold will tend to minimize the false positives but will amplify the error in change-point detection. It is hard to reconcile this trade-off to achieve both high resolution and high specificity. We demonstrate that this is achievable in the proposed integrated framework of segmentation and clustering.

Our proposed integrative approach is designed to dismantle the critical barrier in the field, namely, the number of distinct classes (or clusters) that must be specified a priori for the current methods to work. The proposed method outputs both the change points and data classes without requiring prior information about the data of interest. Our integrative methodology is therefore a significant advance over the existing segmentation methods (19,21,22,29), and also over the present segmentation-classification methods (16–18,30,31), as demonstrated in the later sections. Notably, this relatively simple and straightforward approach performed consistently well in deconstructing artificially constructed, as well as genuine, genomic data that included ‘raw’ genome sequences to ‘processed’ genome hybridization data.

In applications to solving a variety of problems in biology, namely, the identification of ‘alien’ regions in bacterial genomes, the detection of structural variants in human cancer genomes and the alignment-free genome comparison, our proposed method performed either as well as or outperformed the sophisticated state-of-the-art methodologies, and emerged as a powerful statistical tool for deciphering the organizational complexities of genomic data. In what follows, we describe the proposed methodology for genomic data deconstruction and how it can be adapted to solving many different problems in biology.

MATERIALS AND METHODS

The Jensen–Shannon divergence measure

The Jensen–Shannon divergence measure, 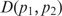, between two probability distributions p₁ and p₂ is defined as (21,32):

(1)

where 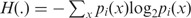is the Shannon entropy function, π_i is the weight factor assigned to p_i, 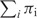= 1. For each probability distribution p_i, 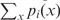) = 1. Note that π_i signifies the importance that a user may want to associate with probability distribution p_i. The Jensen–Shannon divergence measure is related to Kullback–Leibler divergence and also shares the properties of other information theoretic functionals, namely, Jensen difference divergence and φ divergence (21). The following properties make this measure particularly interesting and useful in diverse applications: (i) symmetricity: D(p₁,p₂) = D(p₂,p₁); (ii) weighting: flexibility to assign weights π_i to probability distributions according to their importance in a given context; (iii) bounds: 0 ≤ D(p₁,p₂) ≤ 1; (iv) metricity: D(p₁,p₂) is the square of a metric; and (v) generalization: Jensen–Shannon divergence between n probability distributions, D(p₁, … ,p_n) = 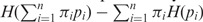. In terms of Kullback–Leiber distance, the Jensen–Shannon divergence between n distributions can be written as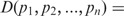 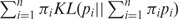, where 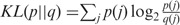for two distributions p and q. 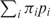is interpreted as the most likely source distribution that has given rise to p_i (i = 1, … ,n) distributions (33). D(p₁, … ,p_n) can thus be interpreted as the weighted mean of the divergence of the distributions p_i from the source distribution.

For symbolic sequence S_i of length l_i represented by alphabet A of size k, let p_i(x) represent relative frequencies f_x of occurrence of symbols x Є A. If the weight factor π_i is assumed proportional to l_i, the Jensen–Shannon divergence between two sequences S₁ and S₂ can be obtained as:

(2)

Here, L = l₁ + l₂, S = S₁⨁S₂, 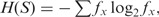(⨁ denotes the concatenation of sequences). Note that we use the annotation D(p₁,p₂) for divergence between probability distributions p₁ and p₂, and D(S₁,S₂) for divergence between sequences/data sets S₁ and S_2. For simplicity, we also refer D(S₁,S₂) as D in the later sections.

Generalization of Jensen–Shannon divergence

The standard Jensen–Shannon divergence measure quantifies the difference between distributions from independent and identically distributed sources. In this premise, for symbolic sequences, each of the symbols is assumed to be generated independently from a source specified by the probability distribution of the symbols. However, in practice, the assumption of independence of symbol occurrence is not valid, and this can be corrected by reformulating the divergence measure to account for order of occurrence of symbols. This is possible in a Markov chain model framework, and the generalized Jensen–Shannon divergence measure for a Markov source of order m is defined as (28,29):

(3)

Here, 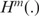is the Shannon entropy function for Markov source of order m,

(4)

where x denotes the symbol that succeeds string w of m symbols, P(x|w) is the probability of making transition from w to x and P(w) is the probability of string w. H^m(.) is thus a conditional entropy function measuring the information content when the occurrence of a symbol i depends on just preceding m symbols string. The standard Jensen–Shannon divergence measure is recovered when model order m equals zero.

Again, as described for the standard measure earlier, when weight factors π_i are proportional to lengths l_i, the generalized divergence measure becomes:

(5)

Here, 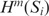is the conditional entropy function for S_i as defined in Equation (3). The values of transition and marginal probabilities can be estimated from the counts of strings w and wx in the sequence S_i: P(w) ≈ N(w) / (l_i − m + 1) and P(x|w) ≈ N(w⨁x) / N(w), where N(.) denotes the count.

Probability distributions of the divergence measures

The analytic approximation of the probability distributions of divergence measures is difficult to obtain, and therefore, in many practical applications, an appropriate threshold is established to assess the significance of values of divergence measures. However, for the Jensen–Shannon divergence measure, analytic expression for the probability distribution was derived for a special case when the weight parameters are proportional to sequence lengths (Equations 2 and 5) (21,28). This allowed to assess the statistical significance of the value of D^m. It was shown that asymptotically, for large L, the probability distribution of D^m approximates as:

(6)

Here, 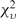is the chi-square distribution function with υ = k^m(k −1) degrees of freedom. Grosse et al. (21) and later Arvey et al. (28) showed that the probability distribution of maximum value of D^m over all possible binary partitions of a given sequence can also be approximated through a chi-square distribution function:

(7)

where β and N_eff are the fitting parameters whose values, for each m, were obtained by fitting the above analytic expression to the empirical distributions obtained via Monte Carlo simulations.

The recursive segmentation and clustering method

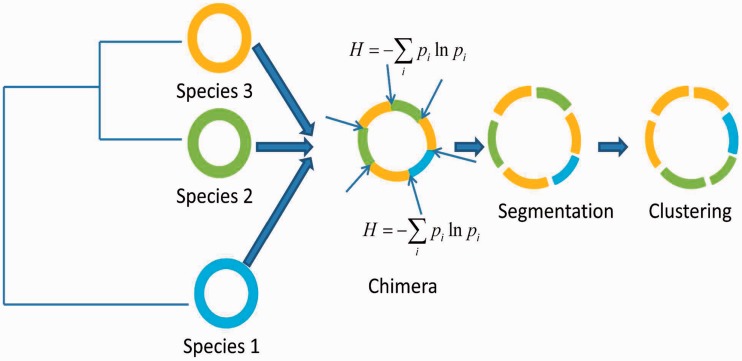
A frequently invoked segmentation approach for understanding the organizational structure underlying genome sequences is based on the Jensen–Shannon divergence measure (19–22). The generalization of this measure to account for short-range nucleotide ordering in the framework of Markov models makes this a powerful tool for mining genomic data (28,29). Briefly, the recursive segmentation procedure proceeds as follows: (i) given as sequence S, compute the difference between sequence segments left and right to each sequence position in S using Jensen–Shannon divergence measure (or its generalization); (ii) find the position of maximum divergence between left and right sequence segments; (iii) if the value of this maximum difference is significantly large, the sequence is segmented at this position; (iv) repeat the aforementioned procedure recursively until none of the resulting sequence segments can be split further. The final output from this procedure is thus a set of sequence segments that are homogeneous within, but heterogeneous between, according to a prespecified criterion. In our proposed framework, in general, the data are hypersegmented to allow accurate detection of transition points or ‘break points’ followed by an agglomerative clustering procedure at relatively relaxed stringencies in two steps: first, the contiguous similar segments are identified, and then, starting with as many number of these segment clusters, grouping of similar clusters is followed recursively until the difference between any two clusters becomes significantly large, preventing further cluster merger. Both the recursive segmentation and clustering are performed within the hypothesis testing framework—the former requires the P-value for the observed Jensen–Shannon divergence between two sequence segments to be less than the preassigned significance level in order for the split to be deemed significant, whereas for the latter, if the P-value for Jensen–Shannon divergence between two clusters is less than the significance threshold, the clusters are deemed statistically different, otherwise they are merged into a single cluster. Note that recursive segmentation proceeds by first deciphering the global heterogeneity, that is, it first splits the given sequence into two and the split point thus obtained guides the next round of segmentation and so on. The earlier obtained segmentation boundaries may not correspond to boundaries of biologically meaningful domains, which may in fact be detected at later steps of the recursive process. We allowed oversegmentation at a relaxed stringency (we recommend any significance threshold between 0.1 and 0.3) to increase the sensitivity of the method in identifying the real break points. However, this might have the undesirable effect of fragmenting the biological domains. To restore the segmental structure, we follow the segmentation with clustering steps at a relaxed clustering stringency (significance threshold < 0.1) to first group the contiguous similar segments, and then group the similar non-neighboring segments. This allows detection of not just the break point points but also different structural or functional types in a given genome sequence (see Figure 1 for an illustration of the proposed procedure for deconstructing a chimeric genome).

Figure 1.

An illustration of the entropy-based technique for the deconstruction of a chimeric genome.

The compositional disparities within a genome sequence have often been assessed directly from the values of Jensen–Shannon divergence measure (34–38). What makes this measure further interesting is the derivability of its probability distribution for a special case: for large L (length of the sequence) and with weight factors π_i lengths l_i of the sequence segments i. Although a vast amount of biological sequences tend to be sufficiently long to validate this assumption (typically of the order of 10³ bases or greater) and π_i l_i could be informative priors in several cases thus allowing a direct assessment of statistical significance of this measure, we show in the next section that different forms of this measure could be adapted to solve a variety of biological problems.

RESULTS

Problem 1: Deconstruction of Chimeric Genomes

Background

Microorganisms are arguably the most versatile creatures on earth. They have the abilities to modulate their physiological capacities through a multitude of evolutionary processes, most notable among them are the lineage-specific gene loss or the acquisition of genes from often unrelated organisms (39–41). The latter, namely, the horizontal gene transfer (HGT), is now recognized as a potent force driving the evolution of microbial genomes (39,42–44). The process of HGT transforms a microbial genome into a chimera of genes with different ancestries. Because the donor genomes have undergone different sets of mutational pressures, the acquired genes appear compositionally distinct in the context of the recipient genome. Understanding the mechanisms and consequences of the process of horizontal gene flow requires deconstruction of chimeric genomes through experimental or computational means. As determining the evolutionary histories of genomic components in laboratories is often not feasible, understanding the microbial evolution has come to rely on the fast growing computational methodologies.

Segmentation methods for deciphering the complex compositional heterogeneities of DNA sequences have a long history (25,26). The problem is essentially formulated as detecting the points of transitions in sequence characteristics. Earlier methods were looking for these change points or break points by dividing a genome into compositionally homogeneous segments or domains (9,19,20). Each domain was considered as an independent entity, described by its own set of sequence properties. Subsequent methods were focused on not just detecting the change points but also the sets of domains that shared similar properties (17,18,27,30,31). The problem of deconstruction of a chimeric genome was thus reformulated as finding k domain sets given N domains in a genome of interest. HMMs (1) provided a natural framework for addressing this problem (3,30,45). Subsequently developed methods were based on Bayesian formalisms and other optimization techniques (16–18,31).

Methods for segmentation and classification

Nicolas et al. (30) implemented an expectation–maximization algorithm for estimating the parameters of an HMM, which had the transition between hidden states (segment or domain classes) governed by a first-order Markov process; this also allowed to infer the most likely hidden state at a sequence position from the posterior distribution of hidden states. Contiguous sequence positions labeled with the same hidden state represented a domain. This method, called RHOM, requires to specify a priori the model order and number of domain classes. Gionis and Mannila’s K-H segmentation method (31) partitions a sequence into K segments arising from H sources by maximizing a likelihood function for fragmentation into K parts. This was accomplished using a dynamic programing algorithm; note that this approach also requires to specify a priori the values of K and H, and the ‘optimal’ combination is inferred through Bayesian information criterion (BIC). Specifically, a given sequence is preprocessed by dividing into equal length blocks, each block is represented by an n-dimensional frequency vector, where n is number of all possible m-letter words (m = 2 or 3). The sequence of these data points (frequency vectors) serves as the input to the K-H method. Boys and Henderson (18) combines the strength of both, HMM and Bayesian technique, to infer all quantities of interest. Here, even the model structure—the number of segment types and the order of Markovian dependence—is also a parameter to be inferred via MCMC technique. The final set of estimated parameters is used to infer the segmentation from the posterior distribution of segment types obtained using the forward–backward algorithm. Keith’s hierarchical Bayesian approach (16,17) is based on a generalized Gibbs sampler, an efficient MCMC sampling technique, that could make possible segmentation of large data sets. The number of segment types has to be specified a priori, and the final value is determined through BIC.

Artificial genomes

To assess the performance of this class of methods, including our proposed entropy-based method, we constructed artificial chimeric genomes by simulating gene transfers from 10 artificial donor genomes into an artificial Escherichia coli genome. Construction of artificial genomes are described in detail in (46). Briefly, a conservative core of a given genome representing the native genes was extracted using a gene clustering method based on Akaike information criterion. The core was partitioned into distinct gene classes using a k-means gene clustering method that used relative entropy as the distance measure for deciding the convergence of the algorithm. Multiple gene models trained on distinct gene classes representing the mutational proclivities of ancestral genome complement were incorporated in the framework of a generalized HMM. This HMM was then used to generate a genome representing the major trends within the ‘core’ of a genuine genome. The donor genomes were modeled after Archaeoglobus fulgidus, Bacillus subtilis, Deinococcus radiodurans, Haemophilus influenzae Rd, Methanocaldococcus jannaschii, Neisseria gonorrhoeae, Ralstonia solanacearum, Sinorhizobium meliloti, Synechocystis PCC6803 and Thermotoga maritima genomes. Approximately 25% of all genes in this chimeric artificial E. coli genome was provided by the 10 donors. As the evolutionary histories of DNA sequences (encompassing one or more genes) within this genome is known with absolute certainty, it serves as a valid test bed for assessing methods for genome heterogeneity decomposition. These methods are expected to identify not just the insertion points of foreign DNAs but also identify regions originating from distinct source genomes.

Assessment on artificial genomes

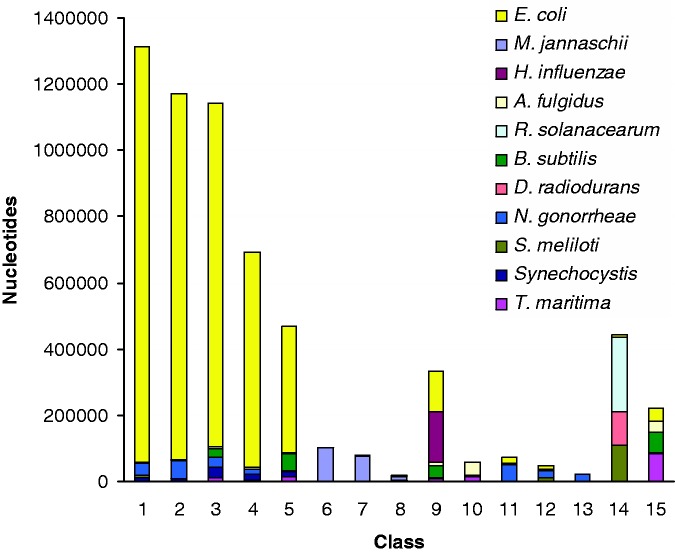
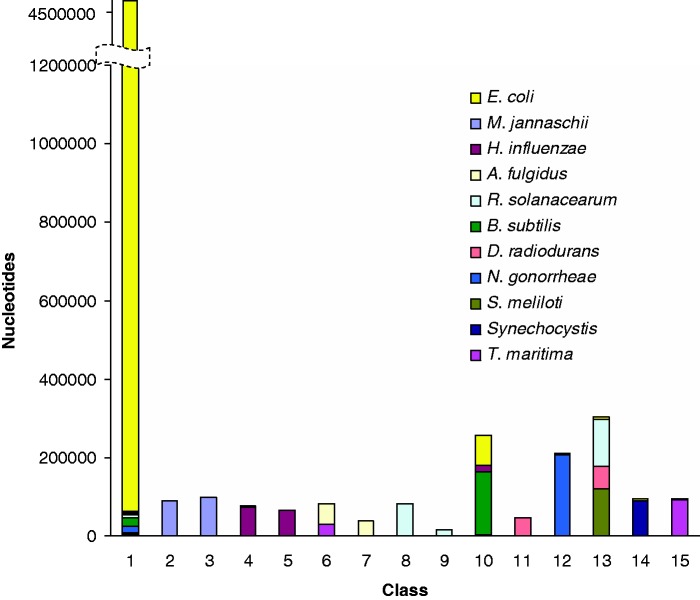
We subjected the five methods described earlier, namely, the HMM-driven Bayesian method (18), the HMM-based method [RHOM, (30)], the generalized Gibbs sampler-based Bayesian method (16,17), the optimization method [K-H segmentation, (31)] and our proposed Markovian Jensen–Shannon divergence (MJSD)-based segmentation-clustering method, to deconstructing the artificial chimeric E. coli genome. As the HMM-driven Bayesian method can not handle sequences of length >60 kb, we excluded it from this test. Figures 2–5 show the cluster configuration generated from the four methods. Ideally, a method should place ‘native’ segments in a large cluster representing the native genome and ‘alien’ segments into several smaller clusters, each representing a distinct donor source. In practice, however, more than one cluster for a genome source may be generated. RHOM, for example, generates several large clusters for the native segments (Figure 2). It could identify only two donors efficiently—M. jannaschii and N. gonorrhoeae. It could also identify B. subtilis and T. maritima, though less efficiently, because of the inability of the method in distinguishing between B. subtilis and H. influenzae segments, and also between T. maritima and A. fulgidus segments. A substantial fraction of alien segments arising from different sources was incorrectly assigned to a large native cluster. The Bayesian method based on a generalized Gibbs sampler also generated several large clusters for native segments (Figure 3). It generated unambiguous clusters for M. jannaschii only, and to an extent for N. gonorrhoeae and A. fulgidus segments. Note that a significant portion of the N. gonorrhoeae squences could not get discriminated from the backbone (E. coli), yet two clusters (# 11 and 13) had most of the sequences from this organism. The K-H segmentation method performed better in assigning alien segments; however, it generated two large native clusters of equivalent size (Figure 4). It could generate clusters of M. jannaschii and Synechocystis segments more efficiently, whereas those of H. influenzae, A. fulgidus, R. solanacearum, B. subtilis, S. meliloti and T. maritima less efficiently. It couldn’t discriminate D. radiodurans from R. solanacearum and N. gonorrheae from the recipient E. coli.

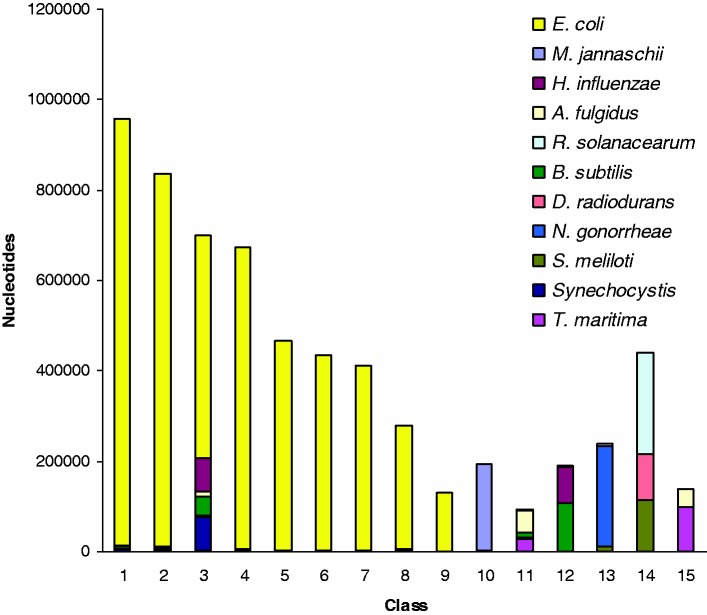
Figure 2.

Assessment of the performance of RHOM, an HMM-based method, in grouping regions inserted into an artificial E. coli genome from 10 donors. The class (or cluster) composition, that is, the amount of nucleotides of different organisms assigned to a cluster (y-axis), is shown for each cluster (x-axis).

Figure 3.

Same as in Figure 2, but for a Bayesian method based on a generalized Gibbs sampler.

Figure 4.

Same as in Figure 2, but for K-H segmentation method.

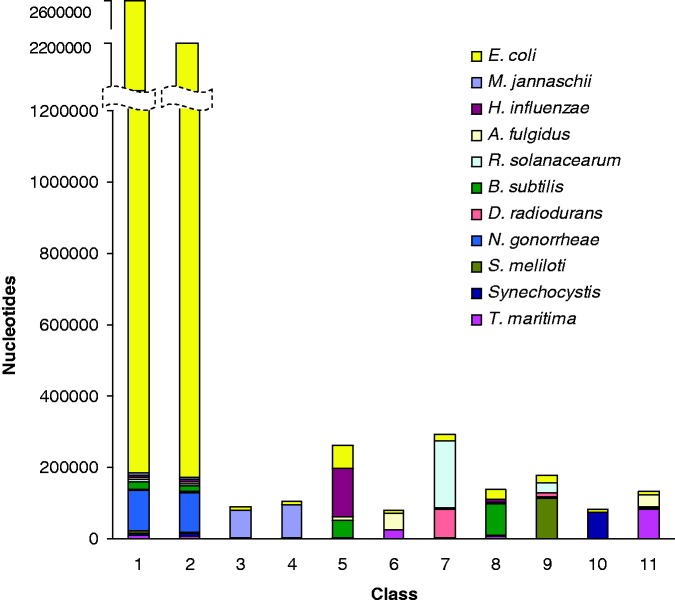
Figure 5.

Same as in Figure 2, but for MJSD-based segmentation-clustering method. The segmentation was performed at the significance threshold of 0.1 followed by a two-step clustering at the significance threshold of 0.001.

In contrast to the aforementioned methods, MJSD based segmentation-clustering method generated a single large cluster for native segments, and also assigned alien segments from different donors to respective source clusters efficiently (model order = 2, segmentation significance threshold = 10⁻¹, clustering threshold = 10⁻³; see Figure 5). Notably, many of the clusters created by this method contained segments from unique donor sources only, namely, M. jannaschii, H. influenzae, A. fulgidus, R. solanacearum and D. radiodurans. Even the clusters of N. gonorrhoeae, Synechocystis and T. maritima were of high purity. Clearly, the MJSD-based method performs well in segregating compositionally distinct regions. Overall, the method identified the recipient E. coli genome and 9 out of 10 donors (by placing majority of their genes or segments in smaller distinct clusters of high purity). This compares favorably with K-H segmentation that performed better than RHOM and Bayesian methods but generated two large E. coli clusters. Note that, in general, bacterial genomes have >60% native or ancestral genes; the genome deconstruction methods are expected to recover this structure of a bacterial genome by placing majority of the genes into a single cluster and rest of the genes into several smaller clusters representing the likely donor sources. The native and alien composition of a genome can thus be easily deciphered from the size of the clusters (largest native and the rest alien). By construction, the artificial chimeric E. coli genome contained 75% genes modeled after the ancestral E. coli genes. Only the MJSD method could place most of these genes into a single large cluster. Further, in comparison to the K-H method whose ‘donor’ clusters were always contaminated with the recipient E. coli sequences, the MJSD method grouped the alien sequences more efficiently and generated more clusters with greater purity. The MJSD method also created distinct clusters for D. radiodurans and N. gonorrheae, which couldn’t be identified by the K-H method.

Although other methods require to specify a priori the number of segments or the number of sources or both, the MJSD-based method generates the number of segments and their clusters corresponding to the inherent genomic heterogeneity. For this test genome, it generated ∼15 segment clusters (excluding 9 tiny clusters each of which identifies unambiguously with a distinct source, see Supplementary Table S1), which is close to the actual number of genome sources (total = 11). As we know a priori the number of segments and their sources for the test genome, we could specify this information for other methods where needed; results were also obtained for other combinations of these parameters including the specifications obtained from the MJSD method. We did not observe any noticeable improvement by varying these parameters (similar results were observed with experiments on genuine genomes also as described later). Both Bayesian and K-H segmentation methods use BIC for determining these parameters; the parameter values that minimize the BIC are selected. This postprocessing step imposes significant computational load on the methods, in particular on the K-H method, where one needs to obtain values of BIC for different combinations of K and H. Surprisingly, though we did not find the BIC-inferred parameter values to be reflective of the inherent heterogeneities of genomes. For example, the optimal number of classes inferred from this criterion was 3 for the Bayesian method, which is far less than than the actual 11. This demonstrates the inherent weakness of these methods in inferring the correct values of these parameters. To test the HMM-driven Bayesian method, we constructed several chimeric genomes of length ∼60 kb; however, all test genomes remained unsegmented, although other methods could deconstruct these genomes with similar relative performance as reported earlier.

Notably, the proposed method is not overly sensitive to the segmentation threshold. In Supplementary Figures S1A and B, we show the cluster configurations generated by the MJSD-based method at further relaxed stringenices of segmentation, at the significance thresholds of 0.2 and 0.3, respectively. Segmentation at the significance threshold of 0.1 generated 1107 segments, whereas segmentation at the significance thresholds of 0.2 and 0.3 generated 1255 and 1391 segments, respectively. However, the subsequent two-step clustering procedure yielded similar cluster configurations for all three cases (compare Figure 5 with Supplementary Figures S1A and B). Relaxing the segmentation stringency further homogenizes the segmentation map, that is, the resulting segments are still more homogeneous, but this comes at the cost of many more segments. Enhanced homogeneity ensures that the optimal clusters could be obtained without overly relaxing the clustering stringency. This is apparent from Figure 5 and Supplementary Figures S1A and B, which display similar cluster configuration retrieved at lesser relaxed clustering stringency as the number of homogeneous segments are increased by relaxing the segmentation stringency.

Assessment on genuine genomes

We also assessed the methods in identifying alien regions in the well-understood Salmonella enterica typhi CT18 genome. Vernikos and Parkhill have compiled a high confidence set of genomic islands (Supplementary Table S2)—large regions with functionally related genes acquired through the process of HGT (47). We subjected all methods to identifying these compositionally distinct regions in S. enterica typhi CT18 genomes. The 375 sequence segments generated by the MJSD method were assigned to 31 clusters (Table 1). The largest cluster contained ∼70% of the genome, whereas the remaining 30% were distributed in the 30 smaller clusters of potentially foreign origin. Approximately 88% of island genome was found to reside in the 30 alien clusters, clearly an indicator that the method has segregated well the native and alien regions. The optimal segmentation by the Bayesian method with number of clusters inferred through BIC results in ∼87% of the genome assigned to the largest cluster and ∼13% to the remaining two smaller clusters, which, however, contained only 27% of the island genome. As RHOM does not determine the optimal number of clusters a posteriori, we obtained results from different numbers of clusters specified a priori. When only two clusters have to be generated by RHOM, 78% of the genome got assigned to one cluster and the remaining 22% to the other cluster, which, however, contained only 44% of the island genome, implying that majority of the islands could not be distinguished from the ancestral genome. Increasing the number of clusters did not resolve this issue, rather the method now seemed to be dividing evenly the ‘native’ or the ‘alien’ clusters (see Table 1). The K-H segmentation method also used BIC to infer the optimal value of K (number of segments) and H (number of classes); we found that the BIC-inferred optimal value of K comes close to or is in fact the number of data points, which is just unrealistic. We have provided in Table 1, the results from various combinations of K and H. Although BIC for K = 6000 and H = 3 (or H = 2) is less than the BIC for K = 100 and H = 2 (implying that the former is a better model for the given data), the latter has aggregated twice the island genome in the alien cluster of equivalent size. For K = 6000 and H = 2, the size of the alien cluster doubled when compared with K = 100 and H = 2, but it assimilated less amount of island genome than the latter. Undesirably, the sensitivity of the method did not improve (rather declined) when the size of the alien cluster increased (results are also shown for K = 300, 400 which are close to the number of segments generated by the MJSD method). Overall, the MJSD method appeared more robust and sensitive in classifying the compositionally distinct regions in both artificial and genuine genomes.

Table 1.

Assessment of the prediction methods in deciphering genomic islands in S. enterica typhi CT18 genome

Methods	Segments	Cluster configuration			Cluster(s) labeled alien	Percentage of whole genome identified alien	Percentage of island genome identified alien
		Total clusters	Largest (% genome)	Others (% genome)
MJSD	375	31	1 (69.3)	2–30 (30.7)	2–30	30.7	87.6
Bayesian		3	1 (86.5)	2–3 (13.4)	2–3	13.4	27.9
RHOM		2	1 (78.3)	2 (21.6)	2	21.6	44.4
		3	1 (40.5)	2 (38.9),	3	20.5	40.1
				3 (20.5)	2, 3	59.4	63.1
					1, 3	61.0	77.0
		4	1 (37.9)	2 (17.6),	1	37.9	33.6
				3 (24.9),	2	17.6	11.1
				4 (19.3)	3	24.9	16.5
					4	19.3	38.6
					1, 4	57.2	72.3
		8	1 (22.4)	2 (3.7),	1	22.4	15.4
				3 (4.5),	2	3.7	0.5
				4 (12.9),	3	4.5	2.5
				5 (12.9),	4	12.9	24.3
				6 (12.9),	5	12.9	10.8
				7 (12.9),	6	12.9	5.3
				8 (12.9)	7	12.9	13.8
					8	12.9	27.0
					4, 8	25.8	51.3
K-H	100	2	1 (87.4)	2 (12.5)	2	12.5	59.8
	300	2	1 (84.1)	2 (15.8)	2	15.8	51.4
	400	2	1 (82.7)	2 (17.2)	2	17.2	53.0
	6000	2	1 (75.5)	2 (24.4)	2	24.4	51.3
	6000	3	1 (49.7)	2 (11.9),	2	11.9	30.6
				3 (38.2)	2, 3	50.1	70.6

Results are shown for second-order Markov models used in MJSD and RHOM.

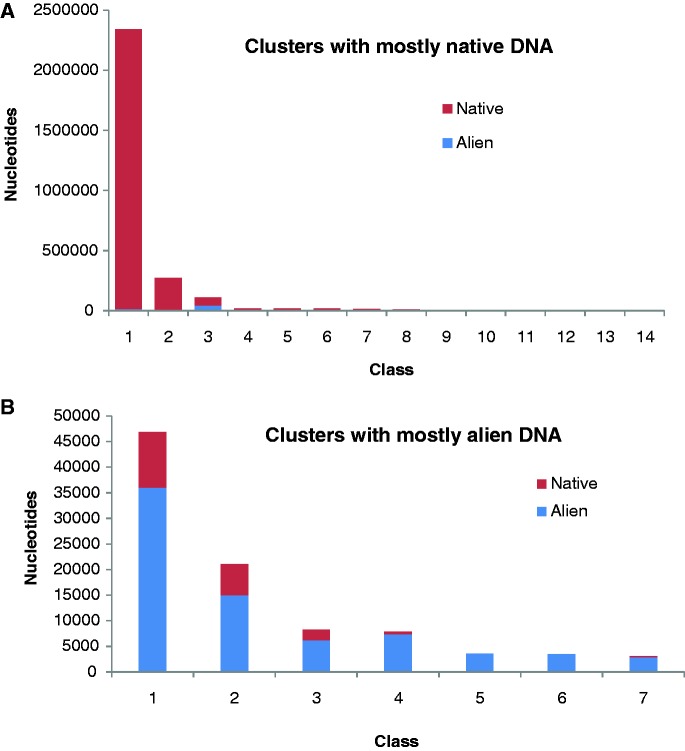
Although genomic islands present a picture of large acquisitions through the process of HGT, alien genes may arrive alone or in company of few other contiguous genes. To assess the performance of the methods in deciphering the genome composition at the genic (or higher) level, we extracted a conservative set of unique and native genes in S. enterica typhi CT18 from the list compiled by Arvey et al. (28). Unique CT18 genes are those which while present in the Salmonella CT18 genome are absent from the genomes of its close relatives (other Salmonella strains and the outgroup taxa). These ‘unique’ genes of limited phylogenetic distributions are likely to have been introduced through horizontal transfer. Specifically, genomes of six Salmonella strains and five non-Salmonella, outgroup taxa were used (Supplementary Table S3). Genes in the CT18 genomes that had matches to all five members of the outgroup taxa were classified as native genes. Here, we assessed how these native (2 792 772 bp) and alien (1 31 346 bp) genome are segregated into distinct classes by different methods (Table 2). MJSD method generated two native clusters—one large and the other relatively much smaller cluster, both containing >99% of the native genome. Seven alien clusters were created, which were of high-level (>90%) to moderate-level (70–90%) purity in terms of the abundance of alien genes in these clusters. One hybrid cluster of low-level purity was also created (native: 62%, alien: 38%). Other smaller native clusters (11, with between 0.001−0.68% of the native genome) were 100% pure but are not shown in Table 2 (see Figure 6 for the composition of all MJSD clusters). The Bayesian method could not distinguish between native and alien genomes, as is evident from the absence of alien clusters in its cluster configuration. RHOM had a similar problem, which persists irrespective of number of distinct clusters. The K-H method was promising at K = 100, H = 2, generating a native cluster and an alien cluster, but its performance declined for higher K’s and H’s (data are shown for values of K and H that results in lower BIC and hence is considered ‘optimal’ by the authors), where the method could no longer discriminate between native and alien genome.

Table 2.

Assessment of the prediction methods in classifying phylogenetically native and alien genes in S. enterica typhi CT18

Cluster	MJSD		Bayesian		RHOM								K-H
					No. of states = 2		No. of states = 3		No. of states = 4		No. of states = 8		K = 100, H = 2		K = 6000, H = 2		K = 6000, H = 3
	Native	Alien	Native	Alien	Native	Alien	Native	Alien	Native	Alien	Native	Alien	Native	Alien	Native	Alien	Native	Alien
1	2 328 423	13 070	2 649 030	84 518	2 498 148	64 974	1 278 877	22 318	1 171 097	46 316	8 67 131	14 403	2 757 199	49 890	2 455 308	56 716	1 667 759	25 064
	(99.4)	(0.5)	(96.9)	(3.0)	(97.4)	(2.5)	(98.2)	(1.7)	(96.1)	(3.8)	(98.3)	(1.6)	(98.2)	(1.7)	(97.7)	(2.2)	(98.5)	(1.4)
2	69 339	41 802	1 28 485	46 709	2 94 624	66 372	1 232 002	48 380	7 97 380	15 465	6 69 939	12 551	35 573	81 456	3 37 464	74 630	1 041 525	59 162
	(62.3)	(37.6)	(73.3)	(26.6)	(81.6)	(18.3)	(96.2)	(3.7)	(98.0)	(1.9)	(98.1)	(1.8)	(30.3)	(69.6)	(81.8)	(18.1)	(94.6)	(5.3)
3	10 872	35 976	15 257	119			2 81 893	60 648	5 61 859	10 760	4 57 456	8758					83 488	47 120
	(23.2)	(76.7)	(99.2)	(0.7)			(82.2)	(17.7)	(98.1)	(1.8)	(98.1)	(1.8)					(63.9)	(36.0)
4	2 70 559	2028							2 62 436	58 805	2 25 980	4647
	(99.2)	(0.7)							(81.6)	(18.3)	(97.9)	(2.0)
5	463	7412									1 76 111	3390
	(5.8)	(94.1)									(98.1)	(1.8)
6	2062	6189									1 54 561	39 626
	(24.9)	(75.0)									(79.5)	(20.4)
7	0	3457									1 23 937	2337
	(0)	(100)									(98.1)	(1.8)
8	6137	14 965									1 17 657	45 634
	(29.0)	(70.9)									(72.0)	(27.9)
9	0	3535
	(0)	(100)
10	138	2912
	(4.5)	(95.4)

For each cluster is shown the amount of ‘native’ and ‘alien’ nucleotides assigned to that cluster (percent native and alien DNAs in a cluster are shown in parenthesis).

Figure 6.

Composition of the S. enterica typhi CT18 gene clusters labeled (A) native and (B) alien by the MJSD-based segmentation clustering method because of the abundance of native DNAs and alien DNAs, respectively, within them. The class (or cluster) composition, that is, the amount of native nucleotides and alien nucleotides assigned to a cluster (y-axis), is shown for (A) native cluster and (B) alien cluster (x-axis).

Recent studies have assessed the accuracy of parametric methods in detecting alien regions as a function of phylogenetic distance of donor source from the recipient organism (28,48). Expectedly, methods appeared less efficient in discriminating genomic segments from phylogenetically similar organisms, such as E. coli and S. enterica. However, a significant interest is in detection of genetic material transfer between highly divergent organisms, particularly in the studies of host–parasite interactions. This motivated us to test the proposed method in a host–parasite setup. We selected N. gonorrhoeae, a bacterial pathogen that lives within human and causes gonorrhea, and has recently been investigated for the presence of human DNA within its genome (49). We performed two experiments. First, a chimeric sequence was constructed by joining equal sized fragments each from N. gonorrhoeae and Homo sapiens, and then the MJSD method was applied to identify the join point in this chimeric genome. The mean error (difference between the segmentation and join point) obtained from 5000 random replicates was plotted as a function of chimeric sequence size (Figure 7). We also obtained the mean errors for 20 kb bacterial chimeras (E. coli sequences concatenated with sequences from different bacterial species). The error was maximum for the Escherichia–Salmonella chimera, which shares ∼98% similarity in their ribosomal DNAs, emphasizing that such transfers would be hard to detect. The interfamily transfers (Escherichia–Vibrio, Escherichia–Haemophilus) could be easier to detect, and perhaps the interdomain transfers, though rare, could be identified with the greatest precision (Figure 7). In the second experiment, we simulated transfer of ten 10-kb segments from human chromosome 22 into the N. gonorrhoeae genome. The MJSD method performed well in grouping the DNAs of the bacterial pathogen and its mammalian host (Figure 8); ∼88% of the N. gonorrhoeae genome was assigned to the largest cluster that was ∼100% pure (that is, contained only N. gonorrhoeae segments). Note that DNAs of both pathogen and host were apportioned in several clusters owing to the heterogeneous composition of these genomes (unlike artificial genomes that were relatively homogeneous by design).

Figure 7.

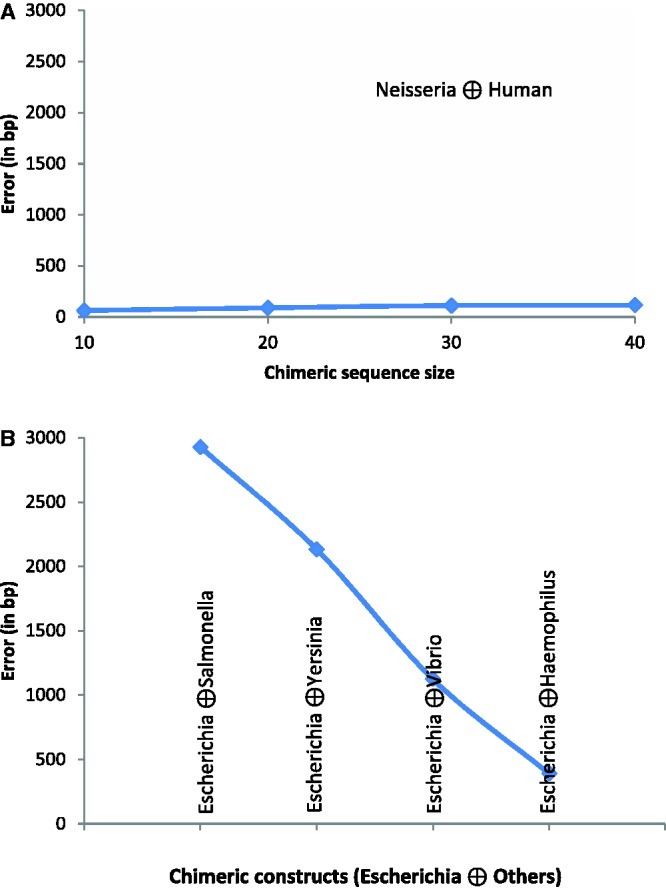
Assessment of the performance of MJSD-based segmentation clustering method in finding the join point of a genomic fragment from one organism concatenated with an equal sized fragment from another organism. The mean error (difference between the segmentation and join point) was estimated from 5000 random replicates. (A) H. sapiens concatenated with N. gonorrhoeae: the mean error is shown as a function of chimeric sequence size, and (B) E. coli concatenated with other bacterial species (in the order of their divergence from E. coli); chimeric constructs were of size 20 kb.

Figure 8.

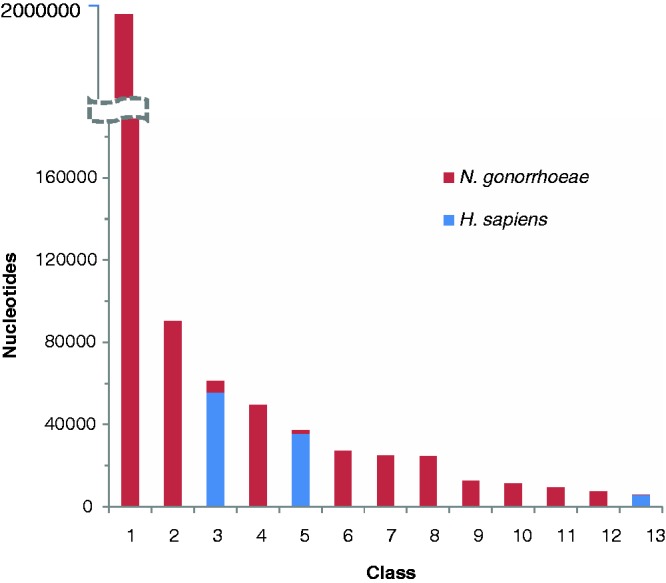
Assessment of the performance of the MJSD method in discriminating the DNAs of a bacterial pathogen (N. gonorrhoeae) from its mammalian host (H. sapiens). Ten 10-kb segments from human chromosome 22 were transferred into the N. gonorrhoeae genome. The class (or cluster) composition, that is, amount of nucleotides of N. gonorrhoeae and that of H. sapiens assigned to a cluster (y-axis), is shown for each cluster (x-axis).

Conclusions

The MJSD-based segmentation-clustering method effectively unravels the underlying segmental structure within genomes, grouping genomic regions representing distinct evolutionary patterns. This is accomplished independent of gene information, making it a useful tool for deconstructing yet characterized, just sequenced genomes.

Problem 2: Detection of Structural Variations in Cancer Genomes

Background

Occurrences of many human diseases are attributed to copy number variations (CNVs), a class of structural variations that changes copy number of DNA at genomic loci (50–52) (note that in what follows, structural variations and CNVs are used interchangeably, both implying amplifications and deletions of DNAs in cancer genomes). The genes responsible for cancers, namely, the oncogenes, and the tumor-suppressing genes, are often localized in regions undergoing copy number changes. Identification of structural variants causing gain or loss of DNA in a tumor genome is thus a significant goal in cataloging cancer-associated genes in human genomes. A normal individual is diploid, carrying two copies of chromosomes; chromosomal aberrations within tumor cells can either increase the copy number by amplification of chromosomal segments or decrease the copy number by deletion of chromosomal segments. Large-scale amplifications or deletions could be up to several megabases of genome, even affecting the entire chromosomal arms. Advances in microarray technologies have greatly advanced our understanding of the CNVs in human genomes. Development of array comparative genome hybridization (aCGH) technique allowed direct assessment of copy number changes in tumors (53); the DNAs from tumor cells are hybridized against the array probes constructed from a reference genome, and the copy numbers are inferred from hybridization (fluorescence) intensities at each probe, a higher value of this measure implying an amplification and a lower value signifying a deletion.

The advent of microarrays has produced new opportunities for large-scale identification of CNVs at a much better resolution; however, this has also brought new challenges to decipher signals from noisy experimental data, and also, not just to predict the presence of CNVs at genomic loci but to predict them precisely. This is a significant computational challenge, and the interest in this area of research is evident from the number of bioinformatics methods developed in the past few years to address this problem (54–62).

Methods for CNV detection

Detection of CNVs is essentially a change-point problem, that is, detecting the break points signifying the transition from normal state to variant state in a genome of interest. Venkatraman and Olshen (57,58) developed a circular binary segmentation (CBS) method that searches recursively for left and right break points for the CNVs in a chromosome with ends joined together; the recursion is continued until the successive break points are deemed statistically significant using a permutation test. However, finding two break points simultaneously in a sequence makes this procedure computationally intensive. Another class of methods that use HMMs to find the most probable sequence of structure types (normal and different classes of variants) underlying a given chromosomal sequence in a probabilistic framework has been frequently invoked to detect CNVs (55,61). A related approach is based on conditional random fields (CRFs) (59); however, despite the sophistications of these methods and the implicit optimality of their solutions, their practical usefulness is constrained by the requirement of training data. Further, they require to specify a priori the model structure, such as the number of structure types, etc., which are often unknown.

Several other approaches are based on a ‘local’ break point procedure that measures variations in the regions within windows along a chromosomal locus of interest (63). Assessment of variations between regions lying within windows of fixed size tends to be much faster than recursive binary segmentation; however, scan window methods are sensitive to window size and are inherently limited in their ability to delineate precisely the break points. The precision of the break points is naturally a function of window step size, as well as window size (smaller size may help detect the break point better but can also lower the signal-to-noise ratio) (28).

Chen et al. (64) have recently shown that the error in measurement of hybridization intensity ratio follows a Gaussian distribution function. Starting with each intensity ratio value assigned to a cluster specified by a Gaussian function, a pairwise Gaussian merging procedure, named SAD, allows to recursively merge clusters with similar Gaussian distribution; this process is halted when the distributions are deemed statistically different. The largest cluster corresponds to the normal state and thus provides the baseline for identification of amplified and deleted regions in the genome. However, this process is prone to generate more false positives and false negatives owing to the presence of outliers in the aCGH data. This was addressed by including a postprocessing step to eliminate the statistical outliers from the final prediction.

As the entropy-driven approach proposed here does not need training data and decodes genome heterogeneities efficiently, it is tempting to apply this approach to deciphering the structural variants in tumor genomes. This problem presents altogether a different challenge to the methodology proposed here—one, the rather continuous numeric data from aCGH platform, which unlike the symbolic sequences cannot be readily interpreted using the Shannon entropy and its derived measures, and the other, the size of the aCGH data—just a few hundreds of data points (hybridization intensity ratios) violates the assumption (sufficiently large data set) implicit in the derivation of probability distribution of divergence measure D (Equations 6 and 7). Here, we show that this approach could still be applied with remarkable success.

Assessment of the proposed entropic method

We assessed the entropic method on the Coriell data set with intensity ratio values for 15 cell lines from aCGH platform (65); this validated data set has frequently been used for evaluating disparate computational methods for copy number variant detection. Given a sequence of hybridization intensity ratio values 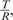where T and R stand for tumor and reference clones for a given cell line, the segmentation procedure proceeds by recursively maximizing the entropic divergence between intensities in the two resulting sequence segments (see Equation 1). The probability of being a part of a cancerous genome, P_T, or a normal genome, P_R, was estimated directly from the intensity ratios 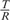for a given sequence segment. 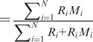That is, given a segment of length N with intensity values P_T and 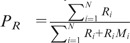(note that here R_i’s equal 1). If the maximum value of the entropic divergence exceeds an established threshold, the sequence was split at that point and the process repeated recursively. In contrast to significance threshold used for large data sets, here, the threshold was a value of entropic divergence that maximized the accuracy of CNV detection (see later for the accuracy measures used for assessment). Finally, copy number variants of similar types were grouped together; note that this data set has broadly three types of structural variations—neutral (copy number = 2), amplification (copy number >2) and deletion (copy number <2).

Results from the application of the entropic method to the Coriell data set are shown in Figure 9 and Supplementary Figures S2A–K (segmentation threshold = 0.000001, clustering threshold = 0.002). Clearly, the method identified most of the variants without generating any false positive. The performance in detecting the variants’ boundaries was quantified through three accuracy measures—Sensitivity, which is the fraction of variants’ boundaries correctly detected by a method; Specificity, which is the fraction of predicted boundaries matching the actual boundaries and F-measure, which is the harmonic mean of Sensitivity and Specificity, F-measure = 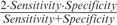. Because of the noisy test data, we allowed offset by a few data points (clones) of the predicted break points from the ‘actual’ boundaries. The values of the accuracy parameters generated by the entropic method are given in Table 3. Also shown alongside are the values of F-measure for three popular methods—CBS (57,58), HMM-based CNA-HMMer (62) and CRF based CRF-CNV (59). Note that like entropy method, CBS also falls in the class of change-point methods that do not require training data; however, it searches for two break points at a time by maximizing the difference using a t-statistics and therefore is computationally more intensive. CBS remains to date the most frequently used method for CNV detection, mainly owing to its unsupervised nature. Our proposed method significantly outperforms the CBS method—F-measure = 0.96 and 0.51 for the former and latter, respectively, for detecting within four data points of the actual boundary. It performed comparably with the more sophisticated supervised methods, namely, CNA-HMMer and CRF-CNV, when the allowed boundary mismatch approached four data points [Table 3, see also (59)]. Note that this level of performance was achieved without resorting to data smoothing or other postprocessing procedures that are routinely used in most current methods.

Figure 9.

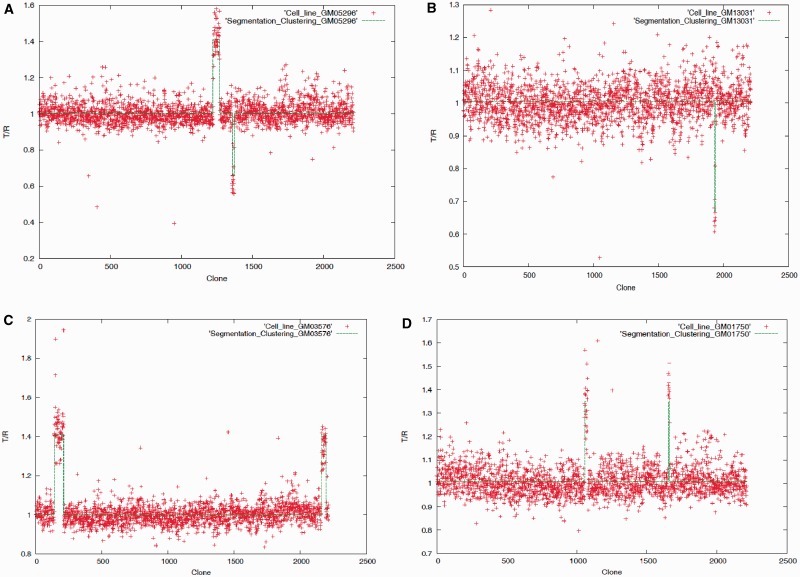
Plot of the aCGH data (T/R ratios, T and R stands for tumor and reference sample,respectively, plotted against the aCGH clone number from chromosome 1 through chromosome 22) for cell lines (A) GM05296, (B) GM13031, (C) GM03576 and (D) GM01750; the recursive segmentation method was first applied to detect the boundaries of the copy number variants followed by an agglomerative clustering for grouping similar variants.

Table 3.

Performance of the CNV detection methods in localizing the variants’ boundaries in genomes from 15 different cancer cell lines

Boundary mismatch	Entropy-based method			Circular binary segmentation	CNA-HMMer	CRF-CNV
	Sensitivity	Specificity	F-measure	F-measure	F-measure	F-measure
0	0.62	0.67	0.65	0.33	0.87	0.63
1	0.74	0.80	0.77	0.50	0.94	0.91
2	0.81	0.87	0.84	0.51	0.94	0.94
3	0.88	0.95	0.91	0.51	0.94	0.96
4	0.93	1.0	0.96	0.51	0.94	0.96

The recently proposed recursive clustering method, SAD, was shown to perform as well as or outperform several existing methods of CNV detection including CGHseg (66), GLAD (56), CBS (57), SW-ARRAY (67) and CNVFinder (68). SAD was shown to outperform both GLAD and CBS on the Coriell data set. Therefore, we assessed our entropic approach vis-à-vis SAD within the similar framework as in SAD; this was accomplished by skipping the segmentation step and directly implementing the clustering procedure but now starting with as many clusters as the number of data points (intensity ratios) as suggested in Chen et al.’s article (64). This helped in identifying more precisely the break points, but both the normal and variant regions appeared fragmented because of the presence of numerous outliers. Postprocessing to remove outliers was needed to restore the actual segmental structure of the genome. Results from both methods are given in Table 4. The entropic clustering method performs comparably with SAD. It is outperformed by SAD for exact boundary match, whereas it performs as well as SAD for one boundary mismatch and outperforms SAD for two boundary mismatches. Interestingly, the prediction output from SAD included a single intensity ratio variant, which was supposed to be filtered during postprocessing and therefore was not considered while computing the accuracy parameters (and as this is a true positive, its inclusion slightly increases the F-measure to 97.7% for one and two boundary mismatch tolerance).

Table 4.

Performance of the two clustering-based CNV detection methods in localizing the variants’ boundaries in genomes from 15 different cancer cell lines

Boundary mismatch	Entropy-based clustering method			Chen et al. SAD method
	Sensitivity	Specificity	F-measure	Sensitivity	Specificity	F-measure
0	0.837	0.857	0.847	0.883	0.863	0.873
1	0.953	0.976	0.964	0.976	0.954	0.965
2	0.976	1.0	0.988	0.976	0.954	0.965

Conclusions

Our entropy-based approach could be easily adapted for deciphering heterogeneities within array CGH data. On tests on experimentally validated data from 15 cancer cell lines, the proposed method performed comparably with other segmentation methods—outperforming CBS and achieving similar performance with supervised methods within four data points of an actual boundary. Within the ‘clustering only’ framework to compare with clustering-based methods, the entropic method performed better in delineating boundaries but required postprocessing to reconstruct the segmental structure.

Problem 3: Alignment-free Genome Comparison

Background

Evolutionary relationships among organisms are often inferred by quantifying the similarity (or dissimilarity) of their molecular sequences through sequence alignment methods (2). However, the efficiency of sequence alignment methods deteriorates when the related sequences have diverged at multiple loci through the evolutionary processes such as genomic arrangements, insertions or deletions. Genomic rearrangements, in particular, disrupt the genomic segment contiguity, which is exploited by sequence alignment methods for reconstructing phylogenies. Frequent rearrangements obfuscate the phylogenetic signals relied on by sequence alignment methods. Coupled with other evolutionary processes, this renders comparison of fast-evolving sequences beyond the limits of these methods. Also, although conserved, mainly, protein-coding or RNA sequences are used for inferring phylogeny, they constitute a small percentage of genome in higher eukaryotes. For example, only ∼1% of human genome is known to encode proteins or RNAs; a significant proportion of the other 99% is known to be conserved and functionally active. Therefore, for reconstructing reliable genome phylogenies, methods must look beyond this 1%. This is a significant computational challenge for alignment methods. The rapidly growing sequence database necessitates development of efficient alternative methods for sequence comparison.

Methods for alignment-free genome comparison

The alignment-free genome comparison methods have a relatively recent history (38,69,70); the importance of this approach is apparent from substantial efforts invested in the past few years. These methods mainly exploit the distributions of oligomer frequencies in measuring the similarity or dissimilarity between genome sequences. The frequently invoked distance measures include Euclidean distance (71), Kullback–Leibler divergence (72), Mahalanobis distance (73), Pearson correlation coefficient (74) and the Kolmogorov complexity metric (75). More recently, genome comparison using Jensen–Shannon divergence measure was reported a better alternative to alignment techniques among the existing alignment-free methods (35–38). One of the main contributions of this work is determining the limits to the oligomer size in describing a given sequence. After initial assessment on synthetic and mitochondrial genomes, this technique was subsequently applied in deducing phylogenies of viruses, prokaryotes and mammals.

Advances in the development of alignment-free methods are mainly directed toward establishing an optimal range of the word or oligomer size appropriate for comparing genomes of different sizes (38,76). Short oligomers provide better statistics, yet longer oligomers have better predictive value. The optimal resolution range balancing this trade-off is essentially a function of the sequence length, and was reported to be between 7 and 14 bp for a genome of size ∼16 kb (38). The number of all possible oligomers of length l is 4^l, and for l = 7, this number is 16 384, which means most of the oligomers will either be missing or occur only once in a sequence of size 16 kb. This scenario will get worse with increasing oligomer length (l > 7). We want to emphasize here that the usage of higher-order oligomers should be done with caution, and show that our approach can achieve comparable or better accuracy even with oligomers of size ≤2.

A proposal for genome complexity decomposition before comparison

Current methods assume distribution of oligomers of size l as a representation of a genome sequence. The difference between these distributions for two genomes of interest is assessed directly, without regard to the inherent heterogeneities within genomes, which are typically chimeras of segments with different ancestries and/or evolutionary constraints, and therefore should be represented by multiple oligomer distributions. A single distribution can have the unwanted effect of ‘averaging out’ evolutionary signals, or in fact, it may not represent any major evolutionary trend in a genome. We posit that this issue can only be resolved if the genome complexity is decomposed first and the similarity is then assessed by comparing the compositionally homogeneous domains within the genomes of interest. To address this issue in the alignment-free genome comparisons, we used our proposed entropic dissection tool and assessed it against the recently proposed feature frequency profiles (FFPs) method by Sims et al. (38), which was shown to outperform several popular methods including ‘Average Common Substring’ and Gencompress. Pairwise genome comparison was done using a metric similar to that suggested by Sims et al. (38): given genomes G₁ and G₂ with M and N classes of similar segments, the genome-wide difference (GWD) between the two genomes can be assessed as:

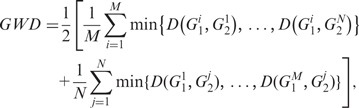where 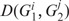refers to the Jensen–Shannon divergence between classes i and j of genomes G₁ and G₂.

Assessment

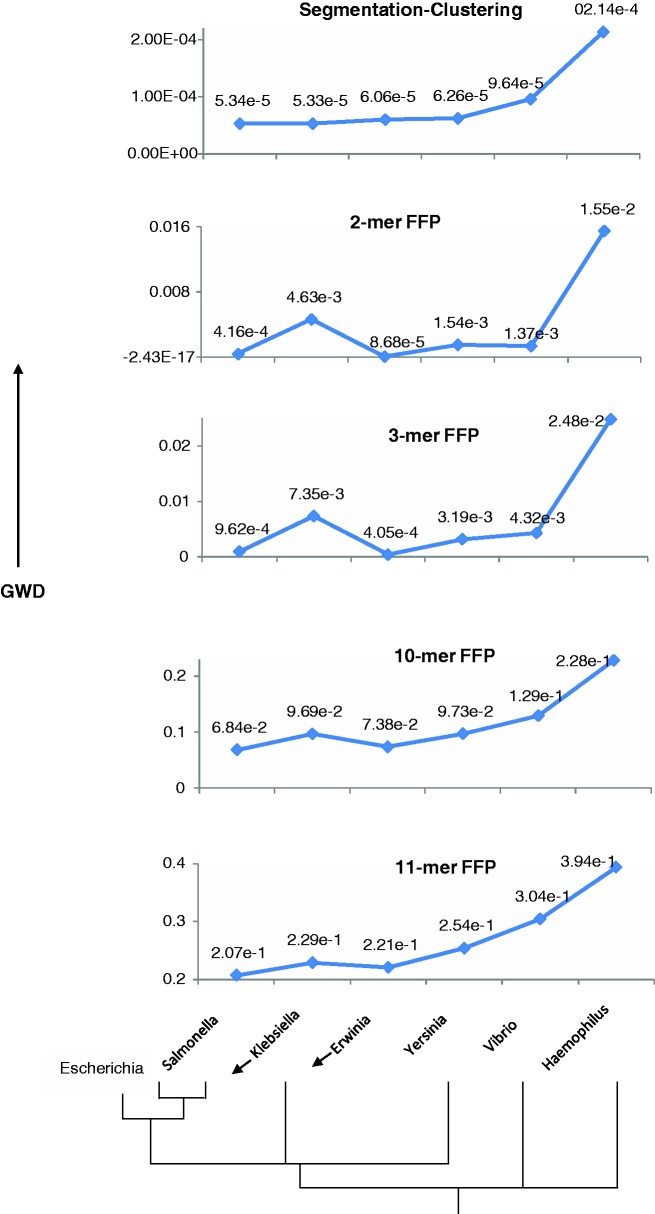
Although the alignment-free methods are expected to outperform alignment driven methods on rapidly evolving sequences, these methods are also expected to perform not much worse than alignment methods on highly conserved sequences that are well suited for the application of the latter methods. Highly reliable organismal relationships have been elucidated using alignment methods, particularly in prokaryotic domain, and we selected one such well-studied bacterial family, Enterobacteriaceae, for reconstructing the phylogenetic relationships among a host of organisms belonging to this family. The representative genomes from this family belonging to the genus Escherichia, Salmonella, Klebsiella, Erwinia and Yersinia were segmented followed by identification of distinct classes of similar segments using the procedure described earlier. Genomes from two outgroup taxa, namely, of genus Vibrio and Haemophilus belonging to Vibrionaceae and Pasteuraellaceae family, respectively, were also included in this study. In Figure 10, we show the GWD between Escherichia and other genomes, signifying the evolutionary divergence of Escherichia from other organisms within and outside of its family. The evolutionary relationships among these organisms are well established through phylogenetic analysis; an illustrative dendogram based on the ribosomal RNA phylogeny of Enterobacteriaceae family is shown at the bottom of Figure 10. The organisms in order of divergence from Escherichia (GC ≈ 51%) are Salmonella, Klebsiella, Erwinia, Yersinia, Vibrio and Haemophilus (GC ≈ 52, 57, 51, 48, 48 and 38%, respectively). Salmonella and Klebsiella share the most recent common ancestor with Escherichia, and therefore could be considered tied in this order. Note that the frequently invoked G+C composition is not a reliable indicator of organismal relationships, and perhaps, this has led researchers to exploit the power of higher order k-mer composition (k defining the oligomer length) in inferring organismal relationships.

Figure 10.

Reconstruction of phylogenetic relationship of E. coli with other members of the Enterobacteriaceae family and two outgroup taxa (represented by genera Vibrio and Haemophilus) by the recursive segmentation clustering method and the FFP method. The phylogenetic relationship inferred from a tree based on ribosomal RNA gene is depicted at the bottom. On y-axis is shown the GWD between Escherichia and other organisms obtained using an alignment-free approach, while the order of divergence of organisms from Escherichia is shown along the x-axis.

Our proposed methodology (top panel) is able to reconstruct this relationship unambiguously. However, irrespective of the oligomer size used, the FFP method could not robustly reconstruct this relationship. The performance was worst at 2-mer resolution as expected, with Erwinia identified closest to Escherichia and Klebsiella farthest from it among organisms in the Enterobacteriaceae family. The outgroup taxon Vibrio was placed within the Enterobacteriaceae family, above Yersinia and Klebsiella. The only improvement observed at 3-mer resolution was the swapping of places between Yersinia and Vibrio, which, however, still remained grouped within the Enterobacteriaceae family. At higher resolutions of 10-mer and 11-mer, which could be considered within optimal range, suggested in Sims et al. and in several subsequent studies (35,36,38,70), the outgroup taxa were correctly placed, but Klebsiella still could not be correctly aligned.

We repeated this experiment with representative genomes from different taxonomic grouping, including the phylum Cyanobacteria, the family Pseudomonadaceae and the genus Mycoplasma. The GWD between Synechocystis sp. PCC and other organisms from the phylum Cyanobacteria is shown in Supplementary Figure S3A (note that the organisms are arranged in order of increasing ribosomal RNA dissimilarity from Synechocystis on the x-axis), between Pseudomonas syringae tomato and other organisms from the family Pseudomonadaceae in Supplementary Figure S3B and between Mycoplasma pneumoniae and other organisms from the genus Mycoplasma in Supplementary Figure S3C. In all instances, we observed segmentation clustering approach to be outperforming the FFP method, reiterating that genome composition deconstruction is a critical step in robust inference of organismal relationships.

Conclusions

We show here that the difficulties of whole-genome comparison lie partly within the current approaches that overlook the inherent heterogeneities of genomes. To demonstrate this unambiguously, the only difference between our approach and the approach taken by FFP methodology was the genome heterogeneity decomposition in the former. That this difference is critical in measuring the GWD between organisms is evident from the results by MJSD-based segmentation clustering method, which could reconstruct the organismal relationships by exploiting just the 2-mer frequencies (Markov model of order 1). Note that GWD was also obtained at the 2-mer resolution. Our objective here was not to develop new methods for genome comparison but to merely demonstrate the usefulness of genome complexity decomposition in inferring organismal relationships. Before reconstructing complex phylogenies, an alignment-free method must have demonstrated its ability to reconstruct simple and well-established organismal relationships such as the ones suggested here. Inclusion of genome heterogeneity decomposition step in the pipelines of novel alignment-free methods can help achieve this goal, as indicated by the outcomes of this study.

DISCUSSION

We show here that when Jensen–Shannon divergence measure (or its generalization) is used in a flexible integrated framework of a recursive segmentation and agglomerative clustering procedure, it unravels a wealth of biological information encoded within the genomic data. In contrast to the methods that used either segmentation to detect large acquired regions (28) or clustering to infer alien genes (48,77), the proposed methodology integrates both approaches in a flexible framework that allows not just to assess the genomic heterogeneity without regard to gene information but also to deconstruct the mosaic organizational structure within the genomic data.

The superior performance of our integrative method is achieved in part because of its ability to detect the break points with greater precision. The method is not highly sensitive to the segmentation threshold, which needs to be relaxed to detect the break points more precisely. In principle, the optimal performance is achieved when all the break points are precisely identified at a certain threshold without incurring false predictions. Relaxing the stringency may divide the segments further, creating more split points in addition to the actual break points. In practice, however, the ‘optimal’ threshold is not known, and further, a method, even at its best, may not detect all break points. Relaxing the segmentation stringency is a way to improve the sensitivity; however, this comes at the cost of specificity. The design of our proposed method allows achieving high sensitivity without sacrificing the specificity. Embedded in the proposed methodology is the flexibility to perform segmentation within a broad range of relaxed stringency and follow this up with a clustering procedure to help recover the segmental structure by eliminating spurious split points. Indeed, this procedure, with segmentation performed at significance threshold of 0.1 (Figure 5), 0.2 (Supplementary Figure S1A) and 0.3 (Supplementary Figure S1B), yielded similar cluster configurations demonstrating the method’s robustness in deciphering the segmental structure irrespective of the choice of segmentation stringency, and, perhaps, because of this, in robustly grouping the similar segments.

Indeed, the classic recursive segmentation procedure, also sometimes called 1 to 2 segmentation or binary segmentation, has often been criticized for being too simple and inherently limited in identifying short variants lying within large homogeneous segments. Olshen et al.’s (57) CBS was developed to circumvent this limitation of being able to detect just one change point at a time. CBS detects two change points at a time and thus augments the power of recursive segmentation in localizing the change points. However, simultaneous localization of two change points makes CBS much more computationally intensive than the binary segmentation. In assessment of CBS with our proposed method that actually used the binary segmentation (but allowing hypersegmentation) in combination with a two-step recursive clustering procedure, we observed that the validated break points were identified much more efficiently by the latter (Table 3). This clearly demonstrates the power of the proposed integrative approach in robust localization of change points within complex genomic data.

Although Bayesian methodology is often invoked for mining biological data, its success depends critically on the prior distribution on the data. The sets of priors used by the two Bayesian techniques tested here were not clearly helpful in deciphering the genome heterogeneities. The HMMs are useful tools; however, often the prior information on the model structure is not available, and also their performance is a function of the quality of training data. Further, the optimal parse provided by HMMs may not adequately represent the multilayer inclusive complexities underlying evolutionary data. These discrepancies were in part addressed through the entropy-based methodology, which does not need any prior information or training data. Our approach consummates both top-down and bottom-up information theoretic approaches yielding a robust integrative methodology for deconstructing genomic data. Importantly, the data heterogeneity was addressed by using multiple stringencies in the segmentation and clustering procedures, allowing hypersegmentation to detect precisely the change points followed by clustering in a non-hierarchical fashion to restore the inherent segmental structure of the data.

Although the usefulness of the Jensen–Shannon divergence measure in interpreting evolutionary relationships among organisms has been demonstrated in a sequel of articles published in the PNAS magazine recently (35–38), we have shown how this interpretation could be confounded by not taking into consideration the inherent compositional heterogeneities within the genome sequences being compared. We emphasize here that it is critical to deconstruct the intragenome heterogeneities in first place before directly comparing two or more genomes using divergence measures. This helps in drawing the bigger picture of evolutionary patchiness and how the parts of the disparate genomes have coevolved leading to fateful evolutionary events including speciation. A faithful deconstruction is feasible within the framework proposed here; this was clearly demonstrated by our experiments on both artificial and genuine genomes in deciphering the compositionally distinct regions.

Although the proposed methodology is readily applicable to symbolic sequences, we have shown here how easily it can be adapted to be applicable to numeric sequences, which are often the case for plethora of biological data including the probe intensity data from aCGH (53) and single-nucleotide polymorphism (SNP) arrays (78), or raw read counts from next-generation sequencing (NGS) platforms (79). Note that the latter two are more recent technologies; development of SNP array technology follows the discovery of millions of SNPs; this platform outputs not just the hybridization intensities but also the relative frequencies of the two alleles (78). More recently, rapid advances in ultra high-throughput NGS technologies have dramatically enhanced the resolution of CNV detection (79,80). After aligning the short reads, typically few tens of bases long, to a reference genome, the amplifications or deletions can be inferred by the increase or decrease in the number of sequence reads at genomic loci relative to the genomic background. Both these technologies bring in essentially a similar set of challenges in detecting CNVs, as is encountered with the aCGH technology. Apparently, CNV detection remains mathematically or computationally the same problem in these instances also; one notable difference is the large volumes of data generated from these platforms, which, however, could be an advantage considering the asymptotic assumptions implicit in the proposed methodology. Future work could focus on the adaptation of this methodology for interpreting data from emerging technologies including NGS technologies.

An alternative to usage of postprocessing, particularly on more complex data sets that may have contiguous outliers as in case of structural variants, could be the application of recursive segmentation to first determine the span of different structural types and then use a clustering procedure similar to one proposed here or as in Chen et al.’s article (64) to refine the break points.

Further, what makes this methodology particularly interesting and widely applicable is its ability to interpret the data without learning the behavior from training data, which are scarcely available in most instances. Additionally, perhaps, because of its unsupervised character, it serves as an exploratory tool for mining yet unknown biological entities. Future work should be directed toward further exploitation of the potential and flexibility of this approach in interpreting biological data of different kinds and sizes.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Tables 1–3 and Supplementary Figures 1–3.

FUNDING

US National Institutes of Health (NIH) [R01-LM008991 to J.L. and R01-GM078092 to R.K.A. as Co-I]; faculty start-up fund from the University of North Texas (to R.K.A.). Funding for open access charge: NIH; University of North Texas.

Conflict of interest statement. None declared.