MuMoD: a Bayesian approach to detect multiple modes of protein–DNA binding from genome-wide ChIP data

Abstract

High-throughput chromatin immunoprecipitation has become the method of choice for identifying genomic regions bound by a protein. Such regions are then investigated for overrepresented sequence motifs, the assumption being that they must correspond to the binding specificity of the profiled protein. However this approach often fails: many bound regions do not contain the ‘expected’ motif. This is because binding DNA directly at its recognition site is not the only way the protein can cause the region to immunoprecipitate. Its binding specificity can change through association with different co-factors, it can bind DNA indirectly, through intermediaries, or even enforce its function through long-range chromosomal interactions. Conventional motif discovery methods, though largely capable of identifying overrepresented motifs from bound regions, lack the ability to characterize such diverse modes of protein–DNA binding and binding specificities. We present a novel Bayesian method that identifies distinct protein–DNA binding mechanisms without relying on any motif database. The method successfully identifies co-factors of proteins that do not bind DNA directly, such as mediator and p300. It also predicts literature-supported enhancer–promoter interactions. Even for well-studied direct-binding proteins, this method provides compelling evidence for previously uncharacterized dependencies within positions of binding sites, long-range chromosomal interactions and dimerization.

INTRODUCTION

Transcriptional regulation is largely governed by interactions between proteins called transcription factors (TFs) and DNA. A TF–DNA interaction can either be direct or indirect through contact with other proteins. In both situations, the protein–DNA complex usually plays a role in regulating the transcription of a target gene. Identifying protein–DNA binding events on a genome-wide scale is therefore crucial for understanding transcriptional regulation.

TF binding sites are commonly identified in vivo through chromatin immunoprecipitation (ChIP) targeting the protein of interest (POI), followed by sequencing (ChIP-Seq) (1) or microarray hybridization (ChIP-chip) (2). A typical ChIP-Seq or ChIP-chip experiment reports regions of length between 50 and 2000 bp, with the resolution depending on the sequencing depth, or the design of the microarray, respectively. The actual TF binding site, however, is far shorter, usually <20 bp (3). Therefore, to identify the precise location of the binding site, the bound regions are fed to de novo motif discovery programs such as MEME (4) or Weeder (5). These tools attempt to find statistically enriched sequence motifs and their locations within the bound regions. However, they suffer from two limitations when applied to ChIP data from higher eukaryotes. First, although the total number of genomic regions may be in thousands, only the top 500 or so regions are typically analyzed to find enriched motifs. As a result, the final motif is indicative of only the high-affinity binding sites and often explains only a fraction of all the bound sequences (6). Although computational constraint is one reason for limiting the number of analyzed regions, the other reason is that increasing the number often does not yield a ‘significantly enriched’ motif. Consider the following scenario: the POI binds with higher affinity to a large, possibly palindromic site through homodimerization, but with a lower affinity to a half-site (Figure 1A and B). In this case, the palindromic site will be enriched in the top few sequences, but will not explain the rest of the sequences. To further complicate matters, the distance between the half-sites may be variable, with each variation having an effect on binding affinity. Figure 1C shows an instance when the POI forms a heterodimer, which could result in yet another binding specificity. Although a traditional motif discovery method may report the half-site in the full set, these variations in the binding modes would be missed. Leucine zipper proteins are classic examples of this kind: they can form homodimers and/or dimerize specifically with other leucine zipper proteins resulting in dimers with different DNA-binding specificities and affinities (7).

Figure 1.

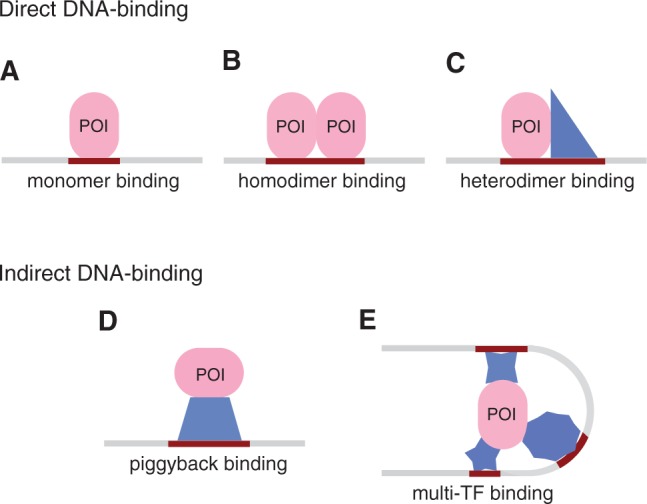
Different modes of protein–DNA binding. The profiled protein is shown as an oval and co-factors as polygons. A direct DNA-binding protein can recognize different sites based on its partner: (A) a half-site as a monomer, (B) a symmetric motif as a homodimer, and (C) two different half-sites as a heterodimer. An indirect DNA-binding protein can immunoprecipitate sequences containing the consensus of (D) one or (E) several co-factors. See Farnham (6) for a discussion on why regions arising from ChIP experiments may not contain a match to the consensus motif.

The second limitation pertains to a POI that is not a direct DNA-binder and has more than one distinct DNA-binding co-factor (Figure 1D and E). In such situations, the bound regions are even less likely to be explained by a single motif. For example, p300, a general activator, binds to several different DNA-binding proteins (8), giving rise to structures similar to the complex in Figure 1E. Assuming that the complex is fairly stable, all three regions will be reported when any of the four constituent proteins are profiled. Although most motif discovery methods have the ability to report multiple motifs, they provide little indication as to how the motifs together explain the full set. Moreover, many of these methods report motifs that are highly similar to each other in content, built from only slightly different subsets of the bound sequences. As a consequence, the decision as to which motifs are meaningful is left for the biologist to make, either through prior expert knowledge or through some threshold for the significance metric(s) accompanying the reported motifs.

The above limitations stem from the fact that traditional motif discovery methods formulate the problem as finding one or more motifs each of which individually explains a majority of the bound sequences. If a subset of POI molecules forms a complex with a DNA-binding protein (Figure 1D) and this subset is relatively small, the motif of the DNA-binding protein will be missed because in the full set of regions bound by the POI, this may not appear to be significantly enriched. Even the faster and specialized motif discovery tools designed to work on large ChIP-Seq datasets (9–11) use the same basic principle of identifying motifs.

In this article, we formulate the problem differently: the goal is to partition the bound sequences such that each partition contains an instance of a motif enriched in that partition. Instead of assuming that a single motif is responsible for the immunoprecipitation of all the regions, we assume that each region is immunoprecipitated due to the presence of one of k motifs. The output therefore, for a given k, is k de novo motifs and k disjoint subsets of the original bound set. For example, in the case of the multi-TF complex in Figure 1E, assuming there are several such complexes in the nucleus and k is set to 3, this method will report three different motifs, characterizing the three DNA-binding proteins interacting with the POI, along with the three corresponding partitions of the bound sequences. The appropriate value of k is determined by applying Bayesian model selection. Since this method attempts to identify the various modes by which the POI binds DNA regions causing them to immunoprecipitate, we call this method MuMoD: Multi-Mode Detection.

We apply MuMoD to several ChIP-Seq datasets reported by different laboratories, targeting a wide range of proteins. In the case of p300, we identify its potential partners in heart cells. Similarly, for the mediator complex, which is also a transcriptional co-activator, we identify co-factors in two different cell types. Furthermore, the identified modes suggest that the mediator complex connects distant enhancers with promoters. Comparison with MEME and Weeder, two conventional motif discovery programs, and with Chipmunk (9) and PeakMotifs (11), programs specifically designed for large ChIP datasets, indicates that MuMoD indeed benefits from this unique approach to motif discovery. Even in the case of proteins that directly bind DNA, MuMoD provides several novel insights: the literature consensus is not necessarily enriched in the very top ChIP regions, POIs can cause immunoprecipitation of other sequences that are bound indirectly, Gata3 probably prefers to bind as a homodimer with an affinity dependent on the gap between the two half-sites, and CTCF-binding sites contain dependencies. Notably, MuMoD requires no additional information such as motif libraries or prior knowledge of whether the POI is a direct binder.

MATERIALS AND METHODS

Model description

Assume the ChIP experiment reports n genomic regions 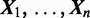for some protein. Each 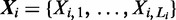is a DNA sequence of length 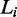, where each 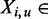{A, C, G, T}. This set of sequences is the only input to MuMoD. We now develop a model class 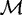with a vector of model parameters 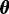to explain the data 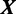. Vector 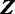of size n denotes the starting location of the binding site in each sequence: 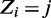if there is a binding site starting at location j in sequence 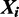. To allow for noise in ChIP experiments, we model the possibility of 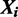having no binding site, which we denote as 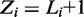. This also accounts for regions that contain binding modes with too many variations to be modeled comprehensively with a motif. This assumption is equivalent to the zero or one occurrence per sequence (ZOOPS) model of MEME (4) or PRIORITY (12). Alternatively, one occurrence per sequence (OOPS) model can be followed by not allowing 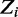to lie outside the sequence.

Model 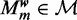assumes there are m different modes in which the POI can bind the sequences: each sequence is explained by the presence of a binding site matching one of m different motifs. The vector 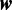represents the widths of the m motifs, which are modeled with m individual position-specific scoring matrices (PSSMs): 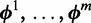. Specifically, motif k with width 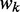is described by 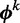, where 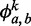is the probability of finding nucleotide b at location a for 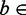{A, C, G, T} and 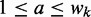. We use 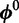, a second-order Markov model built from the input sequences, as the background model. To accommodate the vast heterogeneity in eukaryotic sequences, each sequence has its own background model built from its 3-mers. Indicator vector denotes the type of binding site present in each sequence: 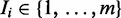. We use 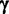to represent the multinomial parameters of 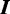: 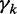represents the probability of the mode being k. Therefore, the parameter vector 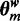for the model 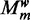contains 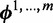, , 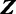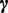and .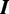

We can compute the likelihood of a sequence 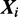as:

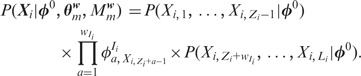(1)

The likelihood of the full data is

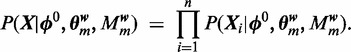(2)

We need to find optimal parameters for model

that maximize the posterior distribution:

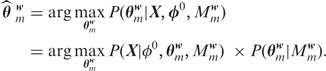(3)

Model learning

Gibbs sampling is a popular technique for parameter estimation: it approximates sampling from the posterior distribution by drawing samples from individual conditional distributions. We use collapsed Gibbs sampling (13) for faster convergence, where 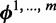and 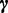are integrated out from the conditional distributions of 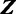and 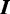. Furthermore, rather than sampling the full vectors 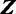and , we iteratively sample 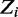and 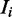for each sequence .

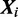Assuming a Dirichlet prior over all 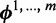, given the current values of parameters in 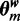except 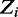, the expression for sampling a value j for 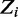reduces to:

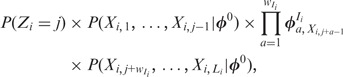(4)

where 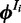is calculated from the nucleotide counts of the sites in all sequences except 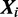having mode 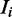. The prior probability over positions 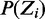can be uniform, as used here, or user-defined (‘Discussion’ section).

Similarly, assuming a Dirichlet prior over 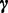, if 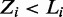, that is, the sequence 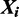contains a binding site of some mode, the expression for sampling the value of k for mode 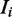reduces to:

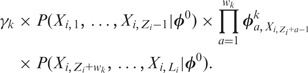(5)

Here 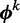is calculated from the nucleotide counts of the sites in all sequences including 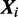which have mode k, while 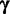is calculated from the counts of all m types of modes in all sequences, except 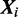. In case 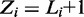, that is, the sequence 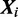does not contain a binding site of any kind, this sampling step is omitted.

Model selection

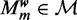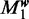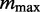Choosing the optimal number of modes m is equivalent to selecting the optimal model . We start with learning all models to for a predetermined maximum number of modes and 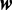drawn from a set of widths. We can compute the probability of a model with m modes with 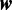widths as

(6)

We assume an exponential prior on the number of free parameters in the model:

(7)

where 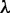is the hyperparameter that controls the penalty given to complex models. The number of free parameters in 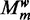is the number of free parameters in the PSSMs used to represent the motifs:

(8)

The first term in Equation (6) can be written as:

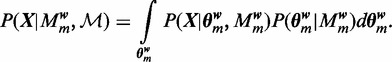(9)

We approximate the integral with the mode of the distribution, which is achieved at 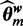in Equation (3), computed using Gibbs sampling. For selecting the best 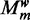, the normalization term in Equation (6), which is the same for all models, is ignored.

For the datasets investigated here, we built models for 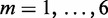and widths were varied between 8 and 16. The optimal number of modes depends on the value of 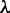, with a value >10 resulting in fewer and less informative motifs, while a value <3 leading to overfitting (Figure 2 and Supplementary Table S1). We obtained reasonable modes with a value of 5, which we use throughout this work. It should be noted, however, that datasets/organisms not explored here may warrant a different value of 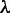(‘Discussion’ section). The prior probability of a sequence not containing a binding site, i.e. 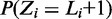was set to 0.1. MuMoD is written in C and is available upon request.

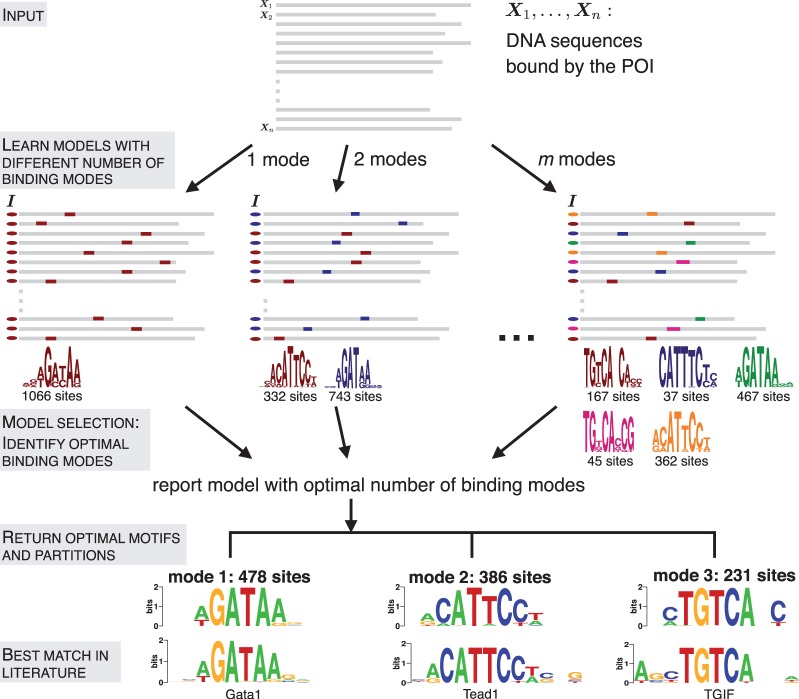
Figure 2.

Identifying different modes of protein–DNA binding. A total of m models having 1 through m modes are learned from the input data. DNA sequences are shown in gray, the indicator vector 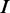on the left of each sequence marks the mode to which it contributes. The motif logos displayed at the bottom correspond to the p300-bound sequences in HL1 cardiomyocytes (14). In the final step, the method reports three optimal partitions, which can be compared with motifs from literature.

Datasets and comparison with other programs

A total of 21 murine datasets were compiled from ChIP experiments conducted at three laboratories:

1. HL1 cardiomyocyte cell line (14): Gata4, Mef2, p300, Nkx2-5, Srf and Tbx5.

2. Murine embryonic stem (ES) cells and murine embryonic fibroblasts (MEFs) (15): Subunits Med1 and Med12 of the mediator complex in ES cells and MEFs, subunit Smc1a of the cohesin complex in ES cells.

3. Ten types of T-cells (16): Gata3.

Processed output after application of peak-calling programs was used directly as reported by the respective laboratories. These programs also report a ChIP enrichment score or peak height. The repeats in the sequences were masked and sequences that contained at least 100 unmasked nucleotides were retained for analysis. The top 5000 sequences based on ChIP enrichment scores were used for all sets except those that reported fewer total sites, in which case all sequences were used. The only exception was the set of sequences that were bound by both cohesin and mediator in ES cells, which contained 11 865 sequences.

Conventional motif discovery programs MEME, Weeder, PeakMotifs and Chipmunk were applied to the same datasets (Supplementary Figures S1–S3). All were asked to report top five motifs. MEME was run with motif widths 8–16, ZOOPS model, E-value <10. Weeder was run with its ‘large’ setting that allows motifs up to width 12 to be discovered. PeakMotifs was run with default parameter settings, and results reported here are using their web-based oligo-analysis tool. Chipmunk was run with its ‘ChIPHorde’ option that allows for multiple motifs to be discovered, with the filter criterion. Web-based tools STAMP (17) and TOMTOM (18) were used to make motif comparisons. Weblogo (19) was used to create logos from identified motifs.

RESULTS

Identifying different modes of TF–DNA binding

MuMoD models the problem as that of identifying the distinct modes by which the POI binds DNA, causing a set of n sequences to be reported by the ChIP experiment. Here, a mode is defined as the motif and the sequences contributing to it. A motif is represented with the commonly used PSSM that records the probability of each nucleotide in every position of the binding site (20). For a predetermined number of modes k, the sequences are partitioned into k sets and the motif most enriched within each set is simultaneously identified (Figure 2). This is done using an iterative algorithm, based on Gibbs sampling (‘Materials and Methods’ section). When k = 1, this is similar to the regular motif discovery problem, where the goal is to find one motif most enriched in the whole set. Even in conventional programs that report multiple motifs, k is implicitly set to 1: additional motifs are identified by masking occurrences of previously found motifs or by exploring different motif lengths. The other extreme case in MuMoD is when k = n, i.e. n different motifs are identified, each derived from exactly one sequence. In addition, a bound sequence is allowed to not contribute to any mode. This accounts for experimental errors and the possibility of the POI binding DNA in a manner that is supported by few instances.

Figure 2 shows models learned from the p300 dataset in the murine HL1 cardiomyocyte cell line (14) containing 1282 sequences. This POI is a transcriptional co-activator that does not bind DNA directly, but instead serves as an adaptor protein facilitating protein–protein interaction and long-range chromosomal (enhancer–promoter) interactions (21), resembling the multi-TF complex in Figure 1B. Looking for one mode results in a weak GATAA motif. Increasing the number of modes refines it, while simultaneously introducing other motifs like CATTCC. This motif closely resembles the binding specificity of Tead1, also implicated in cardiac-related activity (22) and shown to co-precipitate with p300 (14). However, increasing the number of modes beyond a point can cause overfitting (m modes case in Figure 2): the brown/magenta motifs and blue/orange motifs are similar to each other and can perhaps be replaced by one motif each, if the number of sites that contribute to the individual motifs is small. In this case, only 37 sequences contribute to the blue motif in contrast to 362 for the orange motif. Similarly, 45 sequences contribute to the magenta motif when compared with 167 in the case of the brown motif.

The final model selection step identifies the optimal number of modes based on the number of sequences n, the size of each partition and the contribution of the motifs in explaining the dataset. Simply put, models with highly similar motifs get penalized unless they explain the dataset better than a merged motif. Mathematically, the penalty is controlled by a single parameter 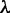; decreasing it biases MuMoD to learn more binding modes. In this specific p300 dataset, MuMoD reports three distinct modes (output in Figure 2). While the first two motifs closely resemble binding sites of the Gata family and of Tead1, the core TGTCA of the third motif matches the specificity of two three-amino-acid extension loop (TALE) homeobox proteins Meis2 and TGIF, both of which may act in competition (23). While both proteins are known to interact with p300 (24,25), Meis2 has also been shown to be active in the heart (26). A total of 187/1282 sequences contain no motif, implying that these sequences may be bound by p300 through many different TFs, none yielding enough sequences to create a high-confidence motif. Interestingly, these sequences are more prevalent in the bottom third of the immunoprecipitated sequences (Supplementary Figure S4) and have a significantly lower ChIP enrichment score (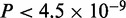) (All P-values for comparing quantities between two sets are based on two-sample two-sided Wilcoxon rank sum tests, unless otherwise indicated.) than the rest of the sequences. These sequences could therefore be a product of noise: a higher significance threshold during peak calling may eliminate these regions from the original set.

We compared motifs reported by MuMoD with the top five motifs found by MEME, Weeder, PeakMotifs and Chipmunk (‘Materials and Methods’ section). These programs together report motifs for Tead1 and Meis2, along with low-complexity variants of the same (Supplementary Figure S1A). Interestingly, none of these programs reports the Gata motif although 77% of the sequences belonging to the Gata family mode identified by MuMoD are indeed bound by Gata4 in the same cell type (14) (hypergeometric ).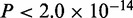

Looking for more than one mode helps recover known TF binding specificity

In addition to p300, He et al. (14) have also profiled Tbx5, Srf, Nkx2-5, Gata4 and Mef2 in the HL1 cell line. The authors performed motif discovery using MEME and Weeder on the top 500 sequences from each set. Here, in order for the motif to not be biased toward the strongly bound sites, we used the top 5000 sequences. The same set was also input to the aforementioned conventional programs.

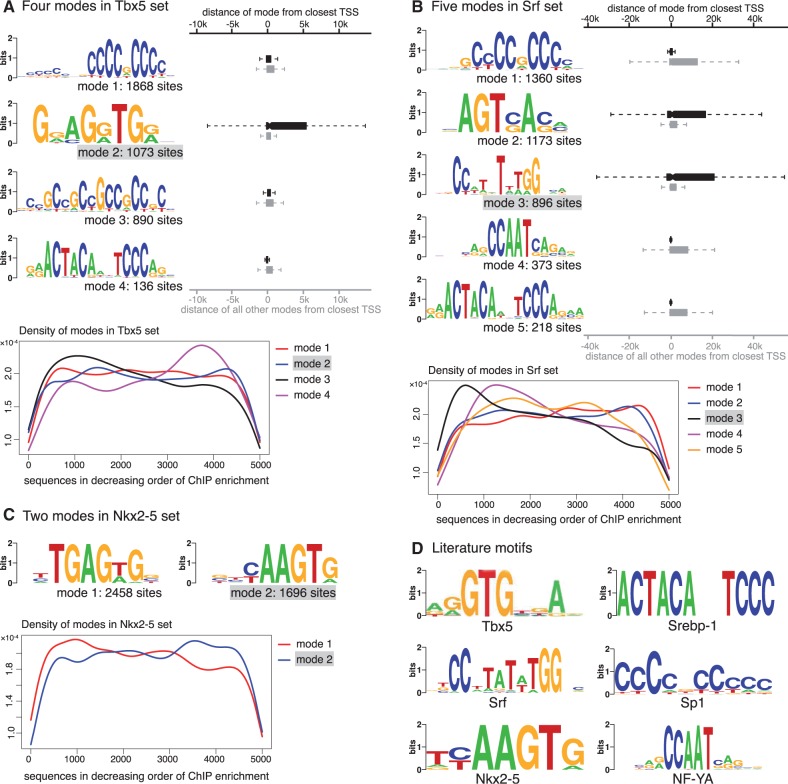
In the case of Tbx5, the authors report that most of the sequences bound by Tbx5 are GC-rich and the removal of these GC-rich sequences results in a motif known to be bound by Tbx5. Since we do not see a rationale for removing these sequences, the full set was investigated here. The optimal number of modes is reported to be 4 (Figure 3A). Motifs corresponding to modes 1 and 3 are highly GC-rich, while the motif corresponding to the second largest mode resembles the binding specificity of Tbx5 (Figure 3D). Interestingly, sequences that are part of this mode are more likely to be distant from the transcription start site (TSS) than other sequences bound by Tbx5 (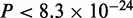, boxplot in Figure 3A). This suggests that Tbx5 binds directly to enhancers, which act in a distance-independent manner, but the resulting protein–DNA complex is close to the TSS causing TSS-proximal regions to be immunoprecipitated during ChIP. TSS-proximal regions are primarily GC-rich, which could explain why the conventional motif discovery methods used in the original study (14) could identify the Tbx5 motif only after their removal from the dataset. Motif 4 matches the consensus of the sterol regulatory element binding protein (Srebp1) (Figure 3D), which is known to be vital for heart function (27,28). None of the conventional motif discovery programs identifies the Tbx5 motif in these top 5000 sequences (Supplementary Figure S1B). Interestingly, the mode matching literature consensus is not especially enriched in the top bound sequences (density plot in Figure 3A). The mode composed by the largest number of sequences, mode 1, occurs uniformly throughout the set, and resembles the Sp1 motif, known to be present in promoters (29,30).

Figure 3.

Modes in three HL1 ChIP-Seq datasets. (A) Four modes are identified in Tbx5-bound sequences: motif for mode 2 matches the literature consensus. The distances to the closest TSS of the sequences in this mode (red boxplot) are significantly larger than sequences in other modes (blue boxplot). The density plot at the bottom illustrates the presence of each mode across sequences sorted by decreasing ChIP enrichment score. (B) Five modes are identified in Srf-bound sequences: motif for mode 3 matches literature consensus. The distances to the closest TSS of the sequences in this mode (red boxplot) are significantly larger than sequences in other modes (blue boxplot). The same holds true also for mode 2. Other three modes are enriched near the TSS. The density plot at the bottom shows that mode 3, which matches the Srf literature consensus, is more prevalent in the top 1000 sequences. (C) Two modes are identified in the Nkx2-5-bound sequences: motif for mode 2 matches literature consensus. The density plot indicates that this mode is slightly more prevalent in the lower half of the sequences. (D) Literature motifs for Tbx5 (reproduced from 31), Srebp1 (32), Srf (33), Sp1 (34), Nkx2-5 (33) and NF-YA (34).

In the case of Srf, we find five modes, of which the motif for mode 3 matches the literature consensus of Srf (Figure 3D). As in the case of Tbx5, this mode is more likely to be present away from the TSS (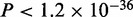). However, in contrast to Tbx5, as indicated by the density plot, this mode is more prevalent in the top sequences and has a higher ChIP enrichment score than sequences contributing to other modes (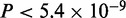). This explains why the Srf motif is found by other motif finders when the top 500 sequences are considered (14). However, none of the four methods used here finds the Srf motif in the top 5000 sequences (Supplementary Figure S1C). Furthermore, one of the modes (mode 5) resembles the Srebp1 motif in this set as well. Motif for mode 4 matches the binding consensus of the nuclear factor Y, alpha (Figure 3D) also known to bind Srf (35). The mode composed of the largest number of sequences, mode 1, resembles the motif for Sp1 here as well (Figure 3D).

In the case of Nkx2-5, we find only two modes in the top 5000 sequences (Figure 3C). Motif for mode 2 matches the literature motif (Figure 3D), but the ChIP peak height of regions in this mode is lower than that of mode 1 (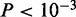). All four conventional motif finders find mode 1, possibly because it is present in a larger number of sequences. Only Weeder additionally finds the literature consensus, which is part of a 10-bp long, weak motif, built from only 463 sites (Supplementary Figure S1D).

In the case of Gata4, all programs find the canonical GATAA motif (Supplementary Figure S1E). MuMoD finds a second smaller mode GATTA, also known to be bound by Gata4 (36). There is no significant difference in the peak heights or distance from the TSS between the two modes. In the case of Mef2, MuMoD finds four modes, the second largest of which matches the known Mef2 consensus (Supplementary Figure S1F). Interestingly, as in the case of Tbx5 and Srf, sequences in this mode are more variable in terms of distance from the closest TSS (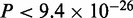, not shown), suggesting that this TF also binds enhancers directly. Similar to the case of Srf, the mode matching the literature consensus of Mef2 has a significantly higher ChIP enrichment (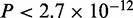) than other sequences. Among the conventional motif finders, only MEME and PeakMotifs identify the Mef2 consensus.

Modes hint at Gata3 homodimerization in T-cells

Gata3 plays a crucial role during T-cell development and differentiation (37). Wei et al. (16) profiled Gata3 binding across 10 different types of T-cells: naive CD4⁺, Th1, Th2, Th17, iTreg, nTreg, NKT, CD8⁺ cells, CD4–CD8 double-positive (DP) and CD3-negative CD4–CD8 double-negative (DN) thymocytes. We applied MuMoD to each of the 10 datasets. Not surprisingly, the WGATAA motif came up in each dataset, a claim that can be made only for Weeder among the conventional motif discovery methods (Supplementary Figure S2A–J). In addition, two related modes were highly prevalent: WGATAnnnATCW was present in nine cell types and WGATAnnATCW was present in four cell types (Figure 4). This suggests that Gata3 may form a homodimer which binds DNA at a palindromic site composed of two WGAT half-sites separated by three or four nucleotides. Our results support an earlier conjecture by Zhang et al. (38) based on gel shift assays stating that Gata3 may bind DNA as a homodimer. However, without additional experimental studies, we cannot exclude the possibility of two Gata3 molecules binding to the half-sites independently, in these cell types.

Figure 4.

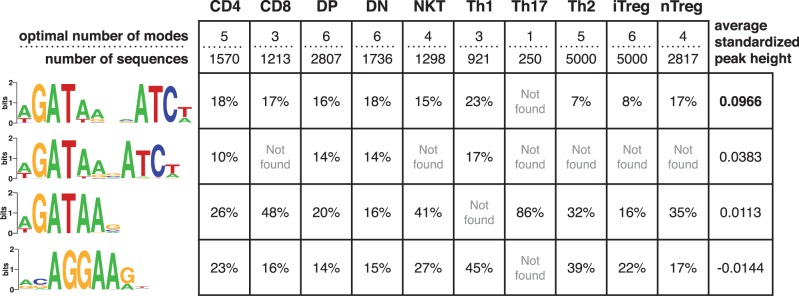
Four modes in Gata3-DNA binding across 10 cell types. The optimal number of modes and the number of sequences in each Gata3 set are shown in the first row of the table. The four motifs on the left are created by aligning sites contributing to similar modes across the different cell types (Supplementary Figure S2A–J). The percentage of the sequences bound by Gata3 in each cell type contributing to the mode is shown in the respective row. The last column indicates the average ChIP enrichment across all cell types for regions in each mode. The heights of all peaks belonging to a mode in each dataset were standardized to remove individual experimental biases. The first palindromic mode has significantly taller peaks (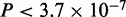) when compared with other modes.

Interestingly, the A following the half-site WGAT is also conserved in the two palindromic motifs. Since each motif is composed of putative binding sites either in the forward or the reverse strand, this result needs to be interpreted as: at least one of A after the first half-site WGAT, or T before the second half-site ATCW is conserved. In contrast, for the single Gata3 site, this A (or T on the opposite strand) is almost always conserved. This suggests that if Gata3 is indeed binding as a dimer, one A at position 5 in either half-site is sufficient to achieve binding in the full site.

The ChIP enrichment is significantly higher for a palindromic site with a gap of four (last column in Figure 4), suggesting a preference for this homodimer–DNA complex. The fourth highly occurring mode, which has the lowest ChIP enrichment among the four modes, resembles the Ets motif AGGAA. Like Gata3, several members of the Ets family, namely, Elf1, Erg, Ets1, Ets2, Fli1, Spi1 and Tel, are also active in the T-cell lineage (39). Some of these have been shown to bind cooperatively with Gata3 (40,16). Since all these TFs have a similar sequence specificity, it is not possible to identify the specific Ets TF associating with Gata3, without additional information. However, not all Ets TFs are active simultaneously (39), and it is likely that Gata3 associates with different Ets TFs at different stages of T-cell differentiation/development.

Some of the motifs identified by MuMoD are also detected by other motif discovery programs, but these programs do not report the partitioning of sequences based on the motifs. Furthermore, many of the reported motifs are highly similar to each other, with the same site contributing to more than one motif. This makes it difficult to assess the significance of each motif. We believe that all modes described in Figure 4 are significant, because together they explain the full set of bound regions.

Multiple modes reveal correlations among positions

The cohesin protein complex has been implicated in several cellular processes such as cell division, DNA repair and DNA loop formation associated with gene regulation (41). The top 5000 sequences bound by Smc1a, a cohesin core complex protein, in mouse ES cells (15) were analyzed by MuMoD. Cohesin has been shown to occupy sites bound by the CCCTC-binding factor CTCF (42) and indeed, all conventional motif discovery methods identify the CTCF motif in this set (Supplementary Figure S3A). MuMoD, however, finds two binding modes, differing at positions 13–15 (Figure 5). Note that the combined motif, which is similar to the canonical CTCF motif (34), has almost equal proportions of G&A at position 14 and of C&G at position 15. However, the two different modes clearly split the sites into two sets, composed of GC and AG at positions 14 and 15, with GG and AC occurring far less often. This shows the dependencies between these two positions in the binding preferences of CTCF, which cannot be captured by a combined motif. Furthermore, an A at position 14 is almost always (97% of the time) preceded by a C at position 13. In contrast, a similar G at position 14 is preceded by a C 78% of the time. This lower enrichment of CG could have implications in DNA methylation.

Figure 5.

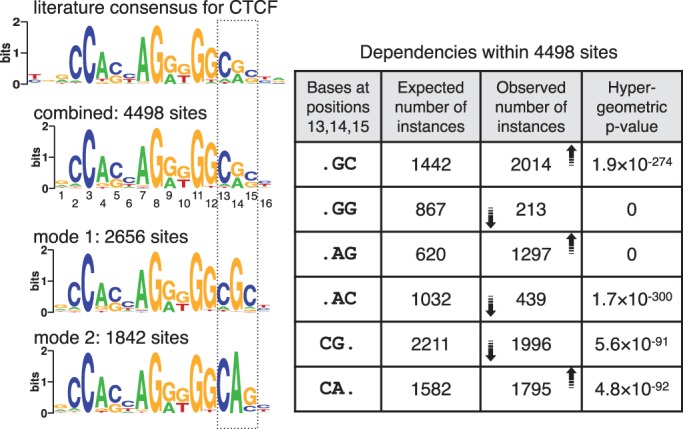
Two modes identified in cohesin-bound sequences in mouse ES cells. Conventional motif discovery programs return a motif similar to the CTCF motif shown on top. MuMoD identifies two modes, whose combination also resembles the CTCF motif. The table on the right describes dependencies within positions 13–15 in the combined motif. The first column considers different dinucleotide combinations; the second column shows the expected number of instances of each combination, assuming that the combined PSSM is an appropriate representation of the binding sites; the third column shows the number of instances actually observed, with the arrows indicating the increase or decrease in numbers with respect to the expected instances; the fourth column shows the hypergeometric P-value of observing similar numbers by chance. The two modes segregate the binding sites into two motifs (left bottom), which together capture these dependencies.

Modes reveal mediator interactions in mouse ES cells

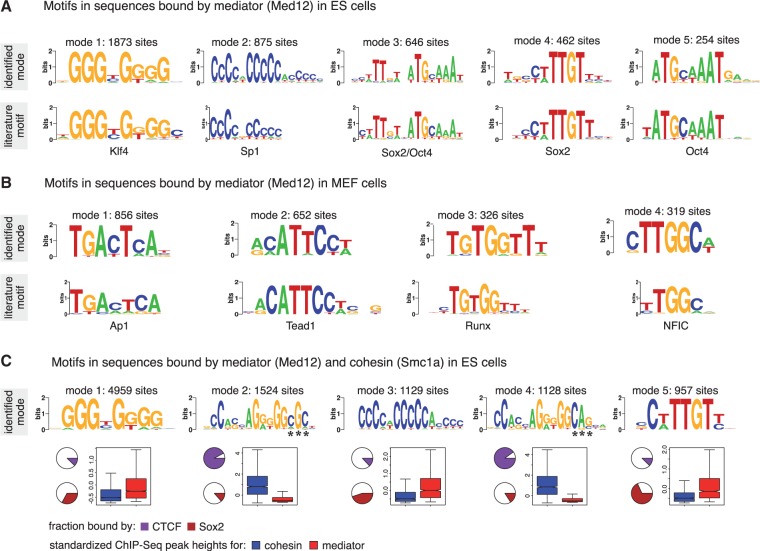
In addition to Smc1a, Kagey et al. (15) have profiled subunits Med1 and Med12 of the mediator complex in mouse ES cells. The mediator complex is a co-activator and acts as a bridge between transcriptional activators and the general transcription machinery (43). MuMoD identifies five modes in the top 5000 sequences bound by Med12 in the ES cells (Figure 6A). For brevity, we discuss results in the Med12-bound regions; we get similar motifs for Med1 (not shown). The largest mode matches the Klf4 motif, while the second largest matches the Sp1 motif. The other three modes resemble the Oct4 motif ATGCAAAT, Sox2 motif CWTTGTT and the motif bound by the Oct4/Sox2 complex (44). Klf4, Sox2 and Oct4 are all known to be active in ES cells (44). Moreover, modes 1 and 2 are significantly closer to the TSS than the other three modes (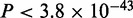; Supplementary Figure S5), suggesting that the mediator complex is indeed connecting distant enhancers bound by Sox2 and/or Oct4 to promoters bound by Klf4 and Sp1. This was supported by ChIP-Seq experiments profiling TFs Sox2, Oct4 and RNA polymerase II (15): modes 3–5 are significantly more enriched for Sox2 and Oct4 binding, while modes 1 and 2 are significantly more enriched for RNA polymerase II. Interestingly, none of the conventional motif discovery methods finds all five motifs (Supplementary Figure S3B): they typically identify only the Klf4 or the Sp1 motif, possibly because they are the dominant modes. Of all the motifs reported by other programs that have a match to JASPAR/TRANSFAC, only MEME finds a motif that MuMoD does not. It resembles the Srebp1 motif, composed of only 74 sites (‘Discussion’ section).

Figure 6.

Modes identified for the mediator complex. (A) Five modes are identified in ES cells, shown on top. The corresponding closest match in the JASPAR (34)/TRANSFAC (33) is shown below. (B) Four modes are identified in MEF cells, with closest match shown below. The motifs in MEF and ES cells are different, corresponding to TFs known to be active in the respective cell types. (C) Five modes are identified in the sequences common to mediator and cohesin. Motifs for modes 1, 3 and 5 match motifs of Klf4, Sp1 and Sox2, respectively. Motifs for modes 2 and 4 resemble the CTCF motif and differ at positions indicated with asterisks. The pie-charts indicate the percentage of sequences belonging to each mode also bound by CTCF and Sox2. Around 90% of modes 2 and 4 are bound by CTCF. In contrast, only 12% of mode 5 is bound by CTCF. Similarly, almost 70% of mode 5 and around 14% of modes 2 and 4 are bound by Sox2. The boxplots indicate the distribution of peak heights resulting from ChIP experiments profiling Smc1a (blue) and Med12 (red). Smc1a is highly enriched at modes 2 and 4 when compared with the other modes. In contrast, Med12 is significantly more enriched at modes 1, 3 and 5.

Applying the method to the same mediator subunit Med12 in MEFs gives entirely different modes (Figure 6B). The resulting motifs match motifs of TFs known to be active in MEFs: Tead1 (45), Ap1 (46), NFIC (47) and Runx (48). This corroborates with our current understanding of the mediator complex acting as a co-activator for other TFs. Again, none of the conventional motif discovery methods finds all these motifs. They typically find Tead1 and Ap1 and report several variants of the same (Supplementary Figure S3C). PeakMotifs finds two other motifs, one is a weak motif resembling Sp1, while the other does not match with anything listed in JASPAR/TRANSFAC.

Through chromosome conformation capture (3C) experiments, Kagey et al. (15) showed interactions between cohesin and mediator at four different loci. To investigate this further on a genome-wide scale, we explored the set of sequences bound by both cohesin and mediator, using the intersection of regions arising from the two respective ChIP-Seq experiments. We found five modes in this set of 11 865 sequences (Figure 6C). Motifs for modes 1, 3 and 5 are similar to those found in the top 5000 Med12 sequences, matching specificities of Klf4, Sp1 and Sox2, respectively, while motifs for modes 2 and 4 are the two variants of the CTCF motif found in the top 5000 cohesin sequences (Figure 5). The overlaps of the modes with regions bound by CTCF and Sox2 support the discovered motifs. More interestingly, the heights of the peaks for the individual cohesin and mediator experiments at the modes are strikingly different. Cohesin is highly enriched at the two CTCF motifs, while mediator is enriched at the other modes. This suggests that cohesin and the mediator target different sites on the genome, but the DNA loops bring them together causing them to co-precipitate. The interactions between cohesin and CTCF and those between mediator and cell type-specific TFs are probably more persistent and therefore get a stronger ChIP enrichment score, while the interactions between cohesin and mediator are more transient in nature. This is further corroborated when we look at the set of sequences bound by Sox2 and CTCF. We find three modes, two for the two variants of CTCF and one matching the Sox2 motif (Supplementary Figure S3E). Here too, we find differential ChIP enrichment for Sox2 and CTCF, with the former being more enriched at the Sox2 mode and the latter in the two CTCF modes.

DISCUSSION

As demonstrated on multiple datasets, MuMoD can be successfully applied to ChIP regions, to identify multiple modes of protein–DNA binding. Bais et al. (49) developed a method that targets the problem of a TF binding to two different motifs depending on the association of the TF with one of two different co-factors. Their method is specific to exactly two co-factors and therefore targets motif pairs. It cannot automatically determine whether the set can be explained better with a single or two motifs. We are not aware of any method designed to work in situations where there are several distinct modes of TF–DNA binding. As a result, for such cases, people typically resort to scanning the regions with motifs from databases such as JASPAR or TRANSFAC. This approach has two pitfalls. First, the set of potentially enriched motifs is restricted to what has been characterized and entered in these databases so far. Second, we strongly believe the criterion to call a certain motif ‘enriched’ is flawed: a motif may appear in very few sequences, but in conjunction with other motifs may explain the full set better. We have therefore proposed an approach here that does not rely on databases, but instead conducts de novo motif discovery, while simultaneously determining the optimal number of modes.

Interestingly, combining sequences from multiple ChIP experiments for detecting multiple modes can sometimes yield more informative results. For instance, in the regions bound by mediator and cohesin in ES cells, MuMoD identifies modes resembling motifs of CTCF and ES-specific factors. This indicates that the regions bound by the mediator and cohesin are likely to not be contiguous regions of DNA, but different pieces of the genome brought together through looping. In a separate study, cohesin was shown to co-localize with tissue-specific TFs, at regions that are not bound by CTCF (50). Considering that CTCF binding is largely ubiquitous across cell types (51), we propose that cell type specificity is attained through cohesin connecting CTCF with tissue-specific TFs through DNA loops. Furthermore, the remarkably different ChIP enrichment scores of these modes in the individual mediator and cohesin ChIP experiments suggest that cohesin-CTCF binding is more persistent than the cohesin-mediator binding.

Although the original motivation for this work came from identifying multi-TF complexes as shown in Figure 1B, we noticed a lot of unexplored biology even in datasets bound by well-characterized direct DNA-binding TFs. Apart from symmetric binding modes for Gata3, MuMoD identified multiple modes for five TFs Srf, Tbx5, Nkx2-5, Gata4 and Mef2 including the known literature motif. None of the conventional motif discovery methods consistently finds the literature motifs: MEME, Weeder and PeakMotifs succeed for two, while Chipmunk for one. Since even these DNA-binding TFs are likely to be part of multi-TF complexes, the immunoprecipitated sequences should be expected to contain motifs for the co-factors. None of the current de novo methods models this fact explicitly. Interestingly, in the cases of Tbx5 and Nkx2-5, the modes that do not match the literature consensus have higher ChIP enrichment. This questions the rationale for selecting the top few enriched sequences for motif discovery in a traditional setting. Even for TFs such as Srf and Mef2, where the literature motif has higher ChIP enrichment, additional insights on possible co-factors and enhancer–promoter interactions are missed by conventional motif discovery methods.

That some TFs display dependencies across positions in their binding sites is now well established (52,53). However, a PSSM, which cannot describe such dependencies, is still the model of choice for representing TF binding sites. This is largely because all other proposed models that model dependencies are more complex and using them in de novo motif discovery involves learning a lot more parameters. By explicitly modeling different modes, we overcome this limitation: MuMoD indirectly identifies dependencies across three positions in the CTCF motif in the cohesin-bound set by identifying two modes. Dependencies within two of these three positions have been observed before by Sharon et al. (54) in CTCF-binding sites in human fibroblast cells. Their method explicitly models dependencies to learn a ‘feature motif model’ instead of a PSSM. While a powerful tool to identify dependencies specifically, it cannot simultaneously report entirely different binding modes. Such dependencies were detected by MuMoD in CTCF-bound regions across 11 other cell types (51) as well (not shown here), suggesting that this is a universal property of CTCF. Given the popularity of PSSMs over all other more complex models, perhaps a mixture of PSSMs (52) may be the ideal way of representing the binding specificity of CTCF.

We note that our method does not try to explicitly distinguish direct from indirect interactions. This has been attempted in yeast (55) and mammalian cells (56,57) using libraries of characterized TFs. Our goal is to identify the reason for each sequence getting pulled down during the ChIP experiment, by identifying the ‘contact’ site within the bound sequence, while not getting biased by motifs of already characterized TFs. The resulting site may be bound directly or indirectly by the profiled protein.

MuMoD is a generalization of conventional motif discovery methods and works well even when there is a single mode of binding. Indeed, when applied to ChIP-chip data from yeast (58), we identified single modes in almost all cases. This does not imply that all protein–DNA binding in yeast is direct, but that there is typically only one primary way in which the POI is binding DNA in the specific environmental condition. The smaller sizes of the bound sets (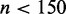, typically) might have influenced the number of modes; lowering the value of penalty parameter 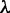may be worth exploring for less complex organisms.

MuMoD does not find co-occurring motifs. However, we understand that there could be two or more distinct modes of binding in the same sequence. For example, MEME identifies the Srebp1 motif in the Mef2-bound regions in HL1 cells (30 sites, Supplementary Figure S1F) and Med12-bound regions in ES cells (74 sites, Supplementary Figure S3B), which MuMoD does not, possibly because the same sequences can be explained by other, more prevalent binding modes. To handle this, the framework can be generalized to learn co-occurring motifs by performing soft clustering: each ChIP region can be modeled to have a multinomial distribution across the motifs. This can explain a sequence being immunoprecipitated due to the presence of a collection of motifs. Moreover, if modes are expected to have different characteristics such as peak height and distance from TSS a priori, these assumptions can be included in the learning process itself. The prior probability of each sequence contributing to a particular mode is currently uniform, but can be changed to reflect prior beliefs. Finally, incorporation of positional information such as sequence conservation (59), chromatin structure (60), distance from the center or end of the genomic regions (11,61), etc. have been shown to benefit motif discovery; these can easily be incorporated into MuMoD as well. While these modifications will no doubt help, the contribution of MuMoD is the fundamental change in the manner in which the problem of motif discovery is formulated. Keeping an open mind with regard to multiple possible modes of protein–DNA interactions can provide novel insights from ChIP experiments.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Table 1 and Supplementary Figures 1–5.

FUNDING

Early career fellowship from Wellcome Trust-DBT India Alliance [500188/Z/11/Z]. Funding for open access charge: Wellcome Trust-DBT India Alliance.

Conflict of interest statement. None declared.