A Review of Modeling Techniques for Genetic Regulatory Networks

Abstract

Understanding the genetic regulatory networks, the discovery of interactions between genes and understanding regulatory processes in a cell at the gene level are the major goals of system biology and computational biology. Modeling gene regulatory networks and describing the actions of the cells at the molecular level are used in medicine and molecular biology applications such as metabolic pathways and drug discovery. Modeling these networks is also one of the important issues in genomic signal processing. After the advent of microarray technology, it is possible to model these networks using time–series data. In this paper, we provide an extensive review of methods that have been used on time–series data and represent the features, advantages and disadvantages of each. Also, we classify these methods according to their nature. A parallel study of these methods can lead to the discovery of new synthetic methods or improve previous methods.

INTRODUCTION

A gene regulatory network (GRN) is a set of genes that interact with each other and with other substances in cells indirectly (through production of proteins and RNA), thereby governing the rates at which genes in the network are transcribed into mRNA. These networks modulate performance of metabolic networks, which leads to structural changes in the physiology of living cells and tissues.[1] Modeling GRNs provides information on gene pathways. This information has many applications in medicine and biology, such as identification of metabolic pathways, identification of genetic diseases, the discovery of new drugs, reducing side-effects of treatment, the study of expression patterns of genes with unknown function and gain ideas about their performance.[2,3] Microarray technology, which allows for the measurement of thousands of gene expression levels in parallel, has created a wealth of data not previously available to biologists along with new computational challenges. Microarray time–series data are a numerical matrix of thousands of rows (indicating genes) and dozens of columns (representing samples or time point). The general form of this data is as follows:

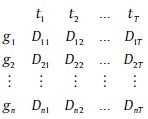
Where, g_i represents genes and t_j represents the time point. D_ij indicates i th the gene expression level at the time point. Thus, the value of j th signal at the time t = j is equal to D_ij. In a gene network, the value of gi(t) is related to itself and to other genes at t – 1. Therefore, the aim of modeling methods is to explore the relationship between genes that determine the dynamics and structure of the network. However, some methods can only determine the structure of the network and others to determine the network structure and dynamics. On the other hand, the proposed model should be adapted to the nature of the data. Noise, missing values and uncertainty is the nature of the microarray time–series data. Some of these modeling methods need pre-processing, such as classification, estimation of missing values and clustering for better performance. For example, methods that are faced with the problem of huge search space, such as Bayesian networks, are associated with cluster analysis.[4] Clustering methods combined with modeling techniques can create new methods for modeling GRNs, called the cluster-based approach.[5] In this article, we will review the basic modeling techniques, which include logical networks, bayesian networks, neural networks, state space models, differential equations and relevance networks, respectively. Section classification of models is dedicated to classify these models according to their nature.

LOGICAL NETWORK

Boolean Network Model

Here, we only think of two levels: ON / 1 and OFF / 0 and, with logical rules governing the functional relationship so an organism of n genes may have (2ⁿ) states. Boolean network (BN) consists of n nodes G = {g₁, g₂,…, g_n} and a list of Boolean functions F = {f₁, f₂,…, f_n}. Each node being a binary variable represents the state (expression) of gene i. The Boolean function shows the way to calculate the value of node g_i (t + 1) = f_i[P_a(g_i)(t))] at the next time point t+1 by the values of its input nodes P_a(g_i) at the current time point t. Changes between states in a network are deterministic and synchronous. Figure 1 depicts a simple BN for the three genes. The upper row lists the state at t and the lower row the state at t+1, while the Boolean function calculating the output from the input is shown below each element.

Figure 1.

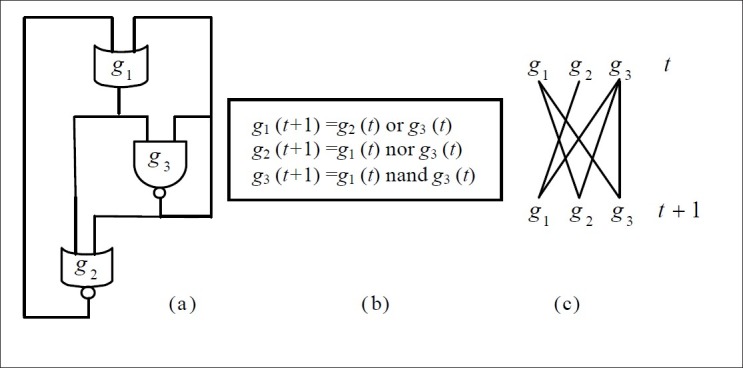
(a) Example Boolean network (BN) and (b) the corresponding equations. In this case, n = 3. (c) Wiring diagram of the BN

To make a BN, you can use literature-based methods with qualitative data available or, if experimental data are available, you can get use of time–series data.[6,7] Two classes of procedure are often used to infer BNs. One is based on correlation measurement to model the topological connections between genes and the other is based on machine learning, in which Genetic Algorithm (GA) is the most common method for network modeling.[8] Because of the shortages of old evolutionary methods in the optimization via local fine-tuning, many new methods have been proposed that use GA with different local search techniques. These include taboo search, hill-climbing, simulated annealing and the simplex method, all using local information to determine probable directions in the search space. Recently, new optimization techniques based on population intelligence, known as swarm intelligence methods including Particle Swarm Optimization (PSO)[9] and Ant Colony System,[10] were recommended as an alternative to old evolutionary algorithms. Now, it is proved that the methods made of combining both evolutionary algorithm and swarm intelligent have further improvements in performance.[8]

The BN method is more efficient than other methods of computational modeling. These networks are used for the analysis of large networks to be successful, but simplify biochemical processes highly. They show only two levels of gene expression, ON or OFF, causing many of the regulatory mechanisms that are based on different levels of expression to not be modeled. To solve this problem, BNs can be extended to the Generalized Logical Networks (GLN).

Generalized Logical Networks

GLN developed by Thomas and colleagues[11] is based on a procedure that generalizes upon BNs, letting variables to have more than two values and transitions to occur synchronously and asynchronously between states.[12] A GLN of n nodes as a dynamical system model in discrete state space includes a directed graph with a Generalized Truth Table (GTT) corresponded to each node.[13]

Let node g_i has Q quantization levels between 0 and Q–1, and is affected by the k parents P_a(g_i) {p_a1, p_a2,/, p_ak} of {Q₁, Q₂,…,Q_k} quantization levels, respectively. The GTT H of nodeis an operator that computes all possible combinations of parent node values (inputs) to values of g_i (output). Therefore, the value of g_i at discrete time t,g_i(t), can be calculated by

The size of H with k parents is Q₁ × Q₂ × … × Q_k, (exponential in k) and poses a memory problem. By generalization of binary decision diagram to diagram the logical choice, there is a space-efficient data structure to accumulate the GTT, eliminating redundancy and false variables.[13,14] Let g(t) be the state vector at discrete time t

illustrating the values of all nodes at discrete time t. Let H be the GTT sets H₁, H₂, …, H_n for all nodes and k₁, k₂,…, k_n be the number of parents for each node. The maximum number of entering edges a node is the network complexity κ, where κ = max{k₁, k₂,…, k_n}.

If the value of some node at time t depends on the parent values from time t − 1 through t − J, the network is J th order. A synchronous network changes the values of all nodes simultaneously through

J th order networks, has the ability to model time varying delays and are plentiful in biological systems. Let g(t -1), g(t - 2),…,g(t - J) be the initial J states of a GLN. A trajectory of length T is defined as g(t -1),g(t - 2),…,g(t - T).

Song et al.[13] reconstructed GLNs by the use of a statistical approach that let them control false positives while other criteria used in network reconstruction, such as the Bayesian information criterion (BIC) used in dynamic Bayesian networks (DBNs) reconstruction and the coefficient of determination (COD) used in BNs reconstruction, do not explicitly enforce false-positive rate control.

GLNs are a good approach to demonstrate the non-linear interactions between genes. Also, those are able to study more about the biological system and its properties by describing state transition diagrams and finite steady states. However, their deterministic nature is incompatible with the stochastic nature of GRNs.

Probabilistic Boolean Network

Unlike the BN and the multi-state generalization, Probabilistic Boolean Network (PBN) is not based on the assumption of deterministic gen–gene interaction.[15] These networks are a probabilistic generalization of BNs by allowing the nodes to have more than one associated Boolean function. In PBN, uncertainty is considered by the transition probability matrix of the system evolution. Therefore, for each node, its corresponding set of Boolean functions is to: F = {F₁, F₂, …, F_n}, where F_i = {f₁⁽ⁱ⁾, f₂⁽ⁱ⁾, …, f_1(i)⁽ⁱ⁾}, is one of the functions that determines the amount of gene expression for gene i and l_(i) is the number of possible Boolean functions. If l_(i) = 1 for all genes, the PBN will be converted to a BN. At any time point, for the gene i, only one of the Boolean functions F_i may be chosen; therefore, for the realization of a PBN, there are altogether Πⁿ_i=1 l_(i) modes. Figure 2 shows the basic building block of a PBN.

Figure 2.

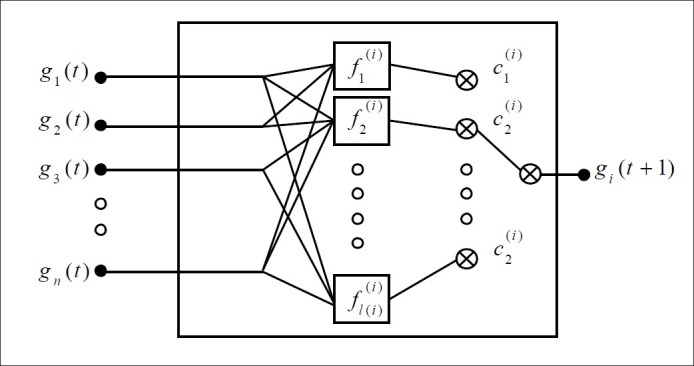
A basic building block of a probabilistic boolean network

Shmulevich et al. used Coefficient of Determination (COD) to select a list of predictors for a given gene.[16] Let G₁⁽ⁱ⁾, G₂⁽ⁱ⁾, …, G_l(i)⁽ⁱ⁾, k = 1,2,…,l_(i) be the sets of gens and f_k⁽ⁱ⁾ (G_k⁽ⁱ⁾) be the predictors of target gene g_i. Therefore, the probabilistic error measure can be illustrated as e(g_k, f_k⁽ⁱ⁾ (G_k⁽ⁱ⁾)). The COD for g_i associated with the conditioning set G_k⁽ⁱ⁾ is defined by.[17]

Boolean functions that are commensurate with the highest CODs will be selected in the probabilistic network.[17]

Marshall et al. executed an inference procedure for PBN that was successful well enough but had a downside of huge need of temporal data for inference.[18] Ching et al. used a more practical way to determine the network known as multivariate Markov model.[19] Here, the state of gene i at time point t has a binary probability distribution marked by vector.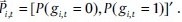

The model assumes[15]

where, τ_ij is the probability transition matrix from gene to gene i and γ_ij is the non-negative weight factor that has

BAYESIAN NETWORK

Static Bayesian Network

A Bayesian network model is a probabilistic- graphical representation of a joint probability distribution for random variables. To define B (Bayesian network), a set of variables B=(G,Θ) is used, where G is a direct acyclic graph (DAG) that indicates conditional dependency relationships between random variables and Θ (series of parameters indicating conditional probability distribution) is used. Let us look at Figure 3 and consider a simple model with Markov assumption. G is relevant to the topology of a GRN, where each node shows a gene as a random variable and each edge shows dependency between nodes. Markov assumption is a basic property of Bayesian networks. This means that the variable g_i with parents is independent of all other variables except the parents and their children. Thus, the joint probability distribution of genes G = {g₁, g₂, …, g_n} is depicted as follows:

Figure 3.

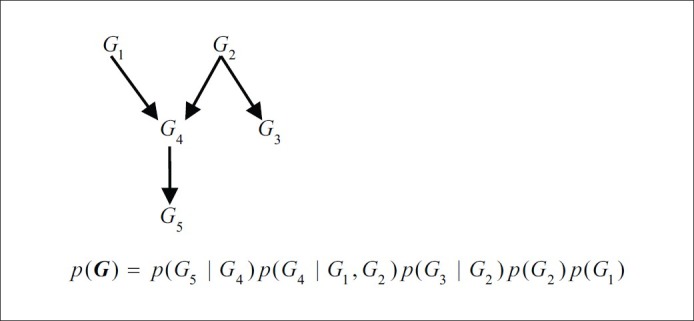
Example Bayesian network consisting of a graph, conditional probability distributions for the random variables, the joint probability distribution and conditional independencies

Where, P_a(g_i) is a set of parents of g_i in G and θ is a statistics from observed data D.

Obtaining a Bayesian network B = (G,Θ) from D means obtaining structure for dependency G and concluding the set of probabilistic parameters Θ. Obtaining Θ is easy if G and D are known, and learning G can be done by finding G* with maximum P(G | D). Learning G given D is a NP-hard problem because the number of possible graph structures increase exponentially as the size of a network increases.[20] Therefore, Bayesian networks focus on small problems in many approaches and need clustering methods for larger ones. One popular heuristic approach is restricting the G to a certain category.[15] In general, there are two methods for learning Bayesian network structure: (1) conditional independence-based learning and (2) learning based on scorings criteria. Methods based on scorings have two components: (a) a function of scorings, which estimates the amount of the matching network with a data set and (b) a technique to search for structures with high score. This method, using the data set, finds the most likely structure for the network.[21] Using the definition of scoring function for different network structures, the structure learning problem becomes an optimization problem. Therefore, the global optimization algorithm, such as GA, PSO… can be used. Among the common scoring functions, we can point to the Bayesian Dirichlet Equivalence (BDE), Bayesian Information Criteria (BIC), Minimum Description Length (MDL) and Maximum Likelihood (ML).[21,22] Given the large number of possible structures, a full-scale search in the space of graphs is not possible. Therefore, heuristic search algorithms such as greedy search, MCMC technique, Hill-Climbing algorithm, K2 algorithm… can be used.[21,22]

The main weakness of Bayesian networks is that they do not consider the dynamic process of gene regulation. Also, they are limited non-circular relations. However, the feedback loop is one of the important methods in real gene networks. To overcome these weaknesses, dynamic Bayesian networks (DBNs) have been proposed as a generalization of Bayesian networks.

Dynamic Bayesian Network

An extension of a Bayesian network model to incorporate temporal concept is a DBN. These networks are able to obtain time-course information and cyclic feedback and feed-forward relation between the random variables and are, therefore, appropriate for modeling the time-dependent phenomena using time-series data. DBNs, in a state transition from time t-1 to t, are defined as a DAG where the nodes represent random variables and the edges represent the relationship between random variables in the transition state, with a set of probability distributions. In comparison with the static Bayesian networks, DBNs include random variables {g_1,t-1, g_2,t-1, …, g_n,t-1}of time step t-1 in addition to {g_1,t, g_2,t, …, g_n,t} of time step t.[15] When between a variable with itself in a state of transition, there is a connection; in the final graph of the network structure, this variable will be a ring. The basic premise of these networks is that the probability distribution of the dependencies is time-invariant or nearly unchanging with time.

Obtaining DBNs can be performed by getting use of the same idea of learning Bayesian networks. Considering additional random variables of time, t–1 is the only difference here. From this point of view, Friedman et al. have evolved some rules to score and learn structures from Bayesian networks to the case of DBNs. Thus, other methods of parameter and structure learning in Bayesian networks can be used here.

Compared with conventional Bayesian networks, the DBN learning process is the heavy computational complexity, because the number of possible graph structures and the parameters are increased, and this should be considered in the search methods of learning algorithms. Therefore, those are mostly applied to small systems in comparison with the study of Bayesian networks.[15]

Structural EM (SEM) algorithm for learning Bayesian networks from incomplete data sets was presented.[23] This algorithm is a generalized EM algorithm for learning the structure. SEM runs the following two steps until convergence: (1) Bayesian network parameter optimization is usually done by the EM algorithm and (2) local search for model structure. In fact, SEM searches the optimum solution in the combined structure and parameter space. Yu Zhang et al. used DBN with Structure Expectation Maximization (SEM) for modeling of gene network from time–series gene expression data of Saccharomyces cerevisiae.[24,25]

DBNs are also an alternative method to demonstrate mechanisms of gene regulation using estimates of the changes described by a system of differential equations with autoregressive models.[26] Specifically, when the gene products have been measured at regularly spaced time points, a simple way to approximate the rate of change dg_i / dt = f_i(g₁, g₂, …, g_n) is possible by a first-order linear approximation. This approach to model the rate of change can be used by the linear Gaussian network.[27] In the linear Gaussian networks, we assume that the variables {g₁, g₂, …, g_n} are all continuous and conditional distributions for each variable with parents as Pa(g_i) = {g_i1, g_i2, …, g_ip(i)} is a Gaussian distribution with mean as a linear function of the parent variables and conditional variance σ_i² = 1/τ_i. Parameter τ_i is called precision. The dependence of each variable to the parents with the linear regression equation is shown as follows:

where the mean μ_i is a linear regression function of the parent variables and regression parameters are (α_i0, α_i1, …, α_ip(i))^T.[26] Ferrazzi et al. proposed a non-linear regression extension of (8) as follows:

where ψ is the hyperbolic tangent function.[28] They used Bayesian approach to model selection that solves the problem as hypothesis test.[26,28]

Let M = {M₀, M₁, …, M_g} is a set of Bayesian networks that each network describes a hypothesis on the dependency structure of the random variables g₁, g₂, …, g_n. According to Bayes’ theory, the prior probability of each model into the posterior probability p(M_h) is revised using the data D as follows:

The Bayesian approach selects the network with maximum posterior probability. The quantity p(D|M_h) is called a marginal likelihood. By averaging out the parameters, the marginal likelihood provides an overall measure of the data generation mechanism that is independent of the values of the parameters.[26] Marginal likelihood is possible by calculating the following integrals:

where θ_h is the vector parameterizing the distribution of g₁, g₂, …, g_n, conditional on M_h, as in the Gaussian network, showing a set of parameters β_ij and τ_i.

Because of the probabilistic nature and dynamic aspect of DBNs, those are one of the most successful methods for modeling GRNs using time–series data.

NEURAL NETWORKS

Recurrent Neural Networks

One of the other methods that can be used to model GRNs is a neural network where each node in the network is corresponded to a gene. A connection between nodes represents a regulatory interaction and the edge weight indicates the stringency and type of regulatory relationship. The most successful of neural network-based model is the recurrent neural network (RNN).[5,29] This model is biologically believable and noise-resistant. The dynamics of a time-discrete neural network of n nodes is described by a system of non-linear update rules for each node value g_i as follows:

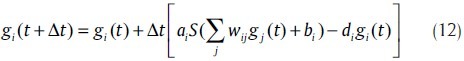
W, a, b, d are the parameters of the model. Weight parameters are W ={w_ij|i, j= 1,…,n}, where w_ij represents the effect of node j on node i. Activation strengths are a = {a_i| i = 1,…,n}, bias parameters are b ={b_i| i = 1,…,n} and degradation rates are d ={d_i| i = 1,…,n}. The activation function (log-sigmoid) is S(x) = 1/(1 + e^–x).[30] This mathematical model executes self-regulation and degradation as well. Back-propagation through time[31] (BPTT) algorithm or other error (parameter) minimization (optimization) algorithms can be used as a learning strategy.[32] This algorithms minimizes the error function as in

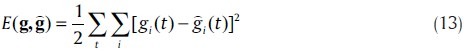
Where 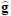, is the computed values vector and the values g are the given expression data of the mRNAs at discrete time points.

By defining an error function as an indicator of network performance, the network learning problem becomes a parameter estimation problem with the goal of minimizing error function (maximizing network performance). Algorithms based on gradient descent, such as BPTT, are efficient to update the parameters in the recursive neural networks. But, in this method, each weight needs a separate learning rate, because the error surface often has a different gradient along each weight direction.[8] Gradient-based optimization algorithms and error back-propagation algorithm are faced with the problem of falling into the trap of local minimum. Many networks have a structure that are not enough regularity for the derivatives used in the gradient-based methods. Therefore, methods such as error propagation are not applicable. In this case, global parameter optimization techniques, including evolutionary algorithms and the swarm intelligence methods (GA and PSO), should be used. However, because of computational complexity, this modeling approach is suitable only for very small systems.[8]

Feed-Forward Neural Network

Artificial feed-forward neural networks (ANN) can be used as molecular models for genetic regulatory networks. ANNs are a powerful method for function approximation. They are the so-called universal operators. In principle, they are able to approximate any function.[33] They suit well for multidimensional problems and they can imitate Boolean logic. For example, the Boolean function called exclusive OR (XOR) can be described with an ANN as Figure 4.

Figure 4.

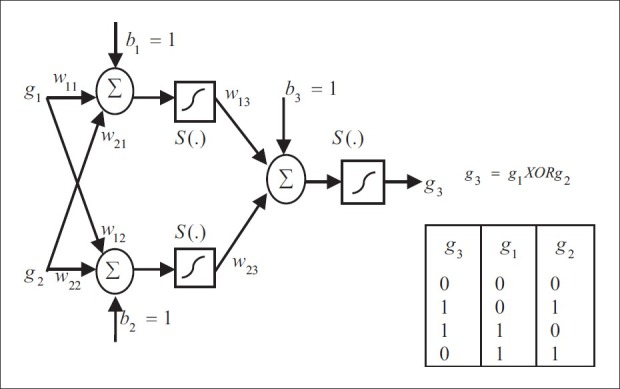
Left: An artificial feed-forward neural network model that can solve the exclusive OR (XOR) problem. Right: The truth table of XOR

Despite the benefits, the artificial neural networks are not often used for modeling of GRNs because of several reasons. Biochemical a priori knowledge, such as the reaction rates, cannot be interpreted by ANNs because the rates may not have any parallel parameter in the ANN model. The most usual algorithm for determining the parameters for ANNs is Back-Propagation, which was presented in section “Recurrent neural networks”. Similar to the BPTT algorithm, the gradients of the error function update the weights with the help of the gradients. The number of parameters of the ANN model may be too large compared with the available data. Instead of a single molecule type, a large artificial neural network may represent the whole genetic regulatory network.[34] That approach and the related optimization issues were already discussed in “Recurrent Neural Networks”.

Stochastic Neural Networks

One of the most important issues in modeling GRNs is the impact of noise in gene regulation by experimental theoretical research and mathematical simulations. There are two major approaches based on detailed biochemical knowledge and rich data sources for studying stochastic occurrence in GRN; stochastic simulation algorithm and stochastic differential equations.[35] Tian et al. introduced stochastic neural network models.[36] They concentrated on stochastic models based on one-stage models (12). In their approach for experimental data with expression levels, they used Poisson processes to describe the synthesis and degradation of expression products. Corresponding to the difference model (12), stochastic models based on Poisson random variables take the form

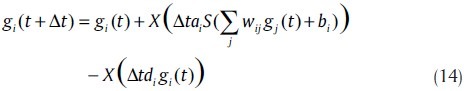
Where, X is a Poisson random variable with mean λ, whose distribution is

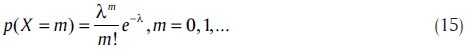
When the gene expression is normalized within a range of unity in order to represent expression levels of a cluster of genes, exponential random variables can be used for realizing variations. Stochastic models with exponential random variables are given by (14), where X is an exponential random variable with mean λ. Using β = 1/λ, the distribution of X is

Similar to Poisson random variables, the distribution of an exponential random variable is determined by the mean. However, the variance of exponential random variables is λ². In order to match the variance, stochastic models can also be constructed with normal random variables, given by

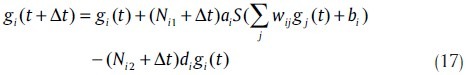
where, N_ik ~ N(0,Δtσ²_ik). In model (17), σ²_ik is an adjustable parameter. The differential equation form of model (17) is

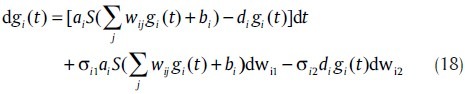
where, w_ik are Wiener processes whose error increments Δw_ik = w_ik(t + Δt) – w_ik(t) are normal random variable N(0, Δt). Model (18) can be considered as a stochastic differential equation of the continuous model. However, it is used just in the normalized concentration case.[36]

STATE SPACE MODEL

Another modeling approach of GRN is a State Space Model (SSM). It can be viewed as an extension to DBNs (Markov model), where it is assumed that the observed measurements depend on some hidden state variables.[15,30] The information of unmeasured variables or effects corresponds to these hidden variables (such as regulating proteins, excluded genes in the experiments, degradations, external signals or biological noise).[30] Schafer and Strimmer proposed a SSM.[37] With the assumption that gene expression levels cannot be directly observed (hidden states), a SSM in the general form is

Equations (19) and (20) show the model of a dynamical system based on the theory of linear systems, where the vector represents the state of the genes for the system, is the observed data for , T is the state transition matrix, C is the state to observation matrix and A and B are the inputs influence matrices for inputs and, respectively. Here δ_{g, t} and δ_{y, t} are white noise terms of system noise and observation noise, respectively. If A = 0 and B = 0, basic linear SSM or standard SSM is extracted.[15]

If the inputs are as the observations from a previous time point, the system is described as

This model has been used by Rangel et al. and Beal et al.[38,39] Please note that the above equation can be rewritten as

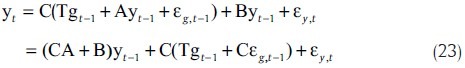
Here, the transition in the observation domain over time, through the hidden states g_t, is determined by the matrix T’ = CA + B The matrix T’ determines the direct gene–gene interactions and the regulation through hidden states over time (indirect interaction). Activation or inhibition of gene j on gene i is determined by a non-zero matrix element [T’]_ij depending on its sign.[30] The parameters of model can be estimated using EM algorithm. Rangel et al. used this approach and constructed a confidence interval on T’ by using bootstrap,[38] while Variational Bayesian EM Algorithm, which can be considered as a Bayesian extension of the standard EM algorithm, was used by Beal et al. to derive a posterior estimation on T’.[39]

DIFFERENTIAL EQUATIONS

Using differential equation models, including ordinary differential equations, non-linear differential equations, partial differential equations and stochastic differential equations, another method for constructing a genetic regulatory network of gene expression is based on time-series data, which can describe the system dynamics more accurately. Although many implementations of this model are only based on linear systems and possibly the model is unsuitable for obtaining the complex phenomena, in general, changes in the expression of a gene in a specific time (discrete or continuous) are determined by a function that shows the effect of activation or inhibition of other genes (regulators of a gene).[8] In other words,

where, g_i is the expression level of gene i at time t, is the number of genes, p_s is parameter set of the system and e is an external perturbation to the system. The function f_i with respect to its ability to describe the system dynamics and complexity can be a linear or non-linear function (such as linear, piecewise linear, pseudolinear, log-sigmoid, tan-sigmoid…).[8]

A simple model of stochastic differential equations describing the process of gene transcription is as follows:

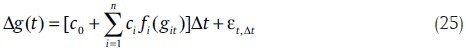
where g(t) and g_ij represent the expression level of target gene and i th is the regulator gene. c_i determines the involvement of the i th gene regulators. f_i is a sigmoid function of the i th regulators and ε_t,Δt is random error with normal distribution N(0,σ²Δt).[35] This model is the model introduced in stochastic neural networks, but in continuous form.

Another most popular non-linear ordinary differential equations (ODE) model is the S-system, which is described by the power law model.[40] In the S-system model, changes in the expression of a gene are a product of power-law functions. It can be described as

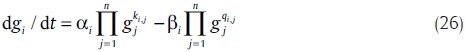
where α_i and β_i are rate constants that show the direction of mass flow. The real number exponents k_i,j and q_i,j are kinetic orders that reflect the intensity of interaction from gene j to i.

Because of their use of continuous variables, the ODE models, especially non-linear ODE models (such as S-system models) can more accurately represent the underlying physical phenomena in comparison with the discrete variable models. This model is useful to describe the theoretical aspects of control systems analysis and design of dynamic systems. Thus, they are able to explain the sensitivity analysis, control analysis, stability analysis and, steady-state evaluation of a given system.[8,41]

To model GRNs using differential equations, one needs to know which genes those regulate each other, while in the case of most biological systems, it is not known. In addition, many data are needed to estimate the parameters of these equations.[42] However, using reverse engineering techniques in discrete space (such as recursive neural networks), the differential equation system can be rebuilt in a continuous mode.

RELEVANCE NETWORKS

Relevance networks are defined using a pairwise measure of interactions between genes. With a set of n genes G = {g₁, g₂, …, g_n} and a set of observations D on genomic profiling (gene expression) for T time points, a relevance between g_i and g_j can be obtained by the use of profiles related to their time-series [g_i,1 g_i,2 … g_i,m] and [g_j,1 g_j,2 … g_j,m]. Among the different relevance measures used to infer relationships, in the first step, correlation for each gene pair is obtained based on different measures like Pearson correlation, Spearman correlation and mutual information. The commonly used Pearson correlation shows the strength of a linear relationship between the genes. In contrast to that, Spearman's rank correlation indicates non-linear correlations as well as mutual information. It seems that if the value of the correlation is not zero then there is a biological relationship between genes going on.[30] Using the data processing inequality (DPI) for that purpose, Basso et al. developed the ARACNe algorithm.[43]

After the first step (correlation for each gene pair), the edges with the lowest mutual information will be removed. In contrast, to eliminate indirect interactions, De la Fuente et al. use partial correlations that have coefficients measuring the correlation between two genes conditioning on one or several other genes in their proposed method.[44] The number of genes conditioning the correlation determines the order of the partial correlation.[30]

An inferred network from a relevance network method is naturally undirected and statistical independence of each data sample is assumed, implying that measurements of gene expression at different time points are to be independent. This predefinition ignores time point dependencies.[30]

CLASSIFICATION OF MODELS

The mentioned methods are classified from different perspectives, such as whether the model is a discrete space or continuous space model. A discrete SSM describes a system using quantized data, while a continuous SSM can describe a system without discretizing the data and loss of information. With this definition, the logical networks and Bayesian networks as models of discrete space. However, neural networks and differential equations are continuous time models. DBNs can also be a continuous space and discrete space.

Another important criterion for classification of these methods is the ability to model the structure and dynamics of GRN. The structure represents all the interconnections among the nodes that generally indicate the relationships between one gene with another gene, or another set of genes. But, structure alone does not completely describe the network. When we are interested in our research on the network response to a specific disorder, or to predict the future behavior of the system, we need a network model that is able to describe the system dynamics. Knowing the dynamics of the system usually provides a mathematical equation that describes the system behavior over time. It can help us in discovering the mechanisms of gene regulation, especially knowing what happens at each stage of the process. It also enables us to be able to intervene in some of these processes at a particular time, such as things that pharmacologists can do to control a disease like cancer. However, for biologists and pharmacologists, knowing the structure of the network has high priority.

Also, the mentioned methods can be a deterministic or a stochastic model. The process of gene regulation is essentially a random process. Therefore, stochastic models are more consistent with the nature of these networks. On the other hand, there is inevitable noise in genomic signals. Thus, a deterministic system does not model the noise term.

Figure 5 shows the classification of models according to the above criteria. This figure shows the intrinsic properties of the model in which each tick mark represents the ability of having a property for a model. But, this figure does not show the superiority of one model over another model. For the modeling of GRNs, a matching model with existing data is more important than a model with the true nature of gene regulation, such as the stochastic, dynamic nature and so on. Hence, for example, a static Bayesian network that is more adapted to the data structure is more efficient than a DBN with fewer matches. Because, according to the above, the structure is far more important than the discovery of dynamics of systems. But, in a similar condition in terms of matching the data, a model that can clearly show the true nature of the network in terms of system dynamics, the probabilistic (stochastic) nature and the continuous-time model is better.

Figure 5.

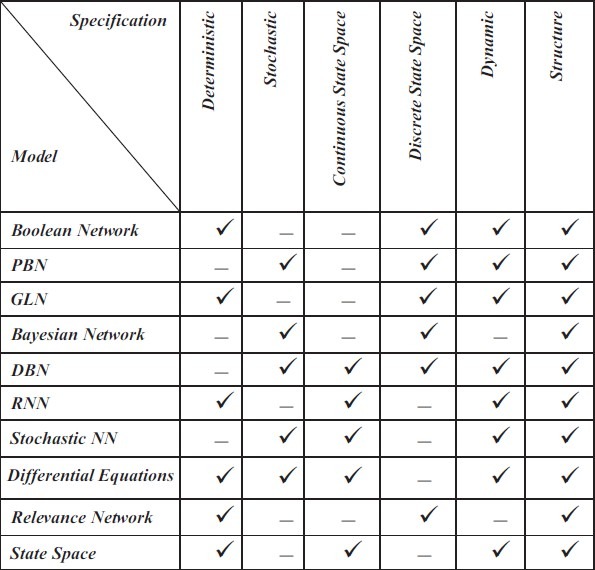
Classification of gene regulatory network reverse engineering models according to their nature

CONCLUSION

In this paper, we have reviewed the modeling and inference of GRN from time-series data. All methods mentioned above are a type of reverse engineering GRNs from time-series data and not really a simulation method. Simulation capabilities of these methods for GRNs depend on the ability to obtain biological knowledge. Some methods are flexible to accommodate biological knowledge, but others are simply a mathematical model that adapt with time-series data. However, the analysis of GRNs is largely based on reverse engineering.

BIOGRAPHIES

Hanif Yaghoobi was born in Salmas, Iran in 1984. He received his bachelor degree from Islamic Azad University, Urmia Branch, Iran, in 2007, in Electrical Engineering (Major Option in Communication Systems). He got his MSc degree in Electrical-Electronic Engineering (Major Option in Biomedical Engineering) from Islamic Azad University, Tabriz Branch, Iran, in 2011. His basic research is about Genomic Signal Processing, Artificial Intelligence and fields of Biomedical Engineering.

Siyamak Haghipour was born in Urmia, Iran in 1974. He received his bachelor degree from Urmia University, Iran, in 1996, in Electrical Engineering (Major Option in Communication Systems). He got his MSc degree from Iran University of Science & Technology, Iran, in 1999 and Ph.D. degree from Islamic Azad University, Science and Research Branch, Iran, in 2006 all in Biomedical-Bioelectric Engineering. His basic research is about Signal & Image Processing, Artificial Intelligence, Bioinformatics and Biological Systems Modeling

Hossein Hamzeiy was born in Tabriz, Iran in 1959. His academic qualifications are Pharm. D: 1984, from Tabriz University, IRAN and PhD: 2002, in Molecular Toxicology, University of Surrey, Guildford, UK. His Positions were and are: 1986-1990: Instructor in medicinal chemistry, 1992-1998: Instructor in pharmacology, 2002-2008: Assistant professor of Molecular Toxicology, 2008: Associate Professor of Molecular Toxicology. His research experiences are about structural as well as functional genomics assays.

Masoud Asadi-Khiavi was born in Meshginshahr, Iran, 1969. He received his MD degree, Shahid Beheshti University of Medical Sciences, Tehran, Iran, in 1996. He obtained his PhD in Pharmacology (Pharmacogenomics), Tabriz University of Medical Sciences, Iran, 2011. His research experiences are about structural as well as functional genomics assays. His Current position is “Assistant Professor of Pharmacology & Toxicology at School of Pharmacy, Zanjan University of Medical Sciences (ZUMS), Zanjan, Iran”.