Abstract
Discovering functional connectivity between and within brain regions is a key concern in neuroscience. Due to the noise inherent in fMRI data, it is challenging to characterize the properties of individual voxels, and current methods are unable to flexibly analyze voxel-level connectivity differences. We propose a new functional connectivity method which incorporates a spatial smoothness constraint using regularized optimization, enabling the discovery of voxel-level interactions between brain regions from the small datasets characteristic of fMRI experiments. We validate our method in two separate experiments, demonstrating that we can learn coherent connectivity maps that are consistent with known results. First, we examine the functional connectivity between early visual areas V1 and VP, confirming that this connectivity structure preserves retinotopic mapping. Then, we show that two category-selective regions in ventral cortex – the Parahippocampal Place Area (PPA) and the Fusiform Face Area (FFA) – exhibit an expected peripheral versus foveal bias in their connectivity with visual area hV4. These results show that our approach is powerful, widely applicable, and capable of uncovering complex connectivity patterns with only a small amount of input data.
Keywords: Functional connectivity, Spatial regularization, fMRI
Introduction
Functional Magnetic Resonance Imaging (fMRI) has been widely adopted by the neuroscience community primarily because it allows researchers to unobtrusively sample activity patterns from populations of neurons across the entire human brain, at a fine spatial scale (typically a few millimeters). However, many methods for identifying distributed functional networks underutilize the spatial resolution of fMRI, considering only the aggregate properties of groups of voxels. For example, when computing functional connectivity between brain regions, activity is often spatially averaged within each Region of Interest (ROI) and simple statistical relationships (e.g. correlation) between these mean timecourses are used as measures of connectivity between the regions (reviewed in Rogers et al., 2007).
ROIs are generally defined by a contrast between two types of stimuli, constrained by rough anatomical location. However, there is no reason to assume that all voxels within an ROI have identical functional properties. Indeed, recent work has achieved some success in dividing existing ROIs into functional subregions. For example, lateral occipital complex (LOC) (defined in Malach et al., 1995) has been shown to contain two functionally distinct subregions (Grill-Spector et al., 1999), and the extrastriate body area (EBA) (defined in Downing et al., 2001) has been split into three separate limb-sensitive areas (Weiner and Grill-Spector, 2011).
Recent work has begun to investigate intra-ROI structure using measures of functional connectivity. These methods have provided evidence of subdivisions within regions such as the thalamus (Zhang et al., 2008), medial frontal cortex (Kim et al., 2010), the amygdala (Roy et al., 2009), anterior cingulate cortex (Margulies et al., 2007), and the precuneus (Margulies et al., 2009), and have been used to uncover the functional connectivity structure of early visual cortex (Heinzle et al., 2011).
However, these methods are unable to jointly model the functional connectivity properties of individual voxels for typical fMRI dataset sizes. Almost all current methods avoid simultaneously learning the connectivity properties for all voxels, by spatially downsampling to a small number of subregions (Margulies et al., 2007; Roy et al., 2009), only learning parameters for one voxel or subregion at a time (Chai et al., 2009; Cohen et al., 2008; Kim et al., 2010; Zhang et al., 2008), or both (Margulies et al., 2009). Each of these approaches has some disadvantages. Downsampling requires prior knowledge of the anatomical subdivisions in a region (Roy et al., 2009) or of the relevant spatial scale of connectivity differences (Margulies et al., 2007), making it ill-suited for exploratory studies. Learning voxel parameters separately can make comparisons between voxels difficult; for example, if two voxels are assigned different levels of connectivity with a seed region, there is generally no way to tell whether these two voxels predict different parts of the seed timecourse, or if one voxel is simply a noisy copy of the other. Jointly learning connectivity weights allows us to pinpoint those voxels that contribute unique information about the seed region, by simultaneously considering the timecourses of all voxels.
Support vector regression (SVR) can learn joint voxel-level connectivity maps, but requires a significant amount of data; for example, Heinzle et al. (2011) use more than 40 min of training data (1600 timepoints) to learn connectivity structures in early visual areas. Scarcity of training data is a common obstacle for characterizing individual voxels in fMRI experiments. Typical fMRI datasets record activity from tens of thousands of voxels in the human brain, but with only about a thousand timepoints per voxel. Several methods have been successfully implemented to boost the number of recorded timepoints (e.g. rapidly scanning only a select portion of the brain, (Bouvier and Epstein, 2011; Scalf et al., 2011)), but all fMRI studies must contend with a severe data shortage for individual subjects caused by this limitation. A recent survey of MVPA techniques (Misaki et al., 2010) has demonstrated empirically that low-complexity models tend to perform better at decoding information from patterns of activity than high-complexity models, which is theoretically plausible given the limited number of timepoints available for model training.
Therefore, there is still a need for a method that can estimate voxel-level connectivity structure with data set sizes more typical of fMRI experiments. For example, when investigating stimulus-category-dependent changes in connectivity patterns, the amount of data for each category can be on the order of only a hundred timepoints. To address this issue, we propose a spatially regularized method for examining connectivity differences within ROIs, which is specifically tailored to small training sets typical in the fMRI setting. Our regularization approach simply imposes the constraint that connectivity properties should vary smoothly across voxels, a highly plausible assumption given the nature of fMRI data. Much prior work has been dedicated to incorporating spatial regularization into MRI and fMRI analyses, with goals such as functional classification and regression (Grosenick et al., 2011; Ng and Abugharbieh, 2011), classification of gray matter concentration maps (Cuignet et al., 2010), and inter-subject alignment (Conroy et al., 2009). However, none of these regularized models are specifically searching for evidence of voxel-level structure within an individual ROI.
In this paper, we present a spatially regularized method for uncovering connectivity differences within ROIs, and demonstrate that it is possible to discover consistent structures using only a small amount of training data. We validate our approach using two different experiments, for which the ground truth connectivity is already known. In the first experiment, we show that we can recover retinotopic connectivity patterns between early visual areas V1 and VP. In the second, we replicate the known eccentricity biases in the connectivity between visual area hV4 and both the Parahippocampal Place Area (PPA) and the Fusiform Face Area (FFA), without using a specialized experimental design.
Materials and methods
Traditional connectivity analysis
The simplest way to characterize functional connectivity between two ROIs is to extract mean timecourses by spatially averaging over all the voxels in each ROI, then computing the Pearson product–moment correlation coefficient (r value) between the two mean timecourses. A high r2 value indicates strong functional connectivity between the pair of ROIs.
We can reformulate this analysis as a linear regression problem in which we use voxel activation values from the first timecourse to predict the second timecourse. Specifically, we choose a slope a and an offset b minimizing
| (1) |
where A1 and A2 are the (# voxels × # timepoints) data matrices from two ROIs, and meanv denotes an average across voxels. The r2 value is then equivalent to the fraction of variance explained (the increase in prediction accuracy from using a and b, as opposed to just predicting the mean of the second timecourse, (Stockburger, 1996)):
where meant denotes an average across time.
We can interpret a · meanv1(A1) as a weighted sum, in which every voxel shares the same weight c=a/(# of voxels in A1). This allows us to rewrite the traditional correlation method as an optimization problem in a more general form:
| (2) |
This is a convex optimization problem, and can be solved using a standard optimization package (all optimization problems in our paper are solved using CVX, a package for specifying and solving convex programs, (Grant and Boyd, 2011)).
Regularized connectivity method
Although the basic connectivity method described above provides valuable insight into the functional organization of the human brain, it lacks a principled way to take into account voxel-level spatial information present in the fMRI signal. However, simply removing the constraint that all voxels must have the same weight leads to severe overfitting on typical fMRI datasets, as will be demonstrated in the results section. Rather than revealing interesting, generalizable connectivity patterns, the learned maps are driven mainly by noise in the training data and fail to replicate across runs. In order to obtain meaningful weight maps, we must place a constraint on the voxel weights which is less restrictive than that of the traditional method (all weights equal), but more restrictive than the unconstrained method (all weights independent).
One plausible assumption is that voxel connectivity properties are likely to be spatially correlated, with nearby voxels typically having more similar connectivity properties than spatially distant voxels. This reflects a common view of cortical organization, and is especially applicable to blood-oxygen-level dependent (BOLD) signals such as fMRI, since the hemodynamic response is spatially smooth.
To incorporate this assumption, we developed a new method of assessing functional connectivity patterns within ROIs (Fig. 1). We define an extension of the original optimization problem (Eq. (2)), replacing the constraint that weights for all voxels must be equal with a spatial regularization term in the minimization objective:
| (3) |
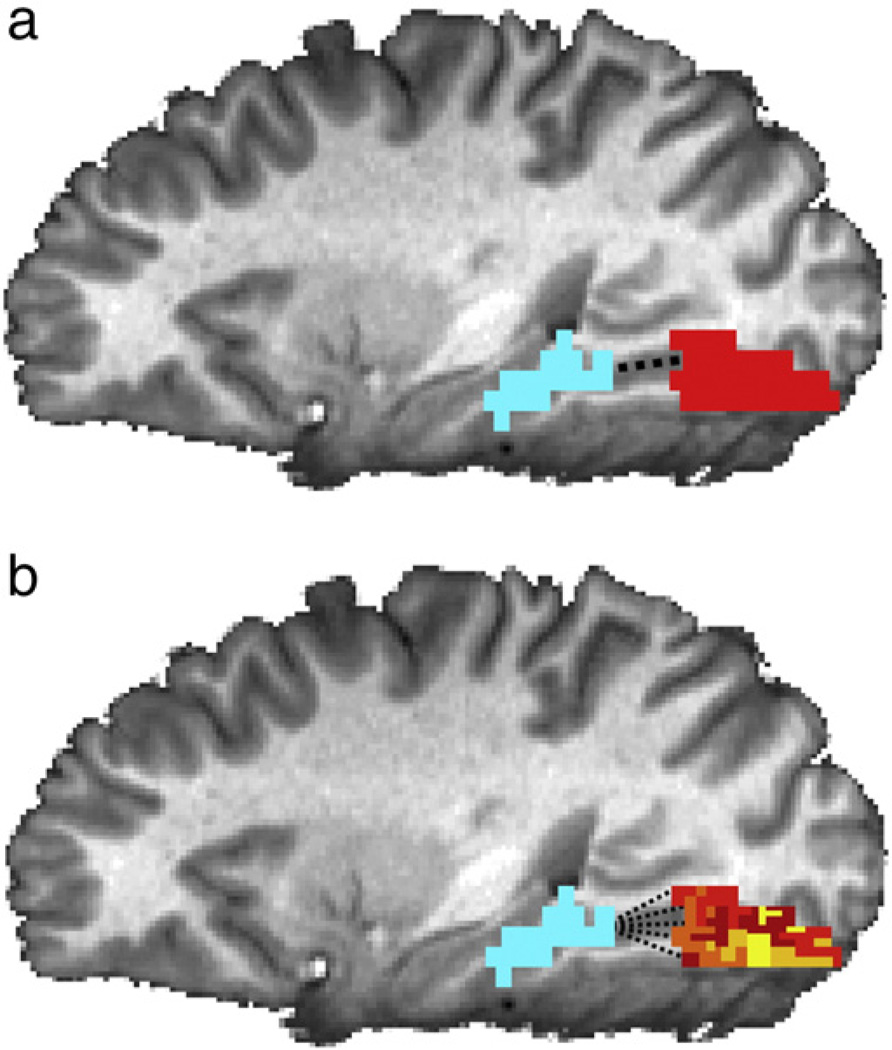
Fig. 1.
Comparison of connectivity maps learned from traditional (a) and regularized (b) methods. (a) In traditional functional connectivity analysis, connectivity with a seed region (blue) is assumed to be identical for all voxels in an ROI (red). (b) Our method can learn a map of weights in an ROI that describes the voxel-level connectivity between each voxel and the seed region. It is possible to learn these maps using a small amount of training data by imposing a spatial smoothness constraint.
D is the voxel connectivity matrix, which we design to penalize the mean squared difference between the weight ai of voxel i, and the weights of voxel i's neighbors. Each row of D represents a directed edge from a voxel i to an adjacent voxel j: all entries in a row are zero, except for the jth element and the kth element , where di is the number of neighbors of voxel i. Thus the regularization term is where N is the number of voxels in A1 and ni is the set of i's neighbors. The hyperparameter λ controls the strength of the regularization, trading off between an a that gives a good prediction of the seed timecourse A2 and an a that is spatially smooth. λ can take on any positive value, with λ→0 producing completely unregularized maps, and λ→∞ producing completely smooth (constant) maps.
In this paper, we define the voxel neighborhoods ni to enforce smoothness along the cortical surface. After mapping an ROI onto a cortical flat map, we define the neighborhood of each voxel to be its k-nearest neighbors. This approach is suitable for ROIs that are known to have retinotopic structure on the cortical surface, such as early visual areas. Alternatively, a more general approach could simply define ni to be all spatially adjacent voxels (touching voxel i at least on a corner in the three-dimensional representation of the particular subject's brain).
As in the traditional method, this optimization problem is convex and therefore has a global optimum that can be found efficiently. On our test machine (with a 3 GHz processor) the optimal a can be found within 5 s, for a typical region with a few hundred voxels and a few hundred timepoints.
Datasets
Human subjects
We tested our functional connectivity method on two separate datasets. Both experiments were approved by the Institutional Review Board of Stanford University, and all subjects gave their written informed consent. Subjects were in good health with no past history of psychiatric or neurological diseases, and had normal or corrected-to-normal vision. 13 subjects (1 female; age: 22–26 years; including one of the authors) participated in the first experiment, and 8 subjects (2 female; age: 23–26; including one of the authors) participated in the second experiment.
Scanning parameters
For both experiments, imaging data were acquired with a 3 Tesla G.E. Healthcare scanner. A gradient echo, echo-planar sequence was used to obtain functional images [volume repetition time (TR), 2 s; echo time (TE), 30 ms; flip angle, 80°; matrix, 128 × 128 voxels; FOV, 20 cm; 29 oblique 3 mm slices with 1 mm gap; in-plane resolution, 1.56 × 1.56 mm]. The functional data were motion-corrected, each voxel's mean value was scaled to equal 100, and linear trends were removed from each run, using the AFNI software package (Cox, 1996). No other preprocessing (e.g. spatial smoothing, slice timing correction, temporal smoothing) was applied. We collected a high-resolution (1 × 1 × 1 mm voxels) structural scan (SPGR; TR, 5.9 ms; TE, 2.0 ms; flip angle, 11°) in each scanning session. Images were presented using a back-projection system (Optoma Corporation) operating at a resolution of 1024 × 768 pixels at 75 Hz.
Visual stimuli and experimental design
For our first experiment, we collected early visual cortex responses from 13 subjects. We used a typical retinotopic mapping protocol, in which a checkerboard pattern undergoing contrast reversals at 5 Hz moved through the visual field in discrete increments (Sayres and Grill-Spector, 2008). First, a wedge subtending an angle of 45° from fixation was presented at 16 different polar angles for 2.4 s each. Next, an annulus subtending 3° of visual angle was presented at 15 different radii for 2.4 s each. Each subject passively observed two runs of 6 cycles in each condition, yielding 512 timepoints per subject (see Fig. 2).
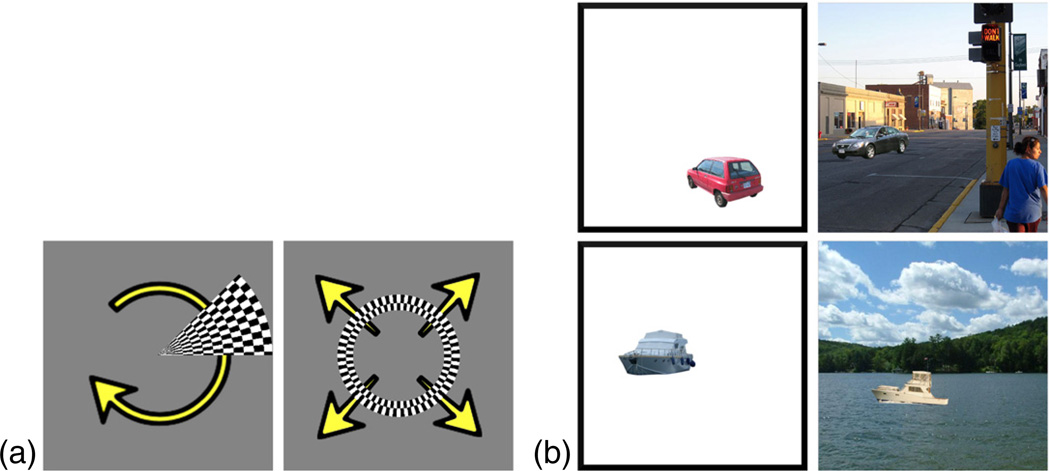
Fig. 2.
Stimuli used in our two datasets. (a) The first dataset consists of responses to two flickering checkerboard patterns: a 45° wedge which rotates clockwise through the visual field, and an annulus subtending 3° of visual angle that expands outward from fixation. (b) The second dataset consists of cars and boats, presented either in isolation or in a scene context.
Our second dataset consists of PPA, FFA, and hV4 responses from 8 subjects. We presented two types of stimuli, as shown in Fig. 2: (1) boats and cars on a blank white background (isolated objects); and (2) boats and cars with a street or water scene background (objects in context). Images (450 × 450 pixels; subtending 24 × 24° of visual angle) were presented 100 pixels (5°) away from fixation in randomly determined directions. Subjects were informed that each image contained either a boat or a car, and were asked to indicate as quickly as possible whether the object was on the left half of the image or the right half of the image (using a button box). Subjects performed 4 runs, with 16 blocks per run (with a 14 s gap between blocks) and 9 images per block. The first 8 blocks of each run showed a boat or car placed in a photographic scene; for each block, the object could violate a semantic relationship (appearing in the wrong type of scene, e.g. a boat on a city street) and/or a geometric relationship (appearing in the wrong position in the scene, e.g. a car above a tree rather than on the street). Each presentation consisted of a 500 ms fixation cross, an image flashed for 100 ms, a 300 ms mask, and then a 1300 ms response period (blank gray screen). The last 8 blocks of each run showed a boat or car on a white background; these images were identical to those presented in the first eight blocks, with the backgrounds removed (and presented in a different random order). Each presentation consisted of a 500 ms fixation cross, an image flashed for 350 ms, and then a 1300 ms response period (blank gray screen). The total number of timepoints for each of the 8 subjects was 1224 (306 per run).
ROIs
In order to measure the eccentricity biases of PPA and FFA in the second experiment, we defined these regions using standard localizer runs conducted in a separate fMRI experiment. Subjects performed 2 runs, each with 12 blocks drawn equally from six categories: child faces, adult faces, indoor scenes, outdoor scenes, objects (abstract sculptures with no semantic meaning), and scrambled objects. Blocks were separated by 12 s fixation cross periods, and consisted of 12 image presentations, each of which consisted of a 900 ms image followed by a 100 ms fixation cross. Each image was presented exactly once, with the exception of two images during each block that were repeated twice in a row. Subjects were asked to maintain fixation at the center of the screen, and respond via button-press whenever an image was repeated. PPA was defined as the top 300 voxels near parahippocampal gyrus for the Scenes > Objects contrast, and FFA was defined as the top 100 voxels near fusiform gyrus for the Faces > Objects contrast. The volume of each ROI in mm3 was chosen conservatively, based on previous results (Golarai et al., 2007). The locations of early visual areas V1, VP, and hV4 were delineated on a flattened cortical surface for each subject, using a horizontal meridian vs. vertical meridian general linear test from the retinotopic mapping data to give the boundaries between retinotopic maps.
Results
VP-V1 connectivity
We know that voxels in early visual cortex exhibit strongly retinotopic population receptive fields (Dumoulin and Wandell, 2008). Recent work has shown that the structure of functional connectivity between early visual areas preserves retinotopic organization. Specifically, the activity of a voxel in V3 is best predicted by voxels in V1 that correspond to the same retinotopic position in the visual field (Heinzle et al., 2011).
In this section, we validate our method by showing how it can be used to discover such connections between retinotopic areas of the early visual cortex. We apply our connectivity method to the early visual cortex dataset with V1 as area A1 and a single voxel in VP (ventral V3, or V3v) as area A2 (Eq. (3)). For each voxel in VP, we obtain a separate connectivity map a of voxel weights in V1.
To quantitatively measure the precision of the learned V1 maps, we first assign a preferred angle and eccentricity to each voxel in V1 and VP. We use the t-statistics from a standard general linear model (GLM) to quantify the preference of each voxel to each wedge angle and each annulus radius (Holmes et al., 1997). Specifically, for each voxel v in the two areas, we take a weighted average of all stimulus angles, with weights proportional to that voxel's t-statistic for that angle θi (ignoring negative t-statistics):
where θi ∈ {0, 22.5, 45, 67.5,…337.5} and is the marginal t-statistic for angle i at voxel v.
Similarly, we compute the preferred eccentricity for each voxel v by taking a weighted average of the stimulus radii Ri:
where Ri ∈ {0.73, 1.46, 2.92, 4.38,…18.98, 19.71} and is the marginal t-statistic for radius i at voxel v.
Finally, we can estimate the position of the population receptive field for v by converting to Cartesian coordinates:
Given the population receptive field locations for each V1 and VP voxel, we can compare the receptive field RF(v) of each voxel v in VP with the receptive fields of the V1 voxels in v's connectivity map. If the V1 connectivity map for voxel v preserves retinotopic organization, then the V1 voxels with high positive weights should have the same retinotopic position as v. We therefore take a weighted average of the V1 receptive fields, in which the weight for each V1 voxel corresponds to its learned connectivity weight (negative weights are set to zero for this computation). This allows us to compare the receptive field of VP voxel v with that generated by the connected voxels in V1, as shown in Fig. 3. To ensure that the receptive field estimates are an independent measure of performance, we compute the receptive field positions using the first run of the wedge and annulus data, and learn connectivity maps using the second run.
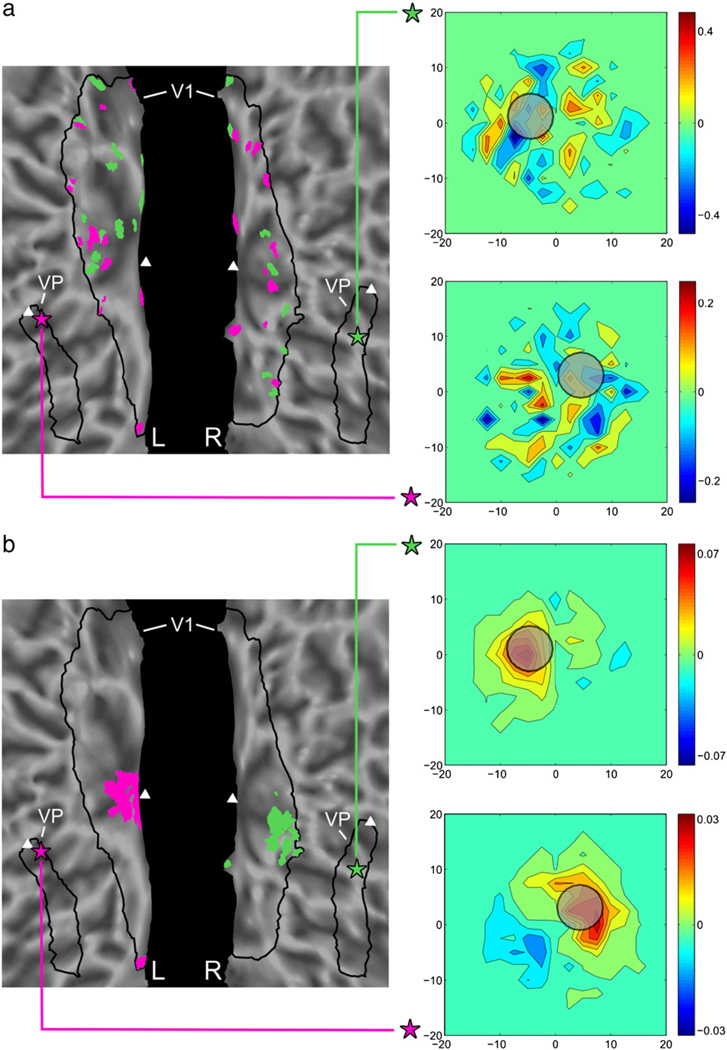
Fig. 3.
Learned connectivity maps and receptive fields for 2 VP voxels, without regularization (a) and with regularization (b). Two VP voxels are denoted by purple and green stars, and the top 30 voxels from the learned connectivity maps are shown in respective color in V1 (triangles indicate the location of the fovea). The inset plots compare the average receptive field of the connected V1 voxels (heatmap) with the actual population receptive field of each VP voxel (gray circle, radius given by the average uncertainty in our receptive field estimates). (a) The unregularized method produces maps with scattered weights, and the receptive fields of the connected V1 voxels are poor predictors of the VP receptive field. (b) The regularized connectivity method learns spatially coherent connectivity maps consistent with retinotopic organization, and the receptive fields of the connected V1 voxels are similar to that of the VP voxel.
Fig. 4 describes the results across all 13 subjects, with λ = 103 and k = 10. We observe a marked decrease in the magnitude of the receptive field differences between VP and V1 when adding regularization, with the median difference reduced by an average of 31% (t(12) = 11.19, p << 0.01, two-tailed paired t-test). With regularization, the V1 maps become much more precise, with the majority of the positive learned V1 weights falling in a retinotopic location similar to that of the VP voxel that generated them. This result demonstrates that our regularized method produces V1 maps that are not only spatially coherent, but also functionally correct. It also shows that our method can perform well even with very little data; we use only 256 timepoints to estimate connectivity maps over all ~1000 V1 voxels. The performance of any connectivity method on this dataset will be limited by the uncertainty in our VP receptive field position estimates (introduced by the limited number of wedge and annulus positions used, and the small number of temporal samples); we can approximate this uncertainty by comparing the RF(v) calculated from a single run to the RF(v) calculated from both runs. This loose error bound is plotted in Fig. 4, indicating that our method makes significant progress toward the optimal result even with such a small number of training timepoints. Similar results for regularized maps are observed over a large range of λ and k values (see Supplementary Fig. 1).
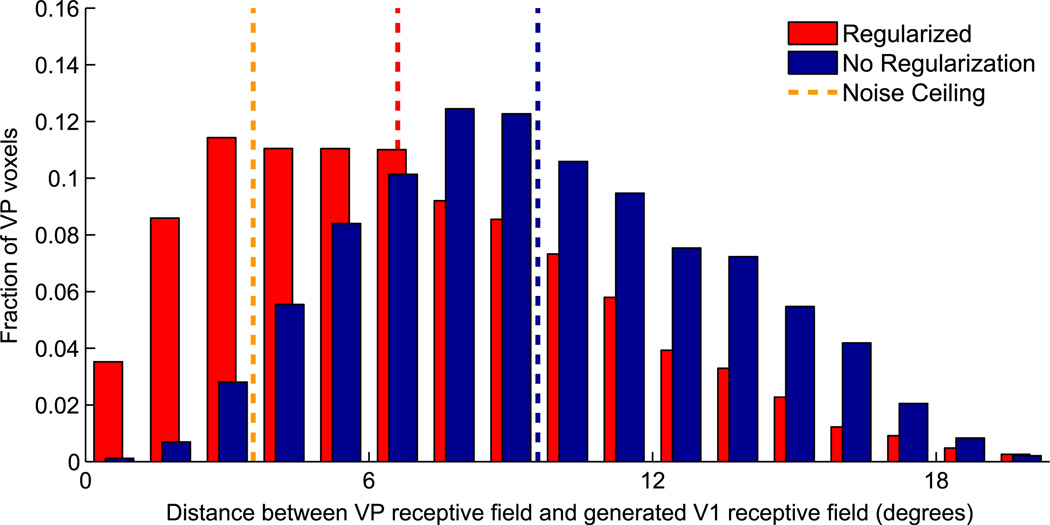
Fig. 4.
Histogram comparing the precision of V1 maps generated from VP voxels. The x-axis indicates the difference between the receptive field locations of VP voxels and the weighted average of the receptive fields in corresponding V1 connectivity maps. Since the actual functional connectivity between V1 and VP is known to preserve retinotopy, each VP voxel and its learned V1 connectivity map should have similar receptive field locations. The y-axis shows the fraction of VP voxels in each difference bin spanning 1.2° of visual angle. Red bars (back) show results for regularized maps (λ = 103,k = 10), which demonstrate significantly smaller differences than blue bars (front), which show results for non-regularized maps (λ = 0). The dotted lines compare the median difference of both methods to a loose lower bound, based on the uncertainty in our receptive field estimates.
hV4-PPA/FFA connectivity
Previous work has shown that there is a preferential response in PPA to peripherally-presented stimuli, and in FFA to foveally-presented stimuli; this effect has been measured both with discrete stimuli (Levy et al., 2001) and with traveling wave methods (Goesaert and Op de Beeck, 2010). Experiments using diffusion tensor imaging (DTI) have provided evidence that this eccentricity bias is also present in the connectivity structure, with projections to early visual areas terminating at peripheral eccentricities for PPA and foveal eccentricities for FFA (Kim et al., 2005). Our connectivity method provides a simple way of revealing such differential connectivity patterns, which does not require a specialized experimental design or a large amount of data. We chose to learn connectivity maps from PPA/FFA to area hV4 (as described in (Wade et al., 2002)), since it is the area in visual cortex most closely connected to ventral regions and is therefore most likely to show strong functional connectivity patterns.
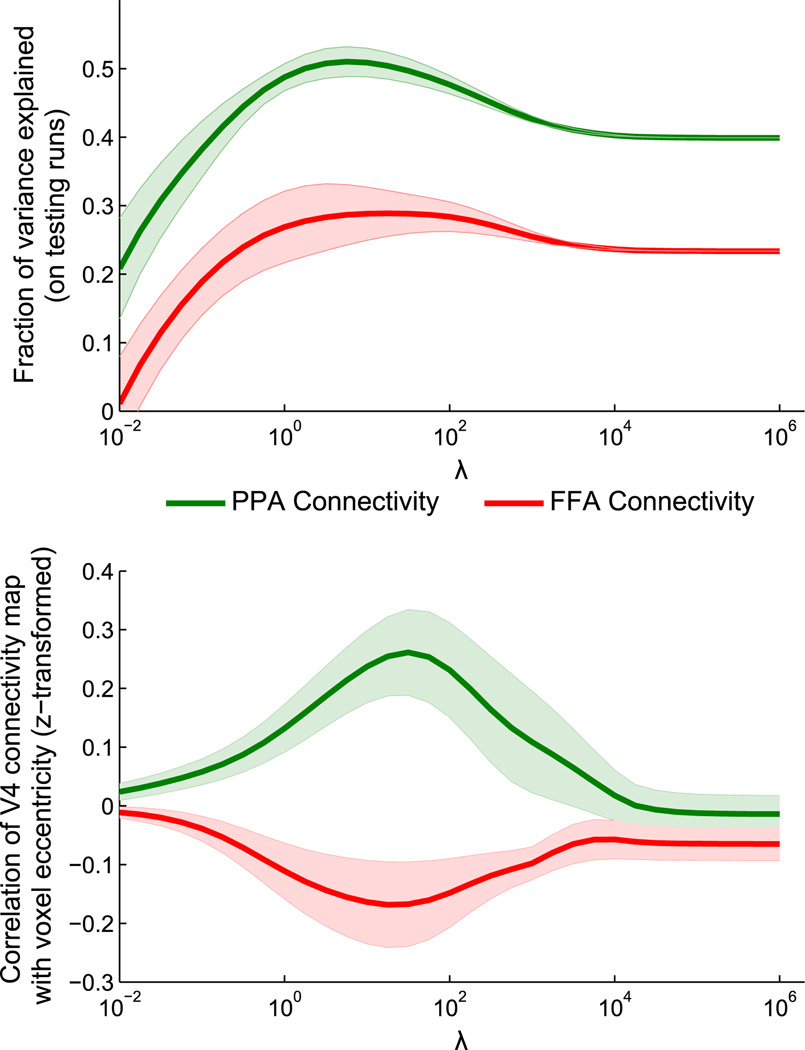
We first examine the effect of varying λ on this dataset, and describe a principled approach for automatically selecting the regularization strength. λ controls the complexity of the learned connectivity patterns; as λ → ∞, we can learn only constant-weight maps, while as λ → 0, the weights are allowed to vary completely independently and maps can be arbitrarily complex.
We now use hV4 as area A1 and either PPA or FFA as area A2 (k = 10); the goal of our optimization is to find a map of weights for the hV4 voxels that allows for the best prediction of the mean PPA or FFA timecourse. For each subject, we train the model parameters on one run and then test on the other three runs (results are averaged across the choice of training run). The testing accuracies across a wide range of λ values (spaced logarithmically with step ratio of 100.25) are shown in Fig. 5 (upper plot). At low values of λ, the connectivity maps are highly complex. These maps severely overfit to the training run, and fail to generalize to testing runs. At high values of λ, testing performance converges to essentially the same result as in the traditional connectivity method, in which all voxels have the same weight (unlike the traditional method, each hemisphere can have a different constant weight). However, the surprising characteristic of the testing accuracy curve is that it does not increase monotonically as λ increases. In every subject, the best testing performance occurred at an intermediate value of λ, which shows that there exists a non-constant connectivity structure which is stable between runs; across subjects, testing performance was significantly increased over the traditional method (λ = ∞) for 10−0.25 <λ <106.75 for PPA and 101.5 <λ <106 for FFA (t(7) <−1.89, p< 0.05, one-tailed paired t-test, uncorrected). This result shows that our method can carefully balance the trade-off between model complexity and data availability. Note that it is not possible to find generalizable connectivity maps using only pre-smoothing rather than spatial regularization (see Supplementary Fig. 2).
Fig. 5.
Effects of changing λ on learned hV4 connectivity maps. Connectivity maps over hV4 were learned with different regularization strengths λ, for seed regions PPA and FFA. An appropriate λ value can be chosen by maximizing the generalization performance of the learned maps, based on held-out testing runs (upper plot). At these values of λ, PPA and FFA show connectivity biases toward peripheral and central eccentricities, respectively (lower plot). Shaded regions indicate standard error across subjects (controlling for performance in the fully-regularized condition for the upper plot).
We obtain the best generalization performance around λ = 101, where we learn maps with a smoothness of approximately 9 mm FWHM (see Supplementary Fig. 3). As shown in the lower plot of Fig. 5, the connectivity maps in this regime have eccentricity biases in opposite directions for the two seed regions, with PPA biased toward peripheral eccentricities and FFA biased toward foveal eccentricities (correlation of learned weights with voxel eccentricities is significantly different for 10−1.25 <λ <103, t(7) > 2.36, p < 0.05, two-tailed paired t-test after z-transform, uncorrected).
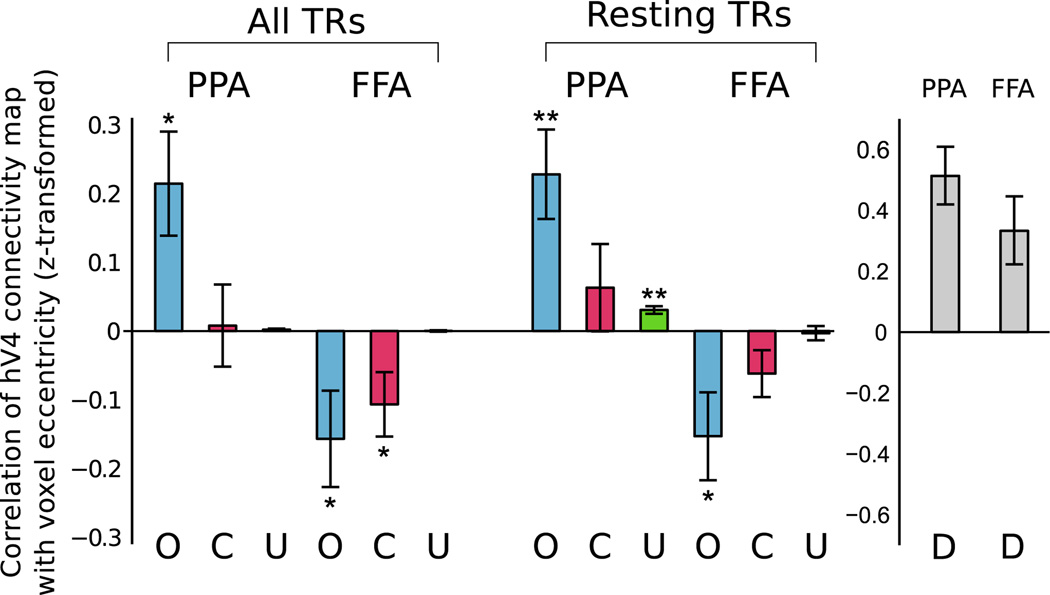
Fig. 6 compares the eccentricity biases of the learned maps, with λ for each subject chosen to maximize generalization accuracy. Using all 306 timepoints from a run, the hV4 connectivity map with PPA is biased toward larger eccentricities, with an average correlation between eccentricity and connectivity weight of 0.21 (t(7) = 2.83, p < 0.05, one-tailed t-test after z-transform) while the hV4 connectivity map with FFA is biased toward smaller eccentricities, with an average correlation of −0.16 (t(7) = −2.24, p <0.05, one-tailed t-test after z-transform) (PPA and FFA eccentricities significantly different, t(7) = 4.19, p< 0.01, two-tailed paired t-test after z-transform). We can obtain similar results using only the 148 “resting” timepoints in between stimulus blocks, in which subjects are simply fixating on a blank screen, suggesting that our method is sensitive to general functional connectivity rather than a stimulus mediated effect (PPA: t(7) = 3.51, p<0.01, one-tailed t-test after z-transform; FFA: t(7) = −2.39, p <0.05, one-tailed t-test after z-transform; Difference: t(7) = 4.88, p <0.01, two-tailed paired t-test after z-transform).
Fig. 6.
hV4 eccentricity differences for optimal values of λ. After choosing an optimal λ value for each subject bfased on generalization performance (see Fig. 5), we compute the eccentricity of hV4 connectivity maps for seed regions PPA and FFA, using our method (O), a voxel correlation method (C), and our method without regularization (U) (results averaged across four runs for each subject). Whether using all timepoints from a run (306 TRs) or using only those timepoints during which no stimulus was presented (approx. 148 TRs), our method finds that connectivity with PPA increases with increasing eccentricity, while the opposite is true for FFA. The correlation and unregularized controls are much less sensitive, showing significantly smaller differences between PPA and FFA eccentricity biases. Additionally, our results cannot be explained simply by local noise correlations; since both PPA and FFA are closer to the anterior (peripheral) side of hV4, such a model would predict similar peripheral eccentricity biases in PPA and FFA (D). Error bars indicate standard error, *p<0.05, **p<0.01.
To demonstrate that our method is more powerful than simpler approaches, the hV4 eccentricity biases for connectivity with PPA and FFA are computed in two additional ways: voxel-wise correlation (C), in which the weight of each hV4 voxel is set to the correlation between the timecourse of that voxel and PPA or FFA; and an unregularized version of our method (U) in which λ = 0. There are only two cases in which these methods give a significant result — the correlation method shows a foveal bias for FFA when using all TRs (t(7) = −2.27, p<0.05, one-tailed t-test after z-transform) and the unregularized method shows a peripheral bias for PPA when using the resting TRs (t(7) = 5.60, p<0.01, one-tailed t-test after z-transform). For both all TRs and the resting TRs, the difference between PPA and FFA eccentricity biases is significantly greater using our method than using the correlation method (all TRs: t(7) = 3.63, p <0.01, resting TRs: t(7) = 3.90, p<0.01, two-tailed paired t-test after z-transform) or using the unregularized method (all TRs: t(7) = 4.20, p <0.01, resting TRs: t(7) = 4.86, p <0.01, two-tailed paired t-test after z-transform). Our approach is therefore significantly more sensitive than either performing independent correlations between individual voxels and the seed region, or learning maps over all voxels without using spatial regularization.
A potential concern regarding functional connectivity measures is that they may be driven by local noise correlations, such that nearby voxels are good predictors of each other even if the underlying neural signals are unrelated. To ensure that our results are not being caused by relative positions of the ROIs, we ran a control analysis in which each hV4 voxel's connectivity weight was simply inversely proportional to its distance from the seed region. For bilateral ROIs, we set the weight of voxel v = 1/(dist from v to left ROI) + 1/(dist from v to right ROI). Since both PPA and FFA are closest to the anterior (peripheral) side of hV4, this model erroneously predicts that PPA and FFA should both show a peripheral eccentricity bias (PPA: t(7) = 5.59, p <0.01; FFA: t(7) = 3.03, p <0.05; two-tailed t-test after z-transform). Our results therefore cannot be explained simply by the physical arrangement of the ROIs.
Discussion
We have shown that our method can successfully extract known functional connectivity structures for two sets of regions. By adding spatial regularization to the traditional functional connectivity measure, our estimate of the connectivity between V1 and VP was made significantly more accurate, showing a clear retinotopic organization. We also demonstrated the expected eccentricity biases in the connectivity between V4 and PPA/FFA; unlike past experiments showing this effect (Levy et al., 2001; Goesaert and Op de Beeck, 2010), this was accomplished without using a specialized experimental design, and could even be estimated from only resting-state data. The success of our method on these two different datasets demonstrates that this technique is likely to be applicable to a wide range of datasets and scientific questions. Note that we are able to learn these connectivity maps using only ~200 timepoints, in contrast to the ~2000 timepoints needed for complex models such as SVR (Heinzle et al., 2011). Therefore, this method could be highly useful for detecting subtle variations in connectivity using small datasets. For example, it could plausibly be used to detect differences in connectivity across stimulus conditions, since only a small amount of data is required for learning.
Although these two experiments examined relatively simple characteristics of the learned weight maps (average retinotopic position or correlation with one of the spatial axes), our method should be applicable to any type of connectivity pattern, including multi-modal weight maps in which two separate sections of an ROI show high connectivity. Since the smoothness of the learned maps is controlled by a continuous parameter λ, our method is highly flexible and can learn arbitrarily complex connectivity maps, given enough training data. For very large datasets, applying regularization will be less important, and the optimal value of λ (giving the best generalization accuracy) will decrease towards zero. Our method is therefore adaptive to the training set size, and will learn maps at finer and finer scales as the amount of training data increases.
Now that this method has been validated with known connectivity results, there are many opportunities to discover new connectivity patterns. One possible application would be to learn connectivity maps in frontal regions, where functional ROIs are difficult to define. By locating the voxels in the frontal lobe that are connected to known ROIs in sensory regions, we may be able to identify how low-level sensory information converges in or is modulated by higher-level regions. Also, given any ROI, we can describe its connectivity with the entire rest of the cortex, by iteratively scanning a seed searchlight through all of cortex and learning a connectivity map over the ROI for each seed position. This will allow us to determine whether certain regions of cortex are connected to specific voxels in our ROI, as in “functional fingerprint” methods (Kim et al., 2010).
There are several ways that our method could be extended in future work. One current limitation is that weights can only be learned over one region at a time; that is, Eq. (3) is not symmetric with respect to A1 and A2. Simply replacing meanv (A2) with a weighted average will yield the degenerate solution a = a2 = 0, so (non-convex) constraints must be added to produce reasonable results. Another possible extension would be to learn weights simultaneously across multiple subjects. After first obtaining a voxel correspondence between subjects using a functional alignment technique (such as Haxby et al., 2011), we could learn a global set of weights that is shared by all subjects. We could also allow the weights to vary between subjects, but introduce a new regularization term that encourages subjects to have similar weight maps.
Conclusions
We have presented a new method for discovering functional connectivity patterns between and within ROIs in the human brain. Our method is specifically tailored to the very small-size datasets typical of fMRI (addressing the known issue of data scarcity in this setting), and is capable of detecting subtle patterns at the voxel level. Our method is fast, can operate efficiently with little input data, gives results consistent with prior work, and has proven to be a good candidate for investigating the structure of functional connectivity in the human brain.
Supplementary Material
Acknowledgments
We thank Stephen Boyd for his suggestions and encouragement, and two anonymous reviewers for their detailed comments.
This work is funded by the National Institutes of Health Grant 1 R01 EY019429 (to L.F.-F. and D.M.B.), a National Science Foundation Graduate Research Fellowship under Grant No. DGE-0645962 (to C.B.) and a William R. Hewlett Stanford Graduate Fellowship (to M.C.I.).
Appendix A. Supplementary data
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2012.07.046.
References
- Bouvier S, Epstein RA. Early vs. late components of category selectivity in the parahippocampal place area: a rapid acquisition fmri study. Presented at the Vision Sciences Society 11th Annual Meeting; Naples, FL. 2011. [Google Scholar]
- Chai B, Walther D, Beck D, Fei-Fei L. Exploring functional connectivity of the human brain using multivariate information analysis. Advances in Neural Information Processing Systems. 2009;22 [Google Scholar]
- Cohen AL, Fair DA, Dosenbach NU, Miezin FM, Dierker D, Van Essen DC, Schlaggar BL, Petersen SE. Defining functional areas in individual human brains using resting functional connectivity MRI. Neuroimage. 2008;41:45–57. doi: 10.1016/j.neuroimage.2008.01.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conroy B, Singer B, Haxby J, Ramadge P. fMRI-based inter-subject cortical alignment using functional connectivity. Advances in Neural Information Processing Systems. 2009;22 [PMC free article] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput. Biomed. Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Cuignet R, Chupin M, Benali H, Colliot O. Spatial and anatomical regularization of SVM for brain image analysis. Advances in Neural Information Processing Systems. 2010;23 [Google Scholar]
- Downing PE, Jiang Y, Shuman M, Kanwisher N. A cortical area selective for visual processing of the human body. Science. 2001;293:2470–2473. doi: 10.1126/science.1063414. [DOI] [PubMed] [Google Scholar]
- Dumoulin S, Wandell BA. Population receptive field estimates in human visual cortex. Neuroimage. 2008;39:647–660. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goesaert E, Op de Beeck HP. Continuous mapping of the cortical object vision pathway using traveling waves in object space. Neuroimage. 2010;49:3248–3256. doi: 10.1016/j.neuroimage.2009.11.036. [DOI] [PubMed] [Google Scholar]
- Golarai G, Ghahremani DG, Whitfield-Gabrieli S, Reiss A, Eberhardt JL, Gabrieli JD, Grill-Spector K. Differential development of high-level visual cortex correlates with category-specific recognition memory. Nat. Neurosci. 2007;10:512–522. doi: 10.1038/nn1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant M, Boyd S. CVX: Matlab software for disciplined convex programming, version 1.21. 2011. http://cvxrcom/cvx. [Google Scholar]
- Grill-Spector K, Kushnir T, Edelman S, Avidan G, Itzchak Y, Malach R. Differential processing of objects under various viewing conditions in the human lateral occipital complex. Neuron. 1999;24:187–203. doi: 10.1016/s0896-6273(00)80832-6. [DOI] [PubMed] [Google Scholar]
- Grosenick L, Klingenberg B, Knutson B, Taylor JE. ArXiv e-prints 1110.4139. 2011. A Family of Interpretable Multivariate Models for Regression and Classification of Whole-brain fMRI Data. [Google Scholar]
- Haxby JV, Guntupalli JS, Connolly AC, Halchenko YO, Conroy BR, Gobbini MI, Hanke M, Ramadge PJ. A common, high-dimensional model of the representational space in human ventral temporal cortex. Neuron. 2011;72:404–416. doi: 10.1016/j.neuron.2011.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinzle J, Kahnt T, Haynes J. Topographically specific functional connectivity between visual field maps in the human brain. Neuroimage. 2011;56:1426–1436. doi: 10.1016/j.neuroimage.2011.02.077. [DOI] [PubMed] [Google Scholar]
- Holmes A, Poline J, Friston K. Characterizing brain images with the general linear model. In: Frackowiak R, Friston K, Frith C, Dolan R, Mazziotta J, editors. Human Brain Function. Academic Press, USA; 1997. pp. 59–84. [Google Scholar]
- Kim M, Ducros M, Ugurbil K, Kim DS. Topography of high-order human object areas measured with DTI and fMRI. Proc. Int. Soc. Magn. Reson. Med. 2005;13:737. [Google Scholar]
- Kim JH, Lee JM, Jo HJ, Kim SH, Lee JH, Kim ST, Seo SW, Cox RW, Na DL, Kim SI, Saad ZS. Defining functional SMA and pre-SMA subregions in human MFC using resting state fMRI: functional connectivity-based parcellation method. Neuroimage. 2010;49:2375–2386. doi: 10.1016/j.neuroimage.2009.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy I, Hasson U, Avidan G, Hendler T, Malach R. Center-periphery organization of human object areas. Nat. Neurosci. 2001;4:533–539. doi: 10.1038/87490. [DOI] [PubMed] [Google Scholar]
- Malach R, Reppas J, Benson R, Kwong K, Jiang H, Kennedy W, Ledden P, Brady T, Rosen B, Tootell R. Object-related activity revealed by functional magnetic resonance imaging in human occipital cortex. Proc. Natl. Acad. Sci. U. S. A. 1995;92:8135–8139. doi: 10.1073/pnas.92.18.8135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies DS, Kelly AM, Uddin LQ, Biswal BB, Castellanos FX, Milham MP. Mapping the functional connectivity of anterior cingulate cortex. Neuroimage. 2007;37:579–588. doi: 10.1016/j.neuroimage.2007.05.019. [DOI] [PubMed] [Google Scholar]
- Margulies DS, Vincent JL, Kelly C, Lohmann G, Uddin LQ, Biswal BB, Villringer A, Castellanos FX, Milham MP, Petrides M. Precuneus shares intrinsic functional architecture in humans and monkeys. Proc. Natl. Acad. Sci. U. S. A. 2009;106:20069–20074. doi: 10.1073/pnas.0905314106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misaki M, Kim Y, Bandettini P, Kriegeskorte N. Comparison of multivariate classifiers and response normalizations for pattern-information fMRI. Neuroimage. 2010;53:103–118. doi: 10.1016/j.neuroimage.2010.05.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng B, Abugharbieh R. Generalized sparse regularization with application to fmri brain decoding. In: Székely G, Hahn HK, editors. IPMI. Springer; 2011. pp. 612–623. [DOI] [PubMed] [Google Scholar]
- Rogers BP, Morgan VL, Newton AT, Gore JC. Assessing functional connectivity in the human brain by fMRI. Magn. Reson. Imaging. 2007;25:1347–1357. doi: 10.1016/j.mri.2007.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy AK, Shehzad Z, Margulies DS, Kelly AM, Uddin LQ, Gotimer K, Biswal BB, Castellanos FX, Milham MP. Functional connectivity of the human amygdala using resting state fMRI. Neuroimage. 2009;45:614–626. doi: 10.1016/j.neuroimage.2008.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sayres R, Grill-Spector K. Relating retinotopic and object-selective responses in human lateral occipital cortex. J. Neurophysiol. 2008;100:249–267. doi: 10.1152/jn.01383.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scalf PE, Dux PE, Marois R. Working memory encoding delays top-down attention to visual cortex. J. Cogn. Neurosci. 2011;23:2593–2604. doi: 10.1162/jocn.2011.21621. [DOI] [PubMed] [Google Scholar]
- Stockburger D. Introductory Statistics: Concepts, Models, and Applications. 1996. [Google Scholar]
- Wade AR, Brewer AA, Rieger JW, Wandell BA. Functional measurements of human ventral occipital cortex: retinotopy and colour. Philos. TransRSoc. Lond. B Biol. Sci. 2002;357:963–973. doi: 10.1098/rstb.2002.1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner KS, Grill-Spector K. Not one extrastriate body area: using anatomical landmarks, hMT+, and visual field maps to parcellate limb-selective activations in human lateral occipitotemporal cortex. Neuroimage. 2011;56:2183–2199. doi: 10.1016/j.neuroimage.2011.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Snyder AZ, Fox MD, Sansbury MW, Shimony JS, Raichle ME. Intrinsic functional relations between human cerebral cortex and thalamus. J. Neurophysiol. 2008;100:1740–1748. doi: 10.1152/jn.90463.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.