Get the Rhythm: Modeling Neuronal Activity

Abstract

The simulation system NEURON is a common research tool for constructing structurally and functionally realistic models of neuronal systems. NEURON allows the development of simulations at any level of complexity, from subcellular components to single cells, cellular networks, and system-level models.

Focusing on an in vitro cell model of a single, acutely isolated thalamic neuron, we used the simulation environment to address and to discuss the following questions in an undergraduate course: (i) Which parts are required to design a single compartment with passive electrical properties? (ii) Which components are necessary to model a single action potential or a train of action potentials? (iii) What can we learn from voltage-clamp and current-clamp experiments? (iv) What kind of cellular parameters are accessible from the modeling data? (v) What are the differences between single-compartment models and multi-compartment models? (vi) What are the advantages and disadvantages of artificial cell models? (vii) Can realistic modeling open up new strategies to discover the way that neurons process information?

Computational models are created to simulate processes observed in a given system in order to understand their function. A realistic model allows predictions about the outcome of natural processes based on a specific set of input parameters. Therefore complicated systems, such as neurons of the central nervous system, are attractive and fascinating targets for modeling approaches, especially when some parameters are not experimentally accessible. Since scientists have begun applying modeling strategies, computational modeling software has grown at an accelerating rate. Supported by increasingly powerful hardware and software, growing numbers and varieties of computational models are being developed to support research, development, and education.

Combining the advantages of active learning methods such as hands-on laboratories and independent research activities with theoretical discussions about the advantages and limitations of neuronal modeling ideas, we offered an undergraduate laboratory course entitled, “Neuroscience Methods – Computational Modeling.” The class was composed of four to six students, who had previous practical neuroscience lessons, taught by a senior research assistant over five consecutive days. In addition to stimulating analytical and critical thinking, working with literature, judging and interpreting experimental data, and developing writing skills, this class focused on introducing computational modeling as a strategy to bridge the gap between information received from different sources (e.g. anatomical parameters, physiological pathways; Barnes et al., 2003). One has to keep in mind that a computational model is just a statement (in computable form) of a conceptual model. Therefore the model cannot decide which of the presented experimental data are relevant to the intended particular function of the system. This judgement must be self-contained and based on biological hypotheses or must incorporate potentially relevant properties to a minimal model and then observe the contributions. It is impossible to mention all facets and varieties of the overall modeling approach, but we are convinced that an introductory class for undergraduates can help to develop educational and research skills.

Before we introduce our model of a simplified neuron, we have to consider both the differences and the similarities of a single-compartment model versus a multi-compartment model. The soma of a neuron can be regarded as a single compartment with the same resting membrane potential everywhere in the compartment. This property is referred to as equipotential or isopotential. If compartments are too large, equipotentiality cannot be assumed and the numerical simulation will produce a poor approximation (Lytton, 2002). However there are realistic models based on anatomical data, containing thousands of compartments and a set of different active conductances, (e.g. for mitral and granule cells of the olfactory bulb, cortical cells, Softky and Koch, 1993; and hippocampal pyramidal neurons, Traub et al., 1991). Because each compartment requires the calculation of several differential equations at each integration time step (normally around 0.1 ms), the simulation of a short period of time with these complex multi-compartment models requires a huge expenditure of computational time (Jackson and Cauller, 1997). As there are advantages and disadvantages to the different types of compartmental models, the investigator has to decide, which one best fits a defined project.

During this undergraduate course we focused on a single compartment model of an acutely isolated thalamic neuron as an example of an excitable cell. Thalamic cells are an interesting target for modeling studies, since they are well characterized by electrophysiology, computational modeling, and anatomical techniques (McCormick and Huguenard, 1992). Moreover, thalamic cells display two characteristic modes of action potential generation: burst firing with two to six action potentials riding on a low-threshold Ca²⁺ spike during periods of slow wave sleep and tonic single spike activity with trains of action potentials during wakefulness (Steriade and Deschenes, 1984).

The approach we used for our undergraduates began with a minimal single-compartment model including membrane capacitance and leakage conductance. Voltage-dependent membrane conductances were then added step by step. This procedure offers opportunities to analyze the influence of the selectively incorporated component on the model cell. Based on the outcome, biological hypotheses concerning the functional relevance of the particular component within the model cell can be tested. This decision is an integral prerequisite to the creation of a computational model, which the model itself cannot accomplish. Kinetics of the active conductances were taken largely from the literature and are provided for download (see appendix). To simplify the procedure further we started with a sodium (Na⁺) and a potassium conductance (K⁺) of the Hodgkin-Huxley formalism and later included further sodium, potassium and calcium channels (see Materials and Methods). A computational cell model has the inherent advantage that active and passive parameters (adding, removing and altering leak conductance, capacitance and ion channels just by a mouse click; see appendix) can be varied. Varying such parameters is not always possible in standard experimental procedures.

MATERIALS AND METHODS

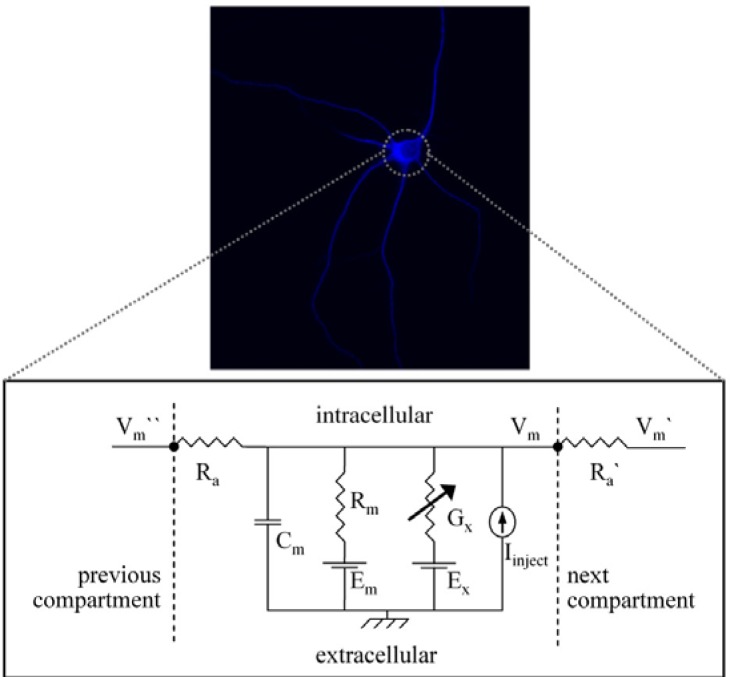
To build a model of a neuron, we first determined the length and the diameter of the dendrites and soma. Figure 1 shows an image of a single cultured thalamic neuron. It is possible to trace neuronal morphology using a microscope linked to a conventional computer to get more anatomical or morphological information. Because neurons are not flat, morphology must therefore be traced through multiple sections.

Figure 1.

Image of a single thalamic relay cell stained against the Ca²⁺-binding protein parvalbumin as a typical marker (upper panel) and a circuit diagram of the somatic single-compartment model (lower panel) consisting of a membrane resistance (R_m) in parallel with a membrane capacitance (C_m) and an axial resistance (R_a). R_a combines the cytoplasmatic and extracellular axial resistance. Channel conductances are represented as variable conductances (G_x) in parallel with R_m. Each of the transmembrane conductances (R_m, G_x) is in series with the appropriate potential (E_m, E_x). These potentials are derived from the reversal potential of the ions passing through the conductances, and are kept fixed in the model. For details on the symbols see Table 3.

To determine all necessary passive and active properties of a neuron to create a realistic neuron model is too challenging for an introductory course. Therefore students determined these properties using selected literature (Tab. 2, Appendix). After all necessary parameters were identified from the literature, an assemblage of conductances, resistances, and a capacitance in the circuit model was constructed (Fig. 1).

After passive and nearly linear components (membrane capacitance, leakage conductance) of the single compartment were set, the model was extended by including additional active conductances. We started with a sodium (I_Na) and a potassium conductance (I_K) of the Hodgkin-Huxley formalism and then included a transient potassium current (I_A), a Ca²⁺ -dependent potassium current (I_C), a hyperpolarization-activated current (I_h), a transient calcium current (I_T), a high-voltage activated calcium current (I_L), and a persistent sodium current (I_{Na persistent}) to the model. A detailed description is given in the appendix and all currents can be downloaded in the publications section of www.patrick-meuth.de. For further information about the modeling procedures, please see the appendix.

RESULTS

Anatomical descriptions, physiological data, correlations between spiking activity and behavior, and lesion effects for thalamic neurons are available; computational modeling provides a means to bridge these different levels of experimental analysis (Hasselmo et al., 2000). Experiencing computational neuroscience is therefore an interesting option for many students.

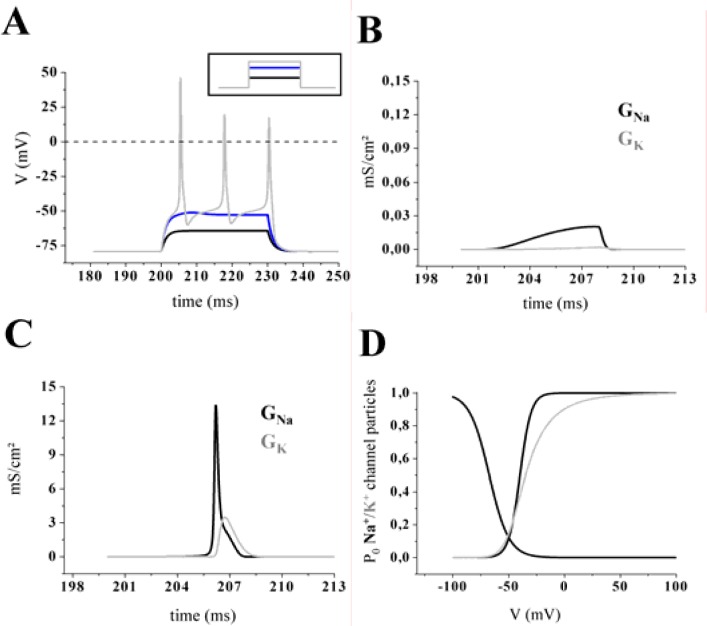
In a first experimental step the passive electrical properties of the model were analyzed. A profile of three different membrane potentials was obtained by applying increasing injection currents to the single-compartmental cell model (Fig. 2A). The stimulus protocol comprised a baseline of 20 ms, followed by three depolarizing current steps of increasing amplitude (30 ms duration) and a final period of 20 ms without injection current (Fig. 2A, inset). When a small positive charge was injected into the neuron, a subthreshold membrane depolarization was produced and the neuron behaved like a simple resistor in parallel with a capacitor. In that case not much of the active conductances (G_Na and G_K) were activated. Figure. 2B and Fig. 2C exemplify the differences between a sub-threshold response and action potential generation regarding the activation level of G_Na and G_K. If the depolarization induced by the injected current was large enough to reach the threshold voltage, the model generated Na⁺/K⁺ action potentials (Fig. 2A, gray line) with overshoots. How does an action potential arise? A strong depolarization caused a sufficient number of voltage-dependent sodium channels to open and sustain a positive feedback mechanism with open channels causing further membrane depolarization and more channels to activate. This can be seen as a rapid increase in the sodium conductance (G_Na; Fig. 2C, black line), which quickly rose to a value much higher than G_K. As a result the membrane potential (V_m) approached the sodium equilibrium potential (E_Na). The process of self-sustained recruitment was stopped when Na⁺ channels started to inactivate. Then the peak value of the action potential is reached and inactivation caused a rapid decrease of G_Na back to its resting level. In parallel, the potassium conductance (G_K) started to increase (Fig. 2C, grey line), resulting in an outward current (I_K). As the outward current surpassed the sodium inward current, the net current flow was then outward (hyperpolarizing), and it began to drive V_m back toward the resting level (Levitan and Kaczmarek, 1997).

Figure 2.

A, A stimulating pulse protocol consisting of three depolarizing current steps (see inset; duration 30 ms) was used to evaluate the behavior below and above the threshold of the cell model. When a positive charge was injected into the cell, a depolarization of the membrane was produced and the neuron behaved similar to a simple resistor in parallel with a capacitor (black and blue line). If the stimulus exceeded a defined threshold of sodium current (I_Na) activation, a train of three action potentials was triggered (grey line). B–C, Ionic movement across the membrane was assumed to flux via channels that were selective to a single ionic species and had two states, open or closed (black line: sodium, grey line: potassium). The conductances were calculated from the Hodgkin-Huxley model for a subthreshold membrane response (B) and during an action potential (C). Note that panel B is magnified 100 fold. D, Steady-state values of the activation and inactivation variables for the fast sodium current (I_Na) as a function of voltage. Note that the steady-state variable for activation was a monotonic increasing function of voltage while inactivation variables were monotonic decreasing functions of voltage. The delayed potassium current (I_K) was characterized by a sigmoidal onset, very slow inactivation and sensitivity to millimolar external tetraethylammonium (TEA). The activation variable was plotted as a function of voltage.

Based on the Hodgkin-Huxley formalism the values of the sodium and potassium conductance were products of the maximal conductance amplitude and the computed open probability (P_O) of channel associated gating particles of activation and inactivation (for details see textbooks or Hodgkin and Huxley, 1952). The parameters of a particle equation were not constant; they were functions of voltage (Fig. 2D; Lytton, 2002). Note that the potassium conductance (Fig. 2D; grey line) revealed no inactivation.

To build a more realistic thalamic neuron we further included a transient potassium current (I_A), a Ca²⁺-dependent potassium current (I_C), a hyperpolarization-activated current (I_h), a transient calcium current (I_T), a persistent sodium current (I_{Na persistent}), and a high-voltage activated calcium current (I_L) to our model neuron. All ionic currents were adapted to NEURON from initial reports (Huguenard and McCormick, 1992; McCormick and Huguenard, 1992). The effect of each current component on the electrophysiological properties of the basic model cell was examined separately.

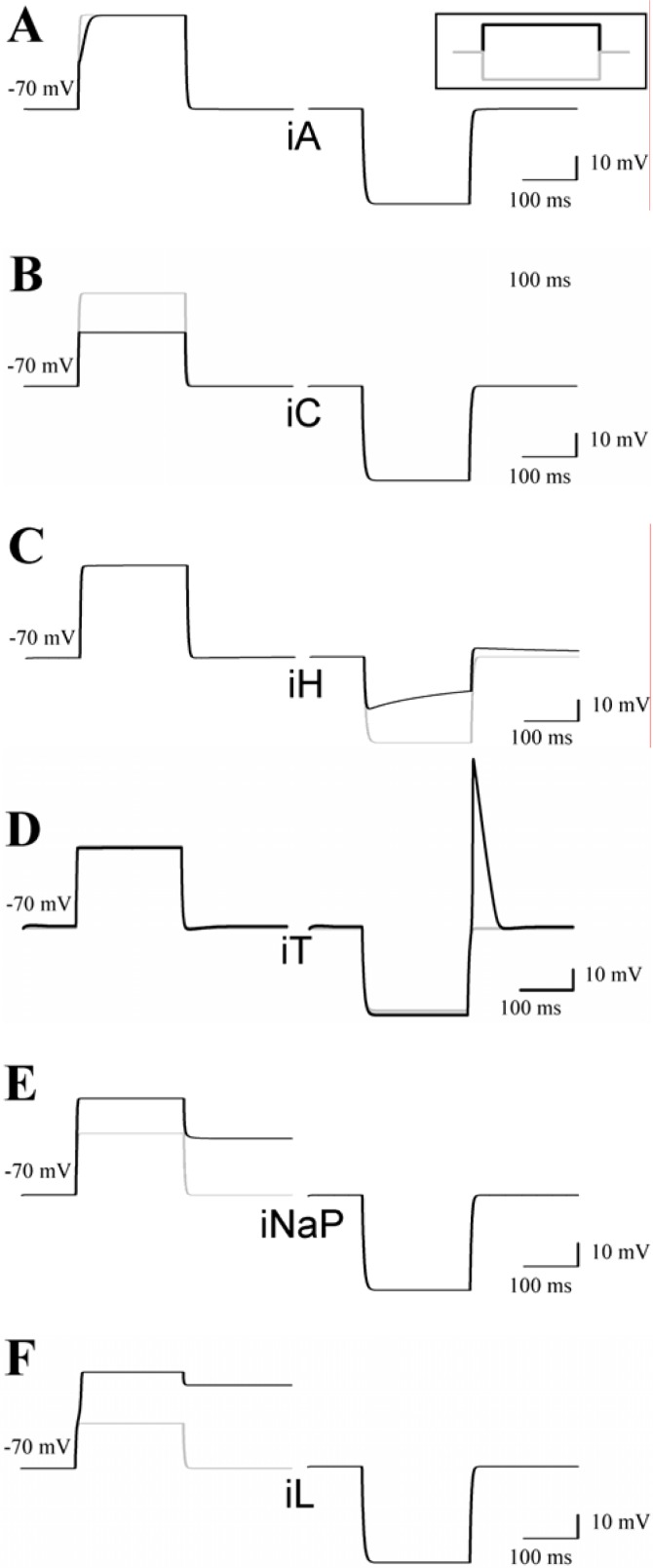
In comparison to the basic model, addition of I_A resulted in a slowing of the rate of rise of the membrane potential in response to a depolarizing current pulse starting from the resting membrane potential (Fig. 3A, left column), leading to the phenomenon of ‘delayed onset of firing’ (Fig. 4C, arrow). In contrast the response of the cell model to a hyperpolarizing current pulse was unaltered by inclusion of I_A (Fig. 3A, right column). Addition of the high-voltage activated Ca²⁺ current I_L and the Ca²⁺-activated K⁺ current I_C also resulted in a marked shift in the response of the model to a depolarizing stimulus, whereas the response to hyperpolarization was unchanged (Fig. 3B,F). Inclusion of the hyperpolarization-activated pacemaker current I_h to the model had no influence on the response to depolarization, but the reaction to a hyperpolarizing pulse was characterized by a time-dependent “sag” of the membrane potential (Fig. 3C). Addition of a transient calcium current I_T led to a rebound calcium spike, a typical feature of thalamic neurons (Fig. 3D). Addition of a persistent sodium current (I_{Na persistent}) or high-voltage activated calcium current (I_L) in our model cell brought a similar increase in response to depolarizing current stimuli (Fig. 3E–F) with the resulting depolarization persisting the stimulus offset.

Figure 3.

Addition of specific ion currents alters the behavior of the model cell. A previously described single-compartment TC neuron model (McCormick and Huguenard, 1992; Huguenard and McCormick, 1992) was adapted to NEURON (Hines and Carnevale, 1997). The model is based on the mathematical description of I_Na, I_K, I_A, I_C, I_h, I_T, I_{Na persistent}, and I_L. A–F, Responses of the cell model to depolarizing (left panels) and hyperpolarizing (right panels) current injections from the resting membrane potential in the presence (black lines) and absence (grey lines) of the indicated ion current.

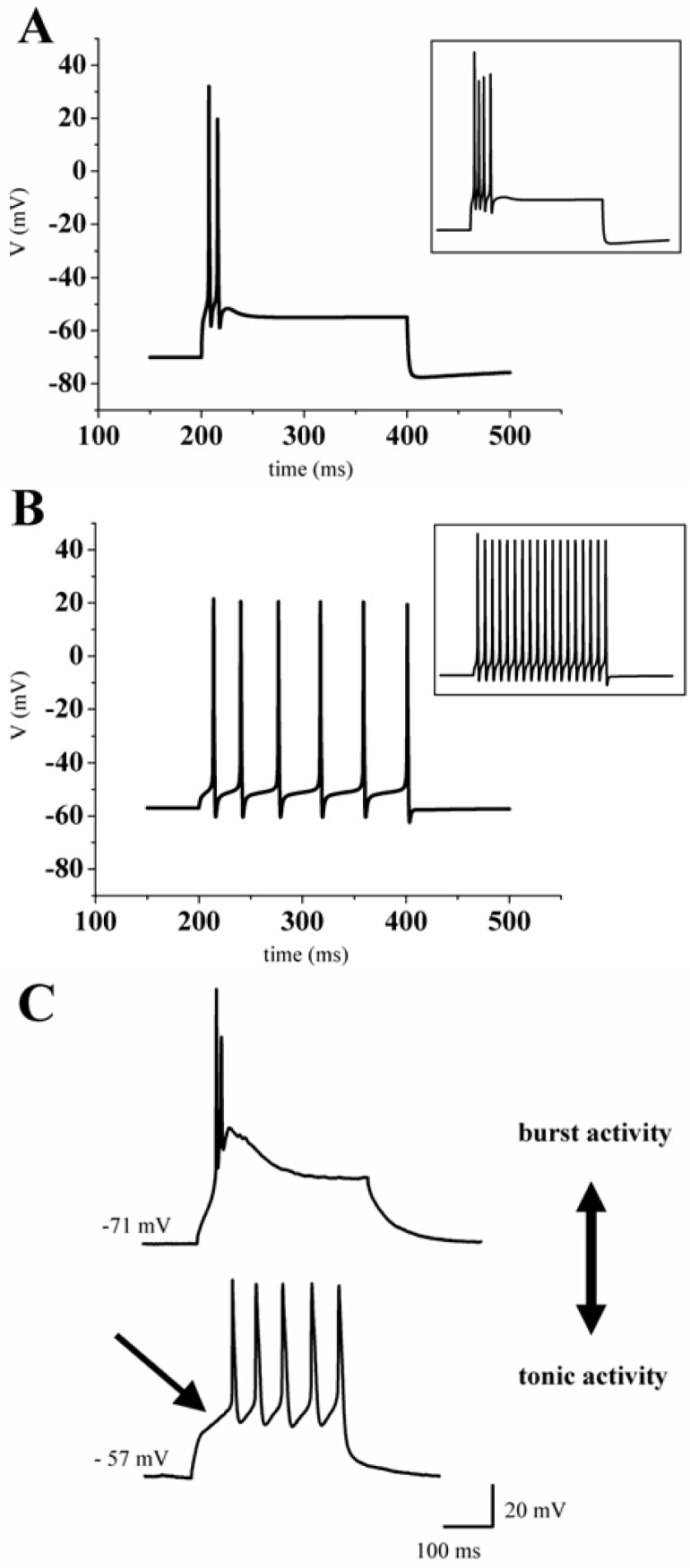
Figure 4.

Two modes of action potential generation in thalamic neurons. Responses to depolarizing current injections are shown. Depending on the membrane potential the model cell (A, B) and a patch-clamped thalamic neuron in vitro (C) displayed bursts of action potentials (A, C upper graph) or a train of action potentials (B, C lower graph). Insets show the response to increased stimuli.

We then considered that even in very detailed models (e.g. the CA3 neuron by Traub et al. (1991) including 19 compartments, each with six active ion conductances (g_Na, g_Ca, g_{delayed rectifier}, g_K(A), g_K, g_{K afterhyperpolarization}, it was not possible to replicate the full range of firing behaviors of these cells (Traub et al., 1994). Furthermore the differential distribution of conductances (e.g. Na⁺ or Ca²⁺) in soma and dendrites endows these cells with the interesting property, that different depolarization induces different firing behaviors (Traub et al., 1991). This differential distribution of ion channels cannot be achieved by a single-compartmental model, like the one we use during this project. Depending on the level of the resting membrane potential, inclusion of all active ionic currents described above results in two fundamentally different modes of action potential generation.

Starting from a hyperpolarized membrane potential (around −70 mV) a depolarizing current pulse evoked a high-frequency burst of Na⁺/K⁺ action potentials ranging on top of a low-threshold calcium spike (Fig. 4A). By enhancing the depolarizing stimulus, the number of action potentials was increased (Fig. 4A, inset).

Interestingly, the generation of these action potentials was comparable to the recordings of a real thalamic neuron in the burst mode (Fig. 4C). At more depolarized membrane potentials the stimulus protocol evoked a train of action potentials (Fig. 4B). Higher stimulus intensity led to an increase in number and frequency of action potentials (Fig. 4B, inset). This so-called tonic activity of thalamic neurons can also be found in whole cell patch-clamp recordings of thalamic neurons (Fig. 4C). Under physiological conditions the burst mode is associated with sleep while the tonic mode underlies states of wakefulness (Steriade and Deschenes, 1984).

Quintessentially, a computational cell model is capable of varying all set parameters, some of which elude experimental manipulation. In this respect the model cell provided here (see appendix) allows simulation of the effects of altered active and passive properties on action potential generation and an exploration of further issues (as suggested in Table 4).

DISCUSSION

Modeling is attractive because it provides a deeper understanding of what is still unknown about a system and thus can guide experiments to avoid generating large amounts of unconnected and difficult to interpret data (Bower and Koch, 1992). By using neuronal modeling in an undergraduate course we demonstrated the versatility and universality of combining modeling strategies with classical, well-established neurobiological methods, such as electrophysiology. With this combination it is possible to incorporate experimental data (judged as relevant for the function of a cell or a system) into a computational model. While it may be necessary to add hypotheses to the model to fill in knowledge gaps, it is also possible to use experimental methods to determine the missing information. Consequently, modeling techniques can help to produce new data, to find gaps in already existing knowledge, to make predictions for living cells, and to open up new strategies for discovering ways that neurons process information.

Like other techniques in neuroscience research, modeling strategies have some major advantages and also some major limitations (Table 1). This list of advantages and disadvantages is far from complete, thus further points and ideas are still open for discussion.

Table 1.

Some major advantages and limitations of neuronal modeling strategies. Further arguments are open for discussion.

advantages
modeling of neuronal activity is a powerful method for simulating morphological and electrical properties of neurons, especially when the experimental question requires a fine-grained model, that embodies a great deal of anatomical or physiological detail (Segev et al., 1985)
general purpose simulation programs like NEURON or GENESIS® offer a straightforward approach to simulate complicated cells, networks or systems
compartmental models are very flexible, since they have no constraints regarding the morphology, physiology or synaptic interactions
computational modeling provides a means for bridging across these different levels of experimental analysis and for linking data at a physiological and anatomical level to the possible functional role (Hasselmo et al., 2000).
disadvantages
idealized cable models remain essential for the estimation of key parameters; with these parameters, a detailed exploration of the compartmental model can be performed and the model can be further refined by comparison with experimental data (Fleshman et al., 1988)
sometimes a hypothesis must be included to the model, since needed parameters are missing due to the uniqueness of the model system
appropriate experimental constraints and reasonable assumptions are necessary to reduce the degrees of freedom in making the choices on which these computations depend (Rall, 1990)

We summarize our strategy for modeling neurons with undergraduates as follows: (i) Based on experimental observations, one must evaluate which components might be relevant for characterizing the system of interest (e.g. single neuron or whole network) morphologically and/or physiologically. This is an essential step since the underlying hypotheses determine the quality and meaningfulness of the resulting model cell. (ii) Then one should construct the passive behavior of the cell model. (iii) In a last step, it is possible, to include active parameters (ion channels) to the model. This initial model can be refined by incorporating additional data or relaxing one or more of the original constraints. Finally, when the model is judged to be sufficiently well behaving and in accordance with known experimental data, it can be used predictively, to examine model behavior under input conditions specific to experimental questions of interest.

Thinking about brain-style computation requires a certain frame of mind, related to but distinctly different from that of the biophysicist. For instance, how should we think of a chemical synapse? In terms of complicated pre- and postsynaptic elements? Ionic channels? Calcium-binding proteins? Or as a non-reciprocal and stochastic switching device that transmits a binary signal rapidly between two neurons and remembers its history of usage? The answer is that we must be concerned with both aspects, with biophysics as well as computation (Koch, 1999).

APPENDIX

NEURON evolved from a long collaboration between Michael Hines (Hines, 1993) and John Moore at Duke University. Initially developed under UNIX, Ted Carnevale’s (Yale University) contribution accommodated common operating systems (MS Windows, MacOS) and therefore NEURON supports a broad range of hardware platforms. Due to NEURON’s modular structure, only minimal effort is necessary to incorporate, extend, or adapt existing implementations (e.g. ion channels or whole network models). Consequently, NEURON is very suitable for undergraduates to experience neuronal computation.

The model cell was created and simulated using a personal computer with the standard distribution of NEURON (version 5.7), available for free download at www.neuron.yale.edu/. This appendix information is intended to provide the reader with fundamental knowledge to understand and reconstruct our model cell. For questions beyond this scope please consult the NEURON documentation of Michael Hines and Ted Carnevale at www.neuron.yale.edu/neuron/papers/nc97/nctoc.htm.

Table 2.

Key references concerning thalamic cell parameters.

McCormick and Huguenard (1992)

A model of the electrophysiological properties of thalamo-cortical relay neurons ⇒ a detailed description of a low-threshold Ca2+ current (IT), a high-threshold Ca2+ current (IL), a Ca2+-activated K+ current (IC), a transient and depolarization-activated K+ current (IA), a hyperpolarization-activated cation current (Ih), a K+ leak current and a Na+ leak current (IKleak; INaleak).

Huguenard and McCormick (1992)

Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons ⇒ they developed Hodgkin-Huxley style mathematical equations that describe the voltage dependence and kinetics of activation and inactivation of four different currents, including the transient, low-voltage- activated Ca2+ current (IT), the rapidly inactivating transient K+ current (IA), the slowly inactivating K+ current (IK2) and the hyperpolarization-activated, mixed cation current (Ih).

Destexhe and Babloyantz (1993)

A model of the inward current Ih and its possible role in thalamocortical oscillations ⇒ kinetic properties of the hyperpolarization-activated inward current (Ih) of thalamocortical neurons.

Destexhe et al. (1998)

Dendritic low-threshold calcium currents in thalamic relay cells ⇒ a combination of in vitro recordings and computational modeling techniques to investigate the function of the low-voltage-activated Ca2+ current (IT) in TC cells.

Mukherjee and Kaplan (1995)

Dynamics of neurons in the cat lateral geniculate nucleus: in vivo electrophysiology and computational modeling ⇒ description of the time domain transformation that thalamocortical relay cells of the cat lateral geniculate nucleus (LGN) perform on their retinal input using computational modeling.

Meuth et al. (2001)

Differential control of high-voltage activated Ca2+ current components by a Ca2+ dependent inactivation mechanism in thalamic relay neurons ⇒ expression of different high-voltage activated Ca2+-channel subtypes in thalamocortical relay neurons and their contribution to a Ca2+- dependent inactivation process.

Hill and Tononi (2004)

Modeling Sleep and Wakefulness in the Thalamocortical System ⇒ sleep is characterized by slow oscillations in cortical activity that can be measured using EEG techniques. These oscillations depend on interactions between the thalamus and the cortex. To investigate these interactions and the switch from wakefulness to sleep, Hill and Tononi have produced a computer model of the thalamocortical circuitry.

We offer two ways of dealing with the appendix information. By working through the step-by-step reconstruction of the model cell, the reader can appreciate the NEURON programming language and develop basic skills to create models. Alternatively the ready-made model (including all necessary resources) can be downloaded at the publications section of www.patrick-meuth.de. Thereby it is possible to gain experience in simulation and usage of NEURON’s GUI (graphical user interface) by performing the suggested experiments without engaging in any programming.

Table 3.

Key definitions of symbols used in the circuit diagram (Fig. 1): F = farad, V = volt, S = siemens, A = ampere, Ω = Ohm.

Cm	membrane capacitance: the membrane capacitance constrains how rapidly Vm can change in response to a fixed current	[F]
Ex	equilibrium potential of a specific ion (x = Na+, K+, Ca2+, Cl−) or a combination of ions	[V]
Em	the “leakage resistance” (Rm) and its associated equilibrium potential (Em) represent the nearly linear channels: these voltage-independent proteins leak ions into and out of a cell down their electrochemical gradient. The flow of the leak ions induces a net leakage current Ileak. The resulting change in Vm is roughly linear with respect to Ileak and follows: $V_m=I_{\mathit{leak}}*R_m$	[V]
Gx	conductance of a specific ion (x = Na+, K+, Ca2+, Cl−) or a combination of ions. Often channels are described by their conductances rather than resistances which is simply the inverse, hence: $G_x=1/R_x$	[S]
Ix	ionic currents where x = Na+, K+, Ca2+, Cl−. Ix is the product of flow of ions via many channels. For voltage-dependent channels, Ix is usually linear with respect to Vm giving: $I_x=G_x*\left(V_m-E_x\right)$	[A]
Ra	axial resistance (interferes with the current flow induced by the longitudinal voltage gradient)	[Ω]
Ra′	axial resistance of the next compartment (interferes with the current flow induced by the longitudinal voltage gradient)	[Ω]
Rm	membrane resistance, Rm is a resistance that characterizes the non-selective pores	[Ω]
Vm	membrane potential (relative to the ground symbol) inside the compartment	[V]
Vm′	membrane potential (relative to the ground symbol) of the next compartment	[V]
Vm″	membrane potential (relative to the ground symbol) of the previous compartment	[V]

Introduction

Each of the following four versions of the modeling exercise includes a framed textbox, which contains the program lines of one of four different versions of the cell model. These boxes mirror the NEURON knowledge that has been introduced up to this point and are intended as patterns to be copied into an ordinary text file (e.g. neuron.txt). After renaming the file into the NEURON specific extension hoc (e.g. neuron.hoc) the program is ready for execution. When NEURON has been installed properly, a double-click on the created text file will automatically start the NEURON interpreter and run the cell model. For all operating systems specific NEURON installation instructions and hints for troubleshooting are provided at the download section of the NEURON website (www.neuron.yale.edu/neuron/install/install.html).

We recommend creating separate folders for each of the four program versions, which should contain only those mechanism files that are explicitly needed. Including unnecessary mechanisms can cause the model to deliver unexpected and misleading data. Each of the used mechanism files can be found in the mechanism folder of the downloadable archive named cell_model.zip (www.patrick-meuth.de; publications section).

Table 4.

Selection of cellular parameters or principles which can be investigated using the provided cell model.

all-or-none phenomenon

one aspect of the action potential generation; in principle a binary phenomenon without any intermediate states

current clamp

in current clamp experiments, one applies a known constant or time-varying current and measures the change in membrane potential caused by the applied current; this type of experiment mimics the current produced by synaptic activity

driving force

difference between the given membrane potential and the reversal potential of an ion, e.g.: ${\text{I}}_{\text{Na}}={\text{G}}_{\text{Na}}*\left({\text{V}}_{\text{m}}-{\text{E}}_{\text{Na}}\right);\text{driving}\hspace{0.17em}\text{force}:\left({\text{V}}_{\text{m}}-{\text{E}}_{\text{Na}}\right)$

frequency

number of action potentials in a defined period of time [Hz = 1/sec]

frequency adaptation

alterations in firing rate over time with a continuing stimulation

holding potential

membrane potential at the beginning of an electrophysiological experiment

hyperpolarization/depolarization

deviations of the membrane potential; to depolarize means to make the membrane potential less negative; to hyperpolarize means to make the membrane potential more negative

interburst interval

time between two bursts (or groups of action potentials); a way to analyze the time domain of neuronal activity

resting membrane potential

membrane potential of a neuron in the absence of stimulation; it should be noted however that natural behavior of neurons includes constant fluctuation of the membrane potential due to intrinsic electrogenic processes and/or extrinsic inputs; a stable resting membrane potential is usually seen only under experimental conditions

reversal potential

a given current through an ion channel reverses direction when the holding potential reaches the reversal potential; according to the Nernst equation the value of the reversal potential depends on the ion selectivity of the investigated ion channel

threshold

defined voltage that has to be reached to evoke an action potential

voltage clamp

see also current clamp; a fixed voltage is delivered while the current is recorded

Morphological and electrical properties

NEURON’s basic building block is the so-called section. Each neuronal structure that is intended to be modeled must be described by at least one of these cylindrical subunits, which are further subdivided into segments (compartments). The number of segments (nseg) within a section is directly proportional to the spatial resolution. Modeling action potentials traveling along an axon is an application example that requires an increased number of segments. For our undergraduate course we reduced the complexity by modeling a single cell body without any axons or dendrites. Thus, one segment was sufficient for our purposes. NEURON is also capable of handling more complex models consisting of several interconnected sections. In this case the axial resistance Ra has to be considered. A section’s morphology is determined by the parameters L (length) and diam (diameter), whereas the electrical properties can be controlled by adapting cm (membrane capacitance). Table 5 summarizes some of the editable section variables.

The following framed textbox illustrates the generation of a section object that can be achieved by the use of the create command followed by a label, through which the object can be referenced within the model. Due to the object-oriented simulation environment references are mandatory for the majority of the available commands. To facilitate further assignments to this section, we used access in combination with the identifier soma, and thus, declared it as the default referenced object. Through this the explicit references to soma for the following two commands could be omitted. To change the section’s length and diameter braces can be used to group multiple variable assignments. The built-in function psection() delivers a print out of the section’s parameters to the console window (Fig. 5) and is, therefore, an useful tool to check the intended changes.

Version 1: Minimal Model

Version 1: Minimal model.

• 1.1 Open NEURON Main Menu:

  After a double-click on Neuron.hoc the NEURON console window (Fig. 5) appears. Enter load_file(“nrngui.hoc”).

• 1.2 Open RunControl:

  Select Tools > RunControl within the NEURON Main Menu (Fig. 7).

• 1.3 Create voltage graph:

  Select Graph > Voltage axis.

• 1.4 Start simulation:

  Click on the Init & Run button.

• 1.5 Evaluate the membrane’s resting potential:

  Right-click within the voltage graph window and select Crosshair at the appearing menu. Point to the voltage graph and keep the left mouse button pressed. While moving left and right explore the window’s bar on top.

• 1.6 Change initial membrane voltage:

  Enter −80 into the Init (mV) input field and hit Init & Run. Evaluate the value of the voltage graph.

• 1.7 Change simulation stop time:

  Enter 500 into the Tstop (ms) input field and notice the x-axis of the voltage graph window.

• 1.8 Recall old input values:

  Click on the red check mark behind Tstop (ms) and notice the effect to the corresponding input field and graph window.

• 1.9 Load session:

  Close the RunControl and voltage graph window by selecting Close. Use File > load session within the NEURON Main Menu to load the session Exp1.ses.

• 1.10 Save session (save values, graphs and windows):

  Change the initial voltage membrane value to −80 and select File > save session. Within the appearing dialog type test.ses and click on Save. After closing the RunControl and voltage graph window load the session test.ses. With respect to session Exp1.ses notice the change in the Init (mV) input field.

create soma

access soma

soma { L = 30 diam = 20}

soma psection()

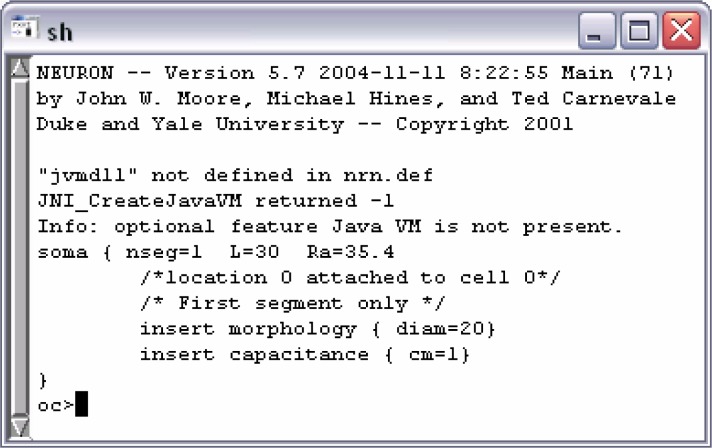
By pasting the above command lines into a text file with the extension hoc and executing the NEURON interpreter by a double-click on it, the source code will produce the output depicted in Fig. 5.

Figure 5.

Output after the execution of the program (Version 1).

Mechanisms

Membrane mechanisms like leak conductances or ionic channels are implemented as software modules in NMODL (extended version of MODL – model description language) and can be recognized by the extension mod. To find appropriate ion channel models the repertoire of freely available channel descriptions should be consulted. These mechanism files are a selection of Arthur Houweling’s NEURON demo (www.cnl.salk.edu/~arthur/, MyFirst-Neuron). Version 2 of the cell model uses the mechanism files leak.mod and HH.mod, which therefore must be copied from the mechanism folder in the archive cell_model.zip (www.patrick-meuth.de; publications section) into the same folder as the model.

Version 2: Expanded Model.

The model is expanded with leak currents and temperature-dependent sodium and potassium channels of the Hodgkin-Huxley formalism. First open the NEURON Main Menu and load session Exp2.ses.

• 2.1 Evaluate simulation temperature:

  Type celsius into the console window.

• 2.2 Change simulation temperature:

  After hitting the Init & Run button evaluate the actual membrane voltage. Type celsius=5 and inspect the voltage difference of a new simulation run.

• 2.3 Change maximum Na⁺ leak permeability:

  Type pna_leak to receive the actual value for the maximum permeability of the Na⁺ leak. Double the result and re-run the simulation for evaluating the new resting membrane potential.

• 2.4 Change maximum K⁺ leak permeability:

  Reset pna_leak to the previous value and increase pk_leak by typing pk_leak=16e-6. Re-run simulation and inspect the new resting membrane potential.

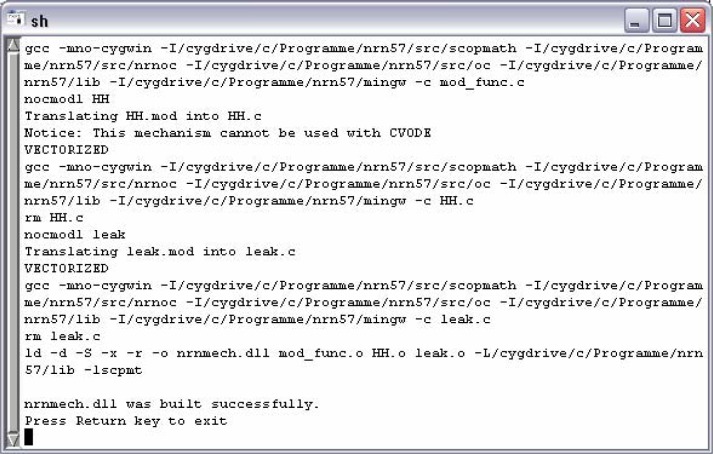
Operating with a mechanism requires that it has been initially compiled through the use of the program mknrndll. During the NEURON installation process an icon for starting mknrndll has been placed either on the desktop or within the start menu. Alternatively, one can execute the file named mknrndll.hoc, which can be found within the NEURON installation folder (e.g. ...\nrn57\lib\hoc\mknrndll.hoc). The next step is to choose the directory where the model and the corresponding mechanism files can be found (e.g. c:/model/version_2). Finally hitting the Make nrnmech.dll button compiles every mechanism within the specified folder. Figure 6 presents the successful compilation of the model version two, merely including leak.mod and HH.mod.

Figure 6.

mknrndll output of the successful compilation of leak.mod and HH.mod.

Mechanisms enhance the model’s range of activities and are incorporated by the insert command. Including leak.mod adds Na⁺, K⁺, Ca²⁺, Cl⁻, and Mg²⁺ leak conductances, through which the model is capable of responding to stimuli in a subthreshold manner (Fig. 2A, lower voltage graphs). Action potential generation (Fig. 2A, upper voltage graph) can be achieved by inserting Na⁺ and K⁺ currents of the Hodgkin-Huxley formalism implemented in HH.mod. Table 6 summarizes the features gained thereby.

Currents are generally measured in mA/cm² and can be expressed in terms of maximum conductance or permeability. In contrast to the standard permeability unit cm³/s (McCormick and Huguenard, 1992), leak.mod uses cm/s. This is due to its internal realization of the Goldman-Hodgkin-Katz current equation; e.g. the Na⁺ leak current is calculated by ina = pna * ghk(v, nai, nao, 1), where the term ghk() delivers a result defined by mC/cm³. To follow the essential rule of global unit consistency pna_leak has to be cm/s for a current in mA/cm².

The simulation’s temperature, controlled by the global variable celsius [°C], should always be kept in mind, since there are several cellular parameters (e.g. ion channel gating) that depend on it. Adapting also the ionic concentrations and the maximum K⁺ membrane permeability leads to a stable resting membrane potential of about −79 mV. Use of the access command omits explicit object references to soma and the over-all source code changes are as follows.

Version 2: Expanded Model

create soma

access soma

{ L = 30 diam = 20}

insert leak

insert HH

celsius = 35

nao = 145

{ki = 135 ko = 3.1}

{cli = 7 clo = 120}

pk_leak=8e-6

psection()

Pointprocesses

IClamp and VClamp are only some of NEURON’s multitude of built-in pointprocesses. Due to their object-oriented character, pointprocesses need to be associated with an arbitrary labelled object reference (objref). Pointprocesses can be inserted at a specific location within a section’s boundaries, so that creating an IClamp object with the new command needs an additional placement parameter given in parenthesis. The location is specified by a number between 0 and 1 representing the distribution along the section in terms of percentage. With no reference provided, the IClamp object will be inserted in the middle of the section soma by default.

The model’s backbone is completed by adjusting the IClamp object’s parameters (Table 7) as shown below.

Version 3: Stimulating the Model

Version 3: Stimulating the Model.

Use current injection; open the NEURON Main Menu and load session Exp3.ses.

• 3.1 Subthreshold membrane answer:

  A current injection of 0.2 nA will be applied after a delay of 200 ms. While the current pulse is injected (200 ms duration) the membrane depolarizes but does not exceed the threshold for action potential generation. Hit the Init & Run button.

• 3.2 Increase injection current:

  Type 0.3 into the amp input field and inspect the changes in the membrane response.

• 3.3 Increase membrane capacitance:

  Type cm into the console window to receive the actual membrane capacitance. Thereafter type cm=10 and explore how the response behavior has changed.

• 3.4 Change cell morphology:

  After resetting the initial membrane capacitance change the cell morphology. This can be achieved by altering either the length (L) or the diameter (diam). Type L=300 or diam=200 and re-run the simulation to recognize the effect.

• 3.5 Active membrane answer:

  After resetting the cell’s morphology change the injection current to 0.5 and inspect the membrane’s behavior.

create soma

access soma

{ L = 30 diam = 20}

insert leak

insert HH

celsius = 35

nao = 145

{ki = 135 ko = 3.1}

{cli = 7 clo = 120}

pk_leak=8e-6

objref stimulus

stimulus = new IClamp(0.5)

stimulus.amp = 0.2

stimulus.del = 200

stimulus.dur = 200

psection()

Graphical User Interface

NEURON’s GUI is a powerful tool to create voltage or current graphs, to control the inserted pointprocesses, and to customize the simulation progression. Executing the statement load_file(“nrngui.hoc”) will successively call all subroutines necessary for the NEURON Main Menu depicted in Fig. 7.

Figure 7.

NEURON’s graphical basis

The first two options of the “Graph” submenu are used to create voltage or current plots. In contrast to voltage graphs, which are automatically associated with the membrane voltage of the default section, a current graph needs an explicitly chosen source. This can be achieved by selecting “Plot what?” in the menu that appears after a right-click within a graph window, where the following dialog delivers all of the model’s variables sorted by sections.

A window for handling each of the included pointprocesses can be opened by using the “point processes viewers”. The execution of Tools > Point Processes > Viewers > PointProcesses > IClamp e.g. summarizes the so far inserted IClamp objects. Selecting a list entry by a double-click on it will open up the corresponding control window.

Several simulation parameters are directly accessible with the aid of the “RunControl”, which is likewise positioned in the “Tools” submenu. Among the buttons to run and stop the simulation, multiple input fields offer the opportunity to control the simulation’s accuracy (“Points plotted/ms”), to set the initial value of the membrane potential throughout the model (“Init (mV)”), and to determine the simulation end (“Tstop (ms)”). A red check mark acknowledges any changes to these fields, whereas removing a check mark recalls the former value. Declaring the nrngui.hoc associated variables v_init and tstop within the source code (see program version 4) will automatically adjust the corresponding field values of the RunControl.

Version 4: Action Potentials.

Finally the model is capable of producing two kinds of action potential generation. Load session Exp4.ses.

• 4.1 Reproduce Fig. 4A:

  Change the amp value in the window labelled IClamp[0] to 0.32 and run the simulation. Try to achieve a membrane response similar to the inset of Fig. 4A by increasing the current pulse in steps of 0.01 nA.

• 4.2 Creating second injection source:

  Enter the following two commands sequentially into the console window:

  objref stimulus2

  stimulus2=new IClamp(0.5)

  Select Tools > Point Processes > Viewers > PointProcesses > IClamp within the NEURON Main Menu. Double-click on the second entry within the appeared list. This opens the control window for the newly created second stimulus source (IClamp[1]).

• 4.3 Reproduce Fig. 4B:

  The values for IClamp[1] must equal: del = 50, dur = 450 and amp = 0.3. The amplitude of the stimulus source IClamp[0] has to be changed to 0.0713. Try to reproduce the inset of Fig. 4B by increasing the amp value of IClamp[0] in steps of 0.005.

After investing time and work in the creation and adaptation of several graph windows and menus the “save session” and “load session” options in the “File” submenu enable the storage of the actual status into a file and the recall, respectively. The session file is denoted by the specific extension ses and includes all visible windows, menus and the actual variable values of them. Therefore, loading a session file will replace the values specified by hoc statements (e.g. tstop).

Final enhancement

Inserting, compiling, and adapting additional channel mechanisms (Fig. 3) enlarges the so far created backbone to a more realistic model of a thalamic relay neuron and is, therefore, capable of reproducing two typical modes of action potential generation (Fig. 4). The inclusion of ia.mod, ic.mod, ih.mod, it.mod, inap.mod and il.mod supplements the features summarized in Table 8.

The convenience of getting a model run under NEURON is exemplified by the following program containing just about 30 lines of source code.

Version 4: Action Potentials

load_file(“nrngui.hoc”)

v_init = −70

tstop = 500

create soma

access soma

{ L = 30 diam = 20}

insert leak

insert HH

insert iA

insert iC

insert iH

insert iT

insert iNaP

insert iL

celsius = 35

nao = 145

{ki = 135 ko = 3.1}

{cli = 7 clo = 120}

pk_leak=8e-6

gkbar_iA = 0.0055

gkbar_iC = 0.00018

ghbar_iH = 0.0006

eh = −40

pcabar_iT = 0.00045

g_iNaP = 17e-5

objref stimulus

stimulus = new IClamp(0.5)

stimulus.amp = 0.2

stimulus.del = 200

stimulus.dur = 200

psection()

Experimental suggestions

The experimental suggestions can be executed without deeper knowledge of NEURON’s programming language. Depending on the reader’s interest the experiments below offer either the practical realization of the so far discussed modeling approaches or a first look on how to deal with simulations and NEURON’s GUI (graphical user interface). All session files following below can be found in the downloadable archive cell_model.zip at the publications section of www.patrick-meuth.de.

Table 5.

Section parameters and their default values [μm = um, μF = uF].

variable	description	default	unit
nseg	number of segments	1	-
Ra	axial resistance	35.4	Ω cm
L	length	100	μm
diam	diameter	500	μm
cm	membrane capacitance	1	μF/cm2

Table 6.

Extensions through the channel mechanisms leak.mod and HH.mod [mho = S].

leak.mod
variable		description	default	unit
ina_leak		Na+ leak current	-	mA/cm2
ik_leak		K+ leak current	-	mA/cm2
ica_leak		Ca2+ leak current	-	mA/cm2
icl_leak		Cl− leak current	-	mA/cm2
img_leak		Mg2+ leak current	-	mA/cm2
pna_leak		max. Na+ membrane permeability	2.07e-07	cm/s
pk_leak		max. K+ membrane permeability	3.45e-06	cm/s
pca_leak		max. Ca2+ membrane permeability	0	cm/s
pcl_leak		max. Cl− membrane permeability	0	cm/s
pmg_leak		max. Mg2+ membrane permeability	0	cm/s
nai / nao		Na+ concentration inside / outside the cell	10 / 140	mM
ki / ko		K+ concentration inside / outside the cell	54.4 / 2.5	mM
cai / cao		Ca2+ concentration inside / outside the cell	5e-05 / 2	mM
cli / clo		Cl− concentration inside / outside the cell	1 / 1	mM
mgi / mgo		Mg2+ concentration inside / outside the cell	1 / 1	mM
HH.mod
variable	description		default	unit
ina	Hodgkin-Huxley Na+ current		-	mA/cm2
ik	Hodgkin-Huxley K+ current		-	mA/cm2
il_HH	non specific leak current		-	mA/cm2
gnabar_HH	max. conductance of ina_HH		0.12	mho/cm2
gkbar_HH	max. conductance of ik_HH		0.036	mho/cm2
gl_HH	max. conductance of il_HH		0.0003	mho/cm2
ena_HH	Na+ equilibrium potential of ina_HH		50	mV
ek_HH	K+ equilibrium potential of ik_HH		−77	mV
el_HH	equilibrium potential of il_HH		−54.3	mV

Table 7.

IClamp object parameters.

variable	description	default	unit
i	injected current	-	nA
amp	max. current amplitude	0	nA
del	stimulus delay	0	ms
dur	stimulus duration	0	ms

Table 8.

Extensions through the channel mechanisms ia.mod, ic.mod, ih.mod, it.mod, inap.mod and il.mod [mho = S]

variable	description	default	unit
ik_iA	transient potassium current	-	mA/cm2
ik_iC	Ca2+ dependent potassium current	-	mA/cm2
ih_iH	hyperpolarization-activated current	-	mA/cm2
iCa_iT	transient calcium current	-	mA/cm2
ina_iNaP	persistent sodium current	-	mA/cm2
ica_iL	high-voltage activated calcium current	-	mA/cm2
gkbar_iA	max. conductance of ik_iA	0.00345	mho/cm2
gkbar_iC	max. conductance of ik_iC	0.00345	mho/cm2
ghbar_iH	max. conductance of ih_iH	4e-05	mho/cm2
pcabar_iT	max. permeability of iCa_iT	0.0001	cm/s
g_iNaP	max. conductance of ina_iNaP	7e-05	S/cm2
pcabar_iL	max. permeability of ica_iL	0.000276	cm/s