Abstract
It is generally believed that students learn best through activities that require their direct participation. By using simulations as a tool for learning neuroscience, students are directly engaged in the activity and obtain immediate feedback and reinforcement. This paper describes a series of biophysical models and computer simulations that can be used by educators and students to explore a variety of basic principles in neuroscience. The paper also suggests ‘virtual laboratory’ exercises that students may conduct to further examine biophysical processes underlying neural function. First, the Hodgkin and Huxley (HH) model is presented. The HH model is used to illustrate the action potential, threshold phenomena, and nonlinear dynamical properties of neurons (e.g., oscillations, postinhibitory rebound excitation). Second, the Morris-Lecar (ML) model is presented. The ML model is used to develop a model of a bursting neuron and to illustrate modulation of neuronal activity by intracellular ions. Lastly, principles of synaptic transmission are presented in small neural networks, which illustrate oscillatory behavior, excitatory and inhibitory postsynaptic potentials, and temporal summation.
Keywords: undergraduate, graduate, neurons, synapses, neural networks, modeling, SNNAP, Hodgkin-Huxley
Teaching the basic principles of neuroscience can be greatly enhanced by incorporating realistic and interactive simulations of neural function. Learning through experimentation and investigation (i.e., inquiry-based teaching) can enhance the student’s understanding and interest (Tamir et al., 1998; Haefner and Zembal-Saul, 2004; Zion et al., 2004; van Zee et al., 2005; for review see National Research Council, 2000). For example, a basic tenet of neuroscience is that neural functions emerge from the interplay among the intrinsic biophysical properties of individual neurons within a network, the pattern of synaptic connectivity among the neurons, and the dynamical properties of the individual synaptic connections (for review see Getting, 1989). The specific role(s) that any one process plays in the overall behavior of a network can be difficult to assess due to such factors as interacting nonlinear feedback loops and inaccessibility of the process for experimental manipulation. One way to overcome this problem is by mathematical modeling and simulating the biophysical and biochemical properties of individual neurons and dynamic properties of the individual synapses. The output of the model network and its sensitivity to manipulation of parameters can then be examined. To do so, it is necessary to have a flexible neurosimulator that is capable of simulating the important aspects of intrinsic membrane properties, synapses, and modulatory processes. Such a simulator can be a tool to aid students to a better understanding of the basic principles of neuroscience and to investigate neural behavior.
Several simulators are available for realistically simulating neural networks (for review of neurosimulators see Hayes et al., 2003). However, only a few neurosimulators have been adapted to a teaching environment (e.g., Friesen and Friesen, 1995; Siegelbaum and Bookman, 1995; Lytton, 2002; Lorenz et al., 2004; Moore and Stuart, 2004; Meuth et al., 2005; Carnevale and Hines, 2006). This paper describes a Simulator for Neural Networks and Action Potentials (SNNAP) that is well suited for both research and teaching environments (Ziv et al., 1994; Hayes et al., 2003; Baxter and Byrne, 2006). SNNAP is a versatile and user-friendly tool for rapidly developing and simulating realistic models of single neurons and neural networks. SNNAP is available for download (snnap.uth.tmc.edu). The download of SNNAP includes the neurosimulator, the SNNAP Tutorial Manual, and over 100 example simulations that illustrate the functionality of SNNAP as well as many basic principles of neuroscience.
This paper illustrates the ways in which several relatively simple models of single neurons and neural networks can be used to illustrate commonly observed behaviors in neural systems and the ways in which models can be manipulated so as to examine the biophysical underpinnings of complex neural functions. The paper begins with a presentation of the most influential model of neuronal excitability: the Hodgkin-Huxley (HH) model (Hodgkin and Huxley, 1952). The HH model describes the flow of sodium, potassium, and leak currents through a cell membrane to produce an action potential. The HH model is used to illustrate several basic principles of neuroscience and nonlinear dynamics. For example, simulations are used to examine the concepts of threshold, the conductance changes that underlie an action potential, and mechanisms underlying oscillatory behavior. A second model (Morris and Lecar, 1981) is used to investigate the role of intracellular calcium as a modulator of neuronal behavior and to develop a bursting neuron model. By manipulating parameters, processes that affect the duration and frequency of activity can be identified. Finally, some basic principles of synaptic transmission and integration are illustrated and incorporated into simple neuronal networks. For example, one of the networks exhibits oscillations and can be used to examine the roles that excitatory and inhibitory synaptic connections can play in generating rhythmic activity. The subject material and “virtual” laboratory exercises that are outlined in this paper are suitable for undergraduate and graduate courses in neuroscience.
MATERIALS AND METHODS
To be useful in a learning environment, a neurosimulator must be both powerful enough to simulate the complex biophysical properties of neurons, synapses, and neural networks and be sufficiently user friendly that a minimal amount of time is spent learning to operate the neurosimulator. SNNAP was developed for researchers, educators and students who wish to carry out simulations of neural systems without the need to learn a programming language. SNNAP provides a user-friendly environment in which users can easily develop models, run simulations, and view the results with a minimum of time spent learning how to use the program.
Installing SNNAP
After downloading the snnap8.zip file, unzip the file and place the snnap8 folder on a local or remote hard drive. SNNAP is written in the programming language Java, which embodies the concept of “write once, run everywhere.” The computer and operating system independence of Java-based programs is due to the machine specific Java Virtual Machine (JVM) that executes Java programs. To determine whether a computer has a JVM installed, run the command java –version from a command prompt, or simply try to launch SNNAP (see below). If JVM is not installed, SNNAP will not run and JVM must be downloaded (www.javasoft.com) and installed. Note, Java does not interpret blank characters in path names. Thus, commonly used folders such as “Program Files” or “My Documents” are not appropriate for installing SNNAP. Also note that European conventions often replace the decimal point in real numbers with a comma. Java does not accept commas in real numbers, and thus, the default system settings of some computers must be modified. For additional details, see the SNNAP web site. The SNNAP download provides an extensive library of example simulations. The present paper illustrates the ways in which some of these examples can be used to teach principles of neuronal function and suggests ways in which students can manipulate the models so as to gain a better understanding of neural function. All of the results in the present paper were generated with SNNAP, and the models are provided at the SNNAP web site. Additional models, which were used in research studies, also are available at the ModelDB web site (senselab.med.yale.edu/senselab/).
Operating SNNAP
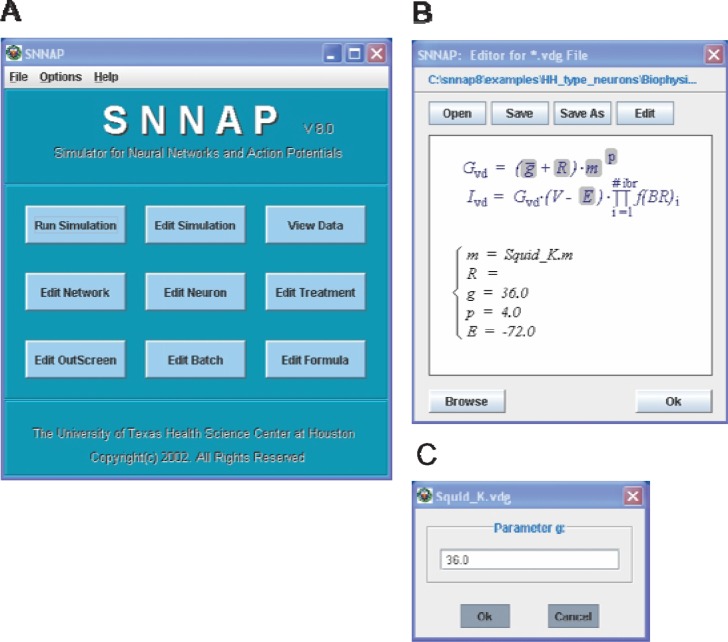
After ensuring that JVM and SNNAP are properly installed, double-click on the snnap8.jar file to launch SNNAP. Alternatively, type java–jar snnap8.jar using the command prompt with the active directory positioned at the snnap8 folder. Launching SNNAP invokes the main-control window (Fig. 1A). The main-control window provides access to the neurosimulator (the Run Simulation button) and to the various editors that are used to develop models and control aspects of the simulation (e.g., setting the duration of the simulation, the integrations time step, or specifying extrinsic treatments that are applied during the simulation). For example, to change the potassium conductance in the HH model, first select Edit Formula (Fig. 1A). This button invokes a file manager (not shown) that allows the user to select the appropriate file for editing (in this case, hhK.vdg). Once the file is selected, the equation is displayed in a separate window (Fig. 1B). The window displays a graphical representation of the equation (upper part of window) and values for parameters (lower part of window). To change a parameter (e.g., the maximal potassium conductance, g̅), click on the parameter with a shaded background, to open a dialogue box (Fig. 1C). The dialogue box allows the user to enter and save a new value for the selected parameter. An extensive selection of examples and step-by-step instructions for how to construct and run simulations are provided in the SNNAP Tutorial Manual.
Figure 1.
User-friendly interface for building models and running simulations. In SNNAP, all aspects of developing a model and running simulations can be controlled via a graphical-user interface (GUI; see also Fig. 3A). A: The simplest way to run SNNAP is to double click on the snnap.jar file. The first window to appear is the main control window. Other features of the neurosimulator are selected by clicking on the appropriate button. B: For example, clicking on the Edit Formula button invokes a file manager (not shown) and allows the user to select the file that contains the specific formula to be edited (in this case the hhK.vdg file). Once selected, the formula is displayed in the formula editor. The parameters in the formula are displayed with a shaded background. The current values for the parameters are listed in the lower portion of the display. C: To change the value of a parameter, click on the parameter. A dialog box appears and the user enters the new value. The SNNAP Tutorial Manual provides detailed instructions for operating SNNAP. The tutorial is available for download at the SNNAP website.
RESULTS
SINGLE-NEURON SIMULATIONS
Neurons are generally regarded as the fundamental units of computation in the nervous system. As input-output devices, neurons integrate synaptic inputs to their dendrites, generate action potentials in response to sufficiently strong inputs, and transmit this electrical signal along their axons in the form of action potentials. The action potentials invade the synaptic terminals, which trigger synaptic transmission to postsynaptic neurons (Shepherd, 2004). At each step of the process, the neural information is modified and the original input signal is processed as it progresses through a neuron and a neural network. For example, a weak input signal may be subthreshold for eliciting a spike and this weak signal is effectively filtered out of the network (see Fig. 10). Alternatively, two weak signals that occur in close temporal proximity may summate and elicit an action potential. The simulations that are outlined below examine some of the biophysical properties of single cells and the ways in which electrical signals are generated.
Figure 10.
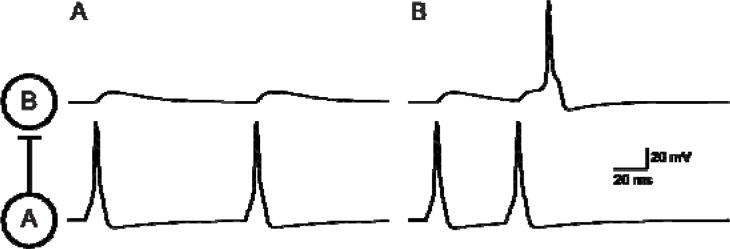
Temporal summation. A network of two neurons with an excitatory synapse from cell A to cell B. A: Two presynaptic action potentials are elicited with an interspike interval of 100 ms. The individual EPSPs are subthreshold for eliciting a postsynaptic spike. B: If the interspike interval is reduced to 50 ms, the EPSPs summate and elicit a postsynaptic spike. The temporal summation of the two EPSPs produces a suprathreshold depolarization in the postsynaptic cell and a spike is elicited.
This section begins by presenting an influential model for nerve cell signaling: the Hodgkin-Huxley (HH) model (for a review of the HH model see Baxter et al., 2004). Using the HH model, the fundamental phenomenon of neuronal excitability is illustrated. In addition, this section illustrates the roles that various parameters (e.g., ionic conductance) play in determining neuronal behavior. In doing so, several experiments are outlined that students can conduct, and thereby, gain an intuitive understanding of the mechanistic underpinnings of neuronal function. This section also illustrates the ways in which terminology from the mathematics of nonlinear dynamics can be used to describe model behavior. Finally, this section illustrates some ways in which more complex patterns of neuronal activity (e.g., oscillations and bursting) can be modeled. A second model, the Morris-Lecar (ML) model (Morris and Lecar, 1981; see also Rinzel and Ermentrout, 1998), is introduced to illustrate mechanisms that underlie bursting.
Hodgkin-Huxley Model of Neuronal Excitability
A widely used model for neuronal behavior is the Hodgkin-Huxley (HH) model (Hodgkin and Huxley, 1952), which earned Alan L. Hodgkin and Andrew F. Huxley the Noble Prize in Physiology or Medicine in 1963. [To view biographical information about Hodgkin and Huxley and other Nobel laureates, visit the Nobel Prize web site at www.nobel.se/nobel. In addition, the lectures that Hodgkin and Huxley delivered when they received the Nobel Prize were published (Hodgkin, 1964; Huxley, 1964), as well as informal narratives (Hodgkin, 1976; 1977 and Huxley, 2000; 2002) that describe events surrounding their seminal studies.] The HH model describes the flow of sodium and potassium ions through the nerve cell membrane to produce an all-or-nothing change in potential across the membrane; i.e., an action potential or spike.
The equivalent electric circuit for the HH model is presented in Fig. 2A. The circuit illustrates five parallel paths that correspond to the five terms in the ordinary differential equation (ODE) that describes the membrane potential (Vm, Fig. 2B). From left to right (Fig. 2A), the circuit diagram illustrates an externally applied stimulus current (Istim), the membrane capacitance (Cm), and the three ionic conductances sodium (gNa), potassium (gK) and leak (gL). Both sodium and potassium have voltage-and time-dependent activation (variables m and n, respectively) and sodium has voltage- and time-dependent inactivation (variable h; Fig. 2B).
Figure 2.
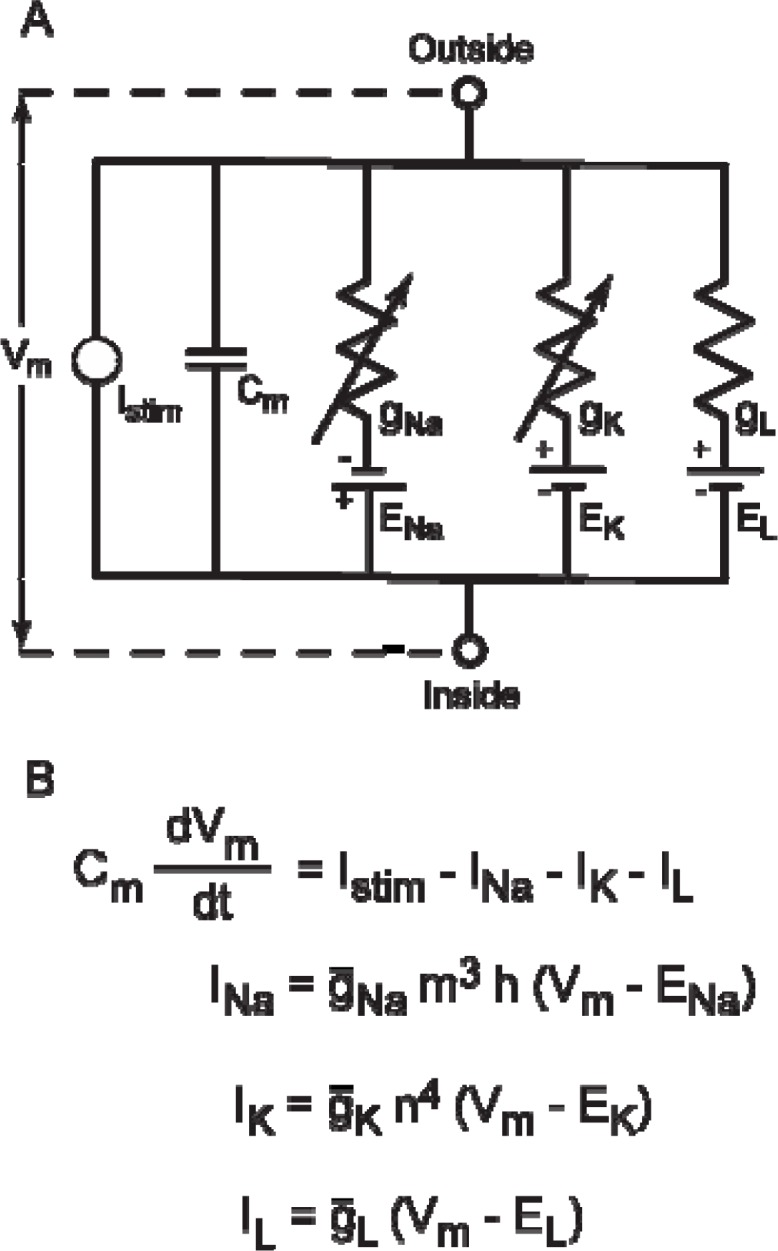
Equivalent electric circuit for HH model. A: Hodgkin and Huxley pioneered the concept of modeling the electrical properties of nerve cells as electrical circuits. The variable resistors represent the voltage- and/or time-dependent conductances. (Note, conductances can also be regulated by intracellular ions or second messengers, see Fig. 7.) The HH model has three ionic conductances: sodium (gNa), potassium(gK) and leak (gL). The batteries represent the driving force for a given ionic current. CM represents the membrane capacitance. Istim represents an extrinsic stimulus current that is applied by the experimenter. B: A few of the equations in the HH model. The ordinary differential equation (ODE) that describes the membrane potential (Vm) of the model contains the ensemble of ionic currents that are present. The HH model is relatively simple and contains only three ionic currents. Other models may be more complex and contain many additional ionic currents in the ODE for the membrane potential (e.g. see Butera et al., 1995; Av-Ron and Vidal, 1999). The ionic currents are defined by a maximal conductance (g̅), a driving force (Vm – Eion), and in some cases activation (m, n) and/or inactivation (h) functions. These equations illustrate many of the parameters that students may wish to vary. For example, values of g̅ can be varied to simulate different densities of channels or the actions of drugs that block conductances. Similarly, values of Eion can be changed to simulate changes in the extracellular concentrations of ions (see Av-Ron et al., 1991).
The HH model for a space-clamped patch of membrane is a system of four ODEs, 12 algebraic expressions, and a host of parameters. The principle ODE of the space-clamped HH model describes the change of voltage across the membrane due to the three currents, sodium (INa), potassium (IK), and leak (IL) currents, as well as an applied external stimulus current Istim (Fig. 2B). The two ions that play the major role in the generation of an action potential are sodium (Na+) and potassium (K+). Sodium ions exist at a higher concentration on the exterior of the cell, and they tend to flow into the cell, causing the depolarization. Potassium ions exist at a higher concentration on the interior of the cell, and they tend to flow outward and cause the repolarization of the membrane back to rest. The key to action potential generation is that sodium activation is faster than the potassium activation (see Fig. 4). At the resting membrane potential (−60 mV), there is a balance between the flow of the inward sodium current, the outward potassium current and the leak current.
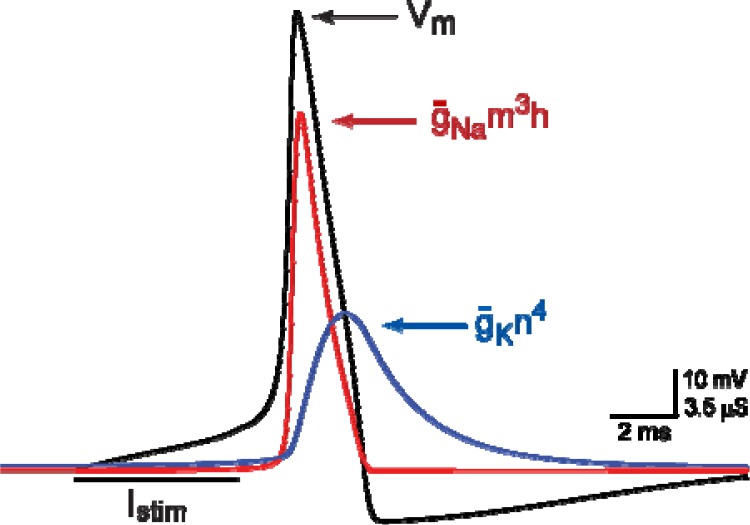
Figure 4.
Conductance changes underlying an action potential. The membrane potential (Vm) is illustrated by the black trace. The sodium conductance (g̅Nam3h) is illustrated by the red trace, and potassium conductance (g̅K n4) is represented by the blue trace (see Fig. 2B). In response to the depolarizing stimulus (Istim), the sodium conductance increases, which depolarizes the membrane potential and underlies the rising phase of the spike. The potassium conductance increases more slowly and underlies the falling phase of the action potential.
An ionic current is defined by several terms: a maximal conductance (g̅), activation (m, n), and/or inactivation (h) variables, which are functions of voltage and/or time (and/or intracellular second messenger or ions, see below), and a driving force (Fig. 2B). The maximal conductance represents the channel density for the particular ion and the activation and inactivation variables describe the kinetics of opening and closing of the channels. By changing the values of g̅, students can simulate the differential expression of ion channels in various cells types or simulate the actions of drugs that block ionic conductances (see below). The activation and inactivation functions also are represented by ODEs (not shown).
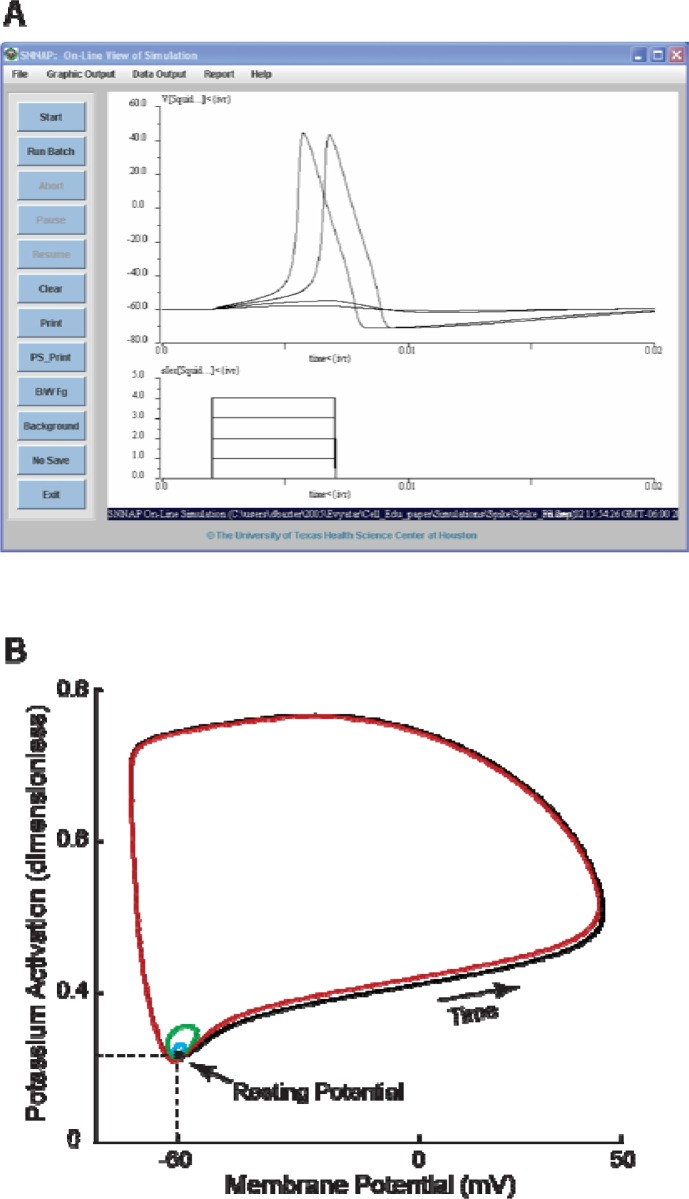
Figure 3A illustrates the overlay of four simulations in which Istim. was systematically increased (lower trace in Fig. 3A). The HH model exhibits a threshold phenomena due to the nonlinear properties of the model. The first two stimuli failed to elicit an action potential, and thus, are referred to as being subthreshold. The final two stimuli each elicit an action potential, and thus, are suprathreshold. Note that both spikes have a peak value of ∼50 mV, hence the spikes are referred to as all-or-nothing.
Figure 3.
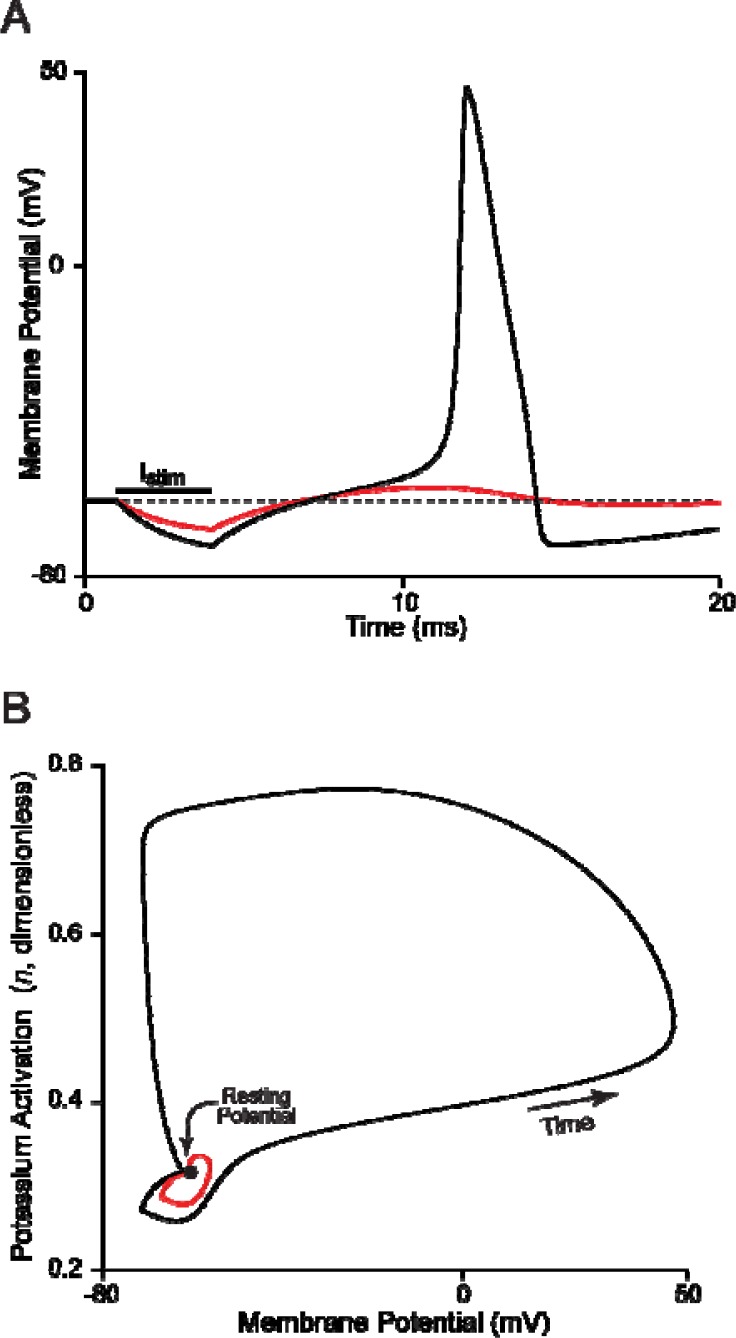
Action potentials and threshold phenomena. A: Screen shot of the SNNAP simulation window. The upper trace illustrates the membrane potential of the HH model. The lower trace illustrates the extrinsic stimulus currents that were injected into the cell during the simulations. With each simulation, the magnitude of the stimulus is systematically increased in 1 nA increments. The first two stimuli are subthreshold, but the final two stimuli are suprathreshold and elicit action potentials. This figure also illustrates several features of the SNNAP simulation window. To run a simulation, first select File, which invokes a drop-down list of options. From this list select the option Load Simulation, which invokes a file manager (not shown). The file manager is used to select the desired simulation (*.smu file). Once the simulation has been loaded, pressing the Start button begins the numerical integration of the model and the display of the results. See the SNNAP Tutorial Manual for more details. B: Phase-plane representation of the threshold phenomena. The data in Panel A are plotted as time series (i.e., Vm versus time). Alternatively, the data can be plotted on a phase plane (i.e., potassium activation, n, versus membrane potential, Vm). Although time is not explicitly included in the phase plane, the temporal evolution of the variables proceeds in a counter-clockwise direction (arrow). The resting membrane potential is represented by a stable fixed point (filled circle at the intersection of the two dashed lines). The stimuli displace the system from the fixed point. If the perturbations are small, the system returns to the fixed point (small blue and green loops). However, for sufficiently large perturbations, the system is forced beyond a threshold and the trajectory travels in a wide loop before returning to the stable fixed point (red and black loops). The system is said to be excitable because it always returns to the globally stable fixed point of the resting potential. For more details concerning the application of phase plane analyses to computation models of neural function see Baxter et al. (2004), Canavier et al. (2005), or Rinzel and Ermentrout (1998).
One advantage of using simulations is that students have access to each component (parameters and variables) in the model. Thus, it is possible to examine the mechanistic underpinnings of complex phenomena. For example, the spike in the membrane potential of the HH model is due to a rapid activation of the sodium conductance, which causes the positive deflection of the membrane potential (Fig. 4). Following a slight delay, the conductance to potassium ions increases, which causes a downward deflection of the membrane potential, which eventually brings the membrane potential back to rest. Only when the input passes a threshold, does the action potential occur. The action potential is an all-or-nothing event (FitzHugh, 1969), which means that an impulse generally reaches a fixed amplitude once the threshold is passed (see Fig. 3A).
Phase-Plane Representations
The mathematics and terminology of nonlinear dynamical systems (Abraham and Shaw, 1992) are often used to analyze and describe neuronal properties. For example, the results that are illustrated in Fig. 3A are represented as a time-series plot; i.e., the dependent variable (Vm) is plotted versus the independent variable time. Alternatively, the data can be represented on a plane of two variables (i.e., a phase plane), Vm and n (Fig. 3B). In the phase plane, the resting state of the system (Vm = −60 mV and n = 0.32) is represented by a stable fixed point (filled circle, Fig. 3B). In response to extrinsic stimuli, the system is momentarily perturbed off the fixed point and displays a loop (Fig. 3B) on the trajectory back to the resting state. Each increasing stimulus displaces the voltage further away from the fixed point, until the membrane potential passes the threshold during the third and fourth stimuli. The action potentials are represented by the two large loops (red and black trajectories). A threshold phenomena is a hallmark of a nonlinear system where for a slight change in input, the system may exhibit a large change in behavior, as seen by the action potential of the HH model. Note that the system always returns to the stable fixed point. Thus, the fixed point is referred to as being globally stable and the system is referred to as excitatory. All trajectories in the phase plane will return to the globally stable fixed point. By modifying model parameters, the stability of the fixed point can be altered and the system can be made to oscillate (see below).
Oscillatory Behavior
In addition to generating single spikes, the HH model can exhibit a second type of behavior, oscillations (Fig. 5A). For a constant stimulus of sufficient magnitude, the HH model exhibits rhythmic spiking activity or oscillations. This oscillatory behavior can be viewed as a limit cycle on a two-variable plane (Fig. 5B). Initially, the system is at rest and the dynamics of the system are defined by the globally stable fixed point. However, the stimulus displaces the system from a resting state and destabilizes the fixed point. The system trajectory progresses towards a limit cycle, which is the stable behavior for the duration of the stimulus. Following an initial transient (the trajectories of the first and second spike), the trajectories of each subsequent spike superimpose, thus the limit cycle is referred to as stable. Once the stimulus ends (not shown), the limit cycle destabilizes and the stability of the fixed point returns and the system returns to the resting potential. There are numerical techniques to calculate the steady state point (SSP) of a system and whether the point is stable or unstable (see Odell, 1980). Alternatively, students can plot the resting potential as a function of stimulating current and observe when the fixed point becomes unstable. Such a plot is referred to as a bifurcation diagram. By systematically increasing the stimulating current, the resting state of the model will be replaced by oscillations and further increases in stimulus intensity will cause the model to oscillate at higher firing frequencies. A plot of the amplitude of the stimulus current versus frequency of oscillations (I-F graph) can be used to determine the input/output properties of the HH model. Students can graph the I-F curve and investigate whether there exists a linear range in the model response as well as determine the maximum firing frequency of the HH model.
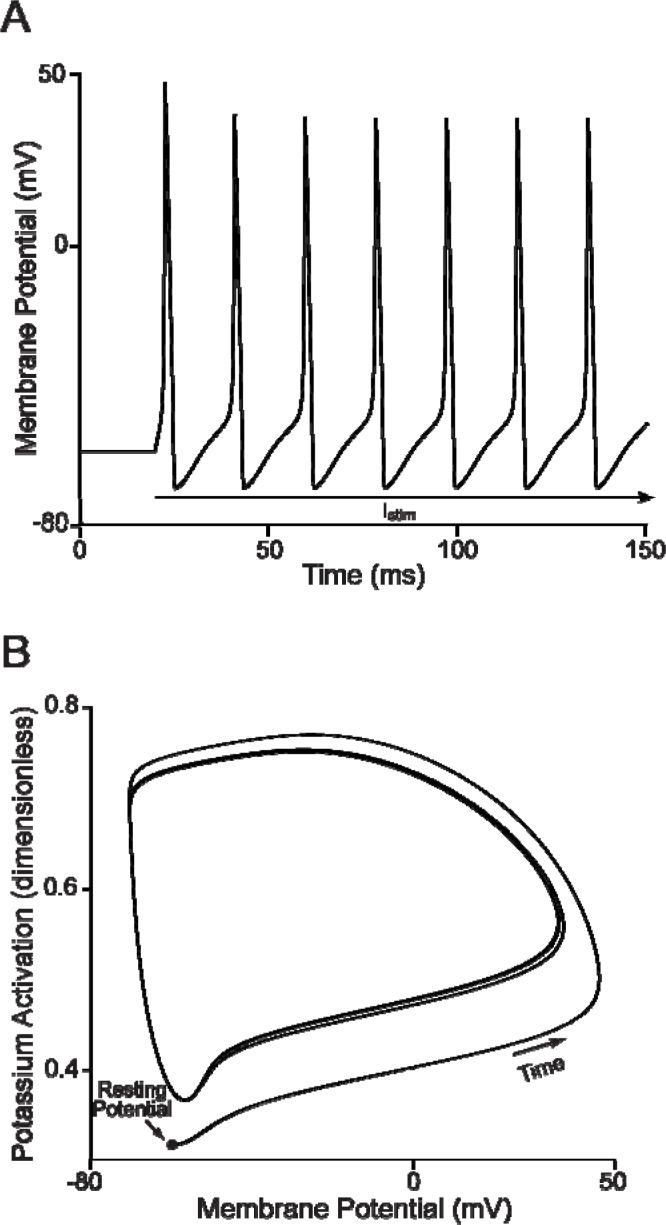
Figure 5.
Induced oscillatory behavior. A: The HH model oscillates if a constant, suprathreshold stimulus is applied. Note that the first spike has a larger amplitude due to the model starting from the resting potential; whereas, subsequent spikes arise from an afterhyperpolarization. B: Limit cycle. The simulation in Panel A is replotted on the Vm-n phase plane. After an initial transient, the trajectory of each action potential superimpose, which indicates the presence of a limit cycle. The constant stimulus destabilizes the fix point and the system exhibits limit cycle dynamics.
Intrinsic Oscillations
The oscillations illustrated in Fig. 5 require the application of an extrinsic stimulus. However, the HH model also can manifest intrinsic oscillations, i.e., oscillations in the absence of extrinsic stimuli. The induction of intrinsic oscillations requires modifying parameters in the model. The HH model contains numerous parameters that can affect the stability of the fixed point. By varying parameters, students can examine the ways in which the different parameters alter the behavior of the model.
The ODE for membrane potential (dVm/dt) of the HH model contains numerous parameters that affect the behavior of the model. Recall that each voltage- and time-dependent ionic current in the HH model is composed of several terms, i.e., a conductance (g̅), activation/inactivation variables (m, n, and h) and a driving force (Vm – Eion; Fig. 2B). The conductance of a current represents the density of channels for that ion. The cell membrane contains many channels that allow the passage of a specific ion, and hence provide for the sodium and potassium currents. Thus, changing the maximal conductance is equivalent to changing the density of channels in the membrane. Different types of neurons have various densities of channels. For example, if the number of potassium channels is reduced, the HH model manifests oscillatory behavior, similar to the oscillations observed in Fig. 5 but without the need of external current stimulation. This oscillatory behavior is due to the reduced strength of the potassium current that normally tends to hyperpolarize the membrane potential. The HH model with g̅K = 16 mS/cm2 (rather than the control value of 36 mS/cm2) exhibits stable oscillations with no extrinsic stimulus; i.e., the system manifests intrinsic oscillations. Students can explore which other parameters can be altered to achieve intrinsic oscillations, such as changing the reversal potential. The SNNAP tutorial provides detailed instructions on how to alter the HH model to exhibit intrinsic oscillations.
Postinhibitory Rebound Excitation
The nonlinearities and complexity of the HH model endow it with a rich repertoire of dynamic responses. For example, extrinsic depolarizing stimuli can elicit either single spikes (Fig. 3) or oscillations (Fig. 5). Paradoxically, extrinsic hyperpolarizing stimuli also can elicit spike activity (Fig. 6A). By injecting a negative (inhibitory) stimulus current, e.g. −25 uA/cm2 for 2 msec (applied to the HH model described in the SNNAP Tutorial manual), the membrane potential becomes more hyperpolarized. When the inhibition is removed, the membrane potential depolarizes beyond the original resting potential. If the recovery of the membrane potential has a sufficient velocity, it passes threshold and produces an action potential. This phenomenon is referred to as postinhibitory rebound excitation (Selverston and Moulins, 1985) or anode break excitation.
Figure 6.
Postinhibitory rebound excitation. A: Response of the HH model to hyperpolarizing current (Istim) injected into the cell. Weak hyperpolarizing current (red curve), strong hyperpolarizing current (black curve). Following these inhibitory inputs, the membrane potential returns toward rest. The recovery of the membrane potential, however, overshoots the original resting membrane and depolarizes the cell. With sufficiently large hyperpolarization, the rebound potential surpasses the threshold and an action potential is elicited. B: The simulations illustrated in Panel A are replotted in the Vm-n phase plane. The hyperpolarizations are represented by hyperpolarizing displacements of the membrane potential and decreases in the value of potassium activation. Following the hyperpolarizing stimulus, the trajectory moves back toward the resting potential, which is represented by a fixed point (filled circle). However, the trajectory that follows the larger hyperpolarization crosses a threshold (also referred to as a separatrix) and an action potential is generated.
By displaying the postinhibitory responses on the Vm-n plane, Fig. 6B, it is clear that the threshold lies between the response curves for the two stimuli. With the stronger inhibitory input, the membrane potential hyperpolarized to a more negative potential, and the trajectory back to rest leads to an action potential. Students can experiment and observe the relationship between duration of stimulus and intensity needed to elicit an action potential.
Additional Simulations with the HH model
The above section illustrated single spike responses to stimuli, oscillations and postinhibitory rebound. The HH model can be used to investigate additional biophysical features of single neurons. The HH model manifests accommodation and students can investigate the ways in which subthreshold depolarizing stimuli can raise the threshold for excitation. Simulations also can examine the absolute and relative refractory periods of the HH model. Voltage-clamp experiments also can be simulated and students can examine the time- and voltage-dependence of membrane currents. Alternatively, students can develop new HH-like models that incorporate a larger ensemble of ionic conductances. For example, SNNAP provides an example of a generic spiking model that can be extended to include currents, such as the transient A-type potassium current and/or a calcium-dependent current (McCormick, 2004). These extended models can be used to examine ways in which more complex neurons respond to input signals.
Bursting Neurons
Neurons exhibit a wide variety of firing patterns (for a review see McCormick, 2004). One pattern that is observed in many neurons is referred to as bursting, alternating periods of high-frequency spiking behavior followed by a period with no spiking activity (quiescent period). Bursting is observed in neurons in various parts of the nervous system. Pacemaker neurons (Smith, 1997), also known as endogenous bursters, are endowed with the intrinsic ability to fire independently of external stimulation. Other neurons have bursting ability that may require a transient input to initiate their burst cycle, known as conditional bursters. Central pattern generators (CPGs; Abbott and Marder, 1998) are neuronal networks that help orchestrate rhythmic activity and CPGs often contain bursting neurons. The rich dynamic behavior of neurons that exhibit bursting has attracted both neuroscientists and mathematicians in an effort to understand the underlying mechanisms that bring about this behavior and its modulation (for reviews see Rinzel and Ermentrout, 1998; Baxter et al., 2004; Canavier et al., 2005).
Neuronal bursting behavior can result from various mechanisms. One common mechanism leading to bursting is the oscillation of a slow-wave calcium current that depolarizes the membrane and causes a series of action potentials as the wave exceeds the spike threshold. When the slow wave ends, the quiescent period begins. In this section, a bursting neuron model is developed; see also the SNNAP Tutorial manual for a description of a SNNAP implementation. The bursting model (Rinzel and Ermentrout, 1998) is based on the Morris-Lecar (ML) model (Morris and Lecar, 1981) (Fig. 7).
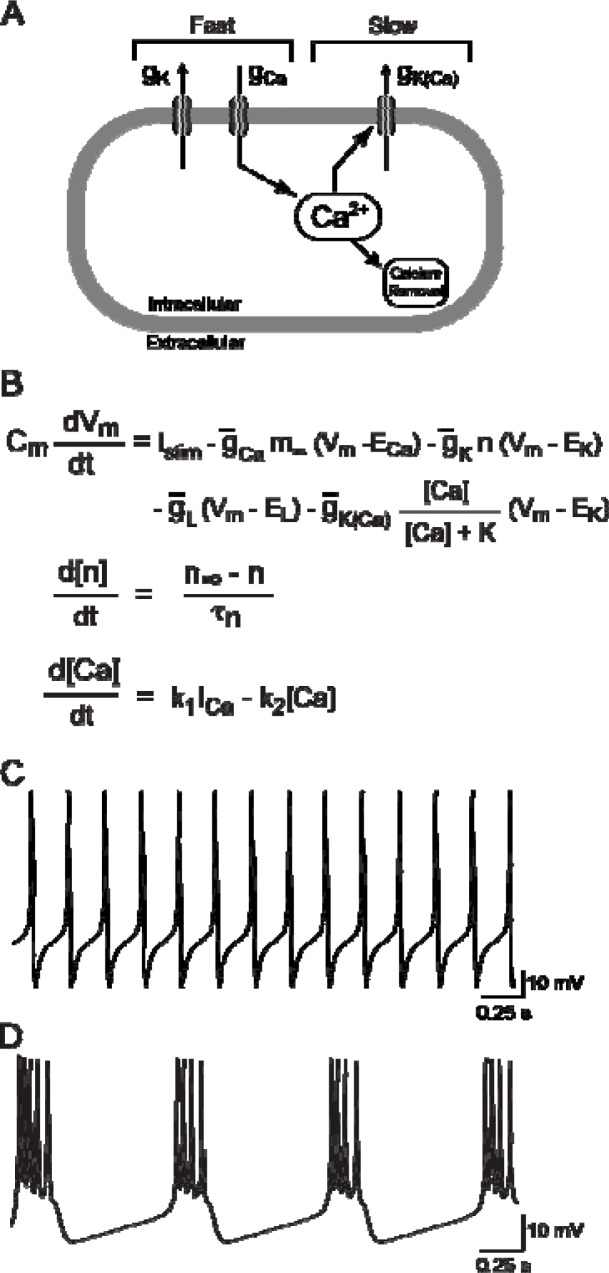
Figure 7.
Morris-Lecar (ML) model. A: Schematic representing elements of the ML model. Similar to the HH model, the ML model has two fast ionic conductances (gCa, gK) that underlie spike activity. However, in the ML model the inward current is calcium rather than sodium. To implement bursting, the ML model was extended to include an intracellular pool of calcium and a second, calcium-dependent potassium conductance (gK(Ca)). The kinetics of the calcium pool are relatively slow and determined the activation kinetics of the calcium-dependent potassium conductance. B: The ordinary differential equations (ODEs) that define the ML model. The ODEs for membrane potential Vm and potassium activation n, are similar to that for the HH model, however, a new term is added to describe the calcium-activated potassium current IK(Ca). The activation of gK(Ca) is determined by a function of calcium concentration ([Ca]/([Ca]+K)), and [Ca] is defined by an ODE in which the calcium current (k1ICa) contributes calcium to the ion pool and buffering (−k2[Ca]) removes calcium from the ion pool. C: If the intracellular pool of calcium and the calcium-activated potassium conductance are not included, the ML model exhibits oscillatory behavior in response to a sustained, suprathreshold stimulus. D: With the intracellular pool of calcium and the calcium-activated potassium conductance in place, the ML model exhibits bursting behavior in response to a sustained suprathreshold stimulus. The burst of spikes are superimposed on a depolarizing wave, which is mediated by calcium current. The interburst period of inactivity is mediated by the calcium-dependent potassium current (see Fig. 8).
The primary advantage of using the ML model is that it contains fewer ODEs, algebraic expressions and parameters than the HH model. Thus, the ML model is a relatively simple biophysical model. The original ML model incorporated three ionic conductances that were similar to the HH model, but in the ML model calcium was the inward current rather than sodium (Fig. 7B). The ML model is simpler than the HH model in two ways. The calcium current has an instantaneous steady-state activation term (m∞) that is dependent only on voltage; i.e., a function of voltage and not a variable dependent on time. In addition, the calcium current does not have an inactivation term. The simplification of the activation term to a voltage-dependent function can be justified when one process is much faster than another. In the ML model, calcium activation is several times faster than potassium activation, and thus, calcium activation is assumed to be instantaneous (see Rinzel and Ermentrout, 1998).
Similar to the HH model, the original ML model exhibits a single action potential in response to a brief stimulus (not shown) and oscillatory behavior in response to a sustained stimulus (Fig. 7C). By incorporating an additional term, a calcium-dependent potassium current, and an ODE, for intracellular calcium concentration, the ML model can exhibit bursting behavior. The new ODE describes the change in intracellular calcium concentration (Fig. 7B). Intracellular calcium ([Ca]) is accumulated through the flow of the calcium current (ICa) and is removed by a first-order process that is dependent on the concentration of intracellular calcium. The additional term describes a new current, a calcium-dependent potassium current (IK(Ca)) (Fig. 7B). This current is different from the currents that were described previously because IK(Ca) is activated as a function of intracellular calcium and not by membrane voltage. When intracellular calcium is high, the activation function approaches one. When intracellular calcium is low, the function approaches zero. The additional potassium current provides a negative feedback mechanism for bursting behavior. By incorporating these two equations, the dynamic property of the model is altered, so that the model may exhibit bursting behavior (Fig. 7D).
In the language of nonlinear dynamics, the bursting behavior exhibited by the ML model is the result of a hysteresis loop (for additional details see Del Negro et al., 1998; Rinzel and Ermentrout, 1998; Baxter et al., 2004; Canavier et al., 2005). Mathematically, the oscillatory behavior is a limit cycle that is more complex than the limit cycle exhibited by the HH model. The hysteresis loop is due to negative feedback, which causes the following behavior. As the intracellular calcium concentration decreases (Fig. 8B), the membrane potential slowly depolarizes until the model begins to exhibit action potentials (Fig. 8A). The concentration of intracellular calcium increases during the period of activity, thereby activating the calcium-dependent potassium current, which in turn halts the neural activity (Fig. 8C). The increase in potassium activation is the negative feedback that causes a decrease in the net inward current, and eventually the calcium slow wave ends and the membrane approaches its resting potential. As intracellular calcium is removed, the calcium-dependent potassium current decreases as well, which allows the membrane potential to depolarize during the quiescent period. During the quiescent period intracellular calcium is removed, until a minimum level is reached and neural activity is resumed. This process repeats itself and is called a hysteresis loop.
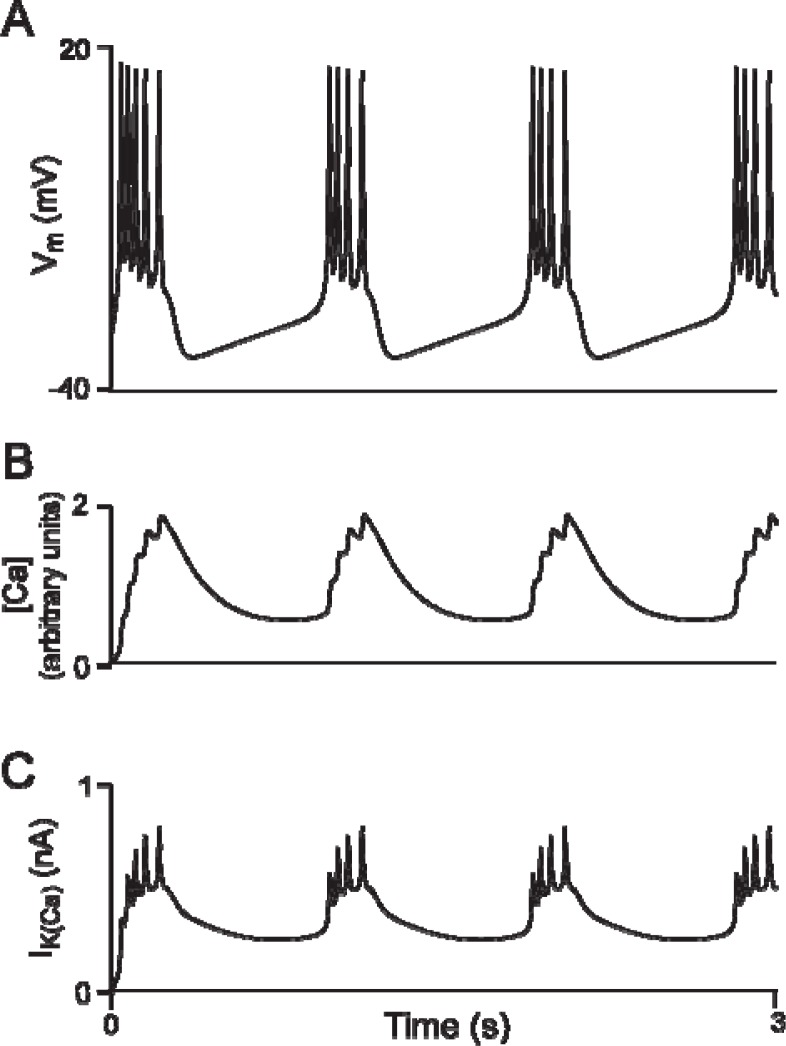
Figure 8.
Mechanisms underlying bursting behavior of the ML model. A: Membrane potential during bursting. B: During the burst of action potentials (Panel A), the intracellular levels of calcium slowly increase. C: As the levels of calcium increase (Panel B), the calcium-dependent potassium conductance increases. Eventually, the calcium-dependent potassium current is sufficiently large to halt spiking and a period of inactivity follows (Panel A). During the quiescent period, the level of calcium falls (Panel B) and the activation of the potassium current decreases (Panel C). This allows the membrane potential to slowly depolarize back toward threshold and another burst of spikes is initiated. Therefore, bursting originates from the interactions between a fast (calcium/potassium) spiking process and a slow (intracellular calcium/calcium-activated potassium) inhibitory process (see Fig. 7A).
The period of an individual bursting cycle is the sum of both active and quiescent durations. Students can manipulate various parameters so as to alter the behavior of bursting neurons. For example, the duration of the burst is dependent on the rate of intracellular calcium accumulation. By reducing the rate of intracellular calcium accumulation (k1 in Fig. 7B) the duration of activity is increased. Simulations can allow students to propose and then test hypotheses regarding what types of changes to which parameters might alter the duration of activity and/or quiescence.
SYNAPTIC TRANSMISSION AND INTEGRATION
The predominate means of communication among nerve cells is via chemical synaptic connections. To model a synaptic connection, the ODE that describes the membrane potential of a cell (see Fig. 2B) is extended to include a new current, a synaptic current (Isyn). Similar to ionic currents, synaptic currents are defined by a maximum conductance (g̅syn), a time-dependent activation function (α) and a driving force (Vm – Esyn) (Fig. 9A). The time-dependent activation can be described by many types of functions, but the most common function is the alpha (α) function (Fig. 9A), which resembles the time course of empirically observed synaptic currents. In addition, some synaptic connections (e.g., NMDA-mediated synaptic current) have a voltage-dependent component. (Although SNNAP can model voltage- and time-dependent synaptic connections, they will not be considered in this paper.)
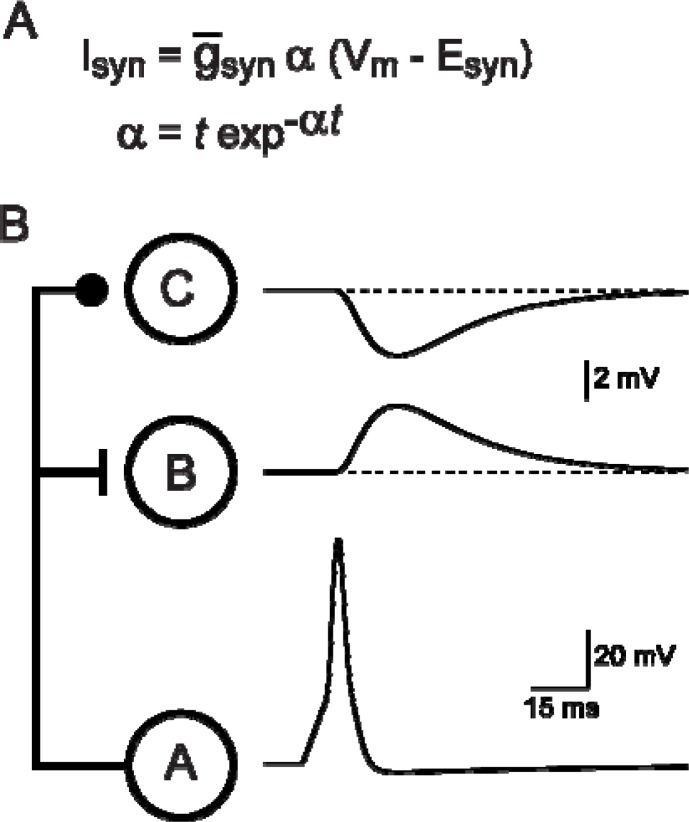
Figure 9.
Excitatory and inhibitory postsynaptic potentials (EPSPs and IPSPs). A: Similar to ionic currents (see Fig. 2B), synaptic currents are defined by a maximum conductance (g̅syn), a time-dependent activation function (α) and a driving force (Vm – Esyn). An expression that is commonly used to define the time-dependent activation function is referred to as an alpha (α) function, which resembles the time course of empirically observed synaptic currents. SNNAP offers several additional functions for defining synaptic activation, including functions that incorporated both time- and voltage-dependency. B: In this simple neural network, a single presynaptic cell (A) makes synaptic connections with two postsynaptic cells (B and C). The connection from A to B is excitatory, whereas the connection from A to C is inhibitory. The only difference between the two synaptic models is the value for Esyn. For excitatory synapses, Esyn is more depolarized than the resting membrane potential; whereas for inhibitory synapses, Esyn is more hyperpolarized than the resting potential.
Postsynaptic potentials (PSPs) are often classified as being either excitatory (EPSP) or inhibitory (IPSP) (Fig. 9B). From a modeling point of view, the only difference between the two types of PSPs is the value assigned to Esyn. If Esyn is more depolarized than the resting potential, the PSP will depolarize the postsynaptic cell and will be excitatory. Conversely, if Esyn is more hyperpolarized than the resting potential, the PSP will hyperpolarize the cell and will be inhibitory. However, remember that hyperpolarizing pulses can elicit spikes in some cells (see Fig. 6) and that subthreshold depolarizations can lead to accommodation in some cells (Hodgkin and Huxley, 1952) and thus inhibit spiking. Students can use simulations to investigate the interactions between EPSPs, IPSPs, and the biophysical properties of the postsynaptic cell.
Temporal Summation
Often, the EPSP elicited by a single presynaptic spike is subthreshold for eliciting a postsynaptic action potential. What is required are several presynaptic spikes in quick succession to elicit a suprathreshold postsynaptic response. This scenario represents an example of synaptic integration known as temporal summation (for review see Byrne, 2004).
Temporal summation occurs when a given presynaptic cell fires several spikes with short inter-spike intervals (Fig. 10). In Fig. 10A, two action potentials are elicited in the presynaptic cell (neuron A). The inter spike interval is 100 ms and each presynaptic spike elicits an EPSP in neuron B. These EPSPs, however, are subthreshold and neuron B fails to spike. In Fig. 10B, the interspike interval is reduced to 50 ms, and the two EPSPs summate. Because of this temporal summation, a postsynaptic action potential is elicited. Whereas a single EPSP may be subthreshold, closely timed EPSPs can summate and elicite a postsynaptic spike. Students can vary the timing between the presynaptic spikes, the duration and amplitude of the EPSP to investigate the ways in which these parameters alter temporal summation. The diversity and complexity of synaptic connections is a key determinant of neural network functionality and students should examine the ways in which various types of synaptic inputs interact with postsynaptic processes.
NEURAL NETWORKS
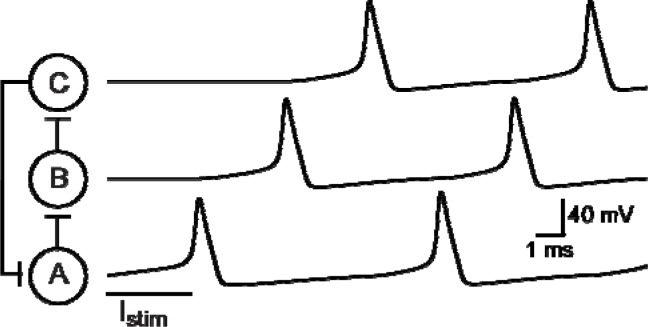
To understand the basic principles of how neural systems function, it is important to investigate the ways in which neurons interact in a network. In this section, a simple neural network composed of three HH neuron models is presented (Fig. 11). The individual neurons exhibit an action potential in response to suprathreshold stimuli and the neurons are interconnected via excitatory chemical synapses. The neurons are connected in a ring architecture and exhibit oscillations once an initial neuron fires an action potential.
Figure 11.
Three cell neural network with recurrent excitation. Three HH models connected in a ring-like architecture. All synaptic connections are excitatory. An initial, brief stimulus to cell A (Istim.) elicits a single action potential, which in turn, produces suprathreshold EPSP in cell B, which in turn, produces a suprathreshold EPSP in cell C. Cell C excites cell A and the cycle repeats itself indefinitely.
Single neurons can exhibit oscillatory behavior (Fig. 5), either as a result of constant stimulation or due to parameter values that destabilize the fixed point. A network can also exhibit oscillatory behavior. The network in Fig. 11 is a three neuron network with excitatory chemical synapses such that cell A excites cell B, cell B excites cell C, and cell C excites cell A. Thus, the network architecture is in the form of a ring. After providing an initial transient stimulus to cell A, the three neurons fire sequentially and the network exhibits stable oscillatory behavior (Fig. 11).
Students can explore the ways in which the firing frequency may be altered by changing the synaptic strength. In addition, students can determine whether the network may oscillate with inhibitory connections between the neurons. With IPSPs, the firing results from postinhibitory rebound (Fig. 6). Applying the same mechanism here, if the synaptic current is changed to a negative current, can oscillations be achieved in the network with inhibitory synaptic connections? The answer is yes, but it requires a large negative current to bring about a postinhibitory rebound action potential. Students can experiment by altering some or all of the synaptic connections and see which current intensity is needed to produce a postinhibitory rebound. Additional investigations can be carried out by incorporating additional neurons into the network. This alters the firing frequency of the network. Students may experiment by varying the network architecture and examining different firing patterns in terms of frequency, propagation speed, and collision events (e.g., initiating two spikes that will cause a collision in the network).
Compartmental Models of Single Cells
There exists a second type of network that scientists use to model neural behavior and that is a compartmental model of a single neuron (for review see Segev and Burke, 1998). Previously, the space-clamped version of the HH model was investigated. Using such a model, the spatial aspects of the neuron are not considered. To describe the physical form of a neuron, the spatial distribution of channels and synapses must be taken into account. One way to model such a neuron is by creating many compartments and connecting them together. Each compartment can be viewed as a HH model, with a resistor between the compartments. Students in advanced courses may wish to examine examples of compartmental models on the SNNAP web site and a recent example of a compartmental model was published by Cataldo et al. (2005). This model used SNNAP to simulate a neuron that spans several body segments of the leech. The input files for this model and for several additional compartmental models are available at the ModelDB web site. Similar models are used to examine the complexities of synaptic integration in mammalian neurons (e.g., Hausser et al., 2000).
DISCUSSION
This paper described several biophysical models and computer simulations that can be used to explore a variety of basic principles in neuroscience. Such models and simulations provide students with tools to investigate biophysical factors and nonlinear dynamics that alter single neuron and neural network behavior. The examples presented in this paper were generated using the neurosimulator SNNAP.
An example of SNNAP used in an undergraduate neurobiology course is at Saint Joseph’s University, Philadelphia. In 2001, Dr. James J. Watrous received a “Teaching Career Enhancement Award” from The American Physiological Society (Silverthorn, 2003). The goals of Dr. Watrous’ project were to develop computer simulations that demonstrate several key principles of neuroscience and to integrate theses simulations into an undergraduate course on neurobiology. Dr. Watrous selected SNNAP for the project. Working with students and members of the SNNAP development team, Dr. Watrous developed simulations that demonstrated excitability, bursting behavior, and neuronal interactions within a network (Hayes et al., 2002; Watrous et al., 2003). In addition to developing simulations, these efforts produced several student research projects (e.g., Pekala and Watrous, 2003; Murray and Watrous, 2004; Pham et al., 2004; Lamb and Watrous, 2005). Currently, students enrolled in the undergraduate neurobiology course are given instruction on the use of SNNAP and provided with the necessary files to construct a network consisting of five neurons. Sufficient excitatory and inhibitory synapse files are also provided so students can individually control the type and properties of each synapse. To encourage active learning, each team is instructed to pose a research question, problem, or situation that they wish to solve or demonstrate; construct a network that would answer the question posed; and develop a presentation showing their hypothesis, the network that was constructed, and their results. Each group presents their findings to the entire class. All of this is accomplished in two, four-hour periods. The published accounts indicate that “student evaluations of this exercise were very positive” (Watrous, 2006). Thus, SNNAP appears to be useful too for teaching undergraduate students basic principles of neuroscience.
There are several applications available for educators that can be used to simulate experiments in neuroscience, e.g., NeuroSim and Neurons in Action. SNNAP differs from these commercial packages in that it is free for download from the Web. SNNAP, based on Java, runs on virtually any platform (different from NeuroSim which runs only on Windows machines). In terms of capabilities, NeuroSim can simulate the Goldman-Hodgkin-Katz constant field equation, which SNNAP in its current version does not (but can be modified relatively easily to incorporate this equation). NeuroSim, though, has a limit of five channel types per simulation, which may become a serious limitation. Neurons in Action is very well suited for single neuron simulations, but lacks examples of networks. SNNAP lacks equations for multiple-state kinetic models of single ion channels but focuses on equations for synaptic modulation as well as compartmental modeling of single and/or networks of neurons.
More complete descriptions of the capabilities of SNNAP can be found on the web site, in the tutorial manual (Av-Ron et al., 2004), and in several publications (Ziv et al., 1994; Hayes et al., 2003; Baxter and Byrne, 2006). A brief list of some of the capabilities of the current version of SNNAP (Ver. 8) is provided below:
-
SNNAP simulates levels for biological organization that range from second messengers within a cell to compartmental models of a single cell to large-scale networks. Within a neural network, the number of neurons and of synaptic connections (electrical, chemical, and modulatory) is limited only by the memory available in the user’s computer.
SNNAP can simulate networks that contain both Hodgkin-Huxley type neurons and integrate-and-fire type cells. Moreover, the synaptic contacts among integrate-and-fire cells can incorporate learning rules that modify the synaptic weights. The user is provided with a selection of several nonassociative and associative learning rules that govern plasticity in the synapses of integrate-and-fire type cells.
SNNAP simulates intracellular pools of ions and/or second messengers that can modulate neuronal processes such as membrane conductances and transmitter release. Moreover, the descriptions of the ion pools and second-messenger pools can include serial interactions as well as converging and diverging interactions.
Chemical synaptic connections can include a description of a pool of transmitter that is regulated by depletion and/or mobilization and that can be modulated by intracellular concentrations of ions and second messengers. Thus, the user can simulate homo- and heterosynaptic plasticity.
SNNAP simulates a number of experimental manipulations, such as injecting current into neurons, voltage clamping neurons, and applying modulators to neurons. In addition, SNNAP can simulate noise applied to any conductance (i.e., membrane, synaptic, or coupling conductances).
SNNAP includes a Batch Mode of operation, which allows the user to assign any series of values to any given parameter or combination of parameters. The Batch Mode automatically reruns the simulation with each new value and displays, prints, and/or saves the results.
SNNAP includes a suite of over 100 example simulations that illustrate the capabilities of SNNAP and that can be used as a tutorial for learning how to use SNNAP or as an aid for teaching neuroscience.
SNNAP is freely available and can be downloaded via the internet. The software, example files, and tutorial manual (Av-Ron et al., 2004) are available at http://snnap.uth.tmc.edu.
Acknowledgments
This work was supported by NIH grants R01-RR11626 and P01-NS38310.
REFERENCES
- Abbott L, Marder E. Modeling small networks. In: Koch C, Segev I, editors. Methods in neuronal modeling: from ions to networks. 2nd edition. Cambridge, MA: The MIT Press; 1998. pp. 363–410. [Google Scholar]
- Abraham RH, Shaw CD. Dynamics: the geometry of behavior. 2nd edition. Redwood City, CA: Addison-Wesley; 1992. [Google Scholar]
- Av-Ron E, Parnas H, Segel LA. A minimal biophysical model for an excitable and oscillatory neuron. Biol Cybern. 1991;65:487–500. doi: 10.1007/BF00204662. [DOI] [PubMed] [Google Scholar]
- Av-Ron E, Vidal PP. Intrinsic membrane properties and dynamics of medial vestibular neurons: a simulation. Biol Cybern. 1999;80:383–392. doi: 10.1007/s004220050533. [DOI] [PubMed] [Google Scholar]
- Av-Ron E, Cai Y, Byrne JH, Baxter DA. Soc. Neurosci. Abstr. Washington, DC: Society for Neuroscience; 2004. An interactive and educational tutorial for version 8 of SNNAP (Simulator for Neural Networks and Action Potentials) Program No. 27.13, 2004 Abstract Viewer/Itinerary Planner. Online: sfn.scholarone.com/itin2004/ [Google Scholar]
- Baxter DA, Byrne JH. Simulator for neural networks and action potentials (SNNAP): description and application. In: Crasto C, editor. Methods in molecular biology: neuroinformatics. Totowa NJ: Humana Press; 2006. in press. [Google Scholar]
- Baxter DA, Canavier CC, Byrne JH. Dynamical properties of excitable membranes. In: Byrne JH, Roberts J, editors. From molecules to networks: an introduction to cellular and molecular neuroscience. San Diego, CA: Academic Press; 2004. pp. 161–196. [Google Scholar]
- Butera RJ, Clark JR, Canavier CC, Baxter DA, Byrne JH. Analysis of the effects of modulatory agents on a modeled bursting neuron: dynamic interactions between voltage and calcium dependent systems. J Comput Neurosci. 1995;2:19–44. doi: 10.1007/BF00962706. [DOI] [PubMed] [Google Scholar]
- Byrne JH. Postsynaptic potentials and synaptic integration. In: Byrne JH, Roberts J, editors. From molecules to networks: an introduction to cellular and molecular neuroscience. San Diego, CA: Academic Press; 2004. pp. 459–478. [Google Scholar]
- Cataldo E, Brunelli M, Byrne JH, Av-Ron E, Cai Y, Baxter DA. Computational model of touch mechanoafferent (T cell) of the leech: role of afterhyperpolarization (AHP) in activity-dependent conduction failure. J Comput Neurosci. 2005;18:5–24. doi: 10.1007/s10827-005-5477-3. [DOI] [PubMed] [Google Scholar]
- Canavier CC, Baxter DA, Byrne JH. Repetitive action potential firing. In: NP Group, editor. Encyclopedia of life sciences. 2005. www.els.net. [Google Scholar]
- Carnevale NT, Hines ML. The neuron book. New York, NY: Cambridge University Press; 2006. [Google Scholar]
- Del Negro CA, Hsiao CF, Chandler SH, Garfinkel A. Evidence for a novel bursting mechanism in rodent trigeminal neurons. Biophys J. 1998;75:174–182. doi: 10.1016/S0006-3495(98)77504-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FitzHugh R. Mathematical models of excitation and propagation in nerve. In: Schwan HP, editor. Biological engineering. New York, NY: McGraw-Hill; 1969. pp. 1–85. [Google Scholar]
- Friesen WO, Friesen JA. NeuroDynamix: computer models for neurophysiology. New York, NY: Oxford University Press; 1995. [Google Scholar]
- Getting PA. Emerging principles governing the operation of neural networks. Annu Rev Neurosci. 1989;12:185–204. doi: 10.1146/annurev.ne.12.030189.001153. [DOI] [PubMed] [Google Scholar]
- Haefner LA, Zembal-Saul C. Learning by doing? Prospective elementary teachers’ developing understandings of scientific inquiry and science teaching and learning. Internatl J Sci Edu. 2004;26:1653–1674. [Google Scholar]
- Hausser M, Spruston N, Stuart GJ. Diversity and dynamics of dendritic signaling. Science. 2000;290:739–744. doi: 10.1126/science.290.5492.739. [DOI] [PubMed] [Google Scholar]
- Hayes RD, Watrous JJ, Xiao J, Chen H, Byrne M, Byrne JH, Baxter DA. New features of SNNAP 7.1 (Simulator for Neural Networks and Action Potentials) for education and research in neurobiology. Washington DC: Society for Neuroscience; 2002. Program No. 22.25, 2002. Abstract Viewer/Itinerary Planner. Online: www.sfn.scholarone.com/itin2002/ [Google Scholar]
- Hayes RD, Byrne JH, Baxter DA. Neurosimulation: Tools and resources. In: Arbib MA, editor. The handbook of brain theory and neural networks. 2nd edition. Cambridge, MA: MIT Press; 2003. pp. 776–780. [Google Scholar]
- Hodgkin AL. The ionic basis of nervous conduction. Science. 1964;145:1148–1154. doi: 10.1126/science.145.3637.1148. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL. Chance and design in electrophysiology: an informal account of certain experiments on nerve carried out between 1934 and 1952. J Physiol (Lond) 1976;263:1–21. doi: 10.1113/jphysiol.1976.sp011620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL. The pursuit of nature: informal essays on the history of physiology. Cambridge, MA: Cambridge University Press; 1977. [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley AF. Excitation and conduction in nerve: quantitative analysis. Science. 1964;145:1154–1159. doi: 10.1126/science.145.3637.1154. [DOI] [PubMed] [Google Scholar]
- Huxley AF. Reminiscences: working with Alan, 1939–1952. J Physiol (Lond) 2000;527P:13S. [Google Scholar]
- Huxley AF. Hodgkin and the action potential. J Physiol (Lond) 2002;538:2. doi: 10.1113/jphysiol.2001.014118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb K, Watrous JJ. Mimicking the electrical activity of the heart using SNNAP (simulator for neural networks and action potentials). Unpublished presentation at the 16th Annual Saint Joseph’s University Sigma Xi Research Symposium; Philadelphia, PA. 2005. [Google Scholar]
- Lorenz S, Horstmann W, Oesker M, Gorczytza H, Dieckmann A, Egelhaaf M. The MONIST project: a system for learning and teaching with educational simulations. In: Cantoni L, McLoughlin C, editors. Proceedings of ED-MEDIA 2004 - World Conference on Educational Media, Hypermedia and Telecommunications. AACE; 2004. [Google Scholar]
- Lytton WW. From computer to brain – Foundations of computational neuroscience. New York, NY: Springer Verlag; 2002. [Google Scholar]
- McCormick DA. Membrane potential and action potential. In: Byrne JH, Roberts J, editors. From molecules to networks: an introduction to cellular and molecular neuroscience. San Diego, CA: Academic Press; 2004. pp. 459–478. [Google Scholar]
- Meuth P, Meuth SG, Jacobi D, Broicher T, Pape HC, Budde T. Get the rhythm: modeling neuronal activity. J Undergrad Neurosci Edu. 2005;4:A1–A11. [PMC free article] [PubMed] [Google Scholar]
- Moore JW, Stuart AE. Neurons in Action: computer simulations with NeuroLab, version 15. Sunderland, MA: Sinauer; 2004. [Google Scholar]
- Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray CE, Watrous JJ. Simulating the behavior of a networked R15 neuron using SNNAP. FASEB. 2004;18:A343. [Google Scholar]
- National Research Council . Inquiry and the National Science Education Standards. Washington DC: National Academy Press; 2000. [Google Scholar]
- Odell GM. Qualitative theory of systems of ordinary differential equations, including phase plane analysis and the use of the Hopf bifurcation theorem. In: Segel LA, editor. Mathematical models in molecular and cellular biology. Cambridge, England: Cambridge University Press; 1980. pp. 640–727. [Google Scholar]
- Pekala A, Watrous JJ. Using SNNAP to simulate barnacle muscles voltage oscillations. Unpublished presentation at the 14th Annual Saint Joseph’s University Sigma Xi Research Symposium; Philadelphia, PA. 2003. [Google Scholar]
- Pham P, Walsh A, Watrous JJ. Geometric model of voltage oscillation in barnacle muscle fiber using SNNAP. Unpublished presentation at the 15th Annual Saint Joseph’s University Sigma Xi Research Symposium; Philadelphia, PA. 2004. [Google Scholar]
- Rinzel J, Ermentrout GB. Analysis of neural excitability and oscillations. In: Koch C, Segev I, editors. Methods in neuronal modeling: from ions to networks. 2nd edition. Cambridge, MA: The MIT Press; 1998. pp. 251–292. [Google Scholar]
- Segev I, Burke RE. Compartmental models of complex neurons. In: Koch C, Segev I, editors. Methods in neuronal modeling: from ions to networks. 2nd edition. Cambridge, MA: The MIT Press; 1998. pp. 93–136. [Google Scholar]
- Selverston AI, Moulins M. Oscillatory neural networks. Annu Rev Physiol. 1985;47:29–48. doi: 10.1146/annurev.ph.47.030185.000333. [DOI] [PubMed] [Google Scholar]
- Shepherd GM. Electrotonic properties of axons and dendrites. In: Byrne JH, Roberts J, editors. From molecules to networks: an introduction to cellular and molecular neuroscience. New York, NY: Academic Press; 2004. pp. 91–113. [Google Scholar]
- Siegelbaum S, Bookman RJ. Essentials of neural science and behavior: NeuroSim a computerized interactive study tool. East Norwalk, CT: Appleton and Lange; 1995. [Google Scholar]
- Silverthorn DE. Teaching career enhancement awards: 2003 update. Adv Physiol Educ. 2003;28:1. doi: 10.1152/advan.00099.2002. [DOI] [PubMed] [Google Scholar]
- Smith JC. Integration of cellular and network mechanisms in mammalian oscillatory motor circuits: Insights from the respiratory oscillator. In: Stein PSG, Grillner S, Selverston AI, Stuart DG, editors. Neurons, networks, and motor behavior. Cambridge, MA: The MIT Press; 1997. pp. 97–104. [Google Scholar]
- Tamir P, Stavy R, Ratner N. Teaching science by inquiry: assessment and learning. J Biol Educ. 1998;33:27–32. [Google Scholar]
- Watrous JJ, Hayes RD, Baxter DA. Using SNNAP 7.1 (Simulator of Neural Networks and Action Potentials) in an undergraduate neurobiology course. FASEB. 2003;17:A391. [Google Scholar]
- Watrous JJ. FASEB; 2006. Group learning neural network education using SNNAP. in press. [Google Scholar]
- van Zee EH, Hammer D, Bell M, Roy P, Peter J. Learning and teaching science as inquiry: a case study of elementary school teachers’ investigation of light. Sci Educ. 2005;89:1007–1042. [Google Scholar]
- Zion M, Shapira D, Slezak M, Link E, Bashan N, Brumer M, Orian T, Nussinovitch R, Agrest B, Mendelovici R. Biomind – a new biology curriculum that enables authentic inquire learning. J Biol Educ. 2004;38:59–67. [Google Scholar]
- Ziv I, Baxter DA, Byrne JH. Simulator for neural networks and action potentials: description and application. J Neurophysiol. 1994;71:294–308. doi: 10.1152/jn.1994.71.1.294. [DOI] [PubMed] [Google Scholar]