Exploring Sensory Neuroscience Through Experience and Experiment

Abstract

Many phenomena that we take for granted are illusions — color and motion on a TV or computer monitor, for example, or the impression of space in a stereo music recording. Even the stable image that we perceive when looking directly at the real world is illusory. One of the important lessons from sensory neuroscience is that our perception of the world is constructed rather than received. Sensory illusions effectively capture student interest, but how do you then move on to substantive discussion of neuroscience? This article illustrates several illusions, attempts to connect them to neuroscience, and shows how students can explore and experiment with them. Even when (as is often the case) there is no agreed-upon mechanistic explanation for an illusion, students can form hypotheses and test them by manipulating stimuli and measuring their effects. In effect, students can experiment with illusions using themselves as subjects.

In addition to their immediate aesthetic appeal, illusions have historically been used to investigate mechanisms of perception. While the success of this approach has been mixed — many illusions do not have accepted explanations or turn out to be more complex than initially thought — illusions are still powerful teaching tools. Not only do they engage student interest, they provide an accessible study subject. Students can alter illusions to determine their salient features, can often measure their strength, can form and test their own hypotheses, and analyze data collected by an entire class. Such activities can be done as in-class demonstrations or as student projects. For the rest of this article, I present several illusions and suggest ways in which they might be used in a class.

Examples shown here and used in the FUN workshop at Pomona came from the PsyCog CD (Wyttenbach 2006; http://www.sinauer.com/detail.php?id=9504). However, free versions of these illusions can be found online or created by an instructor with basic graphic skills. Many can even be created using only the drawing tools and animation options found in PowerPoint™.

NEGATIVE AFTERIMAGE

Nearly everyone has seen negative afterimage illusions, and most textbooks discuss them in the context of trichromatic vision and opponent cells. This illusion is a good place to start because it introduces adaptation and opponent processes, which have bearing beyond color vision, and is tied to a simple model from which students can make straightforward predictions. Figure 1 shows an adapting stimulus, after which a white screen is presented. Students set the color and duration of adaptation and can time the duration of the afterimage.

Figure 1.

Adapting Stimulus. Students set the color and duration of adaptation and can measure duration of the afterimage.

Questions: (1) What color of afterimage do you get with each of the adaptation colors? (2) What color do you expect to see when viewing cyan after adapting to blue? (3) Do you predict an afterimage from adaptation to a black image? (4) Does closing your eyes after adaptation make the afterimage last longer? (5) What do you see if, after adaptation, you move your head closer to or further from the white screen or look at the sky? (6) If you adapt one eye with the other eye closed and then switch eyes, is there an afterimage?

Interpretations: (1) Students should be able to predict the afterimage of any color by using the opponent model. (2) The opponent model also predicts biasing perception of another color; after adaptation to blue, any color should appear less blue (cyan becoming greenish, or magenta becoming redder). (3) The opponent model applies to black and white as well as to colors; it is also interesting to see a whiter-than-white afterimage on even the brightest background, which seems dingy in contrast. This also makes the point (reinforced by the contrast illusions) that perception of brightness depends on relative rather than absolute values. (4) Eye closing extends the afterimage duration, while blinking may restore a faded afterimage; I have not yet found a good explanation of this. (5) When the head moves closer to the screen, the afterimage appears to shrink, while it appears larger when the head is further from the screen or one looks at the sky. The adapted part of the visual field remains the same size (visual angle), but we interpret that size differently depending on distance cues; a given visual angle indicates a larger size when its source is distant than when it is near. (6) In my experience, the negative afterimage does not transfer from one eye to the other. While color is handled at many levels in the visual system, the first color-opponent cells are found in the lateral geniculate nucleus (LGN), before significant binocular processing.

In addition to these questions, students could do experiments testing the duration of the afterimage under different conditions such as very short or long adaptation periods, different levels of color saturation and so on.

MOTION AFTEREFFECT

The motion aftereffect, also known as the waterfall illusion, was first described by Aristotle. After one watches motion in one direction, stationary objects appear to move in the opposite direction. Like negative afterimages, this effect is due to an opponent process system. It poses a rich set of questions but is also just plain fun for students. (Project inward-moving concentric circles and then listen for reactions when students look at their hands.) Figure 2 shows an adapting stimulus, after which a mottled or blank screen is presented. Students set the duration, direction, speed, color, contrast, and size of the moving stimulus, and can time the duration of the aftereffect.

Figure 2.

Motion Aftereffect Stimuli. Left: Inward-moving concentric circles. Students set the direction, speed, colors, contrast, duration, and size of the moving stimulus. Right: After adaptation, a mottled or blank screen is shown. Students can measure the duration of the aftereffect.

Questions: (1) How can you demonstrate the existence of detectors tuned to different directions of motion in the same part of the visual field? (2) Adapt to downward motion and then view horizontal motion. What do you predict? (3) Adapt to downward motion and then switch to upward motion; what do you predict? (4) How can you test whether motion detectors are present throughout the entire visual field? (5) How could you determine whether motion detection is primarily peripheral (retina to LGN) or central (V1 and up)? (6) What do you see if you adapt to motion and then view a blank surface? (7) How do the color and contrast of the adapting stimulus affect the aftereffect? (8) How do the speed of movement and size of the stripes affect the strength of aftereffect?

Interpretations: (1) The same part of the visual field can respond to, and have aftereffects from, motion in any direction. In principle, we could detect any direction from the vector sum of four detectors (right, left, up, down). (2) With downward motion detectors adapted, horizontally moving stripes appear to move diagonally upward. This supports the idea that direction is determined as a vector sum. (3) After adapting to downward motion, upward motion appears faster. This suggests that perceived motion is due to the ratio of responses of opposing detectors rather than to the absolute value of any one detector’s response. (4) The aftereffect is strongest at the periphery, with little motion in the center. This suggests that motion detectors are unevenly distributed. Peripheral vision may be specialized to direct attention to moving objects while central vision is specialized for detailed form. (5) Adapt one eye with the other closed, then check for the aftereffect with the adapted eye closed and the rested eye open. The aftereffect transfers across eyes (albeit more weakly), suggesting that it is due to neurons with binaural input (primary visual cortex or later). Human fMRI studies implicate motion-sensitive areas of visual cortex (area MT) in the aftereffect (Huk et al., 2001). However, this does not rule out a peripheral role. A simple experiment suggests that adaptation also occurs at earlier stages. Simultaneously present upward movement to the left eye and downward movement to the right eye; each eye will have an independent negative aftereffect. (This can be done easily in PsyCog; use a piece of cardboard or pair of tubes to prevent each eye from seeing the display intended for the other.) (6) The motion aftereffect can be seen even on a blank surface. This is interesting because one sees motion without any objects to move. It may reflect the processing of motion and form by different pathways in visual cortex. (7) Color has no effect on the strength of the aftereffect, suggesting that motion detection relies on edges defined by luminance. Contrast also has little effect, and even the lowest-contrast moving stripes can give a robust aftereffect. I have not found a good explanation for this; perhaps motion detectors only require that contrast exceed some low threshold. (8) Strength of the aftereffect is affected not by stripe width and speed per se, but by the number of edge crossings. Thus wide stripes require faster movement or longer movement duration to achieve the same aftereffect as narrow stripes.

As with the negative afterimage, students can measure the duration of aftereffect under various conditions, such as short or long adaptation periods and varying sizes, speeds, contrasts, or colors of adapting stimuli.

ILLUSORY MOTION

In the last two decades, several new motion illusions have been invented. Some of them translate one type of motion into another (e.g., expansion into rotation), while others appear to move when completely stationary. Figure 3 is one of the latter, designed by Akiyoshi Kitaoka. These illusions are not as easily explained as the aftereffect, but students can still benefit from studying them.

Figure 3.

Peripheral Drift. Students can set the colors of the image pieces to determine which stimulus features are essential.

Questions: (1) Is motion equally strong across the visual field? (2) Can you start and stop the motion by looking at the image in different ways? (3) Are all four colors needed? Can you change the strength or direction of motion by altering the color scheme? (4) Can adaptation to illusory motion cause a motion aftereffect?

Interpretations: (1) Most people see little or no motion at the point of fixation, with movement being most apparent in the peripheral visual field. (2) If one makes an effort to stare fixedly at one point without eye movements, motion is reduced or stopped. (3) Only three colors are needed (motion survives replacement of red with black in Figure 3). Motion is usually in the direction of the darker of the two ovals that surround a dark hourglass shape, but exceptions can be found, including some that appear to move weakly and in an ambiguous direction (make all shapes black but one white hourglass). Reducing contrast between light and dark areas reduces the strength of the illusion. (4) After adapting to one large disc, one may get a weak aftereffect.

Although these exercises seem to reveal little about the mechanisms behind this illusion, they reflect the ways in which scientists approach the subject. Observations about weakness in the central visual field, the effect of contrast, and eye movements led to the current explanations of this illusion (Conway et al., 2005; Murakami et al., 2006).

CONTRAST

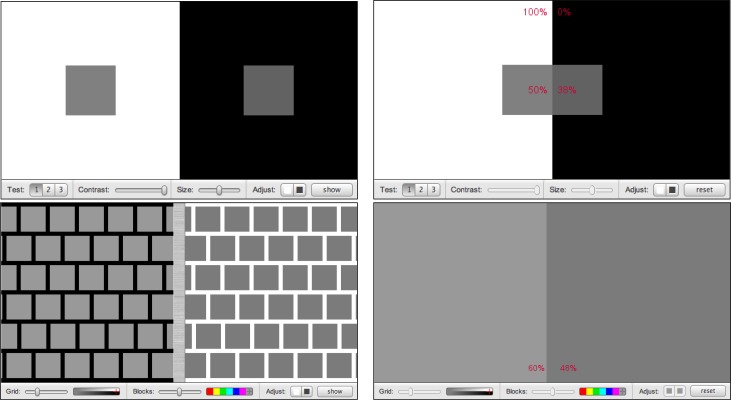
There are many illusions of contrast, both in luminance and color. Despite straightforward explanations invoking lateral inhibition or other local mechanisms, full understanding of these illusions remains elusive. Figure 4 shows two cases in which gray blocks of equal density appear darker or lighter because of their surroundings and one case in which identically colored crosses appear quite different. In PsyCog and many online demonstrations, one can drag blocks together to see that they are in fact equal.

Figure 4.

Contrast Illusions. Top: All small gray squares are the same density. Center: All gray rectangles are the same density. Bottom: Both crosses are the same color.

Questions: (1) Can you predict the outcome of a variety of contrast illusions? How are they usually explained? (2) How do assimilation illusions (e.g., the Munker-White illusion, Figure 4 center) challenge those explanations? (3) How would you measure the strength of a contrast illusion or test whether everyone is “fooled” by the same amount? (4) Can contrast illusions occur in negative afterimages? What would this tell us?

Interpretations: (1) It is not always easy to predict how a patch of color will appear based on its surroundings, since surroundings sometimes enhance contrast (top and bottom panels of Figure 4) and sometimes reduce it (center panel). (2) Explanations invoking contrast or edge enhancement make the wrong predictions in assimilation illusions. In the Munker-White illusion (Figure 4 center panel), gray areas on the right border more white than black and thus “should” darken, while the reverse applies to gray areas on the left. However, our perception is the opposite. That does not mean that the usual explanations are wrong, only that they cannot be applied to all aspects of a scene. They may still apply to other aspects (for example, Mach bands appear in the Munker-White illusion). (3) To measure a contrast illusion, adjust two areas until they are subjectively equal and then measure their difference. Figure 5 illustrates this for a contrast enhancement illusion and an assimilation illusion. As a class project, student could measure their own contrast adjustments and do a statistical analysis of the pooled data. (4) Look at Figure 1 again; its negative afterimage is magenta, but the center of the afterimage is green. Since the original stimulus had no obvious magenta tint in the center, greenness in the afterimage is not itself an afterimage, but contrast enhancement occurring within the afterimage. Thus contrast enhancement is taking place after color-opponent cells, in V1 or later.

Figure 5.

Measuring Contrast Illusions. Top: The basic contrast enhancement illusion with gray squares adjusted to subjective equality by the author and then brought together to show the amount of adjustment. One could then vary parameters such as the contrast between the dark and light surrounding areas and the size of the squares to determine how those affect illusion strength. Bottom: The Bezold effect, an assimilation illusion, with gray squares adjusted to subjective equality by the author. Interestingly, I can never make the gray squares look truly equal. They always seem a bit off and cannot be fixed by lightening or darkening.

These are just a few of the contrast illusions. I have omitted some very striking ones such as the scintillating grid (Schrauf et al., 1995) because of their complexity. They still have use in teaching, both to excite interest and as fodder for mechanistic speculation. For further discussion of contrast illusions, particularly those resistant to easy explanation, see Purves and Lotto (2003).

SIZE AND ORIENTATION

Explanations of size and orientation illusions are still very much in dispute, but they have the advantage of being easy to measure. Nearly everyone has seen the Müller-Lyer illusion (Figure 6), so I use it as an example. The questions it raises apply equally to the Ponzo, Poggendorf, Vertical-Horizontal, Bisection, Lipps, Ebbinghaus-Delboef, Zollner, and Hering illusions and many others.

Figure 6.

Measuring a Size Illusion. Top: The basic Müller-Lyer illusion with red lines adjusted to subjective equality by the author and measured to show the amount of adjustment. Bottom: A variant of the illusion, again with lines adjusted to subjective equality by the author and then measured.

Questions: (1) How would you measure the strength of a size illusion or test whether everyone is off by the same amount? (2) What experimental controls would you need to show that people misperceive size? (3) How could you test the hypothesis that misjudgment of length results from use of perspective cues? (4) Can you train yourself to make accurate size judgments in the Müller-Lyer illusion? If so, do the two lines actually look equal, or are you just compensating to make them equal?

Interpretations: (1) Rather than showing two equal lines that appear unequal, have the observer make the lines subjectively equal. The amount by which they differ is a measure of the illusion’s strength. This turns out to be fairly consistent. Data from a large class (along with controls) could be used for practice in statistical analysis. (2) At a minimum, we should check that people are able to adjust simple lines to equality (we do so easily). (3) If the Müller-Lyer illusion is due to perspective cues, then it should occur when the ends are arrowheads but not when they are circles, brackets, or other shapes that make no sense in the context of depth. As Figure 6 shows, this is not the case. (4) Most people can set the lines equal with practice but still see them as unequal.

Several competing theories attempt to explain illusions of size and orientation. Gregory (1998) and Gillam (1998) argue that the slants and angles in illusions are interpreted as perspective cues. Rock (1995) proposes that the size and orientation of an object are perceived in contrast with those of its local background. Prinzmetal and Beck (2001) attribute several illusions to mechanisms that correct for head tilt. Purves and Lotto (2003) propose that perception is determined by the “statistical relationship between the retinal image and all its possible sources”. None of these theories are mechanistic or based on neural data.

It is interesting that, after years of study, there are still no generally accepted explanations for these ubiquitous illusions. Although disappointing at some level, this makes such illusions ripe for student projects that test competing hypotheses.

RESOURCES

There are so many good (and bad) web sites with visual illusions that it is difficult to keep track of them. These four sites offer explanations along with good graphics:

• http://sites.sinauer.com/wolfe3e/home/startF.htm

  Wolfe et al.’s Sensation and Perception companion site has demonstrations and explanations keyed to the text but available to all.

• http://www.michaelbach.de/ot/index.html

  Michael Bach’s site lets one manipulate many illusions; also includes explanations and references.

• http://www.ritsumei.ac.jp/~akitaoka/index-e.html

  Akiyoshi Kitaoka’s site has many illusions, including his novel illusory motion ones, with links to his research papers on illusions.

• http://illusioncontest.neuralcorrelate.com/

  The Vision Sciences Society has an annual contest for new illusions; the site links to published explanations.

CONCLUSIONS

As even these simple examples show, illusions are often complex and contradictory, with results that are hard to explain with basic textbook-level knowledge. While this can be frustrating at times, it is also exciting. It shows students that science is not simply a recitation of facts, but a process of testing hypotheses about the unknown. Better still, this process is open to students through their own perception of stimuli that they can design and manipulate.

Illusions can be used in introductory classes to stimulate interest and illustrate basic concepts (at the risk of over-simplification). Beyond that, in-class demonstrations can identify critical aspects of stimuli, show the importance of controls, and possibly analyze class-generated data.

More advanced classes might focus on mechanisms and the complexity of an apparently simple illusion. Most illusions combine several effects at once, and a class could work on identifying all features or simplifying an illusion to isolate one mechanism. Students could modify existing illusions or design their own to test specific hypotheses. Term papers and projects could gather data and delve into the extensive literature on illusions.

For instructors, going beyond the usual demonstration and simple explanation poses challenges. How much can we get out of an illusion? How can we present it in an engaging and scientifically valid way? Meeting these challenges should make teaching more fun for instructors as well as their students.