Communication: Origin of the contributions to DNA structure in phages

Abstract

Cryo electron microscopy (cryo-EM) data of the interior of phages show ordering of the interior DNA that has been interpreted as a nearly perfectly ordered polymer. We show surface-induced correlations, excluded volume, and electrostatic forces are sufficient to predict most of the major features of the current structural data for DNA packaged within viral capsids without additional ordering due to elastic bending forces for the polymer. Current models assume highly-ordered, even spooled, hexagonally packed conformations based on interpretation of cryo-EM density maps. We show herein that the surface induced packing of short (6mer), unconnected DNA polymer segments is the only necessary ingredient in creating ringed densities consistent with experimental density maps. This implies the ensemble of possible conformations of polymeric DNA within the capsid that are consistent with cryo-EM data may be much larger than implied by traditional interpretations where such rings can only result from highly-ordered spool-like conformations. This opens the possibility of a more disordered, entropically-driven view of phage packaging thermodynamics. We also show the electrostatics of the DNA contributes a large portion of the internal hydrostatic and osmotic pressures of a phage virion, suggesting that nonlinear elastic anomalies might reduce the overall elastic bending enthalpy of more disordered conformations to have allowable free energies.

The physical confinement of double-stranded DNA within viral capsids is a long studied problem, both theoretically and experimentally.^{1, 2, 3, 4, 5, 6, 7} A proper description of nucleic acids under confinement and/or elastic strain has implications for describing nucleosomal packing, transcription, and other important in vivo processes.^{8, 9} An advantage of phage systems is that they are experimentally well-studied structurally via cryo electron microscopy (cryo-EM),^{10, 11, 12, 13, 14, 15} as well as thermodynamically via single-molecule motor loading force measurements^{16, 17, 18} and osmotic pressure ejection-inhibition experiments.^{19, 20, 21} Asymmetric structural density maps of phages (e.g., P22, epsilon15) have been reconstructed from cryo-electron microscopy.^{10, 12, 13} Also, use of phages has shown potential for safe, low-cost methods of gene transfer, and vaccine delivery vectors.²² A precise, sequence-dependent ability to thermodynamically control packaging and release of nucleic acids would be useful for efficacious drug development and delivery.

Most current models of capsid packing assume the DNA is packed in a highly-ordered spooled conformation.^{3, 4, 5, 6} Such models are based primarily on 3D cryo-EM reconstructions interpreted as showing spherical or ellipsoidal density “shells” of consistent radial width^{10, 12, 13, 15} from 3D reconstructions of various phages (circular or elliptical “rings” in the case of 2D projection averages²³). A more recent model has been proposed^{24, 25, 26} which we herein refer to as the “elastic toroidal” model, which simulates a coarse-grained beads-on-a-string model of DNA “slowly” packaged and equilibrated within capsid-like surfaces, obtaining various conformations of linearly elastic DNA. Averaging over such conformations generates density maps seemingly consistent with cryo-EM. This model suggests a slight departure from the highly-ordered “inverse-spool” models but still assumes a linearly-elastic bending force which results in relatively well-ordered conformations by bending the DNA smoothly and isotropically within the available volume. While structurally consistent with cryo-EM data, the fraction of wild-type genome length is only considered up to 78%. While pressure values similar to the present study were obtained, in contrast to the present study, fully-packaged phages were not considered.²⁴

While higher resolution structures are expected to be pivotal in elucidating detailed physical mechanisms and provide tests of proposed models,¹⁴ a proper physical interpretation of the data is required to obtain thermodynamic mechanistic insight. Historically, cryo-EM reconstructions have imposed symmetry and averaged a large sample size of particles in order to increase resolution. The cost of the symmetry assumption, however, is that only features possessing the imposed symmetry are accurately represented by the averaged density map, and features which do not share this symmetry, such as the packaged genome or tail machinery, will be inappropriately averaged or “smeared.”²⁷

Recently, advances in cryo-EM have allowed for visualization of viral capsids without the need to impose artificial symmetry in what have become known as “asymmetric reconstructions.” This allows for asymmetrical details of structures to be visualized; however, it still relies on the assumption of relative homogeneity of specific features across multiple particles relative to the chosen point of alignment (e.g., the tail). While this may be relatively accurate for proteins that comprise the capsid shell, this assumption is not valid for the DNA packaged within. Typical asymmetric reconstructions, such as that of the P22 phage shown in Figure 1, are obtained by averaging ∼15 000–19 000 particle images.^{12, 13, 15} If the DNA structure differs significantly from particle to particle at a position measured relative to the orientation, then structural elements of the packaged DNA will be an average over position and conformation within individual virus particles.

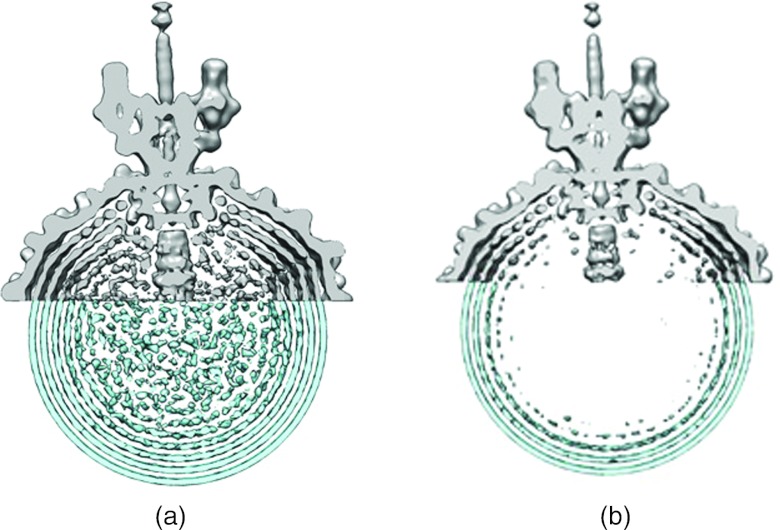
Figure 1.

(a) Comparison of density ring separation in cryo-EM asymmetric reconstruction of the P22 phage (top portion, grey) versus time-averaged density distributions over 100 ns simulation of unconnected segments (bottom portion, blue). (b) Same at lower contour levels.

Because the genomes of phages are on the order of tens of kilo base pairs long, current implementations of all-atom simulations are too computationally demanding to be feasible from proper averaging at this level, and some level of coarse-graining is required.¹⁴ Recent works have utilized coarse-grained models which treat DNA as polymeric chains of ion-penetrable spheres or ellipsoids which interact via electrical double layer interactions. Such models have been successfully applied to free and surface bound microarray experiments of single- and double-stranded DNA sequences.^{28, 29, 30} Therefore, in the present work, we model each six-base pair segment of double-stranded DNA as an ion-penetrable sphere which interacts via an electrostatically-repulsive colloidal potential from classic DLVO theory,³¹ given by

$$V\left(R\right)=\frac{q^2{L}_B}{{\left(1+\kappa a\right)}^2}\frac{\exp \left(-\kappa \left(R-2a\right)\right)}{R},$$

where q = 12e⁻ is the electrostatic charge from backbone phosphate groups L_B = 7.135 Å is the Bjerrum length, κ = 0.31 Å⁻¹ is the inverse Debye screening length, a = 19.9 Å is the radius of the DNA segments, and R is the separation between such segments. Such a potential incorporates the full negative charge from the backbone phosphate groups with simple Gouy-Chapman double layer ionic-screening appropriate to the experimental conditions of 100 mM Na⁺ and 5 mM Mg²⁺.

In order to separate the effects of packing versus the polymer persistence length we de-couple the correlations induced by the polymeric nature of DNA from its packing volume. We first model the enclosed DNA as unconnected segments of six base pairs (“beads”). The enclosed volumes of the expanded lambda phage capsid and the P22 virion are reasonably well-represented by spherical surfaces of radii 290 Å and 266.6 Å, respectively. The entire P22 genome of 41.7 kbp was modeled using 6950 “beads.” This simulation was performed using a modified version of the extended system program (ESP)³² molecular dynamics package (MD) developed by the Pettitt laboratory. The capsid interaction with the surface of the “beads” was modeled through the repulsive part of a WCA decomposition of a Lennard-Jones interaction.³³ The simulation was performed for 100 ns in the microcanonical ensemble at 300 K (with variation less than ±1 K) with a 100 fs time steps. Coordinates were sampled every 2 ps.

As shown in Figure 1, a cross-sectional view of a three-dimensional, time-averaged density distribution map of the simulation shows concentric “rings” of density due to correlations imposed by the capsid surface. Such rings are the consequence of “shells” of density within the full three-dimensional density. Three-dimensional time-average density maps were generated by averaging over the simulation trajectory with the aid of VMD molecular graphics software.³⁴ The spacing between the density shells is shown to be consistent with cryo-EM density maps of the P22 virion by superimposing each within Chimera molecular visualization software,³⁵ as shown in Figure 1. We find that a model with no rope-like polymer tendencies is sufficient to reproduce the spatial data. That is, the spatial data are consequence of packing and do not require a spooled polymer configuration but are, in fact, consistent with an ensemble of configurations which have the potential to be far more disordered.

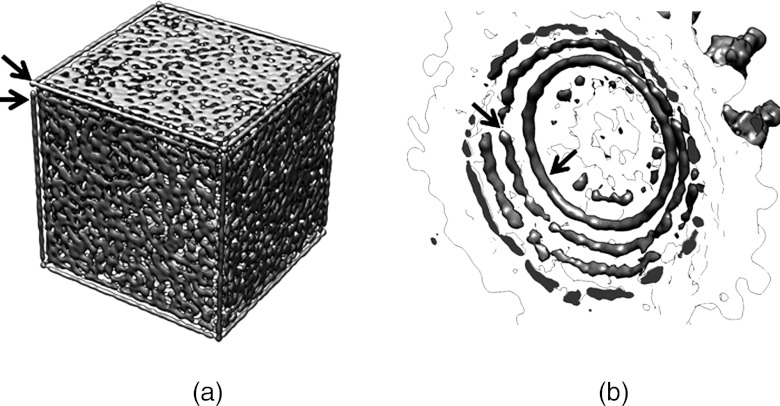
We note that some more rope-like configurations are seen in the corners of the experimental data especially near the portal and at icosahedral corners. To further test our hypothesis that surface-ordering alone is sufficient to obtain the observed structural densities and to clearly demonstrate the effects of sharp edges and corners, simulations were performed with the same number of particles in a cubic box, without periodic boundary conditions, with the same internal volume (and thus density) as our model of the P22 capsid. In Figure 2a the resulting average distribution over a 100 ns simulation clearly shows long “rope-like” densities along the edges of the box. Since these average densities result without any polymeric connections between our DNA segments or “particles,” we find no reason to assume that similar cryo-EM densities within phages, such as those seen in Figure 2b, are necessarily the result of long persistence length polymer correlations, but are, in fact, the result of surface-induced ordering which is consistent with the packing of a possibly more disordered system. Therefore, while the DNA in the phage is clearly DNA polymer chains, we see no evidence to imply the probable orientations of the DNA polymer to be strictly parallel with such “rope-like” densities or the capsid surface.

Figure 2.

(a) Time-averaged density distribution over 100 ns simulation of a non-periodic cubic box at same density (same particle number, same available volume) as our model simulation of phage P22. (b) Close-up view of select densities near phage head within the cryo-EM asymmetric reconstruction of the P22 phage.¹³

Similar simulations were also performed on a comparable model representation of the lambda phage system with similar results (entire 48.5 kbp genome using 8083 “beads” within a 290 Å spherical “capsid”). The average internal pressure over the simulation of our lambda representation was determined to be 30.43 atm with fluctuations of 0.08 atm over a 100 ns of simulation. As this is already on the order of total packaging pressures, a large fraction of the total packing pressure is expected to be due to the electrostatic repulsion, indicating that, for packaging to occur, bending energies may be lower than previously predicted. Indeed this might be the case if phage packaging were shown to induce localized deviations from the linear elasticity of canonical B-form DNA which has a persistence length around 50 nm.³⁶ Since the report by Cloutier and Widom³⁷ highlighted the possible limitations of the worm-like-chain (WLC) model, evidence for nonlinear elastic anomalies within short DNA sequences has been controversial due to experimental issues;^{38, 39, 40, 41} however, recent evidence using different methods has bolstered the original claim.^{42, 43} In addition, theoretical studies have predicted such kinking to be inducible by bending, as well as positive and negative torsional strain, with a significant asymmetry between the effects of over and underwinding.^{44, 45, 46, 47} Significantly higher probabilities of denaturation are predicted for undertwisted sequences.^{48, 49} Recent experimental evidence has shown that the φ29 phage induces negative torsional strain upon packaging.⁵⁰ Deviations from WLC predictions within phages could also allow more disordered conformations to be, not only be structurally consistent with cryo-EM, as we have shown herein, but also thermodynamically allowable by reduction of the overall polymeric bending contribution to the final packing enthalpy and pressure. This would also decrease the entropic penalty to the final packing free energy by enlarging the ensemble of possible conformational states. The contributions of the polymeric correlations may be nontrivial to the thermodynamics but are apparently difficult to reveal by structural experiment.