Development and clinical evaluation of automatic fiducial detection for tumor tracking in cine megavoltage images during volumetric modulated arc therapy

Abstract

Purpose: Real-time tracking of implanted fiducials in cine megavoltage (MV) imaging during volumetric modulated arc therapy (VMAT) delivery is complicated due to the inherent low contrast of MV images and potential blockage of dynamic leaves configurations. The purpose of this work is to develop a clinically practical autodetection algorithm for motion management during VMAT.

Methods: The expected field-specific segments and the planned fiducial position from the Eclipse (Varian Medical Systems, Palo Alto, CA) treatment planning system were projected onto the MV images. The fiducials were enhanced by applying a Laplacian of Gaussian filter in the spatial domain for each image, with a blob-shaped object as the impulse response. The search of implanted fiducials was then performed on a region of interest centered on the projection of the fiducial when it was within an open field including the case when it was close to the field edge or partially occluded by the leaves. A universal template formula was proposed for template matching and normalized cross correlation was employed for its simplicity and computational efficiency. The search region for every image was adaptively updated through a prediction model that employed the 3D position of the fiducial estimated from the localized positions in previous images. This prediction model allowed the actual fiducial position to be tracked dynamically and was used to initialize the search region. The artifacts caused by electronic interference during the acquisition were effectively removed. A score map was computed by combining both morphological information and image intensity. The pixel location with the highest score was selected as the detected fiducial position. The sets of cine MV images taken during treatment were analyzed with in-house developed software written in MATLAB (The Mathworks, Inc., Natick, MA). Five prostate patients were analyzed to assess the algorithm performance by measuring their positioning accuracy during treatment.

Results: The algorithm was able to accurately localize the fiducial position on MV images with success rates of more than 90% per case. The percentage of images in which each fiducial was localized in the studied cases varied between 23% and 65%, with at least one fiducial having been localized between 40% and 95% of the images. This depended mainly on the modulation of the plan and fiducial blockage. The prostate movement in the presented cases varied between 0.8 and 3.5 mm (mean values). The maximum displacement detected among all patients was of 5.7 mm.

Conclusions: An algorithm for automatic detection of fiducial markers in cine MV images has been developed and tested with five clinical cases. Despite the challenges posed by complex beam aperture shapes, fiducial localization close to the field edge, partial occlusion of fiducials, fast leaf and gantry movement, and inherently low MV image quality, good localization results were achieved in patient images. This work provides a technique for enabling real-time accurate fiducial detection and tumor tracking during VMAT treatments without the use of extra imaging dose.

INTRODUCTION

The development of intensity modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT) has provided technical means for dose escalation to the tumor target and better sparing of surrounding normal tissues. However, the ability of obtaining highly conformal dose distributions must be accompanied by an increased accuracy in beam targeting.^{1, 2, 3} Both kilovoltage (kV) and megavoltage (MV) x-ray imaging methods have been used for ensuring the beam targeting accuracy in the radiotherapy process. The kV imaging methods provide better image contrast due to the dominance of the photoelectric effect with kV x rays. However, this benefit is accompanied by additional imaging dose imparted to the patient, which causes concern for the associated risk of secondary malignancies.⁴ The imaging dose delivered in real-time fluoroscopic tumor tracking radiotherapy is rather high and can be unacceptable, as reported by Shirato et al.⁵ On the other hand, imaging with the therapeutic MV beam provides several unique advantages: (1) no additional imaging dose to the patient because the same beams are used both for imaging and therapy; (2) the images are acquired in the beam's-eye view (BEV) that shows what is actually irradiated. The main limitation of MV images is the image quality. Although markerless tumor tracking has been attempted in MV imaging,⁶ the use of implanted metallic radio-opaque markers remains to be a robust solution.

There is much work in the literature addressing the problem of metallic fiducial localization on radiological images. Most of this literature is specific to kV imaging. Fledelius et al.⁷ developed a localization technique based on kV cone-beam CT (CBCT) imaging. They proposed a five-step algorithm that takes into account the trajectory and shape of the cylindrical markers, enabling the localization not only in position but also in orientation in space. They reported a percentage of successes of at least 99.8% in the cases studied. With this technique, the localization was performed with CBCT open fields taken just before or after the treatment. Marchant et al.⁸ also proposed an algorithm for automatic tracking of fiducial markers in CBCT images based on mean shift and sequential random sampling. These algorithms employ kV imaging with open fields. They are based on retrospective processing of the images, and thus cannot be used for real-time or online image guidance purposes. In the context of motion management, Adamson and Wu⁹ have developed a technique to assess prostate intrafraction movement by acquiring kV fluoroscopy image during the step-and-shoot IMRT treatments and employing a previous and a post-treatment CBCT (the latter is used as the baseline for intrafraction motion assessment). Tang et al.¹⁰ developed a tracking system applicable to lung and abdomen tumors based on fixed-gantry kV fluoroscopy that tracks the breathing phase. Using phantoms, Poulsen et al.¹¹ have demonstrated the feasibility of kV tracking with a single imager in VMAT treatments, correcting the motion in real-time by changing the leaves positions.

With respect to MV imaging, Park et al.¹² developed a procedure for marker detection and three-dimensional (3D) localization based on cine MV images. They first employed a Laplacian of a Gaussian (LoG) filter to enhance the small spots caused on the image by the marker. In the second step, they used rigid distances between the markers calculated from the planning CT to assist the localization algorithm. They reported 88.8% detection successes rate in phantom studies, which was improved to 100% after using prior CT information. However, they reported that in patient studies the detection was sometimes hindered by organ deformation. In addition, their method was susceptible to marker misidentification when there was couch rotation, marker blockage, or two markers in proximity. Their work was done in the context of stereotactic body radiation therapy (SBRT) with nonmodulated static fields.

Mao et al.¹³ presented an algorithm applicable to marker tracking based on both MV and kV images. The results were presented for one phantom and five patient studies. This method used pairs of anterior–posterior (AP) and lateral (LAT) orthogonal projection images obtained with MV and kV x ray. The images for fiducial localization were taken with open fields during patient setup, before the treatment. In a following study,¹⁴ they investigated the application of their algorithm to IMRT and addressed the issue of blocking of the fiducials. They presented near real-time tracking speeds for fixed gantry IMRT phantom studies. Next they implemented their algorithm in the clinic for image guidance of fixed gantry IMRT procedures using only cine MV images taken with the electronic portal imaging device (EPID) at different times for different beam treatment angles. They reported retrospective motion measurements both in a phantom and in one patient treatment.¹⁵ They noted several drawbacks in the algorithm performance. First, tracking the fiducial motion with 3D estimation with two images taken at different times allowed the possibility of fiducial movement during gantry rotation. This leads to an error dependent on the rotation time since the 3D estimation assumes no fiducial movement between projections. Furthermore, the ability to detect fiducials at the beginning of a fixed gantry IMRT field was diminished when the aperture was small because the fiducial occlusion was much more likely. Thus, it was possible to deliver a fraction of the total dose before noticing the potential movement. To mitigate this last potential problem, the algorithm relied on having the largest area segment delivered first.¹⁵ However, cases employing many small apertures may be problematic. In these situations, the VMAT with continuous tracking would benefit the beam targeting.

Slagmolen et al.¹⁶ developed a procedure for fiducial localization employing at least two images generated with MV or kV beams. They were able to automatically correct limited intrafraction motion using an open field for the kV image and acquiring the MV images during treatment with IMRT for each fixed gantry at oblique positions. The fiducials were superimposed to the IMRT field, adversely affecting visualization. This was overcome with the use of filters. As with the previous study, one shortcoming was that the fiducial may move in between image acquisitions.

In this work, we present a novel automatic fiducial detection algorithm with 3D tracking applicable on the general situation of complex beam apertures with moving leaves and rotating gantry during VMAT treatment. The approach has several unique features. First, the fiducial detection is based on combined criteria using template matching and image intensity information. The image is filtered to enhance the fiducials and they are identified by morphological similarity using template matching complemented, if necessary, with intensity information. Template matching was proposed by Shirato et al.^{17, 18} to find the fiducial position. This approach was employed in the work by Mao et al.^{13, 14, 15} Here, we improve the method by developing a simple formula as a universal template that takes into account both fiducial rotation and the possibility of partial blockage of the fiducial on the cine MV image by the multileaf collimator (MLC) leaves, which can cause the apparent fiducial to be shorter than its actual length. Furthermore, to dynamically follow the movement of the fiducial, the search area in our method is updated in real-time. The fiducial position is predicted continuously based on its previous positions, and the search for the fiducial is initiated when its predicted position lies in the open beam. This allows us to detect large fiducial shifts with high confidence.

MATERIAL AND METHODS

Outline of the algorithm

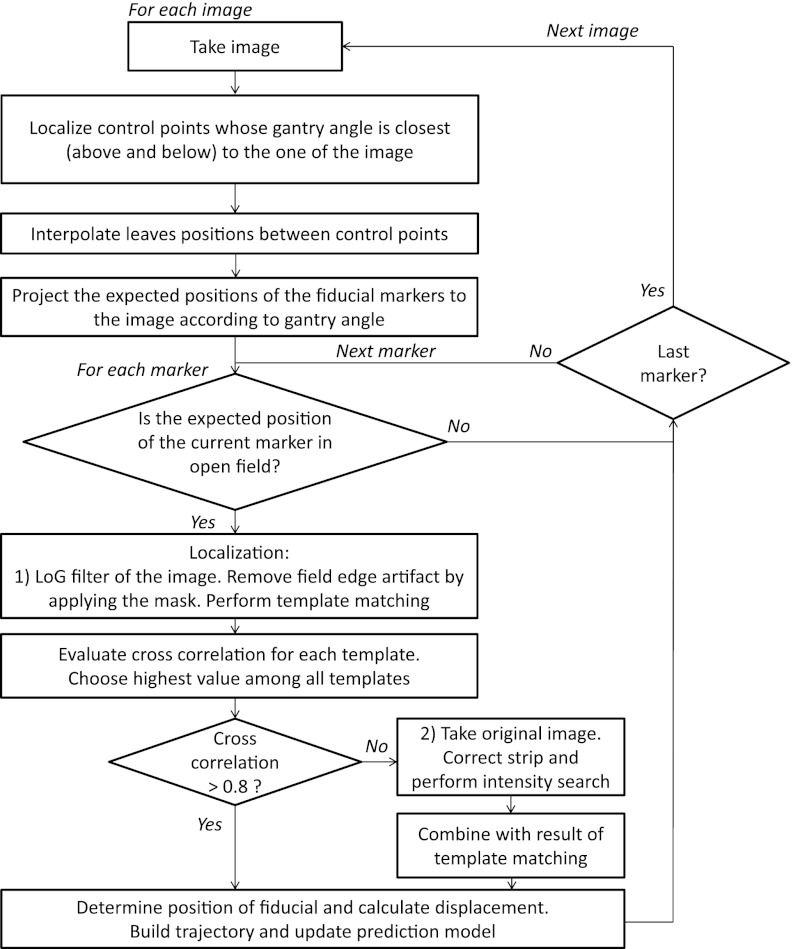
The algorithm structure and workflow is represented in Fig. 1. For each image the search of the fiducial was initiated if its expected position lied in open beam. The expected position for the first image was the one determined by the 2D/2D matching of two kV orthogonal images, which coincided with the projected one from the treatment planning system (TPS) unless the fiducial had migrated. For the remaining images, it was the estimated one based on the tracked position from previous images. An important feature of the algorithm is its ability to deal with varying MLC leaves configurations during VMAT. During the first step, each one of the images was correlated with the control point configuration as specified in the plan file for the gantry angle at which the image was taken, taking into account the gantry rotation direction. Linear interpolation of the leaves positions was performed between subsequent control points.

Figure 1.

Algorithm workflow for fiducial detection in cine MV images acquired during VMAT treatments.

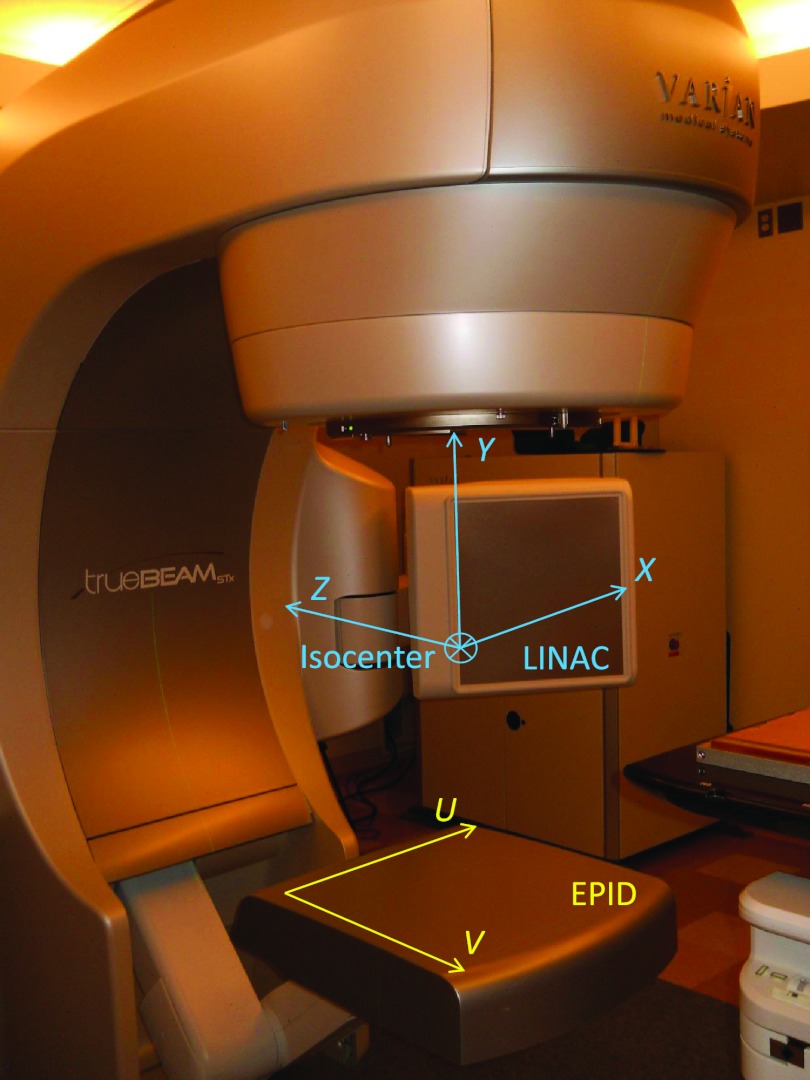
The linear accelerator (linac) employed for VMAT treatments was a Varian True Beam (Varian Medical Systems, Palo Alto, CA) equipped with an EPID. It could acquire cine MV images during treatment at a rate of ∼5 frames/s. The EPID resolution was 0.392 mm/pixel, and it was located at a distance of 150 cm from the beam source.

The transformation between the fiducial coordinates in the linac system {X, Y, Z} and the collimator reference system was done to determine if the expected fiducial position was in open field. It took place in two steps. First, the coordinates were transformed to the gantry rotation system {X^′, Y^′, Z^′}, according to the rotation matrix:

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right],$$ (1)

in which Z was the axis of the gantry rotation and θ is its angle position. Axis rotation in the clockwise (CW) direction was considered in this transformation. After this transformation, a rotation of an angle φ of the collimator axis was considered in the counterclockwise (CCW) direction with respect to the collimator axis Y^′ to represent the fiducial in the collimator reference system {X^″, Y^″, Z^″}:

$$\left[\begin{array}{c}{x}^{\prime \prime }\\ y^{\prime \prime }\\ z^{\prime \prime }\end{array}\right]=\left[\begin{array}{ccc}\cos \phi & 0& \sin \phi \\ 0& 1& 0\\ -\sin \phi & 0& \cos \phi \end{array}\right]\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right].$$ (2)

With this coordinate axis transformation, the expected positions of the fiducial centroids were compared with the leaves aperture from the corresponding control point configuration, and the localization procedure was started if it lied in open field. For all the images until the first one in which the fiducial appeared, its expected position was the projection of its planning CT coordinates onto the image. For the next images a prediction model for the fiducial expected position was used. To perform the fiducial detection in the EPID reference system, its coordinates were projected from the gantry reference system to the EPID distance and its units were changed from mm to pixel values. The linac and EPID reference systems can be viewed in Fig. 2.

Figure 2.

Varian TrueBeam linear accelerator with electronic portal imaging system and reference systems employed in this work. The linac reference system is centered at the isocenter and fixed with respect to the linac room. The EPID reference system rotated with the gantry. Its origin was on the upper left corner of the imager. The reference system employed for comparing the marker with the MLC leaves positions (collimator reference system), as well as the gantry reference system are not represented. The gantry reference system was centered at the isocenter and rotates with the gantry, around the Z≡Z^′ axis.

The localizations were employed to reconstruct the trajectories of the fiducials and to predict their positions in the next images. The expected position of each fiducial in the next image was continuously updated just after each image had been analyzed. The search area was dynamically adapted to track the fiducial motion.

Image enhancement and artifact rejection

Before performing the fiducial search, the image was filtered by using a Laplacian of Gaussian function as implemented in the article by Park et al.¹² This filter enhanced the small spots where the intensity showed a gradient; thus, it is especially suited for fiducials in MV images. Since the field edges were also enhanced by the LoG filter, a mask was further applied to remove them. The mask was built as a binary image with zero value on points with intensity 80% or less with respect to the maximum intensity point and one otherwise. (In one of the cases further presented, number 5, we used 60% of the intensity for defining the mask).

The images acquired by the EPID had an artifact in the form of horizontal strips of varying intensity and fixed height (39 pixels) due to an electrical current that appeared when the EPID was functioning. Consequently, an image preprocessing was necessary to correct these artifacts and improve the image quality. The correction was performed for the search areas which lied in two strips with different intensities, by measuring the mean intensity on a 38 × 41 pixels (14.9 × 16.1 mm²) rectangle on each of the frames with the same x^′ coordinate, and dividing the intensity in the search area by that mean value, taking into account the strip in which each point lied.

Fiducial detection

Adaptive search region

Once the expected fiducial position was determined to be in open field, the searching procedure was initiated. It was performed on the EPID imager reference system. The V direction in our calculations corresponded to the superior–inferior direction of the patient (craniocaudal). The U direction, however, was orthogonal in the plane of the imager, and thus, was rotating with it. A searching area of 25 × 25 pixels (9.8 × 9.8 mm²) was employed. With this size we could reduce the amount of false detection cases. A too large area could include, in principle, more noisy points enhanced by the LoG filter that could lead to algorithm failure. Furthermore, this size had the advantage of reducing the calculation time. Since it was centered in the projected position of the fiducial, and the setup of the patient was performed with a 2D/2D matching for the fiducials between planar images and CT contour projections, good beam targeting was achieved just before the tracking started.

For the subsequent images, the adaptation of the search area to track the tumor motion was performed by 2D and 3D tracking. We employed 2D tracking when the number of analyzed images was not enough to get robust 3D position estimation. In practice, we used 3D estimation when at least five analyzed images were available. In 2D tracking, the search area was centered in the updated expected position using the 2D drift along the superior–inferior (Z≡Z^′) direction of the patient and the trend along the X^′ axis of the gantry reference system. The 2D drift of the fiducial measured at image i was calculated as the average of the displacement of the fiducial with respect to the planned position in the TPS, as measured on the EPID, converted to mm, and projected to the isocenter, for all the previous images in which the fiducial appeared. This quantity was easy to manage and useful, since the 2D drift was defined along the Z≡Z^′ axis, which does not rotate with the gantry. The 2D drift depended slightly on the gantry position of each image, since the measured distance on the EPID was actually a projection of the fiducial position as viewed from the source that rotates with the gantry. However, this dependence is weak and the 2D drift is a robust quantity when estimated from all the previous images in which the fiducial appeared. Defining and using the trend along the X^′ axis was, however, more challenging since it did depend strongly on each image. It was taken as the mean displacement of the fiducial with respect to its expected position for the all the previous images (up to five) to that being considered. This corresponded to a prediction based on images from the last second. The assumption here was that the fiducial did not move more than 12.5 pixels (half of the dimension of the searching area, ∼3.3 mm as projected to isocenter) between two frames, which corresponded to a speed of 16 mm/s.

In cases in which at least five analyzed images were available, a Bayesian approach to estimate the 3D position of the fiducial as proposed by Li et al.^{19, 20} was employed. The 3D tracking was performed by predicting the fiducial position in the image to be analyzed. The drifts of the x, y, and z coordinates on the linac reference system were defined as the mean of all the differences in each one of those coordinates for all the previous images in which the fiducial was localized. The fiducial 3D position was estimated as the initial planned position plus the drifts. The projection of the fiducial on the image being analyzed was the expected fiducial position.

Universal template mathematical form

For a robust algorithm, it was highly desirable to have a template able to localize the fiducials in all patients and situations. The fiducial shape was cylindrical, of dimensions 5 mm in length by 1 mm in diameter. From the physical shape and dimensions of the markers, we defined two sets of templates of dimensions 13 × 13 pixels (5.1 × 5.1 mm²). The fiducial was represented for templates T1–T4 as rectangles of 9 × 3 pixels and for templates T5–T9 as rectangles of 13 × 3 pixels (corresponding to 2.4 × 0.8 mm² for templates T1–T4 and 3.4 × 0.8 mm² as projected to the isocenter). We took into account that, in most situations, the fiducial longitudinal axis would not be completely aligned with the plane of the image so its full length would not be seen. These template dimensions represented a compromise for all situations. In addition to the “vertical” position of the template (T1 and T5), several rotations (45°, 90°, and 135°) were considered. An additional template (T9) represented the case in which the fiducial longitudinal axis was orthogonal to the plane image. In this case, the template was a circle of 5 pixels of diameter.

A challenging situation in the fiducial search was when it lied very close to or was partially blocked by MLC leaves. To solve this problem, another eight templates (T10–T17) were defined by cropping the templates T1–T8 to areas of 7 × 7 pixels (2.74 × 2.74 mm²). In these situations seeing only part of the fiducial was expected. The reduced dimensions of the template contained only part of the fiducial and, since the area of the template was smaller, they were more suitable than the big templates to perform cross correlation search in the edges of a field. The templates can be seen in Fig. 3.

Figure 3.

Template with rotation employed for the detection. The templates T1–T4 represent the fiducial by a 2.4 × 0.8 mm² rectangle, the templates T5–T8 by a 3.4 × 0.8 mm² rectangle. These templates were used to localize the fiducials, whose projected length onto the image depended on its 3D orientation. The template T9 represented the case in which the fiducial was orthogonal to the image. The fiducials T10–T17 were originated from T1–T8 by cropping their area of 13 × 13 pixels (5.1 × 5.1 mm²) to an extension of 7 × 7 pixels (2.74 × 2.74 mm²), to represent the situation in which a fiducial was partially occluded by the leaves. The size of templates T10–T17 relative to that of T1–T9 keeps their proportion. Note that the fiducial dimensions were scaled when projected to the EPID and measured in pixels.

The template square was convolved with a kernel to smooth the edges. We used a 2D Gaussian mathematical formula for the smoothing kernel with a standard deviation of 2 pixels.

Combined detection criterion

A combined criterion of fiducial shape (template matching) and image intensity in the unfiltered original images corrected by the electronic artifact (where the intensity is lower in the fiducial projection area) was considered in this work. Template matching calculations were based on the normalized cross correlation function, γ, defined as

$$\begin{array}{c}\hfill \gamma \left(u,v\right)=\frac{{\sum }_{u^{\prime },v^{\prime }}\left[f\left(u^{\prime },v^{\prime }\right)-{\overline{f}}_{u,v}\right]\left[t\left(u^{\prime }-u,v^{\prime }-v\right)-\overline{t}\right]}{{\left\{{\sum }_{u^{\prime },v^{\prime }}{\left[f\left(u^{\prime },v^{\prime }\right)-{\overline{f}}_{u,v}\right]}^2{\sum }_{u^{\prime },v^{\prime }}{\left[t\left(u^{\prime }-u,v^{\prime }-v\right)-\overline{t}\right]}^2\right\}}^{0.5}},\end{array}$$ (3)

where f was the image, t is the template, $\overline{t}$ was the mean of the template, u, v, u′, v′ were the coordinates of the pixels at the EPID reference system, and ${\overline{f}}_{u,v}$ was the mean of the image under the template. The values for the γ function were contained in the interval [−1, 1]. Cross correlation gave a measure of the similarity of a pattern (template) over a bigger area of search. The function values were highest where the template best matched the shape within the search area. For the template matching procedure, the cross correlation function was calculated for the same search area surrounding the expected fiducial projection, for the available templates. A cross correlation value of at least 0.6 was selected as a threshold for assuming adequate good similarity when applying the big templates. If the maximum cross correlation value was below this threshold (which could be the case near the field edges), the smaller templates (T10–T17) were tried. The position according to the template that led to the highest value in the cross correlation matrix was selected as the fiducial position, as long as its cross correlation value was higher than 0.8.

After template matching, the minimum intensity search was performed only if the maximum cross correlation value was less than or equal to 0.8. In this case, a combined product of cross correlation times the inverse of the intensity was evaluated and the maximum value over the search area was used to localize the fiducial. When the intensity search was performed, the very low intensity in the out-of-field areas as well as the field edges was replaced by very high values to avoid algorithm performance failure. In practice, the selection criterion was for those points whose intensity was less than 60% of the mean intensity in the image. The replacement value was 1000, which is much larger than the intensity values encountered in the images.

Patient treatment

We tested our algorithm with five image sets corresponding to five arcs employed clinically to treat five patients. All of them were implanted with three fiducial markers. The patients were setup in head first and supine position. With this orientation, the positive sign of the AP, LAT, and SI fiducial displacements coincided with the positive orientation of the X, Y, and Z axes. The treatment plans consisted of two VMAT arcs, with a total delivery time of 2 min. The MV photon fluence was modulated using a Varian high definition MLC with 120 leaves (120 HD MLC). It had 32 central pairs of leaves with 2.5 mm of width and the remaining 28 pairs in the periphery with 5 mm width.

RESULTS

Image processing

Image processing in order to improve the ability to detect fiducial markers in MV images consisted of applying the LoG filter for template matching and increasing the image quality by removing the strips with different intensities. Figure 4 represents a two-dimensional (2D) view of a treatment control point with its aperture defined by the configuration of leaves positions at that time. The fiducials could be hardly seen without applying the filter (left) but their location became apparent after its application (center). Furthermore, we applied a mask to remove the edge artifact enhanced by the LoG filter (right).

Figure 4.

MV image of a control point projection acquired with the EPID, without (left) and with (center) Laplacian of Gaussian (LoG) filtering, which enhanced the fiducials, and after the removal of field edges with the mask (right).

Figure 5 displays a zoomed image around the vicinity of a fiducial close to the edge between two strips with different intensity levels. The improved image quality after the processing is apparent.

Figure 5.

Intensity image (left) with frame artifact and (right) after applying the intensity correction to remove it. Clearly the correction enhanced the image quality, prior to performing a minimum intensity search.

Fiducial detection

The fiducial localizations success rates are presented for five patients, as well as their movement assessment. Figure 6 presents the two-dimensional displacement of the fiducials obtained from their detections in the EPID imager for patients 1 and 2. The results were projected to the isocenter, displayed in mm, and plotted with respect to the fixed Z axis and the rotating X^′ axis directions. Bad detections have been removed from the graph. Figure 7 displays the tumor motion data for patient 1. This patient experienced some tumor movement during the arc delivery in that fraction of the treatment. The beam targeting was affected by that movement. The measured data for the displacement in the anterior-posterior (AP), lateral (LAT), and superior-inferior (SI) directions, as well as its absolute value (ABS), are represented. The target motions were calculated from the EPID imager data and the planned 3D positions in the CT, all in the linac reference system. The 3D data corresponding to the images in which there was a bad 2D localization have been removed. The 3D estimation could have limitations of accuracy due to noise if there were few projections available, which was the case of fiducial 1 in the AP and LAT directions between images 165 and 168. The fiducial exhibited much more movement than fiducials 2 and 3. Since fiducial 1 appeared again after several images of being occluded, it was feasible that part of the apparent movement was due to noise in the 3D reconstruction. In Fig. 8 the localization results for patient 2 can be seen, after the 3D estimation data in the images with 2D bad localizations have been removed. In this case, the positioning during the whole treatment was very good, with very small movement of the tumor.

Figure 6.

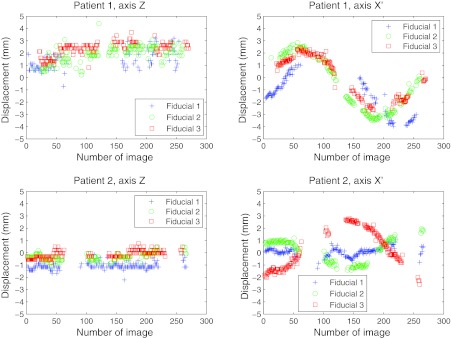
Detection of fiducials in the EPID imager for patients 1 and 2. The 2D displacements as measured from the good fiducial detections were projected to the isocenter and displayed in mm. The directions in which the displacements are presented were the fixed Z axes and the rotating (with the gantry) X^′ axes.

Figure 7.

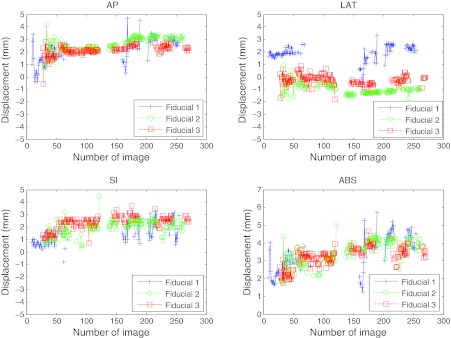
Localization of the three implanted fiducial markers on a set of cine MV images for patient 1. The 3D fiducial positions were calculated from the 2D data obtained by measurement on the EPID imager (displayed in Fig. 6). The bad localizations have been removed. This data correspond to a fraction on a patient where clinically relevant displacement of the fiducials with respect to their planned position was detected. The maximum absolute distance measured for a fiducial from its planned position was 5.7 mm (fiducial 1). Fiducial 1 had a large variation in AP and LAT directions starting in image 165, after being occluded by the leaves. Since the other two fiducials did not experienced that change, part of that difference could be real movement and part could be due to noise in the reconstruction, having had few 2D projections close to that gantry angle. Tracking with at least one fiducial was achieved in 86% of the images.

Figure 8.

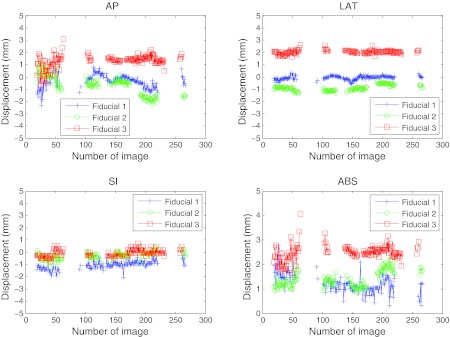
Localization of the three implanted fiducial markers on a set of cine MV images for patient 2. This data corresponds to a fraction on a patient where good positioning during most part of the treatment was achieved (the fiducials were at a position closer than 3 mm from its planned position in most of the treatment). The corresponding 2D detections are presented in Fig. 6. The 3D estimation was robust (especially for the LAT and SI directions). For the AP projection, the estimation was less robust at the starting gantry angles (180° and above), since the direction of estimation was parallel to the gantry angle and some more projections were necessary to get the noise smaller than 1 mm. Tracking with at least one fiducial was achieved in 64% of the images. The relative movement of the three fiducials was quite correlated.

Table 1 lists the algorithm success rate statistics for the five patients. The percentage of images in which each fiducial could be seen, as well as the percentage with at least one fiducial visible, is presented. The percentages of good detections are also given. Last, the mean localization error in mm is displayed, assuming an error of 0.392 mm (the pixel size) for the good localizations, whose percentage averaged for the patient is in the previous column. The localization error for the bad localizations was measured with respect to ground truth values, as determined by manual localization, averaged and weighted by its percentage. The maximum absolute detection error among all the bad detections in all patients studied was 4.24 mm. The mean values for the absolute detection errors for all the bad detections in each patient were 2.88, 3.06, 3.45, 3.09, and 2.52 mm.

Table 1.

Algorithm performance. For all five patients, the percentage of images in which each fiducial was detected, the percentage of images in which at least one fiducial was detected, the percentage of valid detections for each fiducial, the average or valid detections for each patient, and the average detection error are represented in mm. The mean detection error in the 2D images was calculated assuming an error of 0.392 mm (pixel size) for the valid detections, and the measured error with respect to the ground truth as determined by manual introduction for the bad detections.

Case	% Images with localization of the three fiducials (F1/F2/F3)	% Images with at least one fiducial detected	% Valid detections (F1/F2/F3)	Average (%)	Average detection error (mm)
1	49/60/54	86	87/92/97	92	0.6
2	57/47/51	64	99/99/99	99	0.4
3	36/29/26	40	94/91/98	94	0.6
4	39/23/41	58	94/80/91	91	0.6
5	51/65/45	95	89/96/93	93	0.5

Using the 25 × 25 pixels (9.8 × 9.8 mm²) search area dynamically adapted to track the fiducial motion resulted in a good algorithm performance, as well as a reduced computation time for calculating the cross correlation. The maximum fiducial speed that the algorithm could track with this searching area was 16 mm/s. Furthermore, the possibility of algorithm failure due to image noise was greatly reduced by performing a small local search.

Movement assessment

Several statistical data concerning tumor motion are provided in order to test the performance of the proposed localization and tracking algorithm. Table 2 contains the mean absolute displacement with respect to the planned CT position, with its standard deviation (STD), assessed for the five patients (with three fiducials each). The maximum displacement is also reported. For the data presented in Table 2, we have removed the 3D estimated data corresponding to those images in which there was a 2D detection failure. One of the patients (patient 4) had a migration in fiducial 3. The mean value reported in the table for this fiducial was actually a measurement of the magnitude of the migration together with its movement. Without taking this value into account, the maximum displacement measured among all the patients and arcs reported was 5.7 mm.

Table 2.

Motion assessment. The results of the absolute value of the displacement, averaged over all the images, are displayed. The 3D estimation was performed while the detection algorithm was running. After the identification of the bad 2D localizations, the motion assessment data corresponding to those images were removed. The mean displacement between the localized positions and the CT planned position of the centroid of the fiducials is displayed in mm, together with the standard deviation (STD).

	Absolute 3D displacements between the fiducial and its planned position on planning CT (mm)
	Fiducial 1 (F1)	Fiducial 2 (F2)	Fiducial 3 (F3)
	Mean ± STD	Mean ± STD	Mean ± STD
Case	(Max)	(Max)	(Max)
1	3.4 ± 1.0	3.5 ± 0.7	3.2 ± 0.6
	(5.7)	(5.0)	(4.7)
2	1.2 ± 0.4	1.4 ± 0.3	2.5 ± 0.3
	(2.8)	(2.3)	(4.1)
3	1.2 ± 0.4	2.4 ± 0.2	2.9 ± 0.4
	(3.0)	(2.9)	(4.7)
4	1.7 ± 0.4	1.2 ± 0.5	6.7 ± 0.4
	(3.1)	(3.3)	(7.7)
5	1.5 ± 0.5	1.2 ± 0.3	0.8 ± 0.6
	(3.6)	(2.2)	(2.8)

DISCUSSION

Fiducial detection during a VMAT treatment may be complicated by potential occlusion of markers by the multileaf collimator. This was often the situation in the cases studied. The prediction model presented in this work was needed to track the fiducials while they were occluded by the MLC, enabling a robust fiducial detection. The detection robustness was achieved at the cost of the algorithm's sensitivity to track a fast and sudden movement. The reduction of fiducial detectability was particularly apparent in patients 3 and 4, due to the blockage of the prostate, with small, elongated apertures employed. In these cases, it was even more important to have a good prediction scheme to estimate the fiducial position while it was blocked.

Ma et al.²¹ proposed a methodology to enhance the visibility of the fiducials in a general context of four-dimensional (4D) inverse treatment planning. The essence of their method is to encourage/force the fiducials to be visible in the segments of IMRT plan through the introduction of soft/hard constraints during inverse planning. The algorithm was demonstrated using a lung and a pancreatic cancer case. An extension of their work to VMAT planning would provide the basis for cine MV tumor tracking.

The proposed approach of using smaller templates for fiducial detection close to or partially blocked by the leaves has been implemented in a simple and effective way, initiating their use when the best cross correlation achieved with the regular templates was below 0.6. This value has been proven to be a good threshold for properly detecting the fiducials. However, more implementation strategies are possible, like using the smaller templates only when the distance between the expected fiducial position and the leaves is small, of the order of a few mm. These are the situations where the bigger templates are expected to result in an inadequate similarity. Moreover, the smaller template can also introduce an error in the determination of a partially blocked fiducial position with respect to that obtained using a bigger template for the case in which the fiducial is completely lying within the field. To estimate this error, let us assume a half blocked fiducial to which we cannot apply the big template (13 pixels dimension), being the center just in the field edge. If it is detected with the small template (7 pixels dimension), the position is shifted 3.5 pixels (1.4 mm) outwards the blocking leaf.

Figure 7 presents the case of a patient in which tumor motion was detected during the treatment fraction. It is in such cases that the prediction model was especially useful for tracking the fiducial. When analyzing one image, the measured differences along the AP, LAT, and SI directions were averaged among all the previous images. This information was used for predicting the expected fiducial position and updating the starting search position, which enables the localization of the fiducial and further assessment of its displacement. The prediction model based on 3D fiducial position, together with the ability to detect the fiducial close to the aperture's edges, led to a good performance of the algorithm for tracking the fiducial motion based on robust fiducial localization.

An inherent limitation of 3D fiducial position estimation from 2D projections is sparse image data taken during a small arc of gantry movement, are available. This was often the case for the first few projections, or when the fiducial appeared after having been occluded for several images (Fig. 6, fiducial 1 at image 165, where this effect might have hindered the exact motion assessment). The effect was more pronounced in the direction orthogonal to the imager, which was the AP direction at the beginning of the treatments reported here (start at gantry 180°). Although the algorithm was able to predict the fiducial position in the imager and perform the tracking, the motion assessment might have been affected by a few mm due to noise in the 3D estimation. Another limitation is the effect of the false positives when running the algorithm. A strategy consisting on discarding the detected position for a fiducial when the cross correlation value is low can be explored to avoid false positives during the detection process. The detection error magnitude, however, was limited mainly by the searching area employed. When working in real-time, the beam could be stopped after a predefined displacement threshold has been exceeded. An orthogonal kV image would be taken to accurately calculate the 3D position and confirm or not the fiducial displacement. The feasibility of the kV/MV tracking approach has been demonstrated by Wiersma et al.²² and Cho et al.²³ Its applicability for VMAT has been shown by Liu et al.^{24, 25} using phantoms.

A particular circumstance that can lead to algorithm detection failure is when the projections of two fiducials are overlapped on a particular image. This was the case in patient 1, marker 1. Among the 13 images in which the marker was not properly localized, in five of them marker 1 was confused with marker 2. However, we recommend separating the fiducials as much as possible during implantation. Although it is hard to avoid completely having two fiducials overlapped in the same projection, it is expected to prevent most of these situations.

The proposed formalism was designed to be used for real-time tumor tracking. It has been retrospectively tested on prostate patient images to demonstrate its ability to detect fiducials and assess the tumor motion. Since the prostate has unpredictable movement, an appropriate image guidance technique is needed to ensure the tumor coverage with the prescribed dose while sparing the healthy tissue in the surroundings. However, the algorithm formalism is general and can be extended to other localizations.

CONCLUSION

A novel algorithm for automatic detection of fiducial markers in cine MV images acquired during VMAT treatment has been developed. The algorithm has three distinct features: (1) combined use of template matching and image intensity for fiducial detection; (2) dynamic update of the search area based on the previous positions of the fiducials; (3) ability to perform fiducial search at the MLC shaped field boundary. The application of this algorithm to assess motion during VMAT treatments in prostate, as well as in other types of tumors, is work-in-progress and will be reported elsewhere.