The Promises and Pitfalls of Genoeconomics*

Abstract

This article reviews existing research at the intersection of genetics and economics, presents some new findings that illustrate the state of genoeconomics research, and surveys the prospects of this emerging field. Twin studies suggest that economic outcomes and preferences, once corrected for measurement error, appear to be about as heritable as many medical conditions and personality traits. Consistent with this pattern, we present new evidence on the heritability of permanent income and wealth. Turning to genetic association studies, we survey the main ways that the direct measurement of genetic variation across individuals is likely to contribute to economics, and we outline the challenges that have slowed progress in making these contributions. The most urgent problem facing researchers in this field is that most existing efforts to find associations between genetic variation and economic behavior are based on samples that are too small to ensure adequate statistical power. This has led to many false positives in the literature. We suggest a number of possible strategies to improve and remedy this problem: (a) pooling data sets, (b) using statistical techniques that exploit the greater information content of many genes considered jointly, and (c) focusing on economically relevant traits that are most proximate to known biological mechanisms.

1. INTRODUCTION

With the sequencing of the human genome in 2001 (Lander et al. 2001, Venter et al. 2001), and the rapid, ongoing development of new technologies for measuring and analyzing the genome, the study of genetics has been transformed. Until recently, almost no information was available about genetic variation across individuals. Now most common genetic variation can be inexpensively measured.

These advances in genetics are in turn transforming medical research. Some diseases have been linked to single genetic mutations in specific genes (e.g., Huntington's disease and Fragile X syndrome), which can be assayed to diagnose the disease, predict the age of onset and/or severity, and better understand how treatment response varies as a function of genetic characteristics. In the case of complex diseases or conditions, such as macular degeneration and obesity, new methods are beginning to identify the ensembles of genes that, along with environmental forces, account for individual differences. Unfortunately, each genetic variant identified in these studies of complex traits typically explains only a small amount of variation in the trait; therefore, the genetic risk factors identified so far are insufficient for the purpose of accurate medical diagnosis. Instead, the main benefit comes from the identification of new biological pathways and targets for therapeutic intervention. In short, genetics research has identified “new biology” for many major diseases, including diabetes, cancer, and schizophrenia.

Social scientists—including psychologists, anthropologists, political scientists, and, increasingly, sociologists and economists—have begun to measure genetic variation and study how it relates to individual behaviors and outcomes. Early work involved measuring just a few candidate genes in small samples of laboratory participants. The costs of genotyping have now fallen to the point at which comprehensive information on a person's genetic constitution can be obtained at a moderate cost. Consequently, some large-scale social science surveys, such as the Health and Retirement Study, are gathering such data, and others will likely do so soon. With these new data sources, the scale of research at the intersection of social science and genetics will surely explode.

The purpose of this article is to review research at the intersection of genetics and economics, or genoeconomics (Benjamin et al. 2007); to present some new findings that illustrate the current state of the field; and to survey the field's prospects.

In Section 2, we begin by developing a simple conceptual framework that defines some key terms and makes explicit some critical assumptions. In Section 3, we review the economic research conducted in the tradition of classical behavior genetics—primarily involving comparisons between identical and fraternal twins—that seeks to estimate heritability for economic measures: the fraction of the variance that can be explained by genetic factors. A remarkable implication from this work is that in modern Western societies, for most outcomes in life, over half the resemblance of two biological siblings reared in the same family stems from their genetic similarity. Another main implication is that, despite arguably being more complex and “downstream” from biochemical variation than psychological traits such as cognitive ability and personality that are the traditional realm of behavior genetics, economic outcomes and preferences appear to be as heritable as those traits, once adjustment is made for measurement error (Beauchamp et al. 2011a,b).

In Section 4, we present an overview of what we see as the four ways that the intersection of molecular genetics and economics promises ultimately to contribute to economics: (a) identifying and measuring latent traits, (b) identifying biological mechanisms that influence economic behavior, (c) providing exogenous proxies for preferences and abilities that may be used as control variables or—more problematically—as instrumental variables, and (d) predicting the differential effects of policies across individuals with different genetic constitutions. We review the small, but growing body of work that reports associations between specific genes and economic traits. We end the section by outlining the main challenges obstructing progress in genoeconomics and discuss different ways of confronting these challenges.

In Section 5, we illustrate some of these themes with examples from our own work. Using an Icelandic sample, the Age, Gene/Environment Susceptibility-Reykjavik Study (AGES-RS), we searched for associations between a set of outcomes of interest to economists and a set of candidate genes previously associated with cognitive functions or known to be involved in the brain's decision-making circuitry. We found a promising association between a particular genetic variant and educational attainment. The association was biologically plausible, associated with cognitive function, and replicated in a nonoverlapping sample from the same respondent population. The association then failed to replicate in three other samples. We further illustrate the widespread nonreplicability of candidate gene associations by reviewing a systematic study we conducted of previously published associations between cognitive ability and 12 candidate genes. Across three new, large samples, we are unable to replicate these associations. We close Section 5 by proposing a number of strategies for surmounting the challenges that face genoeconomic research. If the genoeconomics enterprise is to bear fruit, it is important that social scientists recognize the many methodological lessons that have been learned in medical genetics over the past decade regarding the frequency of false positives in genetic associations.

This review extends the analysis of Benjamin et al. (2007) and Beauchamp et al. (2011b). Benjamin et al. (2007) provide an initial definition of genoeconomics and survey the potential contributions of genetic studies in economics at a time when no such studies had yet been performed. Beauchamp et al. (2011b) report results from a large-scale genetic association study of educational attainment, which failed to identify any replicable associations. Using those results as a case study, Beauchamp et al. (2011b) reach similar conclusions as those presented here regarding the inferential challenges in genoeconomic research. Although here we primarily review published research at the intersection of genetics and economics and offer our perspective on the emerging field, we also present several new findings. Supplemental Appendix 1 provides details regarding our new behavior genetic results (in Section 3), which use Swedish Twin Registry data to estimate the heritabilities of permanent income and wealth. Supplemental Appendix 2 provides details regarding our molecular genetic analysis (in Section 5) from the Icelandic sample (follow the Supplemental Material link from the Annual Reviews home page at http://www. annualreviews.org).

2. CONCEPTUAL FRAMEWORK

We adopt a conceptual framework that serves three purposes: It defines genetics terms that we use throughout the article, it makes explicit the assumptions typically made in empirical work, and it helps clarify the link between behavior genetics and molecular genetics. We omit many biological nuances to focus on the concepts that are critical to understanding the field.

Human DNA is composed of a sequence of approximately 3 billion pairs of nucleotide molecules, each of which can be indexed by its location in the sequence.¹ This long sequence—the human genome—has subsequences called genes. Humans are believed to have 20,000–25,000 genes. Each gene provides the instructions that are used for building proteins. These proteins affect the structure and function of all cells in the body.

At the overwhelming majority of locations, there is virtually no variation in the nucleotides across individuals. The segments of DNA in which individuals do differ are called genetic polymorphisms (from the Greek poly, meaning “many,” and morphisms, meaning “forms”). For simplicity, our discussion here focuses on the most common kind of genetic polymorphism, called a single-nucleotide polymorphism (SNP). SNPs are locations in the DNA sequence in which individuals differ from each other in terms of a single nucleotide. A single gene may contain hundreds of SNPs, and SNPs are also found in DNA regions that are not part of genes. We index SNPs by j, and we let J denote the total number of SNPs in the genome [currently it is believed that J ≈ 52 million (see the build statistics for Homo sapiens in Natl. Cent. Biotechnol. Inf. 2012)]. Conceptually, we can think of other kinds of genetic polymorphisms in the same way as SNPs, so focusing on SNPs is not misleading given our purposes.²

At the vast majority of SNP locations, there are only two possible nucleotides that occur. The nucleotide of a SNP that is more common in a population is called the major allele, and the nucleotide that is less common is called the minor allele. At conception, each individual inherits half of her DNA from her mother and half from her father. For a given SNP, one allele is transmitted from each parent. The gene, and hence the protein it produces, is affected by the genetic material received from both parents, but it does not matter which material came from which parent. Therefore, for each SNP, there are three possibilities: An individual has zero minor alleles, one minor allele, or two minor alleles. This number is called the individual's genotype, and for individual i for SNP j, we denote its value by x_ij.

Fix some outcome of interest, e.g., educational attainment, income, risk preferences, or body mass index. Let y_i denote the value of this outcome for individual i. The simplest model of genetic effects posits that y_i is determined according to

$$y_i=\mu +\sum _{j=1}^J{\beta }_j{x}_{ij}+{∊}_i,$$ (1)

where μ is the mean value of y_i in the population; β_j is the effect of SNP j; and ∊_i is the effect of exogenous residual factors. Equation 1 embeds a variety of assumptions. For example, the restriction that the genotype's effect is linear in the number of minor alleles is a simplifying assumption that can be, and often is, relaxed. Below we discuss some other important extensions of Equation 1.

β_j should be understood as the treatment effect from an experiment in which one SNP (and nothing else in Equation 1) is changed at conception. Although such experiments are conducted on nonhumans, in humans this treatment effect is a hypothetical construct. If β_j ⁠ 0 for some j, then SNP j is a called a causal SNP. As an example, it is now believed that there is a causal SNP in a gene called FTO on body weight (Frayling et al. 2007).³ There are many ways in which FTO could affect body weight, e.g., by coding for a protein involved in metabolism or by affecting food preferences. Identifying the correct mechanism(s) is an active area of research.

The residual term, ∊_i, is often called the environmental effect, but this terminology is imprecise and potentially misleading. Because the genotypic effects may operate through environmental channels, ∊_i should be interpreted as the component of environmental factors that are not endogenous to genetic endowment (Jencks 1980). For example, if the mechanism through which the FTO SNP affects body weight is a preference for energy-rich foods that leads to increased caloric intake (as suggested in Cecil et al. 2008), then the component of caloric intake that is genetically induced is not part of ∊_i.

Two important assumptions implicit in Equation 1 are quite strong and are therefore relaxed in richer models. First, the genotypes, x_ij and x_ij', for two different SNPs, j and j', may interact in affecting the outcome. Second, a genotype x_ij may interact with factors in ∊_i in affecting the outcome. It is often claimed that such gene-gene interaction and gene-environment interaction effects matter for many outcomes. Indeed, because the treatment effect of a genotype is not a structural parameter, it will vary with some environmental conditions. For example, Rosenquist et al. (2012) report that the effect of the FTO SNP depends strongly on birth cohort.

Most of this article is concerned with potential contributions that the field of genetics could make to the field of economics. We note here, however, a potential contribution that economics could make to genetics. The modeling tradition in economics could help move beyond the crude statistical framework outlined here toward more structural models. For example, a structural model of FTO might allow it to affect the marginal utilities of different foods, and possibly also the (production) function that maps caloric intake to body weight. Such a model would make predictions regarding how the treatment effect of the SNP would vary as a function of the prices and income of an individual, and it might predict compensatory behaviors, such as more exercise to try to reduce elevated body weight. The estimated model could be used to make predictions about the effects of changes in the economic environment. More generally, insights from economics about how environments can amplify or dampen genetic effects (e.g., depending on the degree of substitutability or complementarity) may help geneticists more accurately model, identify, and understand genetic mechanisms.

3. BEHAVIOR GENETICS AND ECONOMICS

Behavior genetics is a field of research concerned with understanding how genetic endowments taken as a whole explain individual-level differences in outcomes. In terms of Equation 1, individual i's genetic endowment is defined as $g_i\equiv {\sum }_{j=1}^J{\beta }_j{x}_{ij}$ The field of behavior genetics predates the availability of genotypic data, and its methods treat genetic endowments as latent variables whose effects are inferred indirectly by contrasting the similarity in outcomes of different pairs of relatives. Much research in behavior genetics focuses on estimating heritability, defined for a given outcome as the ratio of the population variance in genetic endowment to the population variance in the outcome, $\frac{\mathrm{Var}\left(g_i\right)}{\mathrm{Var}\left(y_i\right)}$.⁴ If genetic endowment g_i is independent of residual factors ∊_i, then heritability can be equivalently expressed as the population R² for the regression in Equation 1.

Over the years, there have been a number of misguided attempts to draw policy conclusions from heritability estimates. Goldberger (1979) clarifies the key issues by pointing out that high heritability of an outcome does not imply that policy is impotent in affecting the outcome (see Manski 2011 for a more recent discussion of these issues). High heritability means that existing, naturally occurring variation in ∊_i does not explain much of the variation in y_i. It does not rule out the possibility that a policy could cause a large change in the outcome. In Goldberger's (1979) famous example, even if the heritability of eyesight were 100%, prescribing eyeglasses would still be a policy that passes the cost-benefit test. Conversely, the fact that an outcome has low heritability does not imply that it is especially susceptible to influence by policy.

Despite these important interpretational caveats, we believe there are several reasons why economists may be interested in knowing the heritability of economic outcomes.⁵ First, heritabilities of income, educational attainment, etc., are descriptive facts that constrain the set of theories regarding heterogeneity in preferences and abilities that can be considered plausible. For example, high heritability estimates are challenging for “blank-slate theories” of human nature, which have featured prominently in much social science work (Pinker 2002).

Second, the pervasive finding of nonnegligible heritabilities for economic outcomes confirms the common concern that unobserved genetic endowments may confound attempts to estimate the effect of environmental variables on outcomes of interest, e.g., the effect of parental income on children's outcomes. In the language of econometrics, parental genotypes are omitted variables that correlate with the child's genotype (which influence the child's behavior) as well as influence the child's environmental exposures (through the pathway of parental behavior).

Finally, because heritability can be interpreted as the population R² for the regression in Equation 1, it quantifies the degree to which an individual i's outcome could be predicted if the β_j's were known and the x_ij's were observed (Visscher et al. 2008). This will become an increasingly relevant upper bound as DNA information becomes more widely available and better estimates of β_j's become possible. More immediately, a more heritable outcome may be a better target for efforts to discover particular SNPs that affect it because, all else equal, a more heritable outcome is likely to have more SNPs of larger effect.

The most common method for estimating heritability is the twin study. Twin studies exploit the fact that there are two types of twins: monozygotic (MZ) twins, who are essentially identical genetically,⁶ and dizygotic (DZ) twins, whose genetic endowments are as correlated as those of ordinary siblings. The markedly higher resemblance that is often observed for MZ twins when compared to DZ twins on an outcome is therefore often interpreted as evidence that genetic endowment explains some of the variation in the trait.

Under some strong assumptions, data on the outcome for MZ and DZ twin pairs can be used to obtain a quantitative estimate of heritability. In terms of the conceptual framework described above, begin by assuming that an individual's genetic endowment g_i is independent of residual factors ∊_i. Because the two members of an MZ twin pair, m and m′, have virtually identical genetic endowments, the covariance of their outcomes is given by

$$\mathrm{Cov}(y_m,y_{m^{\prime }})=\mathrm{Var}\left(g_m\right)+\mathrm{Cov}({∊}_m,{∊}_{m^{\prime }}).$$ (2)

Denoting the two members of a DZ twin pair by d and d′, the covariance of their outcomes is given by

$$\mathrm{Cov}(y_d,y_{d^{\prime }})=\frac{1}{2}\mathrm{Var}\left(g_d\right)+\mathrm{Cov}({∊}_d,{∊}_{d^{\prime }}).$$ (3)

The claim that Cov(g_d, g_d∊) equals $\frac{1}{2}$ Var(g_d) is not an immediate consequence of the fact that DZ twins share half their DNA on average (see Falconer & Mackay 1996, chapter 9, for the proof of the claim). The argument relies on the restriction in Equation 1 that the genotypes affect the outcome linearly and additively, and it requires the additional assumption that parents mate randomly (i.e., assortative mating on genetic endowments is ruled out).

If the distribution of genetic endowments and residual factors is the same both among MZ twins and among DZ twins as among the general population, then all three groups have the same population variance of genetic endowments, Var(g_m) = Var(g_d) = Var(g_i), as well as the same population variance of outcomes, Var(y_m) Var(y_d) = Var(y_i).

The final key assumption is that

$$\mathrm{Cov}({∊}_m,{∊}_{m^{\prime }})=\mathrm{Cov}({∊}_d,{∊}_{d^{\prime }})\equiv {\mathrm{Cov}}_{∊}.$$ (4)

Following Jencks (1980), this is how we interpret what is informally called the equal-environment assumption. It requires that the residual factors covary equally for MZ twins as for DZ twins. Of the several strong assumptions in twin studies, this one has generated the most controversy, in part because it is rarely defined precisely, and it is easy to misinterpret. Clearly, MZ twins experience a more similar environment than DZ twins do: For example, they are more similar in college completion and career interests, and because they look the same, they may evoke more similar reactions from others. The terminology “equal-environment assumption” misleadingly suggests that this greater similarity of MZ twins' environments violates the assumption in Equation 4. However, to the extent that this similarity in environment is caused by the similarity in genetic endowment, it is not a violation. Instead, the assumption in Equation 4 would be violated if, e.g., social interactions with an MZ twin generate higher covariance in residual shocks. For example, because he is genetically identical, an MZ twin may learn more about his own preferences from his cotwin's experiences than a DZ twin does. Stenberg (2011) discusses the conceptual issues in interpreting the equal-environment assumption and surveys some attempts to interrogate it empirically.

Now, dividing through Equations 2 and 3 by the respective population variances, we obtain

$$\frac{\mathrm{Cov}(y_m,y_{m^{\prime }})}{\mathrm{Var}\left(y_m\right)}=\frac{\mathrm{Var}\left(g_m\right)}{\mathrm{Var}\left(y_m\right)}+\frac{\mathrm{Cov}({∊}_m,{∊}_{m^{\prime }})}{\mathrm{Var}\left(y_m\right)},$$ (5)

$$\frac{\mathrm{Cov}(y_d,y_{d^{\prime }})}{\mathrm{Var}\left(y_d\right)}=\frac{1}{2}\frac{\mathrm{Var}\left(g_d\right)}{\mathrm{Var}\left(y_d\right)}+\frac{\mathrm{Cov}({∊}_d,{∊}_{d^{\prime }})}{\mathrm{Var}\left(y_d\right)},$$ (6)

Because $\frac{\mathrm{Cov}(y_m,y_{m^{\prime }})}{\mathrm{Var}\left(Y{y}_m\right)}$ and $\frac{\mathrm{Cov}(y_d,y_{d^{\prime }})}{\mathrm{Var}\left(y_d\right)}$ the correlation in outcomes across MZ pairs and DZ pairs, can be estimated from a sample of twins, Equations 2 and 3 define two moment conditions that jointly identify heritability. Although more sophisticated estimation methods are available, the simplest heritability estimator is just to “double the difference” between the correlations,

$$\frac{\widehat{\mathrm{Var}\left(g_i\right)}}{\mathrm{Var}\left(y_i\right)}=2\left(\frac{\widehat{\mathrm{Cov}(y_m,y_{m^{\prime }})}}{\mathrm{Var}\left(y_m\right)}-\frac{\widehat{\mathrm{Cov}(y_d,y_{d^{\prime }})}}{\mathrm{Var}\left(y_d\right)}\right).$$ (7)

Additional moments can be computed from data sets with more sibling types, thereby allowing the identification of more realistic models that relax the equal-environment assumption, the assumption that the effects of genotypes are purely additive, that mating is random, and that genetic endowments do not interact with the environment.⁷ For an illustration of some of these ideas in the context of income heritability, we refer readers to Björklund et al. (2005).

The moment conditions in Equations 5 and 6 also identify $\frac{{\mathrm{Cov}}_{∊}}{\mathrm{Var}\left(y_i\right)}$ which is typically called the common environmental component. This is the proportion of population variance in the outcome explained by residual factors shared among twins. It is often interpreted as the proportion of population variance in the outcome explained by residual factors shared among siblings in general, an interpretation that requires the additional assumption that Cov_∊ is also the covariance in residual factors among nontwin siblings. Although viewed by geneticists as a by-product of the twin method of estimating heritability, this common environmental component is of interest to economists: It is a descriptive statistic measuring how much existing variation in family-rearing environments accounts for variation in outcomes.

A simple example helps build some intuition for why this variance partitioning will often imply nonnegligible heritabilities for outcomes such as income that are many steps removed in the chain of causation from genes and protein production (Jencks 1980). Consider a large sample of identical twins who are separated at birth and then randomly assigned to families. Under these conditions, and if nongenetic shared experiences in the uterine environment are not a source of greater MZ similarity, then any resemblance between the two twins must ultimately result from similarity in genetic endowment. In this case, Cov(∊_m, ∊_m′) = 0, so heritability could be estimated merely by computing the correlation in outcomes. This example illustrates that heritability estimates capture not only “direct” genetic effects, but also “indirect” effects that operate through environmental exposures that are endogenous to genetic endowments. For example, a genotype may be a source of selection into environments that in turn affect outcomes; e.g., genetic variation in cognitive ability may be mediated by self-initiated exposure to books (Lee 2010), which is ultimately caused by genetic influences on preferences. As another example, an individual's genotype may evoke environmental responses, such as parental investments (Becker & Tomes 1976, Becker 1993, Lizzeri & Siniscalchi 2008).

Taubman (1976) introduced twin studies into economics. In a sample of approximately 2,500 white male twins who were all army veterans, he estimated the heritability of income to be between 18% and 41%. The basic finding that income is moderately heritable has now been repeatedly replicated in a variety of samples, including nontwin samples (Rowe et al. 1999, Björklund et al. 2005). Sacerdote (2010) provides a recent review of behavior genetic work in economics, including research on adoptees.

A string of recent papers has shown that measures of economic preferences, usually elicited from either incentivized experiments or surveys, have heritabilities in the 20%–30% range (Wallace et al. 2007; Cesarini et al. 2008, 2009, 2010, 2012; Barnea et al. 2010), although two papers report a considerably higher estimate (Zhong et al. 2009a, Zyphur et al. 2009). Differences in common environment explain little of the variation in these outcomes.

These estimates of heritability (and also those of common environment effects) are likely biased toward zero, however, because of measurement error. Evidence for this view comes from Beauchamp et al. (2011a), who analyze a data set of responses from over 11,000 twins to a battery of survey questions on risk attitudes. A subset of the respondents answered the survey twice. Beauchamp et al. (2011a) find that after adjustment for measurement error (assessed through the subset of repeat respondents), heritability for various survey-based measures of risk taking is estimated to lie in the neighborhood of 40%–50%, quite similar to the consensus estimates for personality and intelligence (Jang et al. 1996, Bouchard & McGue 2003). Just as the original estimates of parent-child correlations in income (Becker & Tomes 1986) were later shown to be greatly attenuated by measurement error (Solon 1992, Zimmerman 1992, Mazumder 2005), so it would appear that twin-based estimates of heritability that fail to adjust for measurement error are quite severely downward biased.

3.1. Heritability of Permanent Income

We now turn to an illustration of the use of twin-study methods by reporting some new estimates of two variables that are of central interest in economics: permanent income and net wealth. Past work has tended to focus on the heritability of current income, but for the purpose of describing inequality in the standard of living, economists are typically more interested in consumption, or permanent income, than in transitory income. Largely because of data limitations, existing studies have focused on the heritability of income measured during a single year (Taubman 1976) or up to three years (Björklund et al. 2005). Here we present heritability estimates of income averaged up to 20 years. For expositional convenience, we relegate a detailed variable and sample description to Supplemental Appendix 1 and only sketch the details here.

We use a Swedish sample of twins from the Screening Across the Lifespan Twin (SALT) study, augmented with a small number of individuals who answered a survey administered by the registry in 1973 (Q73). The SALT sample is described in Lichtenstein et al. (2002) and is composed of twins born between 1926 and 1958. We use panel data on income from 1968 to 2005, drawn from administrative records. We restrict attention to individuals for whom we have complete income data for the 20-year period and whose average yearly income exceeded SEK 1,000 (approximately USD 150).⁸ Such individuals constitute 94% of the original sample (for further information about the sample and summary statistics, see Supplemental Appendix 1). We use the natural logarithm of income, and we residualize on a second-order age polynomial to account for income differences across birth cohorts.

Table 1 reports MZ and DZ correlations for income. In this sample, the estimated MZ correlations for single-year log income are 0.41 for men and 0.27 for women, which are roughly comparable to existing estimates based on US data (Taubman 1976). The male MZ correlation in our sample is a little higher than the figure reported by Björklund et al. (2005). However, when we average over a longer time period, we find that both the MZ and DZ correlations rise, suggesting a larger role for genetic factors in explaining the variation in permanent income. In male MZ twins, the correlation rises from 0.41 to 0.63, and in female MZ twins, the correlation rises from 0.27 to 0.48. The DZ twin correlations also rise, but not as dramatically.

Table 1.

Sibling correlations for log income averaged over multiple years

	Men			Women
	MZ	DZ	p value	MZ	DZ	p value
1 year	0.406 (0.344–0.474)	0.164 (0.123–0.211)	<0.001	0.266 (0.206–0.327)	0.143 (0.095–0.190)	0.002
3 years	0.513 (0.412–0.633)	0.193 (0.150–0.243)	<0.001	0.293 (0.237–0.352)	0.137 (0.099–0.184)	<0.001
5 years	0.512 (0.447–0.574)	0.201 (0.161–0.251)	<0.001	0.297 (0.239–0.361)	0.198 (0.145–0.253)	<0.001
10 years	0.556 (0.486–0.618)	0.241 (0.199–0.285)	<0.001	0.353 (0.293–0.419)	0.226 (0.180–0.272)	<0.001
20 years	0.626 (0.574–0.676)	0.270 (0.223–0.317)	<0.001	0.481 (0.431–0.528)	0.221 (0.170–0.282)	<0.001

Data are from the SALT sample of the Swedish Twin Registry. This table reports the log-income correlations for monozygotic (MZ) and dizygotic (DZ) twin pairs, separately by sex, with log income averaged over 1, 3, 5, 10, and 20 years. Income is defined as the sum of income earned from wage labor, income from own business, pension income, and unemployment compensation. The sample is restricted to those individuals for whom there are income data at ages 31 through 50 and the average income exceeds SEK 1,000 (approximately USD 150). Confidence intervals are in parentheses below the point estimates. Confidence intervals and p values are bootstrapped.

In these data, applying the simple double-the-difference estimator (Equation 7) typically produces a negative estimate of the family environment.⁹ We therefore instead proceed by imposing the restriction that the family environment component is zero and obtain a rough estimate of heritability by taking the average of the MZ correlation and twice the DZ correlation. This estimator suggests that heritability increases from 0.37 to 0.58 in men as we move from single-year income to a 20-year average. The corresponding figures for women are 0.28 and 0.46. These findings suggest that permanent income is more heritable than single-year income. This conclusion partly seems to reflect the fact that measurement error and transitory shocks generate a downward bias in estimates of heritability (Solon 1992, Zimmerman 1992, Mazumder 2005), consistent with our earlier conjecture that the heritability estimates of many other economic outcomes are downward biased.

These patterns of correlations illustrate Turkheimer's (2000) three “laws” of behavior genetics, which are not theoretical necessities, but rather stylized facts that summarize the broad pattern of empirical findings in several decades of behavior genetics studies. The first law states that all behavioral outcomes are heritable. For comparison with our estimates of around 0.50 for permanent income, the heritability of personality traits and cognitive abilities is about 0.40 to 0.60 (Plomin et al. 1994), and the heritability of height is about 0.80 (e.g., Silventoinen et al. 2003). Indeed, although Turkheimer's first law is stated qualitatively, it could be made quantitative: Of the hundreds of outcomes analyzed to date, almost all have heritabilities estimated between 0.20 and 0.80 (see Plomin et al. 2008 for a review). The second law states that common family environment explains less variance than genes do, and the third law states that a substantial part of the variance in the outcome is left unexplained by the sum of genetic and common environment effects. Our results are consistent with the second and third laws, as well.

3.2. Heritability of Wealth

To study wealth, we use data from the SALTY (Screening Across the Lifespan Twin Study: Younger Cohort) survey, which was recently administered by the Swedish Twin Registry. There are a total of 11,418 usable responses, but the wealth questions we study here were only administered to approximately 40% of the survey respondents (for further information and summary statistics, see Supplemental Appendix 1). Because this sample size is far smaller, and because wealth data are generally noisier than income data, our results on wealth are much less precise. Nonetheless, we report these results because, as far as we are aware, this is the first estimate of the heritability of wealth.

We use responses to a series of questions in which survey respondents are asked to indicate their assets in various categories, as well as their total debt. Because wealth results tend to be very sensitive to a few outliers with extreme values, we apply two transformations to the data. The first, which is frequently recommended for wealth data (see, e.g., Pence 2006), is the hyperbolic sine transformation, sinh⁻¹ $\left(x\right)=\ln \left(x+\sqrt{(x^2+1)}\right)$. This transformation is used to reduce the influence of extreme observations while—unlike the log transformation commonly used for other kinds of data—still allowing for negative values. As a robustness check, we also report results with the variable transformed to have a normal distribution. Formally, we first percentile-rank transform the net wealth variable and then take the inverse of the standard normal distribution of the ranking. This ensures that the resulting variable is standard normal.

Table 2 reports MZ and DZ correlations for wealth. The sibling correlations in wealth are quite low and are estimated with less precision than the income correlations because only a subset of the SALTY respondents were asked about their assets and debt. Indeed, in the analyses separately by sex, there is even an instance of the male DZ correlation being higher than the MZ correlation, which we believe is likely to reflect sampling variation. When we pool for males and females, however, we find that the correlations in MZ twins are significantly higher than the DZ correlations, implying heritability levels that range from about 0.20 to 0.40. Nonetheless, given the small sample and the imperfect measurement, we interpret these findings cautiously.

Table 2.

Sibling correlations for wealth

	Men			Women			Pooled
	MZ	DZ	p value	MZ	DZ	p value	MZ	DZ	p value
Hyperbolic sine	0.088 (−0.015–0.249)	0.162 (−0.007–0.375)	0.692	0.446 (0.181–0.573)	0.301 (0.079–0.280)	0.019	0.282 (0.144–0.434)	0.109 (0.013–0.256)	0.054
Standard normal	0.411 (0.277–0.533)	0.378 (0.220–0.524)	0.381	0.380 (0.309–0.569)	0.072 (0.152–0.460)	0.096	0.432 (0.331–0.529)	0.336 (0.219–0.440)	0.084

Data are from the first wave of the SALTY sample of the Swedish Twin Registry. Net wealth is defined as the difference between the total self-reported value of assets and total self-reported debt. The asset classes considered are property (including summer house), stocks, bonds, transportation vehicles, and other. Respondents are asked to prorate in cases of joint ownership of an asset or joint debt. The exact question wording is in Supplemental Appendix 1. Net wealth is transformed as described in the text. The results do not change appreciably if we remove outliers by restricting the sample to individuals with an absolute net wealth lower than SEK 10,000,000 (approximately USD 1,500,000). Confidence intervals are in parentheses below the point estimates. Confidence intervals and p values are bootstrapped.

4. MOLECULAR GENETICS AND ECONOMICS

Molecular genetics is the field of research that studies the structure and function of DNA. Unlike behavior genetics, which draws indirect inferences regarding the effect of genetic endowments as a whole, molecular genetics involves directly measuring the genotypes for particular SNPs. Genoeconomics is an emerging field that incorporates such molecular genetic data into economic research.

4.1. The Promises of Genoeconomics

In our view, genoeconomics will ultimately make significant contributions to economics. We emphasize the word “ultimately” because—as is clear below in our discussion of the pitfalls of genoeconomics—there are many challenges to be overcome before these contributions can be realized. Nonetheless, it is the transformative promise of genoeconomics that makes us believe that, despite the challenges, the enterprise is worth pursuing. We anticipate that the eventual contributions will fall into four main categories.

4.1.1. Direct measures of previously latent parameters

First, measuring genotypes will advance empirical analysis by providing direct and exogenous measures of preferences and abilities. For example, as discussed above, an individual's FTO genotype may be a measure of preference for fatty foods. Preferences and abilities are key parameters in many models but currently must usually be treated as latent, unobserved variables. In principle (although not yet in practice), genetic methods could be used to identify such key parameters and thereby enable estimation of richer structural models.

4.1.2. Biological mechanisms

Second, social scientists will use genotypic data to learn about the biological mechanisms that underlie behaviors of interest. One possibility is that the genetic data can be used for tests of existing hypotheses. For example, experiments in which humans are exposed to the neuropeptide oxytocin suggest that oxytocin causes trusting behavior (Kosfeld et al. 2005). This leads naturally to the hypothesis that variation in the gene OXTR, which encodes the receptor for oxytocin, may be related to variation in trust-related behaviors. Unfortunately, the reported association between genetic polymorphisms in OXTR and trusting behavior (Israel et al. 2009) has not been replicated (Apicella et al. 2010). Nonetheless, the use of genetic data to explore existing hypotheses may bear fruit, and we review a number of efforts along these lines below in the context of candidate gene studies.

Even more intriguingly, analysis of the genetic data might suggest new hypotheses. In medicine, unexpected genetic associations with age-related macular degeneration and Crohn's disease have led to discoveries of new biological pathways for these diseases (Hirschhorn 2009). Although it is difficult to anticipate new hypotheses, we suspect they will arise in economics. We speculate that likely discoveries will involve the nature of preferences. Whereas economists often study individual differences in terms of heterogeneity in “fundamental” preference parameters such as relative risk aversion, the (exponential) discount rate, and a weighting parameter for altruism, these primitive preferences do not (yet) rest on biological foundations—these categories were proposed by economic theorists before the modern age of empiricism. Identifying genetic differences that predict heterogeneity in behavior may provide an empirical basis for decomposing (or even rearranging) crude concepts such as risk aversion and discounting into more primitive attributes with biological microfoundations.

4.1.3. Genes as control variables and/or instrumental variables

Third, social scientists may use genetic markers as control variables, thereby improving the power of standard economic analysis. By controlling for variation that would otherwise be absorbed in residuals, economists will be able to lower the standard errors associated with estimates of nongenetic parameters.

It is also possible that economists will be able to use genes as instrumental variables (IVs) to infer the causal effect of (nongenetic) factor X on (nongenetic) factor Y using observational data. For example, this approach has been used in epidemiology to argue that greater alcohol consumption causes higher blood pressure, using as IVs genetic polymorphisms in genes that code for proteins involved in alcohol metabolism (Chen et al. 2008; for reviews of the genetic IVs in epidemiology, see Davey Smith & Ebrahim 2003 and Lawlor et al. 2008).

There are already a number of economics papers that use genes as IVs (Norton & Han 2008, Ding et al. 2009, Fletcher & Lehrer 2009, von Hinke Kessler Scholder et al. 2010). For example, Fletcher & Lehrer (2009) study the effect of mental health (X) on academic achievement (Y). In effect, the idea is to use the fact that genotypes for polymorphisms affecting mental health are randomly assigned among siblings within a family as a natural experiment. As usual with IVs, the credibility of the analysis depends on whether the assumptions underlying IV estimation are satisfied; the fact that genetic effect sizes are very small, as discussed below in Section 4.6.4, raises the concern of weak instruments, and the fact that most genetic polymorphisms have many effects, as discussed below in Section 4.6.2, suggests that the exclusion restriction will often be violated (Conley 2009, Cawley et al. 2011).

4.1.4. Targeting interventions

Finally, genetic information could eventually be useful for targeting social-scientific interventions, much like it is beginning to be useful for targeting medical interventions. For example, if dyslexia can eventually be predicted sufficiently well by genetic screening, parents with children who have dyslexia-susceptibility genes could be given the option of enrolling their children in supplementary reading programs, years before a formal diagnosis of dyslexia (see Schumacher et al. 2007 for a review of the genetic predictors of dyslexia). For adults, it is generally feasible and more accurate to measure realized preferences and abilities directly rather than relying on genetic predispositions, at least when there is no incentive to misrepresent one's type. For this reason, in the realm of economics, targeting interventions is most likely to take the form of parents obtaining genomic information about their children and then creating a developmental environment that is most likely to cultivate the children's preferences and abilities.

4.2. Estimating Genetic Effects

All these potential payoffs involve knowing the effect on an outcome of one or more particular SNPs. Therefore, most work in genoeconomics to date has been focused on estimating genetic effects, and that is likely to remain true for the foreseeable future. We discuss how genetic effects are estimated, and then we turn to the pitfalls of genoeconomics, most of which involve challenges of estimation and causal inference.

A naïve approach would be simply to estimate Equation 1, $y_i=\mu +{\sum }_{j=1}^J{\beta }_j{x}_{ij}+{∊}_i$. Even if one could measure all J SNPs in the genome, however, this regression would fail the rank condition (unless one had more than 52 million subjects!). For that reason, it is standard instead to run K ⪡ J separate regressions,

$$y_i=\mu +{\beta }_j{x}_{ij}+{∊}_i$$ (8)

one regression for each of K SNPs that have been measured in the sample.

If the genotypes x_i1, x_i2, …, x_iJ were mutually uncorrelated and uncorrelated with ∊_i, then estimating Equation 8 rather than the population regression in Equation 1 would nonetheless yield unbiased estimates of the genetic effect β_j. In fact, however, because of how DNA is transmitted from parents to child, the genotypes of SNPs physically close to each other on the genome are correlated, often highly so. Consequently, a robustly nonzero ${\widehat{\beta }}_j$ estimated from Equation 8 does not necessarily imply that the true β_j from Equation 1 is nonzero. SNP j could be proxying for a nearby, correlated SNP—possibly a SNP that is not included among the K SNPs that have been measured in the sample. For this reason, finding a robust association is the first step in a longer process (not discussed here) of obtaining high-resolution data on the associated SNP and adjacent SNPs to identify which is the causal SNP.

The estimated coefficient on SNP j could also be biased if genotype x_ij is correlated with residual factors ∊_i. Dealing with this possible confound is an important practical issue that we discuss below in Section 4.6.1 under the rubric of “population stratification.”

The two main research strategies when testing for genetic association, the candidate gene approach and the genome-wide association study (GWAS), correspond to the two ways that researchers choose which K SNPs to study.

4.3. The Candidate Gene Approach

In a candidate gene study, a researcher specifies ex ante hypotheses about a small set of K SNPs (with K typically in the 1–30 range), runs the regression in Equation 8 for each, and tests each of the null hypotheses that β_j = 0, usually at the conventional α = 0.05 significance level. Ideally, these hypotheses are derived from the known biological function of the SNP. In practice, the hypotheses are often based on previously reported associations with the same outcome or a related outcome, or the choice of SNPs is a result of their availability in the data set the researchers are using.

The candidate gene approach, or hypothesis-based approach, was the main research strategy in medical genetics prior to the availability of dense SNP chips that made it possible and relatively inexpensive to measure hundreds of thousands, or millions, of SNPs. Candidate gene studies still predominate in the social science literature. Most of the major early successes in medical genetics were candidate gene studies. For example, because the plaques found in the brain of Alzheimer's disease patients contain apolipoproteins, researchers examined whether genotypes in the APOE gene, which codes for an apolipoprotein, are associated with Alzheimer's disease. These genotypes, based on combinations of two SNPs, are now the strongest known genetic predictors of Alzheimer's disease that are common polymorphisms, as opposed to rare mutations (Strittmatter et al. 1993, St. George-Hyslop 2000).

Although the hypothesis-based approach seems intuitively reasonable, aside from the minority of cases in which the hypotheses are direct (such as APOE), it has a poor track record in medical genetics. It is now widely accepted that findings from candidate gene studies typically fail to replicate. In an example that seems typical of the general pattern, a recent study used a sample with more than 20,000 individuals to examine previously reported genetic associations with lung function. Of the over 100 genes examined, only one published association was shown to be robust (Obeidat et al. 2011).

At least three factors seem to account for the apparently high rate of false positives produced by these studies. First, the sample sizes were often relatively small, and thus the statistical power is low, in the studies that initially reported positive findings, as discussed further below. Second, when the hypothesis-based approach is applied to complex diseases (or human behaviors), the basis for the hypothesis is almost always less precise than a direct link between a disease- or trait-relevant protein and the gene that codes for it. Ten years ago, those hypotheses often seemed convincing nonetheless, but today they seem much less so with the benefit of hindsight. That is partly because there are now many more known SNPs that could be hypothesized ex ante to be relevant and partly because it has become clear that—ex post, once an association has been found—it is possible to come up with seemingly plausible hypotheses about why almost any gene should be associated with the outcome of interest. And even if a plausible mechanism linking a gene to an outcome is identified, there is no guarantee that a particular SNP in the gene selected as a candidate will affect the gene's function in the necessary way. Third, publication bias—the tendency for positive findings, as opposed to nonfindings, to be selectively reported by researchers and selectively published by journals—is magnified in genetic association research because the typical data set has data on many outcomes and many SNPs. Hence false positives arise because of multiple hypothesis testing that is not adequately corrected for. The investigation of gene-gene and gene-environment interaction effects, although in theory well motivated, in practice exacerbates the multiple hypothesis-testing problem (see, e.g., Duncan & Keller 2011).

Recognizing these concerns, a leading field journal, Behavior Genetics, has recently adopted strict standards for publication of candidate gene studies (Hewitt 2012). To be considered for publication, candidate gene studies must be well powered and must account for all sources of multiple hypothesis testing, and any new finding must be accompanied by a replication. Today, the consensus view among genetics researchers is that the results from candidate gene studies are intriguing but should be interpreted with great caution.

4.4. Genome-Wide Association Studies

A GWAS is an atheoretical exercise that consists of looking for associations between the outcome and all the SNPs measured on a dense SNP chip (usually K > 500,000, and now typically K ≈ 2,500,000), without any prior hypotheses. The researcher runs the regression in Equation 8 for each of the K SNPs and tests each of the null hypotheses that β_j 0 at the genome-wide significance level, which is α = 5 × 10⁻⁸.

The correlation structure of SNPs in the human genome is now well understood, and the GWAS approach exploits this understanding in two ways. First, the SNPs that are measured on a dense SNP chip are selected such that jointly they cover, or “tag,” much of the nonrare genotypic variation across SNPs in the genome. Second, although the human genome contains approximately 52 million SNPs, because of the correlation structure, there are only effectively approximately 1 million independent SNPs. The genome-wide significance threshold of 5 × 10⁻⁸ therefore approximates the appropriate Bonferroni-corrected significance threshold of 0.05/1,000,000 (Panagiotou & Ioannidis 2012).

GWASs have produced many of the recent major discoveries in medical genetics. For example, the FTO gene mentioned above had not been hypothesized to be linked to body weight, but it repeatedly turned up in GWAS results. As nothing was previously known about this gene, its codename was assigned to represent “fat mass and obesity associated,” and intensive work has begun on discovering its biological functions (Tung & Yeo 2011). In another example, in type 2 diabetes, GWAS-derived genetic discoveries have implicated new biological mechanisms and have linked the disease to other processes, such as circadian rhythms (see Billings & Florez 2010).

4.5. Molecular Genetics and Economics: A Review

To date, most published genoeconomics papers are candidate gene studies of some economic preference parameter or economic behavior measured in the laboratory. All but one (Apicella et al. 2010) of the studies focused on laboratory measures reviewed below are based on samples smaller than 500 subjects, and in some cases smaller than 100 subjects. Ebstein et al. (2010) and Beauchamp et al. (2011b) also provide reviews of the work in genoeconomics to date.

The first genoeconomic association was reported by Eisenberg et al. (2007), who tests whether two genetic polymorphisms near dopamine receptor genes (DRD2 and DRD4) are associated with performance on a hypothetical delay discounting task measuring time preferences. The polymorphism near DRD2 had a significant association with estimated discount rates, and there was an interaction between the DRD2 and DRD4 polymorphisms (but no main effect of the DRD4 polymorphism). Another early paper was by Knafo et al. (2008), who were inspired by findings that genetic variation near the AVPR1a gene causes differences in the social behavior of voles (Hammock & Young 2002, Hammock et al. 2005). In a sample of 203 university students, Knafo et al. find that dictator-game giving was associated with variation in this gene. A number of genoeconomic papers quickly followed suit. These papers tend to study outcomes that can be classified into one of two broad categories: decision making under uncertainty or social preferences.

Several papers inspired by neuroimaging studies of decision making under risk looked for associations between genes involved in the regulation of the dopaminergic system and various measures of risk taking. Kuhnen & Chiao (2009) and Dreber et al. (2009) independently report an association between a particular polymorphism of the DRD4 gene and behavior in incentivized laboratory measures of risk taking. Neither Carpenter et al. (2011) nor Dreber et al. (2011) replicate this reported association. Other papers, also motivated by neuroeconomic theories, have reported statistically significant associations between measures of risk taking and candidate genes (Crisan et al. 2009; Zhong et al. 2009b,c; Roe et al. 2010; Frydman et al. 2011).

There have also been some reported associations with various measures of social preferences. Israel et al. (2009) report an association between a SNP in the gene OXTR and dictator-game giving. Apicella et al. (2010) fail to replicate this result in a larger sample and discuss possible explanations for the failed replication. McDermott et al. (2009) designed an experiment in which 78 genotyped subjects were told that their earnings from a vocabulary task had been reduced by an anonymous third party. Subjects were then offered the opportunity to punish the third party. The subjects were told that either 80% or 20% of their earnings had been taken by the third party. The MAOA genotype predicted the behavioral response only following the more aggressive provocation. Finally, Zhong et al. (2010) report that an interaction between a DRD4 polymorphism and season of birth affects responder behavior in the ultimatum game.

A handful of papers have examined associations between candidate genes and behaviors and outcomes outside the laboratory, such as credit card debt (De Neve & Fowler 2010, De Neve 2011), portfolio risk (Kuhnen et al. 2011), happiness (De Neve et al. 2011), and self-employment (Nicolaou et al. 2011). In a large sample, van der Loos et al. (2011) fail to replicate the reported association with self-employment.

Beauchamp et al. (2011b) is the only example of a GWAS published in an economics journal to date, although van der Loos et al. (2010) describe an ongoing study. In a GWAS of educational attainment with a sample of 7,574 Framingham Heart Study participants, Beauchamp et al. (2011b) report 20 associations that fell short of genome-wide significance. They also report a replication attempt with a sample of 9,535 individuals from a Dutch sample. None of the 20 SNP associations replicated at the 0.05 significance level, and only 9 of 20 even had the same sign. Martin et al. (2011) report on the results for a GWAS of educational attainment in a sample of 9,538 Australians and also fail to find any genome-wide significant associations.

4.6. The Pitfalls of Genoeconomics

Despite the recent explosion in the number of papers reporting genotype-behavior associations, we are pessimistic about the replicability of most findings to date. The most urgent problem—discussed in detail below—is that the most persuasive evidence suggests that true genotype-behavior associations have tiny effect sizes, so current research designs in the social sciences are woefully underpowered. However, even once this problem has been solved, there are a number of further obstacles that must be overcome before the promises of genoeconomics mentioned above—providing direct measures of latent parameters, elucidating biological mechanisms, using genes as controls or IVs, and targeting interventions—can be realized.

4.6.1. Causal inference

The promises of biological mechanisms and genes as IVs require uncovering the causal effect of particular SNPs on behavior, but most existing research designs focus on detecting correlations. There are myriad confounds to a causal interpretation. As discussed above, because of the way DNA is transmitted from parents to children, the genotype of a SNP is often highly correlated with the genotypes of nearby SNPs, necessitating follow-up work to any robustly detected association to identify which SNP is actually responsible. Another common confound is that an individual's genotype is correlated with her parents' genotypes, which in turn are correlated with the individual's family environment. For example, a SNP may be associated with cognitive ability even though it actually causes nurturing behavior; an individual with the nurturing genotype is likely to have parents with that genotype, whose bias toward nurturing behavior may lead them to create a family environment that potentiates the development of higher cognitive ability.

In practice, the most common concern is confounding from population stratification: Different groups within the sample differ in allele frequencies and also differ in their outcome for nongenetic reasons. A famous pedagogical example is the “chopsticks effect” (Lander & Schork 1994): A study concerned with finding the genetic causes of chopstick use would find a significant association for any SNP whose allele frequencies differ appreciably between Asians and non-Asians, even though most variation in chopstick use is explained by cultural factors. This example might seem to suggest that a simple fix would be to control for race or ethnicity. Indeed, it is standard practice to restrict a genetic association study to subjects of a common ethnic background. It has been found, however, that allele frequencies can differ even within ethnically homogeneous populations, such as different regions within Iceland (Price et al. 2009). For this reason, it is a common practice in GWASs to include as control variables the first four or more principal components of all the genotypes measured in the dense SNP chip. These principal components seem to pick up much of the subtle genetic structure within a population (Price et al. 2006). A disadvantage of candidate gene studies relative to GWAS designs is that they are rarely based on samples with dense SNP data and hence cannot control for subtle genetic differentiation using principal components.

In our view, building the case that a robustly identified association is causal will take time and will require convergent evidence from various research strategies. To rule out a number of potential confounds, it would be useful to have evidence for a genetic association in a data set that includes siblings, using the regression in Equation 8 but with family fixed effects. When identifying off of within-family variation, population stratification ceases to be a concern. Moreover, genotypes are randomly assigned to siblings who share the same biological parents. Complementary with such empirical evidence would be experimental evidence from animal models, in which genotypes can be experimentally modified at conception, as well as biological evidence on the function of protein products of the gene.

4.6.2. Pleiotropy

There is a further obstacle to credibly using genes as IVs. For the exclusion restriction to be satisfied, the causal effects of the genes must be understood well enough to rule out alternative pathways (besides X) by which the genes could affect outcome Y. Because many genes code for proteins that have multiple functions and effects—a phenomenon called pleiotropy that in most cases biologists have barely begun to understand—it seems unlikely that we can be confident about all the consequences of any particular genotype in the foreseeable future (Conley 2009).

4.6.3. Missing heritability

Targeting interventions is one of the potential contributions closest at hand because the genetic markers can be merely predictive, rather than causal, and because an index composed of many SNPs can be used, which may in the aggregate have substantial predictive power even if any constituent SNP in the index has little or none.¹⁰ However, although we expect eventual successes, it will likely be slow and challenging to find sufficient predictive power even from an index.

In medical genetics, with the exception of a few, rare, single-gene disorders, there has been a general failure to find sizeable aggregate predictive power from the associated genetic markers identified to date—a problem now called the missing heritability puzzle (see, e.g., Int. Schizophr. Consort. et al. 2009). Consider height, a highly studied physical trait that both is measured with much less error than behavioral traits and is more heritable. Behavior genetics studies on twins and other relatives indicate that about 80% of the variability in height results from genetic factors. Furthermore, recent estimates suggest that, even just using the SNPs measured with current dense SNP genotyping technologies (which leave non-SNP genetic polymorphisms unmeasured), it should be possible to predict 45% of the variance in human height (Yang et al. 2010). Yet the aggregate predictive power from known genotypes is only about 10%, with 0.3% being the largest R² of any one of the SNPs in 180 separate locations in the genome so far found to be associated with height (Lango Allen et al. 2010). This state of affairs for height, and similar states of affairs for a variety of intensively studied medical outcomes, suggests that for these outcomes, the bulk of the genetic variance is carried by many SNPs of miniscule effects that are spread diffusely throughout the genome. If so, unrealistically large sample sizes may be required to identify all these SNPs. Given the failure to find sizeable predictable power in physical traits, the challenge is likely to be at least as large for behavioral traits where the causal mechanisms are probably more complex.

4.6.4. Low power

The most urgent problem, however, is that most efforts in the social sciences to discover genetic associations are underpowered. The fundamental reason is that almost every true genotype-behavior correlation is probably very small. For example, cognitive ability is among the most reliably measured and widely studied outcomes in social science genetics, yet it is unclear whether any purported genetic associations with cognitive ability are robust. In a meta-analysis of 67 independent samples, variation in the COMT gene was found to explain 0.1% of the variance in cognitive ability, although even this estimate is likely to be biased upward because the meta-analysis found evidence of publication bias (Barnett et al. 2008). Even if this effect size were correct, as the strongest associations are more likely to be discovered first, most of the SNPs truly associated with cognitive ability probably have smaller effects. As another example, a recent GWAS of the classic Big Five personality traits (neuroticism, extraversion, openness, agreeableness, and conscientiousness) with a sample size of approximately 20,000 individuals failed to find any genome-wide significant associations (de Moor et al. 2012).

To get a sense of the magnitude of the problem, consider a candidate gene study of a particular SNP. To simplify, suppose there are only two genotypes for the SNP, with carriers of the high variant, as opposed to carriers of the low variant, hypothesized to have a higher value for the outcome. To further simplify, suppose there are only two possibilities: Either there is a true association, or there is not. Imagine the outcome is distributed normally. Suppose it is known that, if there is an association, then the SNP explains R² = 0.1%—a rather large effect size for a single SNP (the same size as the COMT association with cognitive ability). A first question is, what sample size is required for the standard benchmark of 80% power to detect the effect using the regression in Equation 8 at the conventional, two-tailed 0.05 significance level? The answer is 7,845. This is far larger than typical samples to date in genoeconomics, which have numbered from less than a hundred to several hundred in studies using laboratory measures and a few thousand in studies using nonlaboratory data.

Now suppose that in a sample of size N, a researcher observes a statistically significant association at the 0.05 significance level. How large does N have to be for this result to constitute substantial evidence about whether there is an association? The upper half of Table 3 shows how a researcher's posterior belief (after having seen the data) that there is a true association should depend on the researcher's prior belief and on N. Of course, it is difficult to know what an appropriate prior belief is, but for a typical candidate SNP, it is probably much less than 10%. In a GWAS in which millions of SNPs are tested, the prior probability that a typical given SNP has a true relationship is less than 0.01%.

Table 3.

Posterior probability of a true association of R² = 0.1% as a function of prior probability and sample size

		Sample size
		For an association that is statistically significant at p = 0.05
		N = 100 (power = 0.06)	N = 1,000 (power = 0.17)	N = 5,000 (power = 0.61)	N = 10,000 (power = 0.89)	N = 30,000 (power = 0.99)
Prior probability of true association	0.01%	0.01%	0.03%	0.12%	0.18%	0.20%
	1%	1%	3%	11%	15%	17%
	10%	12%	27%	58%	66%	69%

		For an association that is statistically significant at p = 5 × 10−8
		N = 100 (power = 0.00)	N = 1,000 (power = 0.00)	N = 5,000 (power = 0.00)	N = 10,000 (power = 0.01)	N = 30,000 (power = 0.51)
Prior probability of true association	0.01%	0.03%	3%	57%	96%	100%
	1%	3%	47%	99%	100%	100%
	10%	25%	91%	100%	100%	100%

The assumptions underlying these calculations are provided in the text. Power is calculated using Purcell et al.'s (2003) online tool: http://pngu.mgh.harvard.edu/~purcell/gpc/qtlassoc.html. Posterior probabilities are then calculated by Bayes' rule: Pr(true|significant) = (power × prior)/{(power × prior) + [0.05 × (1 − prior)]}.

A proper Bayesian thinker would barely update his posteriors when faced with a statistically significant association in a sample of 100 individuals. Because the effect size is so small, the statistical power—the probability of finding a statistically significant association under the alternative hypothesis that there is truly a relationship—is only 6%. At a significance level of 0.05, there is a 5% probability of finding a statistically significant association under the null hypothesis. Hence finding a statistically significant association at the 0.05 level is almost equally likely under the null hypothesis as under the alternative hypothesis and hence is essentially uninformative regarding which hypothesis is more likely to be correct.

In a sample of 30,000 individuals, where statistical power is 99%, the likelihood of finding a statistically significant association under the alternative hypothesis is about 20 times the likelihood of finding a statistically significant association under the null hypothesis. When the prior probability of a true association is 0.01%, the posterior probability after observing a statistically significant association is 0.20%, which is unfortunately still extremely low. Even if the prior probability of a true association were as high as 10%, the posterior probability after observing a statistically significant association would be 69%, leaving a 31% chance that the reported association is a false positive.

Because the effect sizes are so small, these calculations defy our usual expectations about the robustness of statistically significant findings and suggest that, when evaluating candidate gene studies, it is valuable to conduct such calculations rather than rely on our faulty intuitions. One can see from the upper part of Table 3 that a researcher should conclude almost nothing about a genotype-behavior relationship from a sample size in the hundreds, and sample sizes must be in the many thousands before nontrivial inferences are appropriate.¹¹

5. CAUTIONARY TALES AND CONSTRUCTIVE RESPONSES

In this section, we illustrate some of the challenges of genoeconomics research with two cautionary tales that trace out the trajectory of our research projects in this area, and outline three constructive responses.

5.1. An Icelandic Saga

When we began our work on genoeconomics approximately 10 years ago, before dense SNP chips became relatively inexpensive, the standard empirical strategy in the medical genetics literature was the candidate gene approach, so we followed the same methodology. At the time, there were extremely few data sets that contained both economic and genotypic data. No economic data sets had collected genotypic data, but we were fortunate to team up with the AGES-RS, an Icelandic medical study (described in Harris et al. 2007) that happened to have collected several survey measures of interest to economists. Here we sketch our analysis of this data; full details are available in Supplemental Appendix 2.

Constrained by what was available in the data, we constructed the following eight “economic outcomes” that serve as dependent variables in the analysis: (a) time preference index (an index of present-oriented behaviors, combining measures of alcohol use, cigarette use, and body mass index at age 25), (b) happiness, (c) self-reported health, (d) housing wealth, (e) human capital index (an index of human capital, combining years of education with number of foreign languages learned), (f) income (predicted by occupation held at midlife), (g) labor supply, and (e) social capital index (an index of social capital, combining the amount of regular contact with relatives and friends, attendance at religious services, and participation in social activities).

We then created a list of candidate genes that we believed were most likely to be related to economic decision making, given what was known at the time our study was initiated. We obtained enough funding to have blood samples from 2,349 AGES-RS participants run through a custom-designed microarray that could measure 384 SNPs. We chose which genes to study based on two criteria: published associations with cognition-related outcomes or disorders (e.g., cognitive ability, long-term memory, Alzheimer's disease, schizophrenia, attention deficit hyperactivity disorder) and/or membership in the dopamine or serotonin neurotransmitter systems. If the gene was small enough, we included enough SNPs to capture most of the possible variation in that gene. If the gene was too large, we included only the SNPs on the gene that had been specifically mentioned in published association studies. We supplemented the 384 SNPs we specified with several additional SNPs that had been previously genotyped in AGES-RS for other purposes (e.g., the two SNPs in APOE that define the genotypes associated with late-onset Alzheimer's disease). Adding these additional SNPs, and subtracting the few SNPs that failed to genotype correctly, our total number of SNPs was 415 in a total of 68 genes.

We ran the regression in Equation 8 3,320 times, one for each of the 8 outcome × 415 candidate SNP combinations. The three most statistically significant associations are the social capital index with a SNP called rs17529477 in the gene DRD2 (p < 0.0005), the time preference index with rs908867 in BDNF (p < 0.0001), and the human capital index with rs2267539 in SSADH (p < 0.001). The results are virtually identical when linear controls for age and sex, the standard control variables in medical genetics, are included in the regressions.

Naturally the standard p values (reported above) from such regressions are easily misinterpreted because of multiple hypothesis testing. In 2008, we were able to attempt to replicate these three “top hits” in a nonoverlapping sample of 1,759 AGES-RS participants who had been genotyped using a dense SNP chip (the Illumina Hu370CNV) for a different research project. Although that chip did not directly measure any of the three SNPs that exhibited a promising association, it is standard in genetics to impute data on missing SNPs using observed data on surrounding SNPs, which is usually highly accurate because of the high correlation among nearby SNPs. Although the imputation quality for DRD2 rs17529477 was relatively low, we were able to impute the other two SNPs with high accuracy.¹²

The association between the time preference index and BDNF rs908867 did not replicate (p = 0.531). The association between the human capital index and SSADH rs2267539 not only replicated (p = 0.02), but had similar effect sizes in the two samples: a coefficient of 0.23 with a standard error of 0.07 in the first sample and a coefficient of 0.19 with a standard error of 0.08 in the second sample. Combining the first and second samples, this association has an R² of 0.47%, which is quite large for an individual SNP.

Figure 1a (see color insert) shows, for the first and second samples combined, the average level of the human capital index by genotype. In this case, it turns out that the relationship between the level of the index and the number of A alleles is monotonic. To give a sense of the magnitude of the relationship in natural units, the figure also presents the mean years of education—the main constituent of the index: The years of education for G/G participants were 8.3, and this increased to 8.8 for A/G participants and 8.9 for A/A participants. Table 4 shows, for the combined sample, the regression specification in Equation 8 with controls for population stratification (the first two principal components of the dense SNP data) and regional variation in education.

Figure 1.

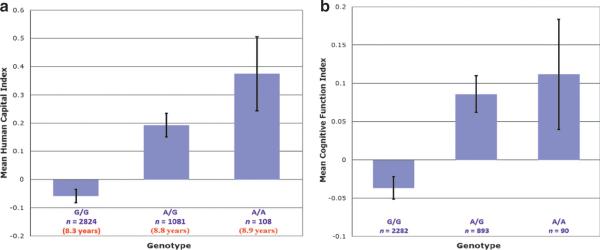
Mean of the human capital index by genotype. (a) The human capital index is a composite variable comprising educational attainment and the number of languages learned. The mean years of educational attainment by genotype are shown in parentheses below the sample size. (b) The cognitive function index is a composite variable comprising digit symbol substitution (WAIS), digit span (forward and backward), spatial working memory, and long-term memory (CVLT recall and recognition). In the cognitive function sample, survey respondents who scored ≤23 on the Mini Mental State Examination are dropped. Both the human capital index and the cognitive function index are standardized to have zero mean and unit variance. The genotype is for SSADH rs2267539. Error bars show ±1 standard error. Data are from the AGES-RS.

Table 4.

Ordinary-least-squares regression of human capital index on genotype

	(1)	(2)	(3)	(4)
Genotype (number of A alleles)	0.218 (0.054)	0.178 (0.060)	0.185 (0.059)	0.185 (0.059)
Birth year	0.055 (0.005)	0.046 (0.006)	0.046 (0.006)	0.046 (0.006)
Female	−0.692 (0.056)	−0.681 (0.062)	−0.682 (0.061)	−0.684 (0.062)
Urban			1.054 (0.242)	1.323 (0.578)
GWAS principal components?	No	Yes	Yes	Yes
Region fixed effects?	No	No	Yes	Yes
Region × urban fixed effects?	No	No	No	Yes
R 2	0.068	0.069	0.100	0.102
N	4,016	3,198	3,198	3,198

Data are from AGES-RS. The human capital index is a composite variable comprising educational attainment and the number of languages learned. It is standardized to have zero mean and unit variance. The genotype is for SSADH rs2267539. Coefficients for the constant term and control variables are suppressed. Standard errors are in parentheses. Urban is a dummy variable for whether the respondent grew up in an urban area. Genome-wide association study (GWAS) principal components refer to the first two principal components of the dense single-nucleotide polymorphism (SNP) data. Region fixed effects are dummies for the nine regions of Iceland (see Price et al. 2009). The first column includes the 2,349 AGES-RS respondents whom we had genotyped with our SNP custom microarray, plus the nonoverlapping subset of 3,198 AGES-RS respondents for whom dense SNP data were available. Because the other columns control for principal components of the dense SNP data, they include only the 3,198 respondents for whom dense SNP data were available.

An association is less likely to be a false positive if there is a plausible biological mechanism for the relationship. The gene SSADH (also known as ALDH5A1) codes for an enzyme that metabolizes GABA, the principal inhibitory neurotransmitter in the brain. This gene matters for cognition: It has been associated with general cognitive ability (IQ; Plomin et al. 2004), it is related to the preservation of cognitive function in the elderly (De Rango et al. 2008), and it may be undergoing recent natural selection (Leone et al. 2006), as might be expected for a gene that has a large effect on a trait that could assist in survival and reproduction. Furthermore, rare mutations of SSADH are associated with mental retardation, and animals in which the gene is experimentally knocked out (i.e., rendered inoperative) are cognitively impaired and develop epileptic seizures (Buzzi et al. 2006, Knerr et al. 2008).

If the gene is related to our human capital index via its effect on cognitive ability, then we should observe that cognitive ability mediates the relationship between the SNP and human capital. To directly test this mechanism, we constructed a measure of cognitive ability using a variety of cognitive tests that had been administered to AGES-RS participants (see Supplemental Appendix 2 for details).

Figure 1b shows that, as expected, this index of cognitive ability is associated with the SNP of interest, SSADH rs2267539. In a regression (Equation 8) with standardized cognitive ability as the outcome, the coefficient is 0.11 with a standard error of 0.03, indicating that a switch of one G allele to an A allele is associated with one-ninth of a standard deviation greater cognitive ability (corresponding to approximately 1.7 points on the IQ scale). This association is highly statistically significant, with a relatively large R² of 0.3%. Also as expected, and consistent with much prior research (e.g., Cawley et al. 2001), a 1-standard-deviation increase in cognitive ability is associated with 1.15 additional years of schooling (p < 0.001, R² = 13%) in our data set. Finally, in the regression in Equation 8 with the human capital index as the outcome, the coefficient on genotype is reduced by including cognitive ability as a control, indicating that cognitive ability is a statistical mediator. Applying the Sobel test for mediation (MacKinnon et al. 2002), we can reject the null hypothesis of no mediation (z = 3.37, p = 0.0008), and we estimate that cognitive ability mediates 51% of the relationship between the human capital index and the SNP.

The best test of whether a finding is a true positive is whether it replicates in multiple new, completely independent samples. Three additional research groups agreed to check in their data whether the association replicates: the Framingham Heart Study, the Wisconsin Longitudinal Study, and a sample of healthy control subjects for the Swedish Large Schizophrenia Study. As we could not construct our human capital index in these samples, we studied only educational attainment, the most important component of the human capital index.

The Framingham Heart Study is a cardiovascular disease study that began in 1948 with a random sample of 5,209 participants from Framingham, Massachusetts. A sample with dense SNP data is available for 7,357 individuals, a mix of original participants and their relatives. Educational attainment is measured via nine categories, which we converted to estimated years of schooling. In this sample, educational attainment is not associated with SSADH rs2267539. In the regression in Equation 8 with standardized years of education as the outcome, the coefficient on the number of A alleles is 0.06 with a standard error of 0.06 (p = 0.30). As the SSADH SNP with the second-strongest association in the AGES-RS sample was not available in the Framingham Heart Study, we examined the SNP in the gene with the third-strongest association. The regression coefficient is 0.02 with a standard error of 0.06 (p = 0.70). (In both cases, the standard errors are adjusted to correct for the presence of relatives.)

The Wisconsin Longitudinal Study is a random sample of 10,317 Wisconsin residents who graduated from high school in 1957, as well as 5,219 siblings who were enrolled later. We obtained genotypes for the three most significant SNPs in AGES-RS from a subsample of 3,408 individuals. Educational attainment is measured as years of schooling. Here it is not associated with any of our three most statistically significant SNPs from AGES-RS, and in fact the point estimates have the wrong sign in all three cases: β = −0.02 (standard error = 0.07) for the most strongly associated SNP, β = −0.00 (standard error = 0.09) for the second SNP, and β = −0.05 (standard error = 0.06) for the third SNP.

Our third non-Icelandic replication sample included 1,235 individuals from the healthy control group for the Swedish Large Schizophrenia Study. These are individuals who were identified from national population registers to match the schizophrenia group (which we do not analyze) along the characteristics of age, gender, and county of residence. Educational attainment is measured on a scale of one to six, ranging from less than nine years to postgraduate education, which we convert to a standardized variable for the purposes of the regression analysis. It is not associated with either our most statistically significant SNP from AGES-RS (β = 0.06, standard error = 0.07, p = 0.45) or our second-most statistically significant SNP from AGES-RS (β = −0.00, standard error = 0.08, p = 0.98).

What explains our puzzling pattern of results—the finding of an association that replicates with a sample similar to the original sample, passes various plausibility and robustness tests, and then fails to replicate in three other samples? We can think of four leading possibilities. First, the association in the AGES-RS data may be spurious due to confounding factors. For example, we attempted to deal with population stratification by controlling for the first two principal components of the whole-genome data, in addition to region dummies, an urban dummy, and region × urban dummies. Even within an ethnically homogeneous population such as Iceland, however, there may be ethnic stratification on a finer scale than would be picked up by these controls. As a purely speculative example (meant just to illustrate the many possibilities), descendants of former nobility/leadership lineages could happen to have more A alleles and also be more educated. Second, the association may be a true positive, but local to the Icelandic environment. This could occur if, for example, cognitive skills that are taught in schools outside of Iceland are instead self-taught within Iceland only by individuals with more A alleles. Third, the association may be a true positive, but local to the Icelandic genome, if the gene in question primarily has effects via its interaction with other genes and those genes differ between Icelanders and other populations. Fourth, our multiple hypothesis tests could have generated a false positive. Only because of chance did we happen to replicate the finding in a smaller sample from the AGES-RS data.

Patterns of results like ours are difficult to interpret. There are reasons to emphasize our replication within AGES-RS—which had exactly the same variable definitions and held constant the environmental and genotypic background—and discount our subsequent replication attempts: The ethnic makeups in the Framingham Heart Study and Wisconsin Longitudinal Study differ substantially from the ethnic makeup in AGES-RS, and the Swedish sample (although ethnically more similar to the Icelandic one) is the smallest study that we had. Yet there are also reasons to discount our plausibility and robustness checks. We chose our set of candidate genes because we thought they were most likely be involved in decision making, so it is not surprising that the association we happened to find “makes sense” biologically. Cognitive ability is correlated with educational attainment, so it is not surprising that a SNP that happened to correlate within AGES-RS with educational attainment also correlates in that sample with cognitive function. Similarly, any confound that might explain the association between the human capital index and our most significant SNP on SSADH would equally well explain the association with other SNPs on SSADH, which are correlated with it.

Our failure to replicate a seemingly robust association illustrates one of the major challenges for integrating genetics and social sciences. But our experience is not unique; indeed, it closely recapitulated a common story line in medical genetics research.

5.2. Wisconsin Tale

When we began our candidate gene study in AGES-RS, we believed—as did most medical genetic researchers at the time—that the candidate gene approach was a reasonable approach. Our experience helped us to appreciate what had become, by the time our failure to replicate was complete, the new consensus view among the medical genetics community: The candidate gene approach is a path strewn with false positives.

These realizations made us skeptical of many published candidate gene associations. Yet social scientists, both authors and referees, seemed much less conscious of the fact that reported candidate gene associations are unlikely to be true. Consequently, we set out to systematically test existing candidate genes for general cognitive ability, also known as “intelligence,” or IQ, which is among the most highly studied psychological traits in molecular genetic work because it is among the most heritable of behavioral traits [estimates range from 0.50 to 0.80 for IQ measured in adulthood (Bouchard & McGue 2003)]. There is a large literature of studies showing associations between many SNPs in various genes and general cognitive ability (see Payton 2009 for a comprehensive review). As is typical of candidate gene studies in the social sciences, many of these results are based on small samples and had not seen any published replications.

As we report in Chabris et al. (2012), we sought to replicate published associations between 12 genetic polymorphisms and general cognitive ability using three independent data sets: the previously described Swedish Twin Registry, Wisconsin Longitudinal Study, and Framingham Heart Study, with a total sample size of 9,755 participants. Of 32 independent tests across all three data sets, only one was nominally significant at the p < 0.05 level.¹³ In the data from the Wisconsin Longitudinal Study, in which we tested all 12 genetic polymorphisms and had the most statistical power, we cannot reject the null hypothesis that the combined effect of those SNPs is zero—even though given our sample size of 5,571 individuals, we had 99% power to detect a combined effect of just R² = 0.52%. Further power calculations suggested that, if the previously reported associations were not false positives, we should have expected between 11 and 15 replicated significant associations in our 32 tests, rather than the one that we found. Our analysis led us to conclude that most published SNP associations with general cognitive ability are probably false positives, most likely because the investigators in those studies inadvertently used samples that were much too small.¹⁴

5.3. Responding to the Inferential Challenges

We believe there are several constructive responses to the inferential challenges posed by the small explanatory power of individual SNPs.

5.3.1. Pooling data to increase power

When it became widely recognized in the medical literature that candidate gene studies were generating a high rate of false positives, and when dense SNP genotyping became sufficiently inexpensive, the standard research design became GWASs. Obviously, relative to a candidate gene study, a GWAS magnifies the multiple-testing problem, but the stringent genome-wide significance threshold of p < 5 × 10⁻⁸, combined with implementing the GWAS in a large sample, has generated findings that have proven much more replicable.

The lower half of Table 3 shows the results of the same Bayesian calculation as the upper half, except for an association that is statistically significant at the p = 5 × 10⁻⁸ level (rather than p = 0.05). Because of the stringent significance threshold, statistical power is much lower at any given sample size N. Indeed, a true association with effect size R² = 0.1% will probably not replicate at a genome-wide significance level for a sample smaller than 10,000 individuals, and there is only a 50% chance that an association known to be true will be detected in a sample of 30,000 individuals. Nonetheless, an association that reaches statistical significance at the genome-wide significance level in a sample of 10,000 or more individuals is almost certain to be a true positive.

Recognizing this, the medical literature has been moving in the direction of forming consortia of data providers. In such a consortium, a GWAS is conducted in each data set, and the “discovery phase” is carried out as a meta-analysis of these GWAS results, a so-called meta-GWAS. In the “replication phase” that follows, the associations implicated in the discovery phase are investigated in independent samples.

On the one hand, the hurdle that genotype-outcome associations must hold in different samples that are typically drawn from populations with different ethnicities and environments—a requirement that is implicit in a meta-GWAS and explicit in the requirement that associations replicate in independent samples—means that GWAS researchers are unlikely to identify genetic associations that exist only in particular environments. The set of associations that are reported will tend to be ones that are among the strongest and the most universal—indeed, the fact that many true associations will not be discovered by a meta-GWAS perhaps helps account for the missing heritability puzzle discussed in Section 4. On the other hand, the samples used in meta-GWASs have proven to be sufficiently large to detect SNP associations with modest effect sizes, and the findings that have emerged from these cooperative studies appear to be more likely to survive the challenges of replication.

Following the lead of the medical genetics community, we, together with Philipp Koellinger, have organized the Social Science Genetic Association Consortium (SSGAC), attempting to include all relevant major data providers that have dense SNP data and social science outcome measures. The SSGAC has had three meetings since its formation in February 2011, under the auspices and guidance of the Cohorts for Heart and Aging Research in Genomic Epidemiology Consortium (Psaty et al. 2009), a successful medical genetic consortium. In forming the SSGAC, we are following in the footsteps of, and proceeding in close coordination with, the “Gentrepreneurship Consortium” that was formed for the purpose of studying genetic associations with self-employment (van der Loos et al. 2010).

5.3.2. Exploiting the cumulative effect of many single-nucleotide polymorphisms

Even in those cases in which sample sizes are too small to discover robust associations, the data may still contain valuable information about the distribution of effect sizes of the SNPs on a dense SNP chip. Yang et al. (2010) developed a method, genomic-relatedness-matrix restricted maximum likelihood (GREML), for estimating the proportion of variance explained jointly by all the SNPs measured on a dense SNP chip. The key assumption is that among individuals who are unrelated—i.e., distantly related, as all humans are related to some extent—residual factors are uncorrelated with differences in the degree of genetic relatedness. Under that assumption, an estimate of heritability can be obtained by examining how the correlation in an outcome between pairs of individuals relates to the genetic distance between those individuals. Unlike in twin studies where relatedness is known, here the relatedness is estimated from the SNP data.

Unlike GWASs, for moderately heritable traits, GREML is well powered for samples of only several thousand unrelated individuals because it aggregates the information contained in the genetic data. The GREML procedure estimates the fraction of variance of an outcome that could be predicted if a researcher had GWAS data and a look-up table that contained the true effect of all SNPs. Under the assumption that large individual-SNP effects are more likely for outcomes where the joint predictive power of all SNPs is larger, GREML can be used to assess which outcomes are the most promising to pursue for GWASs. Applying this method in a sample of 3,925 individuals, Yang et al. (2010) find that the measured SNPs could account for 45% of the variance in human height; Davies et al. (2011) apply the method to cognitive ability and obtain point estimates of 40% for crystallized intelligence (N = 3,254) and 51% for fluid intelligence (N = 3,181); and Chabris et al. (2012) similarly estimate 47% for general cognitive ability. Vinkhuyzen et al. (2012) estimate 6% for the personality trait of neuroticism and 12% for extraversion (N ≈ 12,000, varying somewhat with the outcome variable). Using a sample of 5,727 individuals from the previously mentioned SALT study, Benjamin et al. (2012) estimate 16% for educational attainment. With a smaller sample from SALTY (N ≈ 2,400), Benjamin et al. (2012) also apply GREML to survey measures of risk preference, time preference, fairness concerns, trust, and political attitudes. Although the estimates are noisy, taken as a whole they suggest that the measured SNPs account for a positive share of the variance in these traits.

As with GREML, the basic insight behind polygenic risk prediction (e.g., Int. Schizophr. Consort. et al. 2009) is that even when it is not possible to robustly identify the individual SNPs associated with an outcome, it may still be possible to make statistically efficient use of the joint predictive power of a large number of SNPs. Whereas GREML estimates the amount of predictive power theoretically attainable from the SNP data (but does not enable one to actually predict the outcome), a polygenic risk score is an attempt to use the SNP data in a given sample to actually construct a predictive equation for an outcome in that sample (see footnote 10). Estimating a prediction equation that can predict well out of sample requires precise estimates of the effects of individual SNPs. Because these individual SNP effects are estimated in a finite sample, polygenic risk prediction will achieve much less predictive power than the theoretical bound estimated by GREML. Unfortunately, the out-of-sample predictive power that can be obtained from considering the SNP data simultaneously is presently too small to be of practical use for most outcomes. For example, the International Schizophrenia Consortium reported an out-of-sample predictability of up to 3% from a predictive risk equation estimated in a total sample of 6,907 individuals (Int. Schizophr. Consort. et al. 2009). Benjamin et al. (2012) estimate predictive risk equations for educational attainment (N ≈ 8,300) and for a range of economic preferences and political attitudes (N ≈ 2,900). In all cases, the out-of-sample R² is less than 0.1%. The greatest success to date has been for height, for which the out-of-sample R² is approximately 13% when the predictive risk equation is generated from SNP effects estimated in a meta-GWAS of more than 180,000 individuals (Lango Allen et al. 2010).

5.3.3. Focusing on biologically proximal traits

Regardless of the analytic approach, a major question going forward is which outcomes are the most promising to study. In our view, in the short run this decision will be dictated by which variables are consistently measured across a large-enough number of data sets that the joint sample size will yield reliable results. For this reason, SSGAC's first outcome to study is educational attainment, which is widely measured not only in social science surveys, but also in most medical surveys as a key measure of socioeconomic background.

In the long run, however, we suspect that the most promising economic outcomes will be those that are most closely related to the underlying biology. Distal outcomes, such as educational attainment and self-employment, are likely influenced by an enormous number of genes, each with a tiny effect that will be difficult to detect even in a huge data set. If these distal genetic effects work through different pathways in different local environments, then even true relationships will not robustly replicate across data sets. Proximal outcomes, such as aggressiveness and perhaps impulsivity, are likely to have larger and more direct genetic influences from fewer genes. Outcomes that are also measurable in animals have the additional advantage that the genes can be experimentally manipulated in animal models to directly study their causal effects. Unfortunately, as of now, none of these proximal outcomes is widely measured across many data sets that have dense SNP data. One function we envision for the SSGAC will be to coordinate the collection of harmonized measures of proximal outcomes.

6. CONCLUSION: GENOMICS RESEARCH IN ECONOMICS

Above we discuss a number of ways in which the use of molecular genetic data could benefit economics. For example, genetic data will serve as a powerful lens to identify and study biological mechanisms that generate important, and potentially overlooked (by economists), sources of individual differences (e.g., aggression, ambition, and myopia). Genotypic data will also (eventually) be used as control variables that serve to increase power. Genetic data may also be of interest in and of itself: Economists have used genotypic data to study the effect of intellectual property rights on innovation (Williams 2010) and adverse selection in health insurance markets (Oster et al. 2010). Looking ahead a decade or two, the availability of inexpensive genotypic data is likely to help parents predict learning disabilities such as dyslexia earlier in childhood, facilitating earlier interventions. Potential vulnerabilities to substance abuse, or other kinds of self-destructive behavior, may also one day be predictable from genetic data.

We also predict that methodological challenges—such as multiple testing—will generate many more false positives in the literature, especially in the short run. The press is likely to distort findings and exaggerate the degree to which specific genes “determine” outcomes. In most cases there is no “gene for [insert behavior here],” despite frequent newspaper headlines suggesting that there is. Indeed, for most behaviors, researchers are struggling to find a SNP with an R² that is greater than one-tenth of 1%. Researchers in this field hold a special responsibility to try to accurately inform the media and the public about the limitations of the science.

The inevitable, inexpensive, broad-based availability of genotypic information will raise myriad social, ethical, and legal questions to which economic analysis will provide a valuable perspective. Many geneticists rightly worry that genetic research will prove to be socially harmful by generating discrimination against genetically disadvantaged groups. Genetic information will generate a rich set of new policy problems (in addition to the benefits that we review above). Governments will need to formulate new policies that maximize social welfare in a world where people with genetic advantages will wish to share them with potential employers and insurers, and people with genetic disadvantages will want to shroud them. In some cases, the provision of genetic information can be beneficial (e.g., alerting couples who both possess disease-causing recessive mutations), whereas in other cases, it would be deeply problematic (e.g., sharing genetic data with health insurance companies, which effectively creates an unraveling of some of the social benefit of health insurance). Problems abound in any analysis of optimal access to genetic information, even when the individual herself is the only one who is going to have access to the data. Under what conditions will the benefits to an individual from knowing her own genetic risk factors, such as the ability to prepare well in advance for a likely illness, outweigh the costs of increased anxiety and distress (see Oster et al. 2012)? We predict that research on these different types of questions will soon occupy a much larger fraction of economists' energy as these issues quickly become of immediate practical relevance.

Candidate gene: a genetic polymorphism hypothesized to have a causal effect on some trait (or disease); the hypothesis is based either on what is believed about the biological function of the gene where the genetic polymorphism is located or on previously reported associations between that genetic polymorphism and a related outcome

Gene: a sequence of nucleotides in DNA that provides instructions for building a particular protein or proteins

Genetic polymorphism: a segment of DNA that differs between individuals

Single-nucleotide polymorphism (SNP): a single nucleotide location in the DNA that varies between individuals

Major allele: the nucleotide of a SNP that is more common in the population; for non-SNP genetic polymorphisms with two alleles, the major allele is the term for the more common variant in the population

Minor allele: the nucleotide of a SNP that is less common in the population; for non-SNP genetic polymorphisms with two alleles, the minor allele is the term for the less common variant in the population

Genotype: for a given SNP, an individual's number of minor alleles

Genome-wide association study (GWAS): a study in which hundreds of thousands of genetic polymorphisms are individually tested for association with some outcome, without any prior hypotheses

Genome-wide significance: 5 × 10⁻⁸; the conventional level at which an association is considered to be statistically significant in a genome-wide association study

Pleiotropy: multiple effects of a single gene

Meta-GWAS: a meta-analysis of results from multiple genome-wide association studies