Control of finger force vectors with changes in fingertip referent coordinates

Abstract

The central hypothesis explored in the experiment is that adjustments of fingertip force vectors during object manipulation could result from a simple scaling rule applied to commands to individual digits. The commands have been associated with referent coordinates of the digit tips. The subjects performed quick lifting movements (over 20 cm in under 0.5 s) of a horizontally oriented handle with different combinations of the external load and torque. The prismatic grasp was used with the four fingers pressing on the bottom of the handle and the thumb acting on its top. Principal component and correlation analyses applied to the normal and tangential force vector components confirmed that the force direction of each digit was kept nearly constant in the object-centered referent frame across the loading conditions and movement phases. The middle and ring fingers showed weaker correlations between the force components as compared to the index and little fingers. The differences were likely related to the different roles of the normal force components in the moment of force production. The neural control of the hand, within the studied task, may be adequately described as a simple rule applied to a handful of parameters, such as the referent digit-tip coordinates.

Introduction

Many studies of finger action quantified fingertip forces (and moments of force) and analyzed the relations among different force components such as, for example, normal and tangential forces acting on the object (reviewed in Zatsiorsky and Latash 2008). In particular, finger action on a grasped vertical object is commonly described in terms of coupling between the load forces acting tangential to the surface of the object and normal (grip) forces that ensure adequate friction conditions (Johansson and Westling 1988; De Freitas et al. 2009). One of the frequently accepted hypotheses is that the adjustments of normal forces represent reflections of a feed-forward control process with the purpose to provide consistent magnitude of the safety margin defined as the proportion of the normal force above the slippage threshold (Johansson and Westling 1988; Cole et al. 1999; Flanagan et al. 1999; De Freitas et al. 2009).

When a horizontally oriented object is grasped with a prismatic grasp, with the fingers supporting the weight of the object and the thumb acting on its top, the mechanical roles of the normal and tangential force components change dramatically (Wu et al. 2012a). When the external torque is zero, the thumb does not need to produce any force because the weight of the object is supported by the normal forces of the fingers. The fingers do not have to produce tangential forces; so, friction is a non-issue. When the external torque is non-zero, however, the thumb starts playing a major role in the generation of the total torque, mostly with the tangential force but also with the normal force. The high tangential digit forces require adequate normal forces to ensure sufficient friction. Within this study we assumed that, despite the mechanical complexity of the task with a non-zero external torque, the central nervous system may not distinguish between apparent components of a task, such as the tangential and normal forces, but accept a more universal strategy and use a simple scaling rule to solve the problem of holding and moving a horizontally oriented object. We searched for such a rule and interpreted it within the referent configuration (RC) hypothesis (Feldman 2009).

RC is defined as a body configuration, at which all the muscles are at their thresholds for activation via the tonic stretch reflex loop (Feldman and Levin 1995; Feldman 2009). The RC hypothesis assumes that the central nervous system (CNS) generates actions by changes in neural signals that, within a given force field, lead to changes in the RC. RC can be specified for salient task-specific variables, while all other variables emerge via a chain of few-to-many transformations organized into synergies that stabilize the salient variables (Latash 2010, 2012). Differences between actual and referent configurations lead to muscle activations and force generation. As such, RC shifts are a tool used by the CNS to accomplish the objectives set by the formulation of the motor task. Within this general framework, a simple scaling rule applied to shifts of the referent coordinates of a finger within a referent frame linked to the hand-held object is expected to lead to scaling of the fingertip force vector magnitude without changes in its direction (Pilon et al. 2007; Latash et al. 2010; Martin et al. 2011).

There is evidence that RCs may be specified in different frames of reference, in particular those linked to the body, to a hand-held object, and to the external space (reviewed in Feldman 2009). For example, motion of a hand-held object may be associated with specifying referent coordinates (positions and orientations) of the hand in the external space and referent aperture within an object-linked reference frame (Latash et al. 2010).

Within this study, we assumed that fingertip force vectors during the studied tasks could be defined by scaled shifts of the fingertip referent coordinates along a straight line in an object-centered frame of reference. This assumption leads to a hypothesis that individual digit force vectors will show changes in their magnitude but not direction during holding and moving the object. To test this hypothesis, we analyzed the correlations between the normal and tangential components of the fingertip forces during holding the handle with different external load and torque and during a quick voluntary movement of the handle. If our hypothesis is correct, strong correlations are expected between the normal and tangential forces produced by the individual digits across the loading conditions and movement phases.

Methods

Subjects

Nine subjects, 27 ± 1.1 years of age (7 males and 2 females), were recruited. All of the subjects were right-handed and healthy. None of the subjects had a history of long-term involvement in hand or finger activities such as playing musical instruments. All subjects gave informed consent according to the procedures approved by the Office for Research Protections of the Pennsylvania State University.

Apparatus

A handle (total mass 0.35 kg) was instrumented with force sensors (Nano 17-R; ATI Industrial Automation, Apex, NC, USA) and an electromagnetic tracking device (Polhemus LIBERTY, Colchester, VT, USA). The local axes (x, y, and z) of each sensor were parallel to the global axes (X, Y, and Z), Figure 1. Details on the geometry of the handle can be found in the earlier paper (Wu et al. 2012a). The data were collected using customized software (LabVIEW 9.0, National Instruments, Austin, TX, USA) at 100 Hz. The software also rendered visual feedback on the handle orientation.

Figure 1.

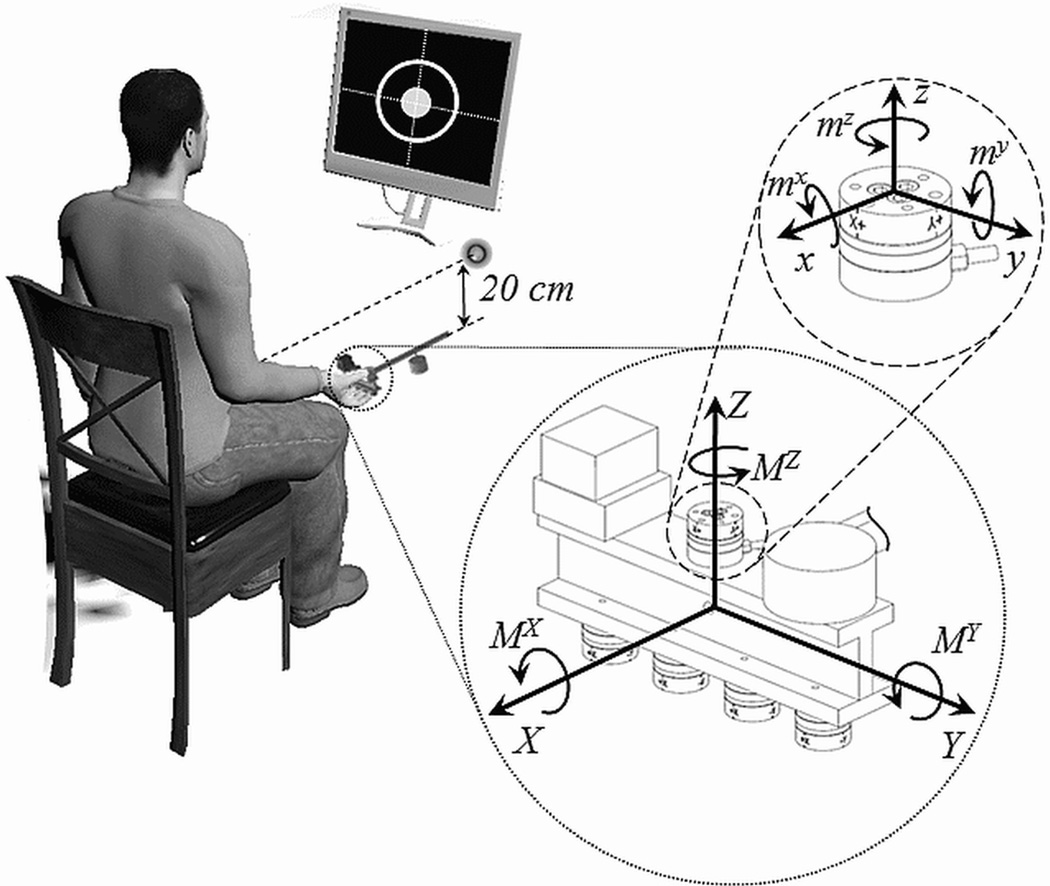
The experiment setup. M^X, M^Y, and M^Z are the moments of force with respect to the global coordinate system with X-, Y-, and Z-axes; m^x, m^y, and m^z are the local moments with respect to the local x-, y-, and z-axes of each sensor. The initial position of the subject’s forearm was 20 cm lower than the elbow joint. The target was at the height of the elbow joint. The handle orientation feedback on the screen helped the subject to maintain horizontal orientation of the handle.

Procedures

Subjects sat in front of the 19” monitor with their right upper arm naturally hanging down and the forearm pointing forward; the elbow and wrist were extended such that the handle was about 20 cm below the elbow, Figure 1. In all trials, the subject was instructed to hold the handle in a horizontal orientation with the hand supinated, the thumb (TH) acting on the top of the handle and the four fingers (I – index; M – middle, R – ring; and L – little) acting on the bottom (prismatic grasp). The horizontal orientation was maintained for about 3 s (static-hold phase) and then the subject lifted the handle in a self-paced manner “very quickly” to a target 20 cm above the initial position (lift stage) and held it there for about 3 s. The visual feedback on the computer screen showed the orientation of the handle. Once reaching the target height, the subject held the handle until the end of the trial. After each trial, the experimenter held the handle and the subject had at least a 20-s rest interval. There were also 5-minite breaks between conditions. The order of conditions was pseudo-randomized, and the total duration of the experiment was about 1.5 h.

The conditions were set by altering the external weight and point of its attachment along the rigid rod attached to the center of the handle and oriented along the X axis (Fig. 1). The five conditions were M₁L₁, M₁L₂, M₁L₃, M₂L₂, and M₃L₂, where M and L denote, respectively, the extra mass (three levels: M_1,2,3 = 0.1, 0.2, and 0.3 kg) and the distance from the center of the handle to the weight (three levels: L_1,2,3 = 0.08, 0.16, 0.24 m). Only five mass-distance combinations were used to minimize fatigue and to have an opportunity to compare conditions with the same mass and different torques and with the same torque and different masses. Twenty trials were performed in a single block for each of the five conditions.

Data Processing

Customized LabView (National Instrument, Austin, TX, USA) software was used to process data off-line. All force and position data were low-pass filtered at 30 Hz with the fourth-order, zero-lag Butterworth filter. The time derivative of the resultant normal force $(F_{\mathit{\text{RES}}}^n)$ acting on the handle was low-pass filtered at 5 Hz.

All force data were time aligned by the lifting onset (T₀) defined as the instant when the derivative of $F_{\mathit{\text{RES}}}^n$ reached 5% of its peak value in that particular trial. Further, the time to reach peak $F_{\mathit{\text{RES}}}^n$ was defined as T_MAX. The force data analyzed in this study were measured at three time instants, T₀, the half-time (T_HT) between T₀ and T_MAX, and T_MAX.

The directions of the force vectors applied by individual digits were analyzed using two approaches, Principle Component Analysis (PCA) in the three-dimensional force space and linear correlation between F^X and F^Z (on the XZ plane) performed for individual digit forces. The averaged force vectors, ${\overline{F}}_j=[{\overline{F}}_j^X,{\overline{F}}_j^Y,{\overline{F}}_j^Z]$ across trials were computed for each subject, condition, and phase for each digit (j = VF, TH, I, M, R and L; VF stands for “virtual finger” – an imagined digit with the mechanical action equal to that of the four fingers combined). PCA was performed on all F⃑_j data within each subject using the covariance matrix. The percentage of total variance expressed by each principle component (PC) was computed. The correlation between F^X and F^Z was computed using the force vectors averaged across repetitive trials within each condition and within each subject; for this analysis, the data for all five conditions and three movement phases were combined. The coefficients of determination (R²) were computed.

Statistics

Analysis of variance (ANOVA) was performed using SPSS software (SPSS 19, IBM, Somers, NY, USA). In the linear correlation analysis, we regressed the normal force components $F_j^Z$ on the tangential force components $F_j^X$, where j = VF, TH, I, M, R and L. Further, we used R² values of linear regressions subjected to Fisher’s z-transform as dependent variables across digits (independent variables). Since the data showed significant heterogeneity of variance, we used the Welch’s one-way ANOVA with a factor DIGIT (6 levels: VF, TH, I, M, R, and L) on the transformed R² values. Turkey’s HSD (Honestly Significant Difference) tests were used in the post-hoc comparisons.

Results

During the lifting action, the subjects kept the orientation of the handle nearly unchanged, at least within the time to peak acceleration (which was, on average, 175 ± 5 ms). Maximal deviation of the handle orientation was seen in the pitch, about the Y axis; it was, on average, 1.49° ± 0.18°. The handle vertical displacement was under 1 cm.

Despite the pronounced scaling of the force vector magnitude across conditions and phases of the movement (as expected from straightforward mechanics, not illustrated), the direction of force vectors showed consistency across all measurements both within individual subjects and when data were averaged across subjects. F_VF and F_TH force vectors, fifteen of each (three phases × five experiment conditions), averaged across subjects, are plotted in Figure 3. Note the consistency in the direction of both F_VF and F_TH vectors.

Figure 3.

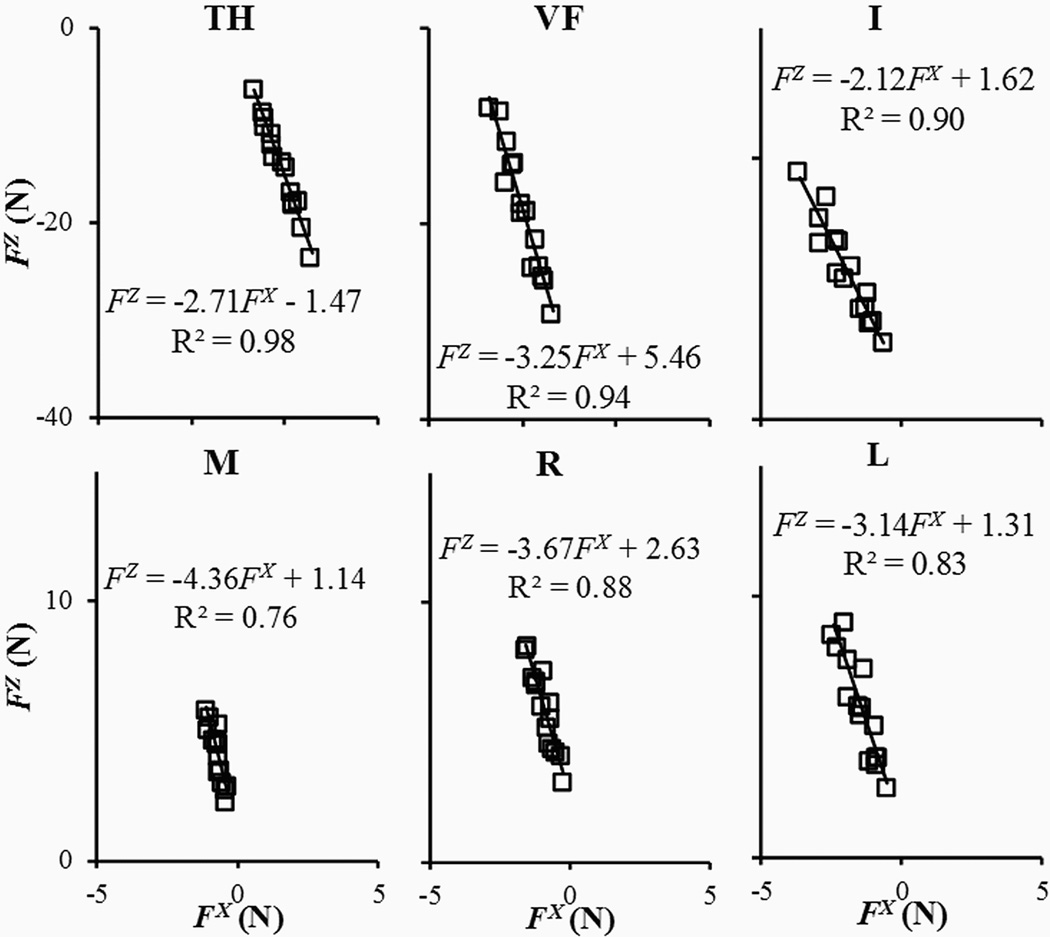
The dependences between the normal and tangential force components for a typical subject. Linear regression equations and coefficients of determination are shown on each graph. Each data point is the mean across trials in one of the fifteen condition × phase combinations.

Principal component analysis in the three-dimensional force space performed using all the data within each individual subject confirmed that much of the total variance was within a single direction for all the digits, TH, VF, I, M, R, and L. For the thumb and VF, the variance explained by the first PC across all subjects ranged from 97.7% to 99.4%, while for the individual fingers (I, M, R, L) is ranged from 88% to 98.9%. There were no statistically significant differences across the digits in the amount of variance explained by PC1 (MANOVA on z-transformed PC1-percentage values).

These results were generally confirmed by linear correlation analysis between two force components, normal (Z) and tangential in the anterior-posterior (X) direction. Figure 3 illustrates the linear regressions for individual digits of a typical subject, while Table 1 presents the data across subjects. This analysis revealed differences among the four fingers. While the data for TH, VF, I and L were consistent with the described PCA results (all these digits showed high coefficients of determination), the correlation coefficients were smaller for the M and R finger. Across subjects, mean R² values were 0.98 (TH), 0.93 (VF), 0.97 (I), 0.56 (M), 0.83 (R), and 0.97 (L). Across subjects, there were no differences in the z-transformed R² values among TH, VF, I and L, while the values for M and R were significantly smaller [F_(5,22.106) = 5.586, p < 0.01; confirmed by Tukey’s post-hoc comparisons].

Table 1.

Results of linear regression analyses between the normal and tangential digit force components

Digit	R2		Linear regression coefficient k
	[Min, Max]	Median	Mean ± SE
Virtual Finger	[0.71, 0.96]	0.92	−2.61 ± 0.34
Thumb	[0.83, 0.98]	0.93	−2.39 ± 0.16
Index	[0.73, 0.98]	0.9	−1.85 ± 0.21
Middle	[0.05, 0.89]	0.27	−2.00 ± 0.81
Ring	[0.01, 0.88]	0.63	−2.10 ± 0.76
Little	[0.57, 0.96]	0.83	−1.94 ± 0.21

The range and median of the coefficient of determination (R²) values, and the mean ± standard error (SE) of the linear regression coefficient k are shown for individual digits across subject.

Discussion

The results of the PCA and the strong linear correlations observed between the tangential and normal force vector components for most digits (the index and little fingers, the thumb, and the virtual finger, VF) support our main hypothesis that digit force vectors changed only their magnitude, but not direction, across the loading conditions and movement acceleration phases. Two fingers (M and R) showed equally consistent behavior of the force vectors according to the PCA results but lower correlation coefficients between the force vector components. An earlier study has shown that the observed close coupling between the normal and tangential force components does not keep the safety margin constant (Wu et al. 2012b; cf. Flanagan et al. 1999; De Freitas et al. 2009). Hence, in this study, we offer a different interpretation for the main results within the framework of the referent configuration (RC) hypothesis (Feldman 2009). We admit upfront that this framework represents our personal preference, and the findings can be interpreted using different theoretical views, for example those based on the assumption of computations performed by the central nervous system. These involve, in particular, theories based on assumed internal models within the central nervous system (reviewed in Kawato 1999) and optimal feedback control ideas (Todorov and Jordan 2002; Diedrichsen et al. 2010).

At the level of action involved in the studied task, considered in two dimensions, RC may be viewed as a combination of three variables, the referent vertical position of the handle (Z_R), the referent aperture (AP_R), and the referent angular rotation (α_R) (see Latash et al. 2010). The differences between these referent variables and the actual values of the handle position, finger aperture, and handle orientation generated the resultant vertical force, grip force, and resultant moment of force, respectively. Note that there were no changes in the finger aperture (constrained by the handle), very little change in the handle orientation (on average, less than 1.5°; cf. Wu et al. 2012b), and a relatively small handle displacement in the vertical direction over the time of analysis (until peak acceleration). So, the observed force and moment patterns were primarily reflective of the RC shift.

The very high correlations between the normal and tangential forces produced by the VF and thumb suggest that a single simple rule was used to adjust the action to changes in the external loading conditions and during the early phase of the lifting action. In other words, the direction of the force vectors stayed unchanged while their magnitude scaled to the task parameters and phase. These results are compatible with the earlier report on a relatively constant percentage of the total moment of force produced by the tangential forces in such tasks (about 80%, Wu et al. 2012a,b). The normal force of the thumb had to be adjusted to ensure sufficient friction (although the safety margin consistently dropped by about 20% during the movement across all conditions; Wu et al. 2012b). The adjustments of the VF normal force served two functions, to ensure sufficient friction and to generate required resultant vertical force against the gravitational and inertial loads. This was reflected in the consistently higher slopes of the linear regressions (regression coefficients k, Table 1) computed for the VF as compared to those computed for the thumb.

The co-adjustments of referent coordinate shifts for the thumb and VF within the handle-centered frame of reference led to a nearly perfect compensation of the resultant referent coordinate shift along the X axis. As a consequence, the resultant tangential force component was always close to zero as required by the task of maintaining equilibrium along that coordinate.

Referent coordinate shifts for individual digits reflected their specificity in prehensile tasks (cf. Zatsiorsky et al. 2003). Note that the two “lateral” fingers (I and L) showed consistently high correlations between the normal and tangential forces, while the “central” fingers (M and R) failed to do this in a number of subjects, as reflected in the overall smaller R² values and high variability of the regression coefficients k (Table 1). An earlier study has shown that the M and R fingers produce consistent non-zero moments by their normal forces, associated with changes in the center of pressure (COP) of the normal force application (Wu et al. 2012a,b). In contrast, the I and L fingers show no consistent COP shifts. This can be interpreted as the I and L fingers using a single simple rule of shifting the referent coordinate along a straight line resulting in the highly correlated force component changes. The control of the M and R fingers may be more complex involving local moment of force production that does not allow using the same simple rule anymore.

This is the first study to demonstrate that a relatively complex mechanical task can be accomplished using a simple rule of scaling the magnitude of digit forces without changing their direction. Whether similar rules apply to other prehensile tasks, such as those involving manipulation of vertical objects or combinations of object rotation and translation, remains to be explored. Using such rules represents an example of a particular strategy by the CNS to avoid solving complex mechanical problems and instead to adhere to simple control rules that are “reasonably sloppy” (Latash 2008; Loeb 2012).

We would like to conclude with the following sequence of main messages that interpret the main results within the RC hypothesis. The system for the control of prehensile actions is hierarchical (cf. Arbib et al. 1985). At the upper level (the VF-TH level), there is a simple rule that defines shifts of the referent coordinates for the thumb and VF. At the lower level (the individual finger level), shifts of the VF referent coordinate are translated into shifts of the individual finger referent coordinates. This is associated with multi-finger synergies stabilizing the VF tangential force but not the VF normal force (Gorniak et al. 2009; Wu et al. 2012a). This difference may be associated with the double role played by the normal forces of the M and R fingers, ensuring adequate normal force magnitude for the desired tangential forces and contributing to the moment of force production with shifts of the point of normal force application. Overall, the neural control of the hand may be adequately described as simple rules (such as shifting fingertip referent coordinates in a prescribed direction) applied to a handful of parameters related to referent values (coordinates) of salient variables in a task-specific frame of reference.

Figure 2.

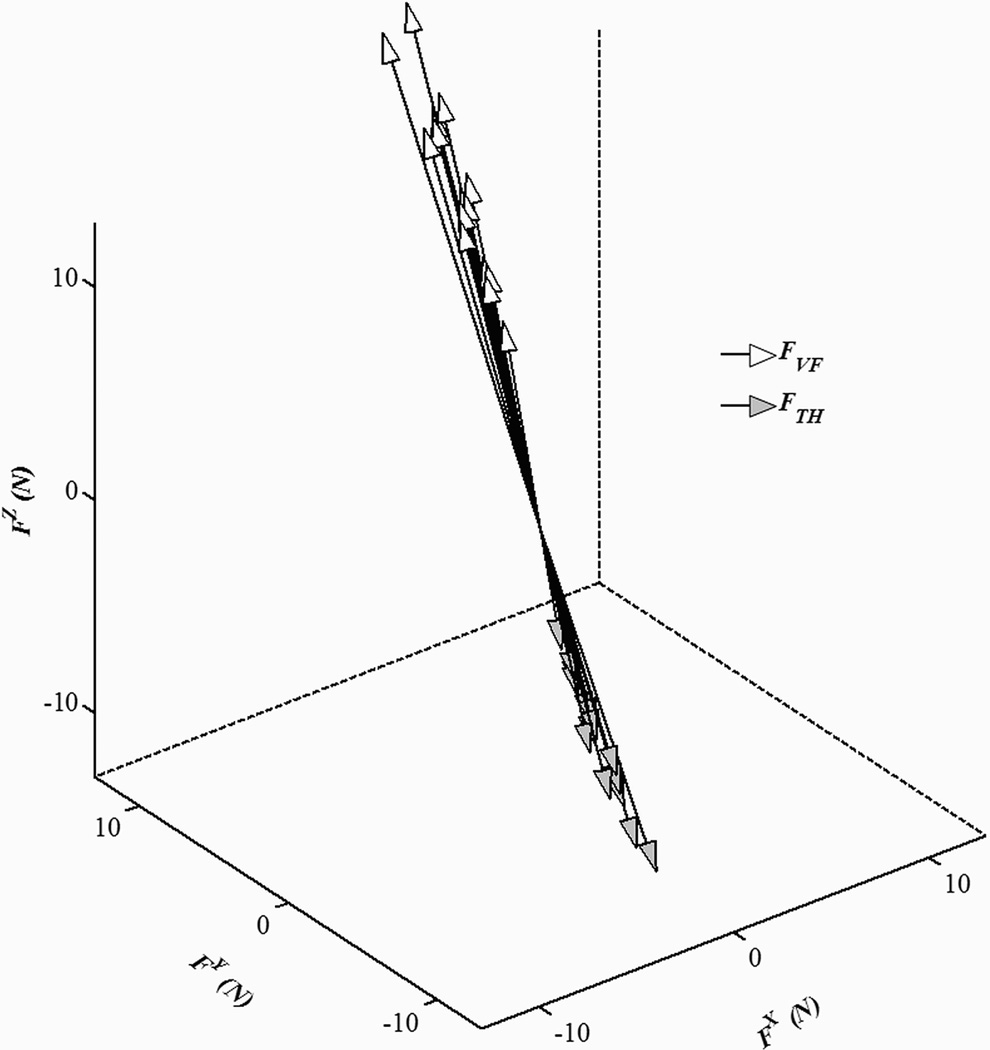
The force vectors of the thumb (TH, gray arrows) and virtual finger (VF, white arrows) across all conditions and movement phases averaged across subjects. Note the consistency in the vector directions for each digit.