Abstract
Objective
To assess various approaches to estimating pressure-induced wall tension in intracranial aneurysms (IA) and their effect on the stratification of subjects in a study population.
Methods
Three-dimensional models of 26 IAs (9 ruptured and 17 unruptured) were segmented from Computed Tomography Angiography (CTA) images. Wall tension distributions in these patient-specific geometric models were estimated based on various approaches such as differences in morphological detail utilized or modeling choices made. For all subjects in the study population, the peak wall tension was estimated using all investigated approaches and were compared to a reference approach – nonlinear finite element (FE) analysis using the Fung anisotropic model with regionally varying material fiber directions. Comparisons between approaches were focused toward assessing the similarity in stratification of IAs within the population based on peak wall tension.
Results
The stratification of IAs tension deviated to some extent from the reference approach as less geometric detail was incorporated. Interestingly, the size of the cerebral aneurysm as captured by a single size measure was the predominant determinant of peak wall tension-based stratification. Within FE approaches, simplifications to isotropy, material linearity and geometric linearity caused a gradual deviation from the reference estimates, but it was minimal and resulted in little to no impact on stratifications of IAs.
Conclusion
Differences in modeling choices made without patient-specificity in parameters of such models had little impact on tension-based IA stratification in this population. Increasing morphological detail did impact the estimated peak wall tension, but size was the predominant determinant.
Keywords: Intracranial aneurysm, Biomechanics, Wall tension, Finite element method, Material models
INTRODUCTION
Estimations of pressure-induced tension or stress resultant in the intracranial aneurysm (IA) sac wall have been proposed as metrics that help stratify patients according to rupture risk – the underlying claim being that aneurysms with high wall tension are more likely to fail [1-2]. Wall tension on patient-specific IAs can be estimated using varying levels of measured information and after making different modeling choices. At its simplest, the ‘size’ of the IA – a standard clinical measure used for diagnosis of severity and treatment planning – may be used to calculate aneurysm wall tension under the assumption that it has a spherical or ellipsoidal shape (depending on whether its ‘size’ is known from one or more orientations, respectively). However, if volumetric image data is available, the aneurysm geometry in its true three-dimensional complexity may be segmented. This rich measured information may be leveraged for estimating a more region-specific distribution of wall tension [3-5]. Region-specific aneurysm wall tension may be estimated in two essential ways: 1) By using the generalized Laplace law for arbitrary convex membranes based on surface principal curvatures [4], 2) By using the finite element (FE) method for stress analysis of the pressurized structure [1-2]. Irrespective of the approach used, one could conceivably claim that the use of rich three-dimensional (3D) aneurysm morphology – as opposed to using just clinical size measurements – will have to yield more reliable estimations of wall tension and better able to distinguish aneurysms vulnerable to high wall tension. But how much more valuable and critical is the 3D morphological information to wall tension estimations? This remains unclear. Answering this question has important practical implications. Consider that wall tension computed from basic size measurements turns out to stratify aneurysms approximately as effectively as 3D FE analyses. The ease of such simple calculations may then permit studies that test the hypothesis that high wall tension correlates to high rupture risk with very large populations. When data collection and analysis is simple, investigators can afford to accommodate study populations that are orders of magnitude greater than if they have to collect volumetric images, and perform segmentation in order to leverage 3D morphological information. Larger study populations can certainly contribute to greater reliability in findings. Further, the ease of calculations would also translate into ease of using wall tension indices in a clinical setting for quick biomechanical assessments.
Now, within studies that leverage patient-specific 3D morphological information, FE analysis itself may be performed by employing differing modeling choices (material or geometric nonlinearity, anisotropy, etc.) [1, 3, 6-11]. In most studies of IA wall tension, these modeling choices are assumed to be consistent across the study population since patient-specific information (e.g. patient-specific material parameters, contact constraints with skull, etc) are not, often, available to be incorporated. When modeling assumptions (and parameter values) are consistently applied to a study population, are the findings – specifically how we interpret them – affected significantly by which models are used? The objective of this study is to assess and document how the wall tension estimates and the ability to stratify aneurysms based on wall tension is affected by these different approaches using a population of aneurysms.
METHODS
Computed Tomography Angiographic (CTA) images of 26 saccular, patient-specific IAs were obtained during routine clinical care at University Central Hospital, Helsinki, Finland. The study was approved by the local ethics committee and the patients or their relative gave informed consent. Aneurysms belonged to diverse locations such as Middle Cerebral Artery (8 unruptured, 4 ruptured), Internal Carotid Artery (4 unruptured,0 ruptured), Anterior Communicating Artery (1 unruptured, 2 ruptured), Basilar Artery(1 unruptured, 1 ruptured), Posterior Communicating Artery (1 unruptured, 1 ruptured) and Pericallosal Artery (2 unruptured, 1 ruptured) as previously reported [12]. Maximum diameter of the aneuryms ranged from 3.96 mm to 12.05 mm with an average of 6.63 mm. Out of the 26 aneurysms, 20 were bifurcation aneurysms while 6 were side– walled. Both basilar aneurysms were terminal aneurysms occurring at the tip of the basilar artery. 3D models of these aneurysms and their contiguous vasculature were created from the source data using levelset segmentation techniques [13-15] as implemented in the Vascular Modeling ToolKit (VMTK-open source software). Aneurysm domes were then isolated from their contiguous vasculature using a cutting plane as previously reported [16].
The wall tension distribution in these patient-specific geometric models were estimated based on approaches listed below in the order of increasing geometric detail followed by increasing realism in material modeling. For all approaches, the aneurysm wall was assumed to be under a spatially uniform static pressure (P) of 100mmHg.
- Sphere: Utilizing a single size measure – using Laplace law for pressurized spherical membranes. The aneurysm was assumed to be a sector of a sphere of diameter, Dmax [16] as measured from its largest dimension.
where T = Tension, P = Pressure and Dmax = Maximum diameter. - Ellipsoid: Utilizing two size measures – using Laplace law for pressurized ellipsoidal membranes. The aneurysm was assumed to be an ellipsoid with the major axes matching the maximum of the two size dimensions – H and Dmax [16] – and the minor axes matching the minimum of the two sizes.
where, P is Pressure; a,b are major and minor axes for ellipsoid and φ is the angle made by the normal, at any point, to the major axis of the ellipsoid [4]. - Utilizing the segmented aneurysm geometry from volumetric diagnostic images.
-
C.1.3D-Laplace: Utilizing generalized Laplace law for arbitrarily shaped pressurized membranes. The spatial distribution of principal curvatures on the aneurysm wall surface was computed [2, 16] from which the distribution of stress resultant was estimated. Assuming the aneurysm wall to be a membrane and its deformation to be axisymmetric [4], stress distribution was obtained using:
where, κm is mean curvature. -
C.2.Using the finite element (FE) method. The FE approach used follows closely our earlier report [2] on the topic but for a few deviations as detailed below. The aneurysm sac wall was modeled as a finite strain 86 μm thick shell. The geometries were subjected to uniform pressure of 100 mmHg while being fixed at the neck and solved using Abaqus (ver. 6.9-1, Dassault Systèmes Simulia Corp., Providence, RI).
-
C.2.i.Employing different material models/behaviors
-
C.2.i.a.Fung-aniso: Fung-anisotropic model. The wall was modeled using the orthotropic Fung model with material parameters reported by Seshaiyer et al. [9]. The material fiber directions were assumed to be aligned along principal curvature directions. Detailed discussion of the model rationale and its implications may be found in our earlier report [2].
with c=28 MPa, c1=17.58, c2=12.19, c3=7.57, c4=4.96 [2, 9] -
C.2.i.b.Fung-iso: Fung-isotropic model. The above model with c = 28 MPa, c1=c2=14.89, (average of c1 and c2 in above model) c3=7.57, c4=4.96 [2].
-
C.2.i.c.Poly-iso: Isotropic polynomial strain energy model. A polynomial functional form that behaves similar to the Fung-isotropic model under uniaxial extension was employed. The polynomial model parameters chosen made this model roughly equivalent to the Fung-isotropic model under biaxial extension [17]:
with a=3.00 MPa, b=−14.35 MPa and c=63.57 MPa. -
C.2.i.d.Hooke-large: Hooke’s model with large deformation. Linearized elasticity model with geometric nonlinearity with elastic modulus of 100 MPa and Poisson’s ratio of 0.49 [2].
-
C.2.i.a.
-
C.2.ii.Hooke-small: Hooke’s model with small deformation. Same as Hooke-large, but with geometric linearity in addition to material linearity.
-
C.2.iii.Employing truncation of FE domain. The exclusion or inclusion of the contiguous vasculature from the FE domain may have some effect on the stress in the aneurysm sac. While inclusion of the vessels would move the boundary away from the sac, it introduces greater computational cost and artifact-prone geometric features that tend to be more common to the neck region, especially in aneurysms at bifurcations (see Figure 1 for illustration). The role of truncation was assessed here.
-
C.2.iii.a.Truncated: Ignoring the contiguous vasculature by truncating the sac.
-
C.2.iii.b.Non-truncated: Including the contiguous vasculature.
-
C.2.iii.a.
-
C.2.i.
-
C.1.
Figure 1.
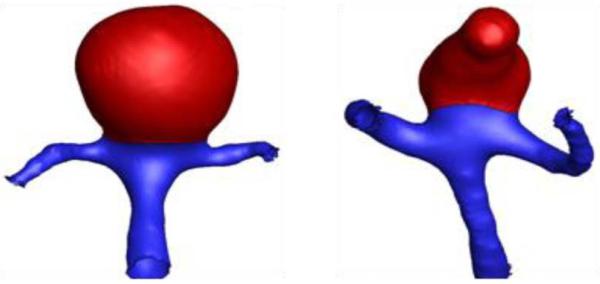
Representative aneurysm models – at a basilar tip and at an MCA (isolated-aneurysm sac highlighted in red)
The peak wall tension index was defined as the 95th percentile value of the wall tension in the spatial domain [18]. Where finite element analysis was employed, wall tension was assumed to be the product of the regionally varying maximum principal stress in the aneurysm wall and the uniform wall thickness used for computations. Statistical treatment involved the comparisons of the peak tension index between each approach and a reference approach – the seemingly most realistic/sophisticated approach. The Fung-aniso was used as the reference approach. One exception was that Poly-iso was used to compare truncated and non-truncated models due to numerical convergence issues in non-truncated models using Fung-Aniso. This is justified mainly because the results clearly showed that Poly-iso generated the same results as Fung-aniso. Three metrics were employed for comparing each approach to a reference approach. The slope of the best fit linear regression without intercept (0 ≤ k ≤ ∞) between two approaches was used as a measure of similarity in the estimated values. When k=1, the wall tension index estimated from an approach is identical to the reference approach. The Pearson’s product-moment correlation coefficient (0 ≤ r ≤ 1) was used as a metric of the similarity in trends between two approaches. When r=1 between two approaches, one approach simply scales up or scales down the indices within a study population compared to the other approach by a constant scale factor. The Spearman’s rank correlation coefficient (−1 ≤ ρ ≤ 1) was used as a metric of the similarity in ranking between two approaches – i.e., how they stratify the aneurysms in the study population based on a given index. When ρ=1 between two approaches, the ranking of the aneurysms in a study population based on one approach is identical to that using the other approach (ρ=0 indicates no similarity). The Pearson’s correlation assesses the level of numerical redundancy between estimates from two approaches. The Spearman’s correlation assesses the impact any existing redundancies will have in clinical trial-type studies where hypotheses on high tension-rupture risk are tested. ρ therefore is the metric directly relevant to our goal, but r provides additional insight. Naturally for all practical purposes, ρ=1 when r=1.
RESULTS
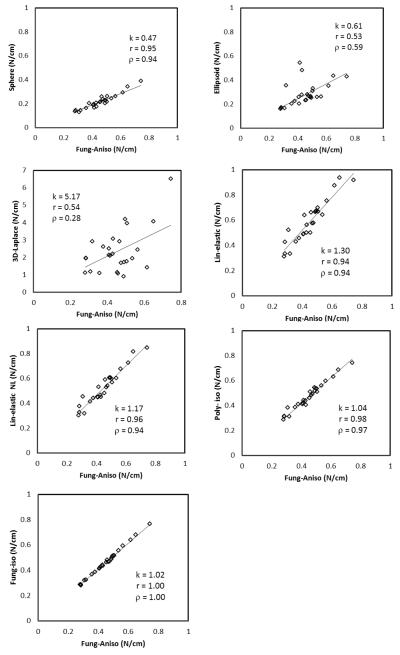
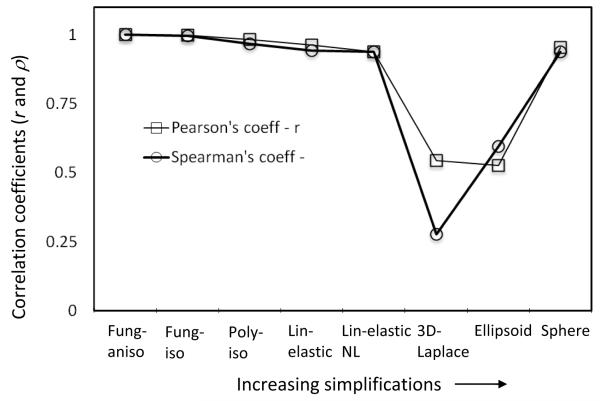
The analyses converged for all approaches and the peak wall tension index computed. The metrics of comparison, k, r and ρ are tabulated in Table 1. Figure 2 shows how various approaches fare in comparison to Fung aniso – the presumed gold-standard model. The Pearson’s and Spearman’s correlation coefficients conform to the visual perception that most approaches – especially the kind where only modeling choices are involved without any new measured information – result in fairly consistent stratification of the aneurysms in the study population (see Figure 3).
Table 1.
Comparison between the seemingly gold-standard approach and other approaches. Between any two approaches, similarity in the estimated peak wall tension index is quantified by the slope; consistency in the dissimilarity, if any, is quantified by the Pearson’s coefficient; and the similarity in the ranking of the aneurysms based on peak wall tension index is quantified by the Spearman’s coefficient.
| Reference approach |
Evaluated approach |
Slope (k) |
Pearson’s correlation coefficient (r) |
Spearman’s correlation coefficient (ρ) |
|---|---|---|---|---|
| Fung-aniso | Fung-iso | 1.02 | 1.00 | 1.00 |
| Fung-aniso | Poly-iso | 1.04 | 0.98 | 0.97 |
| Fung-aniso | Hooke-Large | 1.17 | 0.96 | 0.94 |
| Fung-aniso | Hooke-Small | 1.30 | 0.94 | 0.94 |
| Fung-aniso | Curvature- based |
5.17 | 0.54 | 0.28 |
| Fung-aniso | Ellipsoid | 0.61 | 0.53 | 0.59 |
| Fung-aniso | Sphere | 0.47 | 0.95 | 0.94 |
| Non- truncated |
Truncated | 1.14 | 0.96 | 0.96 |
| Using Max.Principal Stress |
Using Von Mises Stress |
0.92 | 0.98 | 0.97 |
| Refined mesh | Coarse mesh | 1.04 | 0.98 | 0.97 |
| 95th percentile | 100th percentile |
0.77 | 0.95 | 0.96 |
| 95th percentile | 50th percentile |
0.51 | 0.89 | 0.87 |
Figure 2.
Comparison of peak wall tension estimates between various approaches and the seemingly most realistic approach – Funganiso. k is a metric of similarity in estimated value; r is a metric of similarity in the trends; and ρ is a metric of similarity in stratification. The axis scale for 3D-Laplace alone differs from its reference approach for clarity.
Figure 3.
Variation of Pearson’s and Spearman’s correlation coefficients with increasing simplifications in modeling choices and morphological detail. Increasing simplification has an increasing effect on the stratification of aneurysms, but with the exception of 3D Laplace and ellipsoid, this effect is not as dramatic as the simplification may suggest.
DISCUSSION
How would the stratification of IAs in a study population based on peak wall tension be affected by different approaches used to compute it? We sought to address this question using a population of 26 patient specific aneurysms. The approaches investigated here may be categorized based on 1) the morphological detail used, and 2) the modeling choices made. Devoid of an independent baseline-truth, the Fung-aniso was chosen as a gold-standard to compare other estimates to. The reason is three-fold. Among the approaches investigated in this work, Funganiso uses the most realistic morphological detail, makes the most seemingly realistic assumptions on tissue behavior (e.g., finite elasticity, anisotropy with regionally varying material symmetries) and the model parameters are based on the mechanical tests with harvested brain aneurysm tissue performed with rigor [9].
Morphological detail
Reducing the morphological detail in tension estimation from a segmented 3D geometry of the aneurysm (Fung-aniso) to an ellipsoid to a sphere causes a noticeable reduction in the ability to stratify the aneurysms (for ellipsoid - r= 0.53, ρ =0.59, for sphere - r= 0.95, ρ =0.94). The ellipsoid approach does worse than the sphere approach despite having more morphological detail. This may be attributed to the fact that, an ellipsoid defined by H and Dmax as its axes may do worse justice to an irregular-shaped aneurysm than a sphere with diameter of Dmax. But one can’t miss the fact that the sphere approach – a single size measure based idealization of complex aneurysm morphology – turns out to be quite effective in stratifying aneurysms based on tension. Aneurysm wall tension and their stratification based on it are affected by size and shape of the aneurysm. But what is the contribution from each? Is one predominant over the other? In this small study population, the answer is resoundingly clear – size is the predominant factor. In clinical trials where the tension-rupture risk hypothesis need to be tested, there is always a trade-off between the level of detailed information being collected/used and the manageable study population size. Greater the one, lesser the other. If taken at face value, this finding suggests that even studies that collect the minimal morphological detail, but with a large study population (e.g. ISUIA [19]) may offer as much or more valuable insights within the context of wall tension when compared with those that collect detailed information, but with small study populations [1-2]. Of course, as with any finding grounded in empirical data, the representativeness of this small study population would be a legitimate concern.
Suitability of generalized Laplace law for membranes
IA under pressure may be thought of as a classic statically determinate equilibrium problem [20] if its elastodynamics may be ignored [21]. It is natural then to wonder if the generalized Laplace law [4] for arbitrary-shaped membranes applied to the 3D segmented aneurysm geometry may be as effective as a finite element analysis for tension calculations. From the results (see Figure 2 and 3), 3D-Laplace performed the worst of all approaches (k=5.17; r=0.54; ρ=0.28). The drawback with this approach is that the applicability of law of Laplace is questionable at flat, Gaussian and concave regions of the aneurysm wall surface. At approximately flat regions where curvature tends to zero, tension tends to infinity. This is further illustrated by the vast spread in curvature-based tension distribution compared to that calculated using finite element analysis. Either the membrane assumption is not valid everywhere or artifacts in 3D segmentation are causing unrealistic shape features to exist in a pressurized membrane. We have reported here, the use of mean curvature to calculate wall tension. A more generalized approach is to use the individual principal curvatures (κ1 and κ2) to estimate the in-plane components of wall tension –
Peak wall tension calculated by this approach had an even larger and unrealistic spread (k=10.35; r=0.50; ρ=0.40; one extreme outlier data point was not included for clarity). Irrespective, the generalized Laplace law for membranes is not a viable approach in its present form.
Modeling choices
Unlike morphological detail, little by way of patient-specific information is typically available for material behavior – possibly another determinant of wall tension. Thus population-wide modeling assumptions on material behavior become imperative. But what are the most appropriate material modeling choices? Do they even matter? In the present investigation, both the Fung-iso and poly-iso models show a clear linear relationship to Fung-aniso model, despite the latter’s seemingly greater realism (Figure 2 and 3). Thus stratification will be unchanged whether an isotropic or an anisotropic model is used, not to mention any model functional form. Indeed, even the linear elastic model results correlates well with the anisotropic Fung model – accommodating large deformation does slightly better (Figure 2 and 3). These findings are far from surprising. On the one hand, that tension in the IA wall is statically determinable suggests little if any role for material behavior in its estimation. Indeed, our group has demonstrated this earlier by employing the more appropriate inverse elastostatics formulation for stress analysis [20, 22]. Here, we show that even when a forward approach is used, material model choices may have minimal if any impact on the stratification of subjects because the parameters of these models are uniform across the study population. In the past few years, several research groups have calculated wall tension or other wall stress indices in cerebral aneurysms as well as in AAAs [1, 3, 6-10]. More recently, Reeps et al [8] performed a study comparing increasing levels of sophistication in modeling choices made during wall tension estimation in AAAs. As rightly concluded by this study, these modeling choices play a significant role in wall tension estimation when there is more patient-specific information (in addition to patient-specific geometry) that is available to be incorporated across the population under study. However, in clinical studies, biomechanically relevant patient-specific information other than morphology is hard to obtain. This leads to comparative studies being performed with uniform modeling choices applied across the patient population. The data from our study shows that, in such comparative studies, the modeling choices made to estimate wall tension have minimal impact on the ranking of the aneurysms based on wall tension. Further, peak wall tension index tuned out to be quite robust against perturbations in other choices as well including, inclusion of contiguous vasculature (peak tension in the sac region) versus its exclusion, von Mises stress index versus the maximum principal stress (Table 1 and Figure 4), and 95th versus 100th (absolute maximum) percentile values [18]. And finally, one may wonder if the difference in peak wall tension between the ruptured and unruptured group of aneurysms is affected by the approach used. The small study sample aside, we did not see any evidence that approach mattered here either. For example, the Fung-aniso showed the ruptured group to be 5% (group average±SD peak wall tension = 0.543 ± 0.160 versus 0.517 ± 0.121 MPa) higher with the poly-iso approach estimating it to be 5.8% higher (0.569 ± 0.151 versus 0.538 ± 0.126 MPa) – both without statistical significance. In other words, poly-iso approach would have resulted in an almost identical finding regarding tension differences between ruptured and unruptured aneurysms as the Fung-aniso. Incidentally, the sphere approach found it to be 1.2% higher (0.258 ± 0.098 versus 0.255 ± 0.063 MPa) – again without statistical significance.
Figure 4.
Comparison of peak wall tension estimates between (A) truncated and non-truncated models; (B) 100th versus 95th percentile values of wall tension as peak wall tension index; (C) maximum principal stress versus von Mises stress; (D) and between the coarse and fine mesh model. k is a metric of similarity in estimated value; r is a metric of similarity in the trends; and ρ is a metric of similarity in stratification.
In closing, it is worth emphasizing that the insensitivity to modeling choices is only true because the focus is on stratifying subjects with geometry being the only patient-specific information available for use. If additional patient-specific information such as contact constraints, intrasac thrombus or transmural calcifications are involved (none of which have been shown to be ascertainable from noninvasive imaging for brain aneurysms), then modeling choices may indeed start to matter unless shown otherwise. It is therefore not our case that modeling choices do not matter, but rather that they may be secondary or even tertiary factors for patient population studies where these choices are inevitably applied uniformly to all subjects.
ACKNOWLEDGEMENTS
This study was funded in part by the National Institutes of Health grant # 3R01HL083475. The authors are grateful to the Vascular Modeling ToolKit (VMTK) developer and user community for assistance with image processing.
Supported by NIH/NHLBI grant # 3R01HL083475
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest
The authors have no conflicts of interests.
REFERENCES
- 1.Isaksen JG, et al. Determination of wall tension in cerebral artery aneurysms by numerical simulation. Stroke. 2008;39(12):3172–8. doi: 10.1161/STROKEAHA.107.503698. [DOI] [PubMed] [Google Scholar]
- 2.Ma B, et al. Nonlinear anisotropic stress analysis of anatomically realistic cerebral aneurysms. J Biomech Eng. 2007;129(1):88–96. doi: 10.1115/1.2401187. [DOI] [PubMed] [Google Scholar]
- 3.Hademenos GJ, et al. A nonlinear mathematical model for the development and rupture of intracranial saccular aneurysms. Neurol Res. 1994;16(5):376–84. doi: 10.1080/01616412.1994.11740257. [DOI] [PubMed] [Google Scholar]
- 4.Humphrey JD. Review: Computer Methods in Membrane Biomechanics. Comput Methods Biomech Biomed Engin. 1998;1(3):171–210. doi: 10.1080/01495739808936701. [DOI] [PubMed] [Google Scholar]
- 5.Toth M, et al. Sterically inhomogenous viscoelastic behavior of human saccular cerebral aneurysms. J Vasc Res. 1998;35(5):345–55. doi: 10.1159/000025604. [DOI] [PubMed] [Google Scholar]
- 6.Kyriacou SK, Humphrey JD. Influence of size, shape and properties on the mechanics of axisymmetric saccular aneurysms. J Biomech. 1996;29(8):1015–22. doi: 10.1016/0021-9290(96)00010-3. [DOI] [PubMed] [Google Scholar]
- 7.Millan RD, et al. Morphological characterization of intracranial aneurysms using 3-D moment invariants. IEEE Trans Med Imaging. 2007;26(9):1270–82. doi: 10.1109/TMI.2007.901008. [DOI] [PubMed] [Google Scholar]
- 8.Reeps C, et al. The impact of model assumptions on results of computational mechanics in abdominal aortic aneurysm. J Vasc Surg. 2010;51(3):679–88. doi: 10.1016/j.jvs.2009.10.048. [DOI] [PubMed] [Google Scholar]
- 9.Seshaiyer P, et al. Multiaxial Mechanical Behavior of Human Saccular Aneurysms. Computer Methods in Biomechanics and Biomedical Engineering. 2001;4(3):281–289. [Google Scholar]
- 10.Shah AD, et al. Further Roles of Geometry and Properties in the Mechanics of Saccular Aneurysms. Computer Methods in Biomechanics and Biomedical Engineering. 1997;1(2):109–121. doi: 10.1080/01495739708936698. [DOI] [PubMed] [Google Scholar]
- 11.Simkins TE, Stehbens WE. Vibrations recorded from the adventitial surface of experimental aneurysms and arteriovenous fistulas. Vasc Surg. 1974;8(3):153–65. [PubMed] [Google Scholar]
- 12.Elisa L, et al. Intracellular Signaling Pathways and Size, Shape, and Rupture History of Human Intracranial Aneurysms. Neurosurgery. 2012 doi: 10.1227/NEU.0b013e31824c057e. [DOI] [PubMed] [Google Scholar]
- 13.Antiga L, et al. Geometric reconstruction for computational mesh generation of arterial bifurcations from CT angiography. Comput Med Imaging Graph. 2002;26(4):227–35. doi: 10.1016/s0895-6111(02)00020-4. [DOI] [PubMed] [Google Scholar]
- 14.Antiga L, Ene-Iordache B, Remuzzi A. Computational geometry for patient-specific reconstruction and meshing of blood vessels from MR and CT angiography. IEEE Trans Med Imaging. 2003;22(5):674–84. doi: 10.1109/TMI.2003.812261. [DOI] [PubMed] [Google Scholar]
- 15.Piccinelli M, et al. A framework for geometric analysis of vascular structures: application to cerebral aneurysms. IEEE Trans Med Imaging. 2009;28(8):1141–55. doi: 10.1109/TMI.2009.2021652. [DOI] [PubMed] [Google Scholar]
- 16.Ma B, Harbaugh RE, Raghavan ML. Three-dimensional geometrical characterization of cerebral aneurysms. Ann Biomed Eng. 2004;32(2):264–73. doi: 10.1023/b:abme.0000012746.31343.92. [DOI] [PubMed] [Google Scholar]
- 17.Raghavan ML, et al. Three-dimensional finite element analysis of residual stress in arteries. Ann Biomed Eng. 2004;32(2):257–63. doi: 10.1023/b:abme.0000012745.05794.32. [DOI] [PubMed] [Google Scholar]
- 18.Speelman L, et al. Patient-specific AAA wall stress analysis: 99-percentile versus peak stress. Eur J Vasc Endovasc Surg. 2008;36(6):668–76. doi: 10.1016/j.ejvs.2008.09.007. [DOI] [PubMed] [Google Scholar]
- 19.Wiebers DO, et al. Unruptured intracranial aneurysms: natural history, clinical outcome, and risks of surgical and endovascular treatment. Lancet. 2003;362(9378):103–10. doi: 10.1016/s0140-6736(03)13860-3. [DOI] [PubMed] [Google Scholar]
- 20.Zhou X, et al. Patient-specific wall stress analysis in cerebral aneurysms using inverse shell model. Ann Biomed Eng. 2010;38(2):478–89. doi: 10.1007/s10439-009-9839-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shah AD, Humphrey JD. Finite strain elastodynamics of intracranial saccular aneurysms. J Biomech. 1999;32(6):593–9. doi: 10.1016/s0021-9290(99)00030-5. [DOI] [PubMed] [Google Scholar]
- 22.Lu J, Zhou X, Raghavan ML. Inverse method of stress analysis for cerebral aneurysms. Biomech Model Mechanobiol. 2008;7(6):477–86. doi: 10.1007/s10237-007-0110-1. [DOI] [PubMed] [Google Scholar]