Functional characterization of normal and degraded bovine meniscus: Rate-dependent indentation and friction studies

Abstract

The menisci are known to play important roles in normal joint function and the development of diseases such as osteoarthritis. However, our understanding of meniscus’ load bearing and lubrication properties at the tissue level remains limited. The objective of this investigation was to characterize the site- and rate-dependency of the compressive and frictional responses of the meniscus under a spherical contact load. Using a custom testing device, indentation tests with rates of 1, 10, 25, 50, and 100 μm/s were performed on bovine medial meniscus explants, which were harvested from five locations including the femoral apposing surface at the anterior, central, and posterior locations and the central portion at the deep layer and at the tibial apposing surface (n=5 per location). Sliding tests with rates of 0.05, 0.25, 1, and 5 mm/s were performed on the central femoral aspect and central tibial aspect superficial samples (n=6 per location). A separate set of superficial samples were subjected to papain digestion and tested prior to and post treatment. Our findings are: i) the Hertz contact model can be used to fit the force responses of meniscus under the conditions tested; ii) the anterior region is significantly stiffer than the posterior region and tissue modulus does not vary with tissue depth at the central region; iii) the friction coefficient of the meniscus is on the order of 0.02 under migratory contacts and the femoral apposing surface tends to show lower friction than the tibial apposing surface; iv) the meniscus exhibits increased modulus and lubrication with increased indentation and sliding rates; v) matrix degradation impedes the functional load support and lubrication properties of the tissue. The site- and rate-dependent properties of the meniscus may be attributed to spatial variations of the tissue’s biphasic structure. These properties substantiate the role of the meniscus as one of the important bearing surfaces of the knee. These data contribute to an improved understanding of meniscus function, and its role in degenerative joint diseases. In addition, the results provide functional metrics for developing engineered tissue replacements.

Introduction

The menisci of the knee are complex fibrocartilaginous tissues that play important roles in load bearing, shock absorption, and joint lubrication [1]. Until Fairbank’s landmark 1948 study [2], the importance of the meniscus was poorly understood, and meniscectomy was a common orthopedic procedure [3]. Fairbank described three radiological knee joint changes following meniscectomy: formation of a ridge on the femoral condyle; narrowing of the joint space, and flattening of the femoral condyle. These alterations came to be known as ‘Fairbank’s changes’. Since that study, our knowledge of the meniscus has significantly evolved. It is now well established that loss or injury of the meniscus leads to altered loading in the joint [4,5], chondropathy in animal models [6,7], changes in subchondral bone [8,9], and increased incidence of osteoarthritis (OA) [10]. More recent attention is being paid to improving healing of meniscus after damage and to testing replacement options (allografts or engineered menisci) when the tissue is beyond repair [11,12]. These efforts require detailed understanding of mechanical behaviors and material properties of meniscus in both normal and pathological conditions. This knowledge is vital in elucidating the role of meniscus in the development of OA, and establishing functional metrics for successful tissue-engineering applications.

The material properties of meniscus have been studied extensively. However, our understanding of its functional behaviors still remains incomplete. Proctor et al. [13] expanded the cartilage work of Mow et al. [14] and concluded that the meniscus could also be characterized as a biphasic material in which a porous-permeable solid matrix is saturated by interstitial fluid. They found the meniscus to be approximately one-half as stiff in compression and one-sixth as permeable as the cartilage. Several authors [13,15-17] have characterized the compressive behavior of the meniscus, reporting aggregate modulus on the order of 0.1 MPa, and permeability on the order of 1×10⁻¹⁵ m⁴/(N·s). The meniscus has also been tested under tensile loading [13,18,19], and shear loading [20,21]. The values of shear modulus are generally on the same order of magnitude as the compressive modulus (~0.1 MPa) [22] while the tensile modulus typically ranges on the order of 10–100 MPa [23]. These studies demonstrated significant variations among species, anatomical locations, testing directions, and experimental methods.

Cartilage and meniscus are biphasic tribological materials that must support contact forces and lubricate the joint. Ateshain and co-workers have identified two basic testing configurations for lubrication studies of these tissues. The stationary contact area (SCA) is similar to unconfined compression; the sample is squeezed between two large flats and a relative motion is imposed. The defining characteristic of SCA is the stationary contact pressure relative to the tissue surface. Interstitial fluid pressure supports a significant fraction of the load initially and interstitial lubrication provides extremely low initial friction coefficients. Over time, interstitial pressure is lost and the equilibrium friction coefficient results primarily from boundary lubrication and, potentially, other ‘mixed-mode’ contributors. By contrast, the migratory contact area (MCA) occurs when the contact pressure distribution migrates across the tissue surface. Caligaris and Ateshian made a number of critical observations about MCA sliding [24]. Firstly, they showed that MCA articulation maintains interstitial lubrication indefinitely. Secondly, they directly demonstrated that interstitial lubrication is roughly 40 times more effective than boundary lubrication for reducing friction. This study suggests that MCA is an important contributor to joint lubrication during the course of daily activities.

The meniscus directly contacts the femoral condyle and is a primary tribological tissue. The importance of the meniscus on the whole joint lubrication and wear resistance have been established in an in vitro simulation system [25]. There are few quantitative measurements of meniscus friction. Galley et al. [26] used the SCA configuration and found that the equilibrium friction coefficient of ovine meniscus ranged from 0.1 to 0.4 when slid at speeds from 0.2 to 30 mm/s in a bath of phosphate-buffered saline (PBS). Based on the recent work from Ateshian’s group [24], we strongly believe that interstitial pressure is critical for joint function and health and propose that MCA studies are essential for better understanding its functionalities. To date, there have been no investigations on the meniscus in the MCA configuration, and it is unclear if it responds to MCA as cartilage is now known to.

The aim of this study was to systematically characterize the local functional properties of normal and chemically degraded meniscus during rate-controlled indentation and MCA sliding tests. As we showed in a previous study, rate-controlled indentation can be used as a model for MCA sliding (which imposes a rate-controlled deformation of the tissue) [27]. Here, we use rate controlled indentation and MCA sliding to study the relevant biomechanics involved in meniscus load support and lubrication. We test the following hypotheses: 1) equilibrium and functional properties vary spatially throughout the tissue in accordance with location-specific responsibilities in joint mechanics; 2) the functional properties depend on the rate of the corresponding deformation process; 3) functional properties deteriorate as the tissue degenerates. The long-term objective of the research is to improve the understanding of the role of the meniscus in normal and pathological joint mechanics.

Methods

Sample preparations

Sixteen stifles (knee joints) of 12–20 month-old steer were obtained from a local butcher. Each joint was refrigerated before being transported to our laboratory within a couple of days after sacrifice. Samples with any evidence of fibrillation and discoloring were excluded. 10×10×3 mm³ samples were harvested with a surgical scalpel from the medial meniscus at five locations (Fig. 1). Three samples were taken from the femoral aspect (with the testing surface apposing the femoral condyle) at the anterior, central and posterior regions. Two additional samples were taken from the central region of the meniscus at the deep layer and at the tibial aspect (with the testing surface apposing the tibial condyle). The natural articulating surfaces were preserved and efforts were made to ensure that deep layer samples were flat. The effects of sample curvature on testing results were minimized by i) the relatively small size of the probe radius, ii) alignment of the surface normal in the region of interest with the transducer normal force axis using a tilt stage, and iii) accounting for the resulting asymmetry of forward and reverse sliding as described below. The samples were washed and wrapped in PBS saturated gauze and frozen at −50 °C. Samples were thawed and immersed in PBS for 1 h prior to testing. Indentation tests were performed on samples from all 5 anatomical locations (n=5 per location), and sliding tests were only performed on anatomical sliding surfaces of the central femoral and tibial aspect samples (n=6 per surface). All tests were completed within 4 h after thawing, and samples remained in PBS throughout.

Fig. 1.

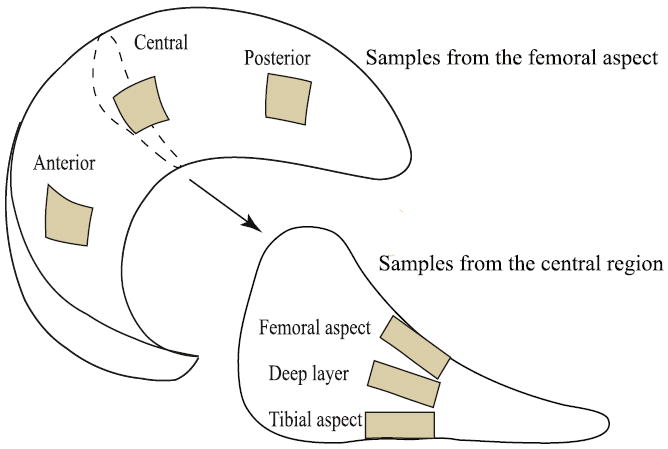
Meniscus tissue explants were harvested from five different locations per bovine medial meniscus (12–20 month-old). The nominal dimensions of each sample were 10×10×3 mm. Drawing not to scale.

To investigate the functional effects of tissue degeneration, papain digestion was used on a separate set of central femoral aspect samples. Papain is a proteolytic enzyme capable of degrading collagen and releasing chondroitin sulfate-peptides from proteoglycans, inducing degenerative changes in the joint similar to those observed in human OA [28]. The papain solution was prepared using 1.25 mg papain (12.5 U/mg, Sigma), 9 mg NaCl, 0.8 mg l-cysteine-HCl, and 9 mg EDTA (disodium salt) per mL distilled water (pH was adjusted to 6.5 at room temperature) [29]. Immediately following ‘pretreatment’ indentation or sliding testing, the samples were immersed in 10 mL of papain solution on a magnetic stirrer plate (~300 rpm) for 30 min. After a thorough wash and rinse in PBS, the samples were subsequently tested. The post-treatment measures were compared with pre-treatment results. The indentation and sliding test sample sets comprised six samples.

Indentation tests

A custom microtribometer described previously [27,30] was used in this study. Briefly, for indentation tests, a vertical piezo stage was commanded to indent the sample via a spherical probe (radius 3.2 mm, 440C stainless steel) attached to the tip of a steel cantilevered beam. The meniscus sample was mounted to a tilting stage using cyanoacrylate adhesive and submerged in a PBS bath. Sample position and alignment with the probe was manually adjusted. Capacitance sensors with sub-nm resolution detected vertical and horizontal beam deflections, from which forces were determined based on the calibrated beam stiffness. Prior to testing, the probe was manually positioned to within 10 μm±5 μm of the meniscus surface and the force sensor zeroed to eliminate bias from fluid surface tension. The indentation protocol included six possible steps (Fig. 2A): the test was initiated by actuating the vertical stage toward the sample (the approach phase). After physically touching the meniscus sample surface (the contact phase), the probe continued to indent the sample at a prescribed rate and target displacement (the indentation phase). Contact was defined to occur when the measured normal force exceeded zero by three standard deviations of previous baseline measures (i.e., noise of 10 kHz signal). The stage position at contact served as the reference location for calculating indentation depth (the advancement of stage minus the beam’s vertical deflection). Each sample was indented at a wide range of indentation speed in the order of 10, 25, 50, 100, and 1 μm/s. For the first four of the five total measurements, the probe was retracted immediately after indentation (the unload phase) to limit matrix consolidation. The 1 μm/s indentation was performed last in order to avoid significant solid consolidation. After the test, the vertical stage was fixed at the target displacement (the equilibration phase) until the system equilibrated (the equilibrium phase) to conclude the series of tests. Between tests a 30 second dwell was used; this dwell was a compromise between ensuring equilibration and reducing total test time to minimize the potential for natural degradation. This time was sufficient to enable equilibration for our four fastest rates due to 1) the presence of significant fluid pressure, 2) the lack of time to exude a significant volume of fluid, 3) the use of unloading to actively pull fluid back into the tissue, and 4) the small indentation depths. Preliminary studies were conducted to ensure repeatable measurements using the protocol as illustrated previously [27].

Fig. 2.

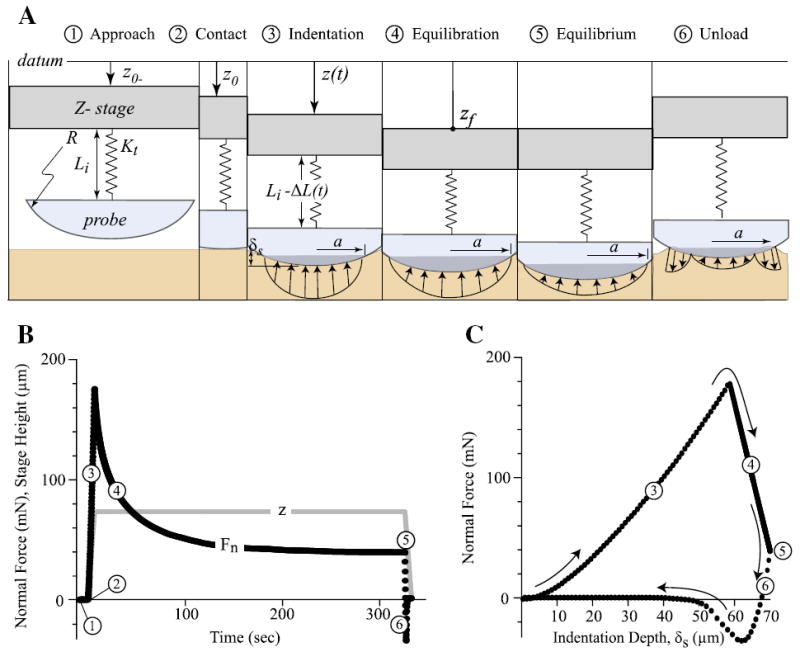
(A) Illustrations of the probe–sample interface during a typical indentation test consisting of six sequential phases. The vertical stage with the spherical probe was actuated toward the sample (the approach phase). After physically touching the meniscus sample surface (the contact phase), the probe continued to indent the sample at a prescribed rate and target displacement (the indentation phase). For most of the tests, the probe was retracted immediately after indentation (the unload phase). For the tests with 1 μm/s, the vertical stage remained at the target displacement while the probe continued to deform the sample (the equilibration phase), until equilibrium was achieved (the equilibrium phase), followed by the unload phase. (B) Representative plots of normal force (F_n) and z-stage position during phases 1 to 6 of a typical test. (C) Normal force plotted as a function of indentation depth for the same test. Equilibrium and effective moduli were obtained from the force and depth data captured at the phases 5 and 3 using the Hertz model.

Equilibrium and effective moduli were determined using Hertz contact theory [32] which provides the relationship between force (F_n), Young’s modulus (E), Poisson’s ratio (ν), sphere radius (R), and penetration depth (δ_s). In our previous studies [27] we defined the contact modulus as:

$$E_c=\frac{E}{1-{\nu }^2}=\frac{3}{4}\frac{F}{R^{0.5}\cdot {\mathrm{\delta }}_s^{1.5}}.$$ (1)

The definition of the contact modulus eliminates the need to characterize Poisson’s ratio and Young’s modulus independently. This equation assumes that the meniscus curvature radius is much larger than the sphere and the sphere is much stiffer than the meniscus. The associated errors are at most 5% and 0.001%, respectively. For reference, the contact radius, α, is equal to the square root of the product of penetration depth and probe radius per Hertz’s theory.

An equilibrium measurement produces a single equilibrium force and depth coordinate that is inserted directly into Eq. (1) to obtain the equilibrium contact modulus, E_c0. The effective contact modulus, E_c, characterizes the non-equilibrium response and comprises contributions from matrix stress and fluid pressure. For these measurements, force and depth data in the range from 50 to 100 μm were fit to Eq. (1). This range of depth was chosen because i) shallower data were subjected to effects of surface irregularities (e.g. surface imperfections, or exposed or broken collagen fibril on deep samples) and ii) deeper data was not available for all measurements (e.g. high speed). The contact modulus, coefficient of determination, and contact modulus uncertainty were determined for each fit.

Sliding tests

The first five phases of the sliding test, identical to those in the indentation test (Fig. 2), aimed to establish equilibrium between the probe and the sample prior to the sliding measurements (Fig. 3). Briefly, the sample was indented at a rate of 10 μm/s to a commanded vertical stage displacement of 200 μm, where the stage remained during the remainder of the test (contact is never broken during MCA testing). Following equilibration, the sample mounted on the horizontally moving stage was commanded to reciprocate beneath the spherical probe at a mean velocity of 5 mm/s over a 1.5 mm long track in physiological sliding direction (anterior–posterior). The initiation of sliding induces fluid pressurization which increases normal force and decreases penetration depth as illustrated in Fig. 3. Interstitial pressure pumps fluid into the contact with reciprocation until the system reaches the associated dynamic equilibrium. Penetration depth, normal force, and friction force were collected continuously during the bi-directional sliding at a rate of 10 kHz. The same sample was subjected to sequential sliding tests in the order of reducing speed (5, 1, 0.25, to 0.05 mm/s), with each segment lasting the larger of 60 s and 5 cycles after reaching a clear dynamic equilibrium. These speeds represent the largest range of speeds that could be easily achieved with the instrument and the protocol reflects a compromise between ensuring equilibration and reducing test time to minimize degradation and wear. Preliminary tests showed no significant effect of test order; i.e. the response at any speed did not depend significantly on the magnitude of the previous speed. Decreasing order of sliding speed was thus chosen for convenience.

Fig. 3.

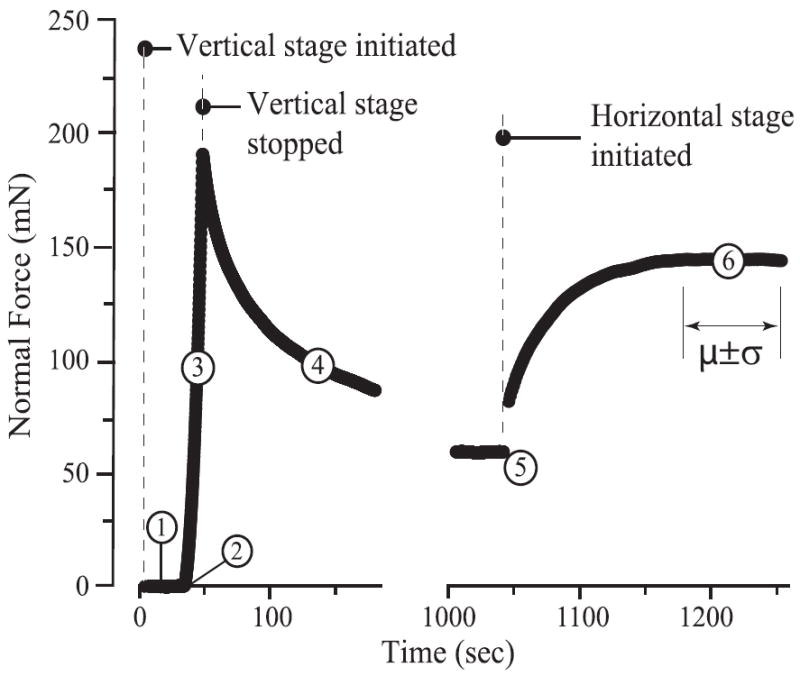
Procedures for sliding tests: the first five phaseswere identical to those in indentation tests (Fig. 2), establishing equilibriumbetween the probe and the sample prior to sliding. During sliding (phase 6), the horizontal stage reciprocated over the probe with a 1500 μm track, resulting in fluid pressurization in the sample and increased normal force until reaching a steady state. The penetration depth, normal and friction forces were collected and analyzed at the center of the sliding track during the steady state.

To minimize the effect of sample curvature on the measured friction coefficient, we adopted a simple reversal method [31] and determined the friction coefficient to be the difference in the forward and reverse tangential forces divided by twice the average vertical force. Although the normal and friction forces were collected over the entire 1500 μm track, only the data within ±10 μm of the location of the indentation/equilibrium measurement were analyzed. This analysis was applied to each cycle of the test, and the mean value was collected for each cycle. All tests were performed at the geometric center of the sample.

Statistical analysis

Descriptive results were reported as the means and standard deviations. Two-way ANOVA with and without repeated measures were performed in SAS software package (SAS Institute Inc, Cary, NC, USA) to detect the influence of either sample location/depth, loading rate, or treatment on the measured contact modulus or friction coefficient, followed by post hoc Tukey tests adjusted for multiple comparisons of means. Significance was defined as p<0.05. The main factors, F statistics, and comparison p values were reported for each test.

Results

Force responses and fitting with the Hertz model

Representative indentation results from the femoral aspect sample group are shown to demonstrate the Hertz fits and the effects of indentation rate and location on the force response (Fig. 4). There was general agreement with the Hertz model. The average coefficient of determination for the entire study was R²=0.986±0.014; one of the posterior femoral aspect sample was a clear outlier (R²=0.668±0.049) and was excluded from the analysis; this exclusion had no effect on the results of the statistical analyses. The worst fit in the data set shown (1 μm/s, R²=0.955, Fig. 4A) is close to the lowest R² value observed for the entire study (R²=0.953). Modulus uncertainty was low in all cases compared to the inter-sample variations; the largest uncertainty in the study was 0.1 MPa and coincided with the largest modulus measurement and lowest coefficient of determination in the study.

Fig. 4.

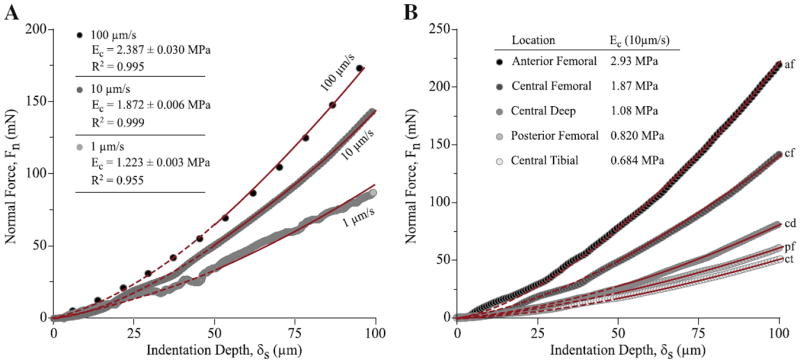
Representative indentation results and illustration of analysis methods. (A) The normal force is plotted versus indentation depth for a central femoral aspect sample at the indentation rates of 1, 10, and 100 μm/s. The line represents the best fit to Hertz model for each measurement. The effective modulus for the fit is given with the corresponding uncertainty and coefficient of determination (R²). The data shown for 1 μm/s was the worst fit in the study. (B) The normal force is plotted versus indentation depth for the five locations at one meniscus under a commanded indentation rate of 10 μm/s. Only data from 50 to 100 μm depth (indicated by thin solid lines) were used in the fitting and analysis.

The force measured at any indentation depth increased as the indentation rate increased (Fig. 4A). This trend with speed was representative of all samples in the study. The effective contact modulus of this sample increased from 1.2 to 2.4 MPa as the indentation rate increased from 1 to 100 μm/s. Likewise, the force and effective contact modulus systematically varied with location (Fig. 4B). During indentation at 10 μm/s on the five locations of one meniscus, the effective contact modulus increased in the superior (tibial → deep → femoral) and anterior (posterior → central → anterior) directions. The spatial variances for the entire data set were reported below.

Site- and rate-dependent material stiffness

In every case, the effective contact modulus was higher than the equilibrium modulus. As an example, the effective contact modulus is plotted as a function of deformation rate for the central femoral aspect samples (n=5, Fig. 5). The contact modulus increased monotonically (at a decreasing rate) with the measured indentation rate. Two-way ANOVA showed that indentation rate (F_5,20 =50.46, p < 0.0001) and specimen donor (F_4,20 =20.36, p < 0.0001) had significant effects. Significant differences detected among means are denoted by different letters (e.g. equilibrium vs. any non-zero indentation rate in Fig. 5).

Fig. 5.

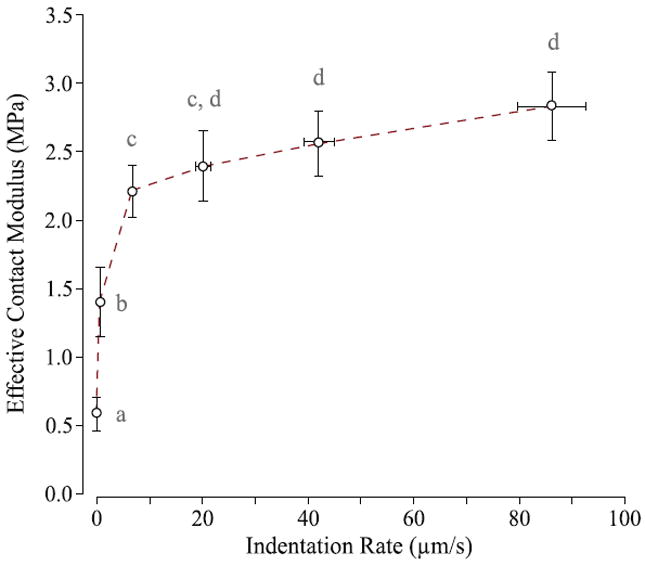
Effective contact modulus plotted versus deformation rate for the central femoral aspect samples (n=5). Samples were indented at commanded rates of 0, 1, 10, 25, 50, and 100 μm/s. Standard deviation bars in the vertical direction represent biological variability between the samples and horizontal standard deviation bars represent one standard deviation of the measured deformation rate. Means with different letters are significantly different (two-way ANOVA with Tukey multiple comparisons, p<0.05).

The effective contact modulus tended to increase in the superior and anterior directions (Fig. 6). Two-way ANOVA (factors: location and specimen donor) was performed separately for equilibrium and effective (10 μm/s) moduli, followed by Tukey post hoc comparison of means. Statistical difference was not detected for equilibrium contact moduli through tissue depth (Fig. 6A, F_2,8 =2.33; p=0.16). However, for the femoral aspect samples (Fig. 6B, F_2,8 =6.89; p=0.018), E_c0 was significantly higher at the anterior location than the posterior location (p=0.015). For all samples analyzed (n=24, excluding one outlier), the mean equilibrium contact modulus was 0.51±0.05 MPa. At an indentation rate of 10 μm/s, statistical difference was detected with tissue depth (Fig. 6A, F_2,8 =11.27; p=0.005) and with the anterior–posterior positioning (Fig. 6B, F_2,8 =27.86; p=0.0002). The mean effective contact modulus for all locations varied from 1.08 MPa (the deep samples) to 3.19 MPa (the anterior samples), increasing by a factor of 2 to 6 compared with equilibrium (Fig. 6). At 10 μm/s indentation rate, the femoral aspect was stiffer than the deep layer (p=0.006) and the tibial aspect (p=0.014) (Fig. 6A). The anterior region remained stiffer than the central (p=0.014) and posterior regions (p=0.0002), and the central region was stiffer than the posterior region (p=0.015). Means with the same letters were not significantly different (Fig. 6).

Fig. 6.

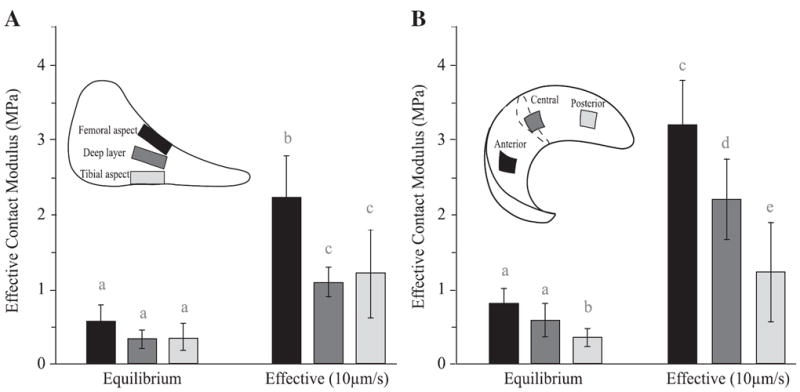
Spatial variations of the equilibrium and effective moduli for (A) the central region with different depths and (B) the femoral aspect samples. Effective moduli were measured with a commanded indentation rate of 10 μm/s. Two-way ANOVA was performed separately for equilibrium and effective moduli; means with different letters are significantly different (Tukey multiple comparisons, p<0.05).

Site- and rate-dependent lubrication properties for normal meniscus

The meniscus exhibited site- and rate-dependent friction during sliding (Fig. 7). Two-way ANOVA with repeated measures showed significant influence from both location (F_1,40 =12.39; p=0.001) and speed (F_3,40 =89.39; p < 0.0001). For both femoral and tibial aspect samples, the friction coefficient decreased by approximately 65% (ca. 0.055 to 0.02) as the sliding speed increased from 0.05 to 5 mm/s. For both locations, the friction coefficient at 0.05 mm/s was significantly higher than those at all other sliding speeds (p<0.0001); differences were also detected between 0.25 vs. 1 mm/s (p=0.015) and 0.25 vs. 5 mm/s (p=0.001) for the tibial aspect samples (Fig. 7). Although the femoral aspect samples tended to have lower friction coefficients than the tibial aspect samples at all sliding speeds, no significance was detected using Tukey multiple comparisons of means.

Fig. 7.

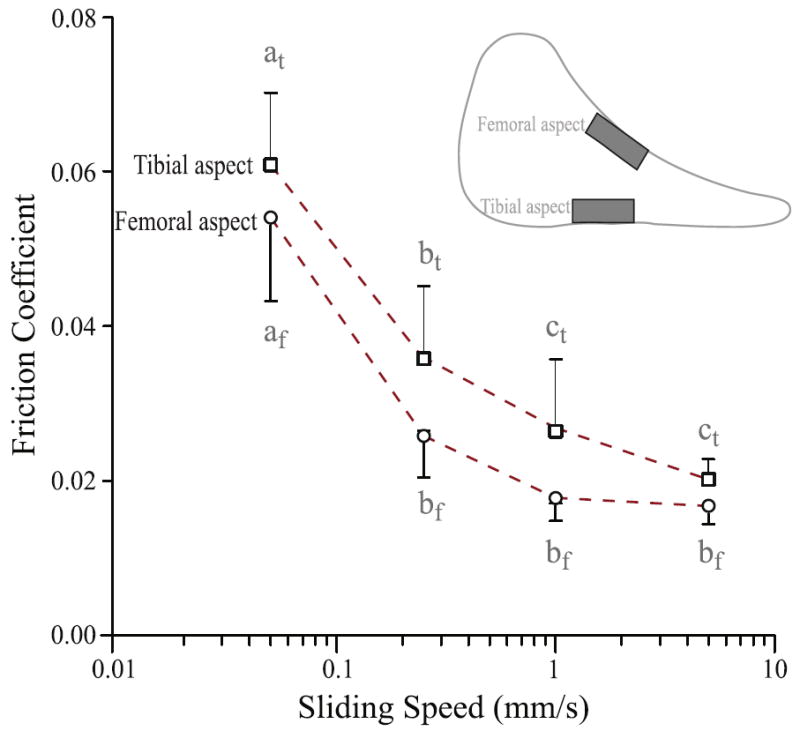
Location and sliding speed significantly affected friction measurements for the central tibial and femoral aspect meniscus samples (two-way ANOVA). Although friction coefficient tended to be lower at the femoral aspect for any sliding speed tested, no statistical difference was detected at any one speed with post-hoc analysis. For both locations, the slowest sliding speed (0.05 mm/s) showed significantly higher friction coefficient than other faster speeds. Means with different letters are significantly different (Tukey multiple comparisons, p<0.05).

Tissue degradation impaired meniscus’ load support and lubrication properties

Tissue degradation by papain digestion tended to decrease the contact modulus of the meniscus and significantly increased the friction coefficient (Fig. 8). For contact modulus prior to and post papain treatment, two-way ANOVA showed that both treatment (F_1,40 =21.77, p < 0.0001) and speed (F_3,40 =13.91, p < 0.0001) had a significant effect (Fig. 8A). The equilibrium contact modulus (labeled as “0 indentation rate” in Fig. 8A, 0.16±0.11 MPa) decreased from pre-treatment (0.51±0.12 MPa). Although the contact modulus of the meniscus was reduced by approximately 50% post-treatment in all the testing indentation rates, the reduction was not significant (p>0.05) (Fig. 8A). Samples exhibited increasing contact modulus with increased speed: pre-treatment contact modulus was significantly higher at 10 and 100 μm/s than at equilibrium (p=0.002, 0.005, respectively) and post-treatment tissue modulus was higher at 100 μm/s than at equilibrium (p=0.02, Fig. 8A). Two-way ANOVA showed that papain treatment had a significant effect on friction coefficient (F_1,40 =122.53, p<0.0001); speed also had a significant effect (F_3,40 =19.39, p < 0.0001) (Fig. 8A). Friction coefficient was increased by a factor of two at every speed post treatment; which was significant compared with its corresponding pre-treatment value (p<0.0002, Fig. 8B). Only the friction coefficient at 0.05 mm/s was significantly higher than those at 0.25, 1, and 10 mm/s when tested pre- and post-treatment (p<0.04 and p<0.002), respectively.

Fig. 8.

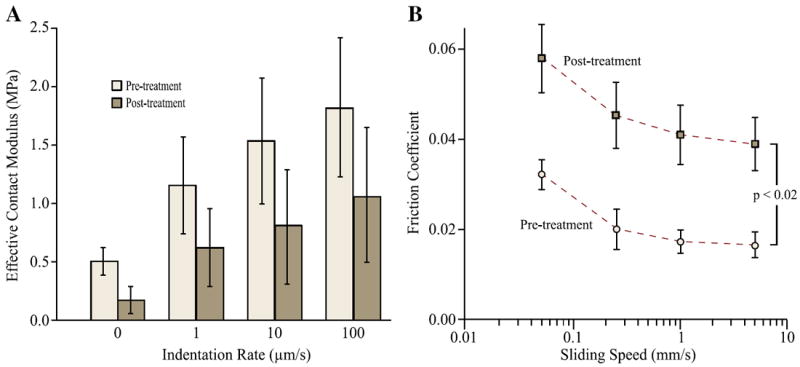
Papain digestion (30 min) tended to soften the meniscus and significantly increased friction. (A) The equilibrium (labeled as zero indentation rate) and effective moduli of six central femoral aspect samples prior to and post digestion treatment. No statistical significance was found between the pre- and post treatment moduli at any of the indentation rates. (B) The friction coefficients of the samples were significantly increased at each of the sliding speed post digestion treatment (Tukey multiple comparisons, p<0.002).

Discussion

This work offers the first direct measurements of meniscus biomechanics and lubrication under the rate-controlled deformation conditions that likely drive the maintenance of interstitial fluid pressure. We observed increased fluid pressurization with increased deformation rates during indentation and sliding, and the anatomical location of the tissue had a significant effect on the biomechanical load support and lubrication responses. These results will benefit future efforts in i) modeling in-vivo joint and tissue mechanics, ii) designing appropriate mechanical stimulations for cell–matrix interactions for enhancing tissue’s intrinsic healing, and iii) testing tissue replacements (e.g., allografts) and establishing functional metrics for tissue-engineering of the meniscus.

Equilibrium contact modulus measurements agreed reasonably well with previous literature using more traditional testing methods; the equilibrium contact modulus is equal to the aggregate modulus only when ν=0. Proctor et al. [13] used confined compression to determine aggregate modulus and permeability of bovine meniscus at different locations and tissue depths. They found no significant difference in modulus with respect to location in superficial specimens. However the deep specimens demonstrated a highly significant variation with locations, with the posterior region being stiffer than the anterior and central-anterior regions. Similar spatial variations were found by Hacker et al. [32] in human meniscus under confined compression. However, using a 0.8–1.0 mm flat ended cylindrical rigid porous indenter tip (50% porous, ~50 μm pore diameter), Sweigart et al. [17] used creep indentation on the menisci from baboon, bovine, canine, human, lapine, and porcine at different locations and found that the bovine meniscus exhibited a higher modulus in the anterior location, which was in direct contrast to the studies by Proctor and Hacker. Our results of the equilibrium moduli for the femoral aspect samples (corresponding to Proctor’s ‘superficial’ location) follow the trend observed in Sweigart et al. in that the anterior location was significantly stiffer than the posterior location (Fig. 6). The magnitude of the moduli measured in this study, however, more closely resembled those of Proctor et al. [13]. Discrepancies among the studies were likely due to differences in tissue sources, sampling locations, and testing methods. Proctor et al. [13] and Hacker et al. [32] used the biphasic theory for curve fitting, while the present study adopted a rigid spherical indentation scheme and applied the Hertz contact theory. Coefficients of determination (R²) were above 0.953 for all the 24 samples analyzed in this study, validating the adoption of Hertz model (Fig. 4).

Significant stiffening occurred when meniscus was indented at increasing rates (Figs. 4-6), which is consistent with its functional role as a shock absorber during joint loading. Compared with the equilibrium modulus (average 0.5 MPa), all locations showed a two- to six-fold increase in effective contact modulus when loaded at 10 μm/s (Fig. 5). Contact modulus increased monotonically with loading rate (Fig. 6). This stiffening effect can be attributed to pressurization of the interstitial fluid during indentation. The fraction of the load carried by fluid pressure is F’=(E_c − E_c0)/E_c [27], such that a 6-fold increase in modulus reflects a fluid load fraction of 83%. The fluid load fractions exceed the 50% limit for a linear biphasic material [33] because the matrix is stiffer in tension than in compression (E*=E_t/E_c >1) [34]. We previously presented a method for fitting variable rate indentation results such as those in Fig. 5 [27]. Fitting Fig. 5 yields a permeability of k=1×10⁻¹⁵ m⁴/(Ns) and E*=4. The permeability is comparable to, if not slightly higher than, prior measurements. However this could be expected based on the fundamental differences in our method and traditional fitting to biphasic theory. We are fitting the entire range of responses including those under high interstitial pressure conditions where consolidation of the matrix is small. Meniscus is at least an order of magnitude stiffer in tension than in compression [13,23] and the result E*=4 suggests that the tensile stresses in our tests were in the ‘toe’ region of the stress–strain curve where collagen bundles have not been fully straightened. The same trend of the site-dependent stiffness (stiffness: anterior>posterior) was found and even amplified under dynamic compression as in Chia et al. [24]. The result is likely due to the narrowed anterior horn which increases the collagen bundle and proteoglycan densities, both of which are expected to increase equilibrium modulus and reduce permeability. The compositional variations of meniscus at different anatomical sites are likely due to the evolution of the meniscus to support varied loading scenarios in the knee joint.

The sliding experiments are analogous to the rate-controlled deformation experiments as we demonstrated previously [27]. While fluid pressurization in rate-controlled indentation is necessarily short-lived, MCA sliding produces a constant deformation rate which maintains high fluid load fractions and low friction coefficients (μ<0.06) under all speed conditions for healthy tissue. The femoral aspect sample produced a relatively low friction coefficient of 0.05 at a speed of 0.05 mm/s (Fig. 7); increasing sliding speed reduced the friction coefficient toward an asymptote of ~0.02, which likely approaches the value achieved in vivo. These results are in close agreement with our cartilage friction coefficient results under nominally identical conditions [30] which suggests that the meniscus is as effective as the cartilage as a bearing material. We expected to find significant frictional difference between the femoral and tibial aspects. Firstly, the tibial aspect sits nominally stationary against the tibial plateau. Secondly, Bullough et al. [36] showed that the tibial aspect surface is dominated by radially oriented tie fibers while the femoral aspect surface is characterized by randomly oriented collagen fibrils. Two-way ANOVA did reveal a significant effect of surface on friction with the friction coefficient being 5–40% higher on the tibial aspect. However, under the same sliding speed, post-hoc analysis revealed no significant difference between the mean friction coefficients of the two surfaces, due to the small sample size (n=6).

Upon disruption of the matrix integrity, both meniscus’ load bearing and lubrication properties were impaired (Fig. 8). After 30 min of digestion, the equilibrium modulus dropped three-fold compared with the pre-treatment value. Although the digested menisci also stiffened at higher indentation rates, they were on average approximately two-fold softer at all indentation rates compared with pre-treatment. A much more significant loss of functionality was observed in the lubrication properties, where the digested meniscus samples exhibited a two-fold increase in friction coefficient. Long-term papain treatment has been found to disrupt the collagen network and cause the loss of proteoglycans from the tissue [28]. Histological staining of proteoglycan and collagen revealed surprisingly little evidence of structural or compositional degradation following the 30 min papain digestion (Fig. 9). This suggests that mechanical testing is of sufficient sensitivity to detect subtle tissue changes that may not be detectable using standard histological staining. Such an approach can be very useful in studying and detecting early stages of OA.

Fig. 9.

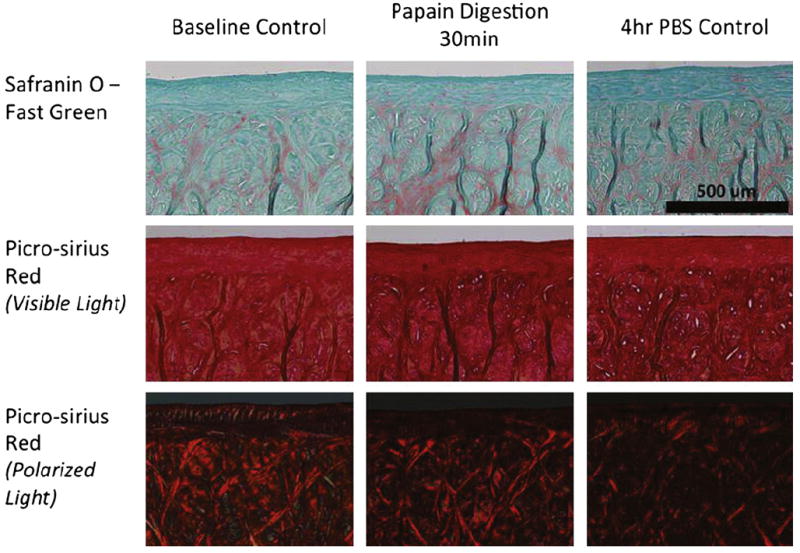
Histological examination of proteoglycan content and collagen content and orientation for three groups: (A) baseline control with no papain digestion or PBS immersion; (B) 30 min papain digestion; and (C) 4 h immersion in PBS solution. No visual changes in tissues after papain digestion or 4 h of immersion in PBS.

The mechanism of significantly increased friction after tissue degradation is not clear, but there are a few possibilities which include i) the removal of endogenous lubricin (surface lubricant) during papain digestion, ii) increased equilibrium friction, iii) increased plowing of the softer matrix, and iv) decreased fluid load support. Although removal of lubricin would contribute to an increase in friction at each speed, previous studies found only modest increases in equilibrium friction (15%) following lubricin removal [35]; we measured a 12% increase in equilibrium friction coefficient during a follow-up test. Increased equilibrium friction would result in divergence of the two curves (pre- and post-treatment) as speed decreased, which is inconsistent with our results. Plowing, which results from asymmetry in the pressure distribution toward the direction of sliding, may have also contributed to the increased friction after treatment. Furthermore, a reduced ratio of the tensile-compression modulus (E*) decreases the fluid load support asymptote, which increases the friction coefficient asymptote. An approach to analyze both in vitro and in vivo indentation and sliding conditions based on Peclet number can be found in our recent paper [27]. In vivo conditions such as meniscus tear, meniscectomy, or loosening of the meniscus anchoring may alter not only the meniscus’ surface congruency, its contact with cartilage, but also hoop stress inside the tissue. These changes, especially the reduced hoop stress, may impair fluid pressurization process and reduce the tissue’s load bearing and lubrication, eventually leading to tissue degradation and osteoarthritis.

There were several limitations in the present studies. Firstly, the counter body was a small, rigid, impermeable, spherical steel ball (3.2 mm radius) as opposed to a large, soft, porous, and geometrically complex femoral condyle. Caligaris and Ateshian [24] showed that the interstitial response to a hard sphere is consistent with the interstitial response to self-mated cartilage. It would be impossible to replicate the physiological environment, so we chose to use well-controlled conditions to enable basic insights into physiological mechanisms. The small probe allowed us to quantify local properties of the meniscus (on the order of 100 μm), which is known to be heterogeneous [13,17,32]. he rigid impermeable surface simplified the boundary conditions and enabled the adoption of Hertz contact theory [24,30]. The equilibrium friction coefficient will depend on the counter surface used. However, our primary interest is the interstitial mechanism and its effect on load support and lubrication. The second concern was the “plowing” effect of the small spherical probe. Our previous studies suggest that plowing is negligible for healthy cartilage under similar conditions [27]. The degree of plowing contributing to increased friction following degradation is indeterminable without direct knowledge of the distribution of fluid pressure around the contact. The third limitation was the use of PBS instead of synovial fluid. PBS was used to minimize contributions from boundary lubrication and thus highlight the contributions from the matrix structure. We anticipate uniformly reduced friction with the use of synovial fluid as demonstrated previously [36]. However, the overall trends of the rate- and site-dependency of meniscus lubrication observed in this study are expected to be held true. Finally, the contact of a small sphere against a square of meniscus is not directly comparable to in-vivo contact. We found a relatively low value of E*=4 which suggests small tensile stresses in the toe-region of the stress–strain curve. Circumferential and radial stresses from in-vivo contacts likely increase E* significantly; this leads to increased fluid load fractions, increased contact moduli, and reduced friction coefficients.

Conclusion

This work has provided the following notable findings: i) the Hertz contact model can be applied to fit the local biphasic response of meniscus; ii) the effective contact modulus was significantly higher anterior versus posterior and femoral versus tibial. iii) the friction coefficient of the meniscus is on the order of 0.02 under migratory contacts 2 and the femoral apposing surface tends to show lower friction than the tibial apposing surface; iv) the meniscus exhibits improved effective contact modulus and lubrication with increased indentation and sliding rates; and v) gross chemical digestion results in significant deterioration of the load bearing and lubrication capacities. This investigation has provided the first local characterization of compressive and frictional responses of the meniscus under a dynamic spherical contact load. The responses were found to exhibit site- and rate-dependency, which may be attributed to the variations in the tissue’s structure and composition. These properties substantiate the role of the meniscus as one of the important bearing surfaces of the knee. Disruption of the matrix integrity by papain digestion significantly impaired the functional load support and lubrication properties of the meniscus. Further studies are needed to elucidate the role of meniscus degradation in the progression of osteoarthritis.