Abstract
The present study uses a systems engineering approach to delineate the relationship between tinnitus and hyperacusis as a result of either hearing loss in the ear or an imbalanced state in the brain. Specifically examined is the input–output function, or loudness growth as a function of intensity in both normal and pathological conditions. Tinnitus reduces the output dynamic range by raising the floor, while hyperacusis reduces the input dynamic range by lowering the ceiling or sound tolerance level. Tinnitus does not necessarily steepen the loudness growth function but hyperacusis always does. An active loudness model that consists of an expansion stage following a compression stage can account for these key properties in tinnitus and hyperacusis loudness functions. The active loudness model suggests that tinnitus is a result of increased central noise, while hyperacusis is due to increased nonlinear gain. The active loudness model also generates specific predictions on loudness growth in tinnitus, hyperacusis, hearing loss or any combinations of the three conditions. These predictions need to be verified by experimental data and have explicit implications for treatment of tinnitus and hyperacusis.
1. Introduction
Tinnitus, also known as ringing in the ear or head, affects 10–20% of the general population (e.g., Shargorodsky et al., 2010). The statistics on hyperacusis, or “reduced tolerance to normal sound level”, are scarce but limited evidence has pointed to concomitant occurrence with tinnitus (e.g., Andersson et al., 2002). Hearing loss 11has been reported consistently as a high risk factor for tinnitus and hyperacusis. Most studies have examined the correlated but not causal relationships among tinnitus, hyperacusis and hearing loss (Nelson and Chen, 2004). A theoretical framework unifying them is still lacking but critically needed to advance our understanding and treatment of these disorders.
The present study takes a systems engineering approach to developing an active loudness model that uses internal noise, linear and nonlinear gain to not only account for but also predict the complicated relationship between tinnitus, hyperacusis and hearing loss. One key principle in systems engineering theory is to quantify the input–output function of the system. The other key principle is to identify the minimal number of modules within the system that can account for the system’s function or behaviors.
2. Loudness functions
Let us first define the loudness input–output function. The input is intensity, usually defined by acoustic pressure level in decibels (dB). The output is loudness, defined by a ratio scale in sones (Stevens, 1936). The input–output function between intensity and loudness is a nonlinear power function; it is also referred to as a loudness growth function and has been quantified in normal-hearing listeners to produce 0, 1, and 256 sones, corresponding to a 1000-Hz pure tone at 0, 40, and 120 dB SPL, respectively (Fastl and Zwicker, 2007). In other words, the input dynamic range from threshold to uncomfortable loudness level is 120 dB, while the output dynamic range is 256 sones. Note in this classic model that loudness at threshold equals 0 sone, a point of interest that we will revisit in this paper.
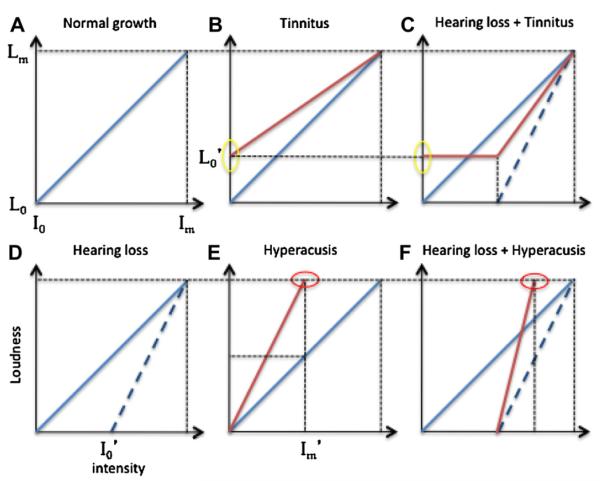
Let us use the input–output function to define hearing loss, tinnitus and hyperacusis. Different from the general term of hearing impairment, which ranges from simple elevated thresholds or more complicated suprathreshold disability in temporal and speech processing, hearing loss here is simply defined as reduced input as a result of elevated threshold. Fig. 1 illustrates how the input–output function changes as a function of hearing loss, tinnitus, hyperacusis, or any combinations of these factors.
Fig. 1.
Loudness growth function in normal hearing (solid diagonal line in panel A) and hearing loss (dashed line in panel D, I0’ denotes the elevated threshold). Loudness function changes with tinnitus (shallower line intercepting the y-axis in panel B) and concomitant hearing loss (panel C). Loudness function changes with hyperacusis (steeper line intercepting the dotted top horizontal line in panel E, Im’ denotes the reduced sound level that reaches the maximal loudness level) and concomitant hearing loss (panel F).
To simplify the matter, normal loudness growth is represented by a straight line (panel A, in which one could imagine the slope equal to 0.3, see Section 2 below for mathematical details). The input dynamic range is the intensity difference between threshold (I0) and uncomfortable loudness level (Im), while the output dynamic range is the loudness difference between L0 and Lm. In cases of hearing loss, the threshold is elevated to I0’ as shown in panel D. Assuming no changes in the uncomfortable loudness level, which is typical in most sensorineural loss cases, loudness appears to grow more steeply than normal (dashed line in panel D), a phenomenon termed loudness recruitment (Fowler, 1928).
Tinnitus refers to a subjectively perceived or internal sound at some loudness even though there is no sound physically present. Tinnitus can occur with or without hearing loss. Without hearing loss (panel B), tinnitus does not affect the input dynamic range but reduces the output dynamic range (=Lm – L0’) by elevating loudness at threshold from L0 to L0’. With concomitant hearing loss (panel C), tinnitus reduces both input and output dynamic ranges as a result of raised “floor” in both intensity and loudness domains.
Contrary to tinnitus, hyperacusis has to manifest itself by engaging an external sound that produces an abnormally loud percept even though the same sound is deemed to be acceptable by a normal-hearing person. Hyperacusis can also occur with or without hearing loss. Without hearing loss (panel E), hyperacusis only reduces the input dynamic range (=Im’ – I0) by lowering the intensity that produces uncomfortable loudness from Im to Im’. Note that the same intensity of Im’ would produce only a medium loud percept under normal circumstances (horizontal dashed line). With concomitant hearing loss (panel F), hyperacusis further reduces the input dynamic range (=Im’ – I0’) as a result of both raised “floor” and lowered “ceiling”. Note again that hyperacusis by itself does not reduce the output dynamic range.
Although more than 30 studies have measured either end of the loudness input–output function, namely tinnitus loudness and the maximal uncomfortable loudness level (e.g., Bauer and Brozoski, 2011; Goldstein and Shulman, 1996; Goodwin and Johnson, 1980;Henry and Meikle, 1999; Tyler and Conrad-Armes, 1983), only 4 studies have measured the entire loudness growth function in tinnitus or hyperacusis subjects (www.pubmed.gov search conducted on March 15, 2012). Penner (1986b) found a steeper than normal loudness growth at the tinnitus frequency in 8 of the 10 subjects with concomitant hearing loss and tinnitus but normal loudness growth at the tinnitus frequency in the remaining 2 subjects without hearing loss. Ward and Baumann (2009) confirmed Penner’s finding by showing steeper growth in tinnitus subjects with ~50 dB hearing loss but normal growth in tinnitus subjects with ~15 dB loss. In 16 tinnitus subjects without hearing loss, Nieschalk and Stoll (1996) found shallower than normal loudness growth (similar to panel B). On the other hand, Formby et al. (2008) showed in a single case that hyperacusis produced steeper loudness growth than even loudness recruitment (similar to panel F).
Overall the present limited data suggest that tinnitus alone reduces the output dynamic range by raising the loudness at or below threshold and produces normal or shallower than normal loudness growth, while hyperacusis alone reduces the input dynamic range by lowering the maximal uncomfortable loudness level and produces steeper than normal loudness growth. Concomitant hearing loss reduces both input and output dynamic ranges while steepening loudness growth. Can we use the current loudness model or do we need to develop a new loudness model to account for these behaviors?
3. Loudness models
To account for loudness growth in normal hearing, Zwicker and Scharf (1965) invented a concept of “specific loudness”, which equals to a power transformation of the intensity summed within a critical band or auditory filter. Zwicker did not specify where the power transformation occurs, but recent studies suggest a cochlear origin of this transformation (e.g.,Epstein and Florentine, 2005; Moore and Glasberg, 1996;Schlauch et al., 1998; Thorson et al., 2012). In this classical model, as shown in Fig. 2A, the brain is passive, performing only linear addition of specific loudness across critical bands to produce the total loudness of a given sound. Zwicker’s loudness model has been modified to account for loudness recruitment associated with typical sensorineural hearing loss. These modifications include widened auditory filters, increased exponent of the power transformation, and raised “internal noise” level (e.g.,Florentine and Zwicker, 1979; Launer et al., 1997; Moore and Glasberg, 2004; Scharf and Hellman, 1966). Most interestingly,Buus and Florentine (2002) argued that the primary cause of loudness recruitment is not the increased exponent of loudness function, but rather abnormally large loudness at an elevated threshold. In other words, loudness at threshold has a small value in normal hearing (~0.005 sones) but increases with elevated thresholds (doubled for every 16 dB loss, see Buus and Florentine, 2002).
Fig. 2.
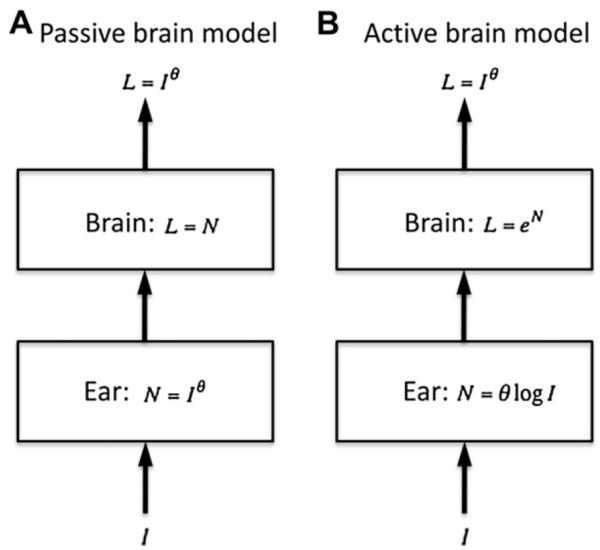
A. Passive brain loudness model. The power transformation occurs in the ear, while only linear addition of loudness occurs in the brain. B. Active brain loudness model. The power transformation is achieved by combining a logarithmic function in the ear with an exponential function in the brain. See text for details.
Although a wide range of applications from audio processing to hearing aid fitting has successfully used this classical loudness model (e.g., Launer and Moore, 2003; Moore et al., 1997), two lines of research have challenged its underlying physiological mechanisms, particularly the passive brain part. First, Heinz et al. (2005) found no evidence for any increased auditory-nerve rate responses following acoustic trauma, despite its apparent effect on reducing the basilar membrane compression in the cochlea. Instead, converging physiological evidence indicates that the neural correlate of loudness recruitment is an increased gain in the central auditory system from the chopper cells in the ventral cochlear nucleus to neurons in the inferior colliculus and cortex (e.g., Cai et al., 2009; Qiu et al., 2000; Szczepaniak and Moller, 1996).
The second line of research arguing for an active brain comes from loudness measurements in cochlear and auditory brainstem implant users who all have an extremely narrow input dynamic range (10–20 dB, e.g. see Zeng and Galvin, 1999) but a highly expansive loudness growth (Zeng and Shannon, 1992). Zeng and Shannon (1994) proposed an active loudness model that has a compression stage in the ear, following by an expansion stage in the brain to achieve the power transformation between sound intensity and loudness (Fig. 2B). In the case of cochlear implants, the compressive stage in the cochlea is bypassed, resulting in an exponential loudness growth.
At present, none of these loudness models have been applied to tinnitus and hyperacusis. One reasonable deduction, though, is the limited utility of Zwicker’s classical model and its modifications in explaining the typical behaviors of tinnitus and hyperacusis (See Section 1). For example, Zwicker’s original model assumes zero loudness at or below threshold, which is inconsistent with tinnitus loudness by definition. Buss and Florentine’s softness imperception model (2002) predicts greater loudness at threshold with elevated hearing loss, which might be true but cannot explain the presence of tinnitus with a normal audiogram profile or minimal hearing loss (e.g., Schaette and McAlpine, 2011). Moore and Glasberg’s modification (2004) does not predict hyperacusis. One has to assume, or accept the fact that loudness perception is a dynamic process that is actively modified by changes in central noise and gain. The next section proposes such an active loudness model and its implications for tinnitus and hyperacusis.
4. An active loudness model
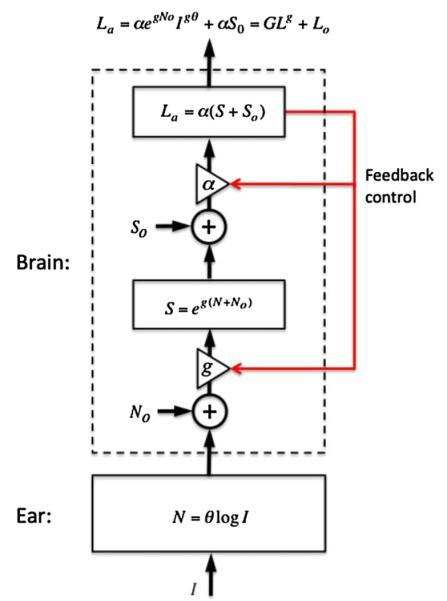
Fig. 3 shows the structure of the proposed active loudness model.
Fig. 3.
An active loudness model incorporating additive noise and gain before (N0 and g) and after (S0 and α) the nonlinear exponentiation process. Both gains can be adjusted by a feedback loop. The output of this active loudness model (La) can be modeled by three parameters, including a linear gain (G), a nonlinear gain (g) and a central noise (L0). See text for details.
The first stage is the same compression (Zeng and Shannon (1994)), modeled as a log function:
| (1) |
where I denotes sound intensity, namely, the input to the ear, N denotes the output of the ear, and θ denotes the amount of compression.
Since we do not know where the increased noise and gain occur, we place them before and after the central exponentiation stage, denoted by No and g for before and So and α for after, respectively. Eq. (2) shows the effect of placing the noise and gain before the central exponentiation stage:
| (2) |
Eq. (3) shows the effect of placing the noise and gain after the central exponentiation stage:
| (3) |
where La is total loudness produced by this active model. Combining Eq. (1)–Eq. (3) produces:
| (4) |
Where
| (5) |
| (6) |
| (7) |
Mathematically, G is viewed as a linear gain in the loudness domain, which contains the post-exponentiation gain α as well as the pre-exponentiation gain g and noise N0. It is worth noting that an additive noise, namely No can be converted into a multiplicative gain after a nonlinear transformation. On the other hand, the pre-exponentiation gain, g, can be viewed as a nonlinear gain that changes the slope of the original loudness growth function (Eq. (6)). The final item Lo is viewed as an additive central noise.
To examine the effects of these three parameters on loudness function, we rewrite Eq. (4) to obtain:
| (8) |
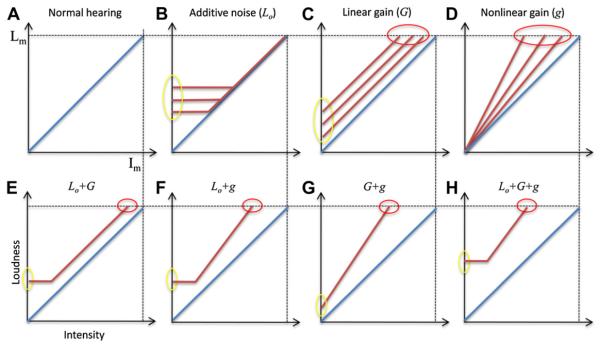
Eq. (8) allows examination of the effects of these three parameters on loudness function and their interactions with hearing loss in the same classical log L versus log I domain. Fig. 4 depicts loudness functions with these parameters varying alone (top panels) and co-varying (bottom panels). Similar to Fig. 1, panel A shows normal loudness function (L = Iθ). The central noise (Lo) would generate tinnitus by raising the floor (see the vertical yellow oval marking the 3 horizontal lines representing three different noise levels in panel B); however the central noise would not produce hyperacusis nor would it change the slope of loudness function. The linear gain (G) would vertically shift the normal loudness function, producing both tinnitus (vertical yellow oval) and hyperacusis (horizontal red oval) but no change in the slope of loudness function (panel C). The nonlinear gain (g) generates only hyperacusis by steepening the normal loudness function (panel D).
Fig. 4.
Normal loudness growth (panel A) and altered loudness growth as a function of central noise (panel B), linear gain (panel C), nonlinear gain (panel D), or a combination of these three factors (bottom panels from E to H). See text for details.
With combinations of any two or all three of these three parameters (bottom panels), both tinnitus and hyperacusis would occur. Not surprisingly the three-parameter combination produces the highest degree of tinnitus and hyperacusis, or the narrowest input and output dynamic range. Overall, this active loudness model predicts that tinnitus is more likely a result of increased noise level, whereas hyperacusis can be a result of either increased linear gain or increased nonlinear gain. The difference between the linear and nonlinear gain is the slope of the loudness function, with the linear gain predicting the same slope and the nonlinear gain predicting a steeper than normal slope.
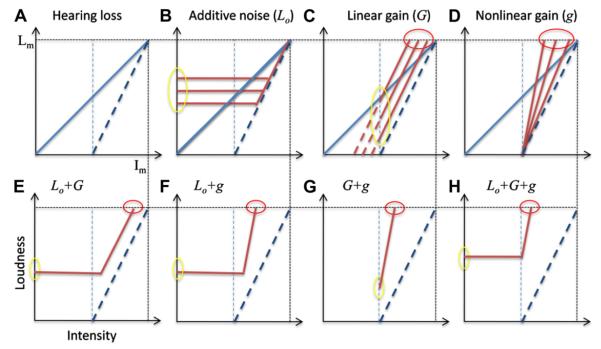
Fig. 5 shows how the central noise, linear gain, and nonlinear gain interact with hearing loss, including the elevated threshold (vertical thin dashed line) and loudness recruitment (slanted thick dashed line). The overall effect of these parameters is similar between normal hearing and hearing loss, except that the degree of the effect is exacerbated with hearing loss. For example, the hearing loss, combined with all three parameters (panel H), produces an extremely narrow input as well as output dynamic range. Two additional observations are worth noting. First, the linear gain is not a sensitivity control per se, because it would not improve thresholds in hearing loss (intersections of the slanted dashed lines on the x-axis in top-third panel). The linear gain amplifies the noise, which would produce the same, if not more elevated threshold in hearing loss. Second, note that the steepened function in loudness recruitment (slanted thick dashed line) is part of continuum of increased nonlinear gain that produces hyperacusis (progressively steepened thick lines in panel D). In other words, hyperacusis and recruitment have the same underlying mechanism. The difference is simply our definition. Indeed, both hyperacusis and recruitment can have the same steepened loudness growth functions, but we define one as hyperacusis in cases of no threshold elevation (Fig. 4D) and another as recruitment in cases of threshold elevation (Fig. 5D). Behaviorally, one has to measure loudness growth to identify hyperacusis in cases of normal audiogram, which may reflect selective damage to high-threshold auditory nerve fibers (Kujawa and Liberman, 2009).
Fig. 5.
Hearing-impaired loudness growth (steeper dashed line in panel A) and altered loudness growth as a function of central noise (panel B), linear gain (panel C), nonlinear gain (panel D), or a combination of these three factors (bottom panels from E to H). See text for details.
5. Discussion
5.1. Model predictions
We argue against the linear gain mechanism in the model for the following reasons. First, it reduces both the input and output dynamic ranges (see Figs. 4 and 5), an ecologically unlikely scenario. Second, the linear gain does not improve thresholds (y-axis in Fig. 4 and dashed vertical line in Fig. 5) because both signal and noise are amplified by the same amount. Third, it raises the overall loudness for all intensities within the reduced dynamic range (see the third panel of top row in Figs. 4 and 5), a prediction that is not supported by present data (see Section 2). Mathematically, a unit linear gain (i.e., G = 1 in Eq. (5)) would require a unit central gain (α = 1) and a zero peripheral noise (N0 = 0).
This simplification (i.e., La = Lg + L0) leaves central noise (S0 = L0) and nonlinear gain (g) as the two key parameters to explain loudness in tinnitus, hyperacusis and hearing loss. The present active loudness model explicitly predicts that the central noise causes tinnitus, whereas the nonlinear gain produces loudness recruitment and hyperacusis. In this model, recruitment and hyperacusis are parsimoniously accounted for by the same mechanism, with hyperacusis simply having higher nonlinear gain. One advantage for increasing the nonlinear gain is its ability to restore the full output dynamic range in response to reduced input dynamic range in hearing loss (panel D in Figs. 4 and 5).
But why does the brain increase the central noise level? Increasing the central noise level does not provide any clear functional benefit to either input or output dynamic range (see panel B in Figs. 4 and 5). The answer may be rooted in the nature of neurodynamic processing in the brain. Because of its intricate excitatory and inhibitory interactions, the brain needs noise to help maintain system stability or some sort of equilibrium (e.g.,Freeman, 1996; Marinaro and Scarpetta, 2004). In the case of increased nonlinear gain, the brain needs more central noise to restore or maintain this equilibrium. This sequence of events suggests that tinnitus is generated by increased central noise, rather than the increased gain per se, as suggested by the recent models (e.g., Norena, 2011; Schaette and Kempter, 2006).
The following examples help further differentiate between the present and previous models. First, increasing central noise and increasing gain are correlated but definitely not dependent on each other in the present model. The central noise can be increased with reduced gain or if the point of equilibrium is tipped by changes in the inhibitory input (Kaltenbach, 2011). Second, behavioral data show that listeners can have tinnitus without hyperacusis, or hyperacusis without tinnitus. Indeed, Penner (1986b) showed that in two subjects with normal thresholds at tinnitus frequency, the slope of loudness function is also normal, suggesting the presence of tinnitus without increased gain (similar results were obtained in the low hearing loss group in Ward and Baumann, 2009). Interestingly, Reavis et al. (2012) found that the slope of loudness growth, a measure of hyperacusis, influences the effect of temporary tinnitus suppression by modulated sounds. Perhaps these modulated sounds affect the central noise, but not the nonlinear gain, thus producing minimal tinnitus suppression in those subjects with steepened loudness growth or presence of hyperacusis. Finally, Penner (1986a) found a shallower psychometric function at tinnitus frequencies than at non-tinnitus frequencies, directly implicating tinnitus as a source of increased internal noise, rather than a result of increased gain.
The above active loudness model leads naturally to either peripheral or central origins of tinnitus and hyperacusis (Fig. 6). It terms of the peripheral origin, hearing loss decreases the input, increasing the nonlinear gain to produce enhanced loudness (recruitment or hyperacusis), which possibly introduces an imbalanced state in the brain and requires it to increase central noise level to maintain balance, thus producing tinnitus. In terms of the central origin, non-hearing loss factors such as somatic modulation, traumatic injury and drug intake can cause an imbalanced state in the brain (Cianfrone et al., 2005; Dehmel et al., 2008; Fausti et al., 2009), requiring it to increase the central noise level and producing tinnitus. If tinnitus interferes with sound detection, the nonlinear gain may also be increased to produce hyperacusis. If it does not interfere, then no gain is needed so only tinnitus is generated without presence of hyperacusis or hearing loss.
Fig. 6.
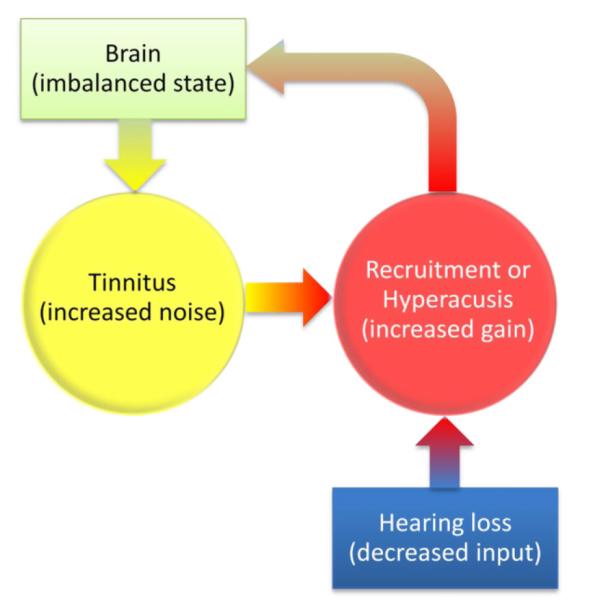
Peripheral (bottom up) or central (top-down) origin of tinnitus and hyperacusis. The peripheral origin: Hearing loss reduces input, leading to increased nonlinear gain in the form of steepened loudness growth as either loudness recruitment or hyperacusis; the increased gain causes an imbalance state in the brain, which requires increased central noise to restore balance, thus generating tinnitus. The central origin: An imbalanced state in the brain increases the central noise, namely, generating tinnitus. If the tinnitus interferes with sound detection, then the nonlinear gain may be increased, producing hyperacusis; If not, then tinnitus occurs without hyperacusis or hearing loss.
At present, the active loudness model cannot predict whether and how an external sound would interact tinnitus, although such interactions are well documented in the form of masking, residual inhibition, and suppression (Formby and Gjerdingen, 1980; Reavis et al., 2012; Roberts et al., 2008; Terry et al., 1983; Vernon, 1981). The reason for not being able to make this prediction is the undefined nature of the central noise in terms of single and population nervous activities. Physiologically, tinnitus has been related to increased synchronous single-neuron activity, namely, “bursting”, or increased synchronous firing between neurons, or increased spontaneous activity in the central nervous system (Roberts et al., 2010). Subjectively, tinnitus may sound tonal, or noisy, or contain more complicated components (Kodama and Kitahara, 1990; Reed, 1960). It is logical to speculate that tinnitus percepts are related to these aberrant neural activities. For example, tinnitus may sound tonal if “the central noise” is due to increased synchronous activity, or noisy if it is due to increased spontaneous activity. Depending on the degree of overlap and similarity between tinnitus-related and sound-evoked neural activities, tinnitus and external sounds can have different types of spectral and temporal interactions. If tinnitus and an external sound generate different neural activities, then it is relatively easy to imagine some of the perplexing interactions such as the requirement of a high-level noise to mask a relatively soft tinnitus (Penner, 1983). Therefore, the next logical extension of the present model is to define the nature of the central noise in order to predict what tinnitus sounds like and how it will interact with external sounds.
In addition, the present model does not predict annoyance – another important aspect of tinnitus and hyperacusis that is partially correlated with tinnitus loudness but strongly related to emotion (Hallam et al., 1988; Hiller and Goebel, 2007). It is conceivable that the present model can be expanded to be part of a general tinnitus and hyperacusis model. For example, the output of the active loudness model can be combined with another parallel pathway, with strong modulation of emotional factors, to help understand and eventually predict annoyance. Indeed, both anatomical and physiological studies have suggested a strong influence of the limbic system in tinnitus and hyperacusis (Rauschecker et al., 2010).
5.2. Experimental evidence for the active loudness model
There is ample experimental evidence supporting the present active loudness model. First, loudness perception changes with hearing aid and cochlear implant usage. Long-term (>6 months) device usage increases the input dynamic range by 4.5 dB in hearing aid users (Olsen et al., 1999) and by a staggering 50% in cochlear implant users (Henkin et al., 2006). However, the increased dynamic range in both users is a result of the “raised ceiling” or an increased input level that produces a loud percept, rather than any substantial changes in the threshold. This change is opposite to loudness recruitment or hyperacusis, suggesting that amplifying external sounds reduces the nonlinear gain in the brain. Interestingly, adding an external noise to cochlear implants can also enhance their dynamic range, but as a result of “lowered floor” or thresholds rather than the “raised ceiling” (Hong et al., 2003). The addition of external noise might reduce the need for central noise, lowering thresholds without changing the nonlinear gain. Implications of these results for sound therapy of tinnitus and hyperacusis will be addressed below.
Several well-known loudness phenomena that occur over second-to-minute scales also support an active loudness model. For example, loudness adaptation, particularly the induced adaptation (Canevet et al., 1985), would be difficult for a passive loudness model, but easy for an active loudness model to explain by changing the gains via a feedback loop (red lines in Fig. 3). Similarly, loudness recalibration in which loudness enhances or reduces depending upon a context sound can be explained by a short-term gain change (Marks, 1994). Cognitive effects such as attention on loudness perception can also be modeled as a gain change (Schlauch, 1992). In particular, Micheyl et al. (1995) found that music training reduces loudness adaptation and suggested the medial olivocochlear system as a possible feedback loop that modulates the gain.
Finally, recent animal studies on the dynamic interplay between environmental sounds and neural responses shed light on possible physiological mechanisms underlying an active loudness model (Dean et al., 2005, 2008; Wen et al., 2009; Zilany and Carney, 2010). These studies show that the auditory nervous system can dynamically (160 ms to tens of seconds) adjust its gain to match the sound level distribution. The gain adjustment is present at the auditory nerve level and becomes greater in the central nuclei. Not surprisingly, the gain adjustment has been suggested to be a result of nonlinear processes, which are abundant in the nervous system from ion channel dynamics and spike generation to homeostatic and network properties. When it comes to physiological manifestation of the increased nonlinear gain in tinnitus, hyperactivity in the dorsal cochlear nucleus is a strong candidate (Kaltenbach and Afman, 2000). Of course, the actual active mechanisms are likely to be more elaborate and complicated than the present active loudness model.
5.3. Implications for sound therapy
The present active loudness model implies that effective tinnitus treatment needs to restore normal central noise level, but the means of achieving it depends upon the cause. If the central noise is increased as a result of the increased nonlinear gain in response to hearing loss, then general amplification usage such as hearing aids and cochlear implants should be effective (Del Bo and Ambrosetti, 2007; Miyamoto and Bichey, 2003). If the central noise is increased as a result of other factors such as excitatory-inhibitory imbalance, or even reduced nonlinear gain, then other forms of sound therapy are needed. Fractal sounds, modulated sounds, notched music sounds, or coordinated reset stimuli might be able to reduce the central noise to some extent (Okamoto et al., 2010;Sweetow and Sabes, 2010; Tass and Popovych, 2012). Other means of reducing central noise would include pharmaceutical, transcranial magnetic stimulation, and cognitive therapy (Darlington and Smith, 2007; Jastreboff and Jastreboff, 2003; Jastreboff et al., 1994; Langguth et al., 2006). At present, hyperacusis has been treated by progressive exposure of louder noise that can change the gain (Formby et al., 2008). Although no data are available, the present model suggests that hyperacusis can also be managed by amplitude compression because it effectively increases the input dynamic range.
6. Summary
The present active loudness model suggests that tinnitus and hyperacusis have different mechanisms: Tinnitus is due to increased central noise whereas hyperacusis is due to increased nonlinear gain. The model predicts two different origins and their sequences of events in tinnitus and hyperacusis generation. For the peripheral origin, hearing loss reduces sound input, leading to increased nonlinear gain (recruitment or hyperacusis), requiring the brain to increase central noise to reach a new equilibrium, generating tinnitus as a result. For the central origin, an imbalanced state in the brain increases central noise, generating tinnitus, which may or may not cause hyperacusis or hearing loss. Due to limited experimental data, the present model is still vague in terms of underlying physiological mechanisms. Nevertheless, the model not only presents a theoretical framework to unify tinnitus, hyperacusis and recruitment, but also suggests different strategies to treat these symptoms.
Acknowledgment
I thank Tom Lu, Myles McLaughlin, Richard Salvi and two anonymous reviewers for their comments on the manuscript.
References
- Andersson G, Lindvall N, Hursti T, Carlbring P. Hypersensitivity to sound (hyperacusis): a prevalence study conducted via the Internet and post. Int. J. Audiol. 2002;41:545–554. doi: 10.3109/14992020209056075. [DOI] [PubMed] [Google Scholar]
- Bauer CA, Brozoski TJ. Effect of tinnitus retraining therapy on the loudness and annoyance of tinnitus: a controlled trial. Ear Hear. 2011 doi: 10.1097/AUD.0b013e3181f5374f. [DOI] [PubMed] [Google Scholar]
- Buus S, Florentine M. Growth of loudness in listeners with cochlear hearing losses: recruitment reconsidered. J. Assoc. Res. Otolaryngol. 2002;3:120–139. doi: 10.1007/s101620010084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai S, Ma WL, Young ED. Encoding intensity in ventral cochlear nucleus following acoustic trauma: implications for loudness recruitment. J. Assoc. Res. Otolaryngol. 2009;10:5–22. doi: 10.1007/s10162-008-0142-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canevet G, Scharf B, Botte MC. Simple and induced loudness adaptation. Audiology. 1985;24:430–436. doi: 10.3109/00206098509078362. [DOI] [PubMed] [Google Scholar]
- Cianfrone G, Pace M, Turchetta R, Cianfrone F, Altissimi G. An updated guide on drugs inducing ototoxicity, tinnitus and vertigo. Acta Otorhinolaryngol. Ital. 2005;25:3–31. [PubMed] [Google Scholar]
- Darlington CL, Smith PF. Drug treatments for tinnitus. Prog. Brain Res. 2007;166:249–262. doi: 10.1016/S0079-6123(07)66023-3. [DOI] [PubMed] [Google Scholar]
- Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat. Neurosci. 2005;8:1684–1689. doi: 10.1038/nn1541. [DOI] [PubMed] [Google Scholar]
- Dean I, Robinson BL, Harper NS, McAlpine D. Rapid neural adaptation to sound level statistics. J. Neurosci. 2008;28:6430–6438. doi: 10.1523/JNEUROSCI.0470-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehmel S, Cui YL, Shore SE. Cross-modal interactions of auditory and somatic inputs in the brainstem and midbrain and their imbalance in tinnitus and deafness. Am. J. Audiol. 2008;17:S193–S209. doi: 10.1044/1059-0889(2008/07-0045). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Bo L, Ambrosetti U. Hearing aids for the treatment of tinnitus. Prog. Brain Res. 2007;166:341–345. doi: 10.1016/S0079-6123(07)66032-4. [DOI] [PubMed] [Google Scholar]
- Epstein M, Florentine M. Inferring basilar-membrane motion from tone-burst otoacoustic emissions and psychoacoustic measurements. J. Acoust. Soc. Am. 2005;117:263–274. doi: 10.1121/1.1830670. [DOI] [PubMed] [Google Scholar]
- Fastl H, Zwicker E. Psychoacoustics: Facts and Models. third ed Springer; Berlin: 2007. [Google Scholar]
- Fausti SA, Wilmington DJ, Gallun FJ, Myers PJ, Henry JA. Auditory and vestibular dysfunction associated with blast-related traumatic brain injury. J. Rehabil. R. D. 2009;46:797–810. doi: 10.1682/jrrd.2008.09.0118. [DOI] [PubMed] [Google Scholar]
- Florentine M, Zwicker E. A model of loudness summation applied to noise-induced hearing loss. Hear. Res. 1979;1:121–132. doi: 10.1016/0378-5955(79)90023-6. [DOI] [PubMed] [Google Scholar]
- Formby C, Gjerdingen DB. Pure-tone masking of tinnitus. Audiology. 1980;19:519–535. doi: 10.3109/00206098009070083. [DOI] [PubMed] [Google Scholar]
- Formby C, Hawley M, Sherlock L, Gold S, Segar A, Gmitter C, Cannavo J. Intervention for restricted dynamic range and reduced sound tolerance. J. Acoust. Soc. Am. 2008;123:3717. [Google Scholar]
- Fowler EP. Marked deafened areas in normal ears. Arch. Otolaryngol. Head. Neck. Surg. 1928;8:151–55. [Google Scholar]
- Freeman WJ. Random activity at the microscopic neural level in cortex (“noise”) sustains and is regulated by low-dimensional dynamics of macroscopic cortical activity (“chaos”) Int. J. Neural. Syst. 1996;7:473–480. doi: 10.1142/s0129065796000452. [DOI] [PubMed] [Google Scholar]
- Goldstein B, Shulman A. Tinnitus - hyperacusis and the loudness discomfort level test – a preliminary report. Int. Tinnitus. J. 1996;2:83–89. [PubMed] [Google Scholar]
- Goodwin PE, Johnson RM. The loudness of tinnitus. Acta Otolaryngol. 1980;90:353–359. doi: 10.3109/00016488009131736. [DOI] [PubMed] [Google Scholar]
- Hallam RS, Jakes SC, Hinchcliffe R. Cognitive variables in tinnitus annoyance. Br. J. Clin. Psychol. 1988;27(Pt. 3):213–222. doi: 10.1111/j.2044-8260.1988.tb00778.x. [DOI] [PubMed] [Google Scholar]
- Heinz MG, Issa JB, Young ED. Auditory-nerve rate responses are inconsistent with common hypotheses for the neural correlates of loudness recruitment. J. Assoc. Res. Otolaryngol. 2005;6:91–105. doi: 10.1007/s10162-004-5043-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henkin Y, Kaplan-Neeman R, Kronenberg J, Migirov L, Hildesheimer M, Muchnik C. A longitudinal study of electrical stimulation levels and electrode impedance in children using the clarion cochlear implant. Acta Otolaryngol. 2006;126:581–586. doi: 10.1080/00016480500443391. [DOI] [PubMed] [Google Scholar]
- Henry JA, Meikle MB. Pulsed versus continuous tones for evaluating the loudness of tinnitus. J. Am. Acad. Audiol. 1999;10:261–272. [PubMed] [Google Scholar]
- Hiller W, Goebel G. When tinnitus loudness and annoyance are discrepant: audiological characteristics and psychological profile. Audiol. Neurootol. 2007;12:391–400. doi: 10.1159/000106482. [DOI] [PubMed] [Google Scholar]
- Hong RS, Rubinstein JT, Wehner D, Horn D. Dynamic range enhancement for cochlear implants. Otol. Neurotol. 2003;24:590–595. doi: 10.1097/00129492-200307000-00010. [DOI] [PubMed] [Google Scholar]
- Jastreboff PJ, Jastreboff MM. Tinnitus retraining therapy for patients with tinnitus and decreased sound tolerance. Otolaryngol. Clin. North Am. 2003;36:321–336. doi: 10.1016/s0030-6665(02)00172-x. [DOI] [PubMed] [Google Scholar]
- Jastreboff PJ, Hazell JW, Graham RL. Neurophysiological model of tinnitus: dependence of the minimal masking level on treatment outcome. Hear Res. 1994;80:216–232. doi: 10.1016/0378-5955(94)90113-9. [DOI] [PubMed] [Google Scholar]
- Kaltenbach JA. Tinnitus: models and mechanisms. Hear Res. 2011;276:52–60. doi: 10.1016/j.heares.2010.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaltenbach JA, Afman CE. Hyperactivity in the dorsal cochlear nucleus after intense sound exposure and its resemblance to tone-evoked activity: a physiological model for tinnitus. Hear Res. 2000;140:165–172. doi: 10.1016/s0378-5955(99)00197-5. [DOI] [PubMed] [Google Scholar]
- Kodama A, Kitahara M. Clinical and audiological characteristics of tonal and noise tinnitus. ORL. J. Otorhinolaryngol. Relat. Spec. 1990;52:156–163. doi: 10.1159/000276126. [DOI] [PubMed] [Google Scholar]
- Kujawa SG, Liberman MC. Adding insult to injury: cochlear nerve degeneration after “temporary” noise-induced hearing loss. J. Neurosci. 2009;29:14077–14085. doi: 10.1523/JNEUROSCI.2845-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langguth B, Hajak G, Kleinjung T, Pridmore S, Sand P, Eichhammer P. Repetitive transcranial magnetic stimulation and chronic tinnitus. Acta Otolaryngol. Suppl. 2006:102–105. doi: 10.1080/03655230600895457. [DOI] [PubMed] [Google Scholar]
- Launer S, Moore BC. Use of a loudness model for hearing aid fitting. V. Online gain control in a digital hearing aid. Int. J. Audiol. 2003;42:262–273. doi: 10.3109/14992020309078345. [DOI] [PubMed] [Google Scholar]
- Launer S, Hohmann V, Kollmeier B. Modeling loudness growth and loudness summation in hearing-impaired listeners. In: Jesteadt W, editor. Modeling Sensorineural Hearing Loss. Lawrence Erlbaum Associates, Inc.; Mahwah, New Jersey: 1997. pp. 175–185. [Google Scholar]
- Marinaro M, Scarpetta S. Effects of noise in a cortical neural model. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2004;70:041909. doi: 10.1103/PhysRevE.70.041909. [DOI] [PubMed] [Google Scholar]
- Marks LE. “Recalibrating” the auditory system: the perception of loudness. J. Exp. Psychol. Hum. Percept. Perform. 1994;20:382–396. doi: 10.1037//0096-1523.20.2.382. [DOI] [PubMed] [Google Scholar]
- Micheyl C, Carbonnel O, Collet L. Medial olivocochlear system and loudness adaptation: differences between musicians and non-musicians. Brain Cogn. 1995;29:127–136. doi: 10.1006/brcg.1995.1272. [DOI] [PubMed] [Google Scholar]
- Miyamoto RT, Bichey BG. Cochlear implantation for tinnitus suppression. Otolaryngol. Clin. North Am. 2003;36:345–352. doi: 10.1016/s0030-6665(02)00165-2. [DOI] [PubMed] [Google Scholar]
- Moore BC, Glasberg BR. A revised model of loudness perception applied to cochlear hearing loss. Hear. Res. 2004;188:70–88. doi: 10.1016/S0378-5955(03)00347-2. [DOI] [PubMed] [Google Scholar]
- Moore BC, Glasberg BR, Baer T. A model for the prediction of thresholds, loudness and partial loudness. J. Audio. Eng. Soc. 1997;45:224–240. [Google Scholar]
- Moore BCJ, Glasberg BR. A revision of Zwicker’s loudness model. Acta Acustica. 1996;82:335–345. [Google Scholar]
- Nelson JJ, Chen K. The relationship of tinnitus, hyperacusis, and hearing loss. Ear Nose Throat J. 2004;83:472–476. [PubMed] [Google Scholar]
- Nieschalk M, Stoll W. Direct loudness scaling in diagnosis of tinnitus. A contribution to loudness perception in tinnitus. HNO. 1996;44:577–584. doi: 10.1007/s001060050057. [DOI] [PubMed] [Google Scholar]
- Norena AJ. An integrative model of tinnitus based on a central gain controlling neural sensitivity. Neurosci. Biobehav. Rev. 2011;35:1089–1109. doi: 10.1016/j.neubiorev.2010.11.003. [DOI] [PubMed] [Google Scholar]
- Okamoto H, Stracke H, Stoll W, Pantev C. Listening to tailor-made notched music reduces tinnitus loudness and tinnitus-related auditory cortex activity. Proc. Natl. Acad. Sci. U S A. 2010;107:1207–1210. doi: 10.1073/pnas.0911268107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsen SO, Rasmussen AN, Nielsen LH, Borgkvist BV. Loudness perception is influenced by long-term hearing aid use. Audiology. 1999;38:202–205. doi: 10.3109/00206099909073024. [DOI] [PubMed] [Google Scholar]
- Penner MJ. The annoyance of tinnitus and the noise required to mask it. J. Speech Hear Res. 1983;26:73–76. doi: 10.1044/jshr.2601.73. [DOI] [PubMed] [Google Scholar]
- Penner MJ. Tinnitus as a source of internal noise. J. Speech Hear Res. 1986a;29:400–406. doi: 10.1044/jshr.2903.400. [DOI] [PubMed] [Google Scholar]
- Penner MJ. Magnitude estimation and the “paradoxical” loudness of tinnitus. J. Speech Hear Res. 1986b;29:407–412. doi: 10.1044/jshr.2903.407. [DOI] [PubMed] [Google Scholar]
- Qiu C, Salvi R, Ding D, Burkard R. Inner hair cell loss leads to enhanced response amplitudes in auditory cortex of unanesthetized chinchillas: evidence for increased system gain. Hear. Res. 2000;139:153–171. doi: 10.1016/s0378-5955(99)00171-9. [DOI] [PubMed] [Google Scholar]
- Rauschecker JP, Leaver AM, Muhlau M. Tuning out the noise: limbic-auditory interactions in tinnitus. Neuron. 2010;66:819–826. doi: 10.1016/j.neuron.2010.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reavis KM, Rothholtz VS, Tang Q, Carroll JA, Djalilian H, Zeng FG. Temporary suppression of tinnitus by modulated sounds. J. Assoc. Res. Otolaryngol. 2012 doi: 10.1007/s10162-012-0331-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed GF. An audiometric study of two hundred cases of subjective tinnitus. AMA Arch. Otolaryngol. 1960;71:84–94. doi: 10.1001/archotol.1960.03770010088009. [DOI] [PubMed] [Google Scholar]
- Roberts LE, Moffat G., Baumann, M., Ward LM, Bosnyak DJ. Residual inhibition functions overlap tinnitus spectra and the region of auditory threshold shift. J. Assoc. Res. Otolaryngol. 2008;9:417–435. doi: 10.1007/s10162-008-0136-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts LE, Eggermont JJ, Caspary DM, Shore SE, Melcher JR, Kaltenbach JA. Ringing ears: the neuroscience of tinnitus. J. Neurosci. 2010;30:14972–14979. doi: 10.1523/JNEUROSCI.4028-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaette R, Kempter R. Development of tinnitus-related neuronal hyperactivity through homeostatic plasticity after hearing loss: a computational model. Eur. J. Neurosci. 2006;23:3124–3138. doi: 10.1111/j.1460-9568.2006.04774.x. [DOI] [PubMed] [Google Scholar]
- Schaette R, McAlpine D. Tinnitus with a normal audiogram: physiological evidence for hidden hearing loss and computational model. J. Neurosci. 2011;31:13452–13457. doi: 10.1523/JNEUROSCI.2156-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharf B, Hellman RP. Model of loudness summation applied to impaired ears. J. Acoust. Soc. Am. 1966;40:71–78. doi: 10.1121/1.1910066. [DOI] [PubMed] [Google Scholar]
- Schlauch RS. A cognitive influence on the loudness of tones that change continuously in level. J. Acoust. Soc. Am. 1992;92:758–765. doi: 10.1121/1.403999. [DOI] [PubMed] [Google Scholar]
- Schlauch RS, DiGiovanni JJ, Ries DT. Basilar membrane nonlinearity and loudness. J. Acoust. Soc. Am. 1998;103:2010–2020. doi: 10.1121/1.421379. [DOI] [PubMed] [Google Scholar]
- Shargorodsky J, Curhan GC, Farwell WR. Prevalence and characteristics of tinnitus among US adults. Am. J. Med. 2010;123:711–718. doi: 10.1016/j.amjmed.2010.02.015. [DOI] [PubMed] [Google Scholar]
- Stevens S. A scale for the measurement of a psychological magnitude: loudness. Psychol. Rev. 1936;43:405–416. [Google Scholar]
- Sweetow RW, Sabes JH. Effects of acoustical stimuli delivered through hearing aids on tinnitus. J. Am. Acad. Audiol. 2010;21:461–473. doi: 10.3766/jaaa.21.7.5. [DOI] [PubMed] [Google Scholar]
- Szczepaniak WS, Moller AR. Evidence of neuronal plasticity within the inferior colliculus after noise exposure: a study of evoked potentials in the rat. Electroencephalogr. Clin. Neurophysiol. 1996;100:158–164. doi: 10.1016/0013-4694(95)00234-0. [DOI] [PubMed] [Google Scholar]
- Tass PA, Popovych OV. Unlearning tinnitus-related cerebral synchrony with acoustic coordinated reset stimulation: theoretical concept and modelling. Biol. Cybern. 2012;106:27–36. doi: 10.1007/s00422-012-0479-5. [DOI] [PubMed] [Google Scholar]
- Terry AM, Jones DM, Davis BR, Slater R. Parametric studies of tinnitus masking and residual inhibition. Br. J. Audiol. 1983;17:245–256. doi: 10.3109/03005368309081485. [DOI] [PubMed] [Google Scholar]
- Thorson MJ, Kopun JG, Neely ST, Tan H, Gorga MP. Reliability of distortion-product otoacoustic emissions and their relation to loudness. J. Acoust. Soc. Am. 2012;131:1282–1295. doi: 10.1121/1.3672654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyler RS, Conrad-Armes D. The determination of tinnitus loudness considering the effects of recruitment. J. Speech Hear Res. 1983;26:59–72. doi: 10.1044/jshr.2601.59. [DOI] [PubMed] [Google Scholar]
- Vernon J. The history of masking as applied to tinnitus. J. Laryngol. Otol. Suppl. 1981:76–79. [PubMed] [Google Scholar]
- Ward LM, Baumann M. Measuring tinnitus loudness using constrained psychophysical scaling. Am. J. Audiol. 2009;18:119–128. doi: 10.1044/1059-0889(2009/07-0033). [DOI] [PubMed] [Google Scholar]
- Wen B, Wang GI, Dean I, Delgutte B. Dynamic range adaptation to sound level statistics in the auditory nerve. J. Neurosci. 2009;29:13797–13808. doi: 10.1523/JNEUROSCI.5610-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng FG, Shannon RV. Loudness balance between electric and acoustic stimulation. Hear. Res. 1992;60:231–235. doi: 10.1016/0378-5955(92)90024-h. [DOI] [PubMed] [Google Scholar]
- Zeng FG, Shannon RV. Loudness-coding mechanisms inferred from electric stimulation of the human auditory system. Science. 1994;264:564–566. doi: 10.1126/science.8160013. [DOI] [PubMed] [Google Scholar]
- Zeng FG, Galvin JJ., 3rd Amplitude mapping and phoneme recognition in cochlear implant listeners. Ear Hear. 1999;20:60–74. doi: 10.1097/00003446-199902000-00006. [DOI] [PubMed] [Google Scholar]
- Zilany MS, Carney LH. Power-law dynamics in an auditory-nerve model can account for neural adaptation to sound-level statistics. J. Neurosci. 2010;30:10380–10390. doi: 10.1523/JNEUROSCI.0647-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwicker E, Scharf B. A model of loudness summation. Psychol. Rev. 1965;72:3–26. doi: 10.1037/h0021703. [DOI] [PubMed] [Google Scholar]