Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 May 11.
Published in final edited form as: J Biomech. 2012 Mar 30;45(8):1517–1521. doi: 10.1016/j.jbiomech.2012.03.016

A platform for dynamic simulation and control of movement based on OpenSim and MATLAB

Misagh Mansouri 1,*, Jeffrey A Reinbolt 1
PMCID: PMC3593123  NIHMSID: NIHMS367478  PMID: 22464351

Abstract

Numerical simulations play an important role in solving complex engineering problems and have the potential to revolutionize medical decision making and treatment strategies. In this paper, we combine the rapid model-based design, control systems and powerful numerical method strengths of MATLAB/Simulink with the simulation and human movement dynamics strengths of OpenSim by developing a new interface between the two software tools. OpenSim is integrated with Simulink using the MATLAB S-function mechanism, and the interface is demonstrated using both open-loop and closed-loop control systems. While the open-loop system uses MATLAB/Simulink to separately reproduce the OpenSim Forward Dynamics Tool, the closed-loop system adds the unique feature of feedback control to OpenSim, which is necessary for most human movement simulations. An arm model example was successfully used in both open-loop and closed-loop cases. For the open-loop case, the simulation reproduced results from the OpenSim Forward Dynamics Tool with root mean square (RMS) differences of 0.03° for the shoulder elevation angle and 0.06° for the elbow flexion angle. MATLAB’s variable step-size integrator reduced the time required to generate the forward dynamic simulation from 7.1 s (OpenSim) to 2.9 s (MATLAB). For the closed-loop case, a proportional–integral–derivative controller was used to successfully balance a pole on model’s hand despite random force disturbances on the pole. The new interface presented here not only integrates the OpenSim and MATLAB/Simulink software tools, but also will allow neuroscientists, physiologists, biomechanists, and physical therapists to adapt and generate new solutions as treatments for musculoskeletal conditions.

Keywords: OpenSim and MATLAB interface, Forward dynamics simulation, Musculoskeletal model, Feedback control, Muscle-actuated control

1. Introduction

Musculoskeletal conditions cost the US economy over $849 billion annually and place great demands on health care systems worldwide (Jacobs et al., 2008). Study and treatment of these conditions could greatly benefit from combined software tools that offer better insights into neuromuscular biomechanics, and predictive capabilities for optimal surgical and rehabilitation treatment planning.

Two general categories of software packages (engineering and musculoskeletal) have been used for modeling and simulation of biomechanical systems. These systems have been studied using engineering software packages such as ANSYS (Otoole et al., 1995), ADAMS (Lemay and Crago, 1996), SD-FAST (Andrews et al., 1998) and MATLAB (Barker et al., 1997). However, it is difficult to use built-in mechanical and electrical elements in these packages to model biomechanical systems. To address this issue, commercial musculoskeletal software packages such as SIMM (MusculoGraphics, Inc.), Visual 3-D (C-Motion, Inc.), and AnyBody (AnyBody Technology) were developed to study different biomechanical systems such as lower limbs (Delp et al., 1990; Kepple et al., 1997), upper limbs (Holzbaur et al., 2005; Damsgaard et al., 2006), and the cervical and lumbar spine (Vasavada et al., 1998; de Zee et al., 2007). Unfortunately, these packages do not share model standards or support data exchange as the engineering packages do. Moreover, neither engineering nor musculoskeletal software packages provide access to, or customization of source code, which makes it difficult for researchers to extend software capabilities.

Currently, there is no freely available, open-source computational tool providing an interface between software packages for modeling and simulation of biomechanical systems with robust design and control. We aimed to develop such an interface based on the popular musculoskeletal and engineering software packages of OpenSim (Delp et al., 2007) and MATLAB/Simulink. OpenSim, a freely available modeling and simulation platform, was developed as an extension to the commercial musculoskeletal software package SIMM (Delp et al., 1990; Delp and Loan, 1995). OpenSim has been successfully used to model musculoskeletal movements such as walking (Thelen and Anderson, 2006; Fox and Delp, 2010), running (Hamner et al., 2010) and predicting surgical outcomes (Fox et al., 2009; Reinbolt et al., 2009). Although users can extend OpenSim by writing their own plug-ins in C++, this software lacks the robust design and control components which are needed for real-time changes to input controls. On the contrary, MATLAB/Simulink (The Math Works, Inc., Natick, MA) as a powerful mathematical computing and control software is a natural choice to complement OpenSim, but it has limited resources (e.g., muscle moment arms) for simulations of biomechanical systems (Hohne, 2000; Lim et al., 2003). Our goal was to develop and disseminate a free interface between OpenSim and MATLAB/Simulink that combines their relevant strengths, such as rapid model-based design, control systems, numerical simulation, and human movement dynamics and simulation.

2. Methods

We start by defining the basic elements of a forward dynamics simulation of a musculoskeletal model and describe how it works in OpenSim. We then explain the basic concepts underlying the new S-function (system function) interface between OpenSim and MATLAB/Simulink. Finally, we demonstrate its application in both open-loop and closed-loop control systems using a model of a human arm.

2.1. Forward dynamics simulation of a musculoskeletal model

A forward dynamics simulation is the integration of the differential equations that define the dynamics of a musculoskeletal model. In forward dynamics, a mathematical model of the system describes how model states (positions, velocities, muscle activations, and fiber lengths) change due to model inputs (muscle excitations, torque actuators, and external forces) according to Newton’s second law (Thelen et al., 2003).

The OpenSim Forward Dynamics Tool (Fig. 1) uses a neural command from an input controls file (e.g., controls.xml) to generate an output states file (e.g., states.sto). Using musculotendon dynamics, the forces actuating the model are computed; next, using musculoskeletal geometry, the joint moments are computed; then, using multibody dynamics, accelerations and other state derivatives are computed. Finally, state derivatives are numerically integrated to determine the model’s new states, including the observed motion.

Fig. 1.

Fig. 1

Open in a new tab

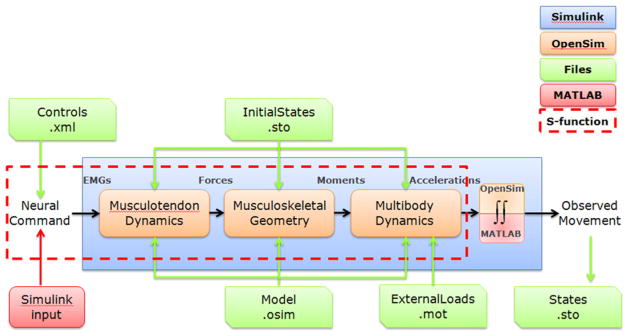
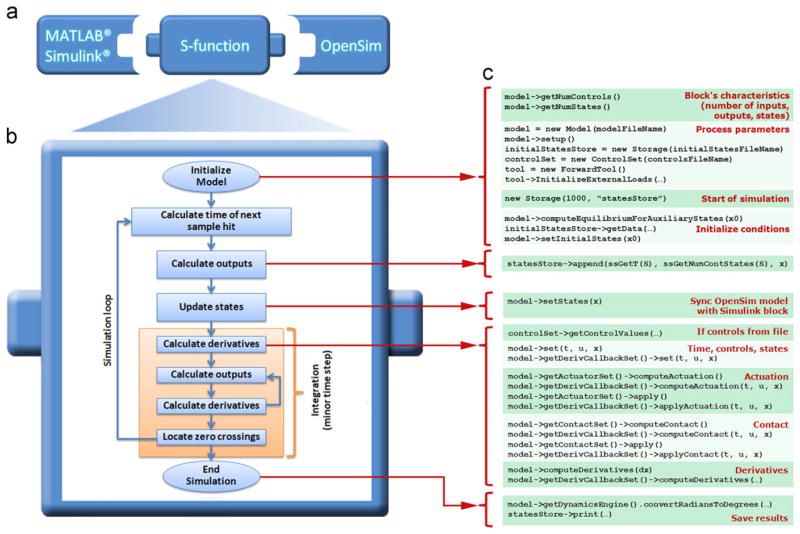
Flowchart illustrating components of forward dynamics in OpenSim and MATLAB/Simulink. Simulink (large blue rectangle) is used instead of the OpenSim Forward Dynamics Tool. The OpenSim transformations (orange rounded rectangles) between a neural command and state derivatives (e.g., joint accelerations) involve musculotendon dynamics, musculoskeletal geometry, and multibody dynamics. Input files (green diagonal corner rectangles) are required by OpenSim for the model, controls (if applicable), initial states, and external loads. The new S-function interface (red dotted rectangle) takes a controls file or Simulink input signal and uses OpenSim to computes state derivatives subsequently integrated by MATLAB integrators instead of OpenSim integrators. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2. Interface between OpenSim and MATLAB/Simulink

We developed a new interface to combine the relevant strengths of OpenSim and MATLAB/Simulink to enable a user to perform musculoskeletal simulations directly in a model-based design and control system environment. The interface uses the well-documented S-function API (application programming interface) to interact with the Simulink engine (Fig. 2). An S-function is a computer language description of a Simulink block written in MATLAB, FORTRAN, C, or C++ language (we chose C++ to have easy access to all OpenSim C++ methods and dynamically linked libraries) and compiled as a MEX-file, a dynamically linked subroutine automatically loaded and executed by MATLAB/Simulink. This interaction is very similar to the interaction that takes place between the engine and built-in Simulink blocks.

Fig. 2.

Fig. 2

Open in a new tab

Overview of the new S-function interface: (a) The interface links the rapid model-based design and control systems strengths of MATLAB/Simulink with the numerical simulation and human movement dynamics strengths of OpenSim. (b) Flowchart illustrating stages for each Simulink simulation. (c) OpenSim v1.9 (higher versions not shown) methods called during each simulation stage.

The S-function interface uses OpenSim’s underlying Simbody dynamics engine and MATLAB integrators to generate the forward dynamics simulation of an OpenSim model (Fig. 1, red dotted rectangle). The user can easily change Simulink configuration parameters (e.g., integration solver, error tolerance) to suit the requirements of the problem at hand.

2.3. Open-loop model application

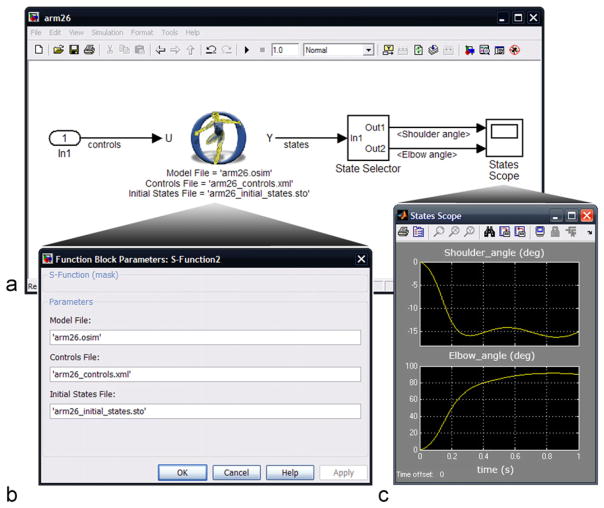
We created a generic open-loop Simulink model (Fig. 3a) that loads and executes the OpenSim-based S-function described above. The interface works with any OpenSim model by defining block parameters for a particular simulation (Fig. 3b).

Fig. 3.

Fig. 3

Open in a new tab

Overview of an open-loop model application for arm flexion. (a) The Simulink graphical editor window shows input controls (U), the new S-function interface (middle), and the output states (Y). (b) The custom Simulink block parameter dialog box shows every input parameter required (or optional) by the OpenSim Forward Dynamics Tool to perform a simulation. The parameter names are identical to those implemented in OpenSim to enable a straightforward transition to the new interface. (c) The output states may be displayed using a State Selector and Scope within the graphical editor or they may be loaded as a motion file in OpenSim to visualize the simulated movement.

To demonstrate the open-loop characteristics and compare how well the S-function in MATLAB/Simulink agrees with the Forward Dynamics Tool in OpenSim, we used a simple human arm model with 2 degrees of freedom (shoulder elevation and elbow flexion) and 6 muscle-tendon actuators (triceps brachii long head, triceps brachii lateral head, triceps brachii medial head, biceps brachii long head, biceps brachii short head, and brachialis) to simulate an elbow flexion movement over 1 s. The motions resulting from the OpenSim and Simulink simulations of elbow flexion were directly compared.

2.4. Closed-loop model application

We extended the open-loop model by adding a proportional-integral-derivative (PID) controller with feedback (Fig. 4). The open-loop model is limited to using predefined input controls that cannot be changed; however, many human movement applications require closed-loop control systems that update input controls to generate a desired output.

Fig. 4.

Fig. 4

Open in a new tab

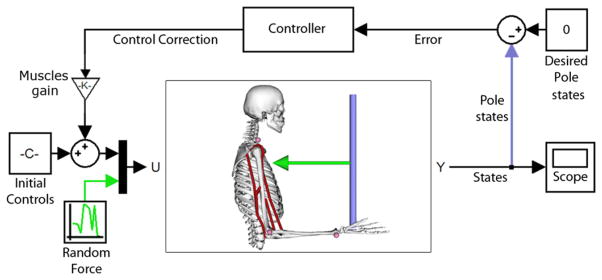
Example closed-loop Simulink model extending the open-loop case with control of a human arm balancing a pole. The desired pole angle was zero and used to compute a pole angle error. The proportional-integral-derivative (PID) controller, along with the muscle gain matrix was used to compute control correction signals for each of the six muscles to balance the pole, despite random force disturbances exerted on the pole.

To demonstrate the closed-loop characteristics, we used a human arm model balancing a pole. The pole was modeled in OpenSim as a cylinder with mass of 10 kg, height of 30 cm, and base radius of 2.5 cm. This biomechanical system had 3 degrees of freedom (shoulder elevation, elbow flexion and pole rotation), 6 muscle-tendon actuators, and a constraint on the hand to move along the horizontal direction. We distributed the PID controller output based on a muscles gain matrix signed to implement the pole angle correction by the muscles and normalized by muscle maximum isometric force, effectively, minimizing muscle activations required for the correction. The PID controller gains were tuned using the Simulink Control Design Toolbox. The initial controls, computed from static optimization, were used to maintain the arm position before a control correction was necessary. Random force disturbances were added to the pole to cause an imbalance and the pole angle error was observed.

3. Results

The new interface between OpenSim and MATLAB/Simulink allows rapid model-based design and numerical simulation of human movement using both open-loop (Fig. 3) and closed-loop (Figs. 4 and 5) control systems.

Fig. 5.

Fig. 5

Open in a new tab

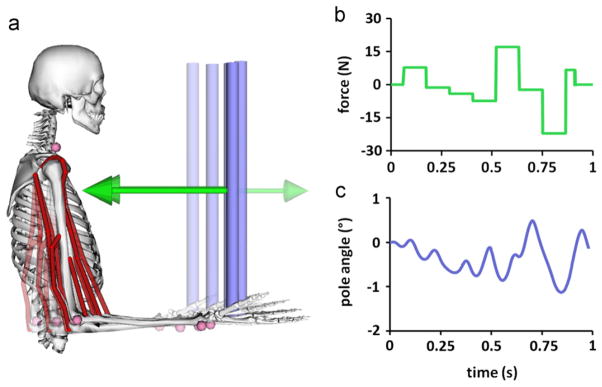
Closed-loop simulation of balancing a pole despite random force disturbances. (a) A PID controlled human arm model balancing a pole (five time frame series from 0.25 s to 0.55 s shown). (b) Random force disturbances were exerted on the pole. (c) The pole angle measured from vertical remained small.

For the open-loop case, the Simulink generated shoulder angle matched the OpenSim generated angle within a 0.03° root mean square (RMS) difference. The RMS difference for the elbow flexion angle was 0.06°. Using the OpenSim integrator error tolerance of 1e-3, the computation time was 7.1 s (computational speed was assessed on a 3.2 GHz Intel® Xeon® workstation with 3.00 GB of RAM). However, it took 2.9 s to generate the same forward dynamics simulation of the arm model using the new interface.

For the closed-loop case, the PID controller successfully rejected random force disturbances ranging between ±30 N (Fig. 5b) and balanced the pole with a maximum pole angle error from vertical of 1.19° (Fig. 5c). Using the MATLAB integrator with the same error tolerance as the open-loop case, the computation time for the closed-loop system was 5.9 s.

4. Discussion

The new S-function interface combines the numerical simulation and human movement dynamics strengths of OpenSim with the robust design, powerful math, and control system strengths of MATLAB. This integrated platform has promise for better understanding movement control and the potential to improve treatment planning.

The S-function interface and control systems software developed in this study had some limitations. First, the compatible versions of OpenSim (v2.3.1), MATLAB (v7.13.0), and Simulink (v7.7) were based on those available at the time of the S-function interface development. Thus, generating the newer versions of the interface may be needed as future versions of these software packages may improve computational efficiency and add new features. However, the current version of the interface, which is compatible with all versions of OpenSim (v1.9–v2.3.1), seems to be sufficient as it contains all of the previous OpenSim features and the new contact modeling capability. Second, the PID control was a simple, classical approach among the many available closed-loop control systems. However, by applying the muscle gain in our closed-loop controller which was designed based on the muscle maximum isometric force, we made the control signal or muscle excitation to act analogous (but not identical) to the human neural command minimizes muscular effort. Whereas the controller development is not a focus of this study, the new interface allows custom, complex controllers to be developed, tested, and refined.

Despite these limitations, the interface allows users to access any OpenSim model within MATLAB/Simulink and perform forward dynamics simulations. OpenSim-required input data files such as controls, initial states, and external forces can be provided by a Simulink signal, a MATLAB workspace variable, or a data file. This flexibility adds the unique ability of real-time changes to input controls (feedback control) which is necessary to study musculoskeletal conditions. For example, gait abnormalities commonly observed in children with cerebral palsy are typically treated by surgically altering muscle functions. Unfortunately, this treatment strategy does not consistently result in improved outcomes. Patient-specific simulations using feedback control have utility to determine the potential efficacy of surgical correction.

Although our interface shares some similarities with other interfaces, this work is fundamentally different from previous work focused on functional electrical stimulation (Davoodi and Loeb, 2002) and finite element analysis (Rasmussen and Ozen, 2007). Others linked their simulation software (MSMS) with MATLAB (Davoodi et al., 2007; Hauschild et al., 2007); however, their package uses the SimMechanics toolbox for simulating musculoskeletal dynamics. In our case, we built on the freely available Simbody dynamics engine and OpenSim software. The users also should not confuse the developed interface with OpenSim’s built-in capability of running the OpenSim Forward Dynamics Tool using the MATLAB command line feature, which only runs OpenSim tool from the system command line using the OpenSim integrator. On the contrary, our tool uses Simbody dynamics engine and MATLAB integrators to create a new platform for forward dynamics as a Simulink block and to add the potential of extending the tool and applying it in closed-loop control systems.

The potential to use OpenSim and MATLAB/Simulink to study and improve treatments for musculoskeletal conditions is exciting. This project not only integrates software tools, but also allows integration of neuroscientists, biomechanists, and physical therapists to adapt and generate new solutions as treatments for musculoskeletal conditions. All of the source code, Simulink model examples, and user documentation related to this work will be available on a SimTK.org project dedicated to the interface (https://simtk.org/home/opensim_matlab).

Acknowledgments

The authors are grateful to Ajay Seth, Ayman Habib, and Scott Delp for their helpful conversations and input. This work was supported by a subaward from the NIH Roadmap for Medical Research U54 GM072970.

Footnotes

Conflict of interest statement

We do not have any financial or personal relationships with other people or organizations that could inappropriately influence our manuscript.

References

  1. Andrews BJ, Davoodi R, Kamnik R, Bajd T. Control of FES in paraplegia: modeling voluntary arm forces. Biomedical Materials Engineering. 1998;8:241–251. [PubMed] [Google Scholar]
  2. Barker TM, Kirtley C, Ratanapinunchai J. Calculation of multi-segment rigid body joint dynamics using MATLAB. Proceedings of the Institution of Mechanical Engineers Part H—Journal of Engineering in Medicine. 1997;211:483–487. doi: 10.1243/0954411981534619. [DOI] [PubMed] [Google Scholar]
  3. Damsgaard M, Rasmussen J, Christensen ST, Surma E, de Zee M. Analysis of musculoskeletal systems in the AnyBody modeling system. Simulation Modelling Practice and Theory. 2006;14:1100–1111. [Google Scholar]
  4. Davoodi R, Loeb GE. A software tool for faster development of complex models of musculoskeletal systems and sensorimotor controllers in Simulink (TM) Journal of Applied Biomechanics. 2002;18:357–365. [Google Scholar]
  5. Davoodi R, Urata C, Hauschild M, Khachani M, Loeb GE. Model-based development of neural prostheses for movement. IEEE Transactions on Biomedical Engineering. 2007;54:1909–1918. doi: 10.1109/TBME.2007.902252. [DOI] [PubMed] [Google Scholar]
  6. de Zee M, Hansen L, Wong C, Rasmussen J, Simonsen EB. A generic detailed rigid-body lumbar spine model. Journal of Biomechanics. 2007;40:1219–1227. doi: 10.1016/j.jbiomech.2006.05.030. [DOI] [PubMed] [Google Scholar]
  7. Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Transactions on Biomedical Engineering. 2007;54:1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
  8. Delp SL, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Computers in Biology and Medicine. 1995;25:21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
  9. Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Transactions on Biomedical Engineering. 1990;37:757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
  10. Fox MD, Delp SL. Contributions of muscles and passive dynamics to swing initiation over a range of walking speeds. Journal of Biomechanics. 2010;43:1450–1455. doi: 10.1016/j.jbiomech.2010.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fox MD, Reinbolt JA, Ounpuu S, Delp SL. Mechanisms of improved knee flexion after rectus femoris transfer surgery. Journal of Biomechanics. 2009;42:614–619. doi: 10.1016/j.jbiomech.2008.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hamner SR, Seth A, Delp SL. Muscle contributions to propulsion and support during running. Journal of Biomechanics. 2010;43:2709–2716. doi: 10.1016/j.jbiomech.2010.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hauschild M, Davoodi R, Loeb GE. A virtual reality environment for designing and fitting neural prosthetic limbs. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2007;15:9–15. doi: 10.1109/TNSRE.2007.891369. [DOI] [PubMed] [Google Scholar]
  14. Hohne G. Computer aided development of biomechanical pilot models. Aerospace Science and Technology. 2000;4:57–69. [Google Scholar]
  15. Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Annals of Biomedical Engineering. 2005;33:829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
  16. Jacobs JJ, Andersson GBJ, Bell JE, Weinstein SL, Dormans JP, Gnatz SM, Lane N, Puzas JE, Clair EW, Yelin EH. The burden of musculoskeletal diseases. Bone and Joint Decade 2008 [Google Scholar]
  17. Kepple TM, Siegel KL, Stanhope SJ. Relative contributions of the lower extremity joint moments to forward progression and support during gait. Gait and Posture. 1997;6:1–8. [Google Scholar]
  18. Lemay MA, Crago PE. A dynamic model for simulating movements of the elbow, forearm, an wrist. Journal of Biomechanics. 1996;29:1319–1330. doi: 10.1016/0021-9290(96)00026-7. [DOI] [PubMed] [Google Scholar]
  19. Lim CL, Jones NB, Spurgeon SK, Scott JJA. Modelling of knee joint muscles during the swing phase of gait—a forward dynamics approach using MATLAB/Simulink. Simulation Modelling Practice and Theory. 2003;11:91–107. [Google Scholar]
  20. Otoole RV, Jaramaz B, Digioia AM, Visnic CD, Reid RH. Biomechanics for preoperative planning and surgical simulations in orthopedics. Computers in Biology and Medicine. 1995;25:183–191. doi: 10.1016/0010-4825(94)00043-p. [DOI] [PubMed] [Google Scholar]
  21. Rasmussen J, Ozen M. AnyBody–ANSYS interface: CAE Technology for the human body. CADFEM Medical 2007 [Google Scholar]
  22. Reinbolt JA, Fox MD, Schwartz MH, Delp SL. Predicting outcomes of rectus femoris transfer surgery. Gait and Posture. 2009;30:100–105. doi: 10.1016/j.gaitpost.2009.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Thelen DG, Anderson FC. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. Journal of Biomechanics. 2006;39:1107–1115. doi: 10.1016/j.jbiomech.2005.02.010. [DOI] [PubMed] [Google Scholar]
  24. Thelen DG, Anderson FC, Delp SL. Generating dynamic simulations of movement using computed muscle control. Journal of Biomechanics. 2003;36:321–328. doi: 10.1016/s0021-9290(02)00432-3. [DOI] [PubMed] [Google Scholar]
  25. Vasavada AN, Li S, Delp SL. Influence of muscle morphometry and moment arms on the moment-generating capacity of human neck muscles. Spine. 1998;23:412–422. doi: 10.1097/00007632-199802150-00002. [DOI] [PubMed] [Google Scholar]

RESOURCES