Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Mar 11;3:1383. doi: 10.1038/srep01383

Graphene-based photovoltaic cells for near-field thermal energy conversion

Riccardo Messina 1,a, Philippe Ben-Abdallah 1,b
PMCID: PMC3593225  PMID: 23474891

Abstract

Thermophotovoltaic devices are energy-conversion systems generating an electric current from the thermal photons radiated by a hot body. While their efficiency is limited in far field by the Schockley-Queisser limit, in near field the heat flux transferred to a photovoltaic cell can be largely enhanced because of the contribution of evanescent photons, in particular for a source supporting a surface mode. Unfortunately, in the infrared where these systems operate, the mismatch between the surface-mode frequency and the semiconductor gap reduces drastically the potential of this technology. In this paper we propose a modified thermophotovoltaic device in which the cell is covered by a graphene sheet. By discussing the transmission coefficient and the spectral properties of the flux, we show that both the cell efficiency and the produced current can be enhanced, paving the way to promising developments for the production of electricity from waste heat.

A hot body at temperature T radiates an electromagnetic field in its surroundings because of local thermal fluctuations. In the close vicinity of its surface, at distances smaller than the thermal wavelength 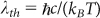Inline graphic, the electromagnetic energy density is several orders of magnitude larger than in far field1,2. Hence, the near-field thermal radiation associated to non-propagating photons which remain confined on the surface is a potentially important source of energy. By approaching a photovoltaic (PV) cell3 in proximity of a thermal emitter, this energy can be extracted by photon tunneling toward the cell. Such devices, also called near-field thermophotovoltaic (NTPV) systems, have been proposed less than twenty years ago4. In presence of resonant surface modes such as surface polaritons, the flux exchanged in near field between source and photodiode drastically exceeds the propagative contribution5,6,7,8,9. This discovery has opened new possibilities for the development of innovative technologies for nanoscale thermal management, heating-assisted data storage10, IR sensing and spectroscopy11,12 and has paved the way to a new generation of NTPV energy-conversion devices13,14,15,16,17. With respect to ordinary far-field photovoltaic cells, these devices are expected to imply an enhancement by several order of magnitudes of the generated electric power, together with the technological advantage of the possible reduction the surface of the cell.

Despite its evident interest, several problems still limit the technological development of NTPV conversion. The main one is the mismatch between the frequency of surface polaritons supported by the hot source and the gap frequency of the cell (typically a semiconductor). Indeed, all photons with energy larger than the frequency gap are not totally converted into hole-electron pair but a part of their energy is dissipated via phonon excitation. Besides, low-energy photons do not contribute to the production of electricity but are only dissipated into heat within the atomic lattice. To overcome this problem, we introduce here a relay between the source and the cell to make the transport of heat more efficient. Graphene is a natural candidate to carry out this function. Indeed, this two-dimensional monolayer of carbon atoms which has proved to be an extremely surprising material with unusual electrical and optical properties18,19,20 can be tailored by modifying the chemical potential to be resonant between the gap frequency of the semiconductor and the resonance frequency of the polariton supported by the source. The modulation of the chemical potential can be achieved, for example, by chemical doping21. In the context of heat transfer, the role of graphene has been recently investigated22,23,24,25, confirming its tunability and paving the way to promising thermal devices such as thermal transistors. Furthermore, a NTPV cell in which a suspended graphene sheet acts as source has been recently considered26. We propose here a modification of the standard NTPV scheme, in which the surface of the cell is covered with a graphene sheet. As we will show, this enables to exploit at the same time the existence of a surface phonon-polariton on the source and the tunability of graphene as an efficient tool to enhance the source-cell coupling.

Results

Figure 1 outlines our novel hybrid graphene-semiconductor NTPV system. A hot source made of hexagonal Boron Nitride (hBN) at temperature Ts, eventually heated by an external primary source, is placed in the proximity of a graphene-covered cell made of Indium Antimonide (InSb) at temperature Tc, having gap frequency 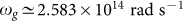Inline graphic. The source supports a surface phonon-polariton resonance at frequency 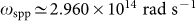Inline graphic, larger than ωg as wished.

Figure 1. Near-field thermophotovoltaic cell.

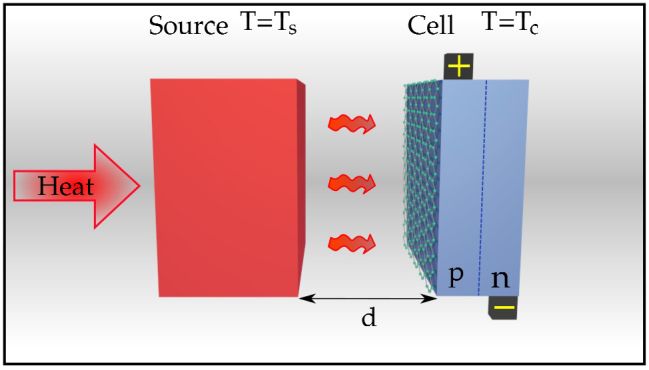
Figure 1

Open in a new tab

A hot source (temperature Ts) is placed in front of a cell at temperature Tc, which is typically a p-n junction. The source is heated by an external radiation flow, and the temperature of the cell is kept constant in time. The radiation flux between source and cell is converted into an electric current inside the cell, extracted by means of the two electrodes connected to the junction. In our case, the source (at temperature Ts = 450 K) is made of hexagonal Boron Nitride (hBN), optically described by a Drude-Lorentz model 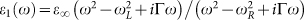Inline graphic with ε∞ = 4.88, ωL = 3.032 × 1014 rad s−1, ωR = 2.575 × 1014 rad s−1 and Γ = 1.001 × 1012 rad s−1 (Ref. 14). This model predicts the existence of a surface phonon-polariton resonance at frequency 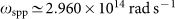Inline graphic. The cell, having temperature Tc = 300 K, is made of Indium Antimonide (InSb), described in the frequency domain of interest by a dielectric permittivity ε2(ω) = (nr(ω) + icα(ω)/2ω)2 m where nr(ω) is the refractive index, α(ω) = 0 for ω < ωg and 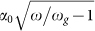Inline graphic for ω > ωg. The value Inline graphic of the gap frequency and the choice α0 = 0.7 μm−1 reasonably reproduce the experimental values of absorption27.

The hybrid configuration will be compared to the case of NTPV system without graphene sheet. The optical properties of graphene are accounted for by means of a 2D frequency-dependent conductivity (see Methods for details)28 as already done in the context of a heat-transfer calculations in25,26. We are going to study the modifications to the radiation flux between the source and the cell, as well as to the power produced by the device, due to the presence of graphene. In particular, our main scope is to investigate whether the presence of graphene is able to enhance the efficiency of the NTPV cell and possibly the output power as well.

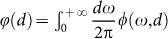First, we need a general expression for the heat flux exchanged between two planar surfaces. This distance-dependent flux Inline graphic can be expressed in near-field regime as Inline graphic, where

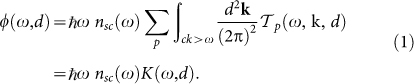graphic file with name srep01383-m1.jpg

This expression implies the sum over all the evanescent modes of the electromagnetic field (identified by the frequency ω, the transverse wavevector k = (kx, ky) and the polarization p taking the values p = TE and p = TM) of the product of the energy 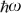Inline graphic carried by each mode (ω, k, p), the difference 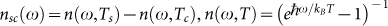Inline graphic being the distribution function inside the reservoir of modes at temperature T, and a transmission probability 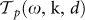Inline graphic through the separation gap assuming values between 0 and 1. In this Landauer-like decomposition29,30,31,32 the transmission probability 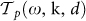Inline graphic represents an absolute measure of the contribution of a given mode to the energy exchange. In the case of two semi-infinite parallel planar media this quantity reads29

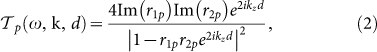graphic file with name srep01383-m2.jpg

where 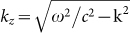Inline graphic is the z component of the wavevector in vacuum, while r1p and r2p are the ordinary vacuum-medium Fresnel coefficients corresponding to polarization p and bodies 1 and 2 respectively. For a NTPV cell, the expression (1) has to be modified in order to take into account the fact that the cell is a direct-gap semiconductor. Hence, the radiative power exchanged between the source and the cell is given by

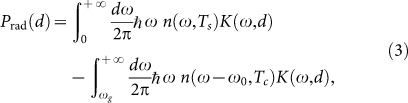graphic file with name srep01383-m3.jpg

where 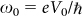Inline graphic, V0 being the potential difference at which the cell is operating, quantity for which we take a value slightly below the theoretical limit 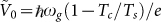Inline graphic (Ref. 26). As for the expression of the electric power which is generated from this flux, it reads

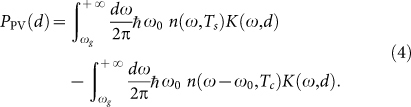graphic file with name srep01383-m4.jpg

It must be highlighted that the expression (1) provides the spectral flux on the two-body system made by the InSb cell and the graphene sheet. On the contrary, we are interested in calculating the flux on the cell alone, neglecting the energy dissipated within the graphene sheet. This analysis can be performed by means of the three-body formalism discussed in Ref.33. Nevertheless, we show in the Methods section that this does not qualitatively modify the physics of our system and produces only a weak reduction of the observed flux. For this reason, we keep in our main analysis a two-body approach allowing to identify in a more transparent way the origin of the amplification mechanism.

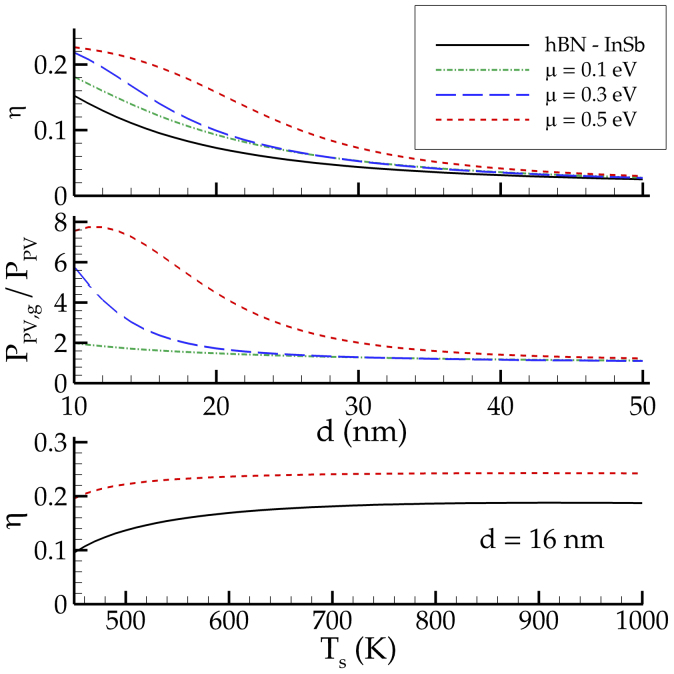
As anticipated, the evolution of both PPV and the cell efficiency η = PPV/Prad has to be followed when modifying a NTPV device, the challenge being their simultaneous enhancement. In Figure 2 we represent both the efficiency and the ratio of electric powers for four different configurations, namely without graphene and with a sheet deposed on the surface of the cell for three different values of the chemical potential μ. We remark here that the contact between the graphene sheet and the p-n junction playing the role of the cell can be actively exploited to modify μ, as discussed e.g. in Ref.34. Regarding the efficiency, we see that graphene produces indeed an enhancement. For example, at d = 16 nm η goes from around 10% in absence of graphene to almost 20% for μ = 0.5 eV, approaching considerably the ideal Carnot limit 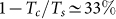Inline graphic. We also see that for larger distances and for any choice of μ the graphene-modified efficiencies tend to the one associated to the standard hBN - InSb system. As for the electric power, the presence of graphene produces an amplification going up to values of the order of 8, showing that both desired conditions are met by our modification scheme. In the same figure the dependence on the source temperature Ts is also analyzed. We observe that for a distance of d = 16 nm the efficiencies both in absence and in presence of graphene (in figure we show the case μ = 0.5 eV) increase by increasing Ts. As far as the difference between the efficiencies is concerned, it goes from around 10% for Ts = 450 K to 5% for Ts = 1000 K. As for the ratio of electric powers (not shown in figure), we have verified that it does not appreciably vary as a function of Ts.

Figure 2. Efficiency and ratio of produced electric power with graphene.

Figure 2

Open in a new tab

The curves in the first two plots correspond to three different values of chemical potential of graphene. For any distance d here represented, the presence of the graphene sheet produces an enhancement of efficiency as well as an amplification of electric power. The overall effect decreases with respect to the source-cell distance d. The third plot shows the efficiency for the standard NTPV cell and in presence of graphene (for μ = 0.5 eV), for a distance d = 16 nm, as a function of the source temperature Ts.

Discussion

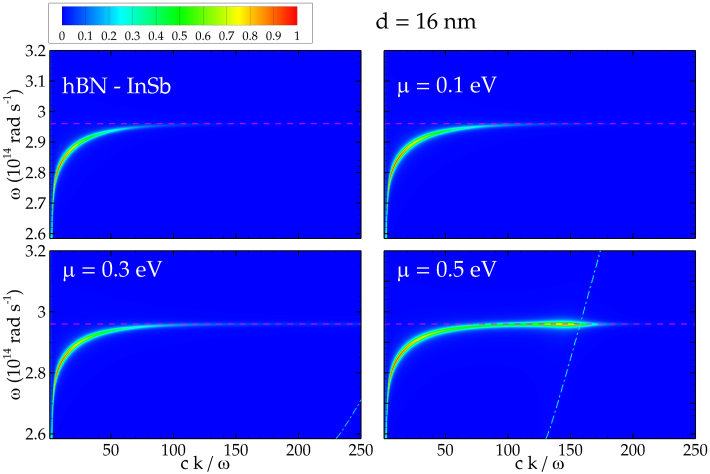
We now show in Figure 3 the transmission probability 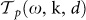Inline graphic for a source-cell distance of d = 16 nm, without and with graphene. We first observe that in absence of graphene the modes contributing to the effect are concentrated in proximity of the surface resonance ωspp of hBN. This resonance branch decays with respect to the wavevector k, and in particular is no longer visible around 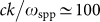Inline graphic. This cutoff, well-known in the theory of radiative heat transfer, is mainly connected to the distance between the bodies and is roughly given by 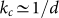Inline graphic (Refs. 29, 30). We remark that the InSb cell does not support any surface mode in the frequency region of interest. This is no longer true in presence of graphene. The modification of the optical properties due to the deposed sheet induces the appearance of a resonant surface mode associated to the graphene-modified cell, represented in figure by the dot-dashed line. This is not visible for μ = 0.1 eV, appears for high wavevectors for μ = 0.3 eV, is clearly visible for the largest chosen value μ = 0.5 eV. The new physical mechanism generated by the presence of graphene can be described in terms of a coupling between the two surface modes. For μ = 0.5 eV this manifestly produces an enhanced region of transmission probability around the intersection point of the two branches, while for μ = 0.1 and 0.3 eV the same coupling, taking place at larger values of ck/ω, gives rise to an increase of the cutoff wavevector kc. The fact that kc is a decreasing function of d and that the graphene-induced resonant modes exist for high values of the wavevector explains why the efficiency enhancement decreases with d. The comparison between the three considered values of μ shows us that the reason for which the coupling is clearly visible for μ = 0.5 eV is that in this case the intersection between the two branches of surface modes takes place at a value of ck/ω not too large with respect to the natural cutoff kc discussed before. As a consequence, we expect this coupling to be manifest even for larger values of μ, for which the coupling would take place at smaller values of ck/ω. Nevertheless, equation (1) proves that modes having larger wavevector contribute more to the flux. These points suggest that μ = 0.5 eV should be a good estimate of the best compromise between these two effects. We have numerically verified this point and for this reason we do not present values of μ larger than 0.5 eV.

Figure 3. Transmission probability with and without graphene.

Figure 3

Open in a new tab

The transmission probability (2) is represented in absence of graphene, and with graphene for μ = 0.1, 0.3, 0.5 eV. The horizontal dashed line represents the frequency ωspp of the surface phonon-polariton resonance of hBN, while the dot-dashed lines describe the resonance of the graphene - InSb system. The enhancement of transmission probability is clearly visible around the intersection point of the two branches for μ = 0.5 eV, whereas the same coupling produces an increase of the cutoff wavevector kc for smaller values of the chemical potential.

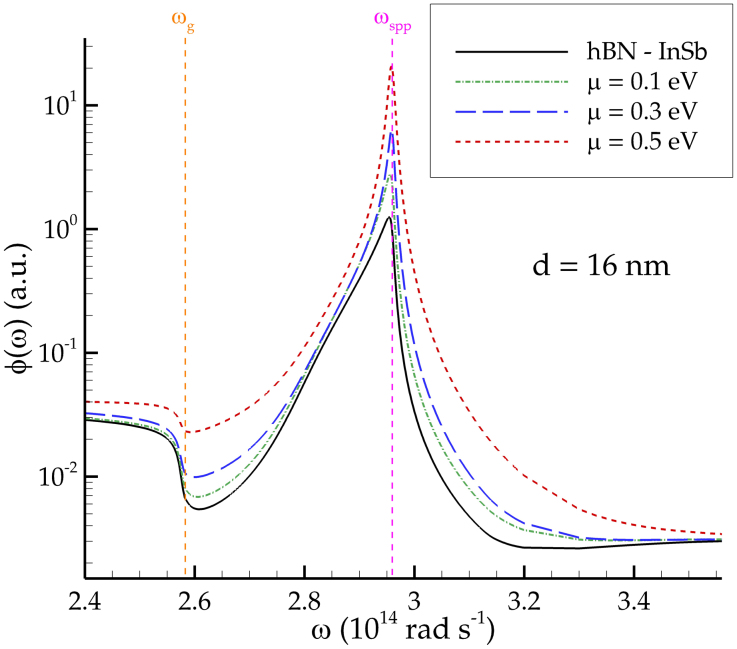
We finally discuss the effect of graphene on the flux spectrum φ(ω) (1). The first manifest effect is the amplification, for any value of the chemical potential, of the peak of the spectrum at ω = ωspp. This clearly corresponds to the enhancement of the cutoff wavevector kc (i.e. an increased number of participating modes) observed for any considered value of μ. Moreover, the coupling discussed for μ = 0.5 eV is here reproduced in terms of enlargement of the peak. These curves clearly explain that both the radiation exchange and the electric power are amplified. Nevertheless, they also allow to explain the enhancement of efficiency. As a matter of fact, the modifications to the spectral properties are more pronounced around ωspp, which is larger than ωg. Thus, since the region ω < ωg contributes only to Prad, this amplification results in a higher value of η as well.

We have proposed a novel setup for NTPV energy conversion in which the PV cell is covered with a graphene sheet. The presence of this two-dimensional system modifies the optical response of the cell, causing in particular the appearance of new surface resonant modes which coupling to the ones belonging to the source produce a significant enhancement of the electric power produced in the cell as well as of the overall efficiency of the NTPV cell. This proves that graphene can play an interesting role in the context of high-efficiency production of electricity from thermal energy.

Methods

A. Optical properties of graphene

We give here a brief overview of the optical properties of graphene used throughout the calculation presented in the paper. The response of the graphene sheet is described in terms of a 2D frequency-dependent conductivity σ(ω), written as a sum of an intraband (Drude) and an interband contribution respectively given by28

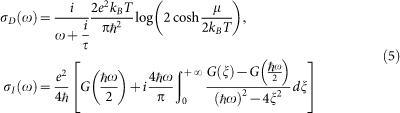graphic file with name srep01383-m5.jpg

where G(x) = sinh(x/kBT)/[cosh(μ/kBT) + cosh(x/kBT)]. The conductivity also depends on the temperature T of the graphene sheet (assumed equal to the temperature of the cell), on the chemical potential μ and on the relaxation time τ, for which we have chosen the value τ = 10−13 s (Ref. 35).

In order to deduce the heat flux between the source and the graphene-covered cell we need the expression of the reflection coefficients for an arbitrary frequency ω, wavevector k and polarization p. To this aim we assume that the graphene sheet is located in z = z0 and that it separates two non-magnetic media 1 (z < z0) and 2 (z > z0) having dielectric permittivities ε1(ω) and ε2(ω) respectively. We assume the presence of an incoming field for z < z0, generating a reflected field in medium 1 and a transmitted field in medium 2. We then impose the continuity of component of the electric field parallel to the graphene sheet and connect the discontinuity of the magnetic field to the surface current on the sheet, proportional to the electric field on the sheet through the conductivity σ(ω). This procedure gives the following expressions of the reflection and transmission coefficients for a given couple (ω, k) and for the two polarizations

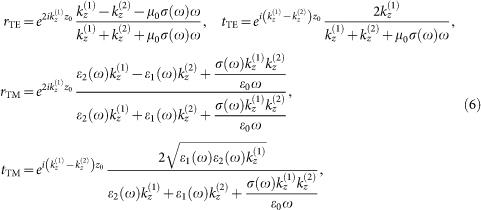graphic file with name srep01383-m6.jpg

where

graphic file with name srep01383-m7.jpg

is the z component of the wavevector inside medium i (i = 1, 2). For the purpose of our calculation we simply have to take ε1(ω) = 1, obtaining

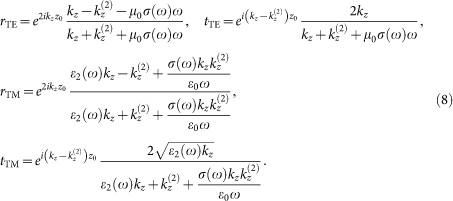graphic file with name srep01383-m8.jpg

The reflection coefficients appearing in eq. (2) correspond to the particular case z0 = 0.

B. Flux absorbed by the PV cell

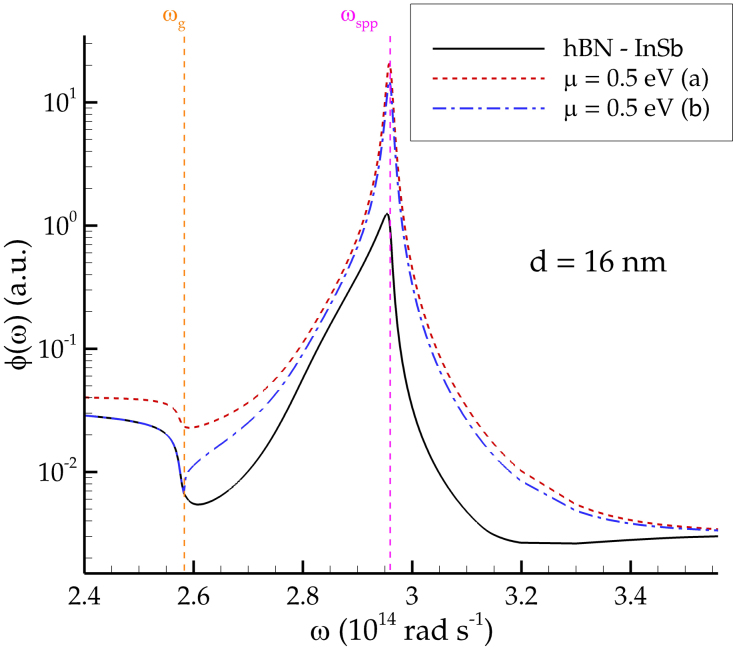
As anticipated in the main text, the use of the two-body expression of the transmission coefficient (2) in conjunction with the reflection coefficients (8) (accounting for the reflection on the PV cell modified by the presence of the graphene sheet) gives back the flux absorbed by the cell and the graphene sheet together. This is a simplified calculation, since the flux entering equations (3) and (4) should more precisely be the flux on the cell alone. This flux can be calculated by considering that our system is made of three separate bodies (the cell, the graphene sheet and the source) and by using the three-body formalism for radiative heat transfer introduced and exploited in Ref.33. It is possible to show that even if the distance between two of the three bodies (the cell and the graphene sheet) is zero, the result is finite without any regularization, in virtue of the fact that both the cell and the graphene sheet are at temperature Tc. We show in Figure 5 the flux for the standard hBN-InSb cell, compared to two fluxes in presence of a graphene sheet of chemical potential μ = 0.5 eV, the former on the cell-sheet system (the same of Figure 4 of the main text), the latter on the cell alone. The figure shows that a part of the energy is indeed dissipated within the graphene sheet, the overall shape of the spectral flux remaining unchanged. In particular, in the case shown in figure, both the radiative and the electric powers exchanged are reduced by a factor of approximately 0.8, while the efficiency undergoes a reduction of only 1%. This validates the physical analysis provided in the main part of the paper.

Figure 4. Spectral distribution of radiative flux.

Figure 4

Open in a new tab

The spectral flux φ(ω) is represented for d = 16 nm in absence of graphene, and with graphene for μ = 0.1, 0.3, 0.5 eV. The curves show an amplification, for any value of the chemical potential, at ω = ωspp. Moreover, for μ = 0.5 eV the width of the peak is significantly enhanced, due to the coupling of surface resonance modes.

Figure 5. Spectral flux on the PV cell.

Figure 5

Open in a new tab

The black curve corresponds to the flux in the standard hBN-InSb configuration. The red dashed line (a) and the blue dot-dashed line (b) are associated to the presence of a graphene sheet of chemical potential μ = 0.5 eV. The former gives the spectral flux on the cell-sheet system, the latter on the cell PV alone (calculated using a three-body approach).

Author Contributions

R.M. and P.B.-A. contributed equally to this work.

Acknowledgments

The authors thank M. Antezza and E. Pallecchi for fruitful discussions. P. B.-A. acknowledges the support of the Agence Nationale de la Recherche through the Source-TPV project ANR 2010 BLANC 0928 01.

References

  1. Joulain K., Mulet J.-P., Marquier F., Carminati R. & Greffet J.-J. Surface electromagnetic waves thermally excited: Radiative heat transfer, coherence properties and Casimir forces revisited in the near field. Surf. Sci. Rep. 57, 59 (2005). [Google Scholar]
  2. Volokitin A. I. & Persson B. N. J. Near-field radiative heat transfer and noncontact friction. Rev. Mod. Phys. 79, 1291 (2007). [Google Scholar]
  3. Basu S., Chen Y.-B. & Zhang Z. M. Microscale radiation in thermophotovoltaic devices – a review. Int. J. Energy Res. 31, 689 (2007). [Google Scholar]
  4. Whale M. D. A Fluctuational electrodynamics analysis of microscale radiative heat transfer and the design of microscale thermophotovoltaic devices. Ph. D. dissertation, Dept. Mech. Eng., MIT, Cambridge, MA, 1997.
  5. Kittel A., et al. Near-Field Heat Transfer in a Scanning Thermal Microscope. Phys. Rev. Lett. 95, 224301 (2005). [DOI] [PubMed] [Google Scholar]
  6. Hu L., Narayanaswamy A., Chen X. & Chen G. Near-field thermal radiation between two closely spaced glass plates exceeding Planck's blackbody radiation law. Appl. Phys. Lett. 92, 133106 (2008). [Google Scholar]
  7. Shen S., Narayanaswamy A. & Chen G. Surface Phonon Polaritons Mediated Energy Transfer between Nanoscale Gaps. Nano Lett. 9, 2909 (2009). [DOI] [PubMed] [Google Scholar]
  8. Kralik T., Hanzelka P., Musilova V., Srnka A. & Zobac M. Cryogenic apparatus for study of near-field heat transfer. Rev. Sci. Instrum. 82, 055106 (2011). [DOI] [PubMed] [Google Scholar]
  9. Ottens R. S. et al. Near-Field Radiative Heat Transfer between Macroscopic Planar Surfaces. Phys. Rev. Lett. 107, 014301 (2011). [DOI] [PubMed] [Google Scholar]
  10. Srituravanich W., Fang N., Sun C., Luo Q. & Zhang X. Plasmonic nanolithography. Nano Lett. 4, 1085 (2004). [Google Scholar]
  11. De Wilde Y. et al. Thermal radiation scanning tunnelling microscopy. Nature 444, 740 (2006). [DOI] [PubMed] [Google Scholar]
  12. Jones A. C. & Raschke M. B. Thermal Infrared Near-Field Spectroscopy. Nano Lett. 12, 1475 (2012). [DOI] [PubMed] [Google Scholar]
  13. DiMatteo R. S. et al. Enhanced photogeneration of carriers in a semiconductor via coupling across a nonisothermal nanoscale vacuum gap. Appl. Phys. Lett. 79, 1894 (2001). [Google Scholar]
  14. Narayanaswamy A. & Chen G. Surface modes for near field thermophotovoltaics. Appl. Phys. Lett. 82, 3544 (2003). [Google Scholar]
  15. Laroche M., Carminati R. & Greffet J. J. Near-field thermophotovoltaic energy conversion. J. Appl. Phys. 100, 063704 (2006). [Google Scholar]
  16. Park K., Basu S., King W. P. & Zhang Z. M. Performance analysis of near-field thermophotovoltaic devices considering absorption distribution. J. Quant. Spectros. Radiat. Transfer 109, 305 (2008). [Google Scholar]
  17. Francoeur M., Vaillon R. & Pinar Mengüç M. Thermal Impacts on the Performance of Nanoscale-Gap Thermophotovoltaic Power Generators. IEEE Transactions on Energy Conversion 26, 686 (2011). [Google Scholar]
  18. Geim A. K. & Novoselov K. S. The rise of graphene. Nat. Mater. 6, 183 (2007). [DOI] [PubMed] [Google Scholar]
  19. Geim A. K. Graphene: Status and prospects. Science 324, 1530 (2009). [DOI] [PubMed] [Google Scholar]
  20. Avouris P. H. Graphene: Electronic and photonic properties and devices. Nano Lett. 10, 4285 (2010). [DOI] [PubMed] [Google Scholar]
  21. Liu H., Liu Y. & Daoben Z. Chemical doping of graphene. J. Mater. Chem. 21, 3335 (2011). [Google Scholar]
  22. Persson B. N. J. & Ueba H. Heat transfer between graphene and amorphous SiO2. J. Phys. Condens. Matter 22, 462201 (2010). [DOI] [PubMed] [Google Scholar]
  23. Volokitin A. I. & Persson B. N. J. Near-field radiative heat transfer between closely spaced graphene and amorphous SiO2. Phys. Rev. B 83, 241407(R) (2011). [Google Scholar]
  24. Svetovoy V. B., van Zwol P. J. & Chevrier J. Plasmon enhanced near-field radiative heat transfer for graphene covered dielectrics. Phys. Rev. B 85, 155418 (2012). [Google Scholar]
  25. Ilic O., Jablan M., Joannopoulos J. D., Celanovic I., Buljan H. & Soljačić M. Near-field thermal radiation transfer controlled by plasmons in graphene. Phys. Rev. B 85, 155422 (2012). [Google Scholar]
  26. Ilic O., Jablan M., Joannopoulos J. D., Celanovic I., Buljan H. & Soljačić M. Overcoming the black body limit in plasmonic and graphene near-field thermophotovoltaic systems. Opt. Express 20, A366 (2012). [DOI] [PubMed] [Google Scholar]
  27. Gobeli G. W. & Fan H. Y. Infrared absorption and valence band in indium antimonide. Phys. Rev. 119, 613 (1960). [Google Scholar]
  28. Falkovsky L. A. Optical properties of graphene. J. Phys. Conf. Ser. 129, 012004 (2008). [Google Scholar]
  29. Ben-Abdallah P. & Joulain K. Fundamental limits for noncontact transfers between two bodies. Phys. Rev. B 82, 121419 (2010). [Google Scholar]
  30. Biehs S.-A., Rousseau E. & Greffet J.-J. Mesoscopic Description of Radiative Heat Transfer at the Nanoscale. Phys. Rev. Lett. 105, 234301 (2010). [DOI] [PubMed] [Google Scholar]
  31. Landauer R. Electrical resistance of disordered one-dimensional lattices. Philos. Mag. 21, 863 (1970). [Google Scholar]
  32. Büttiker M. Four-Terminal Phase-Coherent Conductance. Phys. Rev. Lett. 57, 1761 (1986). [DOI] [PubMed] [Google Scholar]
  33. Messina R., Antezza M. & Ben-Abdallah P. Three-body amplification of photon heat tunneling. Phys. Rev. Lett. 109, 244302 (2012). [DOI] [PubMed] [Google Scholar]
  34. Tongay S., Lemaitre M., Miao X., Gila B. & Appleton B. R. Rectification at Graphene-Semiconductor Interfaces: Zero-Gap Semiconductor-Based Diodes. Phys. Rev. X 2, 011002 (2012). [Google Scholar]
  35. Jablan M., Buljan H. & Soljačić M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 80, 245435 (2009). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES