Abstract
Concerted proton-electron transfer (CPET) reactions in iron carboxy-tetraphenylporphyrin complexes have been investigated using both experimental and theoretical methods. Synthetic heme models abstract H+ and e− from the hydroxylamine TEMPOH or an ascorbate derivative, and the kinetics of the TEMPOH reaction indicate concerted transfer of H+ and e−. Phenylene linker domains vary the electron donor/acceptor separation by approximately 4 Å. The rate data and extensive molecular simulations show that the electronic coupling decay constant (β) depends on conformational flexibility and solvation associated with the linker domain. Our best estimate of β is 0.23 ± 0.07 Å−1, a value that is near the low end of the range (0.2–0.5 Å−1) established for electron transfer reactions involving related linkers. This is the first analysis of β for a CPET reaction.
Keywords: Proton-coupled electron transfer, concerted proton-electron transfer, electronic coupling, molecular dynamics, distance dependence
Electron transfer (ET) reactions accompanied by protonation changes are ubiquitous in chemistry and biology. Many of these proton-coupled electron transfer (PCET) reactions are ones in which both charged particles transfer in a single step (concerted PCET, denoted CPET). CPET is implicated in biological processes that often involve spatial separation of donor/acceptor sites,1–3 as in the oxidation of tyrosine Z in photosystem II, which is thought to proceed by proton transfer (PT) to a nearby histidine in concert with ET to an oxidized chlorophyll P680+ approximately 10 Å away.1 Separated CPET likely also is operative in ascorbate peroxidase,4 with ET between substrate and the heme iron (8 Å) and PT to or from the heme propionate.
A central question in both ET and CPET is how redox center separation and the composition of the intervening medium affect electron/hole transport. This relation provides a basis for controlling the mechanisms and flow of charge in biological and synthetic systems. Studies of the distance dependence of pure ET revealed how linker domains and the associated bridge states impact the electronic coupling between redox sites.5–7 In the current study, we present the first corresponding analysis for a CPET reaction. We have employed rigid linkers in model porphyrin-based systems that allow for comparison of similar reactions at two different separations and therefore an estimate of the donor-acceptor electronic coupling constant (β). Subtle changes in both the preorganization and solvent reorganization energies are shown to play an important role in evaluation of β values from the experimental rate constants.
Syntheses of 5-(4-carboxyphenyl)-10,15-20-triphenylporphyrin, 5-(1,1′-biphenyl-4-carboxylic acid)-10,15,20-triphenylporphyrin, and their iron complexes followed published procedures.8–11 UV-vis and 1H NMR spectra of the two bis(N-methyl imidazole) porphyrin complexes, denoted FeIIIPhCO2H and FeIIIPh2CO2H, exhibited similar features to those of the parent tetraphenylporphyrin (TPP) compounds.10,11
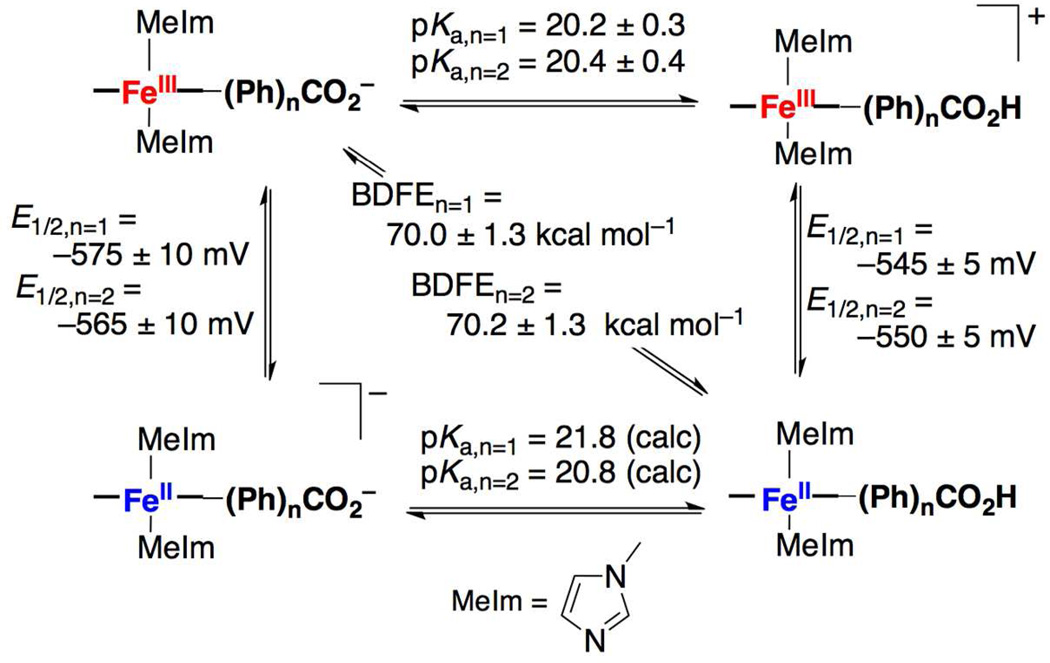
Titrations of FeIIIPhCO2H or FeIIIPh2CO2H with the strong base 1,8-diazabicycloundecane (DBU, pKa = 24.312) in MeCN revealed small UV-vis spectroscopic changes,9 indicative of weak thermodynamic coupling between the iron and benzoate sites.13,14 Titrations of the ferric compounds with Et3N gave the pKa values reported in Scheme 1,9 ca. 1 pKa unit lower than benzoic acid in MeCN (21.515). All titrations were reversible with addition of triflic acid (HOTf).
Scheme 1.
Thermochemical cycle for PCET reactions.
Cyclic voltammograms in MeCN (0.1 M nBu4NPF6) of FeIIIPhCO2H and FeIIIPh2CO2H were reversible with E1/2 = −0.545 and −0.550 V vs. Cp2Fe+/0, respectively. Addition of 1 equiv. DBU (or nBu4NOH) shifted the waves by −30 ± 10 and −15 ± 10 mV for FeIIIPhCO2H and FeIIIPh2CO2H. The shifts in potential were fully reversible upon addition of HOTf. The shifts in E1/2 upon protonation indicate that the small coupling between the heme-iron and the benzoate decreases slightly with increasing linker length. Redox data were used to calculate the pKa of the FeII porphyrins using Hess’ law (Scheme 1). The thermochemical properties of the two iron systems are very similar.
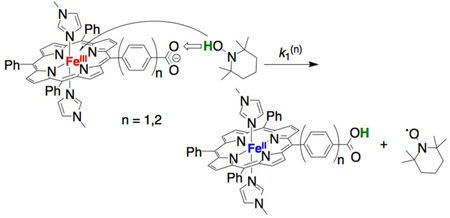
The deprotonated ferric compounds FeIIIPhCO2− and FeIIIPh2CO2− reacted with 2,2´-4,4´-tetramethylpiperidin-1-ol (TEMPOH, eq 1) or 5,6-isopropylidene ascorbate16 (iAscH−, eq 2) to yield the corresponding protonated ferrous species FeIIPhCO2H and FeIIPh2CO2H, as confirmed by UV-vis spectroscopy. The reactions with iAscH− and with ≥ 100 equivalents of TEMPO proceed to completion within minutes, before precipitation of the carboxylate species, which occurs over ~10 min for such dilute (µM) solutions under ambient conditions.
 |
(1) |
 |
(2) |
FeIIPhCO2H and FeIIPh2CO2H have similar O–H bond dissociation free energies (BDFEs, Scheme 1), indicating that their CPET reactions have similar driving forces. Reactions 1(n) (n = 1, 2; eq 1), under conditions of excess TEMPOH at 298 K, follow pseudo-first-order kinetics, with k1(1) = 15.3 ± 1.4 M−1 s−1; k1(2) = 6.5 ± 0.8 M−1 s−1.9 The corresponding reactions with TEMPO–D were markedly slower, such that kinetic measurements and quantitative deuterium kinetic isotope effects (KIEs) were complicated by the competing precipitation; however, the initial rates (d[FeIII]/dt) were clearly slower for D-versus H-transfer in both cases.9
Reactions 2(n) (n = 1, 2; eq 2) proceeded more quickly, requiring stopped-flow spectrophotometry to monitor the kinetics under pseudo-first-order conditions of excess iAscH−. For the reaction of FeIIIPhCO2− with iAscH(D)−, k2(1) = (6.9 ± 0.4) × 105 M−1 s−1, and the corresponding rate constant for the deuterated system is (3.9 ± 0.3) × 105 M−1 s−1, such that kH/kD = 1.8 ± 0.2. For the reaction of FeIIIPh2CO2− with iAscH−, k2(2) = (4.7 ± 0.5) × 105 M−1 s−1 [(4.2 ± 0.4) × 105 M−1 s−1 for iAscD−, kH/kD = 1.12 ± 0.15]. These results are consistent with the small KIEs found for reactions of iAscH− with other iron-porphyrin complexes.17
Possible mechanisms for reactions 1 and 2 include initial ET followed by PT, initial PT followed by ET, or concerted transfer of H+ + e−.1c FeIIIPhCO2− and FeIIIPh2CO2− have little bias towards CPET, since there is virtually no thermodynamic coupling between the redox and acid-base sites (Scheme 1), while TEMPOH strongly favors concerted H+/e− transfer to avoid high-energy intermediates generated from individual ET or PT.1c for concerted transfer from TEMPOH to FeIIIPhCO2− (−3.5 ± 1.1 kcal/mol) is more favorable than ΔGoPT(1) or ΔGoET(1) (+28.5, +29.6 kcal/mol, respectively). The experimentally measured barrier ΔG1(1)‡ = 15.8 kcal/mol is below the ΔGoPT(1) or ΔGoET(1), ruling against these pathways in favor of a CPET mechanism. CPET is similarly likely for reaction 1(2).18
Thermochemical analysis of reaction 2 did not provide evidence for one specific mechanism,9 although the primary KIEs are consistent with CPET. Also, reactions 1 and 2 exhibited qualitatively similar behavior (i.e., k2(1) > k2(2)), consistent with CPET mediated by a (Ph)n bridge.
The rate constants for the reactions of the complex with the n = 2 linker are approximately two times slower than for the analogous k values for the complex with the n = 1 linker (Table 1). This is crudely consistent with previous studies of intramolecular ET.5 To better analyze the measured rate constants for the CPET reactions involving TEMPOH we turned to molecular simulation techniques and the theory of CPET reaction rates.
Table 1.
PCET rate constants for reactions 1 and 2.a
| FeIIIPhCO2− | FeIIIPh2CO2− | k(1)k(2) | |
|---|---|---|---|
| iAscH− | 6.9(4) × 105 | 4.7(5) × 105 | 1.5 |
| TEMPOH | 15(1) | 6.5(8) | 2.4 |
Rate constants in M−1 s−1 for reactions at 298 K. Uncertainty in the last digit indicated in parentheses.
Investigations of ET distance dependence employed photo-initiated unimolecular systems, which constrain the redox centers to a fixed distance, avoiding the formation of multiple, distinct precursor complexes and their associated free energy of formation.5 For the bimolecular CPET reactions studied here, the formation of a hydrogen bond between the donor and acceptor simplifies the analysis of these reactions by providing a well-defined precursor complex.19 In the following analysis, the subscripts that distinguish between reactions 1 and 2 have been suppressed; we focus exclusively on reaction 1 (TEMPOH), which clearly occurs via CPET.
The thermal reaction rate for electronically nonadiabatic CPET in the normal regime assumes the golden-rule form9,20,22
| (3) |
where R is the electron donor-acceptor distance, λ(R) is the CPET reorganization energy given by the sum of the inner- and outer-sphere reorganization energies, wr(R) is the work required for precursor complex formation, ΔGo(R) is the driving force for CPET, HAB(R) is the electronic coupling matrix element, and γ includes the (n- and R-independent) proton coupling matrix elements. Derivation of eq 39 uses the assumption that the proton and electron donor-acceptor distances are statistically uncorrelated for configurations that dominantly contribute to the CPET rate; numerical validation of this assumption is provided in Fig. S18. Numerical support for the n- and R-independence of γ also is provided in Fig. S18 and Section 8.6.9
At a given separation distance, ΔGo(R) can be related to the corresponding value at infinite separation, , and the difference between the works of bringing together the reactant and product species.23
| (4) |
In the electronically nonadiabatic regime, HAB(R) varies exponentially with the electron donor-acceptor distance,23,25
| (5) |
Here, is the coupling matrix element at a reference donor-acceptor distance R°, and β is the associated decay constant. The ratio of the CPET rates for the complexes with n = 1 and n = 2 phenylene linkers is given by eqs 6–8.
| (6) |
| (7) |
| (8) |
The decay constant β can be obtained via numerical solution of eq 6 using the rate constants in Table 1. However, this requires terms wr(R), wp(R), ΔΔGo, and λ(R). Using a combination of MD and electronic structure techniques, we obtained these terms for reactions 1(n) and investigated their relative impact on the interpretation of β.
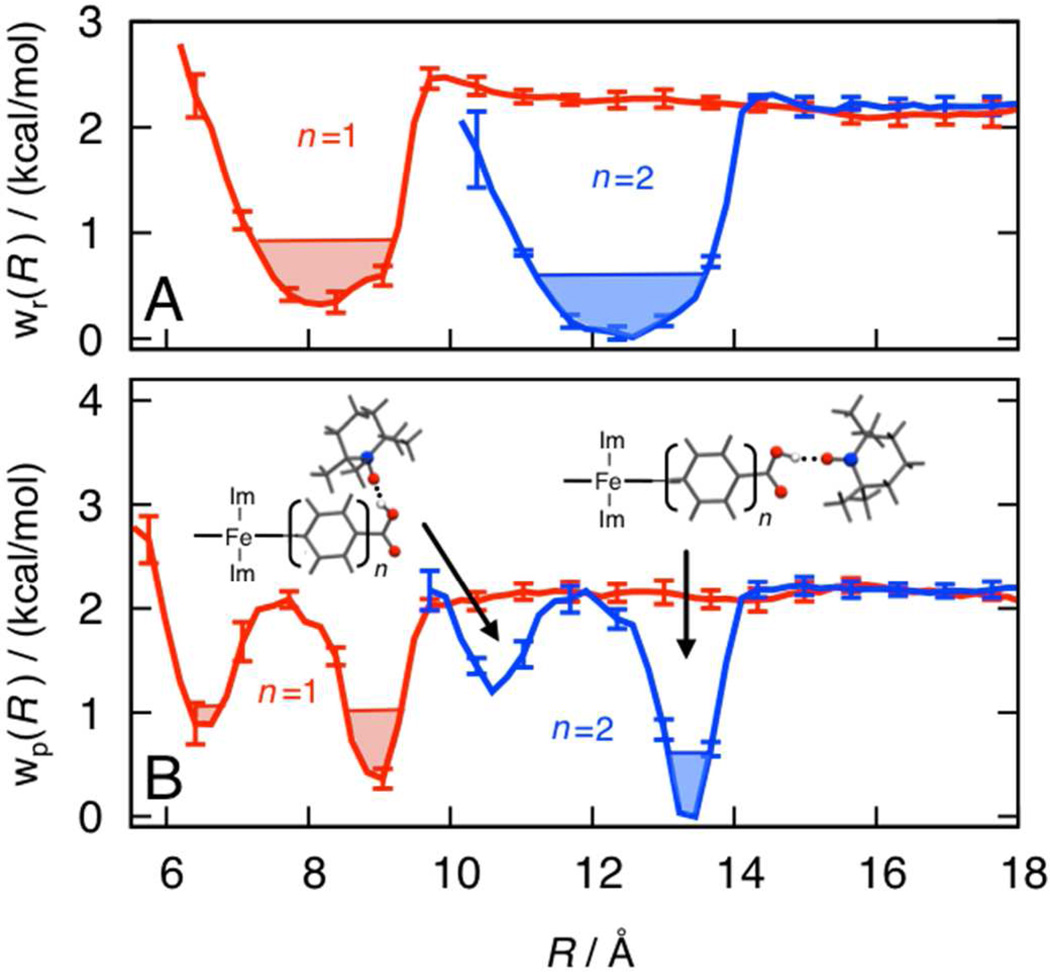
We first considered the work of preorganization for the reactant and product complexes. Calculation of the reactant and product free energy profiles, wr(n)(R) and wp(n)(R), was performed using all-atom MD simulations with a novel setup9 that allows for the direct comparison of free energies obtained with different linker numbers, n. Atomic charges for the MD simulations were obtained at the B3LYP/6-31G(d,p) level of theory. Efficient sampling was achieved by combining two-dimensional umbrella sampling with a three-dimensional implementation of the weighted histogram analysis method;9 nonetheless, a total of 400 ns of simulation time was needed to obtain sufficiently tight convergence for the analysis presented here. The reactant and product free energy profiles are presented in Figure 1.
Figure 1.
(A) Free energy profiles for reactant preorganization, wr(n)(R), associated with the TEMPOH-FeIIIPhnCO2− complexes with n = 1 (red) and n = 2 (blue) linkers. The profiles are plotted as a function of R, defined as the separation between the TEMPOH oxygen and the 5-carbon of the porphyrin ring. Thermally accessible (+1 kT) regions of the free energy profiles are shaded. (B) The corresponding product free energy profiles, wp(n)(R). Molecular structures indicate representative configurations for the complex associated with two basins of stability in the product profiles (with TEMPO• oriented toward the linker or into solution).
The reactant profiles confirm that the longer (n = 2) linker domain increases the electron donor-acceptor distance by approximately 4 Å. The longer linker also leads to a wider basin of stability and slightly stronger binding of TEMPOH due to improved solvation of the hydrogen-bound complex. The product free energy profiles are qualitatively similar, but contain additional structure arising from the torsional potential associated with rotation of the carboxylic acid OH moiety (see inset structures).
Next, we computed the CPET reorganization energy λ(n) (R) for reactions 1(n). As in the calculation of the preorganization work, the outer-sphere contribution to the reorganization energy, , was obtained using all-atom MD simulations.9 We found that is only weakly sensitive to the number of phenylene linkers, n, and to the electron donor-acceptor distance, R (Fig. S11); thermally averaging over R yields kcal/mol and kcal/mol.9 For comparison, we also evaluated the outer-sphere reorganization energy using the frequency-resolved cavity mode (FRCM),26,27 which provides a continuum dielectric representation for the MeCN solvent, yielding kcal/mol and kcal/mol.9 While qualitatively similar, FRCM predicts a stronger n-dependence for than the simulations with explicit solvent. The CPET inner-sphere reorganization energy, , was computed at the B3LYP/6-31G(d,p)||B3LYP/TZVP level of theory9 using a version of Nelsen’s four-point method applied to CPET,9 yielding values of kcal/mol and kcal/mol.
Finally, we computed ΔΔGo, the difference in driving forces for the TEMPOH reactions at infinite separation (eq 8). Driving forces for individual reactions, kcal/mol and kcal/mol, were obtained at the B3LYP/6-31G(d,p)||B3LYP/TZVP level of theory with solvation effects included via the polarizable continuum model.9,28,29 The computed values for the driving forces are in striking agreement with the corresponding experimental measurements ( kcal/mol and kcal/mol) and yielded a difference of ΔΔGo = 0.26 kcal/mol, which we employ throughout the following analysis.
Having computed wr(n)(R), wp(n)(R), λ(n)(R), and ΔΔGo, we examined the impact of these terms in the calculation of the decay constant β using eq 6. We considered a series of three cases (I–III), which provided increasingly complete descriptions of these terms.
In the simplest treatment of eq 6 (Case I), the CPET reaction was assumed to involve only a single electron donor-acceptor distance, R̃(n), and the terms wp, wr and λ were each assumed to be independent of the number of phenylene linkers. Equation 6 then simplifies to a form that resembles what has been employed in the theoretical analysis of ET reactions,23
| (9) |
In this simplest case, the electron donor-acceptor distances for reactions 1(1) and 1(2) were estimated from the distances between the metal center and the carboxyl oxygen in the crystal structures of iron(III) tetra-4-carboxyphenylporphyrin chloride30 and silver(II) 5,10,15,20-tetrakis(4-carboxy-2,6-dimethylbiphenyl)porphyrin,31 respectively. Inserting the relative difference R̃(1) – R̃(2) = −4.2 Å and the experimental values for k1(1) and k1(2) into eq 9 gave β = 0.26 ± 0.04 Å−1. The error bar in this estimate for β reflects the experimental uncertainty in the rate constants; error bars in the subsequent calculations for β additionally incorporate the statistical uncertainty of the numerical simulations.
For Case II, a more detailed treatment of eq 6 included the distance dependence of wr(n)(R) and wp(n)(R), while the dependence of the reorganization energy on the electron donor-acceptor distance and on the linker number was still neglected. Using the experimental values for k1(1) and k1(2), solution of eq 6 via numerical quadrature yielded β = 0.35 ± 0.06 Å−1.
In the most complete treatment of eq 6 (Case III), we included the distance dependence of wr(n)(R) and wp(n)(R), and the distance- and n-dependence of λ. Using the values for λo(R) obtained from the explicit-solvent MD simulations, eq 6 yielded β = 0.23 ± 0.07 Å−1. However, using the (physically reasonable) values for λo(R) from the continuum-solvent FRCM yielded the unphysical result of β = −0.10 ± 0.06 Å−1.
Table 2 presents a summary of these three analyses. Each case yielded a value for β that falls within the established range for ET across phenylene bridges (0.2–0.5 Å−1),13 but inclusion of the various preorganization and solvent reorganization contributions was found to significantly shift β within that range. Specifically, comparison of Cases I and II indicates that inclusion of the difference in preorganization work for the bimolecular reactions leads to an increase of 0.09 ± 0.04 Å−1 in the estimated value of β, emphasizing that even weak n-dependence in the energy of preorganization (~0.3 kcal/mol) leads to a substantial difference in the calculated β. Moreover, comparison of Cases II and III indicates that the weak n-dependence in the solvent reorganization energy leads to a decrease of 0.12 ± 0.04 Å−1 in the calculated β. Although the combined effects of wr(n)(R), wp(n)(R), and λ(n)(R) in Table 2 nearly cancel for this current study, this must be regarded as fortuitous; for systems that do not exhibit this cancellation of error, a careful treatment conformational flexibility and solvent reorganization energy would be necessary to avoid miscalculation of β. The point is further underscored by our finding that approximations in the description of the solvent reorganization (i.e., using implicit vs. explicit solvation) can lead to an unphysical estimate for β.
Table 2.
Electronic decay constant β for three cases.
| Case | Explicitly in eq 6 |
calculated | terms | β / Å−1 | Δβ / Å−1 |
|---|---|---|---|---|---|
| I | ΔΔGo | 0.26(4) | --- | ||
| II | wr(n)(R), wp(n)(R)ΔΔGo | 0.35(6) | + 0.09(4)b | ||
| IIIa |
wr(n)(R), λ(R) |
wp(n)(R), | ΔΔGo, | 0.23(7) | −0.12(4)c |
Using the explicit solvent results for λo(R).
Relative to Case I.
Relative to Case II.
In conclusion, we have examined the bimolecular PCET reactions of FeIIIPhCO2− or FeIIIPh2CO2− with TEMPOH and iAscH−. Thermochemical arguments show that the reactions between FeIIIPhnCO2− and TEMPOH (n = 1, 2; eq 1) follow a concerted mechanism, which may also be exhibited by the ascorbate reactions (eq 2). Adding a phenyl linker and lengthening the electron donor-acceptor distance by ~4 Å leads to a decrease in CPET rate constant of only a factor of 2. Combination of the experimental results with extensive molecular simulations for reactions 1(n) gives the first test of the dependence of CPET reaction rates on the electron donor-acceptor distance. Notably, analysis of the value of β for CPET in reaction 1 is sensitive to the treatment of the preorganization and solvent reorganization energies. The most detailed treatment provided here yields an estimate of β ~ 0.23 Å−1, which is on the low end of the range of values for ET across phenylene bridges (β = 0.2–0.5 Å−1).13 While this is only the first step in characterizing the relationship between β in ET and CPET reactions, the current results suggest that values of β obtained from ET reactions have relevance for electronically nonadiabatic CPET reactions that are central to biological catalysis and energy production.
Supplementary Material
ACKNOWLEDGMENT
Our work was supported by NIH (GM50422 to JMM, DK019038 to HBG, and GM095037 to JJW), the NSF (CHE-1057112 to TFM and DGE-1144469 to JSK), the DOE (DE-SC0006598 to TFM), and the University of Washington (JJW and JMM). TFM acknowledges computing support from the National Energy Research Scientific Computing Center (DE-AC02-05CH11231) and the Oak Ridge Leadership Computing Facility (DE-AC05-00OR22725).
Footnotes
ASSOCIATED CONTENT
Supporting Information. Experimental details and simulation protocols, thermodynamic and kinetics plots. This material is available free of charge via the Internet at http://pubs.asc.org.
References
- 1.Stubbe J, Nocera DG, Yee CS, Chang MCY. Radical Initiation in the Class I Ribonucleotide Reductase: Long-range Proton-Coupled Electron Transfer? Chem. Rev. 2003;103:2167–2201. doi: 10.1021/cr020421u. [DOI] [PubMed] [Google Scholar]
- 2.Huynh MHV, Meyer TJ. Proton-Coupled Electron Transfer. Chem. Rev. 2007;107:5004–5064. doi: 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Warren JJ, Tronic TA, Mayer JM. Thermochemistry of Proton-Coupled Electron Transfer Reagents and its Implications. Chem. Rev. 2010;110:6961–7001. doi: 10.1021/cr100085k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Efimov I, Papadopoulou ND, McLean KJ, Badyal SK, Macdonald IK, Munro AW, Moody PCE, Lloyd R, Emma The Redox Properties of Ascorbate Peroxidase. Biochemistry. 2007;46:8017–8023. doi: 10.1021/bi7006492. [DOI] [PubMed] [Google Scholar]
- 5.Wenger OS. Photoinduced Electron and Energy Transfer in Phenylene Oligomers. Chem. Soc. Rev. 2011;40:3538–3550. doi: 10.1039/c1cs15044h. [DOI] [PubMed] [Google Scholar]
- 6.Helms A, Heiler D, McLendon G. Electron Transfer in bis-Porphyrin Donor-Acceptor Compounds with Polyphenylene Spacers Shows a Weak Distance Dependence. J. Am. Chem. Soc. 1992;114:6227–6238. [Google Scholar]
- 7.Weiss EA, Ahrens MJ, Sinks LE, Gusev AV, Ratner MA, Wasielewski MR. Making a Molecular Wire: Charge and Spin Transport through para-Phenylene Oligomers. J. Am. Chem. Soc. 2004;126:5577–5584. doi: 10.1021/ja0398215. [DOI] [PubMed] [Google Scholar]
- 8.Forneli A, Planells M, Sarmentero MA, Martinez-Ferrero E, O’Regan BC, Ballester P, Palomares E. The Role of para-Alkyl Substituents on meso-Phenyl Porphyrin Sensitised TiO2 Solar Cells: Control of the eTiO2/electrolyte+ Recombination Reaction. J. Mater. Chem. 2008;18:1652–1658. [Google Scholar]
- 9.Full details are given in the supporting information
- 10.Quinn R, Nappa M, Valentine JS. New Five- and Six-Coordinate Omidazole and Imidazolate Complexes of Ferric Tetraphenylporphyrin. J. Am. Chem. Soc. 1982;104:2588–2595. [Google Scholar]
- 11.Warren JJ, Mayer JM. Hydrogen Atom Transfer Reactions of Iron-Porphyrin-Imidazole Complexes as Models for Histidine-Ligated Heme Reactivity. J. Am. Chem. Soc. 2008;130:2774–2776. doi: 10.1021/ja711057t. [DOI] [PubMed] [Google Scholar]
- 12.Kaljurand I, Kütt A, Sooväli L, Rodima T, Mäemets V, Leito I, Koppel IA. Extension of the Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile to a Full Span of 28 pKa Units: Unification of Different Basicity Scales. J. Org. Chem. 2005;70:1019–1028. doi: 10.1021/jo048252w. [DOI] [PubMed] [Google Scholar]
- 13.Manner VW, DiPasquale AG, Mayer JM. Facile Concerted Proton-Electron Transfers in a Tuthenium Terpyridine-4’-Carboxylate Complex with a Long Distance between the Redox and Basic Sites. J. Am. Chem. Soc. 2008;130:7210–7211. doi: 10.1021/ja801672w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Manner VW, Mayer JM. Concerted Proton-Electron Transfer in a Ruthenium Terpyridyl-Benzoate System with a Large Separation between the Redox and Basic Sites. J. Am. Chem. Soc. 2009;131:9874–9875. doi: 10.1021/ja902942g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kütt A, Leito I, Kaljurand I, Sooväli L, Vlasov VM, Yagupolskii LM, Koppel IA. A Comprehensive Self-Consistent Spectrophotometric Acidity Scale of Neutral Brønsted Acids in Acetonitrile. J. Org. Chem. 2006;71:2829–2838. doi: 10.1021/jo060031y. [DOI] [PubMed] [Google Scholar]
- 16.Warren JJ, Mayer JM. Surprisingly Long-Lived Ascorbyl Radicals in Acetonitrile: Concerted Proton-Electron Transfer Reactions and Thermochemistry. J. Am. Chem. Soc. 2008;130:7546–7547. doi: 10.1021/ja802055t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Warren JJ, Mayer JM. Proton-Coupled Electron Transfer Reactions at a Heme-Propionate in an Iron-Protoporphyrin-IX Model Compound. J. Am. Chem. Soc. 2011;133:8544–8551. doi: 10.1021/ja201663p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.For FeIIIPh2CO2− + TEMPOH, ΔGoCPET, ΔGoPT, ΔGoET, and ΔG1,2 ‡ = −3.7, 28.2, 29.4 and 16.3 kcal/mol, respectively
- 19.Mader EA, Mayer JM. The Importance of Precursor and Successor Complex Formation in a Bimolecular Proton-Electron Transfer Reaction. Inorg. Chem. 2010;49:3685–3687. doi: 10.1021/ic100143s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hammes-Schiffer S, Stuchebrukhov AA. Theory of Coupled Electron and Proton Transfer Reactions. Chem. Rev. 2010;110:6939–6960. doi: 10.1021/cr1001436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Costentin C, Robert M, Savéant J-M. Adiabatic and Non-adiabatic Concerted Proton-Electron Transfers. Temperature Effects in the Oxidation of Intramolecularly Hydrogen-Bonded Phenols. J. Am. Chem. Soc. 2007;129:9953–9963. doi: 10.1021/ja071150d. [DOI] [PubMed] [Google Scholar]
- 22.Cukier RI. Proton-Coupled Electron Transfer through an Asymmetric Hydrogen-Bonded Interface. J. Phys. Chem. 1995;99:16101–16115. [Google Scholar]
- 23.Marcus RA, Sutin N. Electron Transfers in Chemistry and Biology. Biochim. Biophys. Acta. 1985;811:265–322. [Google Scholar]
- 24.Gray HB, Winkler JR. Electron Flow through Metalloproteins. Biochim. Biophys. Acta. 2010;1797:1563–1572. doi: 10.1016/j.bbabio.2010.05.001. [DOI] [PubMed] [Google Scholar]
- 25.Cordes M, Giese B. Electron Transfer in Peptides and Proteins. Chem. Soc. Rev. 2009;38:892–901. doi: 10.1039/b805743p. [DOI] [PubMed] [Google Scholar]
- 26.Basilevsky MV, Rostov IV, Newton MD. A Frequency-Resolved Cavity Model (FRCM) for Treating Equilibrium and Non-Equilibrium Solvation Energies. Chem. Phys. 1998;232:189–199. [Google Scholar]
- 27.Newton MD, Basilevsky MV, Rostov IV. A Frequency-Resolved Cavity Model (FRCM) for Treating Equilibrium and Non-Equilibrium Solvation Energies: 2: Evaluation of Solvent Reorganization Energies. Chem. Phys. 1998;232:201–210. [Google Scholar]
- 28.Tomasi J, Mennucci B, Cancès E. The IEF Version of the PCM Solvation Method: an Overview of a New Method Addressed to Study Molecular Solutes at the QM ab initio Level. J. Mol. Struct: THEOCHEM. 1999;464:211–226. [Google Scholar]
- 29.Tomasi J, Mennucci B, Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005;105:2999–3094. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 30.Schareina T, Kempe R. Crystalline Materials with Large Channels or Cavities. Synthesis and Crystal Structure of an Iron(III) Tetra(4-Carboxyphenyl)Porphine. Z. Anorg. Allg. Chem. 2000;626:1279–1281. [Google Scholar]
- 31.Carlucci L, Ciani G, Maggini S, Proserpio DM, Ragaini F, Gallo E, Ranocchiari M, Caselli A. Synthesis and Characterization of New Tetra-Substituted Porphyrins with Exo-Donor Carboxylic Groups as Building Blocks for Supramolecular Architectures: Catalytic and Structural Studies of their Metalated Derivatives. J. Porphyr. Phthalocya. 2010;14:804–814. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.