Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jan 4.
Published in final edited form as: J Biomech. 2012 Nov 28;46(1):192–196. doi: 10.1016/j.jbiomech.2012.10.035

Orientations of wrist axes of rotation influence torque required to hold the hand against gravity: A simulation study of the nonimpaired and surgically salvaged wrist

Jennifer A Nichols a,c,d, Michael S Bednar d,e, Wendy M Murray a,b,c,d,*
PMCID: PMC3593346  NIHMSID: NIHMS419367  PMID: 23199898

Abstract

The wrist is a complex kinematic link connecting the forearm and hand. The kinematic design of the wrist is permanently altered during surgical salvage procedures, such as proximal row carpectomy (PRC) and scaphoid-excision four-corner fusion (SE4CF), which have the unintended consequence of long-term functional impairments to both the wrist and hand. We developed simulations of the nonimpaired, PRC, and SE4CF wrists to evaluate if surgically altered wrist kinematics contribute to functional impairments. Specifically, as a step toward understanding the connection between kinematics and function, we examined the torque necessary to statically maintain functional postures. All simulations included only bone geometry and joint kinematics; soft tissues were excluded. Our simulations demonstrate that the torque necessary to maintain a functional posture is influenced by the orientations of the flexion and deviation axes of rotation relative to each other and the anatomical planes of the radius. The magnitude of torque required to hold the hand against gravity decreased in simulations of the PRC wrist compared to the nonimpaired wrist. In contrast, the torque required increased relative to the nonimpaired wrist in simulations of the SE4CF wrist. These divergent results are directly related to how motion is coupled between the flexion–extension and deviation axes of rotation. This study highlights that, even without considering the effects of soft tissues, changing the kinematic design of the wrist influences function; therefore, kinematics should be considered when surgically redesigning the wrist.

Keywords: Wrist, Kinematics, Computer simulation, Proximal row carpectomy, Four-corner fusion

1. Introduction

The wrist is a complex kinematic link connecting the forearm and hand. As such, a nonimpaired wrist is essential for hand function (Levadoux and Legre, 2003). For example, the ability to produce force with the hand is directly related to the ability to maintain wrist extension (O'Driscoll et al., 1992; Adams et al., 2003). A person with insufficient wrist extension cannot produce the forces necessary to easily perform activities of daily living (Adams et al., 2003).

Difficulty performing activities of daily living is an unintended consequence of surgical salvage procedures on the wrist (Bain and Watts, 2010; Richou et al., 2010). Despite long-term functional impairments, salvage procedures are commonly performed because they successfully relieve the pain associated with degenerative wrist conditions (e.g., osteoarthritis; Mulford et al., 2009) and have a lower complication rate than alternative procedures (e.g., wrist arthroplasty; Levadoux and Legre, 2003; van Winterswijk and Bakx, 2010). However, salvage procedures sacrifice the complex design of the wrist. In particular, carpal kinematics are simplified. In the nonimpaired wrist, carpal motion is distributed across the radiocarpal and midcarpal joints (Ruby et al., 1988). Following a salvage procedure, carpal motion is limited to an altered radiocarpal joint (Stern et al., 2005; Vanhove et al., 2008). Two common salvage procedures are proximal row carpectomy (PRC) and scaphoid-excision four-corner fusion (SE4CF). PRC and SE4CF salvage the radiocarpal joint in different ways (Fig. 1), thereby altering carpal kinematics relative to the nonimpaired wrist and each other.

Fig. 1.

Fig. 1

Open in a new tab

Nonimpaired wrist (left, box) includes 8 carpal bones arranged in two rows. In PRC (right, top), the proximal row is removed, and the hand is shifted to establish a new radiocarpal joint between the capitate and radius. In SE4CF (right, bottom), the scaphoid is removed, and the carpal rows are fused, eliminating motion at the midcarpal joint. Bones marked with R are removed; bones marked with F are fused.

How the kinematic design of the wrist influences wrist and hand function is not fully understood. For example, as described above, both PRC and SE4CF result in simplified carpal kinematics. Yet, the mechanisms responsible for decreased functional capabilities (Cohen and Kozin, 2001; Dacho et al., 2008; Mulford et al., 2009) in surgically salvaged wrists are not known. There is no consensus regarding which procedure better preserves function (Mulford et al., 2009). The functional impact of the altered kinematics introduced by either PRC or SE4CF has not been evaluated.

To examine the impact that different kinematic designs of the wrist have on wrist and hand function, we developed computer simulations of the wrist following PRC and SE4CF. The specific aim of this simulation study is to understand how the orientations of the wrist axes of rotation influence the torque necessary to maintain wrist extension. This work is a step toward understanding whether the simplified wrist kinematics following PRC and SE4CF contribute to post-operative functional impairments.

2. Methods

Kinematic computer models of the PRC and SE4CF wrists were developed to examine biomechanical alterations imposed by surgical salvage procedures. These models were developed in SIMM (Musculographics Inc.; Delp and Loan, 1995) by adapting a validated model of the nonimpaired upper extremity (Holzbaur et al., 2005). All models included only bone geometry and joint kinematics; muscles and other soft tissues were excluded.

To examine different kinematic designs of the wrist, we altered the skeletal geometry and axes of rotation of a nonimpaired wrist model (Holzbaur et al., 2005) to reflect wrist kinematics following PRC and SE4CF. For simulation of PRC, the scaphoid, lunate, and triquetrum were removed and the distal carpal row and hand were translated proximally to establish an interface between the radius and capitate. Axes of rotation for flexion–extension and radial-ulnar deviation following PRC (cf. Fig. 2 red lines) were implemented based on the axes of rotation identified by a cadaveric experiment (Blankenhorn et al., 2007). For simulation of SE4CF, the scaphoid was removed and the lunate, capitate, hamate, and triquetrum were fused using a weld joint, thereby creating a wrist joint in which motion occurred only between the radius and a single, rigid block of carpal bones. To our knowledge, axes of rotation following SE4CF have not been measured. Therefore, we developed two SE4CF models by implementing two possible kinematic designs of the wrist (cf. Fig. 2 blue lines). Unit vectors describing the orientation of all implemented axes are provided in Table 1.

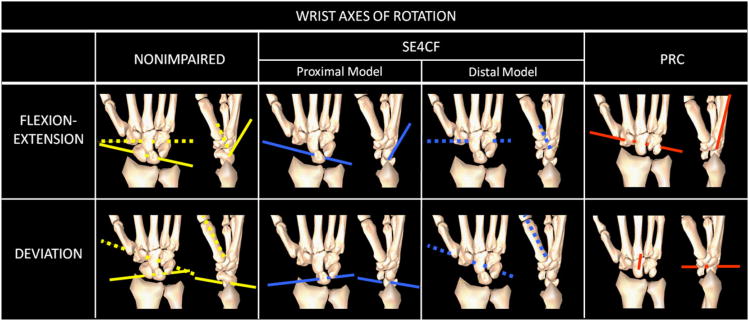
Fig. 2.

Fig. 2

Open in a new tab

Wrist axes of rotation implemented in the nonimpaired, SE4CF, and PRC models. The nonimpaired axes of rotation are separately defined based on Ruby et al. (1988) for the proximal (left, yellow solid lines) and distal (left, yellow dotted lines) carpal rows. The SE4CF axes of rotation (center, blue lines) are defined to be equal to the axes of rotation of the nonimpaired proximal row (left, yellow solid lines) and the nonimpaired distal row (right, yellow dotted lines) in the proximal SE4CF model and distal SE4CF model, respectively. The proximal SE4CF model is based on the assumption that fusion during SE4CF does not directly disturb the articulation between the radius and lunate. The distal SE4CF model is based on the assumption similar to that used in a recent 3D mathematical model of the SE4CF wrist (Dvinskikh et al., 2011). The PRC axes of rotation (right, red solid lines) are defined based on Blankenhorn et al. (2007). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article).

Table 1.

Orientation of wrist axes of rotation.a

Axis Modelb Radial-ulnar (x) Proximal-distal (y) Palmar-dorsal (z)
Flexion- extension Nonimpaired 0.981 −0.189 0.042
PRC 0.982 −0.188 0.034
SE4CF-proximal 0.956 −0.252 0.147
SE4CF-distal 0.997 0.011 −0.075
Radial-ulnar deviation Nonimpaired −0.519 −0.145 −0.843
PRC 0.000 0.000 1.000
SE4CF-proximal −0.819 −0.136 −0.557
SE4CF-distal 0.899 −0.349 −0.264
Open in a new tab
a

All axes are reported as unit vectors in the radius reference frame (see Fig. 3).

b

The nonimpaired axes are a single-axis representation of the axes reported by Ruby et al. (1988).

The nonimpaired, PRC, and SE4CF models were used to evaluate the implications of different kinematic designs of the wrist for maintaining a functional posture. Specifically, we calculated the wrist torque necessary to statically maintain 301 wrist extension. We chose 30° wrist extension because it is a highly functional posture that can be reliably achieved following both PRC and SE4CF (Mulford et al., 2009). 30° wrist extension was defined as a 30° angle between the long axes of the third metacarpal and radius, with the long axis of the third metacarpal constrained to the proximal-palmar plane. This definition made it possible to replicate an identical posture in each model, and is comparable to measurements in clinical assessments. The mass and inertia properties of the wrist and hand were defined to be consistent with those of a 50th percentile male (McConville et al., 1980). Gravity opposed wrist extension.

In each model, the torque necessary to maintain 30° wrist extension was calculated from a static torque balance. In this torque balance, the wrist and hand were held against gravity in 30° wrist extension (as defined above). To specify this posture, rotations about the modeled flexion and deviation axes were calculated using a constrained optimization method (fmincon, Matlab 7.5). We then used the inverse dynamics engine in SIMM (Dynamics Tool - > Joint Torques, v.4.2.1) to solve the static optimization problem examining how torque is distributed across the modeled flexion and deviation axes. The calculated torque, which corresponded to the torque required to support the mass of the hand against gravity while statically maintaining 30° wrist extension, was compared across models. To enable direct comparisons between torques about different axes of rotation, all torques were decomposed into components about a standard radius reference frame (Fig. 4).

Fig. 4.

Fig. 4

Open in a new tab

Magnitude of torque required to hold the hand against gravity following simulated SE4CF (dashed lines) and PRC (bold solid line). For all simulated postures, results are normalized by the magnitude of the maximum torque required to hold the hand against gravity in simulations of the nonimpaired wrist. Simulations were performed at 5° intervals; lines represent spline interpolation.

Due to the fact that the torque necessary to statically maintain 30° wrist extension was substantially different for the nonimpaired, PRC, and SE4CF models, we examined the torque necessary to maintain static postures throughout the functional range of wrist motion. Specifically, we used the technique described above to calculate the torque necessary to maintain static postures spanning from 40° wrist extension to 20° wrist flexion in 5° increments. This range encompasses the functional range of nonimpaired wrist motion as defined by in vivo studies (Brumfield and Champoux, 1984; Palmer et al., 1985).

3. Results

The simulations suggest that the axes of rotation imposed by SE4CF make it more difficult to maintain 30° wrist extension. Relative to the nonimpaired model, the magnitude of torque required to maintain this posture increased between 20.0% and 41.6% (cf. gray bars in Fig. 3A), depending on the simulated axes of rotation implemented in the SE4CF model. For both SE4CF models, the increase in the torque magnitude can be primarily explained by the increase in the component of torque acting about the radial-ulnar axis (cf. gray bars in Fig. 3B; 40.7% increase for proximal row model, 24.1% increase for distal row model). The torque component acting about the palmar-dorsal axis contributed to the increased torque for only the SE4CF model based on the kinematics of the proximal row (cf. gray bars in Fig. 3D; 50.9% increase for proximal row model, 37.8% decrease for distal row model).

Fig. 3.

Fig. 3

Open in a new tab

(A) Magnitude of torque required to maintain 30° wrist extension following simulated SE4CF (gray bars) and PRC (white bar). Results are normalized by the magnitude of torque required to maintain 30° wrist extension in simulation of the nonimpaired wrist. (B-D). The torque (reported in Nm) necessary to maintain an extended wrist posture, decomposed into the (B) radial-ulnar, (C) proximal-distal, and (D) palmar-dorsal components of the radius reference frame. Black bars indicate the results from the simulations of the nonimpaired wrist, gray bars indicate results from the simulated SE4CF wrists, and white bars indicate results from the simulated PRC wrist.

In contrast, the simulations suggest that the axes of rotation imposed by PRC make it easier to maintain 30° wrist extension. Specifically, the magnitude of torque required to maintain this posture decreased by 36.5% (cf. white bars in Fig. 3A) when comparing the PRC model to the nonimpaired model. This overall decrease in torque magnitude reflects the fact that the component of the torque about the radial-ulnar axis decreased by 33.7% (cf. white bars Fig. 3B), while the component acting about the palmar-dorsal axis decreased by 93.7% (cf. white bars in Fig. 3D).

The relative torque magnitudes between the nonimpaired, PRC, and SE4CF models are independent of wrist posture (Fig. 4). Across all postures, the magnitude of torque required to statically hold the hand against gravity increased by 8.7–42.0% for the SE4CF models (cf. dashed lines in Fig. 4) and decreased by 36.3– 42.8% for the PRC model (cf. bold solid line in Fig. 4) when compared to the nonimpaired model.

4. Discussion

Computer simulations of the nonimpaired, PRC, and SE4CF wrists indicate that the torque necessary to hold the hand against gravity is sensitive to the kinematic design of the wrist. Most notably, our results suggest that when compared to the non-impaired wrist, the axes of rotation imposed by SE4CF are more likely to limit the ability to maintain wrist extension than those imposed by PRC. This difference is demonstrated by an increase in torque magnitude for simulations of SE4CF, but a decrease for simulations of PRC (Fig. 4). These divergent outcomes indicate that different kinematic designs of the wrist influence function in different ways, suggesting that kinematics are an important factor to consider when surgically redesigning the wrist.

Examining whether the magnitude of torque necessary to maintain wrist extension changes when different kinematic designs of the wrist are simulated provides valuable insight into how the orientations of the wrist axes of rotation impact function. Importantly, the torque magnitude depends on both the orientation of the axes relative to each other and relative to the anatomical planes of the radius. These orientations influence the torque magnitude because they dictate how motion is coupled between flexion–extension and deviation. Maintaining 30° wrist extension constrained to the proximal-palmar plane requires torque about only the axis normal to the plane (i.e., radial-ulnar axis of the radius). If the flexion–extension axis of the wrist is parallel to the radial-ulnar axis of the radius, no motion coupling is required to maintain wrist extension because torque must be generated about only the flexion–extension axis. Alternatively, if the flexion–extension axis is not parallel to the radial-ulnar axis, wrist extension requires motion coupling because torque must be generated about both the flexion–extension and deviation axes.

The magnitude of torque necessary to maintain wrist extension is directly proportional to the amount of motion coupling imposed by the kinematic design of the wrist. For example, simulations of PRC required the least torque and incorporated the least motion coupling. PRC imposes nearly orthogonal axes of rotation that are closely aligned with the anatomical planes of the radius (Blankenhorn et al., 2007). In contrast, simulations of SE4CF required the most torque and incorporated the most motion coupling. The simulated SE4CF axes of rotation are neither orthogonal to the anatomical planes of the radius nor to each other; in fact the flexion–extension and deviation axes are closer to being parallel to each other than orthogonal (angles between flexion–extension and deviation axes in the SE4CF are 146.2° and 24.2°, for the proximal and distal models respectively). This orientation dictates severe motion coupling because torque about the deviation axis primarily contributes to the radial-ulnar torque direction (Table 1, radial-ulnar component of deviation axis largest for both SE4CF models). This means torque about either the flexion–extension axis or the deviation axis moves the hand in the same primary direction, which makes it difficult to position the hand in the proximal-palmar plane. Simulations of the nonimpaired wrist fall in between those simulated in PRC and SE4CF because the orientation of the axes of rotation fall near the middle of the spectrum of nearly orthogonal to nearly parallel. Therefore, the nonimpaired wrist has moderate motion coupling because torque about the deviation axis is primarily directed about the palmar-dorsal axis of the radius, but also contributes to radial-ulnar torque direction (Table 1, nonimpaired palmar-dorsal component of deviation axis greater than radial-ulnar component). Importantly, because axis orientation does not change with joint posture and the amount of motion coupling is related to the orientation of the axes of rotation relative to the anatomical planes of the radius, the amount of motion coupling is independent of joint posture. Thus, the relative amount of motion coupling across models explains why the relative magnitudes of torque holds for all joint postures (Fig. 4).

How motion coupling influences the torque necessary to maintain functional postures is an important consideration in determining the optimal kinematic design of the wrist. The PRC simulations suggest that a wrist with orthogonal axes of rotation that eliminates motion coupling minimizes the torque necessary to maintain wrist extension. Alternatively, the SE4CF simulations suggest that there is the possibility of designing a wrist with too much motion coupling, potentially limiting the ability of the muscles crossing the wrist to generate the torque necessary to maintain functional postures. However, it is important to realize that torque is not the only factor influenced by motion coupling. For example, the oblique orientation of the axes in the nonimpaired wrist means that the muscles crossing the wrist need to generate more torque to maintain wrist extension, but this orientation has the kinematic benefit of minimizing motion of the proximal carpal row during the dart thrower's motion (Crisco et al., 2005). Additionally, the orthogonal orientation of the axes in the PRC wrist may minimize the torque necessary to maintain extension, but this does not necessarily mean muscles have to generate less force because the orientation of joint axes influences muscle torque-generating parameters, namely muscle moment arm. We believe that biomechanical simulation will be an important tool in understanding how muscles compensate for altered torque requirements following salvage procedures.

Computer simulations of the surgically salvaged wrist provide a means to examine the impact that different kinematic designs of the wrist have on functionally relevant parameters. Our results demonstrate that wrist kinematics alone, without contributions of muscles or other soft tissues, affect the torque required to maintain functional postures. Thus, our work highlights the importance of axis orientation in complex, multi-degree-of-freedom joints, such as the wrist, and demonstrates a simulation method to elucidate the connection between kinematics and function.

Acknowledgments

We would like to acknowledge funding from the Searle Funds of the Chicago Community Trust and the National Institute of Health (NIH R01 HD046774 and NIH T32 HD007418).

Footnotes

Conflict of interest: The authors of this manuscript have no conflicts of interest to disclose.

References

  1. Adams BD, Grosland NM, Murphy DM, McCullough M. Impact of impaired wrist motion on hand and upper-extremity performance. Journal of Hand Surgery, American. 2003;28(6):898–903. doi: 10.1016/s0363-5023(03)00424-6. [DOI] [PubMed] [Google Scholar]
  2. Bain GI, Watts AC. The outcome of scaphoid excision and four-corner arthrodesis for advanced carpal collapse at a minimum of ten years. Journal of Hand Surgery, American. 2010;35(5):719–725. doi: 10.1016/j.jhsa.2010.01.025. [DOI] [PubMed] [Google Scholar]
  3. Blankenhorn BD, Pfaeffle HJ, Tang P, Robertson D, Imbriglia J, Goitz RJ. Carpal kinematics after proximal row carpectomy. Journal of Hand Surgery, American. 2007;32(1):37–46. doi: 10.1016/j.jhsa.2006.10.014. [DOI] [PubMed] [Google Scholar]
  4. Brumfield RH, Champoux JA. A biomechanical study of normal functional wrist motion. Clinical Orthopaedics and Related Research. 1984;187:23–25. [PubMed] [Google Scholar]
  5. Cohen MS, Kozin SH. Degenerative arthritis of the wrist: proximal row carpectomy versus scaphoid excision and four-corner arthrodesis. Journal of Hand Surgery, American. 2001;26(1):94–104. doi: 10.1053/jhsu.2001.20160. [DOI] [PubMed] [Google Scholar]
  6. Crisco JJ, Coburn JC, Moore DC, Akelman E, Weiss AP, Wolfe SW. In vivo radiocarpal kinematics and the dart thrower's motion. The Journal of Bone and Joint Surgery, American. 2005;87(12):2729–2740. doi: 10.2106/JBJS.D.03058. [DOI] [PubMed] [Google Scholar]
  7. Dacho AK, Baumeister S, Germann G, Sauerbier M. Comparison of proximal row carpectomy and midcarpal arthrodesis for the treatment of scaphoid nonunion advanced collapse (SNAC-wrist) and scapholunate advanced collapse (SLAC-wrist) in stage II. Journal of Plastic, Reconstructive and Aesthetic Surgery: JPRAS. 2008;61(10):1210–1218. doi: 10.1016/j.bjps.2007.08.007. [DOI] [PubMed] [Google Scholar]
  8. Delp SL, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Computers in Biology and Medicine. 1995;25(1):21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
  9. Dvinskikh NA, Blankevoort L, Strackee SD, Grimbergen CA, Streekstra GJ. The effect of lunate position on range of motion after a four-corner arthrodesis: a biomechanical simulation study. Journal of Biomechanics. 2011;44(7):1387–1392. doi: 10.1016/j.jbiomech.2010.12.025. [DOI] [PubMed] [Google Scholar]
  10. Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Annals of Biomedical Engineering. 2005;33(6):829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
  11. Levadoux M, Legre R. Total wrist arthroplasty with Destot prostheses in patients with posttraumatic arthritis. Journal of Hand Surgery American. 2003;28(3):405–413. doi: 10.1053/jhsu.2003.50086. [DOI] [PubMed] [Google Scholar]
  12. McConville JT, Churchill TD, Kaleps I, Clauser CE, Cuzzi J. Technical Report AFAMRL-TR-80-119. Aerospace Medical Research Laboratoy, Wright–Patterson Air Force Base; Dayton, Ohio: 1980. Anthropometric relationships of body and body segment moments of inertia. [Google Scholar]
  13. Mulford JS, Ceulemans LJ, Nam D, Axelrod TS. Proximal row carpectomy vs four corner fusion for scapholunate (SLAC) or scaphoid nonunion advanced collapse (SNAC) wrists: a systematic review of outcomes. Journal of Hand Surgery, European. 2009;34(2):256–263. doi: 10.1177/1753193408100954. [DOI] [PubMed] [Google Scholar]
  14. O'Driscoll SW, Horii E, Ness R, Cahalan TD, Richards RR, An KN. The relationship between wrist position, grasp size, and grip strength. Journal of Hand Surgery, American. 1992;17(1):169–177. doi: 10.1016/0363-5023(92)90136-d. [DOI] [PubMed] [Google Scholar]
  15. Palmer AK, Werner FW, Murphy D, Glisson R. Functional wrist motion: a biomechanical study. Journal of Hand Surgery American. 1985;10(1):39–46. doi: 10.1016/s0363-5023(85)80246-x. [DOI] [PubMed] [Google Scholar]
  16. Richou J, Chuinard C, Moineau G, Hanouz N, Hu W, Le Nen D. Proximal row carpectomy: long-term results. Chirurgie de la Main. 2010;29(1):10–15. doi: 10.1016/j.main.2009.10.003. [DOI] [PubMed] [Google Scholar]
  17. Ruby LK, Cooney WP, 3rd, An KN, Linscheid RL, Chao EY. Relative motion of selected carpal bones: a kinematic analysis of the normal wrist. Journal of Hand Surgery American. 1988;13(1):1–10. doi: 10.1016/0363-5023(88)90189-x. [DOI] [PubMed] [Google Scholar]
  18. Stern PJ, Agabegi SS, Kiefhaber TR, Didonna ML. Proximal row carpectomy. Journal of Bone and Joint Surgery American. 2005;87(Pt 2) 1:166–174. doi: 10.2106/JBJS.E.00261. [DOI] [PubMed] [Google Scholar]
  19. van Winterswijk PJ, Bakx PA. Promising clinical results of the universal total wrist prosthesis in rheumatoid arthritis. The Open Orthopedics Journal. 2010;4:67–70. doi: 10.2174/1874325001004020067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Vanhove W, De Vil J, Van Seymortier P, Boone B, Verdonk R. Proximal row carpectomy versus four-corner arthrodesis as a treatment for SLAC (scapholunate advanced collapse) wrist. Journal of Hand Surgery, European. 2008;33(2):118–125. doi: 10.1177/1753193408087116. [DOI] [PubMed] [Google Scholar]

RESOURCES