Parameter estimates for invasive breast cancer progression in the Canadian National Breast Screening Study

Abstract

Background:

The aim of screening is to detect a cancer in the preclinical state. However, a false-positive or a false-negative test result is a real possibility.

Methods:

We describe invasive breast cancer progression in the Canadian National Breast Screening Study and construct progression models with and without covariates. The effect of risk factors on transition intensities and false-negative probability is investigated. We estimate the transition rates, the sojourn time and sensitivity of diagnostic tests for women aged 40–49 and 50–59.

Results:

Although younger women have a slower transition rate from healthy state to preclinical, their screen-detected tumour becomes evident sooner. Women aged 50–59 have a higher mortality rate compared with younger women. The mean sojourn times for women aged 40–49 and 50–59 are 2.5 years (95% CI: 1.7, 3.8) and 3.0 years (95% CI: 2.1, 4.3), respectively. Sensitivity of diagnostic procedures for older women is estimated to be 0.75 (95% CI: 0.55, 0.88), while women aged 40–49 have a lower sensitivity (0.61, 95% CI: 0.42, 0.77). Age is the only factor that affects the false-negative probability. For women aged 40–49, ‘age at entry', ‘history of breast disease' and ‘families with breast cancer' are found to be significant for some of the transition rates. For the age-group 50–59, ‘age at entry', ‘history of breast disease', ‘menstruation length' and ‘number of live births' are found to affect the transition rates.

Conclusion:

Modelling and estimating the parameters of cancer progression are essential steps towards evaluating the effectiveness of screening policies. The parameters include the transition rates, the preclinical sojourn time, the sensitivity, and the effect of different risk factors on cancer progression.

In 2012 in Canada, it is estimated that 22 700 women will be diagnosed with breast cancer and 5100 will die of it; this means 62 newly diagnosed cases and 14 deaths every day (Canadian Cancer Society, 2012). Women aged 50–69 are recommended to have a mammogram every 2 years. Analyses have shown that the net benefits of screening for woman aged 40–49 are less than those for older women (Vainio and Bianchini, 2002; Nelson et al, 2009; Petitti et al, 2010). Part of this lower screening benefit is the number of false-negatives due to the denser breast tissue found in younger women. The incidence rate of cancer in the younger age group is also lower. Therefore, the age at which mammography screening should be started and the frequency with which it should be performed remain under active consideration (Schopper and de Wolf, 2009; US Preventive Services Task Force, 2009; Block, 2010).

The aim of screening is to detect a cancer in the preclinical state when it is still curable by treatment. However, a false-positive or a false-negative test result is a real possibility. The sojourn time is a key factor in assessing a screening policy. The frequency of mammography depends on the distribution of the preclinical detectable sojourn time; a balance should be found between excessive screening and not detecting the cancer in time.

Some researchers use Markov processes to model the progression of breast (Duffy et al, 1996, 1997; Chen et al, 1997a, 1997b, 1998; Weedon-Fekjaer et al, 2005, 2008; Olsen et al, 2006) or other cancers (Prevost et al, 1998; Chen et al, 1999; Sutradhar et al, 2010; Bartolomeo et al, 2011). Several research issues remain to be addressed. Sojourn time and the transition rates between cancer progression states seem likely to be age dependent. However, age is probably not the only influential factor in cancer progression. Other risk factors, including genetics and family history, may affect cancer progression.

We use data from Canadian National Breast Screening Study (CNBSS) and model breast cancer progression using a partially observable Markov model. The CNBSS is one of the eight published randomized controlled clinical trials aimed to evaluate the detection of breast cancer using mammography, but the only one with baseline data for all subjects on breast cancer risk factors (Shen and Zelen, 2001). We estimate the transition rates, the sojourn time and sensitivity of screening procedures for two age-groups 40–49 and 50–59. We also investigate the effect of risk factors on the transition and false-negative rates.

Materials and methods

The Canadian National Breast Screening Study

The CNBSS consists of two randomized screening trials of 98 835 women aged 40–59 recruited at 15 Canadian centres between 1980 and 1985. A woman should not have been pregnant at the time of enrolment, had no history of breast cancer, and no mammography in the previous 12 months. Women aged 40–49 at enrolment were randomly selected to either an annual mammogram and physical examination of the breasts or only an initial physical examination of the breasts with no mammography. Women aged 50–59 were randomly selected to either an annual mammogram and physical examination of the breasts or only an annual physical examination of the breasts. Breast cancer incidence was reported for women who received an annual mammogram and physical examination of the breasts for up to 5 years. Breast cancer diagnoses were determined up to 1994 from the National Cancer Registry for women who did not receive mammography and for women in the screened groups after their four or five planned annual mammogram and physical examination of the breasts.

All women in the study group received an annual mammogram and physical examination of the breasts on the same day, or just a few days apart. If the outcome of either examination revealed an abnormality, the woman was referred to the CNBSS review clinic at which the study surgeon discussed the findings with the study radiologist and decided whether further diagnostic procedures were required. Additional diagnostic procedures and breast biopsies were reviewed and breast cancer diagnoses were confirmed by panels of external pathologists for all those conducted in the study during the period of screening (Miller et al, 2000, 2002).

In the CNBSS, breast cancer mortality and death due to causes other than breast cancer were also identified through linkage with the Canadian Mortality Database at Statistics Canada up to 2006 (Miller et al, 1992a, 1992b; Taghipour et al, 2012a).

Study population and period

We consider 44 690 women aged 40–59 who received both annual mammograms and physical examinations of the breasts for up to 5 years. 25 108 women are in the age-group 40–49 and 19 582 women aged 50–59. We consider 1980–1989 as the study period and exclude breast cancers that were diagnosed <6 months after enrolment to eliminate prevalent breast cancers. To decide about the exclusion period for prevalent cancers we checked the number of diagnosed cancers in each year, and selected the period (i.e., 6 months) whose exclusion from the first year resulted in a similar number of cancer incidents in the first year compared with the second and the subsequent years. An alternative method would be to include potentially prevalent cases but assume that there is an unknown fraction of patients who are already in the preclinical stage at baseline (Yen and Chen, 2007).

By the end of 1989, from 25 108 women aged 40–49, 106 women were diagnosed with screen-detected invasive breast cancer, and 129 were identified with clinical invasive cancer. The number of screen-detected invasive cancers and clinical invasive cancers were 138 and 111, respectively, for women aged 50–59.

We utilise the full history of diagnostic tests and events for each woman. This includes exact dates and results of annual mammograms and physical examinations of the breasts, surgeons and pathologists' findings, and clinical cancer and mortality due to causes other than breast cancer. We identify all records associated with an annual mammogram or physical examination of the breasts. For a series of diagnostic tests, which were requested upon observation of an abnormality in a mammogram or physical examination of the breasts, we consider the result of the last test as the final outcome.

We take into consideration other diagnostic tests that a woman received after her four or five planned screens by the end of 1989. In addition, deaths due to causes other than breast cancer were identified by the end of 1989 and they were recorded as part of history for women who died.

Risk factors

We investigate the effect of ‘age at entry', ‘ever have/had other types of breast disease', ‘families with breast cancer score', ‘menstruation length (years)', and ‘number of live births' on cancer progression and sensitivity of diagnostic procedures. These factors were collected at enrolment (Taghipour et al, 2012a, 2012b). The descriptive statistics of these factors are given in Table 1.

Table 1. Descriptive statistics of the risk factors.

Variable	n=44 690
Age at entry (mean±s.d.)	48.51 (±5.61)
Menstruation length (years) (mean±s.d.)	32.37 (±6.65)
Number of live births
Nulliparous	6537 (14.63%)
≥1	38 153 (85.37%)
Families with breast cancer score (mean±s.d.)	7.17 (±11.30)
Ever have/had other types of breast disease
Yes	7153 (16.01%)
No	37 537 (83.99%)

At the time of enrolment, each woman was asked to specify up to four relatives with breast cancer, such as mother, sister, etc. In order to consider the contribution from all relatives with breast cancer, we first assigned a degree of relationship to each relative (e.g., first degree for ‘mother'). We then assigned a score for relatives with breast cancer to each woman. A woman with no relatives with breast cancer received a score of 1. For women with at least one relative with breast cancer, a contribution of 2^{(6-degree number)} from each relative was made to her score depending on the degree (first, second, third, fourth, fifth degree and above). As an example, a woman with one second degree relative with breast cancer is given a score of 2^(6-2) =16. The family/relative score is considered as a continuous variable in the model in which the risk factors (covariates) are included. The calculation method for score value is adapted from the US Preventive Services Task Force recommendations on genetic risk assessment (US Preventive Services Task Force, 2005).

Statistical analysis

We describe breast cancer progression using a four-state partially observable Markov model and simultaneously estimate the transition rates between the states of the model and the sensitivity of diagnostic procedures. Sensitivity is estimated for combined diagnostic procedures including mammography, physical examination of the breasts, surgeon's review and pathologists' finding, since these all contribute in the final outcome of a series of diagnostic tests. We stratify the data by age at entry and fit a model separately for age-groups 40–49 and 50–59 years.

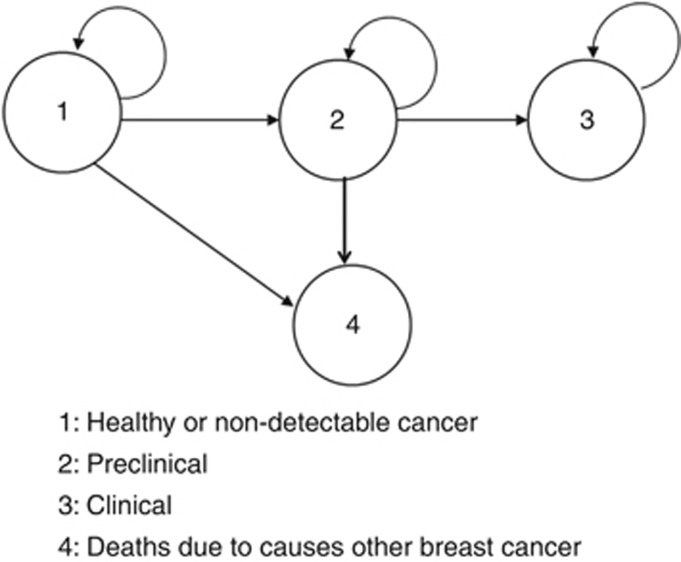
The states of the Markov model are: 1. healthy or non-detectable cancer 2. preclinical (screen-detectable cancer) 3. clinical (symptoms are evident) 4. deaths due to causes other than breast cancer. The transitions between the states are shown in Figure 1. In this model, the transition from one state to another depends on the actual health status of a woman (i.e., whether she has cancer or not, and if she has cancer, what the tumour size is) and the ability of diagnostic tests to detect it (i.e., sensitivity). For example, state 1 describes both cases when a woman is really cancer-free or she has a cancer, but available technology is not able to detect it. Similarly, preclinical state is when cancer tumour has the size that can be detected by mammography. A tumour may reaches to a detectable size sometime before a screening time, therefore, an exact time of transition from healthy state (state 1) to preclinical is not known, but it is known that the transition has happened sometime between the previous and the current screening, at which the cancer is diagnosed. For the clinical state, we assume that exact transition time from preclinical to clinical is known, because the symptoms become evident.

Figure 1.

A four-state breast cancer progression model.

State 2 is subject to misclassification due to a positive probability of false negative of pre-clinical cancer and hence when a subject is observed in state 1 it cannot be determined whether they are truly in state 1 or state 2.The probability of misclassification is equal to one minus sensitivity. We assume that at any screening, there is a positive probability of false negative. Therefore, a woman can be misdiagnosed more than once (since she is taking more than one screen). Although the chance of false negative decreases as a tumour grows, in the model, we consider a constant probability of false negative to be able to simultaneously estimate the progression parameters, including transition rates and sensitivity. Since an abnormality, that is, suspicious cancer cell is confirmed only after a sequence of diagnostic tests, the probability of false positive is zero. In other words, as mentioned earlier, the sensitivity (true positive) and specificity (true negative) are considered for combined diagnostic procedures, and not for a single mammography or physical examination.

It should be noted that the contribution of screening tests to a false-negative diagnosis is expected to be much higher than the subsequent diagnostic tests performed to confirm an abnormal screening test result. For example, if the result of a mammogram or a physical breast examination is negative when a breast cancer is present, the woman will not be referred for follow-up diagnostic testing. However, a false-negative result may also occur because of false-negative diagnostic testing. For example, even though a mammography or physical breast examination may accurately identify a breast cancer, the follow-up surgical testing may fail to confirm the diagnosis (i.e., a false-negative).

States 3 and 4 are fully observable. States 3 and 4 are absorbing states. In Figure 1, the loops on states 1, 2 and 3 indicate the possibility that the Markov process continues to occupy the same state in the next period of time.

Transition from state 2 to state 3 is not directly observed in the data and is estimated based on the transitions from state 1 to 2 and from state 1 to 3. In general, for simultaneous estimation of progression parameters, a likelihood function is constructed, which includes all the information about the unknown parameters. The parameter estimates are then obtained by maximising the likelihood function usually using the Expectation-Maximization algorithm or its variations. Further information on the mathematical modelling of a hidden Markov process and estimating its parameters is given in Jackson et al (2003).

We assume the same transition rates from state 1 to state 4 (healthy to death) and from state 2 to state 4 (preclinical to death), because the death due to non-breast cancer causes should be independent of whether women are in healthy state or preclinical state. For the model with covariates also the same effect of covariates on the transitions to death is considered.

We use the msm package in R (Jackson, 2011) to fit the Markov models. We first find the transition rates and sensitivity without considering the effect of risk factors (covariates) on the transition rates. We then investigate the effect of covariates on the transition rates using a proportional hazards model (Jackson, 2011). We develop the model with no covariate for the situation that the information of risk factors for each individual woman is not available (possibly except age), especially at the population level. In addition, we are also interested to compare the parameter estimates from both models, such as the mean sojourn time and sensitivity.

We conduct univariate analyses (model with a single covariate), and then combine the significant covariates from the univariate models in a multivariate Markov model. To construct the final model, we set to zero the coefficient of a non-significant covariate on a transition rate. The effect of a covariate on a transition is considered significant at a level of 0.1. The effects of covariates on the misclassification probability are also investigated using multinomial logistic regression (Jackson, 2011).

Data preparation

Each woman has several records or observations sorted chronologically. Each record consists of observed state and cumulative time given in years (starting from zero at enrolment) at which the state was observed. All the observations in the dataset are ‘panel observed', except the time to death or time to clinical cancer which are taken as exact. The state of women who were alive by the end of 1989 and no invasive cancer or death were reported for them was considered as censored, and could be either 1 or 2.

Results

From 44 690 women, 244 were diagnosed with screen-detected invasive breast cancers and clinical cancers were reported for 240 women. In all, 164 women were diagnosed with in situ breast cancer and censored at the time of diagnosis, because we were interested only in modelling the progression of invasive breast cancer. From 164 in situ cancers, 147 are screen-detected and the remaining, that is, 17 cancers are clinical. 467 women died due to causes other than breast cancer, which have to be taken into account for proper estimation of transition rates. The majority of women (43 575) were censored at the end of 1989.

Models with no covariate

The results (Table 2) reveal that although younger women have a transition rate from healthy state to preclinical cancer 0.7 times the transition rate from healthy state to preclinical cancer of older women, their screen-detected tumour becomes evident sooner (1.2 times faster). Women in the age-group 50–59 have a transition rate from healthy state to death 2.53 times the transition rate from healthy state to death of younger women. The sojourn times for women aged 40–49 and 50–59 are 2.5 years (95% CI: 1.7, 3.8) and 3.0 years (95% CI: 2.1, 4.3), respectively. Sensitivity of diagnostic procedures is higher for older women and is estimated to be 0.75 (95% CI: 0.55, 0.88), while women in the age-group 40–49 have a lower sensitivity (0.61, 95% CI: 0.42, 0.77).

Table 2. Parameters of the models with no covariate for age-groups 40–49 and 50–59.

Age group	40–49	50–59
Transition	Estimate (95% CI)	Estimate (95% CI)
Healthy to preclinical	0.00194 (0.00164, 0.00230)	0.00278 (0.00239, 0.00324)
Healthy to death	0.00095 (0.00082, 0.00111)	0.00240 (0.00215, 0.00268)
Preclinical to clinical	0.39540 (0.26150, 0.59790)	0.33670 (0.23490, 0.48250)
Preclinical to death	0.00095 (0.00082, 0.00111)	0.00240 (0.00215, 0.00268)
Mean sojourn time (95% CI)	2.529 (1.672, 3.825)	2.970 (2.072, 4.257)
Sensitivity (95% CI)	0.608 (0.417, 0.771)	0.748 (0.554, 0.876)

Abbreviation: CI=confidence interval.

Models with covariates

For both age groups (Tables 3 and 4), the transition rates, sojourn times and sensitivities obtained from these models are relatively similar to the results of the models with no covariate.

Table 3. Parameters of the model with covariates for age-group 40–49.

	Healthy to preclinical	Healthy to death	Preclinical to clinical	Preclinical to death
Transition rate (95% CI)	0.00184 (0.00155, 0.00219)	0.00092 (0.00078, 0.00108)	0.40180 (0.26720, 0.60410)	0.00092 (0.00078, 0.00108)
Log-linear effect of covariate on transition rate (90% CI)
Age at entry	0.05116 (0.01442, 0.08790)	0.09212 (0.04725, 0.13700)	0 a	0.09212 (0.04725, 0.13700)
Absence of history of breast disease	−0.4374 (−0.6914, −0.1835)	0	0	0
Family with breast cancer score	0.0155 (0.00755, 0.02345)	0	0	0
Mean sojourn time (95% CI)	2.489 (1.655, 3.742)
Sensitivity (95% CI)	0.614 (0.423, 0.776)

Abbreviation: CI=confidence interval.

^aThe effect of the covariate on the transition is constrained to zero, since the covariate has statistically no effect on this transition.

Table 4. Parameters of the model with covariates for age-group 50–59.

	Healthy to preclinical	Healthy to death	Preclinical to clinical	Preclinical to death
Transition rate (95% CI)	0.00267 (0.00228, 0.00313)	0.00230 (0.00205, 0.00259)	0.32940 (0.22970, 0.47250)	0.00230 (0.00205, 0.00259)
Log-linear effect of covariate on transition rate (90% CI)
Age at entry	0	0.10210 (0.06843, 0.13570)	0	0.10210 (0.06843, 0.13570)
Absence of history of breast disease	−0.3787 (−0.6331, −0.1243)	0	0	0
Menstruation length (years)	0.02821 (0.01466, 0.04176)	−0.01641 (−0.02888, −0.003948)	0	−0.01641 (−0.02888, −0.003948)
Number of live birthsa	−0.5654 (−0.8124, −0.3185)	−0.3095 (−0.549, −0.07008)	0	−0.3095 (−0.549, −0.07008)
Mean sojourn time (95% CI)	3.035 (2.116, 4.354)
Sensitivity (95% CI)	0.712 (0.536, 0.841)

Abbreviation: CI=confidence interval.

^aThe baseline is a woman with no live birth.

Except age, none of the covariates were found to have a significant effect on the misclassification. Therefore, we estimated the misclassification probability and sensitivity for age-groups 40–49 and 50–59 years separately.

For women aged 40–49 years, ‘age at entry (i.e., age at enrolment)', ‘having history of breast disease' and ‘families with breast cancer score' are found to be significant. Age is a detrimental factor for both transitions from healthy state to preclinical (HR 1.05, 90% CI: 1.01, 1.09) and from healthy to death due to causes other than breast cancer (HR 1.10, 90% CI: 1.05, 1.15). In other words, 1 year increase in ‘age' increases the hazard ratio by 1.05 and 1.10 for preclinical cancer and death, respectively. The baseline age is 40 years old for the age-group 40–49. Considering ‘age at entry' as a covariate allowed us to investigate how the variation in age within each age-group affects the transition rates.

A woman who does not have a history of breast disease compared to a woman with the same age but with the history of breast disease is at lower risks of being diagnosed with breast cancer (0.65 times less). Having families with breast cancer is increasing the likelihood of breast cancer incidence (HR 1.02, 90% CI: 1.01, 1.02). A woman with one first degree family with breast cancer is at 1.64 (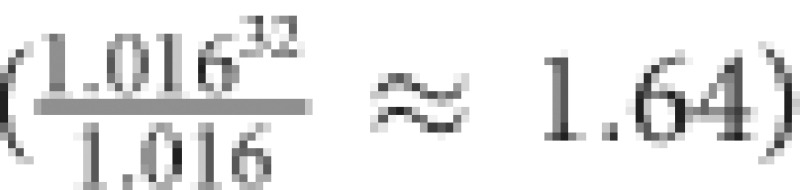) times higher risk of being diagnosed with breast cancer compared to another woman with the same characteristics but with no family with breast cancer. It should be noted that the covariate ‘families with breast cancer score' is considered as a continuous variable, thus one unit increase in the score value is associated with 1.016 (exp(0.0155)∼1.016) greater relative risk of breast cancer. The mean sojourn time and sensitivity for age-group 40–49 years are estimated to be 2.49 years (95% CI: 1.66, 3.74) and 0.61 (95% CI: 0.42, 0.78), respectively.

For the age-group 50–59 years, age shows an effect only on the transition from healthy to death due to other causes (HR 1.11, 90% CI: 1.07, 1.15). The baseline age is 50 years old for the age-group 50–59. Having no history of breast disease is protective for transition from healthy state to preclinical (HR 0.68, 90% CI: 0.53, 0.88). The longer menstruation length, the higher is the risk of being diagnosed with breast cancer (HR 1.03, 90% CI: 1.01, 1.04), and slightly lower is the probability of death due to causes other than breast cancer (HR 0.98, 90% CI: 0.97, 0.996). Women who have at least one live birth are at lower risk of being diagnosed with breast cancer (HR 0.57, 90% CI: 0.44, 0.73) and mortality (HR 0.73, 90% CI: 0.58, 0.93). For women in the age-group 50–59 years we obtained 3.04 years (95% CI: 2.12, 4.35) and 0.71 (95% CI: 0.54, 0.84) for the mean sojourn time and sensitivity, respectively.

The results of both models with covariates reveal a higher probability of false negative for younger women (0.39, 95% CI: 0.22, 0.58) compared to older women (0.29, 95% CI: 0.16, 0.46). These probabilities are 1−sensitivity, and describe the false-negative probability of combined diagnostic procedures.

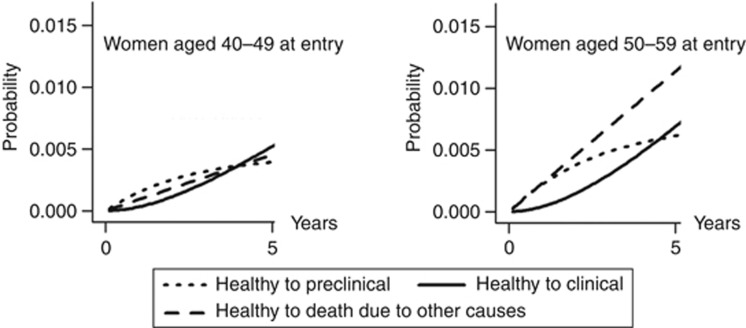
Transition probabilities

We use the models with covariates to estimate the 5-year transition probabilities from state healthy to other states (Figure 2). We set the covariate values to their means in the data, so the probability estimates are obtained for overall population within each age-group. The matrix of transition probabilities are obtained from the matrix of transition intensities (Q, given in Tables 3 and 4) using P_t exp(tQ), where t is 5 years here.

Figure 2.

Five-year transition probabilities from state healthy to preclinical, clinical and death due to causes other than breast cancer for age-groups 40–49 and 50–59.

The probabilities of transition from state healthy to clinical diagnosis and death increase almost linearly. For women aged 50–59 years, the probability of transition from healthy state to death is always higher than to clinical state; while after 4 years of follow-up, women in the age-group 40–49 years have higher probability of transition to clinical state than to mortality.

Discussion

This study presents for the first time estimates for the sojourn time of preclinical invasive breast cancer and sensitivity of the diagnostic procedures for women in the age-groups 40–49 years and 50–59 years from the CNBSS. The breast cancer model discussed in this paper is a unidirectional progression model, with partially observable hidden Markov as its underlying process. We only consider the progression of invasive cancer. Our study has several improvements over other published research which estimated the sojourn time and sensitivity based on these data. First, we estimate the parameters of invasive breast cancer progression, which are of more interest to be studied for evaluating the effectiveness of screening policies on breast cancer mortality.

Second, we utilise all observations for each woman, including exact observation time and the observed state. Moreover, additional diagnostic tests received by a woman within and after her planned screening programme are also considered for up to 1990. In addition, a longer follow-up of women provides more information about the incidence rate of cancer, particularly when no clinical cancer is reported for a large number of women by 1990.

Third, excluding prevalent cancers strengthens the assumption that all women are in state 1 at the beginning of the follow-up. This allows us to estimate the transition rate from healthy/non-detectable cancer state to preclinical state. Fourth, we take into consideration the mortality of women over the follow-up period (1980–1989). Ignoring the deaths due to causes other than breast cancer can overestimate the transition rate to breast cancer incidence, since some women may die before even experiencing breast cancer. Finally, we investigate the effect of several risk factors on the transition rates and sensitivity, which to the best of our knowledge have not been considered in other multi-state models of breast cancer progression; a few studies incorporated some covariates in their models constructed from other clinical trials (Perez-Ocon et al, 2001; Hsieh et al, 2002; Weedon-Fekjaer et al, 2008a).

Other studies based on the CNBSS (Shen and Zelen, 2001; Cong et al, 2005; Chen et al, 2010) have used the published results by Miller et al, 1992a, 1992b for the detection rates of breast cancer, including in situ, by year of screen (5 years). The detection rate is given separately for each detection method, including mammography, physical examination of the breasts, both mammography and physical examination of the breasts, and the overall detection rate, which is the sum of all detection rates.

The data utilised by other researchers is grouped-data and includes number of participants at each screen, the number of screen-detected cancers (invasive and in situ cancers are combined and are not differentiated), and the number of clinical interval cancers presenting between screens. These studies assume 1-year interval between two screens, and no mortality is taken into account in estimating the parameters. Moreover, the prevalent cancers are included in their analyses, which results in a higher detection rate of cancer at the first screen. This can cause underestimation of sojourn time and overestimation of sensitivity.

Although considering only invasive cancers in our study prevents us from directly comparing our estimates with the other published estimates based on the CNBSS (Shen and Zelen, 2001; Cong et al, 2005; Chen et al, 2010), relative comparison of the results is still possible. Shen and Zelen (2001) use the detection rates of mammography, physical examination of the breasts, and the overall detection rate of combined modalities for four annual screens and estimate the sensitivity separately for each detection method stratified by age-groups 40–49 and 50–59 years. The average sensitivities obtained for the combined modalities for both age-groups (0.91 and 0.82) are higher than the sensitivity of each diagnostic procedure alone, which requires proper interpretation. Moreover, the estimated overall sensitivity for younger women (0.91) is higher than older women (0.82); despite younger women have lower number of screen-detected and higher number of clinical cancers. The mean sojourn time obtained for women aged 40–49 years (1.87 years) is lower than our estimate from the model with covariates (2.49 years). Their mean sojourn time for older women (3.09 years) is still comparable with our estimated sojourn time for women aged 50–59 years (3.04 years).

Chen et al (2010) use the overall cancer detection rate and estimate 2.55 years for the mean sojourn time and 0.70 for the sensitivity for women aged 40–49 years. For women aged 50–59 years, they obtained 3.15 years and 0.77 for the mean sojourn time and the sensitivity, respectively. These results are relatively comparable with our results, even though we obtained lower sensitivity for younger women. Our estimates have narrower confidence intervals, which is an indicator of a more precise estimation. Cong et al (2005) combine two age-groups 40–49 and 50–59 years and obtain the estimates which are close to the estimates of (Shen and Zelen, 2001) presented for the combined modalities.

The mean sojourn time of 2.5 years and sensitivity of 0.70 obtained for women aged 40–64 years in the HIP study (Shen and Zelen, 2001) are relatively comparable with our results. Duffy et al (1996, 1997) and Chen et al (1997a, 1997b) estimated 2.46 years and 0.83 for the mean sojourn time and mammography sensitivity for women aged 40–49 years in the Swedish Two-County study. Their estimates for women aged 50–59 years are 3.70 years and 1.0 for the mean sojourn time and mammography sensitivity, respectively. The estimate obtained for the mean sojourn time for women aged 45–64 years in the Edinburgh study is 4.3 years, much higher than our estimate.

The models discussed in this paper can be extended to consider both in situ and invasive cancers. In addition, a semi-Markov process can be considered, which better describes the transition from state 1 to state 2. In a Markov process, the sojourn times have an exponential distribution, while in a semi-Markov process the sojourn times can have a general distribution.

Conclusions

Modelling cancer progression is one step towards evaluating the effectiveness of screening strategies. The preclinical sojourn time, transition rates between the stages of cancer progression, sensitivity of diagnostic tests, and the effect of different risk factors on cancer progression and sensitivity, all are important factors that should be taken into account in deciding about the best screening frequency and starting and ending ages of screening.

The authors declare no conflict of interest.