A comprehensive assessment of the impact of errors in the cancer registration process on 1- and 5-year relative survival estimates

Abstract

Background:

When making international comparisons of cancer survival, it is essential reported differences are real effects and not an artefact of potential errors in cancer registration.

Methods:

We use simulation methods to assess the impact of various cancer registration errors on commonly reported outcomes of cancer survival (1-, and 5-year relative survival estimates). We draw two samples of patients diagnosed with cancer from one population and introduce potential registration errors in one of the sample populations under various assumptions. We investigate the effect of errors individually as well as the composite effect when combined with other registration errors.

Results:

The results indicate that high levels of cancer registration errors are necessary to make a noticeable effect on commonly reported metrics of cancer survival. Differences of up to 3 percentage units in the 5-year relative survival proportion are seen under plausible scenarios.

Conclusion:

This study is a comprehensive assessment of cancer registration errors and the consequent impact on commonly reported survival statistics. We show that under plausible scenarios, it is very unlikely that these biases are large enough to explain the variation in international comparisons of cancer survival. Registration errors will also impact on other metrics reported from registry data, such as incidence.

Comparisons of cancer survival statistics between countries, regions and differing groups within a given population (e.g. socio-economic) are frequently performed. International comparisons of cancer survival statistics have become increasingly common (Sant et al, 2009, Møller et al, 2010, Coleman et al, 2011). It is important when making these comparisons and drawing conclusions that affect health policies, the differences that are reported are real effects and not artefacts of differences in data collection processes and errors in cancer registration.

Cancer registration is important for measuring the burden of cancer in a population. Many countries around the world have established cancer registries to record and collect data on incidence of cancer. However, the process of cancer registration varies from country to country and the various processes are each susceptible to the introduction of potential errors, which may in turn bias the survival measures.

One possible error relating to cancer registration is to miss the earliest possible date that the cancer registration ‘could have been made' (see the Definition in Box 1 from the United Kingdom association of cancer registries (UKARC, 2011)). If the cancer registration process in a given country allows registrations to be recorded from a variety of sources, it is possible that the registration may be made at a later point in time than the objective date of tissue diagnosis. The registration date could then be recorded as, for instance; a date of a follow-up visit for the treatment or assessment of the cancer or a date of recurrence of the disease. The key point is that the consequent survival time that would be recorded for this patient will be too short. In some cases, a cancer patient may be completely missed and thus omitted from the cancer register. This will have important implications in the incidence statistics that are reported from the registry. It may also be the case that those patients that are missed entirely are different in some way in terms of survival outcomes to those that are caught by the registration process. Under this scenario, the survival estimates obtained from the incomplete data will also be biased.

Box 1. Definition—Date of Diagnosis.

The date of the first event (of the six listed below) to occur chronologically should be chosen as the incidence date. If an event of higher priority occurs within 3 months of the date initially chosen, the date of the higher priority event should take precedence.

Order of declining priority:

1. Date of first histological or cytological confirmation of this malignancy (with the exception of histology or cytology at autopsy). This date should be in the following order:

   1. date when the specimen was taken
   2. or date of receipt by the pathologist
   3. or date of the pathology report

2. Date of admission to hospital because of this malignancy.

3. When evaluated at an outpatient clinic only: date of first consultation at the outpatient clinic because of this malignancy.

4. Date of diagnosis, other than (1), (2) or (3).

5. Date of death, if no information is available other than the fact that the patient has died because of malignancy.

6. Date of death, if the malignancy is discovered at autopsy.

Robinson et al (2007) investigated the effect of incomplete cancer registration and the presence of death certificate only (DCO) cases on the estimates of 5-year survival. The authors made adjustments to the UK Thames Cancer Registry data under plausible assumptions based on the DCO proportions and the estimates of the incompleteness of the registry based on the method of Bullard et al (2000). The authors conclude that it is important to take differences in DCO proportions and varying levels of completeness into account when making comparisons between populations.

A simulation to address questions over errors in the UK cancer registry data has recently been conducted (Woods et al, 2011) in response to a Beral and Peto editorial (Beral and Peto, 2010). Adjustments were made to the UK cancer registry data under two key scenarios based on the major criticisms of the UK data given in the editorial. First, the UK registry data was supplemented with long-term survivors of varying proportions to assess the impact on 1-, and 5-year relative survival. Second, a proportion of the patients had their survival time artificially inflated in order to counter the assumption that for some patients the date of recurrence is recorded rather than the original date of diagnosis. Again, the impact on 1 or 5-year relative survival was considered. The authors conclude that massively unrealistic errors would be necessary to reproduce the differences that are seen in international comparisons with, for instance, Sweden.

Another recent publication (Møller et al, 2011) used the Hospital Episode Statistics data from England to assess the completeness of case ascertainment achieved by the UK cancer registries. The analysis conducted was a response to the criticisms levelled at the UK data by the BMJ editorial by Beral and Peto (2010). The paper concludes that survival outcomes are biased by incomplete case ascertainment in the UK; however, this bias is of trivial magnitude.

If the date is properly recorded at diagnosis for a given patient, it is common for a cancer registry to link information with a national death register in order to ascertain whether the patient is still alive. When a patient dies, the link to the death register then provides information on how long the patient lived after their cancer registration; this is the recorded survival time, which is a commonly used measure for evaluating cancer treatment and care. If the link to the death register fails, this results in the patient being recorded as still alive beyond their date of death. Failure to correct this error results in inflated survival times for the patients in question. Brenner and Hakulinen (2009) performed a study based on failure to ascertain when a registered case has died comparing overall and relative survival for a range of scenarios. They observe that if deaths are missed then the effect of long-term survival can be quite substantial, particularly if the cancer type under study is associated with a poor prognosis.

Often registries want to directly compare their obtained outcome measures with those of other registries (either nationally or internationally). For this reason, estimates of relative survival are often favoured; these estimates are intended to be independent of the background risk of death in a given population while also not relying on accurate cause of death information. If the data quality is different between two compared populations, then this may in turn lead to difficulty in making a fair comparison between the estimates. Wide-scale international comparisons of relative survival statistics are regularly undertaken (Sant et al, 2009, Coleman et al, 2011).

In this paper, we report a study using entirely simulated data based on real-life scenarios. Using simulation methods ensures that the true answer is known and provides the best method for quantifying and understanding bias. It is also possible to assess which of the potential errors has the largest impact on the survival outcome measures that are commonly reported by cancer registries. Starting from completely simulated data rather than making alterations to existing registry data allows a true assessment of the impact of the various errors that are introduced and ensures that there is an appropriate comparison to the ‘perfect' cancer registry. The fact that we rely on entirely simulated data also means that it is possible to investigate the effect of each registration error individually as well as the composite effect when combined with other errors in the registration process.

Materials and methods

Outline of simulation

The simulation involves a comparison between a ‘perfect' cancer registry (Population 1) and a registry that suffers from various cancer registration errors (Population 2). The simulation strategy is outlined below (further technical details of the simulation strategy are contained in the Appendix):

• Draw two samples of patients diagnosed with cancer of equal size from the same underlying population. A survival time is generated for each patient that is dependent on age and that accounts for competing risk mortality from other causes.

• Adjust one of the sample populations (Population 2) according to the error process using realistic parameter values (see Figure 1); e.g., percentage of individuals missed at diagnosis.

• Compare the survival of the adjusted population to the sample with no adjustment in terms of key survival quantities, i.e. 1-, and 5-year age-standardised relative survival.

• On the basis that the effects of the various biases may vary over follow-up time, comparisons can also be made by calculating a time-dependent excess hazard ratio (Population 2 vs Population 1) to directly compare the two populations.

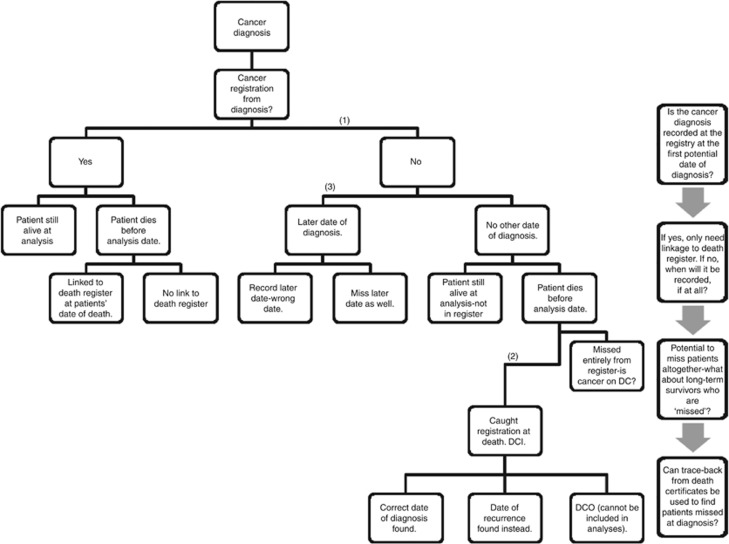
Figure 1.

Flow chart showing the process used for the simulation.

To ensure a comparison that is valid across a range of cancer types, three different true populations will be used with varying levels of relative survival. The survival of the true population was varied by changing the parameter values in the data generation process of the survival distribution according to the method set out by Bender et al (2005). Full details of the data generation process are given in the Appendix.

Cancer registration errors

Various forms of cancer registration error were considered as part of the simulation. However, each of the simulated errors stem from the initial ‘miss' of the first true date of diagnosis (point (1) of Figure 1). This date has an important role in the simulation and will be defined as the date at which, under normal circumstances (following the rules given in Box 1), a cancer registration would be made. This differs from the onset of the disease and provides an achievable date of registration for each patient that may well be ‘missed' due to various factors associated with how cancers are registered. Two assumptions can be made further to having missed the initial date of diagnosis (see Figure 1). Either, the patient is registered at a later date (a delayed cancer registration—see point (3) of Figure 1), or the cancer patient dies having not had a cancer registration made. For those patients that have a delayed cancer registration, we assume that the delayed date of diagnosis is a maximum of 2 years after the true date of diagnosis. This means that those patients with a survival time of >2 years had a uniform chance of a recorded date of diagnosis across the first 2 years of their follow-up. For those patients who died within the first 2 years, the recorded date of diagnosis could occur uniformly across their follow-up time.

Death certificate-initiated (DCI) cases (see point (2) of Figure 1) are often subject to tracing back through medical records in order to establish the date of diagnosis if that patient is not already in the cancer register. We will refer to this process as traceback and it will be assumed for a large proportion of the conducted simulations. As we simulate cause of death (see Appendix), we know what each simulated individual died from. Therefore, those patients that are missed initially, but who die from their cancer can be assumed to be subject to a successful traceback procedure, or there could be assumed to be an error in a proportion of these cases where a misspecification of the true date of diagnosis occurs instead.

Figure 1 shows a flow chart that explains how the introduction of the error process was undertaken for Population 2. Varying parameter values were chosen for the likelihood of any given patient progressing down any arm of the flow chart. The parameter values that can be varied and the range of values that were used are detailed in the list below. The numberings in the list given below are related to those given at the junctures of the flow chart in Figure 1.

Population characteristics

• Shape and scale parameter for Weibull:

  • – Low relative survival (λ=1, γ=0.5), medium relative survival (λ=0.5, γ=0.5), high relative survival (λ=0.02, γ=0.5).
• Effect of age (⩽44, 45–54, 55–64, 65–74, ⩾75):

  • – Excess hazard ratio values: 0.8, 0.9, 1, 1.2, 1.4, respectively

Registration errors

• (1) Initial miss proportion

  • Percentage missed at diagnosis:

    • 10%, 20%, 30%
• (2) Traceback

  • Is DCI traceback allowed?

    • Yes, No
  • Percentage of DCI cases that find the true date:

    • 90%, 95%, 100%
  • DCI: If not true date, what date?

    • Uniform over 2 out of 3 years.
• (3) Delayed diagnosis

  • Percentage of patients who have a second chance of diagnosis:

    • 0%, 85%, 90%, 100%
  • When is the second chance of diagnosis recorded?

    • Restricted to a maximum of 2 years.

The flow chart indicates the parameters that need to be set in order to simulate the error process for the data. The shape and scale parameters selected for the three Weibull distributions represent three cancer-relative survival curves. The high survival curve has an age-standardised 5-year relative survival estimate of 95.4%, the medium survival curve has an age-standardised value of 5-year relative survival of 31.6%, whereas the low survival curve has an age-standardised 5-year relative survival value of 10.4%.

A number of different scenarios for the values contained in Figure 1 were considered. First, to understand the direction of the respective biases, the errors were introduced one at a time (firstly error (1) alone, then error (1) in combination with error (2), and then error (1) in combination with error (3)). Following this, plausible levels of error were applied to attempt to understand the joint effect of all of the biases; some of the biases cancel each other out at certain points in follow-up, whereas others act in the same direction causing a more severely biased estimate of the outcome measures of interest. For the plausible scenarios, we used two sets of estimates that we felt were suitable for the UK cancer registry data. In scenario (A), we assumed that 15% of patients missed the true date of diagnosis, and that 85% of those patients who missed this date had a delayed cancer diagnosis by up to a value of 2 years. For those patients that died of cancer in this scenario before being registered, we allowed them to be traced back from their death certificates; however, in 10% of these cases we assumed that the date was mis-specified. In scenario (B), we assumed that 30% of patients missed the true date of diagnosis, and that 90% of those patients who missed this date had a delayed cancer diagnosis by up to a value of 2 years. For those patients that died of cancer in this scenario before being registered, we allowed them to be traced back from their death certificates; however, in 5% of these cases we assumed that the date was mis-specified.

Model fit and methods of comparison

It is likely that the biases introduced through the cancer registration errors have a varying impact over the time since diagnosis. Assuming a proportional effect for the comparison between the populations masks the time-dependent nature of the effect. A time-dependent excess mortality rate ratio between the populations informs where in follow-up the various biases have the largest impact. Therefore, flexible parametric excess mortality models (Royston and Parmar, 2002, Royston and Lambert, 2011) are used as the modelling framework due to the ease in which the model can incorporate time-dependent effects. We use a common lifetable for populations 1 and 2 to obtain the relative survival estimates. Simulation techniques allow a direct comparison with a ‘true', unbiased population, which can highlight at which point in follow-up the errors are likely to have the largest impact. This can then be translated to a comparison between the standard outcome measures that are reported by the cancer registries (1-, and 5-year relative survival).

The overall sample size for the simulations was chosen to be a cohort of size 25 000 over a 5-year diagnosis period. The simulations were run 100 times and the average of the excess mortality rate ratio over time for the 100 simulations will be reported. All of the analyses were carried out using the statistical software package Stata (StataCorp, 2011 Sata Statistical Software: Release 12, College Station, TX: SataCorp LP (2011).

Results

Missed individuals initially, no facility for a delayed date of diagnosis, no traceback employed; (‘No Traceback'—Error (1) only)

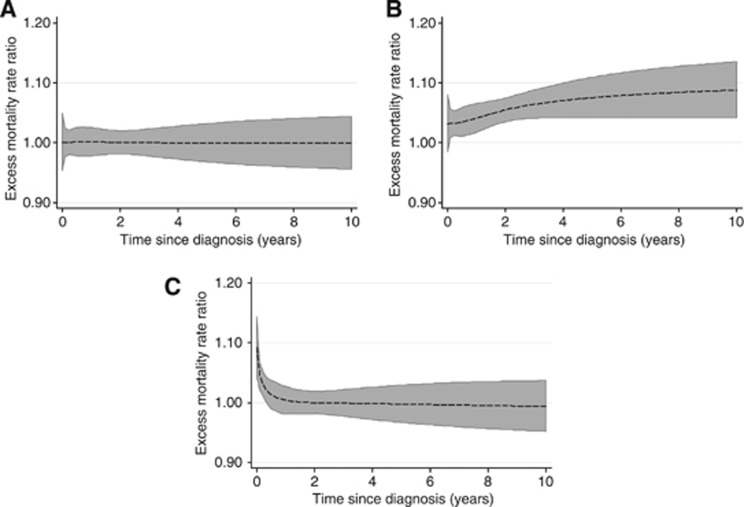
Figure 2A shows the excess mortality rate ratio for the medium survival scenario comparing the two populations if 10% of registrations are missed at diagnosis, and there is no facility of capturing those registrations at a later date (i.e., a 0% probability of making a diagnosis at a later available date and traceback being disallowed). The missingness was assigned at random in the population; this leads to the relative comparison between the two being unbiased (although there is a small increase in uncertainty). The likelihood of no information becoming available (later hospital visits, information on death certificates) is unlikely in a population-based registration setting. However, this highlights that provided the data is missing at random, little effect is had when comparing across populations in terms of the relative effects and the absolute estimates of relative survival. The incidence statistics will of course still be biased for the population with the 10% of patients missed at diagnosis.

Figure 2.

Combined figure for scenarios. The three subfigures relate to scenarios with 10% missing at diagnosis. The figures show the excess mortality rate ratio with associated 95% confidence interval comparing Population 2 (with the introduced errors) to Population 1. The plotted lines are an average over the 100 simulations. (A) The effect with no traceback from DC and no facility for delayed registration. (B) shows the effect with traceback from DC with no facility for delayed registration. (C) The effect where each patient that is missed initially has a delayed date of registration within a 2-year period.

The ‘No Traceback' row of Table 1 shows the estimated bias in 1 and 5-year relative survival for three values for the proportion of individuals who have a missed date of diagnosis (10%, 20% and 30%). The table also contains information on the three different true populations that have varying severity of disease (labelled low, medium and high relative survival). There is negligible bias introduced for the survival estimates even when the proportion of patients missed in Population 2 is increased to 30% (average percentage unit bias of −0.03, 0.02 and −0.02, respectively, for the three levels of survival; low, medium and high). If the patients are missing at random, then this has very little impact on the estimated survival estimates for the population with an introduced error structure. These results are in line with the excess mortality rate ratio represented in Figure 2A, which shows an excess mortality rate ratio comparison between the two populations over follow-up that differs little from 1.

Table 1. The average percentage unit bias in age-standardised relative survival for Population 2 is given for all scenarios at both 1 and 5 years.

		Low relative survivala			Medium relative survivalb			High relative survivalc
		Missing at diagnosis			Missing at diagnosis			Missing at diagnosis
Scenario	Years (RS)	10%	20%	30%	10%	20%	30%	10%	20%	30%
No traceback
	1	−0.033	−0.008	−0.030	0.013	0.001	0.015	−0.019	−0.006	−0.023
	5	−0.012	−0.025	−0.019	−0.006	−0.009	0.051	−0.018	−0.004	−0.041
Traceback
	1	−0.511	−0.981	−1.457	−1.022	−2.139	−3.365	−0.230	−0.491	−0.781
	5	−0.618	−1.255	−1.884	−1.642	−3.451	−5.332	−0.496	−1.018	−1.679
Delayed diagnosis
	1	−1.058	−1.923	−2.691	−1.058	−2.158	−3.311	−0.251	−0.509	−0.779
	5	−0.278	−0.593	−1.012	−0.476	−1.275	−2.364	−0.307	−0.673	−1.106

The values are given for the three scenarios, the three values for missing percentage at diagnosis, and for the three Weibull distribution values for varying the severity.

^aTrue values: 1 year=35.66, 5 year=10.39.

^bTrue values: 1 year=57.79, 5 year=30.52.

^cTrue values: 1 year=97.58, 5 year=94.99.

Missed individuals initially, no facility for later (delayed) diagnosis, traceback employed; (‘Traceback' –Error (1) and (2) combined)

Figure 2B highlights the impact of having a perfect traceback system from DCI cases in the case where 10% of initial diagnoses are missed. This can be compared with Figure 2A where traceback from death certificates was not employed. The fact that only cancer deaths are introduced when using the traceback from death certificates introduces a bias when comparing back to the complete population. It is only possible to begin the traceback procedure if cancer is mentioned on the death certificate. This is also likely to be associated with prognosis; with those who survive a shorter time more likely to have cancer mentioned on the death certificate. This is accounted for in the simulation because perfect cause of death information is simulated. However, in reality cause of death registration errors will occur and lead to further biases. In addition, the inability to perform the traceback procedure perfectly could also introduce further biases for the survival time estimates. However, the traceback system is of benefit for reducing the bias in the incidence statistics that are reported by cancer registries.

The ‘Traceback' row of Table 1 shows the estimates of the percentage difference in survival between the true age-standardised values and the average estimated values for the population that has a proportion of the patients missing (Pop 2). In these simulations a perfect traceback procedure has been employed for those patients that died of cancer. This ensures that those patients that are missed initially but then die of their cancer, have their correct date of diagnosis recorded, whereas those patients who do not die of cancer will still be missing from the register. This introduces a bias in the compared estimates across the two populations, which is in contrast to the results displayed in the ‘No Traceback' row of Table 1. For example, there is a downward bias for 5-year age-standardised relative survival of 1.6, 3.5 and 5.3 percentage units, respectively, for 10%, 20% and 30% of subjects initially missed for the medium survival scenario.

Missed individuals initially, facility for later (delayed) diagnosis for all missed patients; (‘Delayed diagnosis'—Error (1) and (3) combined)

Figure 2C shows the excess mortality rate ratio comparing the two populations if 10% of registrations are missed at diagnosis, and 100% of registrations are caught at a later date (the later date is uniformly spread across a 2-year period, or uniformly across the patient's follow-up time if they survive for <2 years). The early effect on the excess mortality rate ratio is greater because the delayed diagnosis only has an impact in the short-term. However, it is clear from Table 1 that the long-term effects are also seen for survival estimates because survival is a cumulative measure. Traceback from the death certificates does not have a role in this scenario because 100% of patients who are missed are caught at a later date in follow-up. Therefore, the impact on the excess mortality rate ratio and relative survival seen in Figure 2C and Table 1 is solely due to a delay in a proportion of cancer registrations up to a period of 2 years.

The ‘delayed diagnosis' row of Table 1 shows a comparison between the true value and the population when a proportion of the cancer registrations are delayed (10%, 20% and 30%) by up to 2 years. It is clear that this leads to bias in the estimates of relative survival. The bias is increased as the proportion of patients that are missed is increased. The table also shows the effect on three levels of cancer survival; which are labelled as low, medium and high. A bias of over 3 percentage units for 1-year relative survival for the medium survival scenario is seen when the proportion missing at diagnosis is 30%.

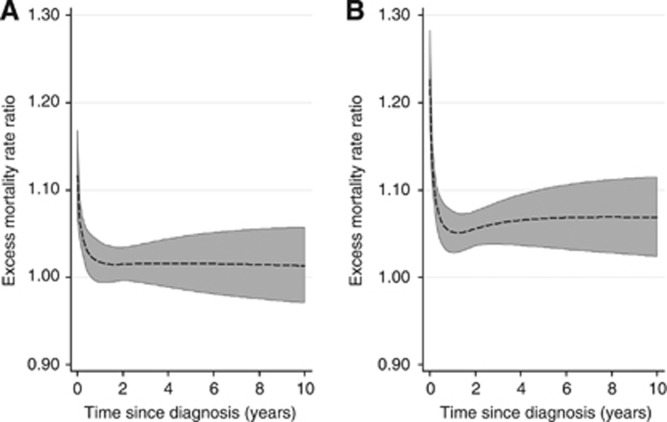
Combining errors; ‘Plausible' parameter values

Table 2 shows a comparison between the two populations when a combination of registration errors have been introduced. The results of the two plausible scenarios are given graphically as excess mortality rate ratios in Figure 3A and B. The values selected for the scenarios presented in Table 2 have been chosen to represent plausible levels of error in the cancer registration process. It is clear that the bias in the age-standardised relative survival is modest for the less extreme scenario (labelled (A)) but becomes more substantial for the second scenario (B).

Table 2. Estimated bias and age-standardised relative survival at 1 and 5 years for Population 2 for realistic parameter values.

		Low relative survival			Medium relative survival			High relative survival
Scenario	Years (RS)	Truth	Pop 2	Bias	Truth	Pop 2	Bias	Truth	Pop 2	Bias
(A) 15% Missing, 85% secondary diagnosis, 10% mis-specified if DCI (3-year uniform), traceback allowed
	1	35.66	34.31	−1.354	59.478	57.790	−1.688	97.928	97.582	−0.346
	5	10.34	9.911	−0.475	31.639	30.519	−1.119	95.427	94.991	−0.436
(B) 30% Missing, 90% secondary diagnosis, 5% mis-specified if DCI (2-year uniform), traceback allowed
	1	35.66	33.07	−2.591	59.478	56.047	−3.431	97.928	97.168	−0.760
	5	10.34	9.27	−1.112	31.639	28.966	−2.673	95.427	94.369	−1.057

Bias as given as the difference in percentage units between the simulated truth and the population. The errors in cancer registration have been introduced in Population 2.

Figure 3.

Excess mortality rate ratios comparing Population 2 to Population 1. (A) 15% missed initial diagnosis, 85% delayed registration (of those initially missed), 10% mis-specified diagnosis date when DCI (bias uniform over 2 years). Traceback from DC allowed. (B) 30% missed initial diagnosis, 90% delayed registration (of those initially missed), 5% mis-specified diagnosis date when DCI (bias uniform over 2 years). Traceback from DC allowed.

Other methods to show differences

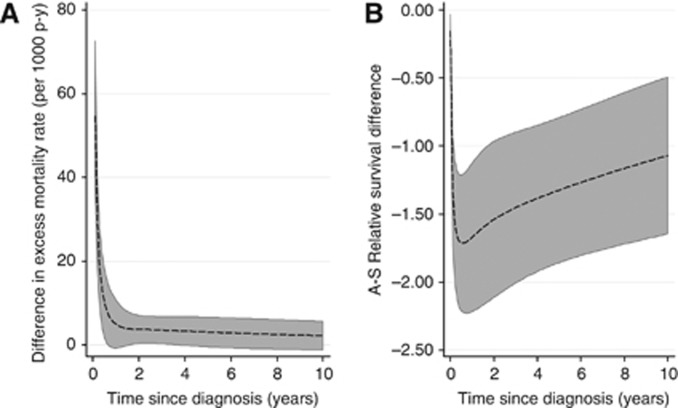
Figure 4A shows the difference in excess mortality between the two populations per 1000 person-years for the first plausible scenario (A). Plotting the results as a difference in excess mortality rates gives a measure of absolute risk, compared with the relative risk estimates given in Figure 3A. The difference in the excess mortality rate is much higher early in follow-up under this scenario.

Figure 4.

Graph highlighting different measures to show differences for the scenario with 15% missed initial diagnosis, 85% delayed registration (of those initially missed), 10% mis-specified diagnosis date when DCI (bias uniform over 2 years) with traceback from DC allowed. (A) The excess mortality rate difference between Population 2 and Population 1 per 1000 person-years. (B) The percentage point difference in age-standardised relative survival between Population 2 and Population 1. Note that the scales and units of the two subfigures are different.

Figure 4B shows the difference in age-standardised relative survival between the two populations as a function of time for the same plausible scenario (A). The data given in Table 2 for the difference in 1-, and 5-year relative survival is a subset of the information contained in this figure. Most of the change in the age-standardised relative survival between Population 2 and Population 1 occurs early on follow-up.

Discussion

Although there have been various publications looking at errors in the cancer registration process, few of the publications have looked at the consequent impact on the reported survival estimates (Robinson et al, 2007, Møller et al, 2011). Through the use of simulation techniques, it has been possible to assess this impact by using realistic parameter values. Using this methodology, it is also possible to assess the level of errors that are required in order to produce a set level of observed difference between two populations in terms of commonly used metrics in population-based cancer research.

The key feature of the simulation is providing realistic inputs for the parameter values. Realistic estimates can be approximated by using cancer registry data and expert input. However, it is also of interest to try the extremes of the range of possible values in order to answer the question ‘What is the maximum impact that data registration errors can have?' on any given output.

International comparisons of cancer survival statistics are becoming increasingly common (Sant et al, 2009, Møller et al, 2010, Coleman et al, 2011). As has been highlighted in a recent publication, the cancer registration errors necessary to explain differences that are seen between the ‘best' European countries and the UK would need to be of an unrealistic magnitude (Woods et al, 2011). The simulation carried out by (Woods et al, 2011) made modifications to pre-existing data to illustrate the point. Here, we have concentrated on entirely simulated data; this results in having a direct comparison with a truth in order to assess levels of bias that are introduced. However, the conclusions from the two approaches were likely to be similar and this proved to be the case.

A modification on the method that has been outlined here would be to alter both of the compared populations in order to account for different levels of error between two comparison populations. This would allow a direct estimate of the differences that can occur between two populations purely due to differences in cancer registration processes. Both of the compared populations are drawn from the same overall population; therefore, any observed differences (beyond random variation) are purely due to the introduction of error into the cancer registration process.

The concept of the ‘date of diagnosis' is a key element in cancer registration and public health monitoring of cancer occurrence and survival. The date of diagnosis establishes the calendar period for incidence reporting, and provides the starting point for population-based survival analysis. There is no clear analogue in clinical medicine where occurrence of disease is usually replaced by provision of service, and where survival analyses typically start at the time of an intervention rather than at disease occurrence. A clear definition of date of diagnosis is required in order to give meaning to the idea of a ‘later than true' diagnosis date. The definition that we have used given in Box 1 allows the distinction between the date of diagnosis that would be used as standard by the cancer registry at the earliest possible occurrence of the cancer compared with a date that is later than that specified in this definition.

In this analysis, we concentrate on the effect of registration errors on cancer patient survival. Registration errors also have an impact on other measures that are reported using registry data, such as incidence and prevalence estimates. Although the impact on survival estimates is shown to be modest in this analysis, it is also important to consider that any ‘missed' case will have an impact on the incidence and prevalence estimates reported by the registry.

In summary, cancer registration errors can have an impact on the survival statistics that are reported by cancer registries. Therefore, it is important to make considered judgements when evaluating the results of international comparisons. However, for UK data and countries with established cancer registration systems it is unlikely that registration errors will have a major impact on survival statistics. The results of the simulation indicate that modest errors in registration do not lead to large survival differences.

Appendix

In order to simulate relative survival, each individual was simulated a time to death due to cancer, and a time to death due to other causes; the minimum value from these two was then taken as the value for the time to death for that individual. The simulation of the all-cause survival time estimates is similar to previously published work (Rutherford et al, 2012). The data simulation was carried out as follows:

• Times of death due to cancer were generated from a Weibull distribution according to the method set out by Bender et al (2005). Different shapes for survival curves were generated by altering the parameter values of the Weibull distribution, referred to as the scale and shape parameters, commonly denoted λ and γ, respectively. A value of 0.5 was used for γ, and λ was varied over 1, 0.5 and 0.02 for each scenario.

• Time to death due to other causes was calculated by using a population mortality file and using an exponential distribution for each attained age during follow-up.

• Overall time to death was calculated by taking the minimum of the cancer-specific time to death, and the expected (background) time to death.

• An age distribution was simulated from a normal distribution with a given mean (60), and s.d. (13).

• The effect of age was simulated by using preselected excess hazard ratios (0.8, 0.9, 1, 1.2, 1.4) for the defined age groups (<45, 45–54, 55–64, 65–74, >74) with the central age group as the reference.

The simulation approach outlined above was used for each of the two populations. One of the populations was then modified in line with the error process introduced for each scenario. The simulation was repeated 100 times for each scenario, with a sample size of 25 000 over a 5-year diagnosis window.