Abstract
Purpose
Blood flow is an important factor in bone production and repair, but its role in osteogenesis induced by mechanical loading is unknown. Here, we present techniques for evaluating blood flow and fluoride metabolism in a pre-clinical stress fracture model of osteogenesis in rats.
Procedures
Bone formation was induced by forelimb compression in adult rats. 15O water and 18F fluoride PET imaging were used to evaluate blood flow and fluoride kinetics 7 days after loading. 15O water was modeled using a one-compartment, two-parameter model, while a two-compartment, three-parameter model was used to model 18F fluoride. Input functions were created from the heart, and a stochastic search algorithm was implemented to provide initial parameter values in conjunction with a Levenberg–Marquardt optimization algorithm.
Results
Loaded limbs are shown to have a 26% increase in blood flow rate, 113% increase in fluoride flow rate, 133% increase in fluoride flux, and 13% increase in fluoride incorporation into bone as compared to non-loaded limbs (p < 0.05 for all results).
Conclusions
The results shown here are consistent with previous studies, confirming this technique is suitable for evaluating the vascular response and mineral kinetics of osteogenic mechanical loading.
Keywords: 18F fluoride, 15O water, bone blood flow, mechanical loading
Introduction
Adequate vascular perfusion is critical for the viability of any biological system. Bone is typically highly vascularized; when blood flow is disrupted, necrosis and hypoxia may occur [1]. As a result, the integrity of the skeletal vasculature system is an important clinical consideration in scenarios such as severe trauma and non-union fractures. Maintaining adequate perfusion is essential for the successful repair of large bony defects using bone grafts [2, 3]. In addition, bone blood flow has been implicated as a crucial factor during both skeletal development [4] and repair [1].
Fatigue loading of bone can produce a stress fracture and stimulate new bone formation. Skeletal blood flow is likely crucial for this process because bone formed after this type of mechanical loading is produced by mechanisms similar to fracture repair [5]. While different bone formation responses have been generated through a variety of mechanical loading configurations [6, 7], the resulting perturbation in blood flow rate as a result of any type of osteogenic mechanical loading has not been reported. Although angiographic imaging techniques have historically been used to measure blood flow, quantifying blood flow in and around bone with X-ray-based techniques can be difficult due to the high density of bone [8]. The heterogeneity of the vascular network in bone compounds this issue [9]. Thus, other in vivo methods for measuring skeletal blood flow are needed to examine the response to osteogenic mechanical loading.
Positron emission tomography (PET) is an established in vivo, dynamic imaging technique suitable for evaluating rates of flow and metabolism. Commonly used for both clinical and research applications, its specificity is determined by the radiopharmaceutical used for the scan. 15O water PET has been used previously to evaluate blood flow in many tissues, including pancreas [10], lung [11], heart [12], and brain [13], since it freely diffuses throughout the body. In addition, 18F fluoride PET has been used to evaluate skeletal kinetics and diagnose skeletal diseases [14, 15]. 18F fluoride is preferentially incorporated into bone by replacing a hydroxyl group in bone hydroxyapatite to form fluoroapatite [16]. Although not suitable for directly measuring blood flow rates, 18F fluoride has been used to find the overall bone metabolic activity [17]. In previous studies, we have used 18F fluoride PET to analyze the skeletal response after damaging fatigue loading [18]. In the tradition of standard bone scintigraphy, only standard uptake values from 2D regions of interest were considered, and the study did not attempt to quantify blood flow rates. Importantly, uptake of 18F fluoride in loaded bones was significantly different from control seven days after loading. Here, we extend the PET analysis of the skeletal response using the same loading model at the seven day time point.
The objective of this work is to develop a dynamic in vivo technique suitable for analyzing vascular and bony outcomes following osteogenic mechanical loading. This technique will facilitate studies examining the connection between bone formation and vascularity. By performing serial imaging with 15O water and 18F fluoride PET, both blood flow rate and skeletal kinetics can be determined simultaneously [19]. In this paper, we evaluate blood flow and skeletal kinetics in a pre-clinical stress fracture model of osteogenesis in rats using PET.
Materials and Methods
Experimental Design
Eight male Fischer F344 rats (Harlan, Indianapolis IN) were obtained at 13–14 weeks of age and housed under standard conditions until age 20 weeks (± 2 weeks). The right forelimb of each animal was mechanically loaded using established methods [20]. Briefly, rats were anesthetized using isoflurane gas (1–3%) and weighed (359 ± 40 g). The forelimb was axially compressed by placing the olecranon process and the flexed carpus into specially designed fixtures. A material testing system (Instron Electropuls 1000) was used to apply force and monitor displacement. First, a 0.3 N compressive pre-load was applied. Next, a cyclic haversine waveform of 18 N at 2 Hz was applied to the forelimb until 65% of the displacement to fracture was achieved (1.3 mm, relative to the 10th cycle). The left forelimb did not receive any mechanical loading, and was used as an internal control. Following the procedure, rats were given an intramuscular injection of analgesic (0.05 mg/kg Buprenex) and allowed unrestricted cage activity with ad libitum access to water and food.
Seven days after loading, whole-body PET scans were completed using a combined PET/CT microPET®-Inveon™ system (Concorde Microsystems Inc., Knoxville TN). 15O water (30 – 55 MBq) was administered by tail vein injection in a short bolus, immediately followed by a 10 minute scan (1x3s, 6x2s, 5×5s, 11×10s, 5×30s, 5×60s). Next, 18F fluoride (9 – 15 MBq) was administered in the same manner, followed by a 60 minute scan (1×3s, 6×2s, 9×5s, 6×10s, 4×30s, 2×60s, 2×120s, 10×300s). Images were reconstructed using filtered back projection with CT-based attenuation correction. All protocols were approved by our institution’s Animal Studies Committee. Statistical significance was considered using two-tailed Student’s t-test of unequal variance, where p < 0.05 was considered to be significant.
Regions of Interest
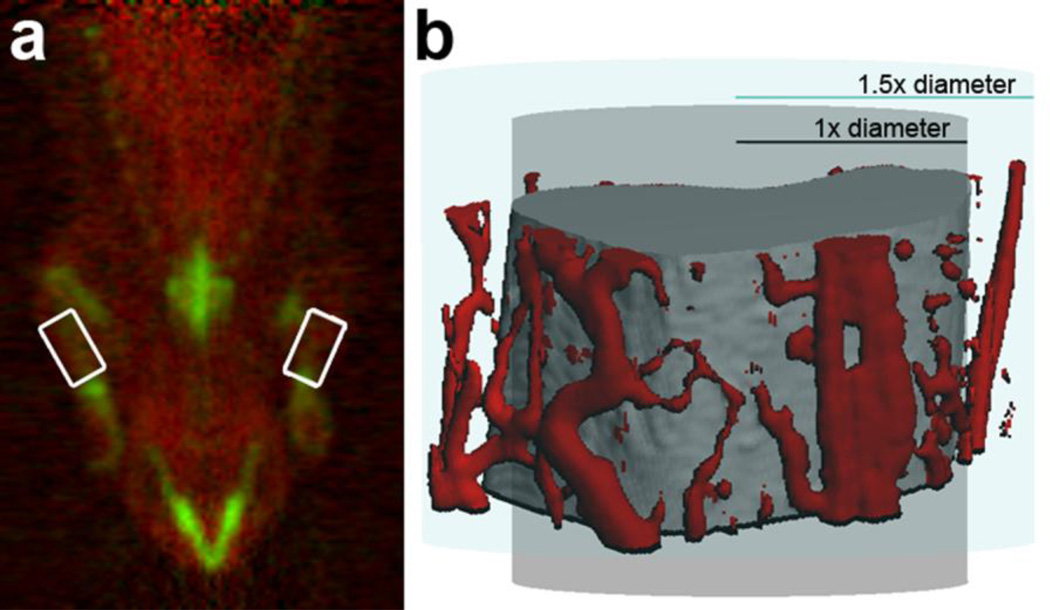
Since 15O water PET images have no significant anatomical landmarks, the 18F fluoride scan was used to draw ROI for each scan (Fig. 1a). All frames of the 18F fluoride scan were summed to form a single image. Using the summed image, cylindrical 3D ROI were created with 1.5 times the diameter of the bone and 1/3 the length of the bone. These ROI are intentionally larger than the visible bone, because vessels may be found in the periosteal region that is dramatically expanded after mechanical loading [21], as illustrated in Fig. 1b. ROI were overlaid onto 18F fluoride and 15O water dynamic sequences to create time-activity curves for each forelimb.
FIGURE 1.
a) The 15O water PET scan (red) has been superimposed on the 18F fluoride scan (green). The areas where ROIs were drawn are highlighted with white boxes. b) Using CT angiography, vessels surrounding the bone in the region of interest have been colored red. Since an ROI of the diameter of the ulna may fail to include some vessels, an ROI 1.5 times the diameter of the ulna was used for this experiment.
Input Function Generation
To visualize the heart clearly, the first 30 seconds of the 18F fluoride scan was summed into a single image. Using this image, a small cylindrical ROI (r=0.5 mm, l=1 mm) was drawn on the left ventricle. This ROI was transferred onto the 15O water and 18F fluoride scans, and input functions were obtained from the time-activity curve of the heart. To account for dispersion of the injected bolus that occurs between the heart and arrival at the forelimb, the time-activity curve was convolved with a Gaussian function as:
| (1) |
where C0(t) is the time activity curve measured at the heart. In preliminary analysis, σ was treated as a fit parameter, and a value of approximately 0.5 s minimized the residual for all samples. As a result, σ was set to be 0.5 s in all subsequent kinetic analyses.
15O Water Kinetics
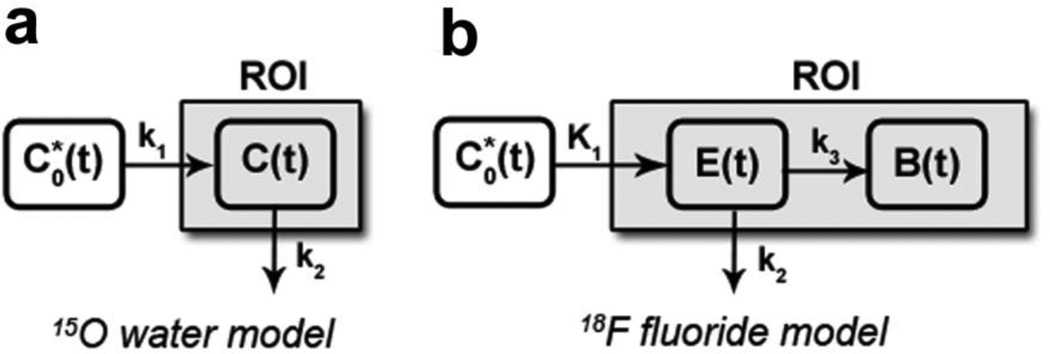
After injection into the tail vein, 15O water travels freely throughout the vasculature, so its kinetics provides an in vivo estimate of blood flow. The kinetics of 15O water was modeled with a one-compartment (bone), two-parameter (uptake and clearance) model, similar to Kety [22] and others [10–13] (Fig. 2a). An additional parameter was included to account for fractional blood volume (V). The rate of change of concentration in the compartment is:
| (2) |
The solution can be found by Laplace transform as:
| (3) |
where C(t) denotes the concentration of 15O water in the region of interest (ROI). Note that the measured input function at the limb is the convolution of 0C (t) with a Gaussian kernel as described in Input Function Generation (Equation 1). The solution for the entire region of interest is therefore:
| (4) |
FIGURE 2.
a) 15O water model: is the input function (blood), k1 is the uptake (flow in), k2 is the clearance (flow out), and C(t) represents the concentration of 15O water in the compartment. b) 18F fluoride model: is the input function (blood), K1 is the uptake into the extravascular space, k2 is the clearance from the extravascular space, k3 is the uptake into the bound compartment, and E(t) and B(t) are the concentration of 18F fluoride in the extravascular and bound compartments, respectively. In both figures, the shaded compartment (ROI) represents the scope of the measured region of interest.
18F Fluoride Kinetics
18F fluoride is preferentially incorporated into the hydroxyapatite-like mineral of bone. After escaping the vasculature, fluoride binds to bone mineral in a concentration dependent fashion. Multiple model configurations were considered to characterize the kinetics of 18F fluoride. First, a two-compartment, four-parameter model was constructed. In preliminary testing, the flow rate of fluoride from the bound compartment to the extravascular compartment was near zero. Subsequently, similar to Hawkins et al. [23], the fourth parameter was eliminated, and a two-compartment (extravascular and bound), three-parameter model (Fig. 2b) was used to model the kinetics of 18F fluoride near the site of bone formation. An additional parameter was included to account for fractional blood volume (V). The rate of change of concentration in the two compartments is:
| (5) |
| (6) |
where denotes the input function at the limb per Equation 1, E(t) denotes the concentration in the extravascular compartment, and B(t) denotes the concentration in the bound compartment. The solution to this system of equations can be found by Laplace transform as:
| (7) |
| (8) |
The solution for the entire region of interest is therefore:
| (9) |
The total flux of fluoride into the bone, Ki, is given directly from the model as:
| (10) |
Data Optimization
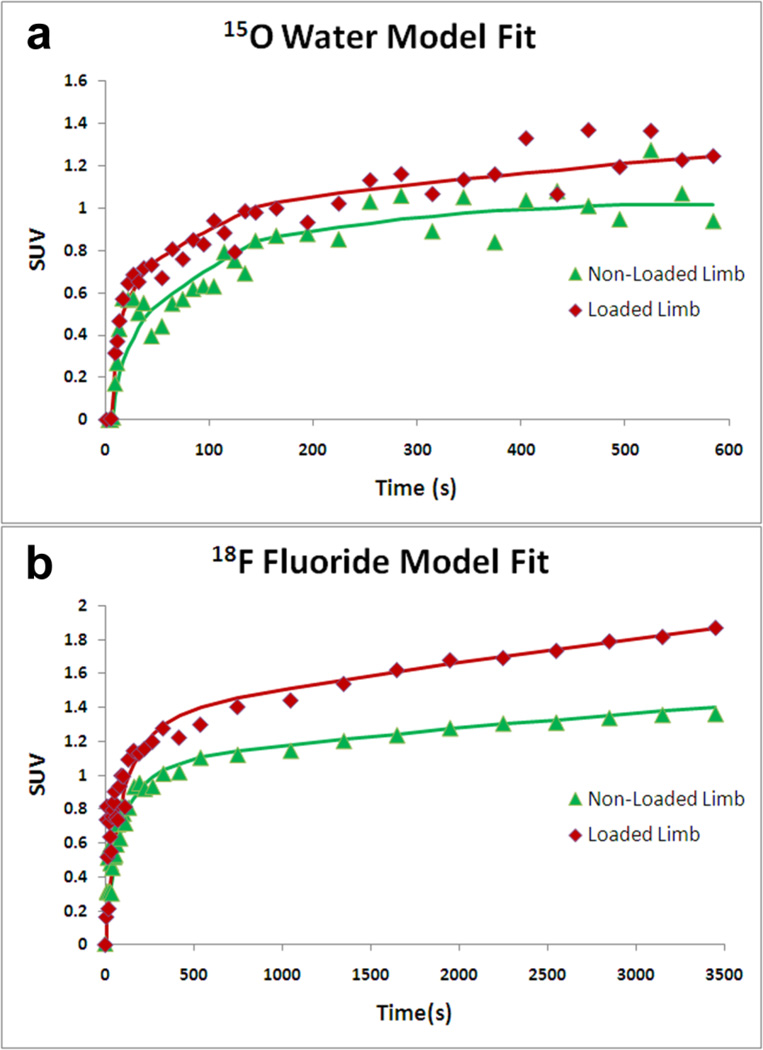
Equations 4 and 9 were fit to the experimental data, denoted as ROI (t) , using a non-linear least squares method utilizing the Levenberg-Marquardt algorithm (MATLAB, Natick MA). Parameter limits were determined after extensive test model fitting. For 15O water PET, the parameter limits were [0, 1] for both k1 and k2. For 18F fluoride PET, the limits were [0, 0.5], [7, 9], and [0.5, 1] for K1, k2, and k3 respectively. For all scans, the parameter V was fit on the interval [0,1]. To obtain the best fit to the data, initial conditions for the fitted parameters were randomly generated between the minimum and maximum limit for that parameter. After optimizing 100 fits from random initial conditions, the five fits with the lowest residuals were averaged to obtain the final parameters. These five fits were generally within 1% of each other, and often identical. Fig. 3 illustrates the resulting model fits for both 15O water and 18F fluoride.
FIGURE 3.
Example model fits to the experimental data for A) 15O Water and B) 18F Fluoride. In general, non-loaded limbs (triangles) exhibited less overall uptake than loaded limbs (diamonds).
Static Analysis
A static analysis approach was also investigated. Although dynamic analysis is appropriate for determining blood flow rate and skeletal kinetics, static analysis may provide a simplified means to assess changes in uptake. Additionally, the analysis is less computationally and labor intensive. To form a static image, 3D ROI were drawn centered on the ulna with 1.5 times the diameter of the bone and 1/3 the length of the bone. The first 60 minutes of mean activity within the ROI was summed for 18F fluoride, while the first 2 minutes of mean activity within the ROI was summed for 15O water. The resulting values were corrected for the injected activity and the animal weight.
CT Imaging
CT imaging was performed concurrently with PET imaging. The thickness of the ulna was determined at the top, bottom, and middle of the ROI using commercial software (Inveon Research Workplace 3.0, Siemens Medical Solutions, USA). These measurements were used to assess the need for partial volume correction, as well as any differences between loaded and non-loaded limbs.
Results
15O Water Kinetics
The results from the fit to the 15O water compartment model are given in Table 1. Of the three fit parameters (k1, k2, and V), only the blood flow rate (k1) was significantly different between the loaded and non-loaded limbs (p=0.02). On average, the loaded limbs exhibited a 26% increase in blood flow rate versus the non-loaded limbs.
TABLE 1.
Parameters from 15O water compartment model, given as mean ± standard deviation.
|
15O Water Compartment Model | |||
|---|---|---|---|
| Limb | k1 (mL g−1 s−1) | k2 (s−1) | V |
| Loaded | 0.0038 ± 0.0007 * | 0.97 ± 0.03 | 0.0001 ± 0.0001 |
| Non-Loaded | 0.0031 ± 0.0006 | 0.95 ± 0.04 | 0.0001 ± 0.0003 |
indicates a significant difference (p < 0.05) between loaded and non-loaded limbs.
18F Fluoride Kinetics
The results from the fit to the 18F fluoride compartment model are given in Table 2. Of the five parameters fit or computed (K1, k2, k3, V, Ki), the loaded limbs were significantly different in K1, k3, and Ki from the non-loaded limbs (p<0.05). On average, loaded limbs exhibited a 113% increase in fluoride flow rate, a 13% increase in fluoride incorporation, and 133% increase in total fluoride flux versus non-loaded limbs.
TABLE 2.
Parameters from 18F fluoride compartment model, given as mean ± standard deviation.
|
18F Fluoride Compartment Model | |||||
|---|---|---|---|---|---|
| Limb | K1 (mL g−1 s−1) | k2 (s−1) | k3 (s−1) | Ki (mL g−1 s−1) | V |
| Loaded | 0.17 ± 0.08 * | 7.79 ± 0.61 | 0.68 ± 0.07 * | 0.014 ± 0.008 * | 0.18 ± 0.25 |
| Non-Loaded | 0.08 ± 0.03 | 7.62 ± 0.81 | 0.60 ± 0.04 | 0.006 ± 0.003 | 0.11 ± 0.01 |
indicates a significant difference (p < 0.05) between loaded and non-loaded limbs.
Static Analysis
The static analysis is an overall analysis of uptake in the region of interest. As such, similar trends were observed – loaded limbs had a 47% increase over non-loaded limbs in 15O water, while loaded limbs experienced a 63% increase over non-loaded limbs in 18F fluoride (Table 3). The comparisons between loaded and non-loaded limbs were significant (p < 0.05) for both radioisotopes.
TABLE 3.
Results from static analysis on 15O water and 18F fluoride given in arbitrary units as mean ± standard deviation.
| Static Analysis | ||
|---|---|---|
| Limb | 15O Water | 18F Fluoride |
| Loaded | 9.86 ± 2.14 * | 41.87 ± 4.23 * |
| Non-Loaded | 6.87 ± 1.73 | 26.26 ± 3.52 |
indicates a significant difference (p < 0.05) between loaded and non-loaded limbs.
CT Imaging
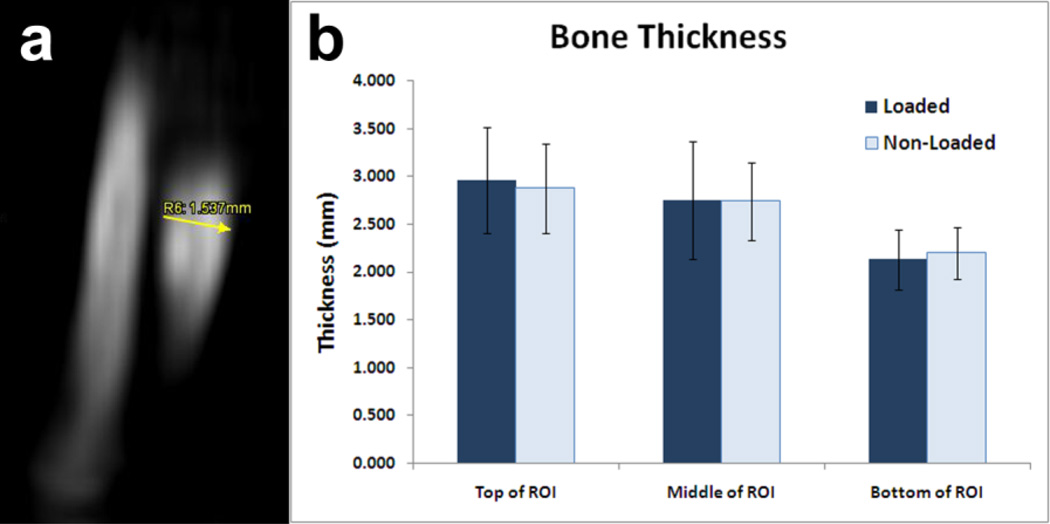
Fig. 4 shows the results from the CT imaging. Although the thickness of the ulna changes throughout the length of the limb, there were no significant differences between loaded and non-loaded limbs at each site. As a result, we concluded that any partial volume effects were comparable between loaded and non-loaded limbs; therefore, no correction was necessary.
FIGURE 4.
a) Example of a 2D measurement of bone thickness by CT b) Bone thickness measured for loaded and non-loaded limbs at top, middle, and bottom of the ROI. Plotted as mean ± standard deviation. No significant differences were found between loaded and non-loaded limbs. References
Discussion
Here, we developed PET imaging techniques for evaluating blood flow and skeletal kinetics after osteogenic mechanical loading. Using a cohort of eight rats, we have implemented compartment models and demonstrated the ability to detect increases in blood flow rate (k1), fluoride flow rate (K1), fluoride flux (Ki), and fluoride incorporation into the bone (k3). A static analysis approach was also investigated, and significant differences between loaded and non-loaded limbs were demonstrated for both 18F fluoride and 15O water. We did not observe significant differences in bone dimensions between the loaded and non-loaded limbs suggesting that, while partial volume effects may affect quantitative measures, these effects are similarly applied to both the loaded and non-loaded limbs.
Comparisons to Previous Studies
Because blood flow rate is widely disparate in and around the bone, it is difficult to directly compare our study to other studies with similar scope. However, the blood flow rates reported here from 15O water PET for non-loaded limbs (0.0031 mL g−1 s−1) are in the normal range for bone blood flow [9, 24], while the loaded limbs (0.0038 mL g−1 s−1) are above this range, as expected.
In 2004, Brenner et al. evaluated the relationship between 18F fluoride compartment model analysis, Patlak graphical analysis, and SUV (static) analysis [25]. Their results indicate that outcomes from Patlak analysis and SUV were highly correlated with measures derived through compartment modeling. Here, we report similar findings – the results from our compartment model analysis display similar trends as our static analysis for both 15O water and 18F fluoride. Our results also compare favorably with previously published standard uptake values of 18F fluoride PET scans after fatigue loading, as we noted substantial (>60%) and significant (p<0.05) increases in loaded limbs versus non-loaded limbs [18].
In the present study, the fluoride uptake parameter (K1) was well correlated with the overall flux of fluoride into the bone (Ki) but not the blood flow rate (k1). Since fluoride uptake is influenced by both blood flow and available bone surface [26, 27], this result suggests that K1 was dominated by the surface area of bone rather than blood flow. This correlation may be expected, as the bone surface was greatly increased within the region of interest due to the initiation and propagation of a stress fracture in the bone during mechanical loading [27].
Although some groups have shown linear correlations (r2 ranging from 0.52 to 0.93) between Ki and the blood flow rate in humans and pigs [15, 19], this trend was not evidenced in this experiment. This discrepancy may be due to differences in tissue kinetics – the cited experiments were carried out in high-uptake areas (spine, hip) while a relatively low-uptake area was considered here (distal forelimb). Interestingly, our modeling results did not indicate any changes in clearance parameters (k2) in either 15O water or 18F fluoride PET analysis. In addition, we observed high clearance values for 18F fluoride kinetics. It is not clear if these are aberrant or typical; to our knowledge, results of 18F fluoride PET modeling in rodents have not been previously published. These observations require further investigation, but may suggest vascular remodeling is affecting clearance mechanisms.
We reported a fractional blood volume (V) for both 15O water and 18F fluoride, although the values were relatively dissimilar. In practice, the fractional blood volume parameter accounts for discrepancies between tissue and blood kinetics; the absolute value depends on the kinetic model as well as the magnitude of the input function. It is not a physical parameter, as other factors may be inadvertently included. For 15O water, the kinetic model fit closely matched the observed data, so V was negligible. This parameter could be effectively eliminated from the model, as has been published in the past [11], but was included to reduce fit residuals.
Confirmation from Other in vivo Measurements
The results from this study correlate well with previous findings considering angiogenic outcomes after osteogenic mechanical loading. Matsuzaki et al. [21] examined periosteal vascularity on histological sections after osteogenic mechanical loading at four different fatigue displacement levels. The results from the same displacement level used in our study (65% fatigue displacement) indicated a 275% increase in vessel number, a 72% increase in average vessel area, and a 510% increase in total vessel area when comparing loaded limbs to non-loaded limbs 7 days after mechanical loading. Similarly, Wohl et al. [5] examined osteogenic and angiogenic gene regulation after osteogenic mechanical loading. Considering the 65% fatigue displacement group, angiogenic markers (VEGF, PECAM-1) were upregulated (2.7 and 3.5 fold). Additionally, osteoblast transcriptional regulators (Msx2, Runx2, and Osx) were increased (2.5, 5.9, and 11.4 fold). Finally, they noted that bone markers (BMP2 and BSP) were also increased (4.8 and 23.2 fold). All of these results were significant (p < 0.05) when comparing loaded limbs to non-loaded limbs. Therefore, although these measurements cannot be directly compared to our study, the increased periosteal vascularity and increased gene expression profiles noted after osteogenic mechanical loading are consistent with results presented here.
Future Applications
Our results both reinforce and clarify the relationship between bone formation and vascularity after mechanical osteogenic loading. In previous studies, we have shown that osteogenic mechanical loading produces robust woven bone [28] and increased fluoride uptake [18]. Here, we have demonstrated increases in skeletal blood flow accompany increases in fluoride metabolism, indicating that angiogenesis is concurrent with osteogenesis after mechanical loading. We plan to use this method to determine the time course of angiogenesis after mechanical loading.
Since our method provides data on skeletal blood flow as well as the kinetics of mineral metabolism, it may prove useful for exploring the nuances between other osteogenic stimuli. Although we used rats for this study, these techniques will scale for both larger and smaller animal models, as the specificity of 15O water and 18F fluoride is not species dependent. Since the current generation of PET imaging scanners has spatial resolutions on the order of 2 mm, depending on the radioisotope and in-plane placement of animals, resolution may be a concern for smaller animals. Notwithstanding, 18F fluoride and 2-deoxy-2-[18F]fluoro-D-glucose PET imaging have been performed in mice to assess fracture healing [17] and bone metastasis [29], suggesting that the scaling of this technique to mice is feasible, but may require correction for partial volume effects.
Conclusion
We have evaluated blood flow and skeletal kinetics in the rat forelimb after osteogenic mechanical loading using PET imaging. Our results indicated significant increases in blood flow and fluoride flow rates, in addition to increased fluoride incorporation into the bone, following mechanical loading. This work is validated by previous studies considering quantification of periosteal vascularity, gene expression, and PET standard uptake. In the future, we plan to use the techniques presented here to explore differences in blood flow and fluoride kinetics using a variety of osteogenic mechanical loading methods.
Acknowledgements
Funded by a grant from the National Institutes of Health (AR050211). The authors would like to acknowledge Nikki Fettig, Lori Strong, Dr. Richard Laforest, and JR Rutlin for their assistance in PET scanning.
Footnotes
Conflict of Interest
The authors declare that they have no conflict of interest.
References
- 1.Glowacki J. Angiogenesis in fracture repair. Clin Orthop Relat Res. 1998 Oct;(355S):S82–S89. doi: 10.1097/00003086-199810001-00010. [DOI] [PubMed] [Google Scholar]
- 2.Pliefke J, Rademacher G, Zach A, et al. Postoperative monitoring of free vascularized bone grafts in reconstruction of bone defects. Microsurgery. 2009;29(5):401–407. doi: 10.1002/micr.20662. [DOI] [PubMed] [Google Scholar]
- 3.Banic A, Hertel R. Double vascularized fibulas for reconstruction of large tibial defects. J Reconstr Microsurg. 1993;9(6):421–428. doi: 10.1055/s-2007-1006751. [DOI] [PubMed] [Google Scholar]
- 4.Pechak DG, Kujawa MJ, Caplan AI. Morphological and histochemical events during first bone formation in embryonic chick limbs. Bone. 1986;7(6):441–458. doi: 10.1016/8756-3282(86)90004-9. [DOI] [PubMed] [Google Scholar]
- 5.Wohl GR, Towler DA, Silva MJ. Stress fracture healing: fatigue loading of the rat ulna induces upregulation in expression of osteogenic and angiogenic genes that mimic the intramembranous portion of fracture repair. Bone. 2009;44(2):320–330. doi: 10.1016/j.bone.2008.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hsieh YF, Silva MJ. In vivo fatigue loading of the rat ulna induces both bone formation and resorption and leads to time-related changes in bone mechanical properties and density. J Orthop Res. 2002;20(4):764–771. doi: 10.1016/S0736-0266(01)00161-9. [DOI] [PubMed] [Google Scholar]
- 7.De Souza RL, Matsuura M, Eckstein F, et al. Non-invasive axial loading of mouse tibiae increases cortical bone formation and modifies trabecular organization: a new model to study cortical and cancellous compartments in a single loaded element. Bone. 2005;37(6):810–818. doi: 10.1016/j.bone.2005.07.022. [DOI] [PubMed] [Google Scholar]
- 8.Dyke JP, Aaron RK. Noninvasive methods of measuring bone blood perfusion. Ann N Y Acad Sci. 2010;1192:95–102. doi: 10.1111/j.1749-6632.2009.05376.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McCarthy I. The physiology of bone blood flow: a review. J Bone Joint Surg Am. 2006;88(S3):4–9. doi: 10.2106/JBJS.F.00890. [DOI] [PubMed] [Google Scholar]
- 10.Kubo S, Yamamoto K, Magata Y, et al. Assessment of pancreatic blood flow with positron emission tomography and oxygen-15 water. Ann Nucl Med. 1991;5(4):133–138. doi: 10.1007/BF03164627. [DOI] [PubMed] [Google Scholar]
- 11.de Langen AJ, Lubberink M, Boellaard R, et al. Reproducibility of tumor perfusion measurements using 15O-labeled water and PET. J Nucl Med. 2008;49(11):1763–1768. doi: 10.2967/jnumed.108.053454. [DOI] [PubMed] [Google Scholar]
- 12.Rimoldi O, Schafers KP, Boellaard R, et al. Quantification of subendocardial and subepicardial blood flow using 15O-labeled water and PET: experimental validation. J Nucl Med. 2006;47(1):163–172. [PubMed] [Google Scholar]
- 13.Raichle ME, Martin WR, Herscovitch P, Mintun MA, Markham J. Brain blood flow measured with intravenous H2(15)O. II. Implementation and validation. J Nucl Med. 1983;24(9):790–798. [PubMed] [Google Scholar]
- 14.Doot RK, Muzi M, Peterson LM, et al. Kinetic analysis of 18F-fluoride PET images of breast cancer bone metastases. J Nucl Med. 2010;51(4):521–527. doi: 10.2967/jnumed.109.070052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Temmerman OP, Raijmakers PG, Heyligers IC, et al. Bone metabolism after total hip revision surgery with impacted grafting: evaluation using H2 15O and [18F]fluoride PET; a pilot study. Mol Imaging Biol. 2008;10(5):288–293. doi: 10.1007/s11307-008-0153-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grynpas MD. Fluoride effects on bone crystals. J Bone Miner Res. 1990;5(S1):S169–S175. doi: 10.1002/jbmr.5650051362. [DOI] [PubMed] [Google Scholar]
- 17.Hsu WK, Feeley BT, Krenek L, et al. The use of 18F-fluoride and 18F-FDG PET scans to assess fracture healing in a rat femur model. Eur J Nucl Med Mol Imaging. 2007;34(8):1291–1301. doi: 10.1007/s00259-006-0280-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Silva MJ, Uthgenannt BA, Rutlin JR, et al. In vivo skeletal imaging of 18F-fluoride with positron emission tomography reveals damage- and time-dependent responses to fatigue loading in the rat ulna. Bone. 2006;39(2):229–236. doi: 10.1016/j.bone.2006.01.149. [DOI] [PubMed] [Google Scholar]
- 19.Piert M, Machulla HJ, Jahn M, et al. Coupling of porcine bone blood flow and metabolism in high-turnover bone disease measured by [(15)O]H(2)O and [(18)F]fluoride ion positron emission tomography. Eur J Nucl Med Mol Imaging. 2002;29(7):907–914. doi: 10.1007/s00259-002-0797-2. [DOI] [PubMed] [Google Scholar]
- 20.Torrance AG, Mosley JR, Suswillo RF, Lanyon LE. Noninvasive loading of the rat ulna in vivo induces a strain-related modeling response uncomplicated by trauma or periostal pressure. Calcif Tissue Int. 1994;54(3):241–247. doi: 10.1007/BF00301686. [DOI] [PubMed] [Google Scholar]
- 21.Matsuzaki H, Wohl GR, Novack DV, Lynch JA, Silva MJ. Damaging fatigue loading stimulates increases in periosteal vascularity at sites of bone formation in the rat ulna. Calcif Tissue Int. 2007;80(6):391–399. doi: 10.1007/s00223-007-9031-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kety SS. Theory of blood-tissue exchange and its application to measurement of blood flow. Methods Med Res. 1960;(8):223–227. [Google Scholar]
- 23.Hawkins RA, Choi Y, Huang SC, et al. Evaluation of the skeletal kinetics of fluorine- 18-fluoride ion with PET. J Nucl Med. 1992;33(5):633–642. [PubMed] [Google Scholar]
- 24.Bloomfield SA, Hogan HA, Delp MD. Decreases in bone blood flow and bone material properties in aging Fischer-344 rats. Clin Orthop Relat Res Mar. 2002;(396):248–257. doi: 10.1097/00003086-200203000-00036. [DOI] [PubMed] [Google Scholar]
- 25.Brenner W, Vernon C, Muzi M, et al. Comparison of different quantitative approaches to 18F-fluoride PET scans. J Nucl Med. 2004;45(9):1493–1500. [PubMed] [Google Scholar]
- 26.Blau M, Ganatra R, Bender MA. 18 F-fluoride for bone imaging. Semin Nucl Med. 1972;2(1):31–37. doi: 10.1016/s0001-2998(72)80005-9. [DOI] [PubMed] [Google Scholar]
- 27.Genant HK, Bautovich GJ, Singh M, Lathrop KA, Harper PV. Bone-seeking radionuclides: an in vivo study of factors affecting skeletal uptake. Radiology. 1974;113(2):373–382. doi: 10.1148/113.2.373. [DOI] [PubMed] [Google Scholar]
- 28.Uthgenannt BA, Kramer MH, Hwu JA, Wopenka B, Silva MJ. Skeletal self-repair: stress fracture healing by rapid formation and densification of woven bone. J Bone Miner Res. 2007;22(10):1548–1556. doi: 10.1359/jbmr.0070614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hsu WK, Virk MS, Feeley BT, et al. Characterization of osteolytic, osteoblastic, and mixed lesions in a prostate cancer mouse model using 18F-FDG and 18F-fluoride PET/CT. J Nucl Med. 2008;49(3):414–421. doi: 10.2967/jnumed.107.045666. [DOI] [PMC free article] [PubMed] [Google Scholar]