T₂ Relaxometry with Indirect Echo Compensation from Highly Undersampled Data

Abstract

Purpose

To develop an algorithm for fast and accurate T₂ estimation from highly undersampled multi-echo spin-echo (MESE) data.

Methods

The algorithm combines a model-based reconstruction with a signal decay based on the slice-resolved extended phase graph (SEPG) model with the goal of reconstructing T₂ maps from highly undersampled radial MESE data with indirect echo compensation. To avoid problems associated with the nonlinearity of the SEPG model, principal component decomposition is used to linearize the signal model. The proposed CUrve Reconstruction via pca-based Linearization with Indirect Echo compensation (CURLIE) algorithm is used to estimate T₂ curves from highly undersampled data. T₂ maps are obtained by fitting the curves to the SEPG model.

Results

Results on phantoms showed T₂ biases (1.9% to 18.4%) when indirect echoes are not taken into account. The T₂ biases were reduced (<3.2%) when the CURLIE reconstruction was performed along with SEPG fitting even for high degrees of undersampling (4% sampled). Experiments in vivo for brain, liver and heart followed the same trend as the phantoms.

Conclusion

The CURLIE reconstruction combined with SEPG fitting enables accurate T₂ estimation from highly undersampled MESE radial data thus, yielding a fast T₂ mapping method without errors caused by indirect echoes.

Introduction

Spin-spin (T₂) relaxation is one of the main contrast mechanisms in MRI. Although most clinical applications use qualitative (visual) information derived from T₂-weighted images, there is an increasing interest in T₂ mapping (1–10).

Because single-echo spin-echo T₂ mapping requires long acquisition times, its translation to the clinic has been limited by its time inefficiency. In order to reduce the acquisition times it is customary to use multi-echo spin-echo (MESE) pulse sequences, where several echo time (TE) points are acquired per repetition time (TR) period by using a train of 180° refocusing pulses after the initial 90° excitation pulse. To further accelerate T₂ data acquisition a fast (or turbo) spin-echo approach where several k-space lines of data are acquired per TR period is commonly used. For the sake of speed in T₂ mapping (while maintaining high spatial and temporal resolution), the use of TE data sets that are undersampled in k-space has been proposed in conjunction with a fast spin-echo approach. Several algorithms have been described to recover T₂ information from these highly reduced TE data sets (11–16). Recently, the focus has been on model-based T₂ mapping algorithms. Doneva et al. proposed to exploit the temporal sparsity of the exponential decay while reconstructing all TE images under the framework of compressed sensing (13, 16). Block et al. proposed a model-based algorithm for radial fast spin-echo acquisitions to directly reconstruct I₀ and R₂ (1/T₂) maps from the measured k-space data (11). Because I₀ and R₂ values have very different scales the gradient-based minimization process requires a scaling factor which needs to be fine tuned for accurate T₂ estimation (12). Our group has recently developed the REPCOM (REconstruction of Principal COmponent coefficient Maps) algorithm which linearizes the signal model using principal component analysis (PCA). REPCOM exploits the spatial and temporal sparsity of the TE images, and provides accurate T₂ estimates from highly undersampled data without the need of a scaling factor for the fitted parameters.

The algorithms described above, including REPCOM, rely on the assumption that the signal follows an exponential decay. However, in MESE acquisitions the decay is generally contaminated by indirect echoes (echoes leading to signal generation after more than one refocusing pulse such as stimulated echoes) including differences in the signal intensities between even and odd echoes, thus, altering the single exponential nature of the T₂ decay observed in a single-echo spin-echo experiment. The indirect echoes are the result of refocusing pulses not attaining the ideal 180° flip angle (FA) due to nonrectangular slice profiles, static (B₀) and transmit field (B₁) inhomogeneity, and B₁ calibration errors (17).

To alleviate the pulse imperfection due to nonrectangular slice profiles, a thick refocusing slice technique has been proposed by Pell et al. (5). This technique employs a refocusing slice that is thicker than the excitation slice. B₀ and B₁ inhomogeneity, and calibration errors, however, are not corrected for by this approach. Echo editing techniques that use crusher gradients around the refocusing pulses have also been proposed to reduce the signal resulting from pathways leading to indirect echoes (18–20). However, not all pathways can be crushed effectively and the method has only been demonstrated with non-selective refocusing pulses, which limits the use of the method to single slice applications. Recently, Lebel and Wilman proposed the slice-resolved extended phase graph (SEPG) fitting algorithm (17), for accurate T₂ estimation from MESE data contaminated by indirect echoes. Their method is based on the extended phase graph (EPG) model proposed by Hennig (21) which provides decay curves for any given refocusing FA. The EPG model assumes perfectly rectangular slice profiles whereas the SEPG model includes the known slice profile for both excitation and refocusing pulses. The fitting algorithm fits the measurements to the SEPG model to obtain the T₂ estimates. The method is robust to B₁ inhomogeneity and calibration errors and it has been shown that accurate T₂ estimation can be obtained from MESE data acquired with reduced FAs (<180°).

So far, the SEPG fitting algorithm has been demonstrated for fully sampled or 60% partial k-space Cartesian data. The main limitation of combining the SEPG fitting algorithm with a model-based reconstruction approach for T₂ estimation from highly undersampled data (< 10% sampled with respect to Nyquist sampling theorem), is the non-linearity of the SEPG model. In this work we propose to extend the PCA approach used in the REPCOM algorithm to linearize the SEPG model. The proposed CUrve Reconstruction via pca based Linearization with Indirect Echo compensation (CURLIE) algorithm aims to obtain accurate T₂ decay curves from highly undersampled data in the presence of B₁ imperfections or non-180° refocusing pulses. The T₂ values of the reconstructed curves can then be obtained by applying SEPG fitting. Although only radial data is used in this work, the methodology can be translated to other trajectories.

Theory

Hennig’s EPG model provides a way to calculate the signal intensity of a specific echo point for MESE sequences with the assumption that all spins experience the same FA. Given the excitation pulse FA, α₀, the FAs of the N refocusing pulses, α_j (j=1, … N), the sensitivity of transmit B₁ field, and the I₀, T₁ and T₂ values of a voxel, the signal intensity at the j^th spin echo, S_j, can be expressed as according to ref.21:

$$S_j=I_0·\mathit{EPG}(T_1,T_2,B_1,{\alpha }_0,\dots ,{\alpha }_j,j).$$ [1]

The function EPG(•) does not have an explicit expression, but can be computed numerically. Based on the EPG model, Lebel and Wilman recently proposed the SEPG model. With the prior knowledge of the prescribed slice profile of the excitation pulse along the z direction, α₀(z), the prescribed slice profiles of the refocusing pulse along the z direction, α_j (z) (j=1, …, N), the SEPG model can be obtained by integrating the EPG model throughout the slice:

$$C_j(I_0,T_1,T_2,B_1,{\alpha }_0(z),\dots ,{\alpha }_j(z))=I_0·\underset{z}{\int }\mathit{EPG}(T_1,T_2,B_1,{\alpha }_0(z),\dots ,{\alpha }_j(z),j)dz.$$ [2]

The SEPG fitting algorithm fits T₂ decay curves acquired with a MESE sequence to Equation [2]. Given N TE measurements s_j (j=1, …, N), the SEPG fitting algorithm can be written as:

$$I_0,T_1,T_2,B_1=arg{min}_{I_0,T_1,T_2,B_1}\{\sum _{j=1}^N{\Vert C_j(I_0,T_1,T_2,B_1,{\alpha }_0(z),\dots ,{\alpha }_j(z))-s_j\Vert }^2\}.$$ [3]

In Ref. 17, it has been shown that the SEPG model is insensitive to T₁ values when T₁/T₂ ratio is large, hence it has been proposed to fix T₁ to +∞ in order to simplify the signal model and the fitting algorithm:

$$C^{\prime }(I_0,T_2,B_1,{\alpha }_0(z),\dots ,{\alpha }_j(z),j)=I_0·\underset{z}{\int }\mathit{EPG}(T_1=+\infty ,T_2,B_1,{\alpha }_0(z),\dots ,{\alpha }_j(z),j)dz,$$ [4]

$$I_0,T_2,B_1=arg{min}_{I_0,T_2,B_1}\{\sum _{j=1}^N{\Vert {C_j}^{\prime }(I_0,T_1=+\infty ,T_2,B_1,{\alpha }_0(z),\dots ,{\alpha }_j(z))-s_j\Vert }^2\}.$$ [5]

In the published work of the SEPG fitting algorithm, the amplitude images were obtained from fully or 60% sampled Cartesian k-space. For highly undersampled data (< 10% sampled), the fitting algorithm relies on a reconstruction algorithm which can accurately recover the decay curves. Thus, it is intuitive to combine the SEPG model with a model-based algorithm (11, 22):

$${\mathbf{I}}_0,{\mathbf{T}}_2,{\mathbf{B}}_1=arg{min}_{{\mathbf{I}}_0,{\mathbf{T}}_2,{\mathbf{B}}_1}\{\sum _{j=1}^N{\Vert FT\{{C_j}^{\prime }(I_0,T_1,T_2,B_1,{\alpha }_0(z),\dots ,{\alpha }_j(z))\}-{\mathbf{K}}_j\Vert }^2\},$$ [6]

where I₀,T₂,B₁ are the vectors of I₀, T₂, B₁ of all voxels, FT is the forward Fourier transform, K_j is the (undersampled) k-space data acquired at the j^th TE. Due to the large dimensionality of the problem, it is impractical to use a global minimization algorithm to solve Equation [6], hence a local minimization algorithm (such as the gradient-based minimization algorithm) can be used. However, the SEPG model is non-linear as a function of T₂ and B₁ and it is difficult to obtain the gradient for minimization purposes.

In the REPCOM algorithm (12), we use PCA to linearize the exponential T₂ decay model, thus overcoming non-linear minimization problems. In CURLIE we extend the PCA approach to approximate the SEPG model. The principal components (PCs) are calculated for given TE points using a training set of decay curves given by the SEPG model for a certain range of T₂ and B₁ values. With the PCs obtained from the training curves, the T₂ decay curves with indirect echoes can be approximated by a weighted linear combination of the PCs.

Let v⃗ be a vector representing a noiseless T₂ decay curve with indirect echoes. Let L be the number of PCs to be used in the approximation and p⃗_i the i^th PC vector. v⃗ can be approximated by a linear combination of p⃗_i:

$$\overrightarrow{v}={\sum }_{i=1}^L{m}_i{\overrightarrow{p}}_i,$$ [7]

where m_i is the weighting of the i^th principal component. P̂ = (p⃗₁, p⃗₂, …, p⃗_L) is the matrix consisting of the vectors of the first L PCs. Let M⃗_i be the vector of m_i for all the voxels and M can be formed as (M⃗₁, M⃗₂, …, M⃗_L). Let P̂_j denote the j^th row of the matrix P̂. Note that $\mathbf{M}{\widehat{\mathbf{P}}}_j^T$ yields the image at TE_j from the L principal component coefficients. Equation [6] can be reformulated as:

$$\widehat{\mathbf{M}}=arg{min}_{\mathbf{M}}\{{\sum }_{j=1}^L{\left|\right|{FT}_j(\mathbf{M}{\widehat{\mathbf{P}}}_j^T)-{\overrightarrow{\mathbf{K}}}_j\left|\right|}^2\}.$$ [8]

When the complex coil sensitivity profiles S_l and the sparsifying penalties Penalty_i (·) (with corresponding weights λ_i) are given (12), the algorithm can be written as:

$$\widehat{\mathbf{M}}=arg{min}_{\mathbf{M}}\{{\sum }_{l=1}^{\#\mathit{coils}}{\sum }_{j=1}^L{\left|\right|{FT}_j({\mathbf{S}}_l\mathbf{M}{\widehat{\mathbf{P}}}_j^T)-{\overrightarrow{\mathbf{K}}}_{l,j}\left|\right|}^2+{\sum }_i{\lambda }_i{\mathit{Penalty}}_i(\mathbf{M})\}.$$ [9]

The penalty terms are used to exploit the spatial compressibility of the PC coefficient maps in the framework of compressed sensing and have been shown to improve the quality of the reconstructed T₂ maps (12). The decay curves are reconstructed from M̂ which can be obtained by a conjugate gradient minimization algorithm.

The SEPG fitting algorithm (Equation [5]) can then be applied to the curves reconstructed by CURLIE to obtain T₂ estimates. As mentioned above, Lebel and Wilman proposed to fix the T₁ to be +∞ for the fitting (17). As an alternative, an optimized T₁ value can be used in the SEPG fitting based on the prior knowledge of the anatomy being imaged as indicated by Sénégas et al. (23).

The flow chart of the CURLIE reconstruction algorithm and the SEPG fitting is shown in Figure 1. Different from REPCOM, the new method includes the effects of indirect echoes in the T₂ estimation process by incorporating the SEPG model in the generation of the training curves and in the estimation of the principal components coefficients (via the CURLIE algorithm) as well as in the fitting of the TE images to obtain the final T₂ map.

Figure 1.

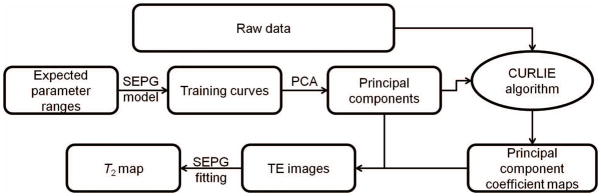
Flow chart depicting the CURLIE-SEPG fitting algorithm.

Methods

All radial MESE data were acquired on a 1.5T Signa HDxt GE (General Electric Healthcare, Milwaukee, WI) MR scanner using a previously developed radial fast spin-echo (radFSE) pulse sequence (24). A “bit-reversed” angular ordering was used to minimize artifacts from T₂ decay and motion (25). The slice profiles of the excitation and refocusing pulses were generated from the Fourier transform of the RF waveforms provided by the manufacturer for fast spin-echo pulse sequences. The refocusing slice RF profiles are calibrated by the techniques in Ref. 26. It should be noted that in the manufacturer’s pulse sequence the full-width half-maximum of the refocusing pulses is designed to be about 1.6 times as thick as the corresponding excitation pulse.

Computer simulation

Curves were generated according to the SEPG model assuming an ETL = 16 and echo spacing =12.11 ms with the slice discretized into 63 points along the slice profile. A total of 765 curves were generated for T₂ values varying from 50 ms to 300 ms with a step size of 5 ms, B₁ values varying from 0.5 to 1.2 with a step size of 0.05, and T₁ = +∞. The PCs were trained from these 765 curves.

Phantom Data

A physical phantom, containing three 10 mm glass tubes filled with MnCl₂ solutions of different concentrations (50 μM, 75 μM, and 170 μM) to yield data at different T₂’s, was prepared. RadFSE data were acquired with a single channel transmit/receive coil, with an echo train length (ETL) of 16 with echo points spaced by 12.11 ms, TR = 1 s, excitation slice thickness = 8 mm, receiver bandwidth = ±15.63 kHz, field of view (FOV) = 10 cm. The acquisition matrix for undersampled data was 256×256 yielding 16 radial k-space lines for each of the 16 TE data sets. For comparison purposes, another data set was acquired with an acquisition matrix of 256×4096 to yield 256 radial k-space lines for each TE; all other acquisition parameters were kept the same. Although for radial acquisition a data set with 256 radial lines and 256 sampling points per line is 64% sampled (according to the Nyquist theorem a fully sampled data set requires 402 radial lines for 256 sampling points per line), the data set gives good quality images and accurate T₂ maps for most clinical applications (as well as for our phantom work). In this work, this data set is referred to as “standard sampled”.

Cartesian single-echo spin-echo data (not contaminated by indirect echoes) of the phantom were also acquired to obtain the gold standard T₂ values. Data were acquired with a single channel transmit/receive coil, TR = 5 s, excitation slice thickness = 8 mm with the refocusing slice being approximately 5 times as thick as the excitation slice, receiver bandwidth = ±15.63 kHz, and FOV = 10 cm. Data for 4 TE points (12, 24, 36 and 48 ms) were acquired with the acquisition matrix per TE point set to 64×64. A lower resolution was used for the single-echo spin-echo sequence due to its long acquisition time. Gold standard T₂ values were obtained by fitting the data to a single exponential decay.

In vivo data

Each in vivo data set (brain, liver and heart) were acquired from a separate volunteer under informed consent with a protocol approved by the local Institutional Review Board.

In vivo brain data were acquired using the radFSE pulse sequence with an 8-channel receiver head coil, 16 TE points equispaced by 12.93 ms, excitation slice thickness = 8 mm, receiver bandwidth = ±15.63 kHz, TR = 4 s, and FOV = 24 cm. The acquisition matrix for the standard sampled data set was 256×4096 to yield 256 radial lines per TE. The acquisition matrix for the undersampled data set was 256×512 yielding 32 radial lines per TE (8.0% sampled compared to fully sampled data). Experiments were conducted with the refocusing RF pulses FAs prescribed to be 180° and 120°.

In vivo liver data were acquired in a breath hold using the radFSE pulse sequence with an 8-channel receiver torso coil, 16 TE points equispaced by 8.93 ms, slice thickness = 8 mm, receiver bandwidth = ±31.25 kHz, TR = 1.5 s, FOV = 48 cm, and acquisition matrix = 256×256 to yield 16 radial lines per TE (4.0% sampled compared to fully sampled data). To evaluate the estimated T₂ values, three tubes containing either MnCl₂ or agarose for T₂ variation were placed on the subject’s chest. The gold standard T₂ values of the three tubes were estimated to be 56.0 ms, 77.9 ms and 64.0 ms in a separate experiment using a single-echo spin-echo sequence.

In vivo cardiac data were acquired using a radFSE pulse sequence which included a double-inversion preparation period for nulling the signal from flowing blood (27). Data were acquired with an 8-channel receiver cardiac coil, 16 TE points equispaced by 9.46 ms (for refocusing pulses with prescribed FA=180°) or 6.85 ms (for refocusing pulses with prescribed FA=155°), slice thickness = 8 mm, receiver bandwidth = ±31.25 kHz, TR = 1 RR, and FOV = 48 cm. The acquisition matrix was 256×256 resulting in 16 radial lines per TE (4.0 % sampled compared to fully sampled data). Imaging of a slice was completed within a breath hold (~ 15–18 s).

Data Reconstruction

All algorithms were implemented in Matlab (MathWorks, Natick, MA). The training curves for PC (P̂) generation were provided by the SEPG signal model using Equation [3]. Equation [8] was solved iteratively by using the nonlinear Polak-Ribiere Conjugate Gradient algorithm (28). The spatial penalty terms used in Equation [9] consisted of the 1-norms of the wavelet transform (Daubechies 4, code obtained from http://www-stat.stanford.edu/~wavelab) and total variation of the PC coefficient maps.

T₂ estimates were obtained either by conventional exponential fitting or by SEPG fitting. SEPG fitting was performed using Equation [4]; during the fitting, T₂ was allowed to vary between 30 – 5000 ms and B₁ was limited to 0 – 3. The T₁ values used in the SEPG fitting were fixed to an optimal value using prior information. For each in vivo image a single T₁ was chosen based on reported values for the anatomy of interest: gray matter for brain (950 ms) (29), liver (500 ms) (30) and myocardium (700 ms) (31). For the phantom data, where there was a wide range of T₁ values among the different vials used, the optimal T₁ was determined as proposed in Ref. 23. In brief, a set of simulated curves were generated using the SEPG model with T₁, T₂, and B₁ varying independently between 300~2000 ms, 50~300 ms, and 0.5~1.2, respectively. SEPG fitting was then performed on these curves for each of the T₁ values in the selected range. The T₁ value that minimized the T₂ estimation error according to the 2-norm was selected to be the optimized T₁.

For comparison, T₂ maps were also reconstructed using the REPCOM algorithm. The T₂ values for the PC training were between 35 ms to 300 ms equi-spaced by 1 ms. Total variation and wavelet transforms were used as the sparsifying transform with proper weightings as in Ref. 12.

Results

Proof-of-Concept

In order to demonstrate that a small number of PCs are sufficient to characterize the T₂ decay curves in the presence of indirect echoes, we first performed simulations. Figure 2a shows 4 out of the 765 curves generated according to the SEPG model. The curves show the expected signal modulation due to indirect echoes with modulations increasing with B₁. Figure 2b shows the 2-norm of the approximation error when 6 PCs are used to represent the curves after these are normalized so that the 2-norm is unity. Note that the 2-norms of the approximation error are all below 0.006 and most of the errors have 2-norm < 0.003. Figure 2c shows the distribution of the % error of the T₂ values estimated by SEPG fitting caused by the PC approximation. As shown, the % errors in T₂ values estimated from the curves recovered from 6 PCs are all < 3.5% with majority of the errors being < 1.5%. These experiments show that it is sufficient to use L = 6 to represent the training curves accurately under the given conditions and that the approximation error caused by using only the first 6 PCs is small.

Figure 2.

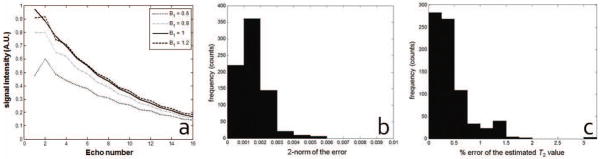
(a) Selected training curves for T₂ = 100 ms, T₁ = + ∞ and B₁ ranging from 0.6 to 1.2. Curves were simulated numerically using the SEPG model. An echo spacing of 12.11 ms was used in the simualtions to cover a TE range similar to in vivo data. (b) The distribution of the 2-norms of the approximation error for training curves generated according to the SEPG model using only 6 PCs; (c) The distribution of the % error of the T₂ values caused by the approximation error when 6 PCs are used to represent the training decay curves. Note that the 2-norms of the approximation error are all below 0.006 and the % error of the T₂ values are all less than 3.5% which indicates that the curves are well represented with only 6 PCs.

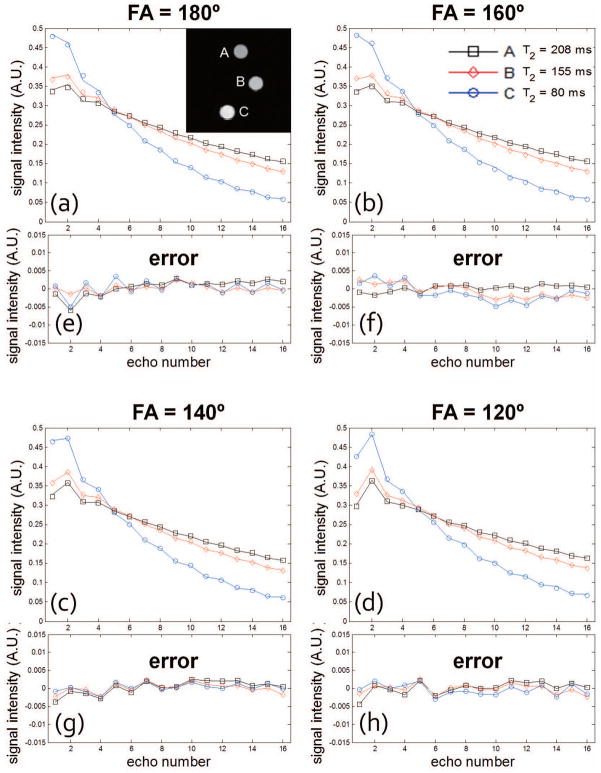
Experiments using physical phantom data were performed to further investigate the accuracy of the linear approximation using principal component decomposition. Phantom data were acquired with radFSE using standard sampled data (256 radial lines per TE with 256 points per radial line). Figure 3a–d show decay curves reconstructed directly from the acquired data for each of the three phantom tubes shown in the image and for various refocusing FA. Each point in the decay curves corresponds to the averaged signal from voxels within an ROI for each tube; each curve is the fitted decay curve according to the SEPG model from fitting parameters using the SEPG fitting (T₁ = +∞). The curves are normalized (2-norm=1). As shown, the fitted curves are well matched to the acquired data for all the four FAs. Figure 3e–g show the approximation error of the corresponding curves recovered from the 6 PCs used to generate Figure 2b–c. The errors are all below 0.01 with most under 0.005. The 2-norms of the approximation error are between 0.0018 and 0.0042 for all FAs which also show that 6 PCs can represent the decay curves of the acquired data well. Note that the same PCs were used for all FAs (FA changes are equivalent to B₁ changes under the model). In this experiment T₁ was not optimized and assumed to be +∞.

Figure 3.

(a–d) Decay curves for each of the three tubes in the phantom for different refocusing FA obtained from a standard sampled radial MESE data set (i.e. 256 radial views with 256 points per view). Data were acquired with echo spacing of 12.11 ms to mimic the TE coverage in vivo. Each point in the decay curves corresponds to the averaged signal from voxels within an ROI for each tube; each curve is the fitted curve according to the SEPG model. The curves are normalized (2-norm=1). (e–h) The approximation error when 6 PCs are used to represent the decay curves. Note that the errors are all below 0.01 (with most under 0.005) for all FAs which show that 6 PCs can represent the decay curves of the acquired data well.

We then evaluated the accuracy of T₂ estimation using the curves recovered from 6 PCs using the standard sampled phantom data. Table 1 compares the bias in T₂ estimates obtained from the “recovered curves” to those from curves obtained directly from the TE images (“original curves”). The table shows results for various FA and for three fitting algorithms: exponential fitting, SEPG fitting with T₁ = +∞, and SEPG fitting with T₁ optimized. It can be observed that for each fitting algorithm the bias of T₂ estimates obtained from the original and recovered curves are very similar. The differences in T₂ bias are all below 0.3%, which further demonstrates the accuracy of the PC approximation for representing the acquired decay curves. The results also show that the exponential fitting of MESE data overestimates T₂ values. The estimation bias increases as T₂ increases and as the FA diverges from 180° due to the more pronounced indirect echo effect; for FA = 120°, the bias of the exponential fitting can be up to 18.4% (with the larger bias for T₂=210 ms). The bias of the SEPG fitting with T₁ = +∞ is less than 6% which is significantly smaller than the bias of the exponential fitting. When an optimized T₁ (500 ms) was used, the largest error is further reduced to 3.6% which demonstrates that the optimized T₁ can be used in the SEPG fitting to improve T₂ estimation.

Table 1.

Percent error of T₂ estimates (relative to the gold standard) for the of the physical phantom shown in Figure 3. The table shows % error of T₂ values estimated from curves derived directly from the TE images (original curves) and curves recovered from the first 6 PCs. Results shown are for standard sampled radial data (i.e., data for each TE time point has 256 radial lines with 256 points per line).

Exponential Fitting
	Vial	Gold standard	FA=180	FA=160	FA=140	FA=120
Original curves	A	210.0	5.7%	5.7%	9.6%	18.3%
	B	159.3	3.6%	2.8%	5.9%	13.4%
	C	80.7	3.2%	2.1%	5.0%	12.0%
Recovered curves	A	210.0	5.6%	5.7%	9.8%	18.4%
	B	159.3	3.6%	2.7%	6.0%	13.6%
	C	80.7	3.1%	1.9%	5.0%	12.0%

SEPG fitting with T1=+∞
	Vial	Gold standard	FA=180	FA=160	FA=140	FA=120
Original curves	A	210.0	0.7%	−0.9%	−2.0%	−3.7%
	B	159.3	−1.2%	−3.0%	−4.0%	−5.5%
	C	80.7	−0.5%	−2.9%	−4.2%	−5.8%
Recovered curves	A	210.0	0.8%	−0.9%	−1.9%	−3.8%
	B	159.3	−1.2%	−3.0%	−4.0%	−5.6%
	C	80.7	−0.6%	−2.9%	−4.2%	−5.8%

SEPG fitting with T1 optimized (500 ms)
	Vial	Gold standard	FA=180	FA=160	FA=140	FA=120
Original curves	A	210.0	2.4%	1.2%	1.8%	3.2%
	B	159.3	0.0%	−1.6%	−1.6%	−0.8%
	C	80.7	−0.4%	−2.5%	−3.2%	−3.6%
Recovered curves	A	210.0	2.4%	1.2%	1.8%	3.1%
	B	159.3	0.0%	−1.6%	−1.6%	−0.9%
	C	80.7	−0.4%	−2.5%	−3.2%	−3.6%

T₂ estimation from highly undersampled data

So far, we have demonstrated that a few principal components can accurately represent the T₂ decay curves contaminated with indirect echoes using standard sampled data. For highly undersampled data we need to use the CURLIE algorithm described in Equation [8], where the PCA-based signal model is used to match the acquired k-space data. Using the three-tube physical phantom and highly undersampled radFSE data (i.e., data with only 16 radial lines per TE) we tested the accuracy of CURLIE for reconstructing the decay curves using 6 PCs. Figure 4 shows the difference between curves reconstructed from highly undersampled data using CURLIE and curves obtained from the standard sampled data (64% sampled) for various FAs. In general, the differences between the curves are small despite the fact that the highly undersampled data has 16 times less samples than the standard sampled data. The 2-norms of the differences are between 0.0035 and 0.0095 which demonstrates that decay curves from highly undersampled data can be accurately reconstructed by CURLIE. The T₂ estimates for the three tubes in the phantom, obtained with SEPG fitting, are shown in Table 2. Note that the T₂ bias of undersampled data is similar to the T₂ bias obtained for standard sampled data (data from Table 1): less than 5% for T₁ = +∞ and less than 3.6% for T₁ = 500 ms. This demonstrates that the decay curves reconstructed by CURLIE from highly undersampled data have the same T₂ characteristics as the decay curves obtained from the standard sampled data.

Figure 4.

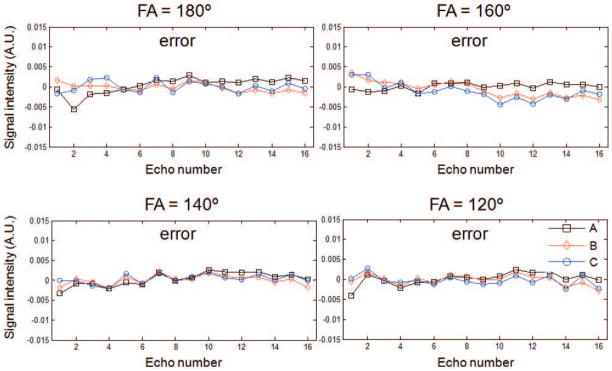
The errors of the decay curves of the three-tube phantom shown in Figure 3 reconstructed from highly undersampled radial MESE data (4% sampled relative to the Nyquist condition) by using the CURLIE algorithm. Data were acquired with echo spacing of 12.11 ms to mimic the TE coverage in vivo. Note that the differences between the curves are small (the 2-norms of the differences are between 0.0035 and 0.0095) which demonstrates that decay curves from highly undersampled data can be accurately reconstructed with the CURLIE algorithm.

Table 2.

Percent error of T₂ estimates (relative to the gold standard) for highly undersampled data (4% sampled compared to fully sampled radial data). Data shown corresponds to the vials of the physical phantom shown in Figure 2. T₂ estimation was performed using CURLIE for the generation of curves followed by SEPG fitting with T₁= +∞.

Fitting algorithm	Vial	Gold standard	FA=180	FA=160	FA=140	FA=120
SEPG fitting with T1=+∞	A	210.0	−0.9%	−2.1%	−3.5%	−4.0%
	B	159.3	0.3%	−0.9%	−4.0%	−4.7%
	C	80.7	0.5%	−0.4%	−4.6%	−4.8%
SEPG fitting with T1=500 ms	A	210.0	1.0%	−0.1%	−0.2%	2.3%
	B	159.3	1.6%	0.5%	−1.8%	−0.1%
	C	80.7	0.6%	0.0%	−4.0%	−2.7%

CURLIE was tested in vivo using brain data. Two experiments were conducted: one where the prescribed FA of the refocusing pulses was 180°, another where the prescribed FA was 120°. The same 6 PCs used in Table 2 were used for the reconstruction of the undersampled brain data. In Figure 5, the decay curves of the shown ROI obtained from standard sampled data (directly from the TE images) are compared to the curves reconstructed from 32 radial lines per TE (8.0% sampled) using CURLIE. Note that the curves generated from under- and standard sampled data are very similar (the error for all echo points for each of the two FA are below 0.01). The T₂ values obtained from the decay curves using SEPG fitting are also shown in the figure. The differences between the T₂ values obtained from under- and standard sampled data are below 3%. These results show that the curves reconstructed from highly undersampled in vivo data agree well with the decay curves obtained from standard sampled data. Also, note that the T₂ values estimated from data acquired with 180° and 120° FAs are similar.

Figure 5.

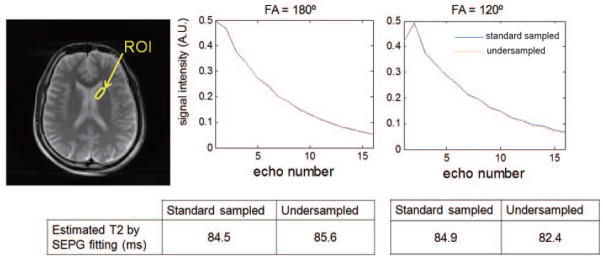
Decay curves of the ROI obtained from standard sampled and 8 times less sampled radial MESE data acquired with FAs of the refocusing pulses prescribed to 180° and 120°. The T₂ values for standard sampled data were obtained directly from the reconstructed TE images using SEPG fitting. The T₂ values for undersampled data were obtained using CURLIE followed by SEPG fitting. T₁= +∞ was used for the SEPG fitting. Data were acquired with echo spacing = 12.93 ms. Note that the curves generated from undersampled data via CURLIE are similar to the standard sampled curves (obtained directly from the acquired data). The differences between the T₂ values obtained from under- and standard sampled data are below 3%. Also, the T₂ values estimated from data acquired with 180° and 120° FAs are similar.

A voxel-wise brain T₂ map obtained using CURLIE and SEPG fitting for data acquired with prescribed FAs of 180° is shown in Figure 6a. Figure 6b shows the difference map between data acquired with prescribed FAs of 180° and 120° but reconstructed with the REPCOM algorithm (i.e. where the training curves do not take into account indirect echoes and single exponential fitting is used for T₂ estimation). The % difference maps between T₂ maps obtained by CURLIE with SEPG fitting from data acquired with prescribed FAs of 180° and 120° is shown in Figure 6c and 6d for T₁=+∞ and T₁=950 ms, respectively. The same 6 PCs as in previous figures were used for both FAs. In the % difference maps, the ventricles are masked out due to the fact that the T₂ of cerebrospinal fluid (~ 2000 ms) is much larger than the white and gray matter, and the TE coverage used here is not suitable for the accurate estimation of long T₂s. The means of the difference map are: 8.3% for the map derived from the REPCOM reconstruction and 4.9% and 3.1% for the maps derived from CURLIE and SEPG fitting with T₁ = +∞ and T₁ = 950 ms, respectively. The small means in the difference maps support the concept that the CURLIE reconstruction followed by SEPG fitting significantly reduces the effect of indirect echoes in T₂ estimation in vivo. When an optimized T₁ is used in the SEPG fitting the % difference T₂ map obtained by SEPG fitting with optimized T₁ is generally smaller. It is noteworthy to point out that since the data sets with 180° and 120° FAs were obtained by two separate acquisitions, there is slight difference between the two imaging slices due to inter-scan movement even though the same slice was prescribed.

Figure 6.

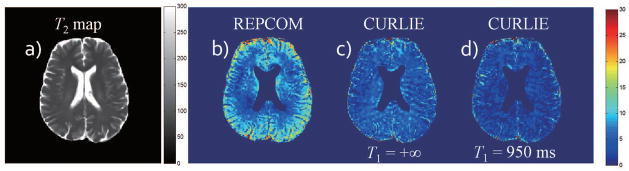
(a) Voxel-wise T₂ map obtained by CURLIE and SEPG fitting (T₁=950 ms) from the data acquired with the FAs of the refocusing pulses prescribed to 180°. (b–d) The %difference between T₂ maps obtained from data acquired with prescribed FAs of 180° and 120° using REPCOM (which ignores indirect echoes) and CURLIE with SEPG fitting. Each difference map was obtained from the T₂ maps obtained by the same fitting algorithm for the prescribed FAs of 180° and 120°. The difference maps support the concept that the CURLIE reconstruction followed by SEPG fitting significantly reduces the effect of indirect echoes in T₂ estimation.

We also investigated the utility of T₂ mapping with CURLIE and SEPG fitting for abdominal imaging where high undersampling is needed due to the acquisition time constraint imposed by the breath hold. Figure 7 shows the anatomical images and the voxel-wise T₂ maps of an abdominal slice. The maps were reconstructed from highly undersampled data (16 radial k-space lines per TE; 4.0% sampled) by REPCOM and CURLIE with optimized T₁ SEPG fitting. Three phantoms with known T₂ values were placed above the subject during data acquisition and used as the gold standard (due to the breath hold limitation, it was not possible to obtain a gold standard data set for the liver T₂ map). The CURLIE reconstructions were performed with L = 6. The PCs were obtained from training curves generated for a T₂ range of 35 – 350 ms, T₁ = +∞ and B₁ = 0.5 – 1.2. As shown in the figure, the T₂ estimates obtained from the REPCOM reconstruction increase when the FA decreases from 180° to 120°, while the T₂ maps reconstructed by CURLIE with SEPG fitting (optimized T₁ = 500 ms) are comparable for the two different FAs. Note that since the data sets with 180° and 120° FAs were obtained from two separate breath hold acquisitions the slices are similar but not exactly the same.

Figure 7.

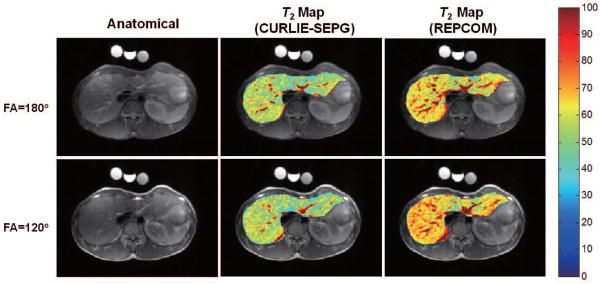
(left) Anatomical abdominal images reconstructed from the same data used for T₂ map generation. (middle) Liver T₂ maps (overlaid onto the anatomical image) obtained by CURLIE and SEPG fitting (T₁ = 500 ms) from undersampled data acquired with two refocusing pulses (FA=180° and 120°). (right) The T₂ maps reconstructed by REPCOM (which ignores indirect echoes) using the same undersampled data sets as in the CURLIE reconstruction. Note that the T₂ estimates obtained from the REPCOM reconstruction increase when the FA decreases from 180° to 120°, while the T₂ maps reconstructed by CURLIE with SEPG fitting are comparable for the two different FAs.

The T₂ estimates of the phantoms imaged with the liver subject are summarized in Table 3. For both 180° and 120° prescribed FAs, the T₂ estimates by CURLIE with SEPG fitting have < 3.5% error compared to the gold standard T₂. When the effect of indirect echoes is not taken into account in the reconstruction (as in REPCOM), the error can be up to 14% and 38% for FAs of 180° and 120°, respectively. The trend is similar as that shown in Figure 7, and the fact that the T₂ values obtained from CURLIE with SEPG fitting are very similar to the gold standard T₂ values indicates that the CURLIE T₂ maps shown in Figure 7 are accurate.

Table 3.

Percent error of T₂ estimates (relative to the gold standard) for the phantoms acquired with the liver data shown in Figure 7. T₂ curves were reconstructed from undersampled data (4% sampled) using CURLIE or the REPCOM algorithm (which does not compensate for indirect echoes). T₂ estimates from the CURLIE curves were obtained by SEPG fitting with “optimized” T₁ (500 ms). T₂ estimates from REPCOM were obtained using an exponential fit to the data.

	Gold Standard (ms)	FA = 180°		FA = 120°
		CURLIE+SEPG	REPCOM	CURLIE+SEPG	REPCOM
a	53.2	−2.3%	6.4%	−3.2%	20.7%
b	77.9	1.0%	14.4%	3.1%	38.9%
c	64.0	−2.0%	12.0%	−1.3%	36.4%

CURLIE with optimized T₁ SEPG fitting can also be applied for T₂ mapping of the myocardium using data acquired in a single breath hold. In cardiac imaging it is desirable to keep the echo train as short as possible to avoid cardiac motion during data acquisition thus, a short refocusing pulse (i.e., FA< 180°) is typically used. Figure 8, shows the anatomical short-axis cut of the heart acquired with a double-inversion radFSE sequence and T₂ maps reconstructed via CURLIE with SEPG fitting (optimized T₁ = 700 ms) and REPCOM. The maps were reconstructed from 16 radial k-space lines per TE (4.0% sampled). Similar to the observation made for the liver, the T₂ maps reconstructed by CURLIE with SEPG fitting are comparable for the two different refocusing pulses, whereas the T₂ maps reconstructed by REPCOM show a greater disagreement between the two refocusing pulses.

Figure 8.

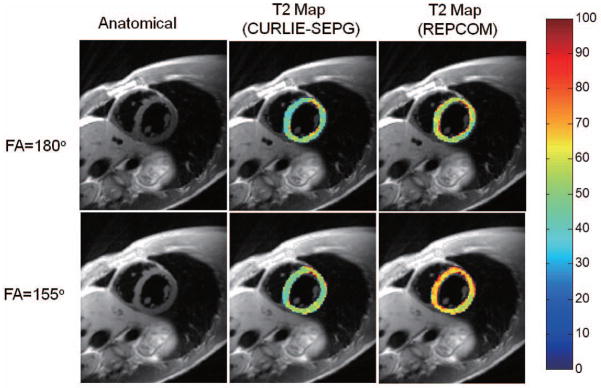
(left) Anatomical cardiac images reconstructed from the same data used for T₂ map generation. (middle) T₂ maps of the left ventricular heart wall (overlaid onto the anatomical image) obtained by CURLIE and SEPG fitting (T₁ = 700 ms) from undersampled data for normal refocusing pulses (FA =180°) and the short-duration refocusing pulses (FA =155°). (right) The T₂ maps reconstructed by REPCOM (which ignores indirect echoes) using the same undersampled data sets as in the CURLIE reconstruction. T₂ maps reconstructed by CURLIE with SEPG fitting are comparable for the two different refocusing pulses, whereas the T₂ maps reconstructed by REPCOM show a greater disagreement between the two refocusing pulses.

Discussion

In this work, we have introduced CURLIE and showed that it can accurately reconstruct the decay curves with indirect echoes from highly undersampled radial MESE data. CURLIE uses a linear approximation of the signal decay allowing for the incorporation of the highly non-linear SEPG model to account for the effects of indirect echoes. Moreover, the TE images generated via CURLIE have high spatial and temporal resolution. As a result, CURLIE combined with SEPG fitting enables accurate T₂ estimation from highly undersampled radial MESE data allowing for the reconstruction of T₂ maps from data acquired in a short period of time. For instance T₂ maps of the whole brain can be achieved in 4 min or less (depending on the degree of undersampling used). Maps of the thoracic cavity and abdomen can be obtained in a breath hold.

As shown in this work, the indirect echoes which are inherent to MESE acquisitions cause a significant (positive) T₂ bias if data are reconstructed assuming an exponential decay. The indirect echo effect is more pronounced for longer T₂s and as the FA of the refocusing pulses deviate from the ideal 180°(17). Thus, without indirect echo compensation, the T₂ estimates from MESE data will depend on the profile of the RF pulse, B₁ imperfections, as well as the TE coverage used in the experiment (number of TE points and echo spacing). As a result, the inter-site or inter-scan reproducibility of T₂ measurements can be greatly impacted. Indirect echoes also limit the use of MESE for T₂ mapping at higher fields (field strength ≥ 3T) where SAR limits the use of 180° refocusing pulses or in cardiac applications where shorter refocusing pulses are used to reduce the acquisition window and minimize the effects of motion.

Our results showed that when curves are reconstructed with CURLIE followed by SEPG fitting the T₂ bias of phantoms (compared to a gold standard) are small and not dependent on the T₂ values and FAs of the refocusing pulses even for data acquired with a high degree of undersampling. The same trend in seen vivo: the T₂ maps of brain, liver and heart reconstructed from highly undersampled data with CURLIE and SEPG fitting are not affected by the prescribed FA of the refocusing pulses as those reconstructed from the REPCOM algorithm. Overall, the technique should provide a fast method for T₂ mapping that is less dependent on the experimental conditions including the magnetic fields strength. These unique characteristics should make the technique practical for clinical use.

In this work SEPG fitting was performed for T₁ = +∞ or an optimized T₁, however, in the reconstruction of the decay curves via CURLIE, T₁ was fixed to infinity. This can be optimized using prior information of the object being imaged and the scanner and imaging parameters. Similar optimization can be performed for the T₂ and B₁ for the generation of the PCs. The T₂ range used to generate the training curves can also be optimized by using prior knowledge based on the anatomy being imaged, or estimated by prior T₂ mapping using a different algorithm (e.g. REPCOM or the echo sharing algorithm described in Ref. 14). In this work we used 6 principal components to approximate the signal model and showed that the T₂ can be accurately estimated in phantoms and a series of in vivo applications such as brain, myocardium and liver. In this work, the number of principal components (L) was determined empirically for the given training set. It is expected that smaller L could yield similar results for an optimized training set. However, given the ranges and/or distributions of T₂, T₁ and B₁, the optimal L and design of the training curves remain open problems.

Although SEPG fitting yields fitted B₁ maps in addition to the T₂ maps, the fitted B₁ maps estimated from our algorithm showed T₁ effects. These manifested as fluctuations along interfaces between tissues with very different T₁s (eg, gray-white matter tissue and CSF or liver parenchyma and blood vessels). However, the nature of the B₁ maps did not affect the T₂ results. We verified this experimentally by comparing the T₂ maps obtained from the CURLIE-SEPG method to those resulting from just SEPG fitting (using standard sampled data when available) or by a using smoothing constraint for the B₁ maps before T₂ estimation. The T₂ maps were similar regardless of the B₁ maps.

For the non-optimized Matlab code used here, the reconstruction took about 40 min using a single core of a desktop computer (Intel Core 2 Quad CPU, 2.4 GHz) for a single slice when the data were acquired with eight coils, 256 k-space lines. However, a significant reduction in reconstruction time is expected when the reconstruction code is optimized and parallelized since most of the computation time was spent on matrix multiplication.

Conclusions

In this work, it has been shown by numerical simulation, phantom and in vivo data that the proposed CURLIE algorithm can accurately reconstruct the decay curves with indirect echoes from highly undersampled radial MESE data. Accurate T₂ estimates can then be derived from the TE curves via SEPG fitting. The use of highly undersampled radial MESE data allows for the fast acquisition of data. The correction for indirect echoes reduces inaccuracies in T₂ mapping due to imperfect refocusing pulses making T₂ mapping with MESE accurate when the FA of the refocusing pulses are less than the ideal 180°; this is particularly important at higher magnetic fields as well as in certain cardiac applications. Overall, the CURLIE algorithm combined with SEPG fitting enables fast T₂ estimation which is less dependent on the experimental conditions used for data acquisition. These improvements should make T₂ mapping more practical for clinical use.