Abstract
Force spectroscopies have emerged as a powerful and unprecedented tool to study and manipulate biomolecules directly at a molecular level. Usually, protein and DNA behavior under force is described within the framework of the worm-like chain (WLC) model for polymer elasticity. Although it has been surprisingly successful for the interpretation of experimental data, especially at high forces, the WLC model lacks structural and dynamical molecular details associated with protein relaxation under force that are key to the understanding of how force affects protein flexibility and reactivity. We use molecular dynamics simulations of ubiquitin to provide a deeper understanding of protein relaxation under force. We find that the WLC model successfully describes the simulations of ubiquitin, especially at higher forces, and we show how protein flexibility and persistence length, probed in the force regime of the experiments, are related to how specific classes of backbone dihedral angles respond to applied force. Although the WLC model is an average, backbone model, we show how the protein side chains affect the persistence length. Finally, we find that the diffusion coefficient of the protein’s end-to-end distance is on the order of 108 nm2/s, is position and side-chain dependent, but is independent of the length and independent of the applied force, in contrast with other descriptions.
Keywords: internal diffusion, potential of mean force, protein elasticity
The development of single-molecule force spectroscopies [atomic force microscopy (AFM), and optical or magnetic tweezers] in the last two decades has opened a whole new and exciting field (1, 2). It is now possible to manipulate biomolecules directly at a molecular level and to study their behavior under force (3). It is therefore not surprising that these techniques have been applied in a broad gamut of contexts, in particular for proteins. In some cases, including enzyme catalysis (4), protein–ligand interaction (5), or folding and unfolding events (6), force is used as a probe, altering the free-energy landscape and the dynamics of the protein (7), and provides valuable kinetic and mechanistic insights. For other systems, force is of direct biological relevance [e.g., cellular adhesion (8) or muscle elasticity (9)].
The elasticity of a polypeptide is typically modeled using the worm-like chain (WLC) (1, 2) model of polymer elasticity. Although this simple model from polymer physics has proven remarkably successful at describing and interpreting experimental data, it lacks molecular details associated with proteins extended under force. However, substrate flexibility to adopt the right geometry is key in many situations, including, e.g., molecular recognition (10) or enzymatic reactivity (11). Therefore, a precise understanding of how force modulates and influences protein flexibility at a single-amino acid level is essential and is not provided by the aforementioned model.
From a dynamical perspective, it is still unclear how applied force affects internal diffusion of a polypeptide along the pulling trajectory. A joint experimental and theoretical study has suggested that increasing force greatly enhances internal friction along the end-to-end coordinate with a power law dependence (12). Indeed force spectroscopy measurements have reported values on the order of 102–104 nm2/s (12–14) about five orders of magnitude slower than that obtained for unfolded protein in the absence of force as measured by fluorescence techniques (15, 16). However, we recently suggested that the slow diffusion coefficients of proteins estimated by force spectroscopies are due to the viscous drag on the microscopic objects (beads, tips, surfaces) they are necessarily tethered to (14). Diffusion of untethered protein under force as studied in molecular dynamics (MD) simulations occur on a much faster timescale (typically 108 nm2/s), close to that obtained from fluorescence techniques where the probes are of molecular size. These similarities suggest that force would have a limited impact on diffusion along the longitudinal coordinate. However, the effect of the tether may be of relevance for comparison with diffusion in vivo since force is necessarily exerted with a tethering agent.
Here, we combine MD simulations of a full protein system in explicit solvent to unveil some key molecular aspects of protein relaxation under force. We start by showing that the WLC model successfully explains our simulation data and is also in very good agreement with available experimental results. We then show that the molecular details arising from the dihedral angles lead to WLC behavior. Changes in both the dihedral angles and their fluctuations appear to be necessary and sufficient to give rise to the success of the WLC. Analysis of the molecular dynamics show that the applied force has no influence on the diffusion coefficient along the pulling coordinate (the end-to-end distance) and that the diffusion coefficient of the end-to-end distance is length independent but is position and side-chain dependent.
Results and Discussion
WLC Model and Comparison with Experiments.
The WLC model is a very popular and successful model from polymer physics to describe proteins and other biomolecules under force (1, 2, 7). The polymer is considered to be a semiflexible rod whose behavior is uniquely and totally defined by its total length (contour length Lc) and a persistence length p. This latter is a measure of the polymer local stiffness, i.e., the length scale above which the rod can be curved. Proteins are relatively flexible polymers whose persistence length is usually on the order of a nanometer (6, 17), which corresponds to the length scale of a single peptide unit.
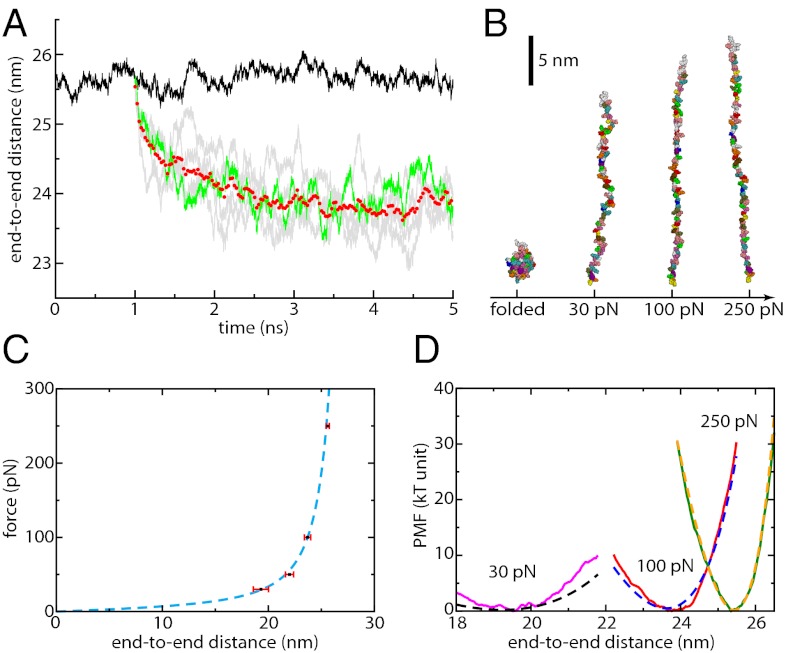
We first verify that our simulations agree with prediction from the WLC model. Trajectories of all-atom ubiquitin in explicit solvent at 300 K are generated at different forces as described in the Materials and Methods. Examples of such trajectories are given in Fig. 1A, which shows both equilibrium fluctuations of the end-to-end distance at 250 pN and how the protein shrinks when the force is reduced (force-quenched) to 100 pN. At each force, including others not depicted in Fig. 1A, equilibrium properties are averaged over tens of nanoseconds once plateauing of the end-to-end distance is observed. Typically, this takes between 3 (at 100 pN) and 60 ns (at 30 pN) after the force has been quenched. Snapshots of the protein at representative forces are shown in Fig. 1B, suggesting that, although no secondary structure is formed, the protein is not yet totally extended and exhibits some lateral fluctuations and local structure.
Fig. 1.
(A) End-to-end distance as a function of time for ubiquitin under an applied force of 250 pN (black curve). Relaxation trajectories are obtained by quenching force from 250 to 100 pN (gray curves, one highlighted in green) and averaged over five such trajectories (red circles). Equilibrium data are then accumulated once the average end-to-end distance has reached a plateau. A similar procedure is applied at other forces. (B) Snapshots of ubiquitin in a folded configuration (Left) and at different forces (30, 100, and 250 pN). Solvent molecules are not represented. (C) Force-extension profile at each force (black squares, average; red bars, standard deviation) and the corresponding WLC fit (dashed blue line). (D) PMF as a function of end-to-end distance at different forces (30 pN, magenta curve; 100 pN, red curve; 250 pN, green curve) and comparison with the WLC predictions (30 pN, dashed black curve; 100 pN, dashed blue curve; 250 pN, dashed yellow curve).
We show in Fig. 1C that the average end-to-end distances L obtained at different forces down to 30 pN, are well fitted by a WLC chain force-extension profile (see expression in Materials and Methods) with Lc = 28.4 nm [corresponding to a peptide unit’s length of 0.38 nm, in agreement with the experimental estimate of 0.4 ± 0.02 nm (18)] and p = 0.39 nm. Because the fit of the force-extension data can lead to uncertainties in the determination of the total contour length of the protein, we also use an alternate technique to estimate the peptide unit’s length that leads to the same value of 0.38 nm (SI Text and Fig. S1). The persistence length value of 0.39 nm for unfolded ubiquitin is in remarkable agreement with that obtained by AFM experiments, including some on the same protein (2, 19, 20), which suggest that simulations reach equilibrium. However, the WLC model alone is expected to break down at forces lower than 10–20 pN for then the barrier to collapse to a more compact and stable state should be low enough that hopping will be observed in the experiment on the timescale of seconds (21). For such low forces, protein simulations on a nanosecond or even a microsecond timescale might see the protein get trapped in a metastable state. As an illustration, we repeated our simulations applying a force of 15 pN and did not observe any convergence of the end-to-end distance even after 150 ns of simulation.
As force decreases, fluctuations of the end-to-end distance around its average value become more important (Fig. 1C and Fig. S2). In Fig. 1D we further compare the potential of mean force (PMF) as a function of the end-to-end distance determined in our simulations (using the umbrella sampling technique) with the WLC predictions using the parameters determined independently from the force-extension profile of Fig. 1C. A very good agreement is found at 250 pN but the PMF increasingly deviates from the WLC prediction when force is decreased. We also note that no roughness is observed in the free-energy profile (PMF) at high applied force—the PMF is very smooth. This observation contrasts with a recent suggestion that local roughness of at least 4kBT could offer an explanation to the very slow effective diffusion coefficient of the end-to-end distance in this regime of forces and extensions (12). At worst, roughness on the order of 1kBT starts appearing at the lowest force investigated, which may be explained by the existence of contacts between adjacent side chains, a feature absent from the simple WLC model (7).
The overall similarities between our simulations and the WLC model, both in the force-extension profile and in the PMF along the end-to-end distance, clearly demonstrate the applicability of the model, especially at high stretches. The absence of significant roughness suggests that the projection onto the end-to-end coordinate provides a dynamically relevant energy landscape.
Finally, one could argue that, because of the limited timescale readily accessible to our simulations, the protein could be “trapped” in a metastable state and that the end-to-end distance could further decay toward its true average value if much longer simulations were performed. Three complementary arguments suggest convergence is reached: our force-extension results agree very well with experimental data, the average end-to-end distance corresponds to the true minimum of the PMF at each force (assuming there is no trapping in the sampling of the PMF), and the timescale of internal diffusion (as discussed later) is fast enough so that a good sampling is ensured on a nanosecond timescale.
Structural Aspects of Protein Relaxation.
In the simulations of ubiquitin acted upon by forces ranging from 30 to 250 pN, no secondary structure and no native contacts between residues were observed. This is consistent with the sudden increase in length observed experimentally upon unfolding of a protein under mechanical force, which generally corresponds to the release of the totality of its amino acids (19): proteins are thus almost fully extended in this force regime. It is, however, evident from Fig. 1 that proteins at different forces exhibit distinct structural features that must be implicated in the variations of the end-to-end distance under force.
We thus examine the effect of force on the backbone degrees of freedom of a protein. Bond lengths and bend angles appear to be insensitive to the subnanonewton forces usually used in experiments (SI Text and Fig. S3). This observation may not be surprising given the magnitude and the stiffness of the associated potentials. Hence a force of 1 nN is typically required to stretch a bond (or a bend angle) by ≲5%. (Investigation of such high-energy effects would require more accurate force fields for bond bending and bond stretching, but such effects are not our main focus here.) For comparison, ubiquitin at 800 pN is more than 35% longer than it is at 30 pN. Thus, the elastic response probed in most force spectroscopy experiments does not involve the elongation of bonds and bend angles.
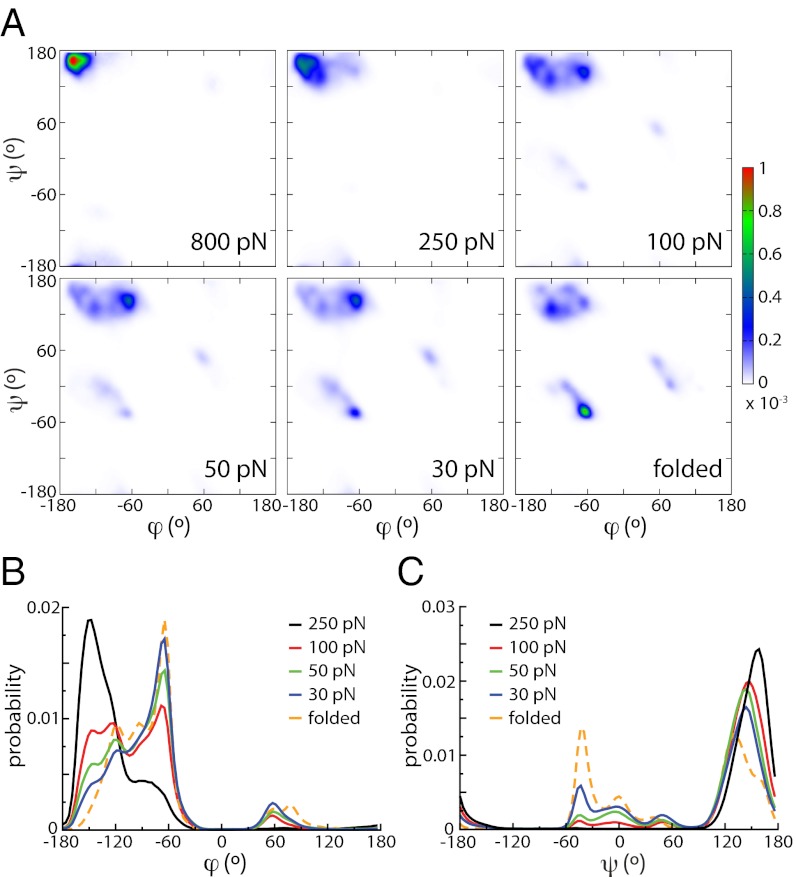
In contrast, the backbone dihedral angles usually defined as ϕ = C(−1)NCαC and ψ = NCαCN(+1) are dramatically affected by force (the third backbone dihedral angle ω = Cα(−1)C(−1)NCα is readily close to 180° in the absence of force because of the planarity imposed by conjugation). The Ramachandran plots presented in Fig. 2A illustrate these large differences. At high force (250 pN and above), most of the population is concentrated in the top left corner with (ϕ, ψ) values close to (−180°, 180°), corresponding to a fully extended backbone. The Ramachandran plot is radically different from that of the folded structure in the absence of force. Upon relaxation to more moderate forces (e.g., 50 pN), dihedral angles start exploring lower angle values and the backbone becomes more compact. The peak around (−180°, 180°) becomes more spread out and the populations at positions characteristic of the coil fragments of the Protein Data Bank (PDB) (22) grow, mainly in the polyproline II region approximately (−75°, 150°), the region that is also populated in chemically unfolded proteins (23). Nevertheless, we again stress that no secondary structure is formed.
Fig. 2.
(A) Ramachandran plots of ubiquitin (Upper, from Left to Right: 800 pN, 250 pN, 100 N; Lower, from Left to Right: 50 pN, 30 pN, and folded at no force). (B) Distribution of the ϕ dihedral angle for unfolded ubiquitin at different forces and compared with the distribution for the folded, equilibrium protein at no force. (C) Same plot for the ψ dihedral angle.
Changes are more prominent if we consider the distributions of angles ϕ (Fig. 2B) and ψ (Fig. 2C), corresponding to projections of the Ramachandran plot onto the respective axes. The two angles behave differently with force. ϕ is definitely the more sensitive (Fig. 2B): when force is lowered, the peak close to −180° progressively shifts to higher values while disappearing, and sharp peaks around −60° and 60° (similar in terms of the corresponding peptide end-to-end distance) that are absent at 250 pN rise. It is remarkable that the distribution at the lowest force investigated here (30 pN) is very similar to that of the folded structure in the absence of force. However, although the distributions are similar, they are very different in nature, as shown in SI Text. For the folded state, the heterogeneous distribution arises from static heterogeneities among the amino acid sequence, whereas under force, most of the amino acids along the sequence sample significant part of the distribution, which is therefore due to dynamic disorder (Fig. S4) (the same observation is made for the ψ angle). The force dependence of ψ is more subtle (Fig. 2C) and differs from that of ϕ in some key aspects. First, a sharp peak is present close to 180° at any force although its position shifts and its amplitude decreases as force is decreased. Even if smaller angles are found at the smaller forces, the distribution at 30 pN is markedly different from that of the folded protein. In particular, the sharp peaks between −60° and 0°, leading to shorter peptide end-to-end distance is not totally present (Fig. 2A).
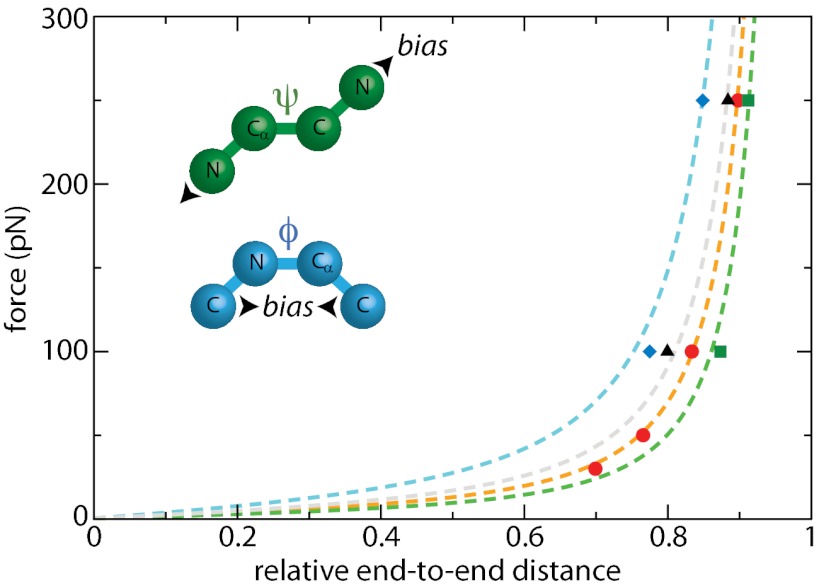
Although major variations of dihedral angles are observed upon relaxation of the force, it is still unclear at this point whether this is a cause or a consequence of the relaxation of the end-to-end distance. We now investigate whether artificially altering the dihedral free-energy surfaces in the MD simulations leads to a different WLC behavior. In realistic force fields, different types of interactions contribute to the dependence of the free-energy profile on the dihedral angles. One of them accounts for the regular nonbonded (van der Waals and electrostatic) interactions between the different atoms involved. However, this alone usually fails to reproduce the specific dihedral angle potential obtained from more precise, ab initio calculations. Some cosine-based corrections are therefore added to give better agreement with high level theory. In most cases, the magnitude of these corrections is small (∼0–1 kcal/mol) with respect to the contribution of electrostatic and van der Waals interactions. To explore the specific effect of ϕ and ψ backbone dihedral angles on the WLC behavior, we artificially modify the corresponding dihedral potentials in our simulations. To introduce a significant perturbation, we have therefore repeated our simulations using either a ψ or a ϕ potential 10 times larger than the unperturbed one (SI Text). Although of similar magnitude, these potentials fundamentally differ in that sense that they bias the angle toward 0° for ϕ but toward ±180° for ψ. The resulting end-to-end distances at two representative forces and the corresponding WLC fits are shown in Fig. 3. For this fit, we fix the contour length to be the same than that determined for the unperturbed system (28.4 nm), the persistence length being the only free parameter. To reduce the computational effort, we only repeated our simulations at 100 and 250 pN so that the results of these fits should be considered as qualitative. For high ϕ dihedral potentials, we find a persistence length p = 0.19 nm, which is one-half that of the unperturbed protein (p = 0.39 nm): in this case, the protein is more flexible because of the bias toward ϕ = 0°. On the contrary, the persistence length if using high ψ dihedral potentials is p = 0.59 nm, showing that the polypeptide is stiffer in this case. These results unambiguously show that the WLC behavior and thus protein flexibility are intimately tied to the free-energy profile along the ψ and ϕ dihedral angles. Artificial alteration of the corresponding potentials leads to different values of the persistence length.
Fig. 3.
Effect of dihedral angles and side chains on the WLC behavior (red, regular potentials; blue, biasing the ϕ potential toward 0°; green, biasing the ψ dihedral potential toward 180°; black, polyglycine analog of ubiquitin); points represent simulation data, and dashed lines show the best WLC fits using Lc = 28.4 nm.
The above study demonstrates how the applied force affects the dihedral angle distributions and through this the protein flexibility. The protein collapse upon force-quench is found to be due to a decrease in the average backbone dihedral angles whose trajectories in the Ramachandran space correlate well with that of the end-to-end distance (Fig. S5). These dihedral angles are also responsible for the fluctuations of the end-to-end length at a given force (Figs. S2 and S5).
Additional confirmation of the key role played by dihedral angles comes from the effect of side chains on protein flexibility. Earlier studies showed that a purely entropic chain analog of ubiquitin, where all attractive interaction between the protein atoms was removed, is much stiffer, with a persistence length of 1.2 nm (24) (three times larger than that of regular ubiquitin). Indeed the distribution of a given dihedral angle mainly result from both energetic and steric interactions between the atoms or groups of atoms defining this angle. We have examined the variations of ϕ and ψ for each residue independently (SI Text and Fig. S6). In most cases, fluctuations are broad and poorly correlated with the size of the side chains. Only two amino acids are found to behave very differently: glycine and proline. The proline side chain is involved in the backbone through a five-atom cycle, and it is therefore well known that it constrains dihedral orientations. For example, its ϕ remains always close to −60° for any force. For glycine, major differences are observed and both angles can explore lower angular values more easily because of the absence of a side chain. As a consequence, the end-to-end C–C distance for each glycine is more sensitive to force, and thus more flexible. Similar observations were made for short protein fragments whose flexibility is sensitive to the glycine content (25). To confirm this particular behavior, we performed simulations of an all-glycine analog of ubiquitin, i.e., a protein containing the same number of residues but all mutated to glycine. The resulting end-to-end distances as a function of applied force are shown in Fig. 3. As predicted, this homopolymer is more flexible with p = 0.31 nm, which is ∼25% shorter than that of the wild-type ubiquitin. At any force, the Ramachandran plots of polyglycine are also very different from that of ubiquitin (Fig. S7). Thus, a direct connection is made between this increased flexibility and the different distributions of dihedral angles, again showing the strong interplay between these two aspects as well as the role of side-chain interactions (both energetic and steric) in determining the persistence length.
Here, we show how dihedral angles determine a persistence length p ∼ 0.4 nm for an unfolded protein. This observation may seem in contrast with some force-ramp and constant-velocity measurements showing a static disorder of p on a second timescale among different collapse or extension trajectories (17, 26), especially at the lower forces. Possible explanations include the effect of the ionic environment of the experimental buffer solutions that could alter the dihedral free-energy profile, or the strong effect of tethering on the protein internal diffusion (14) that could result in different pathways in the Ramachandran space and in out-of-equilibrium states.
Dynamical Aspects of Protein Relaxation.
We now investigate how internal diffusion (i.e., diffusion along the end-to-end distance) in ubiquitin is affected by applied force and the resulting extension. The fast, nanosecond relaxation observed upon force-quench (Fig. 1A) at any force suggests that diffusion occurs on a very fast D ∼ 2 × 108 nm2/s timescale (using a very approximate estimation detailed in SI Text, later confirmed by more precise calculations as detailed below). These values are in close agreement to that measured in fluorescence techniques (15, 16), but five to six orders of magnitude faster than observed in atomic force spectroscopy measurements (12–14). We and collaborators have recently suggested that the observed slow diffusion coefficients seen in force spectroscopies experiments result from the viscous drag on the microscopic objects (beads, tips, surfaces) they are necessarily tethered to (14), and do not correspond to an intrinsic property of the protein. Diffusion is much faster in the simulations because in the usual steered MD setup force is directly applied to one extremity of the protein, the other one being fixed, without any intermediate tethering agent. This conclusion contrasts with that of a previous attempt to separate the dynamics of a polypeptide from that of the AFM tip it is tethered to where measured diffusion coefficients were found to be as much as six orders of magnitude smaller than those measured in bulk solution without tethers (12). These values were interpreted in terms of a frictional WLC model, predicting a power-law dependence of friction on force as F3/2, and also that friction is inversely proportional to the protein contour length Lc. Fair agreement was claimed to be found between this model and the experimental data (12). These results are surprising because one would expect that force would only affect the free-energy surface on which the protein is moving, not the diffusion dynamics itself. Interestingly, another popular model [the Rouse model (27)] has been recently applied to interpret simulation results on diffusion dynamics of short polypeptides under force (28) and that of unfolded proteins in Förster resonant energy transfer experiments (29). The protein is modeled as a chain of N beads connected by springs. Although such aspect was not the focus of these previous works, this model predicts that diffusion along the end-to-end distance slows down as N increases, i.e., as Lc increases.
Here, we use a method described previously (30, 31) to estimate D at different positions and forces (SI Text and Fig. S8). Briefly, an additional harmonic potential bias is used to constrain the end-to-end distance L around a target value LT. Under the assumption that the free-energy surface is locally harmonic, which is ensured by using a bias potential that is stiff enough with respect to the actual PMF, D(F, LT) is recovered from the autocorrelation function δL = L −〈L〉as 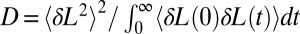 .
.
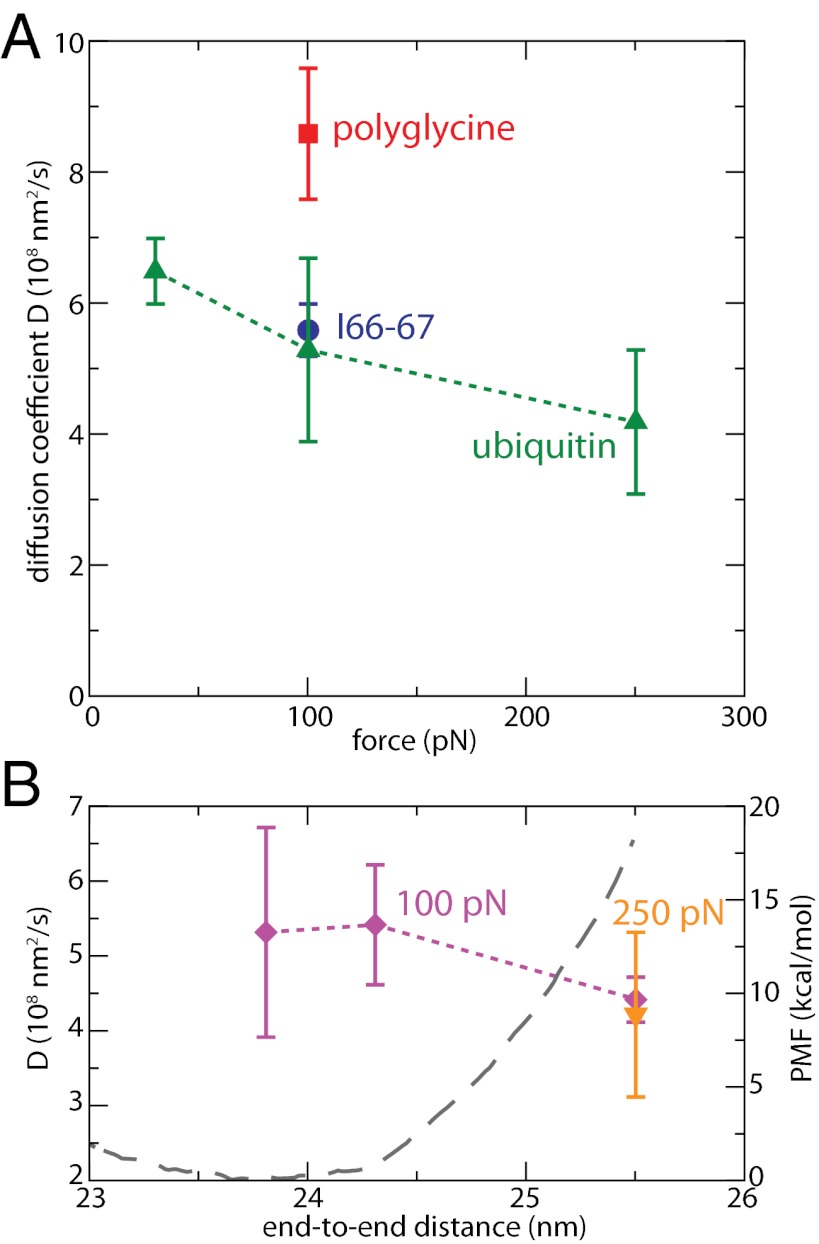
The evolution of D(F, Leq(F)) as a function of force, evaluated at the equilibrium position at each force Leq(F) (Fig. 1B), is shown in Fig. 4A. We note a very weak dependence of D upon force: when force is multiplied by ∼10, from 30 to 250 pN, D is only reduced by less than 30%, in strong contrast with the model and the measurements mentioned above (12), which would predict a difference by a factor ∼25. In addition, these surprisingly low experimental values of the internal diffusion coefficient were attributed to the roughness of the free-energy surface (12). As predicted by Zwanzig (32), local barriers of ∼4kBT would be required to explain these low effective diffusion coefficients (12). Our results rather suggest that the PMF is smooth and that no large local barriers are present, especially at high forces (Fig. 1C). As a consequence, surface roughness can probably be ruled out as an explanation of these large differences. The low values of experimentally measured diffusion coefficients may be due to the effect of the tip, which was not totally removed in the analysis of the data and has been shown to lead to such low values of the diffusion coefficient (14).
Fig. 4.
Diffusion coefficients D along the end-to-end distance. (A) D as a function of force, for regular ubiquitin (green triangles), its polyglycine analog at 100 pN (red square) and the longer I66-67 (blue circle) at 100 pN. Here, D is calculated for each force at the corresponding average end-to-end distance L. Error bars are estimated after block averaging. (B) D as a function of length at 100 pN (violet diamonds); D at F = 250 pN and L = 25.5 nm, the equilibrium position at this force, is given for comparison. The PMF at 100 pN is also shown in gray dashed line.
Instead, we propose that the observed (weak) force dependence at the respective equilibrium end-to-end distances is in fact a position dependence. When we repeat the measurement for L = 25.5 nm (equilibrium distance at 250 pN) and F = 100 pN (Fig. 4B), the respective diffusion coefficients at 100 and 250 pN are very similar, suggesting that, for a given protein configuration, increasing force does not lead to a larger friction coefficient. Force’s effect on friction is rather indirect, simply altering the PMF (Fig. 1D) and subsequently the average end-to-end distance. In the absence of force, the extent of the variations of D along the PMF describing folding and unfolding is still controversial, although it was shown to strongly depend on the coordinate that was considered (33). However, the observed changes are often smaller than one order of magnitude. Some studies have suggested that these changes occur because of the formation of native contacts such as hydrogen bonds, locally increasing the friction around specific positions (28, 33). For an extended polypeptide under force, we do not observe any strong position dependence over the limited range accessed by the protein (Fig. 4A): L varies between ∼20 and ∼25 nm over the 30- to 250-pN force range. At a given force, a similar weak dependence is observed along the PMF (Fig. 4B), mostly lying within error bars. These results are in agreement with our prior observation that neither secondary structure nor native contacts are formed at these forces.
To investigate the length dependence of the diffusion coefficient, we have performed simulations of a 188-residue fragment of the giant protein titin consisting of the two domains I66 and I67 (9) using the same setup as already discussed for ubiquitin. Ig domains of titin have been extensively studied by force spectroscopy techniques (2, 9) and we have chosen this system both for convenience and to show that our conclusions hold for a protein very different from ubiquitin. In particular, this unfolded fragment is much longer, reaching an average end-to-end distance Leq(250 pN) = 63.0 nm at 250 pN. The resulting value of D is shown in Fig. 4A and is seen to be very similar to that of ubiquitin at the same force: internal diffusion does not appear slowed down as the polymer length is increased, in strong contrast with earlier predictions (12).
The diffusion coefficients (∼ 5 × 108 nm2/s) reported here are consistent with the value of ∼8 × 108 nm2/s for the end-to-end diffusion of a short polypeptide in the absence of force and described by the same force field (34). Once corrected for threefold lower viscosity of our water model, our diffusion coefficients also closely agree with the estimate of 1.8 × 108 nm2/s from triplet-state contact quenching (16). Finally, the values obtained using very stiff biasing potentials are in fair agreement with the approximate estimation from the collapse trajectories of ∼2 × 108 nm2/s (SI Text). Now how can we relate the measured value for D with the importance of dihedral angles and side chains in providing flexibility to the protein? Because relaxation of an extended polypeptide upon force-quench is largely due to large changes in the dihedral angles, as shown above, diffusion along the end-to-end distance is likely to correspond to diffusion along the dihedral coordinates. Indeed, our results are in surprisingly good agreement with previous calculations on the dialanine dimer in water (30), where diffusion along the ω (Cα(−1)C(−1)NCα) dihedral angle was found to be almost position independent and close to ∼0.2 rad2/ps. Once converted in terms of end-to-end distance using the relationship D(L) = D(ω) × (dL/dω)2, the values correspond to ∼1−5 × 108 nm2/s in the 180–90° range, reaching a maximum at 90°. Although the system is different and another dihedral coordinate has been considered, the agreement is remarkable. In particular, the small increase in D when L decreases coincides with the increase in (dL/dω) in the 180–90° range for a fixed value of diffusion along the dihedral coordinate. Therefore, the internal diffusion of protein under force shows striking similarities with the diffusion along dihedral coordinates. A direct consequence is that the importance of side chains is nonnegligible: diffusion of the polyglycine analog of ubiquitin is almost twice as fast as that of regular ubiquitin at similar extension and force (Fig. 4A).
Concluding Remarks
In this paper, we combine molecular dynamics simulations of a full protein system in explicit solvent to uncover some key molecular aspects of protein elasticity under force. We first show that, at forces F ≥ 30 pN, the WLC model successfully explains the simulation data, especially at high applied force. Both the contour length and the persistence length are in very good agreement with available experimental data. We find evidence for a very strong interplay between the protein elasticity and the response of the backbone dihedral angles to force, and show how this interplay leads to the success of the WLC model. We provide a sensitivity analysis of different classes of dihedral angles to force, and show how side chains affect the persistence length of proteins through their effect on the exploration of backbone dihedral space. For example, we show that a polyglycine analog is ∼25% more flexible than a regular protein. Finally, artificial alteration of the dihedral potentials in the simulations is found to significantly affect the persistence length.
From a dynamical perspective, we show that the applied force should have practically no influence on the diffusion coefficient along the pulling coordinate (the end-to-end distance) in force spectroscopy experiments. We show that this internal diffusion coefficient is position and side-chain dependent, but length independent. Thus, applied force does not dramatically affect intramolecular friction, but does change the free-energy surface (PMF) the protein is moving along. We also show that diffusion is several orders of magnitude faster for untethered proteins in simulations than for tethered proteins (as studied experimentally), as we suggested earlier (14).
Since being introduced to treat experimental data from the first force spectroscopy measurements (1, 2), the WLC model has been very successful in a wide variety of systems and contexts. This study provides an explanation of why the WLC model has enjoyed such success based on molecular details. Our detailed analysis shows how the dihedral angles determine the protein’s persistence length and diffusion dynamics along the end-to-end distance. Protein elasticity and dynamics, especially the timescale of fluctuations along the end-to-end distance, depends crucially on how protein dihedral angles explore key regions of the Ramachandran space. Because the length scale of dihedral motions is that of a single peptide unit, it is therefore not surprising that proteins are very flexible polymers, in contrast with, e.g., nucleic acids.
Because force can modulate flexibility, this molecular picture can help complement and provide an understanding of the experimental data that simple continuous models fail to explain. Several studies have shown that when force is applied to the proteins in certain enzyme–substrate complexes, the relaxation is very sensitive to strength of the applied force, sometimes in a nonlinear fashion (4). An analysis of the kind presented here might shed light on this sensitivity.
Materials and Methods
Molecular Dynamics.
All-atom steered MD simulations of wild-type ubiquitin (PDB ID code 1UBQ) and I66-67 protein fragment (PDB ID code 3B43) in explicit solvent were carried out with the software NAMD 2.8, using the CHARMM27 force field for the protein and the TIP3P-CHARMM water model. Details about the system preparation, equilibration, calculation of the PMF, and diffusion coefficients are given in SI Text.
WLC Model.
A WLC is fully described by its contour length Lc (total length) and its persistence length p (which corresponds to the chain spatial “memory”). The end-to-end distance L of the polymer under force is approximated by Eq. 1 as follows:
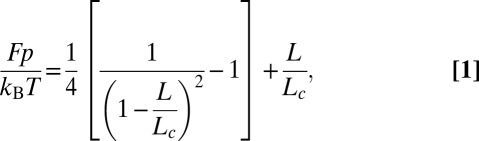 |
and the PMF force along the end-to-end distance W(L) by the following:
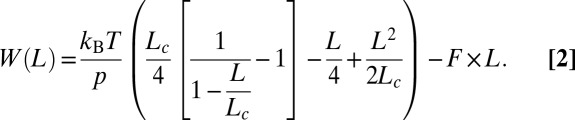 |
Supplementary Material
Acknowledgments
We thank Ronen Berkovich, Glen Hocky, and Joe Morrone (Columbia University) for fruitful discussions and comments on the manuscript. This work was supported by grants from the National Institutes of Health [NIH-GM4330 (to B.J.B.)] and in part by the National Science Foundation through TeraGrid resources provided by National Center for Supercomputing Applications (MCA08X002).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1300596110/-/DCSupplemental.
References
- 1.Bustamante C, Marko JF, Siggia ED, Smith S. Entropic elasticity of lambda-phage DNA. Science. 1994;265(5178):1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 2.Rief M, Gautel M, Oesterhelt F, Fernandez JM, Gaub HE. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 1997;276(5315):1109–1112. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- 3.Neuman KC, Nagy A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat Methods. 2008;5(6):491–505. doi: 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Perez-Jimenez R, et al. Diversity of chemical mechanisms in thioredoxin catalysis revealed by single-molecule force spectroscopy. Nat Struct Mol Biol. 2009;16(8):890–896. doi: 10.1038/nsmb.1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Merkel R, Nassoy P, Leung A, Ritchie K, Evans E. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 1999;397(6714):50–53. doi: 10.1038/16219. [DOI] [PubMed] [Google Scholar]
- 6.Schlierf M, Li H, Fernandez JM. The unfolding kinetics of ubiquitin captured with single-molecule force-clamp techniques. Proc Natl Acad Sci USA. 2004;101(19):7299–7304. doi: 10.1073/pnas.0400033101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Berkovich R, Garcia-Manyes S, Urbakh M, Klafter J, Fernandez JM. Collapse dynamics of single proteins extended by force. Biophys J. 2010;98(11):2692–2701. doi: 10.1016/j.bpj.2010.02.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thomas W. Catch bonds in adhesion. Annu Rev Biomed Eng. 2008;10:39–57. doi: 10.1146/annurev.bioeng.10.061807.160427. [DOI] [PubMed] [Google Scholar]
- 9.Hsin J, Strümpfer J, Lee EH, Schulten K. Molecular origin of the hierarchical elasticity of titin: Simulation, experiment, and theory. Annu Rev Biophys. 2011;40:187–203. doi: 10.1146/annurev-biophys-072110-125325. [DOI] [PubMed] [Google Scholar]
- 10.Rini JM, Schulze-Gahmen U, Wilson IA. Structural evidence for induced fit as a mechanism for antibody-antigen recognition. Science. 1992;255(5047):959–965. doi: 10.1126/science.1546293. [DOI] [PubMed] [Google Scholar]
- 11.Benkovic SJ, Hammes-Schiffer S. A perspective on enzyme catalysis. Science. 2003;301(5637):1196–1202. doi: 10.1126/science.1085515. [DOI] [PubMed] [Google Scholar]
- 12.Khatri BS, et al. Internal friction of single polypeptide chains at high stretch. Faraday Discuss. 2008;139:35–51, discussion 105–128, 419–420. doi: 10.1039/b716418c. [DOI] [PubMed] [Google Scholar]
- 13.Kawakami M, Byrne K, Brockwell DJ, Radford SE, Smith DA. Viscoelastic study of the mechanical unfolding of a protein by AFM. Biophys J. 2006;91(2):L16–L18. doi: 10.1529/biophysj.106.085019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berkovich R, et al. Rate limit of protein elastic response is tether dependent. Proc Natl Acad Sci USA. 2012;109(36):14416–14421. doi: 10.1073/pnas.1212167109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Haas E, Katchalskikatzir E, Steinberg I. Brownian-motion of ends of oligopeptide chains in solution as estimated by energy-transfer between chain ends. Biopolymers. 1978;17(1):11–31. [Google Scholar]
- 16.Lapidus LJ, Steinbach PJ, Eaton WA, Szabo A, Hofrichter J. Effects of chain stiffness on the dynamics of loop formation in polypeptides. appendix: Testing a 1-dimensional diffusion model for peptide dynamics. J Phys Chem B. 2002;106:11628–11640. [Google Scholar]
- 17.Walther KA, et al. Signatures of hydrophobic collapse in extended proteins captured with force spectroscopy. Proc Natl Acad Sci USA. 2007;104(19):7916–7921. doi: 10.1073/pnas.0702179104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ainavarapu SRK, et al. Contour length and refolding rate of a small protein controlled by engineered disulfide bonds. Biophys J. 2007;92(1):225–233. doi: 10.1529/biophysj.106.091561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Carrion-Vazquez M, et al. Mechanical and chemical unfolding of a single protein: A comparison. Proc Natl Acad Sci USA. 1999;96(7):3694–3699. doi: 10.1073/pnas.96.7.3694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Carrion-Vazquez M, et al. The mechanical stability of ubiquitin is linkage dependent. Nat Struct Biol. 2003;10(9):738–743. doi: 10.1038/nsb965. [DOI] [PubMed] [Google Scholar]
- 21.Berkovich R, Garcia-Manyes S, Klafter J, Urbakh M, Fernández JM. Hopping around an entropic barrier created by force. Biochem Biophys Res Commun. 2010;403(1):133–137. doi: 10.1016/j.bbrc.2010.10.133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jha AK, et al. Helix, sheet, and polyproline II frequencies and strong nearest neighbor effects in a restricted coil library. Biochemistry. 2005;44(28):9691–9702. doi: 10.1021/bi0474822. [DOI] [PubMed] [Google Scholar]
- 23.Jha AK, Colubri A, Freed KF, Sosnick TR. Statistical coil model of the unfolded state: Resolving the reconciliation problem. Proc Natl Acad Sci USA. 2005;102(37):13099–13104. doi: 10.1073/pnas.0506078102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gräter F, Heider P, Zangi R, Berne BJ. Dissecting entropic coiling and poor solvent effects in protein collapse. J Am Chem Soc. 2008;130(35):11578–11579. doi: 10.1021/ja802341q. [DOI] [PubMed] [Google Scholar]
- 25.Cheng S, Cetinkaya M, Gräter F. How sequence determines elasticity of disordered proteins. Biophys J. 2010;99(12):3863–3869. doi: 10.1016/j.bpj.2010.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li H, et al. Multiple conformations of PEVK proteins detected by single-molecule techniques. Proc Natl Acad Sci USA. 2001;98(19):10682–10686. doi: 10.1073/pnas.191189098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rouse PE. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J Chem Phys. 1953;21:1272–1280. [Google Scholar]
- 28.Schulz JCF, Schmidt L, Best RB, Dzubiella J, Netz RR. Peptide chain dynamics in light and heavy water: Zooming in on internal friction. J Am Chem Soc. 2012;134(14):6273–6279. doi: 10.1021/ja211494h. [DOI] [PubMed] [Google Scholar]
- 29.Soranno A, et al. Quantifying internal friction in unfolded and intrinsically disordered proteins with single-molecule spectroscopy. Proc Natl Acad Sci USA. 2012;109(44):17800–17806. doi: 10.1073/pnas.1117368109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hummer G. Position-dependent diffusion coefficients and free energies from bayesian analysis of equilibrium and replica molecular dynamics simulations. New J Phys. 2005;7:34. [Google Scholar]
- 31.Straub JE, Borkovec M, Berne BJ. Calculation of dynamic friction on intramolecular degrees of freedom. J Phys Chem. 1987;91:4995–4998. [Google Scholar]
- 32.Zwanzig R. Diffusion in a rough potential. Proc Natl Acad Sci USA. 1988;85(7):2029–2030. doi: 10.1073/pnas.85.7.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Best RB, Hummer G. Coordinate-dependent diffusion in protein folding. Proc Natl Acad Sci USA. 2010;107(3):1088–1093. doi: 10.1073/pnas.0910390107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yeh IC, Hummer G. Peptide loop-closure kinetics from microsecond molecular dynamics simulations in explicit solvent. J Am Chem Soc. 2002;124(23):6563–6568. doi: 10.1021/ja025789n. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.