Real-time 3D imaging of Haines jumps in porous media flow

Abstract

Newly developed high-speed, synchrotron-based X-ray computed microtomography enabled us to directly image pore-scale displacement events in porous rock in real time. Common approaches to modeling macroscopic fluid behavior are phenomenological, have many shortcomings, and lack consistent links to elementary pore-scale displacement processes, such as Haines jumps and snap-off. Unlike the common singular pore jump paradigm based on observations of restricted artificial capillaries, we found that Haines jumps typically cascade through 10–20 geometrically defined pores per event, accounting for 64% of the energy dissipation. Real-time imaging provided a more detailed fundamental understanding of the elementary processes in porous media, such as hysteresis, snap-off, and nonwetting phase entrapment, and it opens the way for a rigorous process for upscaling based on thermodynamic models.

There are several important processes in nature and technology that present particularly complex problems for our understanding of the nonsteady flow of multiple immiscible phases in porous structures. In sedimentary rocks, these processes include carbon and nutrient cycling in the critical zone, the spread and long-term fate of sequestered carbon dioxide (1, 2), the mobilization of trapped hydrocarbon phases in enhanced oil recovery (3), and drying processes (4); they also include mass transfer in porous catalysts (5) and membrane-based fuel cells (6). The most widely accepted criterion for partitioning the pore space of porous materials is based on a cellular, equivalent-capillary conceptualization of individual pores, in which individual pore bodies are divided by openings or constrictions and, when delineated this way, contribute to a characteristic pore-size distribution. This concept is most relevant to the hydraulic behavior of two-phase immiscible fluids such as water and air in (porous) soils. A particularly intricate characteristic of such flows are the “Haines jumps” (7), events showing a sudden drop in capillary pressure when the nonwetting phase (e.g., air, oil, mercury) passes from a pore neck into a wider pore body displacing the wetting phase (e.g., water), which were first recognized more than 80 y ago. This effect was studied in detail by high-resolution monitoring of capillary pressure fluctuations in very slow rate-controlled mercury porosimetry experiments (8) using the term “subison” to classify the events. The pore openings control the matrix pressure, p, at which pores empty, whereas the wider pore bodies control the pressure at which pores fill. For example, as soil dries and p decreases, water gradually retreats as the air–water interface (meniscus) becomes more curved. At the narrowest part of the filled pore opening, the meniscus can no longer gradually increase its curvature, so it suddenly retreats to the next narrow capillary constriction, emptying the pore instantaneously through this capillary. An analogous phenomenon occurs when the wetting phase front advances during wetting or imbibition. When the wetting layers in a narrow restriction between two pores touch and coalesce, an instability—called snap-off (9)—occurs, leading to disconnection and (capillary) trapping of the nonwetting phase. This phenomenon ultimately leads to hysteretic behavior in water retention curves, which is well known in soil science (10), and also affects oil recovery efficiency (3) and mass transfer in porous catalysts and membrane-based fuel cells. Measuring Haines jump pore volumes provides important information on residual nonwetting phase saturation (8) because the Haines jump pore system volume distribution represents, in principle, the size distribution of the residual nonwetting phase (e.g., oil or air) ganglia.

Filling of Pore Space

Pore-space filling in a typical fluid displacement event is controlled by the geometry of the pore itself and by the fluid distribution in the adjacent pore network, i.e., how much fluid volume is “buffered” in the menisci and available for spontaneous local rearrangement (8). When the associated intrinsic relaxation time scale is comparable to the time scale for the general advancement of fluid front propagation or an externally imposed main flow rate (11), the fluid configuration is not in capillary equilibrium (12), leading to the well-known rate dependency of the flow parameters (11, 12), which is not captured by the commonly used two-phase extended Darcy description (13, 14).

These rapid pore-scale events are essential to the upscaling of multiphase flow because they make up a significant fraction of the energy dissipation within the system (15, 16) and contribute to relative permeability (14) and to macroscopic nonequilibrium effects (12). An estimate of the Helmholtz free-energy balance (15), ΔF, of the Haines jumps, using

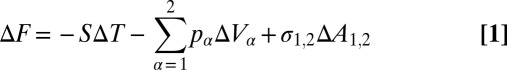now can be made on the basis of the pressure–volume work, −pΔV, and changes in interfacial energy, σ_1,2ΔA_1,2, where σ_1,2 is the interfacial tension and ΔA_1,2 is the change in interfacial area between the two fluid phases. The reliable parameterization of this fundamental equation presents the nontrivial problem of determining the characteristic volume, ΔV, and the change in interfacial area, ΔA, of the Haines jump events. These parameters are not necessarily equal to the averages determined from the pore-size distribution because typically only fractions of the connected pore space are subject to Haines jump hysteresis.

To date, the experimental quantification of pore-scale displacement dynamics has been based on constricted glass capillaries, artificial micromodels (17), glass bead packs (18), and other model systems (19) that allow in situ optical access (4). However, these systems differ from most natural systems in dimensionality (20), flow regime (18), and the degree to which displacement events contribute to energy dissipation (15, 16). Consequently, the contribution of pore-scale events to fluid displacement often has been underestimated. In classical pore-network modeling inspired by 2D micromodels, the relative permeability, k_r,α, is computed from the connected phase flow only, which leads to notable differences from the use of direct hydrodynamic approaches (21). Concepts derived from these model systems therefore may not always be applicable to natural rock, in which direct optical observation of these events is not possible because of the opacity of the minerals.

An objective of these models is to predict the state of the residual nonwetting phase (“oil”) correctly, following displacement by the wetting phase (“water”) in a porous medium. To make such a prediction, it is important to know how the pressure field affects the number and sequence of nonsteady pore-scale events, given an initial condition and the pore structure. However, it is not yet known whether more than one jump can take place simultaneously. Clearly, the jumping process causes an unsteady pressure field near the microscopic water/oil interface for which Darcy’s law no longer applies. The externally imposed displacement rate determines the number of such jumps per cross-sectional area unit and unit of time, but the ratio of the number of simultaneous to the number of successive jumps is unknown, and this is essential to provide a correct displacement length scale per unit time (11) and to predict the amount and structure of the residual nonwetting phase. Multiphase hydrodynamic simulations increasingly are capable of modeling relevant system sizes, and might correctly account for the discrete pore-scale event contributions; therefore, they may provide a means of consistently upscaling to the macroscopic scale. These simulations require adequate experimental validation by direct observation.

Three decades ago, Shell scientists adopted a medical CT (X-ray computed tomography) scanner for use with geological samples (22–24). CT techniques gradually matured since then and now are capable of a spatial resolution in the micrometer range (micro-CT, “μ-CT”) suitable for mesh computational fluid dynamics, with the now visible complex pore space (1, 25–34). However, the temporal resolution of μ-CT needed to be improved to visualize the relevant pore-scale processes. The work presented here makes a contribution to a key aspect of pore-scale visualization. Never before have pore-scale displacement events in natural sandstone been visualized directly at a time resolution matching their actual occurrence using dynamic micro–X-ray CT. This method previously could be used only at time resolutions that were some orders of magnitude too low [typical scanning times at synchrotron beamlines were on the order of 1 h (26) in 2001 and 5 min in 2011 (32)] compared with the intervals between individual pore-scale displacements, which are on the order of seconds (35), and the intrinsic time scales for relaxation and fluid rearrangement. Therefore, the method could be used only to investigate quasistatic situations in which flow had been stopped before taking a scan to avoid fluid motion and blurring effects during scanning. However, after flow stopped, i.e., pressure gradients ceased, fluids were rearranged in a static capillary equilibrium. Hence, when flow resumes, pore-scale fluid distributions typically are different from when the flow was stopped. Here, we report the dynamic imaging of pore-scale displacement using fast synchrotron-based μ-CT (36), which differs from the previously discussed quasistatic imaging in that flow, pressure gradients, and the viscocapillary balance are always maintained (also during imaging). By comparison with pressure data recorded at subsecond time resolution, we demonstrate later that a temporal resolution of 10–30 s actually is sufficient to capture pore-scale fluid distributions of uninterrupted Haines jump sequences. Using this method at millisecond exposure time for each projection (36) (Methods and Materials), we could create a time series of visualized individual pore-filling events under drainage conditions, with oil displacing the water that initially was present in the rock, as shown in Figs. 1–3 (with respective pressure data displayed in Fig. 4).

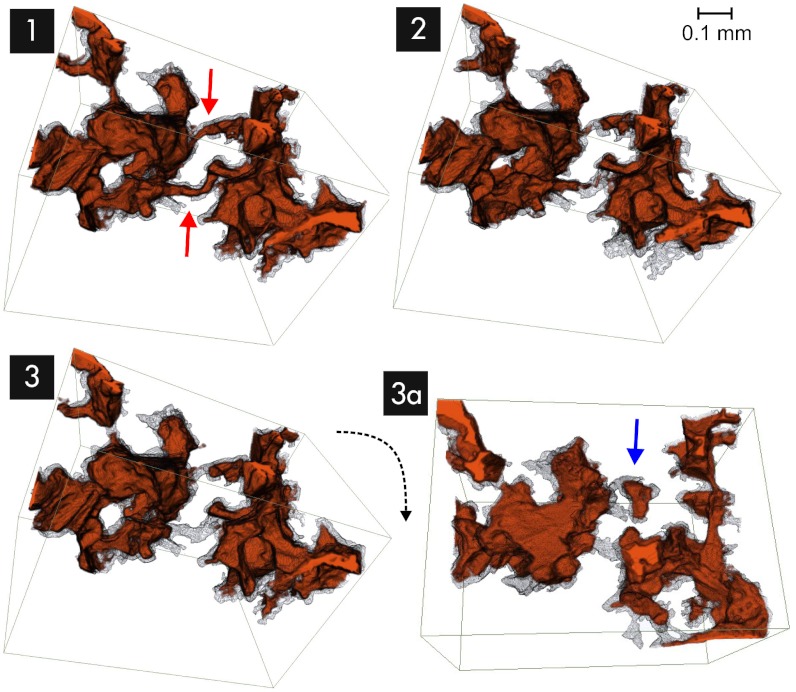
Fig. 1.

Sequence of scans during drainage, at time intervals (Δt) of 16.8 s and with a voxel size of 3 μm. The volume change (ΔV) from time steps 3 to 4 was 14 nL.

Fig. 3.

A pore system–filling event during drainage, with Δt = 16.8 s and ΔV = 34 nL, extending over several geometrically defined pores.

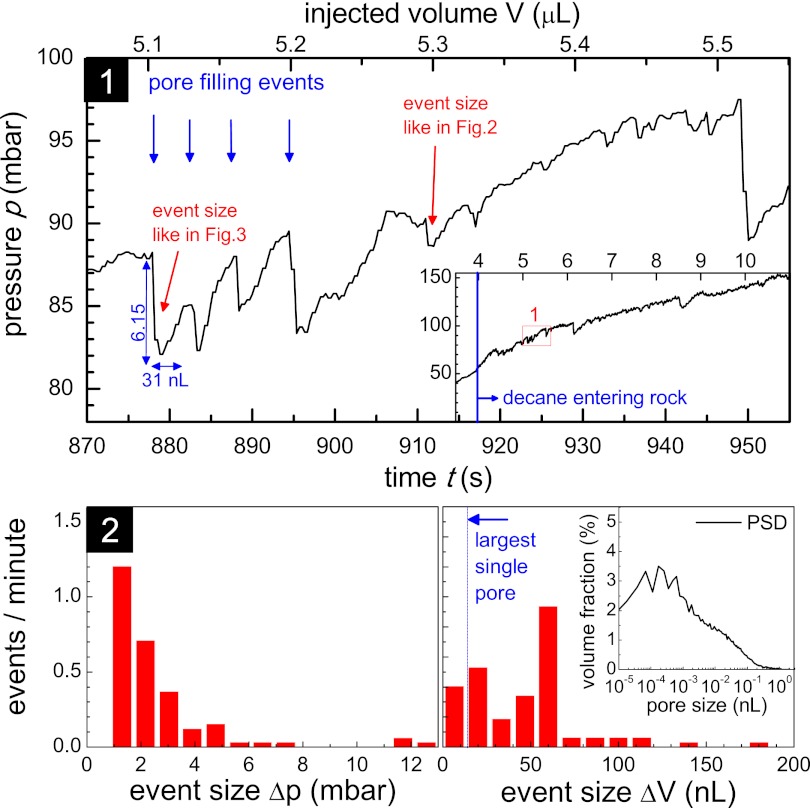
Fig. 4.

(1) Pressure drop, p, for a sequence of seven scans showing individual pore-filling events (entire drainage experiment in the Inset). (2) Δp and ΔV size distributions, with Inset showing the pore size distribution (PSD).

Snap-Off During Imbibition

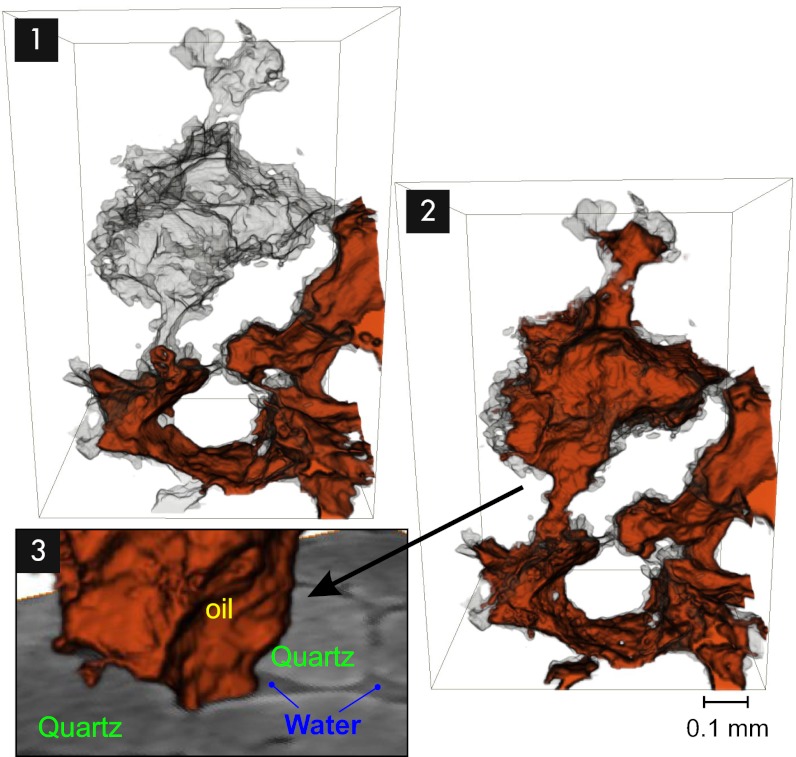
Fig. 5 shows an example of imbibition, in which the wetting phase invades the pore space and “snaps off” (9), causing the nonwetting phase to form isolated clusters at narrow pore throats (rotated view, Fig. 5, 3A). This constitutes irreducible nonwetting phase saturation. The competition between the wetting water phase at the pore throats choking the oil neck and the advancing oil head menisci jumping past the pore throats tends to favor the latter at increasing imbibition rates.

Fig. 5.

Sequence of snap-off events (time steps 1–3) during imbibition (Δt = 16.8 s) occurring at the narrowest pore throats (red arrows), leading to the trapping of oil (rotated view, 3A, blue arrow).

Cooperative Pore-Filling Events

We now consider the details of the drainage process, in which the nonwetting oil, injected at a constant rate, displaces the water initially present in the rock. The injection pressure, p, generally increases steadily, as shown in Fig. 4, as a consequence of the nonwetting oil phase being forced into the water-wet rock (3). However, a more detailed view shows that this continuous increase is modulated by many small nonsteady fluctuations (Fig. 4, Inset), as has already been observed in rate-dependent high-resolution mercury porosimetry (8). This is because once p exceeds the capillary entry pressure of a pore throat (Fig. 2), the accessible pore body volume, ΔV, is filled rapidly (11, 35). These pore-filling events (as in Figs. 1 and 2) may be seen as discrete (negative) pressure jumps in p. (Note, however, that synchronization between images and pressure curves are hampered by the fact that events documented in the pressure data may also have occurred outside the field of view, which covers only approximately one quarter of the sample.) During a jump, capillary driving forces accelerate the meniscus, which is opposed by inertial forces and the viscous resistance in the bulk fluid and rough boundary layers at the pore walls. The inertial forces initially are larger than the viscous forces, i.e., the ratio of the Reynolds and the capillary number (11) far exceeds 1, i.e., Re/Ca ≈ σρr_pore/μ² ≫ 1. In our study, Re/Ca ≈ 2⋅10³ (for r_pore = 100 μm). So, the fluid motion was capillary-inertial controlled and the jump time was estimated to be proportional to the mass of the accelerated fluid (11), i.e., as an order of magnitude estimate, 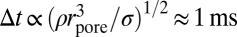, which is consistent with acoustic measurements reported by DiCarlo et al. (35). From the example shown in Fig. 2, the rate of such a pore-filling event might be estimated as ΔV/Δt = 5.9 nL/1 ms = 5,900 nL/s, which far exceeds the feed flow rate of 5.8 nL/s. The fluid volume, ΔV, required to fill a pore body is supplied mainly by fluid rearrangement (8, 15) from liquid–liquid menisci in pore throats, i.e., via the relaxation from a more to a less convex shape, accompanied by a rapid decrease in (capillary) pressure, Δp, and the dissipation of (elastic) energy. Continuous injection resupplies the volume, ΔV, building up the liquid–liquid menisci curvature and the pressure again. Finally, the pressure exceeds its magnitude before the filling event, at which point another Haines jump occurs (8).

Fig. 2.

(1 and 2) Oil-filling event in a single pore during drainage, with ΔV = 5.9 nL (subset of Fig. 1, transition from time steps 2 to 3). (3) Cross-section at the toroidal pore throat with the water wetting films and the oil neck after the transition from step 1 to 2. The rough wall causes draping menisci (collars not visible because of remaining spatial resolution limitations), essential for the presence of pressure connections for the wetting water.

In this way, the irreversible instantaneous pressure jumps and overall reversible continuous increases (15) allow fluid displacement–based partitioning of the pore space (8). Real-time imaging, however, showed that displacement-based partitioning differs from a purely geometrical definition of pore throats and pore bodies. The ΔV event size distribution for most filling events involved pores up to a factor of 10 larger than individual geometrically defined pores. (Using the pore size distribution from the imaging data shown in Fig. 4, 2, Inset for comparison, the biggest pores have a radius of ≈ 100 μm and a volume of 14 nL). Such major filling events therefore may be seen to be cooperative, involving many individual pores. They occur frequently, rather than being exceptional, as the event size histogram in Fig. 4 clearly shows. The examples shown in Figs. 1 and 3, with ΔV = 34 nL (including about 20 individual pores), agree with the Haines jump statistics obtained from pressure data (Fig. 4), making it clear that an imaging interval of a few seconds ensures that jumps are not missed. As evident from the pressure data in Fig. 4, which are sampled at a subsecond time resolution, pore-scale displacement events occur every dozens of seconds in the whole sample, typically not at the exact location but at different locations at the (disperse) flow front. Therefore, we found a time resolution between 10 and 30 s actually is sufficient to capture differences in fluid front configurations in dynamic flow experiments.

Energy Dissipation and Upscaling

In a Haines jump, the elastic energy initially contained in the liquid–liquid menisci is converted into kinetic energy, with substantial inertial contributions from the high Reynolds number (18), and finally dissipated. Our data (Fig. 4) revealed that only 39% of the displaced volume occurs through the filling of pore throats by reversible laminar flow [rison events (8)], whereas 61% occurs via rapid irreversible events [subison events (8)], which dissipated 64% of the total work of drainage, 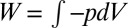, confirming previous reports on Berea sandstone (16).

Measurements of the external pressure, p, required to quantify the externally performed work, may be complemented by in situ estimation of the phase pressures; however, although this method is feasible in principle, it is still under development (37). This approach also includes the disconnected nonwetting phase clusters, through the measurement of the curvature in the liquid–liquid menisci by image analysis and by calculating the pressure using the Laplace equation. Apart from the pressure–volume work for an energy balance as formulated in Eq. 1, the newly created interface and the associated interfacial energy also must be considered. In the event shown in Fig. 2, the interfacial area, including the area in which thin water films separate oil and water-wet rock, is ΔA_1,2 = 5.7 × 10⁻⁷ m². This corresponds to an interfacial energy, for this specific event, of 36% of the displacement pressure–volume work. The remainder is dissipated, as accounted for in Eq. 1 by the entropy term −SΔT. The associated increase in temperature, ΔT, is small (a few millikelvins) and is equilibrated quickly because of the relatively large heat capacities and thermal conductivities of the surrounding liquids and solids (15).

Most approaches to upscaling from the pore to the macro scale, particularly numerical upscaling, use a volume average, but it is not clear how big the averaging volume should be, i.e., how big the two-phase representative elementary volume (REV) (38) is. Georgiadis et al. (39) showed (based on the discontinuous nonwetting phase cluster size distribution) that for two-phase flow, the averaging volume is substantially larger than the single-phase REV. In addition to the fluid (cluster) distribution, it may be important to consider the distance over which Haines jump pressure pulses (Fig. 4) can propagate, and over what volume they can be averaged, that the macroscopic two-phase properties (evaluated using the average pressure drop) are independent on averaging volume.

Niessner et al. (14) have shown that pore-scale dissipative displacement events are important contributors to macroscopic transport coefficients, leading to rate dependency. By following an argument based on reversibility and dissipation of drainage work in the framework of a thermodynamically based approach (40), it has been shown that relative permeability in the traditional two-phase Darcy formulation (3) has contributions originating from hydraulic conductivity and from dissipative pore-scale events. This leads to a saturation gradient and, implicitly, a rate dependency for the relative permeability (14), which has been observed many times (e.g., ref. 41). The consequence of this is that commonly used steady-state (no saturation gradient) and unsteady-state [large saturation gradient caused by the Buckley–Leverett shock front (42)] techniques for measuring relative permeability give different results (e.g., ref. 43).

Materials and Methods

A cylindrical sample of Berea sandstone (44) [4-mm diameter and 10-mm length, approximately three times the REV (38), with open porosity ∼19.9% and permeability ∼700 millidarcies = 0.7 μm² measured on a twin sample] was fitted tightly inside a polycarbonate cylinder and initially saturated with water [with 40% (wt/wt) CsCl to increase the X-ray contrast] with a free-water level 1 mm above the top of the sample. A micro–piston pump integrated into the sample holder (our own design) is the key to conducting experiments without displacement artifacts caused by the bending of external flow lines during rotation during X-ray tomography or when opening and closing the valves. For drainage experiments, n-decane was injected from bottom to top at a constant flow rate of 0.35 μL/min, corresponding to a linear flow velocity of 1.54 μm/s (0.4 ft/d) and a (microscopic) capillary number, Ca, of 4 × 10⁻⁸ (at an interfacial tension of 35 mN/m determined by the pendant-drop method), which is representative of typical (field-relevant) viscocapillary flow regimes (3). A piezoresistive miniature pressure sensor (Keller 2 Mi) recorded the injection pressure (at a rate of 3 Hz), which for the open outlet configuration, approximately corresponded to the pressure drop over the sample plus the ambient pressure. The X-ray tomography experiments were performed at the TOMCAT beamline at the Swiss Light Source, Paul Scherrer Institut, Villigen, Switzerland. The sample was exposed to a parallel beam of monochromatic synchrotron X-ray radiation at 21.25 keV. The transmitted X-rays were converted into visible light by a 100 μm–thick cerium-doped lutetium aluminum garnet (LAG) scintillator and projected at 3.7× magnification onto a high-speed CMOS camera (pco.dimax; PCO AG) with 1,440 × 896 pixels, leading to an effective voxel width of 3 μm and a field of view covering approximately a quarter of the sample, starting at 2 mm from the bottom of the sample. A sample–detector distance of 80 mm gave a small amount of edge enhancement in the images. Each tomogram was computed from 1,401 projections (12 ms exposure time) over 180° rotation (leading to a total acquisition time of 16.8 s) by a gridded Fourier transform–based reconstruction algorithm (45) with a Parzen filter. The projections for seven tomograms were recorded in series, limited only by the camera memory (36 GB). The reconstructed volumes were filtered with a 3 × 3 × 3 median filter, segmented with local connectivity-based thresholding, and processed furthered and visualized using Avizo (Visualization Sciences Group). The pore size distribution was determined with GeoDict (Fraunhofer ITWM) using a maximum sphere algorithm. The pressure data were analyzed using Matlab (MathWorks Inc).

Overall, four experiments were performed that showed similar behavior, and in each experiment, events of comparable magnitude were similar, but only the data with best quality after image processing were selected for this publication.