Abstract
Outer hair cells (OHCs) drive cochlear amplification that enhances our ability to detect and discriminate sounds. The motor protein, prestin, which evolved from the SLC26 anion transporter family, underlies the OHC’s voltage-dependent mechanical activity (eM). Here we report on simultaneous measures of prestin’s voltage-sensor charge movement (nonlinear capacitance, NLC) and eM that evidence disparities in their voltage dependence and magnitude as a function of intracellular chloride, challenging decades’ old dogma that NLC reports on eM steady-state behavior. A very simple kinetic model, possessing fast anion-binding transitions and fast voltage-dependent transitions, coupled together by a much slower transition recapitulates these disparities and other biophysical observations on the OHC. The intermediary slow transition probably relates to the transporter legacy of prestin, and this intermediary gateway, which shuttles anion-bound molecules into the voltage-enabled pool of motors, provides molecular delays that present as phase lags between membrane voltage and eM. Such phase lags may help to effectively inject energy at the appropriate moment to enhance basilar membrane motion.
Keywords: hearing, molecular motor
Outer hair cells (OHC) foster mechanical feedback within the mammalian cochlear partition that enhances perception of auditory stimuli by 2–3 orders of magnitude; this is known as cochlear amplification (1, 2). Following the molecular identification of prestin (3), an SLC26 family member (a5) that recapitulates the electromechanical properties of the native OHC's voltage sensor/motor (4, 5), a preponderance of evidence pointed to prestin-based electromotility (eM) as the basis of this boost (6, 7). During the last couple of decades, measures of nonlinear charge movement or capacitance (NLC), an electrical correlate of voltage-dependent conformational changes within the motor protein prestin, have served as surrogate, indeed as signature, of voltage-evoked eM of the OHC (8–12). Intracellular chloride plays an important role in prestin function (13), and recent evidence indicates that anions serve a modulatory, allosteric-like role (14–17). For the most part, anion effects, as well as many other influences on prestin, have been limited to the study of NLC, on the assumption that NLC reports on steady-state characteristics of OHC eM. We now show that this assumption is wrong.
Using simultaneous measures of charge movement and eM, we show disparity between deduced characteristics of prestin motor protein conformation. That is, a dissociation in magnitude and voltage dependence of NLC and eM is revealed by lowering intracellular chloride to physiological levels (≤ 10 mM; ref. 6), all previous comparisons having been made with abnormally high intracellular chloride levels. Furthermore, this chloride effect, which presents as a function of rate and polarity of voltage stimulation, uncovers a mechanism predicted to be frequency dependent in vivo, and likely plays an important role in frequency selectivity and efficiency of cochlear amplification. A very simple kinetic model, which recapitulates most known behaviors of prestin, indicates that the chloride effect is due to intermediary, non-voltage-dependent transitions, the kinetics of which are very much slower than those of prestin’s chloride-binding or voltage-dependent state transitions. These slow conformational changes likely derive from prestin’s lineage as a slow anion transporter, providing lags between voltage stimulation and mechanical activity, possibly contributing to productive cochlear amplification.
Methods
Recordings were made from single isolated OHCs from the organ of Corti. Hartley albino guinea pigs were overdosed with isoflurane, the temporal bones excised, and the top turns of the cochleae dissected free. Enzyme treatment (1 mg/mL Dispase I, 10 min) preceded gentle trituration, and isolated OHCs were placed in a glass-bottom recording chamber. A Nikon Eclipse E600-FN microscope with 40× water immersion lens was used to observe cells during voltage clamp. Experiments were performed at room temperature.
Solutions.
Chloride levels were set to bracket the intracellular level in intact OHCs, namely ∼10 mM (6). An ionic blocking solution was used to remove ionic currents, allowing valid measures of membrane capacitance. The base high Cl solution contained (in millimoles): NaCl 100, tetraethyl ammonium-Cl 20, CsCl 20, CoCl2 2, MgCl2 1, CaCl2 1, Hepes 10. Lower chloride concentrations (10 and 1 mM) were achieved by substituting chloride with gluconate. In a subset of experiments, aspartate was used as the substitute. Base intracellular solutions contains (in millimoles): CsCl 140, MgCl2 2, Hepes 10, and EGTA 10. The intracellular and extracellular Cl concentration was set the same to guarantee levels in the subplasmalemmal space of the OHC.
Manipulation of the subsurface cytoskeletal integrity was made with diamide and latrunculin. Diamide works on spectrin to unbundle actin filaments and reduce OHC stiffness (18). On the other hand, latrunculin results in actin depolymerization (19). OHCs were treated with 2 mM diamide in extracellular solutions for 30 min before recordings. Latrunculin A (0.01 µM) was perfused both intracellularly (via patch electrode) and extracellularly during recording. All chemicals used were purchased from Sigma.
Cell Capacitance and Mechanical Response.
An Axon 200B amplifier was used for whole cell recording. Coupled voltage ramps (depolarizing followed immediately by hyperpolarizing ramp) of varying durations from 100 to 5,000 ms were delivered to the cells from a holding potential of 0 mV. In a subset of cells, ramp order was reversed after routine collection and comparison of the two yielded no significant differences. The ramp voltage was set between –250 and +250 mV maximum, but span was fixed at 360 mV. For each individual cell, the ramp voltage was set according to Vh of NLC permitting responses to reach steady state to ensure good Boltzmann fits. No averaging was done.
Nonlinear capacitance was measured using a continuous high-resolution (2.56-ms sampling) two-sine stimulus protocol (10 mV peak at both 390.6 and 781.2 Hz) superimposed onto the voltage ramp (20, 21). Capacitance data were fit to the first derivative of a two-state Boltzmann function (9) (see Supporting Information for equation), providing Qmax, the maximum nonlinear charge moved, Vh the voltage at peak capacitance or equivalently, at half maximum charge transfer, z, the valence, and Clin, the linear membrane capacitance.
Simultaneous eM measurements were recorded with a Prosilica GE680 camera (Allied Vision Technologies). Video sampling of 3.3 ms were achieved with binning and reduced region of interest. Video image resolution was 2.83 pixels per micrometer. The eM video recordings were digitally analyzed with jClamp (www.SciSoftCo.com), allowing synchronous assessment of eM and NLC in time and voltage. The edge of the cuticular plate was used to track OHC length change, the patch electrode providing a fixed point at the basal end of the cell. Sigmoidal fits (four parameters) provided estimates of Vh, maximal movement and slope factor b. Shift of motility against NLC is calculated by subtracting NLC Vh from eM Vh.
Model Assessment.
The kinetic model was assessed using Matlab Simulink in conjunction with jClamp. jClamp provides an automation link to Matlab, which allows voltage stimuli to be delivered to and current responses to be obtained from Simulink models. The kinetic model was interfaced to jClamp via a model of the patch clamp amplifier and OHC. The linear component of the patch-cell model possessed an Rs of 5 MΩ, Rm of 500 MΩ, and Clin of 15 pF. The nonlinear component, NLC derived from charge movement of the prestin model, parameters laid out in Results. The exact same voltage stimuli and exact same analysis of model two-sine currents were performed as with the biophysical data. Mechanical contraction data of the model, namely eM, was taken as the accumulated residence in the C state. Fits of model NLC and eM were performed the same way as the biophysical data.
Although this parallel approach provides for powerful comparisons between model and biophysical data, it is laborious. Thus, only visual “fits” to the data are presented because no automatic iteration is possible. Instead, each set of model parameters was selected and compiled in Matlab. Then jClamp was used to stimulate, collect, and analyze the resulting model data, as was done with OHCs. The data were then plotted for comparison with biophysical data, followed by visual determination of goodness of fit. Another choice of model parameters was then made and the process repeated. In consequence, an enormous amount of time was invested in obtaining model data.
Results
Experiment.
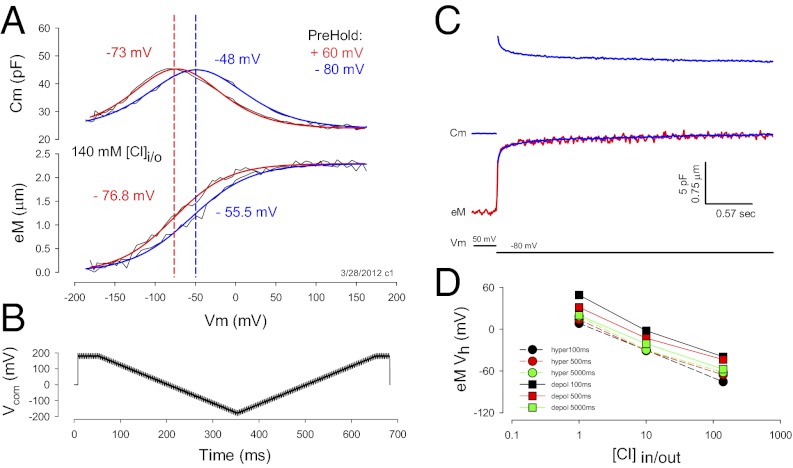
Under voltage clamp, OHCs display an NLC that is bell shaped with its peak magnitude residing at a voltage (Vh), where prestin’s charge is equally distributed on either side, similar in behavior to an ionic channel’s voltage-sensor charge (22) (Fig. 1A). Coupled to this nonlinear charge movement is a mechanical response of the whole cell (a length change; eM) that follows the charge’s voltage dependence. Shifts in NLC Vh along the voltage axis, known to be induced by changing the long-term holding potential (prepulse) of the OHC or prestin-transfected cells (4, 20, 23), are accompanied by corresponding shifts in eM voltage dependence. In this example (Fig. 1A), a Vh shift of 25 mV for OHC NLC arises, along with a parallel Vh shift of 21.3 mV for eM. Furthermore, Fig. 1C illustrates that the time course of OHC length change follows the time course of NLC during step voltage stimulation, each showing stretched (multi) exponential behavior (23). This tight coupling between NLC and eM is observed when intracellular chloride is high, e.g., 140 mM, the typical intracellular level used for experimentation during the last few decades to study OHCs.
Fig. 1.
Nonlinear capacitance and eM are coupled. (A) OHCs possess a capacitance that is nonlinear with voltage. Its peak resides at a voltage, Vh, that changes depending upon holding potential. In this case, Vh is −73 mV after holding the cell at +60 mV for one minute (red line). Vh shifts to −48 mV after holding the cell at −80 mV for one minute (blue line). Similar shifts are observed for eM. Fits: (red) NLC Vh −73.10, z 0.69, Qmax 3.15, Clin 23.86; eM Vh −76.81, b 33.96, eMmax 2.42; (blue) NLC Vh −48.76, z 0.63, Qmax 3.42, Clin 23.90; eM Vh −55.48, b 37.13, eMmax 2.41. (B) Voltage stimulus used for the collection of capacitance and eM. Dual sine superimposed on ramps is used to evaluate Cm (Methods). Measures shown in A were obtained with hyperpolarizing ramps. The effects of ramp duration and polarity are described in subsequent figures. (C) A step voltage from 50 to −80 mV induces an elongation of the OHC (red trace) and simultaneous jump in Cm (blue trace). Cm relaxes with a stretched (multi) exponential time course that is mirrored by eM. The Cm trace was inverted, scaled and overlaid onto the eM trace (blue trace on red), showing similar time courses. (D) eM shifts in the depolarizing direction when intracellular chloride is reduced. The eM and NLC were measured simultaneously with hyperpolarizing and depolarizing ramps at the indicated ramp durations/rates. Regardless of polarity or rate, a large shift of Vh is observed, but the absolute values of Vh are more depolarized with longer depolarizing ramps. Number of cells averaged is the same as indicated in Fig. 3 A–C. SEs are not plotted for clarity. They are for 1, 10, and 140 mM Cl: black squares, 4.5, 3.7, and 3.8 mV; red squares, 5.0, 3.8, and 2.7; green squares, 7.3, 3.8, and 9.6; black circles, 4.6, 4.2, and 3.8; red circles, 3.5, 5.2, and 4.3; and green circles, 5.4,6.0,and 10.6.
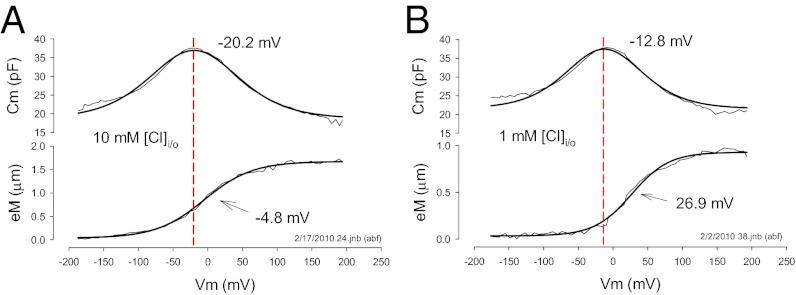
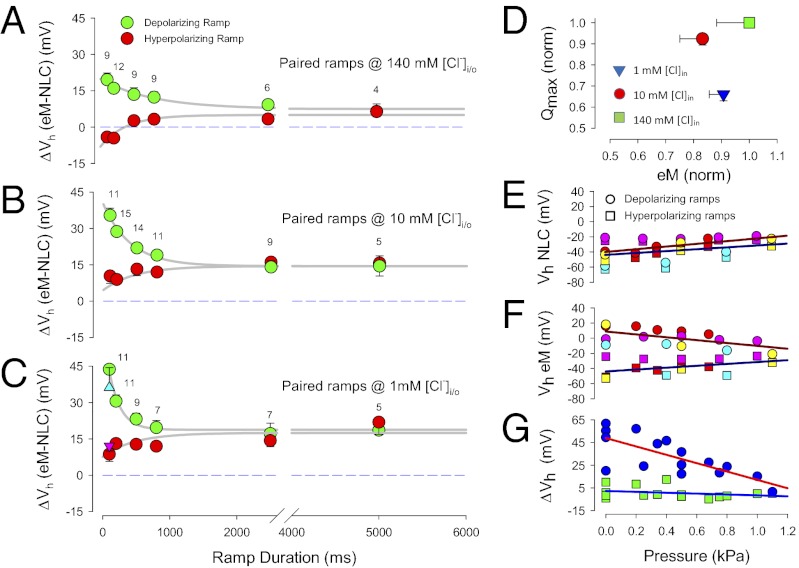
Recently, the level of intracellular chloride was estimated to be ≤10 mM in OHCs (6). As noted above with hyperpolarizing prepulses, lowering intracellular chloride is known to shift NLC Vh to depolarized levels (14). We confirm that the same is true for eM (Fig. 1D). Here, voltage ramps (±180 mV) of different duration/rate (100–5,000 ms or equivalently 4–0.08 mV/ms) and polarity drove eM, while simultaneously summed high-frequency dual-sine stimuli reported on NLC (see Methods for details; refs. 20, 21). Although eM Vh shifted to depolarized levels regardless of protocol rate, the faster depolarizing ramps produced a more depolarized Vh. It was surprising that, although lowering intracellular chloride levels shifts both NLC Vh and eM Vh to positive voltages, a disparity between Vh of NLC and eM arises (Fig. 2). As chloride levels reduce, Vh of eM is shifted further to the right than Vh of NLC. In the examples shown, 10 mM chloride produced a disparity of 15.3 mV, and 1 mM chloride produced a disparity of 39.7 mV. This disparity is dependent not only on chloride level, but also on rate and polarity of voltage ramp stimulation (Fig. 3 A–C). Note that there is a chloride-dependent ΔVh disparity that is greater in the depolarizing ramp direction as rate is increased, reaching an average disparity of about 45 mV with depolarizing 100-ms ramps; but even at very slow ramp rates, a chloride-dependent disparity remains. A large disparity is also observed when we instead use aspartate to replace chloride (Fig. 3C). Finally, there is a decrease in disparity with shorter ramp durations in the hyperpolarizing direction, and with 140 mM chloride, little disparity exists, which accounts for assertions of good electromechanical coupling during the last couple of decades (8–12).
Fig. 2.
Reduction of intracellular chloride toward physiological levels reveals disparity in NLC and eM operating voltage range. (A) The 10 mM chloride condition evidences a Vh disparity of 15.3 mV with eM more depolarized than NLC. Fits: NLC Vh −20.15, z 0.59, qmax 3.17, Clin 18.66; eM Vh −4.87, b 34.58, eMmax 1.64. (B) Under 1 mM chloride conditions the disparity is larger, namely, 39.7 mV. Fits: NLC Vh −12.87, z 0.68, qmax 2.38, Clin 21.50; eM Vh 26.92, b 26.78, eMmax 0.9.
Fig. 3.
The eM and NLC are disparate. (A) The eM and NLC operating voltage disparities are dependent on chloride levels, ramp durations/rates, and polarity. With 140 mM chloride intracellular, polarity effects are symmetrical but offset in the depolarizing direction. (B) For 10 mM chloride, the offset is larger, and a depolarizing asymmetry arises at short ramp durations. (C) With 1 mM chloride, the depolarizing offset is larger still, and the depolarizing asymmetry at short ramp durations is also greater. Errors bars are SE and numbers of cells are indicated. Triangles (up, blue: depolarizing ramp; down, purple: hyperpolarizing ramp) depict results obtained with aspartate as the chloride substitute at 100 ms duration ramp. Compare with model results in Fig. 5 B–D. (D) Qmax and eMmax are not strictly correlated. Normalized Qmax and eMmax are derived from 500 ms hyperpolarizing ramp data. As chloride levels decrease, Qmax decreases, but eM does not follow. Error bars are SE, number as in Fig. 3 A–C. Compare with model results in Fig. 5E. (E) Membrane tension reduces Vh disparity between eM and NLC. Vh of NLC shifts in the depolarizing direction with increase in membrane turgor pressure regardless of ramp polarity. (F) Vh of eM also shifts in the depolarizing direction with hyperpolarizing ramps as tension increases. However, eM Vh shifts in the hyperpolarizing direction when measured with depolarizing ramps. (G) Net effect of shifts in Vh is to reduce Vh disparity as membrane tension increases. ΔVh obtained by subtraction of data in A and B; n = 4. Compare with model results in Fig. 5 F–H.
In addition to disparity in voltage dependence, there is disparity in correspondence between maximal charge movement (Qmax), estimated from Boltzmann fits to NLC, and maximal eM (eMmax), estimated from sigmoidal fits to eM. Qmax has been taken to report on the number of elementary charged motors (prestin) in the OHC (8, 9), and consequently, there is a correlation between prestin surface expression and Qmax (24). Because it is undisputed that prestin conformational changes drive eM (25), the number of active prestin molecules should correspond to measures of eM, with eMmax correlated with Qmax. Fig. 3D shows that this is not the case; that is, although chloride reduction significantly reduces Qmax, eM does not follow. For example, eMmax values (mean ± SE in micrometers; n = 9–14) for 500-ms hyperpolarizing ramps were 2.19 ± 0.12 @ 1 mM; 2.01 ± 0.20 @ 10 mM; and 2.41 ± 0.28 @ 140 mM chloride. Corresponding Qmax values (mean ± SE in picocoulombs, n = 9–12) were 2.04 ± 0.09, 2.86 ± 0.09, and 3.10 ± 0.03. Neither eMmax nor Qmax magnitude was significantly different for hyperpolarizing or depolarizing ramps. The slope factor (b; Methods) of eM with 140 mM at this 500-ms ramp rate was 34.8 ±> 0.84 mV, which translates to 17.3 nm/mV maximal sensitivity (eMmax/4b). This is similar to previously reported values (26, 27).
Iwasa (28) first identified the membrane tension dependence of OHC NLC and introduced a mechanical energy term in the Boltzmann model of prestin (29). In confirmation of its molecular nature, tension dependence was subsequently shown to have direct action on the motor/prestin (4, 5, 10). The susceptibility of fast ramp rate effects to perturbations of whole-cell mechanics is illustrated with turgor pressure manipulations (Fig. 3 E–G). Increasing turgor pressure, which increases membrane tension, eliminates the disparity (ΔVh) evidenced with 100-ms ramps. Also revealed are disparate changes in Vh of NLC and eM. Whereas, the Vh of NLC shifts in the depolarizing direction during increases in membrane tension regardless of ramp polarity, the direction of Vh shift of eM depends on ramp polarity. That is, hyperpolarizing ramps cause near-equivalent depolarizing shifts in Vh of eM and NLC; depolarizing ramps, on the other hand, cause a hyperpolarizing shift in eM Vh. It is this differing behavior that accounts for the elimination of ΔVh during increases in membrane tension, and points to a molecular phenomenon.
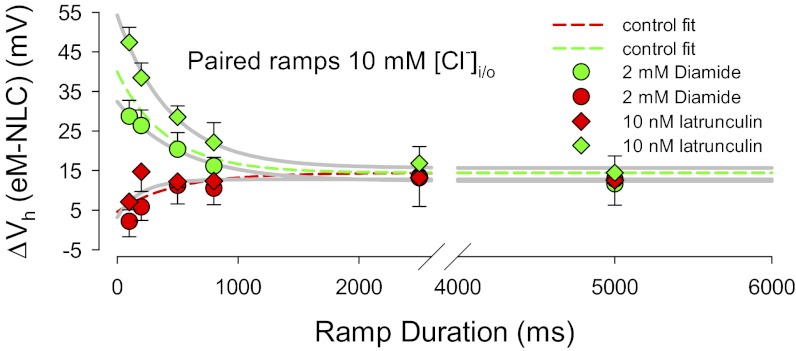
To ensure that the observations that we observe derive from molecular actions of prestin, rather than mechanical characteristics of the cell, we perturbed the cytoskeleton. We treated OHCs with latrunculin (an agent causing actin depolymerization) and diamide (a spectrin, actin-bundling protein antagonist), each of which is expected to modify the OHC cortical cytoskeleton. Fig. 4 illustrates that only minor changes in the fast rate effects are evident. These small effects we attribute to the influence of the cytoskeleton in controlling tension delivered to the membrane.
Fig. 4.
The eM and NLC Vh disparity is little influenced by cytoskeletal integrity. The dotted lines are fits from the 10 mM chloride plot of Fig. 3B. The effects of diamide and latrunculin are absent with hyperpolarizing ramps (red symbols). On the other hand, diamide slightly reduces and latrunculin slightly increases fast ramp effects.
Model.
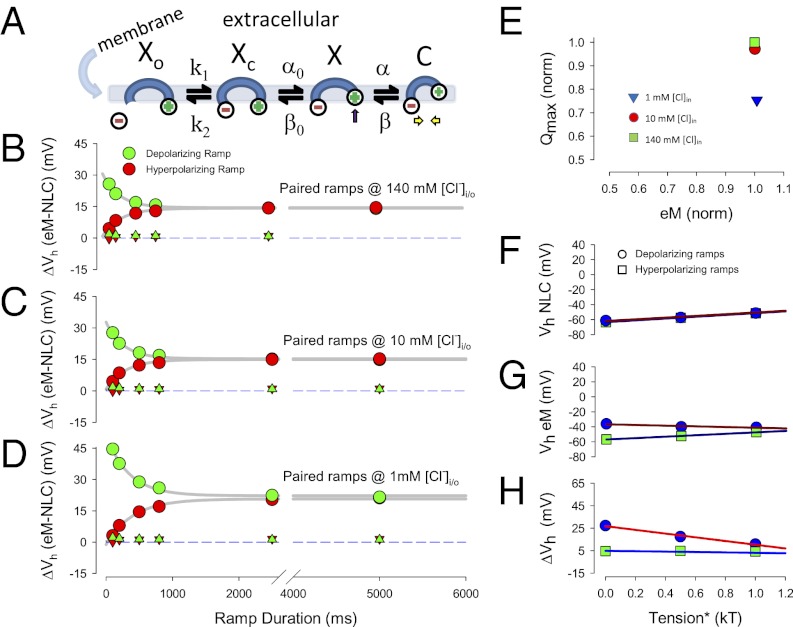
In the two-state area motor model of OHC electromotility (29, 30), the accumulation of prestin motors into the contracted state (small surface area) will shorten the cell, and accumulation into the expanded state (large surface area) will lengthen the cell. This two-state model cannot reproduce our data (see below). To understand the molecular events underlying our time- and chloride-dependent observations, we developed an extended, yet very simple kinetic model, schematized in Fig. 5A.
Fig. 5.
Kinetic model of prestin. (A) Simple kinetic model of prestin activity within the plasma membrane. Xo state is unbound by anion. The Xc state is bound by anion but intrinsic voltage-sensor charge is not responsive to membrane electric field. Slow conformational transition to X state enables voltage sensing of electric field (arrow depicts positive charged sensor movement into the membrane field). Depolarization moves positive sensor charge outward within the membrane field, simultaneously resulting in compact state C, which corresponds to cell contraction (yellow arrows). (B–D) Kinetic model recapitulates ΔVh disparity of biophysical data. Plots correspond to those plots of Fig. 3 A–C. Note increasing Vh disparity with chloride reduction and shorter ramp durations. There is a slight asymmetry at fast ramp rates for the 1 mM chloride condition. Triangles depict results obtained when the intermediate transition rates were increase by a factor of 1e8. No disparity is detected under these conditions, as expected for a simple fast two-state model. (E) Kinetic model recapitulates uncorrelated Qmax and eMmax of biophysical data. As chloride levels decrease, Qmax decreases, but eM does not follow. Compare with biophysical data of Fig. 3D. (F–H) Kinetic model recapitulates membrane tension dependence of biophysical data. Plots correspond to those plots of Fig. 3 E–G. Note similarity of model behavior and biophysical behavior, resulting in reduced ΔVh disparity as membrane tension increases.
Similar to carbonic anhydrase (31), we assume very fast anion (chloride) binding and unbinding transitions (Xo↔Xc). Because the voltage-dependent mechanical activity of prestin is greater than 80 kHz (32), we also assume very fast voltage-dependent conformational transitions (X↔C). The transition to state C carries a unit charge, q; Qmax, total charge moved, will reflect the maximal accumulation of motors in that state. The number of motors in state C also equates to magnitude of eM (contraction), providing a Boltzmann-like sigmoidal response. Nestled between the anion-binding and voltage-dependent transitions, resides a non-voltage-dependent transition (Xc↔X), which is very much slower than the other two transitions. The kinetics of these slow transitions is set to have the model resemble prestin’s electromechanical behavior. The differential equations describing the model are listed in the Supporting Information, where k1 = 107 * [Cl]in, k2 = 107 * kd, α0 = 75 * exp(tm), β0 = 5.58 * 108 * exp(−Ea/RT), α = 106 * exp(zFVm/2RT), β = 583 * 109 * exp(−zFVm/2RT + tm/2 – Ea/RT), kd = 0.001, T = 296 K, Ea = 38.36 * 103 J/mol, F = 9.648 * 104 C/mol, R = 8.315 J/Kmol, k = 1.381 * 10−23 VC/K.
The rates α0 and β are tension sensitive, because tension is known to increase prestin residence in the expanded (X) state (10, 28), tm in units kT (eRT/F); rates β and β0 are equally temperature sensitive, with Arrhenius activation energy, Ea. Here, α and β are voltage dependent, with sensor valence z. At T = 296 K, Vm= 0 mV, Tm = 0 kT, and [Cl]in = 0.14 M, initial rates are k1 = 1.4e6, k2 = 1e4, α0 = 75, β0 = 95, α = 1e6, and β = 1e5.
Model results recapitulate our biophysical data. Stimulation of the model is with the same voltage protocols used to collect the biophysical data, and analysis is the same. Fig. 5 B–D shows chloride-, rate-, and polarity-dependent disparity similar to the biophysical results illustrated in Fig. 3 A–C. The polarity dependence of the fastest rates with low chloride levels is not as rectified as the biophysical data, the model showing only minor differences, and may result from the extraordinary simplicity of the model. The triangles depict results obtained when intermediary rates, α0 and β0, are set 8 orders of magnitude faster. Under such conditions, the model resembles a fast two-state model, with no disparity between NLC and eM. We reason that at high chloride levels the population of voltage-enabled Cl-bound motors is enriched, and the fast kinetics of the voltage-dependent transitions work on this population to dominate the cell response, thus appearing more similar to a fast two-state process.
Fig. 5E illustrates that the model, similar to the biophysical results in Fig. 3D, exhibits poor correlation between Qmax and magnitude of eM. In this case, Qmax estimates can reduce with essentially no change in eM. Fig. 5 F–H illustrates the effects of tension on kinetic model behavior and shows similarity to the biophysical data of Fig. 3 E–G. Namely, a reduction of the fast ramp (100 ms) ΔVh disparity results from inverse shifts of polarity dependent eM Vh. NLC Vh, on the other hand, shifts in the depolarizing direction for both polarity ramps. It is important to note that Fig. S1 A–D illustrates that a variety of perturbations to the model recapitulate biophysical behavior of NLC observed during the previous two decades, including prepulse effect, chloride concentration effect, temperature effect, and exponential relaxations of Cm induced by voltage step. The success of the model strongly suggests that an intermediary slow transition governs prestin behavior.
Given that the model recapitulates most of the available biophysical data, we are confident that it can be used to investigate other expected qualities that enable the OHC to function effectively as cochlear amplifier. To this end, we tested the phase characteristics of the model. Fig. S1 E–G shows that (i) eM phase lags that of stimulating membrane potential, (ii) the phase lag is chloride and voltage dependent, and (iii) depending on intermediary gateway kinetics, the phase lag exhibits variable frequency dependence. Fig. S2 confirms that we do find small phase lags in OHC eM.
Discussion
OHC eM is voltage dependent and necessarily coupled to its charged voltage sensor (8, 9, 12, 26, 27, 33). Thus, it is expected that sensor-charge movement, measured as displacement currents or NLC, should correspond to mechanical movements of the cell. In fact, a strict correspondence is predicted based on two-state Boltzmann models that incorporate transition speeds that match the very fast voltage-induced mechanical response (>80 kHz) (32). The incongruence of our data with this scheme, especially at physiological chloride levels, requires rethinking of prestin’s molecular mechanism.
Measures of prestin’s NLC alone are not sufficient to rule on the existence of kinetic schemes above two states, given that Cm-Vm functions can be fit equally well by two-state Boltzmann or multistate Langevin functions within physiological voltage ranges (34, 35). However, by evaluating simultaneous measures of NLC and eM, we are able to identify at least three state transitions, including fast anion-binding and voltage-dependent ones, and an intermediary slow one. The intermediary state transition controls the delivery of primed (anion bound) motors into a voltage-enabled pool, and likely corresponds to the allosteric-like behavior we have observed previously (16, 17). Thus, rather than a typical allosteric mechanism, chloride binding to the evolutionary ancient transport-binding site functions to effect a slow conformational change that enables a process (voltage sensing and eM) unrelated to transport per se. We had previously separated NLC and anion transport via mutations in prestin, and identified charged amino residues that contribute to charge movement (36). In consequence, the intermediate transition serves as a gateway controlling the magnitude and voltage dependence of eM, and underlies the disparity between measures of NLC and eM.
We emphasize that our data do not suggest that NLC and eM are intrinsically separable, but that they only appear disparate because our measuring techniques are subject to intermediate rate effects that the disparity highlights. This is somewhat analogous to the recently observed need to integrate sensor charge across long time ranges to reconcile large shifts in the voltage sensor domain Q-V function of Shaker channels (37). Thus, we find that the apparent operating voltage range of prestin depends on the frequency of interrogation of its behavior. With our measures of NLC, we are studying a nonstationary population of voltage-dependent motors, varying according to the kinetics of the intermediary gateway. That is, NLC measures that characterize the voltage-dependent conformational change in prestin at discrete frequencies cannot provide steady-state behavior as previously thought, because we are not dealing with an invariant fast two-state system. The kinetic model starkly illustrates this: when intermediate rates are set very fast, model behavior is similar to fast two-state behavior. As a correspondence, we find that differing Vh is obtained by varying integration times of step-induced charge movement. Thus, past estimates of steady-state prestin behavior have been influenced by this gateway. For example, we and others had assumed that lowering intracellular chloride levels shifts eM correspondingly with NLC in the positive direction along the voltage axis. We now know that eM shift is greater. Physiologically, acoustic frequency stimulation in vivo will be influenced by intermediary kinetics corresponding to its equivalent frequency bandwidth. This may underlie some of the differences between low- and high-frequency cochlear behavior. It is important to note that the simple model we provide here has single exponential kinetics, whereas previously observed kinetic characteristics of NLC (e.g., see Fig. 1 NLC time course), which we can now ascribe to this gateway, clearly show that the transition actually has stretched exponential behavior providing control ranging from the submillisecond to the seconds timescale (20, 23). Implementing this kinetic diversity will certainly increase the complexity of the model, but may improve its correspondence with biophysical data. For example, at the present time we needed to decrease the transition rates from the millisecond to the second timescale to obtain the voltage prepulse effect as in Fig. S1A. As noted above, NLC relaxations do have components in this slower time range.
Anions and eM.
The operating voltage range of eM is dependent on chloride level (Fig. 1D), showing a greater dependence than that of NLC. In a similar way, Qmax estimates of charge movement do not correlate well with eM. The disparities may be explained because NLC only reports on the voltage-enabled population of motors at interrogation frequencies, whereas eM is evaluated at ramp rates much slower than that of the intermediate transition rates. Still, it is interesting to note that steady-state eM magnitude is little affected by chloride removal. It was previously observed that removal of intracellular chloride abolished eM (13). That observation involved replacement of chloride with pentane sulfonate, which we subsequently showed causes NLC Vh to shift to very hyperpolarized voltages, effectively shifting eM outside practical interrogation voltage ranges (16). In the present study, we successfully evaluate the full range of eM at various chloride levels and show robust mechanical responses, despite large reductions in chloride. We and others have determined the Kd for prestin, ranging from 1 to 6 mM, using measures of NLC (13, 15, 17). Our robust eM observations along with clear indications that NLC measures may not faithfully depict prestin’s steady-state properties indicate that the Kd for prestin mechanical activity needs reassessment.
Models of Prestin.
The earliest molecular models of prestin, based on OHC NLC and eM, were simple two-state Boltzmanns (8, 9, 29, 30), corresponding to two area states, compact and expanded. The first observation of tension effects on OHC NLC led to a modified Boltzmann model, where a mechanical energy term supplemented that of electrical energy (28, 29). Those whole-cell experiments correctly implicated a molecular basis, as subsequent experiments revealed (4, 5, 10). Here we find that the disparity between eM and NLC is susceptible to membrane tension, thus directly implicating molecular underpinnings. To be sure, the hallmark of the intermediate transition rate, the Cm relaxation indicative of the shifting Q-V function, is impervious to intracellular pronase treatment (20), does not depend on OHC length (23), and is found in prestin transfected cells (4), as expected for a membrane-based phenomenon. Indeed, the minor effects of present cytoskeletal perturbations on the ΔVh disparity confirm those observations. In accordance, it must be emphasized that water movements into and out of the OHC that can alter OHC shape are expected to be slow (38), and thus their greatest contribution to the disparity in ΔVh would be during long ramps, which is just the opposite of what we find. In fact, chloride (water) movement into or out of the cell should depend on ramp polarity but at long durations disparity remains the same for each polarity ramp. In addition, the order of ramp delivery is without effect on the data. We conclude that our results cannot be due to whole-cell mechanical properties or chloride/water movements during stimulation, and that the success of our model derives from its accurate description of prestin’s molecular behavior.
Recently, extensive models, some deriving from OHC measures, incorporating transporter or multistate behavior have been devised to replicate some of the available biophysical data, mostly prestin’s anion dependence (39–41). Prestin’s anion transporter capabilities are controversial, some groups championing transport, others not (36, 42–44). However, another simple four-state model (sum of two voltage-dependent Boltzmanns) was found to rival an earlier model (45) in goodness of fit of NLC and salicylate’s effect on OHC NLC (41). In a subsequent addition (33), the authors suggest that chloride binding could screen intrinsic voltage-sensor charge thus underlying Vh shifts; however, ions of any one polarity are not expected to produce extreme Vh shifts in both positive and negative directions, as has been measured in OHCs (16). In any case, their model cannot reproduce our data, as chloride binding leads directly to fast voltage-dependent reactions. It should be noted, that we previously identified a voltage dependence of NLC relaxations, which could signal that the slow intermediate transition may possess some measure of voltage dependency (23). In subsequent model renditions we intend to evaluate this possibility, and the possible effects of electric field on anion binding. In its present form, however, our simple model derives from typical ligand gated channels (e.g., ACh receptor channels) where fast ligand-binding kinetics leads to very much slower conformational changes that gate open conductance (46, 47). For prestin, the slower, voltage-independent intermediate conformational change enables voltage sensing. It is well known that a voltage-independent transition can affect the characteristics of a linked voltage-dependent one (37, 48, 49). It may be that the other more complicated, although untested (re the host of biophysical data available), models of prestin possess some of the qualities of our model, but to date our model is the simplest capable of recapitulating the widest known set of OHC biophysical data. In league with the transporter models, however, we speculate that the transporter lineage of prestin underlies the slow transition process that controls the fastest known molecular motor.
What Is Required of the OHC as an Amplifier?
To provide amplification within the cochlear partition, the OHC must exert its force fast and at the right time. OHCs can respond to sinusoidal voltage stimulation above 80 kHz (32), and although resistor-capacitor (RC) filtering posed initial skepticism due to expected decreases in eM driving force at high acoustic frequencies (26, 50), much work has basically eliminated this concern (14, 51–55). However, one of those potential mechanisms that we envisioned to overcome the RC problem does not survive tests with our model. We previously suggested (14) that should chloride levels fluctuate at acoustic rates near prestin (analogous to stereocilia mechano-electrical transducer Ca2+ flux effects on bundle mechanics), this could drive high-frequency mechanical responses, bypassing an RC limit. Our observations indicate that such fluctuations are of limited effect because prestin’s intermediary rates will low pass filter responses, with the intermediate transition imposing its time dependence on chloride-driven eM. Nonetheless, chloride flux at rates at or below intermediary rates could significantly affect eM.
Some cochlea models require a phase lag between OHC voltage and OHC force, typically 1.57 rad, thereby delivering force to the basilar membrane at an appropriate phase angle to cancel viscous drag (56–58). This requires a delay between receptor potential and activation of eM. Although various mechanisms have been invoked to establish phase lags in cochlear models, none have been based on intrinsic biophysical mechanisms of the OHC motor. We suggest that the disparity that we observe between NLC and eM may represent a delay proffered by the additional states required to replicate the biophysical data. To this end, we find in the model that phase lags between membrane voltage and eM are generated by the intermediary gateway, and that chloride level and membrane resting potential control lag magnitude (Fig. S1). It must also be remembered that the gateway is actually multiexponential, thus in addition the model can generate frequency-dependent phase delays depending on the kinetics of the gateway. However, we find that model lag magnitudes are a fraction of 1.57 rad. Indeed, we find a small phase lag in our physiological measures of eM (Fig. S2), thus contributing to those model phase requirements. It should be mentioned, however, that more recent models of OHC-based amplification do not have lags required of older models (59). Based on new concepts, it is not OHC action on the basilar membrane, but instead on the fluid micromechanics of the subtectorial membrane space that affords amplification (60, 61). Although our data are in harmony with the phase-lag requiring models, it remains to be seen how our predicted phase characteristics of the OHC motor impact on newer models, and whether the throttling kinetics of prestin’s intermediary gateway can influence amplification.
Supplementary Material
Acknowledgments
This research was supported by National Institutes of Health National Institute on Deafness and other Communication Disorders Grant DC00273 (to J.S.-S.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1218341110/-/DCSupplemental.
References
- 1.Brownell WE, Bader CR, Bertrand D, de Ribaupierre Y. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 1985;227(4683):194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
- 2.Ashmore J, et al. The remarkable cochlear amplifier. Hear Res. 2010;266(1-2):1–17. doi: 10.1016/j.heares.2010.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zheng J, et al. Prestin is the motor protein of cochlear outer hair cells. Nature. 2000;405(6783):149–155. doi: 10.1038/35012009. [DOI] [PubMed] [Google Scholar]
- 4.Santos-Sacchi J, Shen W, Zheng J, Dallos P. Effects of membrane potential and tension on prestin, the outer hair cell lateral membrane motor protein. J Physiol. 2001;531(Pt 3):661–666. doi: 10.1111/j.1469-7793.2001.0661h.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ludwig J, et al. Reciprocal electromechanical properties of rat prestin: The motor molecule from rat outer hair cells. Proc Natl Acad Sci USA. 2001;98(7):4178–4183. doi: 10.1073/pnas.071613498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Santos-Sacchi J, Song L, Zheng J, Nuttall AL. Control of mammalian cochlear amplification by chloride anions. J Neurosci. 2006;26(15):3992–3998. doi: 10.1523/JNEUROSCI.4548-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dallos P, et al. Prestin-based outer hair cell motility is necessary for mammalian cochlear amplification. Neuron. 2008;58(3):333–339. doi: 10.1016/j.neuron.2008.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ashmore JF. Forward and reverse transduction in the mammalian cochlea. Neurosci Res Suppl. 1990;12:S39–S50. doi: 10.1016/0921-8696(90)90007-p. [DOI] [PubMed] [Google Scholar]
- 9.Santos-Sacchi J. Reversible inhibition of voltage-dependent outer hair cell motility and capacitance. J Neurosci. 1991;11(10):3096–3110. doi: 10.1523/JNEUROSCI.11-10-03096.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kakehata S, Santos-Sacchi J. Membrane tension directly shifts voltage dependence of outer hair cell motility and associated gating charge. Biophys J. 1995;68(5):2190–2197. doi: 10.1016/S0006-3495(95)80401-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kakehata S, Santos-Sacchi J. Effects of salicylate and lanthanides on outer hair cell motility and associated gating charge. J Neurosci. 1996;16(16):4881–4889. doi: 10.1523/JNEUROSCI.16-16-04881.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang X, Yang S, Jia S, He DZ. Prestin forms oligomer with four mechanically independent subunits. Brain Res. 2010;1333:28–35. doi: 10.1016/j.brainres.2010.03.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Oliver D, et al. Intracellular anions as the voltage sensor of prestin, the outer hair cell motor protein. Science. 2001;292(5525):2340–2343. doi: 10.1126/science.1060939. [DOI] [PubMed] [Google Scholar]
- 14.Rybalchenko V, Santos-Sacchi J. Cl- flux through a non-selective, stretch-sensitive conductance influences the outer hair cell motor of the guinea-pig. J Physiol. 2003;547(Pt 3):873–891. doi: 10.1113/jphysiol.2002.036434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Song L, Seeger A, Santos-Sacchi J. On membrane motor activity and chloride flux in the outer hair cell: Lessons learned from the environmental toxin tributyltin. Biophys J. 2005;88(3):2350–2362. doi: 10.1529/biophysj.104.053579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rybalchenko V, Santos-Sacchi J. Anion control of voltage sensing by the motor protein prestin in outer hair cells. Biophys J. 2008;95(9):4439–4447. doi: 10.1529/biophysj.108.134197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Song L, Santos-Sacchi J. Conformational state-dependent anion binding in prestin: Evidence for allosteric modulation. Biophys J. 2010;98(3):371–376. doi: 10.1016/j.bpj.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Adachi M, Iwasa KH. Effect of diamide on force generation and axial stiffness of the cochlear outer hair cell. Biophys J. 1997;73(5):2809–2818. doi: 10.1016/S0006-3495(97)78310-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Morton WM, Ayscough KR, McLaughlin PJ. Latrunculin alters the actin-monomer subunit interface to prevent polymerization. Nat Cell Biol. 2000;2(6):376–378. doi: 10.1038/35014075. [DOI] [PubMed] [Google Scholar]
- 20.Santos-Sacchi J, Kakehata S, Takahashi S. Effects of membrane potential on the voltage dependence of motility-related charge in outer hair cells of the guinea-pig. J Physiol. 1998;510(Pt 1):225–235. doi: 10.1111/j.1469-7793.1998.225bz.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Santos-Sacchi J. Determination of cell capacitance using the exact empirical solution of dY/dCm and its phase angle. Biophys J. 2004;87(1):714–727. doi: 10.1529/biophysj.103.033993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bezanilla F. How membrane proteins sense voltage. Nat Rev Mol Cell Biol. 2008;9(4):323–332. doi: 10.1038/nrm2376. [DOI] [PubMed] [Google Scholar]
- 23.Santos-Sacchi J, Navarrete E, Song L. Fast electromechanical amplification in the lateral membrane of the outer hair cell. Biophys J. 2009;96(2):739–747. doi: 10.1016/j.bpj.2008.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bian S, Koo BW, Kelleher S, Santos-Sacchi J, Navaratnam DS. A highly expressing Tet-inducible cell line recapitulates in situ developmental changes in prestin’s Boltzmann characteristics and reveals early maturational events. Am J Physiol Cell Physiol. 2010;299(4):C828–C835. doi: 10.1152/ajpcell.00182.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liberman MC, et al. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature. 2002;419(6904):300–304. doi: 10.1038/nature01059. [DOI] [PubMed] [Google Scholar]
- 26.Ashmore JF. A fast motile response in guinea-pig outer hair cells: The cellular basis of the cochlear amplifier. J Physiol. 1987;388:323–347. doi: 10.1113/jphysiol.1987.sp016617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Santos-Sacchi J, Dilger JP. Whole cell currents and mechanical responses of isolated outer hair cells. Hear Res. 1988;35(2-3):143–150. doi: 10.1016/0378-5955(88)90113-x. [DOI] [PubMed] [Google Scholar]
- 28.Iwasa KH. Effect of stress on the membrane capacitance of the auditory outer hair cell. Biophys J. 1993;65(1):492–498. doi: 10.1016/S0006-3495(93)81053-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Iwasa KH. A membrane motor model for the fast motility of the outer hair cell. J Acoust Soc Am. 1994;96(4):2216–2224. doi: 10.1121/1.410094. [DOI] [PubMed] [Google Scholar]
- 30.Santos-Sacchi J. Harmonics of outer hair cell motility. Biophys J. 1993;65(5):2217–2227. doi: 10.1016/S0006-3495(93)81247-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Prabhananda BS, Rittger E, Grell E. Kinetics and mechanism of anionic ligand binding to carbonic anhydrase. Biophys Chem. 1987;26(2-3):217–224. doi: 10.1016/0301-4622(87)80024-8. [DOI] [PubMed] [Google Scholar]
- 32.Frank G, Hemmert W, Gummer AW. Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proc Natl Acad Sci USA. 1999;96(8):4420–4425. doi: 10.1073/pnas.96.8.4420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Homma K, Dallos P. Dissecting the electromechanical coupling mechanism of the motor-protein prestin. Commun Integr Biol. 2011;4(4):450–453. doi: 10.4161/cib.4.4.15463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Huang G, Santos-Sacchi J. Mapping the distribution of the outer hair cell motility voltage sensor by electrical amputation. Biophys J. 1993;65(5):2228–2236. doi: 10.1016/S0006-3495(93)81248-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Scherer MP, Gummer AW. How many states can the motor molecule, prestin, assume in an electric field? Biophys J. 2005;88(5):L27–L29. doi: 10.1529/biophysj.105.059782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bai JP, et al. Prestin’s anion transport and voltage-sensing capabilities are independent. Biophys J. 2009;96(8):3179–3186. doi: 10.1016/j.bpj.2008.12.3948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lacroix JJ, Labro AJ, Bezanilla F. Properties of deactivation gating currents in Shaker channels. Biophys J. 2011;100(5):L28–L30. doi: 10.1016/j.bpj.2011.01.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ashmore J. Cochlear outer hair cell motility. Physiol Rev. 2008;88(1):173–210. doi: 10.1152/physrev.00044.2006. [DOI] [PubMed] [Google Scholar]
- 39.Muallem D, Ashmore J. An anion antiporter model of prestin, the outer hair cell motor protein. Biophys J. 2006;90(11):4035–4045. doi: 10.1529/biophysj.105.073254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schaechinger TJ, et al. A synthetic prestin reveals protein domains and molecular operation of outer hair cell piezoelectricity. EMBO J. 2011;30(14):2793–2804. doi: 10.1038/emboj.2011.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Homma K, Dallos P. Evidence that prestin has at least two voltage-dependent steps. J Biol Chem. 2011;286(3):2297–2307. doi: 10.1074/jbc.M110.185694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schaechinger TJ, Oliver D. Nonmammalian orthologs of prestin (SLC26A5) are electrogenic divalent/chloride anion exchangers. Proc Natl Acad Sci USA. 2007;104(18):7693–7698. doi: 10.1073/pnas.0608583104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tang J, Pecka JL, Tan X, Beisel KW, He DZ. Engineered pendrin protein, an anion transporter and molecular motor. J Biol Chem. 2011;286(35):31014–31021. doi: 10.1074/jbc.M111.259564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schänzler M, Fahlke C. Anion transport by the cochlear motor protein prestin. J Physiol. 2012;590(Pt 2):259–272. doi: 10.1113/jphysiol.2011.209577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Santos-Sacchi J, Navarrete E. Voltage-dependent changes in specific membrane capacitance caused by prestin, the outer hair cell lateral membrane motor. Pflugers Arch. 2002;444(1-2):99–106. doi: 10.1007/s00424-002-0804-2. [DOI] [PubMed] [Google Scholar]
- 46.Del Castillo J, Katz B. Interaction at end-plate receptors between different choline derivatives. Proc R Soc Lond B Biol Sci. 1957;146(924):369–381. doi: 10.1098/rspb.1957.0018. [DOI] [PubMed] [Google Scholar]
- 47.Osterrieder W, Noma A, Trautwein W. On the kinetics of the potassium channel activated by acetylcholine in the S-A node of the rabbit heart. Pflugers Arch. 1980;386(2):101–109. doi: 10.1007/BF00584196. [DOI] [PubMed] [Google Scholar]
- 48.Colquhoun D. Binding, gating, affinity and efficacy: The interpretation of structure-activity relationships for agonists and of the effects of mutating receptors. Br J Pharmacol. 1998;125(5):924–947. doi: 10.1038/sj.bjp.0702164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shirokov R. What’s in gating currents? Going beyond the voltage sensor movement. Biophys J. 2011;101(2):512–514, discussion 515–516. doi: 10.1016/j.bpj.2011.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Santos-Sacchi J. Asymmetry in voltage-dependent movements of isolated outer hair cells from the organ of Corti. J Neurosci. 1989;9(8):2954–2962. doi: 10.1523/JNEUROSCI.09-08-02954.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Santos-Sacchi J, Kakehata S, Kikuchi T, Katori Y, Takasaka T. Density of motility-related charge in the outer hair cell of the guinea pig is inversely related to best frequency. Neurosci Lett. 1998;256(3):155–158. doi: 10.1016/s0304-3940(98)00788-5. [DOI] [PubMed] [Google Scholar]
- 52.Ospeck M, Dong XX, Fang J, Iwasa KH. Electromotility in outer hair cells: A supporting role for fast potassium conductance. ORL J Otorhinolaryngol Relat Spec. 2006;68(6):373–377. doi: 10.1159/000095280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Spector AA, Brownell WE, Popel AS. Effect of outer hair cell piezoelectricity on high-frequency receptor potentials. J Acoust Soc Am. 2003;113(1):453–461. doi: 10.1121/1.1526493. [DOI] [PubMed] [Google Scholar]
- 54.Johnson SL, Beurg M, Marcotti W, Fettiplace R. Prestin-driven cochlear amplification is not limited by the outer hair cell membrane time constant. Neuron. 2011;70(6):1143–1154. doi: 10.1016/j.neuron.2011.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Corbitt C, Farinelli F, Brownell WE, Farrell B. Tonotopic relationships reveal the charge density varies along the lateral wall of outer hair cells. Biophys J. 2012;102(12):2715–2724. doi: 10.1016/j.bpj.2012.04.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Neely ST. A model of cochlear mechanics with outer hair cell motility. J Acoust Soc Am. 1993;94(1):137–146. doi: 10.1121/1.407091. [DOI] [PubMed] [Google Scholar]
- 57.Markin VS, Hudspeth AJ. Modeling the active process of the cochlea: Phase relations, amplification, and spontaneous oscillation. Biophys J. 1995;69(1):138–147. doi: 10.1016/S0006-3495(95)79883-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Geisler CD. A realizable cochlear model using feedback from motile outer hair cells. Hear Res. 1993;68(2):253–262. doi: 10.1016/0378-5955(93)90129-o. [DOI] [PubMed] [Google Scholar]
- 59.Yoon YJ, Steele CR, Puria S. Feed-forward and feed-backward amplification model from cochlear cytoarchitecture: An interspecies comparison. Biophys J. 2011;100(1):1–10. doi: 10.1016/j.bpj.2010.11.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nowotny M, Gummer AW. Vibration responses of the organ of Corti and the tectorial membrane to electrical stimulation. J Acoust Soc Am. 2011;130(6):3852–3872. doi: 10.1121/1.3651822. [DOI] [PubMed] [Google Scholar]
- 61.Guinan JJ., Jr . Mechanical excitation of IHC stereocilia: An attempt to fit together diverse evidence. In: Shera C, Olson E, editors. What Fire Is in Mine Ears: Progress in Auditory Biomechanics. Melville, NY: American Institute of Physics; 2012. pp. 90–96. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.