Abstract
Colloidal suspensions exhibit shear thinning and shear thickening. The most common interpretation of these phenomena identifies layering of the fluid perpendicular to the shear gradient as the driver for the observed behavior. However, studies of the particle configurations associated with shear thinning and thickening cast doubt on that conclusion and leave unsettled whether these nonequilibrium phenomena are caused primarily by correlated particle motions or by changes in particle packing structure. We report the results of Stokesian dynamics simulations of suspensions of hard spheres that illuminate the relation among the suspension viscosity, shear rate, and particle configuration. Using a recently introduced sampling technique for nonequilibrium systems, we show that shear thinning can be decoupled from layering, thereby eliminating layering as the driver for shear thinning. In contrast, we find that there is a strong correlation between shear thinning and a two-particle measure of the shear stress. Our results are consistent with a recent experimental study.
Keywords: colloids, rare-event sampling, Nonequilibrium Umbrella Sampling, rheology
Flowing colloidal suspensions exhibit many nonlinear response phenomena, prominent among which are shear thinning and thickening, i.e., the decrease and increase, respectively, of the suspension viscosity with increasing shear strength (1–5). In the last four decades, many experimental studies and computer simulations have attempted to identify changes in particle configurations responsible for these phenomena (6–16), but no conclusive signature has yet been identified. In early experimental studies of dense colloidal suspensions of hard spheres (8, 17) (solid or glass at equilibrium) and of dilute charge-stabilized suspensions that crystallize at equilibrium (18, 19), sliding layers were observed when the systems were subjected to shear flow. This layering structure, characterized by a nonuniform density distribution along the shear gradient direction, was independently predicted to occur by nonequilibrium molecular dynamics (NEMD) simulations without hydrodynamic interactions (20, 21). The organization of the suspension into layers was thought to explain the shear-thinning behavior observed, but later experimental studies of less dense systems (with liquid-like order at equilibrium) using light scattering (22, 23) or small-angle neutron scattering (24–27) yielded mixed signals relevant to the existence of this layering structure in the shear-thinning regime, thereby implying that layering might not be necessary for shear thinning. This implication is supported by Stokesian dynamics simulations (28, 29), which differ from earlier NEMD simulations by incorporating hydrodynamic interactions between the particles. The Stokesian dynamics simulations find no shear-induced layering of hard spheres in the shear-thinning regime in bulk systems that are liquid-like at equilibrium (9, 30).
It is certainly the case that diffraction from an assembly of particles is sensitive to ordering and many body correlations associated with complicated structures on many length scales. Determination of the structure of the assembly on those many length scales from diffraction data requires that the Fourier space complementary to real space is adequately sampled. The scattering studies of sheared colloidal systems that have been reported cover a small part of the Fourier space complementary to the real space particle arrangement, and are determined by particle correlations on the pair level only. In an equilibrium state of a fluid of particles with pair interactions that depend only on the pair separation, the pair correlation function determined from scattering measurements adequately describes the structure. In a nonequilibrium state of a fluid of particles, the statistical weight of each configuration depends explicitly on the way the system is driven out of equilibrium and cannot be obtained from the pair correlation function alone. Thus, although the light scattering and small-angle neutron scattering experiments hint that layering does not drive shear thinning, they do not provide unique evidence for that conclusion and the notion that shear thinning is associated with formation of particle layers persists (3, 14–16).
The experimental study of shear thinning has recently been advanced via simultaneous rheological and structural measurements on confined colloid suspensions, with single-particle resolution, using fast confocal microscopy (7). The results of this experiment, unlike the results of previous Stokesian dynamics simulations (9, 30), show simultaneous appearance of the layering structural change and the shear thinning. The difference in results with respect to the existence of layering in the fluid may be a consequence of the difference in boundary conditions between the experiment and the simulations. Specifically, confinement by planar boundaries, as used in the experiments, enhances layer formation in the dense colloidal suspension. However, the use of a periodic boundary condition in the velocity gradient direction [or the more elaborate Lees–Edwards boundary conditions (31)], as used in the referred to Stokesian dynamics simulations of bulk colloidal suspensions, can repress layering in the suspension because particles in the top layer of the simulation cell are in direct contact with particles in the bottom layer of the simulation cell.
Although the experimental data imply that the simultaneous appearance of layering and shear thinning is coincidental rather than causal, they are not adequate to resolve this issue because the shear strength and layering cannot be independently varied. Advances in simulation algorithms now make resolution of the relationship between shear thinning and layering in the suspension possible. The Stokesian dynamics simulations (28, 29) we report in this paper exploit the same methodology as used in previous studies (9, 30) except that we use boundary conditions that are consistent with those used in the experiment by Cheng et al. (7). We furthermore use nonequilibrium umbrella sampling (32–34) to observe otherwise rare configurations. Our results show that shear thinning in a suspension of confined hard spheres is accompanied by other structural changes in addition to layering, and in particular a two-particle measure of the shear stress is demonstrated to be strongly correlated with shear thinning.
Results and Discussion
Observations of Shear Thinning.
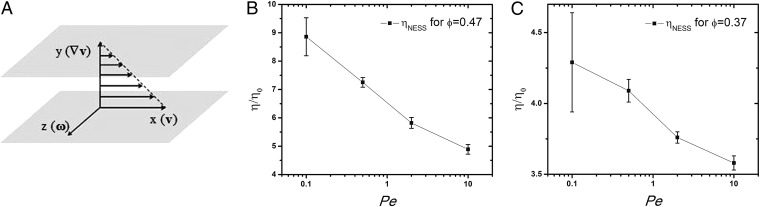
Our Stokesian dynamics simulations use the methodology developed by Brady and coworkers with boundary conditions as detailed in Methods. The shear applied to the N hard spheres is in the x direction, the shear gradient is in the y direction, and the vorticity is in the z direction (Fig. 1A). The sheared hard sphere fluid is characterized by the sphere diameter 2a, the packing fraction 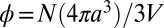 and the Peclet number
and the Peclet number 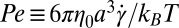 , where
, where 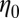 is the viscosity of the supporting liquid and
is the viscosity of the supporting liquid and 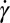 is the shear rate. The Peclet number measures the magnitude of particle motion induced by shear relative to that associated with thermal motion. Simulations were carried out for packing fractions
is the shear rate. The Peclet number measures the magnitude of particle motion induced by shear relative to that associated with thermal motion. Simulations were carried out for packing fractions 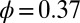 and
and 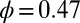 , similar to the packing fractions used in the experiments of Cheng et al. (7) These packing fractions lie below that at which the hard sphere fluid crystallizes. The dependence of the steady-state shear viscosity,
, similar to the packing fractions used in the experiments of Cheng et al. (7) These packing fractions lie below that at which the hard sphere fluid crystallizes. The dependence of the steady-state shear viscosity, 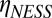 (NESS stands for nonequilibrium steady state) on Pe over the range
(NESS stands for nonequilibrium steady state) on Pe over the range 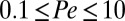 is displayed in Fig. 1 B and C. These data clearly show that up to
is displayed in Fig. 1 B and C. These data clearly show that up to 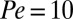 these suspensions are shear thinning, and the simulations are in general agreement with recent experimental data (7) for shear thinning and with the results of earlier simulations of bulk suspensions (29). The quantitative differences between our results and earlier results are attributable to the different boundary conditions used.
these suspensions are shear thinning, and the simulations are in general agreement with recent experimental data (7) for shear thinning and with the results of earlier simulations of bulk suspensions (29). The quantitative differences between our results and earlier results are attributable to the different boundary conditions used.
Fig. 1.
Characterization of shear thinning. (A) Illustration of the coordinate system. (B) Shear viscosity 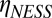 as a function of
as a function of 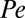 for suspensions with
for suspensions with 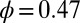 , showing strong shear-thinning behavior. (C) Shear viscosity as a function of
, showing strong shear-thinning behavior. (C) Shear viscosity as a function of 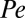 for suspensions with
for suspensions with 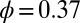 , showing moderate shear-thinning behavior. Each data point shown in both B and C is the average of 100 independent simulations (Methods), and the bars show the SD.
, showing moderate shear-thinning behavior. Each data point shown in both B and C is the average of 100 independent simulations (Methods), and the bars show the SD.
Study of the Relation Between Shear Thinning and Layer Ordering.
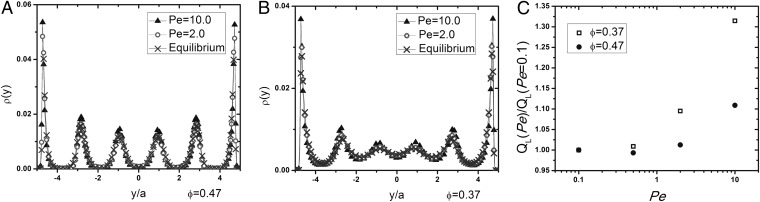
Owing to the confinement, there is layering of the colloidal suspension in the equilibrium state, and that layering is enhanced with shear. Our simulations reproduce the enhanced layering structure in the sheared fluid observed in recent experiments (7). This layering structure can be characterized qualitatively by the peaks in the density profile of the system along the shear gradient direction y (Fig. 2 A and B). To quantitatively investigate how the shear thinning depends on layering structure, we quantify the strength of the layering by the scalar parameter 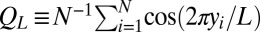 , where
, where 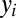 is the y-position of sphere i, and L is the separation between two neighboring layers of particles (Fig. 2C). It is important to note that the increase in
is the y-position of sphere i, and L is the separation between two neighboring layers of particles (Fig. 2C). It is important to note that the increase in 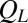 is much stronger for Pe > 1 than for Pe < 1, yet the rate of decrease in suspension viscosity over the range
is much stronger for Pe > 1 than for Pe < 1, yet the rate of decrease in suspension viscosity over the range 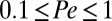 is very close to that over the range
is very close to that over the range 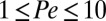 (Fig. 1). This finding strongly implies that enhancement of layering with increasing Pe is not essential to shear thinning.
(Fig. 1). This finding strongly implies that enhancement of layering with increasing Pe is not essential to shear thinning.
Fig. 2.
Characterization of layer ordering. Density profiles of the suspension along the y direction with 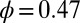 (A) and
(A) and 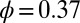 (B). Note the layer enhancement due to increased shear. (C) Scalar parameter
(B). Note the layer enhancement due to increased shear. (C) Scalar parameter 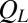 as a function of
as a function of 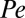 , normalized by its value at
, normalized by its value at 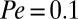 for suspensions with
for suspensions with 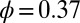 (empty squares) and with
(empty squares) and with 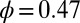 (black circles).
(black circles).
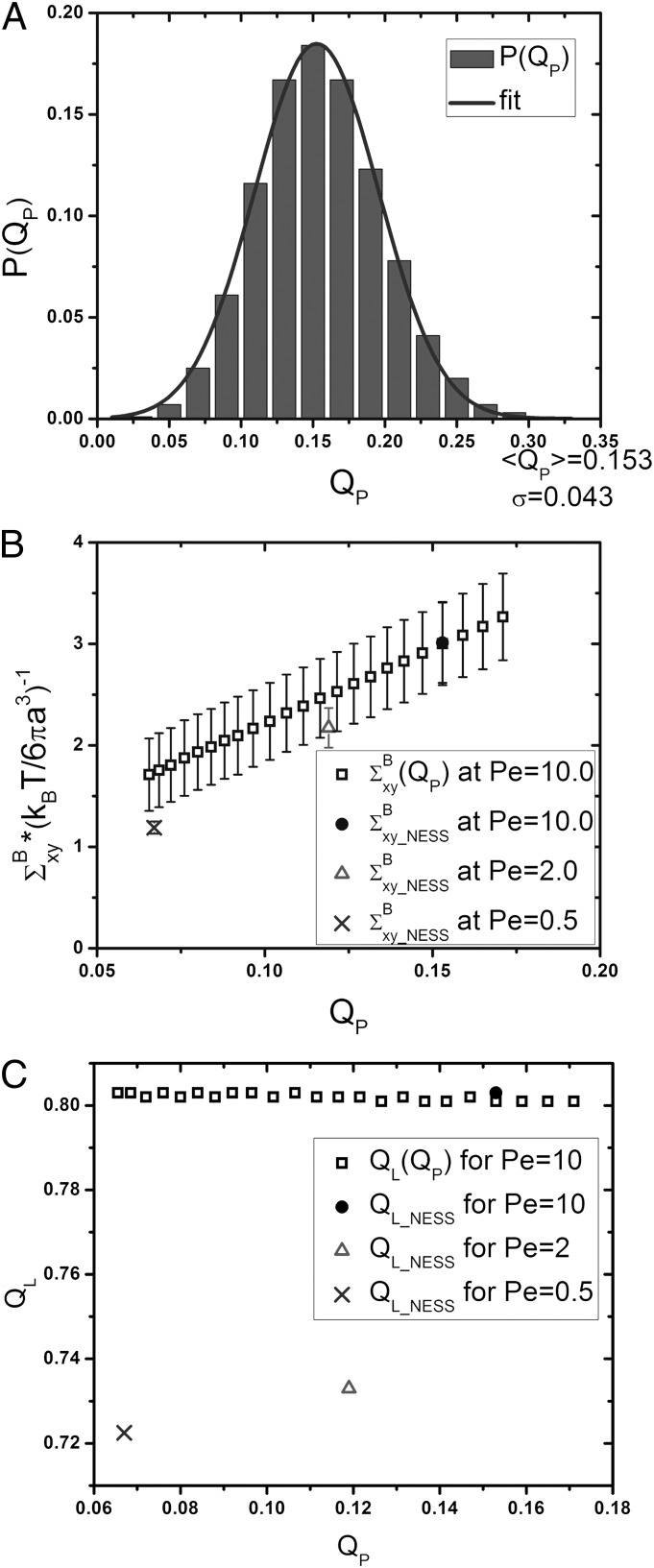
To strengthen the conclusion implied by the results just described, we now demonstrate that the layer structure of a confined colloidal suspension and the decrease in viscosity with increasing Peclet number are uncorrelated. Using 100,000 steady-state colloid configurations for the suspension with 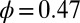 and
and 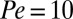 , we construct a histogram of values of
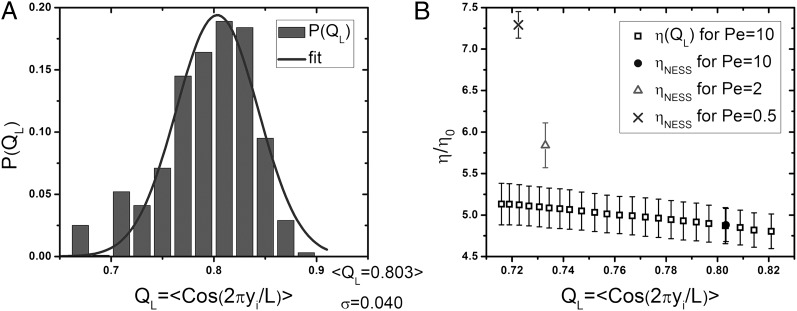
, we construct a histogram of values of 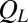 (Fig. 3A). The distribution of values of
(Fig. 3A). The distribution of values of 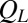 delineates the amplitude of fluctuations, and it is well represented by a Gaussian function with mean of 0.803 and SD of 0.040. If we can harvest a sufficient number of configurations in the small
delineates the amplitude of fluctuations, and it is well represented by a Gaussian function with mean of 0.803 and SD of 0.040. If we can harvest a sufficient number of configurations in the small 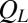 tail of this distribution, we can calculate the viscosity associated with those configurations and compare the values found with the values for
tail of this distribution, we can calculate the viscosity associated with those configurations and compare the values found with the values for 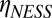 obtained at smaller Pe. Doing so is challenging because these configurations are rare. Consequently, we use nonequilibrium umbrella sampling (32–34) (Methods). This numerical technique preserves the dynamics of a system but allows sampling to be focused on low-probability regions of a steady-state distribution by selectively branching and pruning stochastic trajectories in an order parameter-dependent fashion. Using this method, we can readily obtain configurations with
obtained at smaller Pe. Doing so is challenging because these configurations are rare. Consequently, we use nonequilibrium umbrella sampling (32–34) (Methods). This numerical technique preserves the dynamics of a system but allows sampling to be focused on low-probability regions of a steady-state distribution by selectively branching and pruning stochastic trajectories in an order parameter-dependent fashion. Using this method, we can readily obtain configurations with  values that we would normally associate with Pe < 1 while maintaining Pe = 10. In this way, we can independently explore layering and shear strength. For each value of
values that we would normally associate with Pe < 1 while maintaining Pe = 10. In this way, we can independently explore layering and shear strength. For each value of 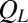 , we calculate the corresponding viscosity
, we calculate the corresponding viscosity 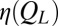 . If changes in layering underlie shear thinning, we expect that the viscosity will be strongly correlated with
. If changes in layering underlie shear thinning, we expect that the viscosity will be strongly correlated with 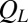 . However, we find that the dependence of
. However, we find that the dependence of 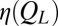 on
on 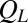 when Pe = 10 is weak, and the values of
when Pe = 10 is weak, and the values of 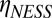 obtained from the simulations at small Pe are larger than
obtained from the simulations at small Pe are larger than 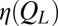 at the same
at the same 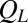 . This result leads us to the conclusion that, at least for the model suspension studied, changes in viscosity and layering are coincidental rather than causal.
. This result leads us to the conclusion that, at least for the model suspension studied, changes in viscosity and layering are coincidental rather than causal.
Fig. 3.
Viscosity–layer relation. (A) Histogram of 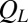 for 100,000 steady-state configurations of the suspension with
for 100,000 steady-state configurations of the suspension with 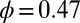 and
and 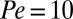 (bars), fitted to a Gaussian function (line) with average value
(bars), fitted to a Gaussian function (line) with average value 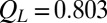 and SD
and SD 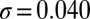 . (B) Dependence of
. (B) Dependence of 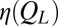 on
on 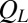 for the suspension with
for the suspension with 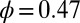 and
and 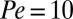 (empty squares) compared with
(empty squares) compared with 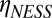 , the average viscosity for the indicated Pe (Fig. 1B). Each data point shows the average of results from 100 independent simulations; the bars show the SD.
, the average viscosity for the indicated Pe (Fig. 1B). Each data point shows the average of results from 100 independent simulations; the bars show the SD.
Mechanism of Shear Thinning: Study of a Two-Particle Structure.
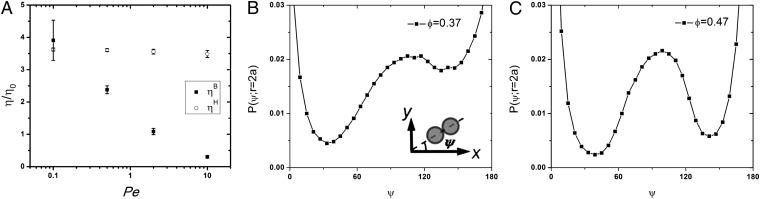
What then is the basis for the observed shear thinning? It is conventional to represent the shear stress S in the complex colloidal fluid as the sum of three contributions (28, 35): a thermodynamic component associated with the stochastic motions of particles, called the Brownian stress SB, an interaction component associated with the particle–particle forces, called the interaction stress SP, and a hydrodynamic component associated with the shear flow, called the hydrodynamic stress SH. The Brownian stress arises from the fluctuations in position of a colloidal particle that induce flows that interact with all other particles in the system, the spatial configuration of which also fluctuates on the same timescale as individual colloidal particle motion. Because of the many-particle dependence of the hydrodynamic resistance on the configuration, and the coupling of the fluctuation timescales, this contribution has a nonzero value when averaged over a time long compared with the Brownian relaxation time 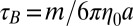 , where m is the mass of a colloidal particle. The interaction stress is zero for a hard-sphere system (9). In general, shear thinning is a consequence of the fact that the change in the thermodynamic component with Peclet number is unable to keep up with the increase of shear strain (9). Indeed, our Stokesian dynamics simulations reproduce the earlier results (9, 35) that both SB and SH increase with increasing
, where m is the mass of a colloidal particle. The interaction stress is zero for a hard-sphere system (9). In general, shear thinning is a consequence of the fact that the change in the thermodynamic component with Peclet number is unable to keep up with the increase of shear strain (9). Indeed, our Stokesian dynamics simulations reproduce the earlier results (9, 35) that both SB and SH increase with increasing 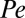 , but the rate of increase of SB cannot match the rate of increase of SH. As a result, the stochastic component of the viscosity,
, but the rate of increase of SB cannot match the rate of increase of SH. As a result, the stochastic component of the viscosity, 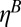 , decreases as Pe increases and eventually becomes negligible at large Pe, while the hydrodynamic component of the viscosity,
, decreases as Pe increases and eventually becomes negligible at large Pe, while the hydrodynamic component of the viscosity, 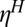 , stays almost constant up to
, stays almost constant up to 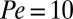 (Fig. 4A).
(Fig. 4A).
Fig. 4.
Structural signature for shear thinning. (A) 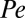 dependence of the Brownian component (black squares) and the hydrodynamic component (empty circles) of the viscosity of the suspension with
dependence of the Brownian component (black squares) and the hydrodynamic component (empty circles) of the viscosity of the suspension with 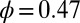 . Angular probability distributions of contact pairs in the xy-plane
. Angular probability distributions of contact pairs in the xy-plane 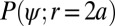 versus
versus 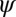 for suspensions with
for suspensions with 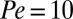 and
and 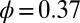 (B); and
(B); and 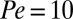 and
and 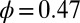 (C). Inset in B defines the angle
(C). Inset in B defines the angle 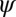 for a contact pair when projected onto the xy-plane. Each data point shown in A is the average of 100 independent simulations, and the bars show the SD.
for a contact pair when projected onto the xy-plane. Each data point shown in A is the average of 100 independent simulations, and the bars show the SD.
Brady (36) has shown that at large packing fraction the Brownian stress is well approximated by the contact integral 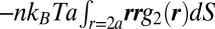 , where
, where 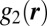 is the pair correlation function. We are concerned with the xy-component of the Brownian stress and its dependence on
is the pair correlation function. We are concerned with the xy-component of the Brownian stress and its dependence on 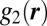 , or more specifically
, or more specifically 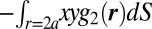 . This integral is 0 for suspensions at equilibrium as a result of system symmetry. As the colloidal suspension is subject to simple shear motion, this symmetry is broken, and as a result
. This integral is 0 for suspensions at equilibrium as a result of system symmetry. As the colloidal suspension is subject to simple shear motion, this symmetry is broken, and as a result 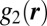 , when projected on the xy-plane, exhibits strong distortions as the colloidal suspension shear thins (7, 9). This observation is also reproduced in our simulations for steady states under shear (Fig. 4 B and C). To quantitatively examine this dependence, we introduce a scalar parameter defined as
, when projected on the xy-plane, exhibits strong distortions as the colloidal suspension shear thins (7, 9). This observation is also reproduced in our simulations for steady states under shear (Fig. 4 B and C). To quantitatively examine this dependence, we introduce a scalar parameter defined as 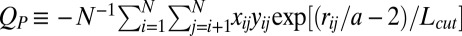 , where
, where 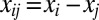 ,
, 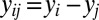 ,
, 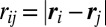 and the pair correlation function at contact is approximately obtained by counting pairs at surface distance
and the pair correlation function at contact is approximately obtained by counting pairs at surface distance 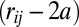 with a rapidly decaying weight
with a rapidly decaying weight 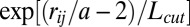 , which assures that the dynamics of
, which assures that the dynamics of 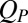 is smooth. When projected onto the xy-plane, a pair at contact has a strong positive contribution to
is smooth. When projected onto the xy-plane, a pair at contact has a strong positive contribution to 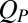 when aligned along the 135° axis and a strong negative contribution when aligned along the 45° axis (Fig. 4B, Inset). We use
when aligned along the 135° axis and a strong negative contribution when aligned along the 45° axis (Fig. 4B, Inset). We use 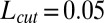 for the calculation shown, and find that the results are insensitive to variations between 0.05 and 0.1.
for the calculation shown, and find that the results are insensitive to variations between 0.05 and 0.1.
As in the case of the analysis of 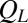 , we constructed a histogram of values of
, we constructed a histogram of values of 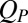 using 100,000 steady-state colloid configurations for the suspension with
using 100,000 steady-state colloid configurations for the suspension with 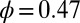 and
and 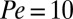 (Fig. 5A), and using nonequilibrium umbrella sampling we sampled configurations that are associated with different values of
(Fig. 5A), and using nonequilibrium umbrella sampling we sampled configurations that are associated with different values of 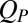 . For each value of
. For each value of 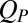 , the associated colloid configurations were analyzed to obtain the xy component of the Brownian stress
, the associated colloid configurations were analyzed to obtain the xy component of the Brownian stress 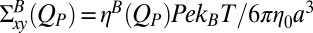 . A comparison of
. A comparison of 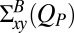 with the values of
with the values of 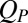 calculated for the steady states of the same suspension subject to different shear rates shows a strong correlation between
calculated for the steady states of the same suspension subject to different shear rates shows a strong correlation between 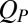 and the shear stress (Fig. 5B). We conclude that alteration of the pair structure, rather than the layering, in the suspension is the dominant mechanism underlying shear thinning. This interpretation is consistent with earlier suggestions that “entropic” (i.e., Brownian) contributions to the stress become small compared with hydrodynamic ones as the system is sheared more strongly (7, 9).
and the shear stress (Fig. 5B). We conclude that alteration of the pair structure, rather than the layering, in the suspension is the dominant mechanism underlying shear thinning. This interpretation is consistent with earlier suggestions that “entropic” (i.e., Brownian) contributions to the stress become small compared with hydrodynamic ones as the system is sheared more strongly (7, 9).
Fig. 5.
Structural signature for shear thinning. (A) Histogram of 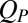 for 100,000 steady-state configurations of the suspension with
for 100,000 steady-state configurations of the suspension with 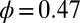 and
and 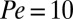 (bars), fitted to a Gaussian function (line) with average value
(bars), fitted to a Gaussian function (line) with average value 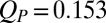 and SD
and SD 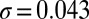 . (B) The xy component of the Brownian stress contribution
. (B) The xy component of the Brownian stress contribution 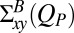 as a function of
as a function of 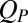 for suspensions with
for suspensions with 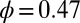 and
and 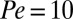 (empty squares), compared with
(empty squares), compared with 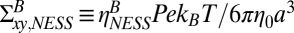 . (C) The layering of the suspension as described by scalar
. (C) The layering of the suspension as described by scalar 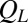 as a function of
as a function of 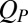 for suspensions with
for suspensions with 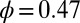 and
and 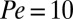 (empty squares), compared with
(empty squares), compared with 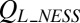 , the steady-state average of
, the steady-state average of 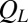 at different
at different 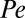 . Each data point shown in B is the average of 100 independent simulations, and the bars show the SD.
. Each data point shown in B is the average of 100 independent simulations, and the bars show the SD.
Given that the changes in the viscosity and layering are simultaneous, it is natural to ask whether they share the same origin: the alteration of the pair structure as characterized by 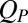 . As we increase Pe, the steady-state average of
. As we increase Pe, the steady-state average of 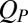 increases as contact particle pairs align along the 135° direction when projected onto the xy-plane. However, as indicated by our nonequilibrium umbrella sampling results, this structural change on the pair level has very little correlation with the layering (Fig. 5C). The mechanism that causes the enhancement of layering is of strong interest (37) but is not resolved by the present study.
increases as contact particle pairs align along the 135° direction when projected onto the xy-plane. However, as indicated by our nonequilibrium umbrella sampling results, this structural change on the pair level has very little correlation with the layering (Fig. 5C). The mechanism that causes the enhancement of layering is of strong interest (37) but is not resolved by the present study.
Conclusions
The use of nonequilibrium umbrella sampling for studying rare events far from equilibrium allows us to decouple particle configurations from the shear strength. Our results have demonstrated that, for hard-sphere colloidal suspensions, the dominant mechanism underlying shear-thinning behavior is alteration of the pair distribution function, rather than layering, which is a single-particle measure. As also demonstrated from our results, the fact that the structural change on the pair level has no correlation with the layering is consistent with the observation that scattering measurements only yield information about the system on the pair level and make no prediction about the layering as the system is driven far from equilibrium by shear flow. In fact, we see that layering of the system can vary substantially with virtually no changes in the pair structure (Fig. 3B), and the pair structure of the system can vary substantially with almost no change in layering (Fig. 5C).
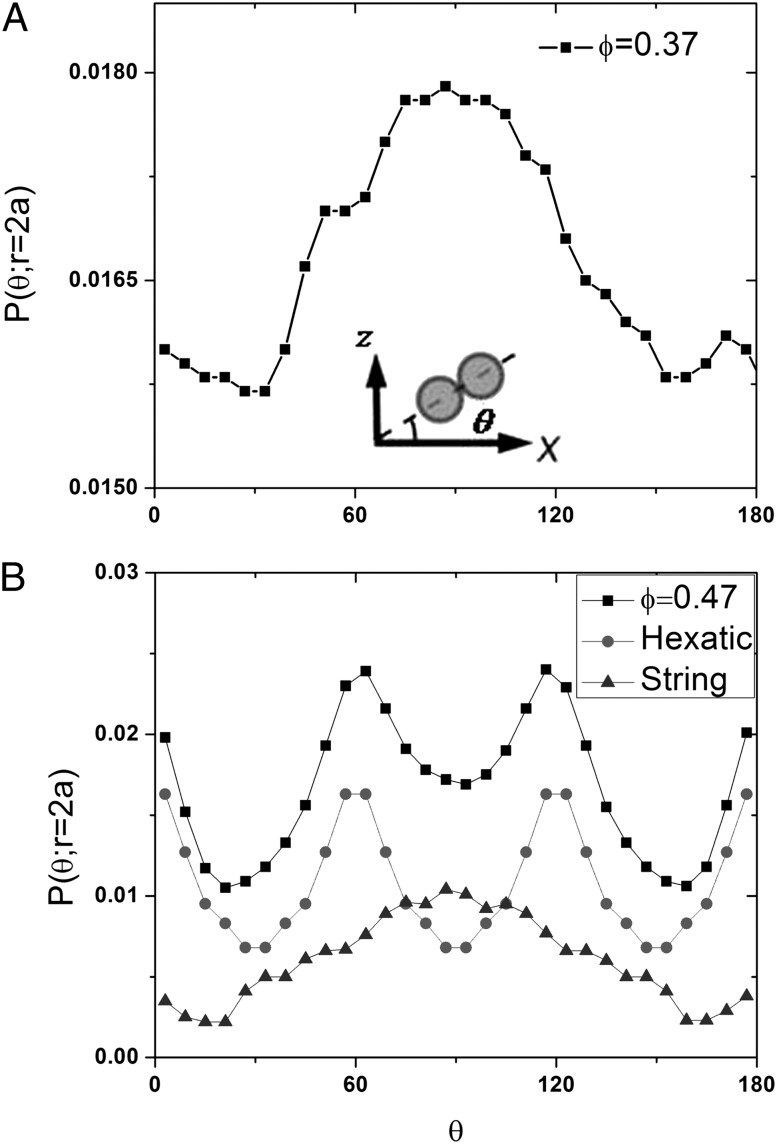
The particle structure within each layer is another aspect of the suspension that is of great interest. In our simulations, we observed a rich variety of structures within each layer as we vary the packing fraction and Pe. If we maintain 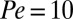 , at
, at 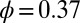 we observed a weak string configuration of particles (an anisotropic distribution in favor of the vorticity direction, as illustrated in Fig. 6A), in qualitative agreement with our earlier results (38). At higher density
we observed a weak string configuration of particles (an anisotropic distribution in favor of the vorticity direction, as illustrated in Fig. 6A), in qualitative agreement with our earlier results (38). At higher density 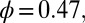 which is very close to the bulk crystallization density for hard spheres, we observed distorted hexatic ordering (Fig. 6B). The existence of this hexatic ordering is in qualitative agreement with the results of earlier studies of suspensions that are solid at equilibrium. However, it is not clear to us whether the patterns observed in our system arise solely from shearing (30), or whether the strong confinement of the suspension plays a key role. The distortion of the hexatic ordering observed can be written as a sum of a perfect hexatic part and a string phase part (Fig. 6B). Clearly, determining the detailed relationship between the particle structures within each layer and system parameters such as
which is very close to the bulk crystallization density for hard spheres, we observed distorted hexatic ordering (Fig. 6B). The existence of this hexatic ordering is in qualitative agreement with the results of earlier studies of suspensions that are solid at equilibrium. However, it is not clear to us whether the patterns observed in our system arise solely from shearing (30), or whether the strong confinement of the suspension plays a key role. The distortion of the hexatic ordering observed can be written as a sum of a perfect hexatic part and a string phase part (Fig. 6B). Clearly, determining the detailed relationship between the particle structures within each layer and system parameters such as 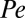 or packing fraction
or packing fraction 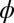 requires more quantitative studies.
requires more quantitative studies.
Fig. 6.
Structures within each layer. The black squares show the angular probability distribution of contact pairs in the xz-plane 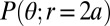 versus
versus 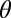 for suspensions with
for suspensions with 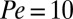 and
and 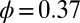 (A); and
(A); and 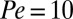 and
and 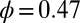 (B). Inset in A defines the angle
(B). Inset in A defines the angle 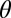 for a contact pair when projected onto the xz-plane.
for a contact pair when projected onto the xz-plane. 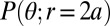 in B is also shown as a sum of a perfect hexatic phase (circles) and a string phase (triangles).
in B is also shown as a sum of a perfect hexatic phase (circles) and a string phase (triangles).
It is important to note that our simulation applies a boundary condition, via an external potential, that confines only the colloidal spheres in the shear gradient direction but not the solvent flow. This boundary condition is not the same as that imposed by the planar walls used in the experiment (7). It has been shown that, for the systems we have studied, with moderate planar separations and high packing fractions, the behavior is dominated by the sphere–sphere interactions and the effect of hydrodynamic interactions between the spheres and the walls can be ignored (39). However, in other situations, for example with dilute suspension, the rheology of the system can be greatly influenced by the sphere–wall interactions.
Despite the fact that confinement induces or enhances layering within the suspension, we expect our conclusions to be generally valid in the absence of additional sources of stress (e.g., strong particle–particle magnetic repulsion) because we make comparisons between relative numbers for consistently defined systems. We also note that our results are complementary to those obtained from earlier simulations of bulk colloidal suspensions (9) that use periodic boundary conditions, which could repress layer structures. Looking forward, we plan to build on the present approach to address the broader problem of determining how to attribute suspension properties to particle interactions and structure changes in situations with additional sources of stress (40).
Methods
Stokesian Dynamics Simulations.
We use Stokesian dynamics to simulate the dynamics of a monodisperse suspension of N hard spheres of unit radius. The influence of hydrodynamic interactions on the particle motions is incorporated through the resistance tensor, which is evaluated based on the configuration at the beginning of each time step of length ∆t = 4 × 10−4. The centers of the spheres are restricted to a rectangular box spanning 0 < x < 11.4, 0 < z < 11.4, and –5.0 < y < 5.0. We apply periodic boundary conditions in the x and z directions and an external potential along the y direction that is 0 for 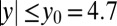 and
and 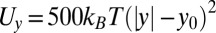 otherwise. We have N = 130 and 167 for
otherwise. We have N = 130 and 167 for 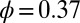 and
and 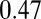 , respectively, as packing fraction
, respectively, as packing fraction 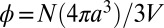 and volume
and volume 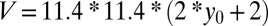 . Although this potential is meant to mimic the confinement imposed by the shear cell used in ref. 7, it is important to note that the potential confines only the colloidal spheres and not the solvent flow. The unit time of the simulation is defined in terms of the characteristic timescales of the system: the diffusive timescale
. Although this potential is meant to mimic the confinement imposed by the shear cell used in ref. 7, it is important to note that the potential confines only the colloidal spheres and not the solvent flow. The unit time of the simulation is defined in terms of the characteristic timescales of the system: the diffusive timescale 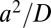 when
when 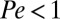 and the inverse shear rate
and the inverse shear rate 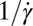 when
when 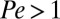 , where D is the short time diffusion constant of an isolated colloidal particle in an infinite suspension. Spatial configurations of the suspension at successive time steps are recorded and used to compute structures and properties of the system. For example, the viscosity of the suspension is evaluated using eqs. 20 and 21 in ref. 28. To compute the average properties for the nonequilibrium steady state for each packing fraction and Pe, 100 independent simulation runs were initialized using the Monte Carlo method. In each run, the system was equilibrated for 30,000 time steps of Δt = 4 × 10−4 before applying shear. Another 50,000 time steps were taken after the onset of the shear motion to allow the system to settle into the nonequilibrium steady state, after which 100,000 time steps were taken for analysis of averaged properties.
, where D is the short time diffusion constant of an isolated colloidal particle in an infinite suspension. Spatial configurations of the suspension at successive time steps are recorded and used to compute structures and properties of the system. For example, the viscosity of the suspension is evaluated using eqs. 20 and 21 in ref. 28. To compute the average properties for the nonequilibrium steady state for each packing fraction and Pe, 100 independent simulation runs were initialized using the Monte Carlo method. In each run, the system was equilibrated for 30,000 time steps of Δt = 4 × 10−4 before applying shear. Another 50,000 time steps were taken after the onset of the shear motion to allow the system to settle into the nonequilibrium steady state, after which 100,000 time steps were taken for analysis of averaged properties.
Nonequilibrium Umbrella Sampling.
We use nonequilibrium umbrella sampling for efficient sampling of rare configurations of our sheared system. In this approach, a space of order parameters (here 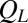 and
and  ) is divided into a number of regions with arbitrarily chosen sizes, and a copy of the system is simulated in each region. Simulations proceed independently according to the original dynamics except when a step would take a copy out of its region. In such an event, a series of bookkeeping variables for determining the physical weights of the copies are updated, the configuration is saved, and the copy is reinitialized from a previously saved entry into its region [see the study by Dickson et al. (34) for details]. In this way, the procedure enforces uniform sampling over the regions regardless of the probabilities of the ranges of order parameter values, without distorting the underlying dynamics.
) is divided into a number of regions with arbitrarily chosen sizes, and a copy of the system is simulated in each region. Simulations proceed independently according to the original dynamics except when a step would take a copy out of its region. In such an event, a series of bookkeeping variables for determining the physical weights of the copies are updated, the configuration is saved, and the copy is reinitialized from a previously saved entry into its region [see the study by Dickson et al. (34) for details]. In this way, the procedure enforces uniform sampling over the regions regardless of the probabilities of the ranges of order parameter values, without distorting the underlying dynamics.
We initialized the simulations for each order parameter from 100 independent configurations randomly chosen from the steady-state configurations of a Stokesian dynamics simulation with 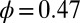 and
and 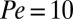 . From each of these configurations, we ran 100 independent nonequilibrium umbrella sampling simulations. In each simulation, the one-dimensional parameter space is divided into 30 regions, where the sizes of the middle regions range from 10 to 20% of the SD of the steady-state histogram of the corresponding order parameter with
. From each of these configurations, we ran 100 independent nonequilibrium umbrella sampling simulations. In each simulation, the one-dimensional parameter space is divided into 30 regions, where the sizes of the middle regions range from 10 to 20% of the SD of the steady-state histogram of the corresponding order parameter with 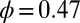 and
and 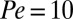 (Figs. 3A and 5A). The regions without a copy initially were OFF and only turned ON once a copy naturally crossed into them [the progressive activation scheme in the study by Dickson et al. (34)]. The simulations run in terms of cycles. Within each simulation cycle, we simulated the dynamics within each active region for 40 time steps of
(Figs. 3A and 5A). The regions without a copy initially were OFF and only turned ON once a copy naturally crossed into them [the progressive activation scheme in the study by Dickson et al. (34)]. The simulations run in terms of cycles. Within each simulation cycle, we simulated the dynamics within each active region for 40 time steps of 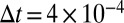 , yielding on average about two crossings per active region. After all of the desired regions were activated, which took on average about 150 cycles, we ran an additional 100 cycles for viscosity and stress analysis.
, yielding on average about two crossings per active region. After all of the desired regions were activated, which took on average about 150 cycles, we ran an additional 100 cycles for viscosity and stress analysis.
Acknowledgments
We thank J. Brady, J. Morris, and J. Swan for help with the Stokesian dynamics simulations and for useful discussions. X.X. also thanks A. Dickson for help with the nonequilibrium umbrella sampling method and N. Guttenburg for help on multithreading parallel computing. We acknowledge the financial and central facilities assistance of The University of Chicago Materials Research Science and Engineering Center, supported by National Science Foundation Grant DMR-MRSEC 0820054.
Footnotes
The authors declare no conflict of interest.
References
- 1.Larson RG. The Structure and Rheology of Complex Fluids. Oxford: Oxford Univ Press; 1999. [Google Scholar]
- 2.Wagner NJ, Brady JF. Shear thickening in colloidal dispersions. Phys Today. 2009;62(10):27–32. [Google Scholar]
- 3.Chen DTN, Wen Q, Janmey PA, Crocker JC, Yodh AG. Rheology of soft materials. Annu Rev Condens Matter Phys. 2010;1:301. [Google Scholar]
- 4.Coussot P. Rheometry of Pastes, Suspensions and Granular Materials. Hoboken, NJ: Wiley; 2005. [Google Scholar]
- 5.Morris JF. A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol Acta. 2009;48(8):909–923. [Google Scholar]
- 6.Dauchot O, Marty G, Biroli G. Dynamical heterogeneity close to the jamming transition in a sheared granular material. Phys Rev Lett. 2005;95(26):265701. doi: 10.1103/PhysRevLett.95.265701. [DOI] [PubMed] [Google Scholar]
- 7.Cheng X, McCoy JH, Israelachvili JN, Cohen I. Imaging the microscopic structure of shear thinning and thickening colloidal suspensions. Science. 2011;333(6047):1276–1279. doi: 10.1126/science.1207032. [DOI] [PubMed] [Google Scholar]
- 8.Hoffman RL. Discontinuous and dilatant viscosity behavior in concentrated suspensions. I. Observation of a flow instability. J Rheol (N Y N Y) 1972;16:155–173. [Google Scholar]
- 9.Foss DR, Brady JF. Structure, diffusion and rheology of Brownian suspensions by Stokesian Dynamics simulation. J Fluid Mech. 2000;407:167–200. [Google Scholar]
- 10.Kalman D, Wagner NJ. Microstructure of shear-thickening concentrated suspensions determined by flow-USANS. Rheol Acta. 2009;48(8):897–908. [Google Scholar]
- 11.Dullens RPA, Bechinger C. Shear thinning and local melting of colloidal crystals. Phys Rev Lett. 2011;107(13):138301. doi: 10.1103/PhysRevLett.107.138301. [DOI] [PubMed] [Google Scholar]
- 12.Brown E, Jaeger HM. Dynamic jamming point for shear thickening suspensions. Phys Rev Lett. 2009;103(8):086001. doi: 10.1103/PhysRevLett.103.086001. [DOI] [PubMed] [Google Scholar]
- 13.Vermant J, Solomon MJ. Flow-induced structure in colloidal suspensions. J Phys Condens Matter. 2005;17:R187–R216. [Google Scholar]
- 14.Genovese DB. Shear rheology of hard-sphere, dispersed, and aggregated suspensions, and filler-matrix composites. Adv Colloid Interface Sci. 2012;171–172:1–16. doi: 10.1016/j.cis.2011.12.005. [DOI] [PubMed] [Google Scholar]
- 15.Brader JM. Nonlinear rheology of colloidal dispersions. J Phys Condens Matter. 2010;22(36):363101. doi: 10.1088/0953-8984/22/36/363101. [DOI] [PubMed] [Google Scholar]
- 16.Stickel JJ, Powell RL. Fluid mechanics and rheology of dense suspensions. Annu Rev Fluid Mech. 2005;37:129–149. [Google Scholar]
- 17.Hoffman RL. Discontinuous and dilatant viscosity behavior in concentrated suspensions. II. Theory and experimental tests. J Colloid Interface Sci. 1974;46(3):491–506. [Google Scholar]
- 18.Ackerson BJ, Clark NA. Shear-induced melting. Phys Rev Lett. 1981;46(2):123–126. [Google Scholar]
- 19.Chen LB, Ackerson BJ, Zukoski CF. Rheological consequences of microstructural transitions in colloidal crystals. J Rheol (N Y N Y) 1994;38(2):193–216. [Google Scholar]
- 20.Loose W, Hess S. Rheology of dense model fluids via nonequilibrium molecular dynamics: Shear thinning and ordering transition. Rheol Acta. 1989;28(2):91–101. [Google Scholar]
- 21.Woodcock LV. Origins of thixotropy. Phys Rev Lett. 1985;54(14):1513–1516. doi: 10.1103/PhysRevLett.54.1513. [DOI] [PubMed] [Google Scholar]
- 22.Ackerson BJ, Pusey PN. Shear-induced order in suspensions of hard spheres. Phys Rev Lett. 1988;61(8):1033–1036. doi: 10.1103/PhysRevLett.61.1033. [DOI] [PubMed] [Google Scholar]
- 23.Wagner NJ, Russel WB. Light scattering measurements of a hard-sphere suspension under shear. Phys Fluids A. 1990;2(4):491–502. [Google Scholar]
- 24.Johnson SJ, de Kruif CG, May RP. Structure factor distortion for hard-sphere dispersions subjected to weak shear flow: Small-angle neutron scattering in the flow-vorticity plane. J Chem Phys. 1988;89(9):5909–5921. [Google Scholar]
- 25.Ackerson BJ, van der Werff J, de Kruif CG. Hard-sphere dispersions: Small-wave-vector structure-factor measurements in a linear shear flow. Phys Rev A. 1988;37(12):4819–4827. doi: 10.1103/physreva.37.4819. [DOI] [PubMed] [Google Scholar]
- 26.Laun HM, et al. Rheological and small angle neutron scattering investigation of shear-induced particle structures of concentrated polymer dispersions submitted to plane Poiseuille and Couette flow. J Rheol (N Y N Y) 1992;36(4):743–787. [Google Scholar]
- 27.Maranzano BJ, Wagner NJ. Flow-small angle neutron scattering measurements of colloidal dispersion microstructure evolution through the shear thickening transition. J Chem Phys. 2002;117(22):10291–10302. [Google Scholar]
- 28.Bossis G, Brady JF. The rheology of Brownian suspensions. J Chem Phys. 1989;91(3):1866–1874. [Google Scholar]
- 29.Phung TN, Brady JF, Bossis G. Stokesian dynamics simulation of Brownian suspensions. J Fluid Mech. 1996;313:181–207. [Google Scholar]
- 30.Kulkarni SD, Morris JF. Ordering transition and structural evolution under shear in Brownian suspensions. J Rheol (N Y N Y) 2009;53(2):417–439. [Google Scholar]
- 31.Lees AW, Edwards SF. The computer study of transport processes under extreme conditions. J Phys C Solid State Phys. 1972;5(15):1921–1929. [Google Scholar]
- 32.Dickson A, Dinner AR. Enhanced sampling of nonequilibrium steady states. Annu Rev Phys Chem. 2010;61:441–459. doi: 10.1146/annurev.physchem.012809.103433. [DOI] [PubMed] [Google Scholar]
- 33.Warmflash A, Bhimalapuram P, Dinner AR. Umbrella sampling for nonequilibrium processes. J Chem Phys. 2007;127(15):154112. doi: 10.1063/1.2784118. [DOI] [PubMed] [Google Scholar]
- 34.Dickson A, Maienschein-Cline M, Tovo-Dwyer A, Hammond JR, Dinner AR. Flow-dependent unfolding and refolding of an RNA by nonequilibrium umbrella sampling. J Chem Theory Comput. 2011;7:2710–2720. doi: 10.1021/ct200371n. [DOI] [PubMed] [Google Scholar]
- 35.Bender JW, Wagner NJ. Optical measurement of the contributions of colloidal forces to the rheology of concentrated suspensions. J Colloid Interface Sci. 1995;172(1):171–184. [Google Scholar]
- 36.Brady JF. The rheological behavior of concentrated colloidal dispersions. J Chem Phys. 1993;99(1):567–581. [Google Scholar]
- 37.Zurita-Gotor M, Bławzdziewicz J, Wajnryb E. Layering instability in a confined suspension flow. Phys Rev Lett. 2012;108(6):068301. doi: 10.1103/PhysRevLett.108.068301. [DOI] [PubMed] [Google Scholar]
- 38.Cheng X, Xu XL, Rice SA, Dinner AR, Cohen I. Assembly of vorticity-aligned hard-sphere colloidal strings in a simple shear flow. Proc Natl Acad Sci USA. 2012;109(1):63–67. doi: 10.1073/pnas.1118197108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Swan JW, Brady JF. The hydrodynamics of confined dispersions. J Fluid Mech. 2011;687:254–299. [Google Scholar]
- 40.Brown E, Jaeger HM. Materials science. Through thick and thin. Science. 2011;333(6047):1230–1231. doi: 10.1126/science.1211155. [DOI] [PubMed] [Google Scholar]