Abstract
Conventional electronics are based invariably on the intrinsic degrees of freedom of an electron, namely its charge and spin. The exploration of novel electronic degrees of freedom has important implications in both basic quantum physics and advanced information technology. Valley, as a new electronic degree of freedom, has received considerable attention in recent years. In this paper, we develop the theory of spin and valley physics of an antiferromagnetic honeycomb lattice. We show that by coupling the valley degree of freedom to antiferromagnetic order, there is an emergent electronic degree of freedom characterized by the product of spin and valley indices, which leads to spin–valley-dependent optical selection rule and Berry curvature–induced topological quantum transport. These properties will enable optical polarization in the spin–valley space, and electrical detection/manipulation through the induced spin, valley, and charge fluxes. The domain walls of an antiferromagnetic honeycomb lattice harbors valley-protected edge states that support spin-dependent transport. Finally, we use first-principles calculations to show that the proposed optoelectronic properties may be realized in antiferromagnetic manganese chalcogenophosphates (MnPX3, X = S, Se) in monolayer form.
Keywords: antiferromagnetism, valleytronics
The exploration of novel electronic degrees of freedom (1–4) has been a fairly important topic recently because of their potential in next-generation electronics. The intrinsic degrees of freedom of an electron, namely its charge and spin, have been the basis for the society-transforming information technologies, i.e., electronics and spintronics. Additional electronic degree of freedom, if present, will offer immense potential for information encoding and manipulation at the microscopic level. The notion of valleytronics (1) on honeycomb lattices has received considerable attention in recent years (5–10). When the centrosymmetry of the honeycomb lattice is broken, such as in gapped graphene, there arises an inequivalent, degenerate pair of valleys in the momentum–space electronic structure. The valley excitations, protected by the suppression of intervalley scattering, have contrasting optical and transport properties ensured by quantal helicity (5, 6). In the most recent experimental progress in monolayer group VI transition metal dichalcogenides, the identity of valleys manifests as valley-selective circular dichroism (CD), leading to substantial valley polarization with circularly polarized light, offering a potential arena to the eventual realization of valleytronics (7, 9, 10).
Evidently, it is important to broaden the choice of materials, beyond transition metal dichalcogenides (7–10), with which novel degrees of freedom (beyond charge and spin) of Bloch electrons may be accessed. Central to these endeavors are two tasks, namely developing theoretical paradigms and subsequent materials discovery, the latter of which makes possible experimental measurements that put the theory (5–7) to test (7, 9, 10). In previous theoretical and experimental developments, attention was paid to the absence of an inversion center in the lattice space group. Here, we show that the pseudospin symmetry in the initially symmetric honeycomb lattice hints at a nontrivial transformation, which leads to an emergent degree of freedom characterized by the product of spin and valley indices. We further propose that such a fermionic system may be observed on a bipartite honeycomb lattice that assumes the Néel antiferromagnetism (afm), which may possess chiral electronic excitation concomitant to the spin-density wave, as well as spin-dependent transport properties on the edge states. In the last part of the paper, we use first-principles calculations to show that the proposed physics may be realized in antiferromagnetic manganese chalcogenophosphates (MnPX3, X = S, Se) in monolayer form. We also analyze the general consequence of symmetry in the afm fermionic honeycomb lattice. A potential transition to the topologically nontrivial quantum spin Hall state is briefly discussed.
Theory of the Antiferromagnetic Honeycomb Lattice
Model Hamiltonian.
Valley as an electronic degree of freedom has been suggested in a spinless fermion model on a honeycomb lattice with a symmetry-breaking perturbation to the sublattices (5, 6). A honeycomb lattice may be defined as a three-connected 2D net, with the connection vectors for bond length b pointing toward its three nearest neighbors (NNs), 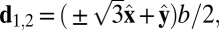 and
and 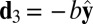 . The corresponding lattice constant
. The corresponding lattice constant 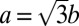 . The two sublattices of a honeycomb structure is conventionally denoted A and B, respectively, which correspond to a binary degree of freedom called isospin. The low-energy quasiparticle states at
. The two sublattices of a honeycomb structure is conventionally denoted A and B, respectively, which correspond to a binary degree of freedom called isospin. The low-energy quasiparticle states at 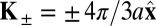 are assigned a valley index τ = ±1, indicating the valley contrasting physics. It is tied to physical measurables, such as the orbital magnetic moment,
are assigned a valley index τ = ±1, indicating the valley contrasting physics. It is tied to physical measurables, such as the orbital magnetic moment, 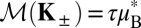 , where
, where 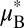 is the effective Bohr magneton (5). Concomitant to the orbital magnetic moment are nonvanishing Berry curvatures (11), Ω(K±) = ħℳ(K±)/eɛ(K±), where e and ɛ(K±) are the electronic charge and the band energy at K±, respectively (6).
is the effective Bohr magneton (5). Concomitant to the orbital magnetic moment are nonvanishing Berry curvatures (11), Ω(K±) = ħℳ(K±)/eɛ(K±), where e and ɛ(K±) are the electronic charge and the band energy at K±, respectively (6).
When the spin degree of freedom (s = ±1/2) is taken into account, spontaneous symmetry breaking becomes viable in the dichromatic Shubnikov group. Imposing dichromatic coloring on the spin and lattice, we propose a spin-full Hamiltonian for the low-energy quasiparticles near K± of a honeycomb lattice,
where p is the momentum operator and vF is the massless Fermi velocity. Here, τα, σα, and sα (α = x, y, z, 0) are the Pauli matrices for the valley, isospin, and spin degrees of freedom, respectively. The mass term, m, corresponding to a symmetry-breaking perturbation, admits a band gap Δ = 2m for both spins. The relevance of the model Hamiltonian will become clear shortly (Eq. 4). With the spin-dependent Hamiltonian, 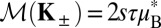 . Therefore, the product of spin and valley indices identifies a new degree of freedom of electrons, which we call the coupled spin–valley, s ⋅ τ, degree of freedom. The s ⋅ τ index bears the virtue of a good quantum number, for so long as intervalley scattering is suppressed it mimics the two spin states of an electron.
. Therefore, the product of spin and valley indices identifies a new degree of freedom of electrons, which we call the coupled spin–valley, s ⋅ τ, degree of freedom. The s ⋅ τ index bears the virtue of a good quantum number, for so long as intervalley scattering is suppressed it mimics the two spin states of an electron.
As the spinless fermion model describes a nonmagnetic system (5), the dichromatic Hamiltonian of Eq. 1 represents an antiferromagnetic system. Inspection of Hamiltonian (1) reveals that the s ⋅ τ degree of freedom arises upon engaging the electrons with a spin-dependent on-site Hubbard potential, 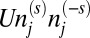 , which characterizes the Coulomb interaction of opposite spins on site j = A, B. Here, U is the on-site Coulomb parameter, and
, which characterizes the Coulomb interaction of opposite spins on site j = A, B. Here, U is the on-site Coulomb parameter, and 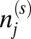 the number operator of site j and spin s (12). Within the Hartree–Fock approximation, the on-site Coulomb energy of two spins can be decoupled as
the number operator of site j and spin s (12). Within the Hartree–Fock approximation, the on-site Coulomb energy of two spins can be decoupled as 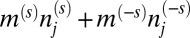 , upon an immaterial energy shift. We define a spin-dependent mass term,
, upon an immaterial energy shift. We define a spin-dependent mass term,
where
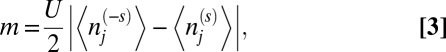 |
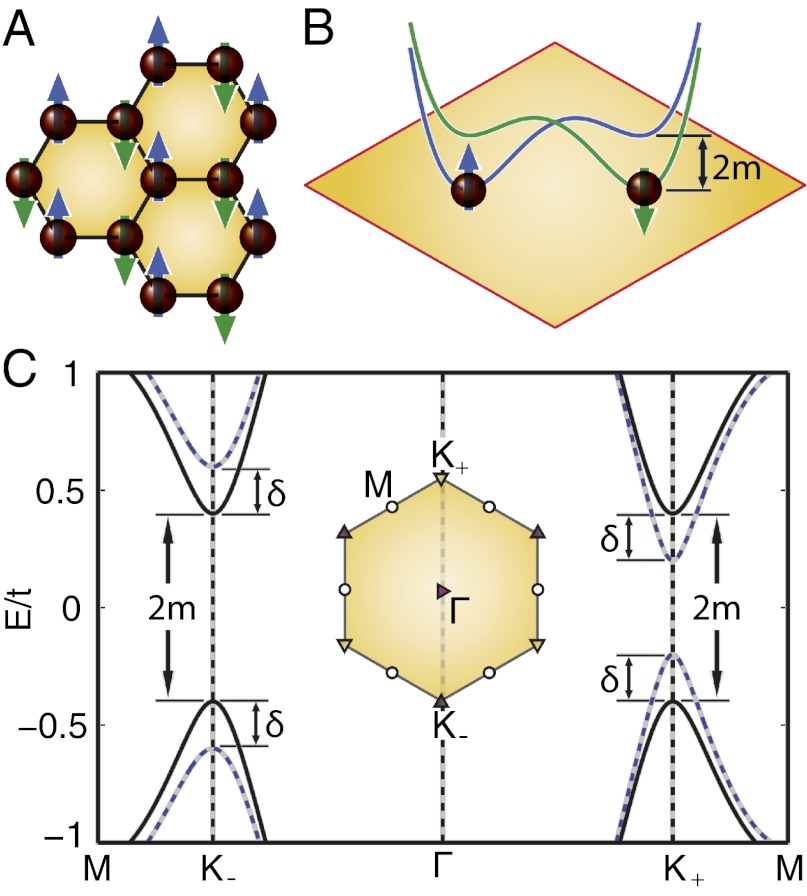
characteristic of an afm spin-density wave (Fig. 1A). It now is apparent that with the afm order, each spin sees different potentials on the two sublattices, as represented by m(s) (Fig. 1B) and described by Eq. 1.
Fig. 1.
The antiferromagnetic honeycomb lattice. (A) Néel afm of a honeycomb lattice. ↑ and ↓, staggered spin-density wave. (B) Spin-dependent lattice potential corresponding to the afm order. (C) Low-energy quasiparticle bands of an NN hopping afm Hamiltonian. Solid lines assume zero spin–valley coupling, whereas dashed lines take into account the spin–valley coupling. With the hopping parameter t as the energy unit, the mass and the spin–valley coupling parameter are set to m = 0.4t and δ = 0.2t, respectively. The zero of energy is set to midgap, the Dirac point energy when m = 0 and δ = 0. (Inset) Brillouin zone and high-symmetry points.
To pinpoint the essential physics of spin and valley on an afm honeycomb lattice, we analyze a tight-binding Hamiltonian invoking the spin-dependent mass term above and an NN hopping, t,
which in the neighborhood of K± may be linearized to Eq. 1. The NN hopping is given as
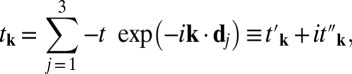 |
where dj are the vectors pointing toward the three NNs. We use that notation where 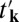 and
and 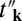 are the real and imaginary parts of tk, respectively. The band structure is shown in Fig. 1C. The bands are spin degenerate at each k-point. Band gaps Δ = 2m indeed are opened at the valleys. An ad hoc spin–valley coupling may be introduced with the parameter δ, as
are the real and imaginary parts of tk, respectively. The band structure is shown in Fig. 1C. The bands are spin degenerate at each k-point. Band gaps Δ = 2m indeed are opened at the valleys. An ad hoc spin–valley coupling may be introduced with the parameter δ, as  . The spin–valley coupling preserves the spin degeneracy, but leads to a renormalization of the valley gaps. The band gaps become enlarged at one valley and reduced at the other, that is, Δ = 2(m − τδ). The fact that spins remain degenerate in this system has to do with the invariance of the Hamiltonian under simultaneous time reversal
. The spin–valley coupling preserves the spin degeneracy, but leads to a renormalization of the valley gaps. The band gaps become enlarged at one valley and reduced at the other, that is, Δ = 2(m − τδ). The fact that spins remain degenerate in this system has to do with the invariance of the Hamiltonian under simultaneous time reversal 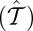 and spatial inversion
and spatial inversion 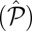 , although neither
, although neither 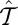 nor
nor 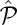 alone commutes with the Hamiltonian. We revisit this symmetry,
alone commutes with the Hamiltonian. We revisit this symmetry, 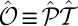 , later in Discussion.
, later in Discussion.
Physics of the Spin–Valley Degree of Freedom.
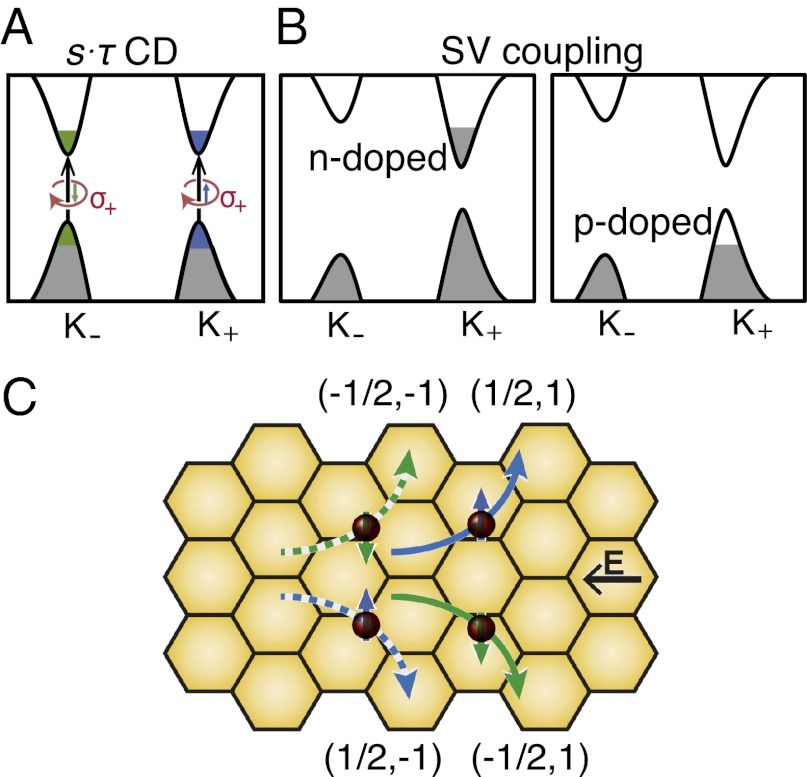
A few interesting experiments immediately become compelling, to probe and manipulate the s ⋅ τ degree of freedom. When the spin–valley coupling is absent or weak, the two valleys may be considered degenerate (Fig. 2A). The system will have s ⋅ τ–selective CD, owing to the two spins adopting opposite masses. That is, the optical selection rule at Kτ has η(s, τ) = 2sτ, where η is the degree of circular polarization (6, 7), in contrast to gapped graphene (6) and monolayer MoS2 (7–10), where the optical selectivity depends only on valley. As illustrated in Fig. 2A, when left-polarized light (σ+) illuminates the sample, spin-up electrons are excited to the conduction band at K+, as well as the spin-down electrons at K−. On the contrary, when a right-polarized photon is absorbed, it excites down-spins of K+ and up-spins of K−.
Fig. 2.
Spin and valley physics of an afm honeycomb lattice. (A) s ⋅ τ–selective CD in the absence of spin–orbit coupling. (B) When spin–valley coupling is present, the valleys can be doped asymmetrically. (C) Electron spin (bottom of conduction bands) fluxes under the action of Berry curvature of the Bloch bands and in-plane electric field. The spin-up and spin-down currents are shown in blue and green, respectively. Solid and dashed lines stand for the currents from K+ and K−, respectively. The spin and valley, (s, τ), indices are indicated in parentheses. E is an applied in-plane electric field.
Berry curvature also induces topological quantum transport that allows for electric detection of s ⋅ τ polarization, via the anomalous velocity of Bloch electrons, va ∼ E × Ωk, where E is the applied in-plane electric field (11). In the above dynamical polarization of charge carriers, the spin or spin holes under the action of Berry curvature, Ω(k, s), of the Bloch bands will exhibit a CD Hall effect (CDHE). Because of the relation with orbital magnetic moments, both Berry curvature and transversal conductivity (σxy) depend on s ⋅ τ. Charge carriers with s ⋅ τ = ±1/2 (excitable by left- and right-polarized lights, respectively) will have opposite transversal conductivity, as shown in Fig. 2C. Therefore, CDHE is a nonequilibrium charge Hall effect in the presence of a circularly polarized radiation field.
If we dope the system with electrons or holes at equilibrium, then an applied in-plane electric field will drive a transversal “valley” current. Spin currents from all s ⋅ τ = ±1/2 contribute to the transversal transport, resulting in a net accumulation of valley moments and orbital magnetization at the upper and lower edges of the sample (Fig. 2C) with zero transverse charge current. This is the valley Hall effect. In the case of strong spin–valley coupling, the gaps at K± become different and thus have different levels of doping. Suppose we dope the system, say, at K+ with electrons (Fig. 2B). Under an in-plane electric field, the carriers will produce a net transversal spin current without charge current, that is, the pair of currents with (s, τ) = (±1/2, 1) in Fig. 2C. This is the anomalous spin Hall effect (SHE). When we switch from n-doping to p-doping (Fig. 2B), the SHE will be characterized by a transversal spin current in the opposite direction, arising from spin holes.
Domain Walls.
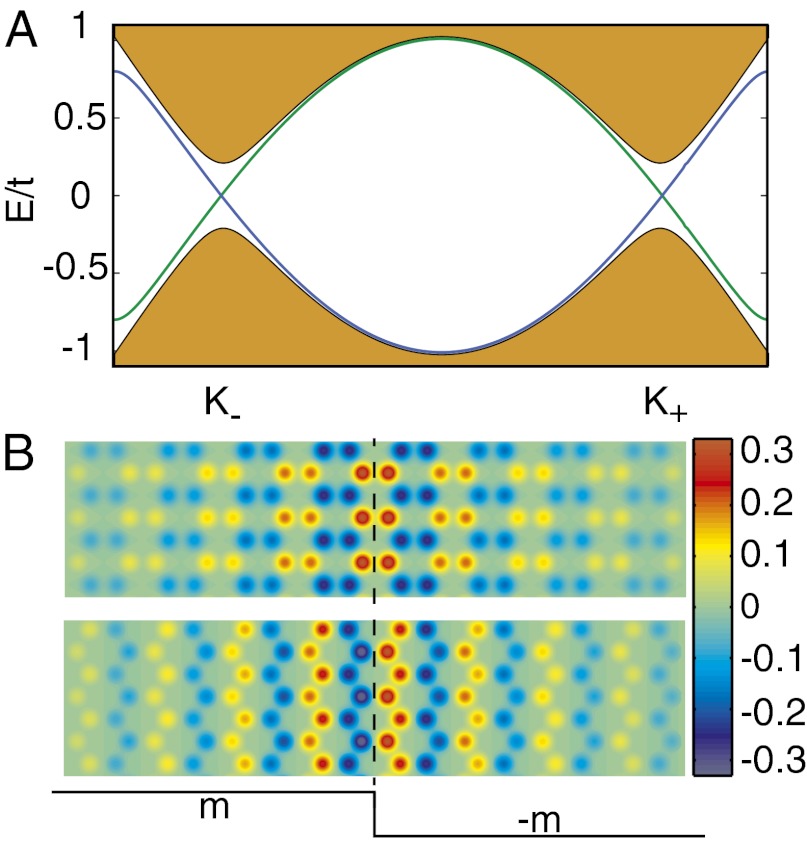
Also to be assessed is the topological domain walls that occur naturally with the afm order, the band structure of which is shown in Fig. 3A. There are two spin-polarized bands that arise at the domain wall and intersect to yield a pair of Dirac points, whereas the bulk states are always spin degenerate. The spin and momentum clearly are locked at individual Dirac points. Unlike the edge states in a topological insulator, these edge states cannot offer the spin-selective channels. However, if a spin is injected into the edge with a prescribed direction of momentum, it can migrate ballistically, enjoying the suppression of back scattering offered by valley protection. It is also of interest to note that the wavefunctions (Fig. 3B) at the same Dirac points have opposite parity for opposite spins. The odd and even parity boundary states may be used as spin and/or valley filters, as linear defects in graphene (13).
Fig. 3.
Spin-polarized edge states. (A) Band structure in the presence of a zigzag magnetic domain on the afm honeycomb lattice, derived from NN hopping Hamiltonian. A model of a zigzag domain wall is used, which extends 50 unit cells on both sides. The bulk states are lumped into shaded blobs. With the hopping parameter t as the energy unit, the mass is set to m = t/2. The edge states of two spins are shown in blue and green. (B) Wavefunctions of two spins at the same Dirac points. The amplitudes are convolved on 2D Gaussians centered on lattice sites for visualization (scale bar in arbitrary units).
Antiferromagnetic MnPX3
Taking one step from the above theoretical exposition, here we suggest actual materials in which the proposed spin and valley physics may be observed. The selection of materials should meet a few criteria. The candidate materials must (i) have characteristic afm order on a honeycomb lattice; (ii) be a semiconductor, with direct band gaps at high-symmetry K+, K−; and (iii) have interband transitions in the neighborhood of valleys that exhibit CD.
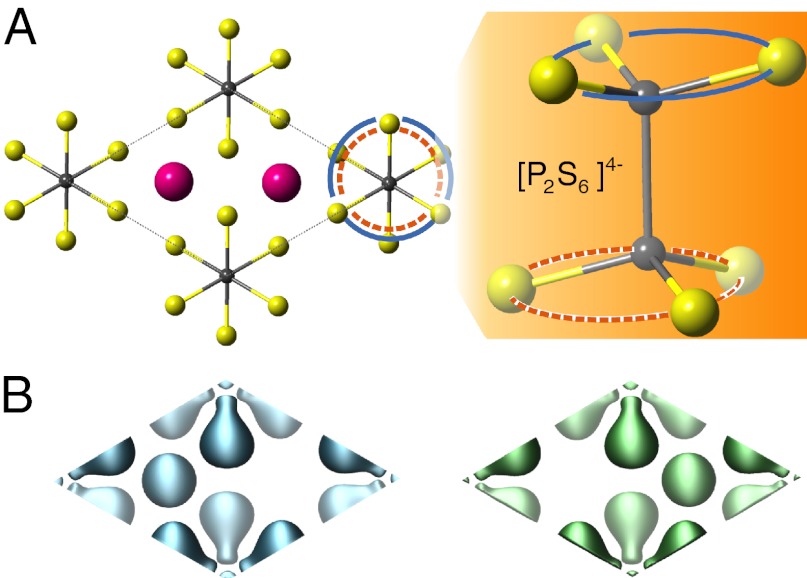
These criteria then lead us to manganese chalcogenophosphates, MnPX3, X = S, Se (14), in monolayer form. Manganese chalcogenophosphates are layered crystalline materials, in which the interlayer coupling is the relatively weak van der Waals interactions. In principle, all van der Waals–bonded layered compounds can be thinned to the monolayer limit by the micromechanical exfoliation technique (15, 16). Hence, monolayer MnPX3 in all likelihood can be produced. As shown in Fig. 4A, each unit cell in the monolayer MnPX3 is composed of two Mn2+ and one [P2X6]4− cluster, the latter isostructural and isoelectronic to molecular ethane (C2H6) in the staggered conformation. The most crucial feature of these compounds is that each Mn2+ ion, assuming an 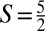 high-spin state, is antiferromagnetically coupled to its three NNs, forming the afm honeycomb lattice.
high-spin state, is antiferromagnetically coupled to its three NNs, forming the afm honeycomb lattice.
Fig. 4.
Structure and afm of monolayer MnPX3. (A) Structure showing the unit cell. Purple spheres are Mn, yellow X, and gray P. Some of the computed bond lengths are P–P = 2.22 Å, P–S = 2.04 Å for MnPS3, and P–P = 2.24 Å, P–Se = 2.22 Å for MnPSe3. (B) Spin densities in one unit cell, presenting the antiferromagnetic configuration (the isosurface of 0.4 e/Å3). (Left) up-spin; (Right) down-spin.
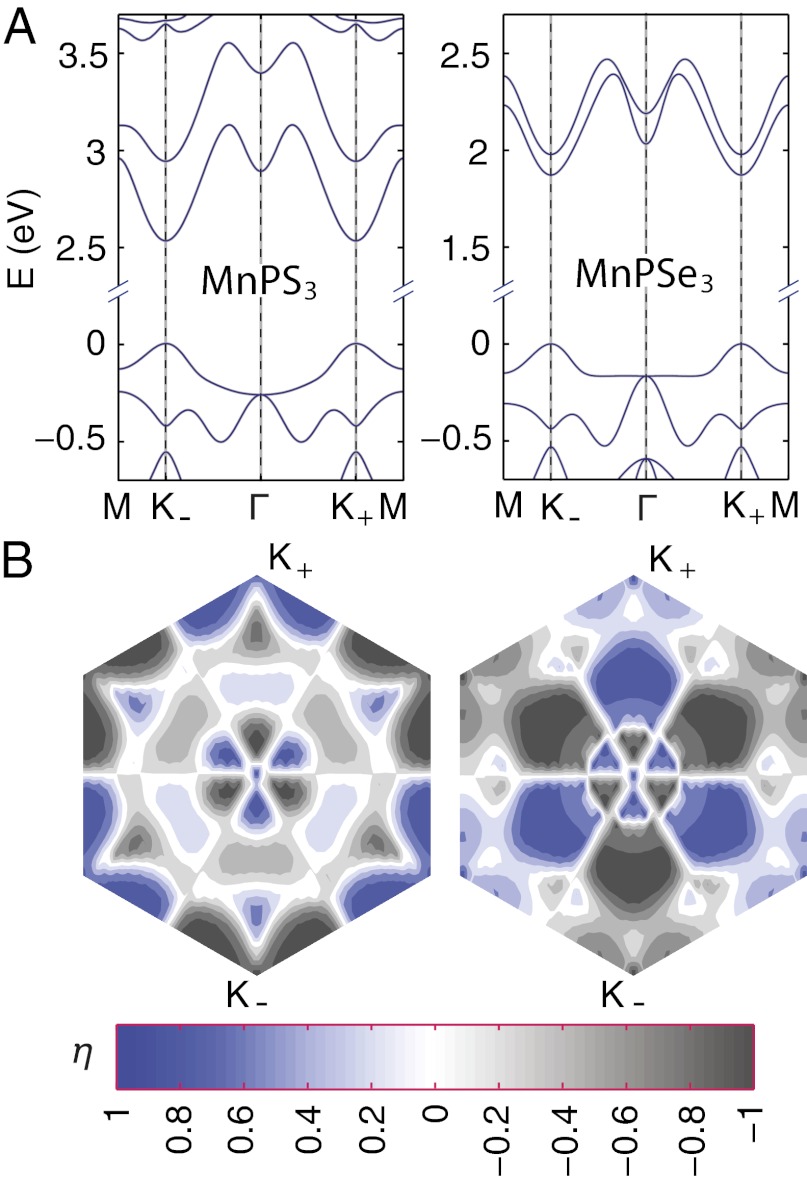
The spin-density isosurfaces for MnPS3, computed with the density functional theory (refer to Methods for computational details), are displayed in Fig. 4B. The spin densities for the up- and down-spins show little difference on the [P2X6]4− framework. However, the densities for two spins on Mn are indeed well separated and localized on the two Mn ions, providing the expected spin-contrasting asymmetric potential (Fig. 1B). The band structures of monolayer MnPX3 are shown in Fig. 5A. We observe that the band widths near the band gap are quite narrow for MnPX3, between 0.17 and 0.63 eV. The ratio of U to the band widths (a measure of U/t) for MnPX3 is greater than 7, indicating that the afm insulating state is expected to be stable in the monolayer limit (12). MnPS3 and MnPSe3 both show direct band gaps at K± (2.53 and 1.87 eV, respectively), falling well within the optical range. This is advantageous for the realization of optical polarization of charge carriers. Within the collinear treatment of magnetism, the Bloch states of two spins are degenerate everywhere in the momentum space. When treating the spins in the noncollinear formalism to account for possible spin–orbit (or spin–valley) interactions, the spins remain degenerate, but band gaps become renormalized as expected. For MnPS3, the gap difference between K± is negligibly small. However, for MnPSe3, the gaps at K± differ by up to ∼43 meV, offering a window for realizing the SHE with equilibrium n- or p-doping (compare Fig. 2B).
Fig. 5.
Electronic structure of manganese chalcogenophosphates from density functional theory (DFT) calculations. (A) The band structures of MnPX3 (X = S, Se) near the band gaps. The energy scales are zeroed to the Fermi level. (B) The momentum-resolved degrees of circular polarization of MnPX3 (X = S, Se), η(s)(k), between the top of valence bands and the bottom of conduction bands. Only the values of one spin are presented, as in our calculations the other spin takes values equal in magnitude but with opposite signs over the Brillouin zone. At Γ, the computed optical selectivity is nonzero. This is a numerical artifact because of indeterminacy in η(s)(k) in the presence of band degeneracy (apart from the spin degeneracy) in the valence bands (A).
To assess the optical selectivity of valleys by circularly polarized light, we compute the spin-dependent degree of circular polarization, η(s)(k) (6, 7), between the top of valence bands and the bottom of conduction bands. This quantity is computed using the density functional linear response approach, defined as
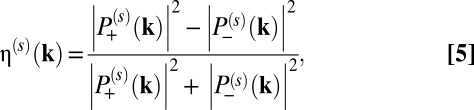 |
where 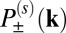 are the interband matrix elements of, respectively, left- and right-polarized radiation fields for spin s at k, defined for a vertical transition from band n to band n′, as
are the interband matrix elements of, respectively, left- and right-polarized radiation fields for spin s at k, defined for a vertical transition from band n to band n′, as 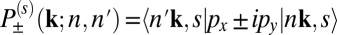 , assuming spin flip is absent in the optical processes. The value of η(s)(k) quantifies the relative absorption rates of left- and right-handed photon. As shown in Fig. 5B, monolayer MnPX3 is computed to have perfect CD in the neighborhood of K±. For one spin component, they show the valley-selective CD as previously found for MoS2 (7), and for opposite spins they show a spin–valley dependent selectivity lending corroboration to our theoretical model. The computed selectivity decays as we move away from the high-symmetry K±, yet substantial polarization is achievable owing to the sizable regions of nonvanishing selectivity.
, assuming spin flip is absent in the optical processes. The value of η(s)(k) quantifies the relative absorption rates of left- and right-handed photon. As shown in Fig. 5B, monolayer MnPX3 is computed to have perfect CD in the neighborhood of K±. For one spin component, they show the valley-selective CD as previously found for MoS2 (7), and for opposite spins they show a spin–valley dependent selectivity lending corroboration to our theoretical model. The computed selectivity decays as we move away from the high-symmetry K±, yet substantial polarization is achievable owing to the sizable regions of nonvanishing selectivity.
Discussion
The optical selectivity of valley interband transitions was discussed in earlier papers (see, e.g., refs. 6–8). Here, we phrase it in the language of group theory. Central to the selectivity is the rotational symmetry, 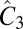 , and the associated pure rotational group, C3. The point group of a staggered honeycomb lattice (A and B sites are inequivalent) is C3v (i.e., for MnPX3 there is no in-plane mirror reflection). The symmetry at K±, however, is C3; i.e., this is an abelian group that does not allow degeneracy (apart from spin degeneracy). Because band degeneracy is absent, when we operate
, and the associated pure rotational group, C3. The point group of a staggered honeycomb lattice (A and B sites are inequivalent) is C3v (i.e., for MnPX3 there is no in-plane mirror reflection). The symmetry at K±, however, is C3; i.e., this is an abelian group that does not allow degeneracy (apart from spin degeneracy). Because band degeneracy is absent, when we operate 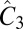 on an eigenstate at a k that respects C3 rotational symmetry, we have
on an eigenstate at a k that respects C3 rotational symmetry, we have 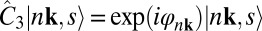 , where φnk = lnk2π/3. The azimuthal quantum number, lnk, is an integer determined up to modulo 3. Consider the following transform:
, where φnk = lnk2π/3. The azimuthal quantum number, lnk, is an integer determined up to modulo 3. Consider the following transform:
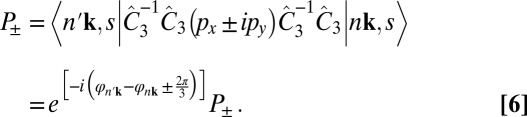 |
Clearly, the optical selection rule is modulo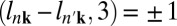 for left- and right-polarized radiation fields, respectively (SI Symmetry Analysis of the Optical Selectivity). This is a mere restatement of the conservation of angular momentum in the absorption of a single photon absent spin flip. The azimuthal quantum number of the Bloch state, lnk = lL + lM, is the sum of two terms—(i) lL arising from lattice phase winding of the Bloch phase factor, eik⋅r (6), and (ii) lL = ml, where ml is the magnetic quantum number of the local atomic basis sets (or, Wannier-like functions)—that contribute an additional phase under
for left- and right-polarized radiation fields, respectively (SI Symmetry Analysis of the Optical Selectivity). This is a mere restatement of the conservation of angular momentum in the absorption of a single photon absent spin flip. The azimuthal quantum number of the Bloch state, lnk = lL + lM, is the sum of two terms—(i) lL arising from lattice phase winding of the Bloch phase factor, eik⋅r (6), and (ii) lL = ml, where ml is the magnetic quantum number of the local atomic basis sets (or, Wannier-like functions)—that contribute an additional phase under 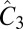 . The effect of the local orbital symmetry and orbital ordering at the two valleys has an important role in determining the selection rules, as demonstrated in previous work (7). Because of the multiband nature of the states across the band gaps in MnPX3, an effort that is currently underway is to develop a more elaborate model to appreciate the symmetry of the valley states, beyond the two-band model in Eq. 1.
. The effect of the local orbital symmetry and orbital ordering at the two valleys has an important role in determining the selection rules, as demonstrated in previous work (7). Because of the multiband nature of the states across the band gaps in MnPX3, an effort that is currently underway is to develop a more elaborate model to appreciate the symmetry of the valley states, beyond the two-band model in Eq. 1.
We also note how the spin–valley optical selection rule develops as a consequence of symmetry breaking in a fermionic honeycomb lattice. The threefold rotational invariance of the Hamiltonian implies 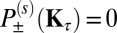 for either left- or right-handed (±) polarization field, when conduction and valence bands are separately nondegenerate (this is not the spin degeneracy, and is ensured when the point group is abelian) (7). The antiferromagnetic Hamiltonian of Eq. 1 violates both time-reversal symmetry and parity, but accommodates the joint operation
for either left- or right-handed (±) polarization field, when conduction and valence bands are separately nondegenerate (this is not the spin degeneracy, and is ensured when the point group is abelian) (7). The antiferromagnetic Hamiltonian of Eq. 1 violates both time-reversal symmetry and parity, but accommodates the joint operation 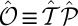 as a symmetry; that is,
as a symmetry; that is, 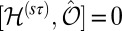 . When operating on a Bloch state,
. When operating on a Bloch state, 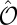 preserves its wavevector while inverting the spin. Consequently, the Bloch states of the same k and opposite spins are degenerate. Moreover,
preserves its wavevector while inverting the spin. Consequently, the Bloch states of the same k and opposite spins are degenerate. Moreover, 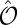 changes the chirality of light, which implies
changes the chirality of light, which implies 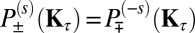 , to within a phase factor. This is concordant with the notion that the spin–valley index s ⋅ τ constitutes a degree of freedom, which defines chiro-optical selectivity (as well as orbital moments).
, to within a phase factor. This is concordant with the notion that the spin–valley index s ⋅ τ constitutes a degree of freedom, which defines chiro-optical selectivity (as well as orbital moments).
Of note, the proposed optical selectivity may be a convenient assay for antiferromagnetic order in an extremely thin sample, e.g., a monolayer or few-layer sample. This is especially relevant to the recent interest in the yet-to-be-uncovered spin liquid phase on a honeycomb lattice in the intermediate U regime (12). The neutron-scattering technique commonly used to determine the antiferromagnetic order will become impractical for thin samples. The circularly polarized photoluminescence, on the contrary, works well for these atomically thin samples, with sufficient sensitivity (7, 9, 10). In the spin liquid phase, ground-state fluctuations are incessant at T = 0 K, whereby obliterating the afm order and, hence, the optical selectivity will be absent. Entrance into the symmetry-broken afm ordered regime, on the other hand, is accompanied by the proposed optical selectivity.
A nontrivial variation of the proposed Hamiltonian of Eq. 1 occurs when the spin–orbit interaction becomes overwhelming, compared with the afm order, m. Clearly, when |δ| = m (Fig. 1C), the band gap closes in one of the valleys. When |δ| > m, band inversion of one valley will drive the system into a topological quantum spin Hall state (17, 18). In the limit m = 0, the model reduces exactly to that of Kane and Mele (17), which affords time-reversal symmetry-protected edge states. However, when m is finite but smaller than |δ|, time reversal is lost. The corresponding topological classification depends on detailed symmetry of actual crystal. If the x–y plane is a mirror plane, then the system may be classified by the mirror Chern number. If, on the other hand, the x–y mirror symmetry is absent, the system may be classified by its spin Chern number (19). This topic and the strategy for tuning the ratio |δ|/m in real materials are issues worth further pursuit.
We also note that bilayer or few-layer MnPX3 also may have similar optical selectivity, similar to a spontaneous symmetry-broken few-layer graphene system (20). Different kinds of stacking and magnetic order of bilayer MnPX3 (X = S, Se) with intralayer afm and ferromagnetism are evaluated in our calculations (SI Bilayer Manganese Chalcogenophosphates). Two AA-stacked bilayers with intralayer afm are nearly degenerate in energy and more stable than other stacking and magnetic orders. They differ by the interlayer magnetic configuration; that is, the two layers can couple ferromagnetically or antiferromagnetically. By computing the momentum-resolved spin-dependent degree of circular polarization, we find that the s ⋅ τ CD is present in the ferromagnetically coupled bilayer, which has no inversion center in the magnetic space group. The chiral optical selection rule is absent in the case of antiferromagnetic interlayer coupling, as expected. The computed perfect spin–valley-dependent optical selectivity of both monolayer and ferromagnetically coupled bilayer MnPX3 attests to the emergent electronic degree of freedom presented in the foregoing mode. It is, therefore, of interest to study these materials in monolayer and few-layer forms experimentally, to characterize their optoelectronic and transport behaviors and to explore their potential for application in novel operating paradigms for advanced electronics.
Methods
We use density functional theory (21) calculations within the generalized gradient approximation (GGA) (22) to investigate the basic electronic structure of monolayer and bilayer MnPX3. For monolayer MnPX3, we use the Perdew–Burke–Ernzerhof exchange-correlation functional (23). To consider different kinds of stacking and magnetic order of bilayer MnPX3, van der Waals corrections within GGA are included by the optB86b-vdwDF method (24, 25). The projector-augmented wave potentials are used, as implemented in the Vienna Ab initio Simulation Package (26, 27). A planewave cutoff of 600 eV and a Monkhorst–Pack k-point mesh of 30 × 30 × 1 per reciprocal unit cell are adopted. Vacuum slabs at least 15 Å thick are inserted between monolayer MnPX3 to minimize interaction between periodic images. Structure optimizations are performed with a convergence threshold of 0.01 eV/Å on the interatomic forces. To account for the magnetic structure of the divalent transition metal Mn, we use a GGA+U approach to describe the on-site electron–electron Coulomb repulsion (28). The value of the isotropic U is set to 5 eV, as suggested by a previous assessment of this parameter for the divalent Mn2+ (29). As a calibration for the choice of U, the band gap of 2.4 eV is obtained for bulk MnPS3, to be compared with the experimental band gap of bulk MnPS3 of 2.7 eV (30). For both bulk and monolayer MnPX3, the antiferromagnetic order of MnPX3 is indeed the more stable in our calculations, compared with the nonmagnetic and ferromagnetic states by at least 45 meV per unit cell. The magnetic moment on each Mn is computed to be about 4.6 Bohr magnetons, in good agreement with the experiments (14). Therefore, the choice of U is reasonable and used in all calculations. We compute the interband transition matrix elements using density functional theory at the linear response level (7, 31).
Supplementary Material
Acknowledgments
We are grateful to Prof. Shuang Jia and Dr. Fan Zhang for useful discussions. We acknowledge financial support from the National Science Foundation of China (NSFC Project 11174009) and China 973 Program (Project 2013CB921900).
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1219420110/-/DCSupplemental.
References
- 1.Rycerz A, Tworzydlo J, Beenakker CWJ. Valley filter and valley valve in graphene. Nat Phys. 2007;3:172–175. [Google Scholar]
- 2.Gunawan O, et al. Valley susceptibility of an interacting two-dimensional electron system. Phys Rev Lett. 2006;97(18):186404. doi: 10.1103/PhysRevLett.97.186404. [DOI] [PubMed] [Google Scholar]
- 3.Takashina K, Ono Y, Fujiwara A, Takahashi Y, Hirayama Y. Valley polarization in Si(100) at zero magnetic field. Phys Rev Lett. 2006;96(23):236801. doi: 10.1103/PhysRevLett.96.236801. [DOI] [PubMed] [Google Scholar]
- 4.Eng K, McFarland RN, Kane BE. Integer quantum Hall effect on a six-valley hydrogen-passivated silicon (111) surface. Phys Rev Lett. 2007;99(1):016801. doi: 10.1103/PhysRevLett.99.016801. [DOI] [PubMed] [Google Scholar]
- 5.Xiao D, Yao W, Niu Q. Valley-contrasting physics in graphene: Magnetic moment and topological transport. Phys Rev Lett. 2007;99(23):236809. doi: 10.1103/PhysRevLett.99.236809. [DOI] [PubMed] [Google Scholar]
- 6.Yao W, Xiao D, Niu Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys Rev B. 2008;77:235406. [Google Scholar]
- 7.Cao T, et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat Commun. 2012;3:887. doi: 10.1038/ncomms1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xiao D, Liu GB, Feng W, Xu X, Yao W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys Rev Lett. 2012;108(19):196802. doi: 10.1103/PhysRevLett.108.196802. [DOI] [PubMed] [Google Scholar]
- 9.Mak KF, He K, Shan J, Heinz TF. Control of valley polarization in monolayer MoS2 by optical helicity. Nat Nanotechnol. 2012;7(8):494–498. doi: 10.1038/nnano.2012.96. [DOI] [PubMed] [Google Scholar]
- 10.Zeng H, Dai J, Yao W, Xiao D, Cui X. Valley polarization in MoS2 monolayers by optical pumping. Nat Nanotechnol. 2012;7(8):490–493. doi: 10.1038/nnano.2012.95. [DOI] [PubMed] [Google Scholar]
- 11.Xiao D, Chang MC, Niu Q. Berry phase effects on electronic properties. Rev Mod Phys. 2010;82:1959–2007. [Google Scholar]
- 12.Meng ZY, Lang TC, Wessel S, Assaad FF, Muramatsu A. Quantum spin liquid emerging in two-dimensional correlated Dirac fermions. Nature. 2010;464(7290):847–851. doi: 10.1038/nature08942. [DOI] [PubMed] [Google Scholar]
- 13.Gunlycke D, White CT. Graphene valley filter using a line defect. Phys Rev Lett. 2011;106(13):136806. doi: 10.1103/PhysRevLett.106.136806. [DOI] [PubMed] [Google Scholar]
- 14.Ressouche E, et al. Magnetoelectric MnPS3 as a candidate for ferrotoroidicity. Phys Rev B. 2010;82:100408. [Google Scholar]
- 15.Novoselov KS, et al. Electric field effect in atomically thin carbon films. Science. 2004;306(5696):666–669. doi: 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- 16.Novoselov KS, et al. Two-dimensional atomic crystals. Proc Natl Acad Sci USA. 2005;102(30):10451–10453. doi: 10.1073/pnas.0502848102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kane CL, Mele EJ. Quantum spin Hall effect in graphene. Phys Rev Lett. 2005;95(22):226801. doi: 10.1103/PhysRevLett.95.226801. [DOI] [PubMed] [Google Scholar]
- 18.Kane CL, Mele EJ. Z2 topological order and the quantum spin Hall effect. Phys Rev Lett. 2005;95(14):146802. doi: 10.1103/PhysRevLett.95.146802. [DOI] [PubMed] [Google Scholar]
- 19.Hsieh TH, et al. Topological crystalline insulators in the SnTe material class. Nat Commun. 2012;3:982. doi: 10.1038/ncomms1969. [DOI] [PubMed] [Google Scholar]
- 20.Zhang F, Jung J, Fiete GA, Niu Q, MacDonald AH. Spontaneous quantum Hall states in chirally stacked few-layer graphene systems. Phys Rev Lett. 2011;106(15):156801. doi: 10.1103/PhysRevLett.106.156801. [DOI] [PubMed] [Google Scholar]
- 21.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. 1965;140:A1133–A1138. [Google Scholar]
- 22.Langreth DC, Mehl MJ. Easily implementable nonlocal exchange-correlation energy functional. Phys Rev Lett. 1981;47:446–450. [Google Scholar]
- 23.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77(18):3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 24.Klimeš J, Bowler DR, Michaelides A. Chemical accuracy for the van der Waals density functional. J Phys Condens Matter. 2010;22(2):022201. doi: 10.1088/0953-8984/22/2/022201. [DOI] [PubMed] [Google Scholar]
- 25.Klimeš J, Bowler DR, Michaelides A. Van der Waals density functionals applied to solids. Phys Rev B. 2011;83:195131. [Google Scholar]
- 26.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter. 1996;54(16):11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 27.Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B. 1999;59:1758–1775. [Google Scholar]
- 28.Dudarev SL, Botton GA, Savrasov SY, Humphreys CJ, Sutton AP. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys Rev B. 1998;57:1505–1509. [Google Scholar]
- 29.Franchini C, Podloucky R, Paier J, Marsman M, Kresse G. Ground-state properties of multivalent manganese oxides: Density functional and hybrid density functional calculations. Phys Rev B. 2007;75:195128. [Google Scholar]
- 30.Jeevanandam P, Vasudevan S. Magnetism in MnPSe3: A layered 3d5 antiferromagnet with unusually large XY anisotropy. J Phys Condens Matter. 1999;11:3563–3570. [Google Scholar]
- 31.Gajdoš M, Hummer K, Kresse G, Furthmüller J, Bechstedt F. Linear optical properties in the projector-augmented wave methodology. Phys Rev B. 2006;73:045112. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.