Circular representation of human cortical networks for subject and population-level connectomic visualization

Abstract

Cortical network architecture has predominantly been investigated visually using graph theory representations. In the context of human connectomics, such representations are not however always satisfactory because canonical methods for vertex–edge relationship representation do not always offer optimal insight regarding functional and structural neural connectivity. This article introduces an innovative framework for the depiction of human connectomics by employing a circular visualization method which is highly suitable to the exploration of central nervous system architecture. This type of representation, which we name a ‘connectogram’, has the capability of classifying neuroconnectivity relationships intuitively and elegantly. A multimodal protocol for MRI/DTI neuroimaging data acquisition is here combined with automatic image segmentation to (1) extract cortical and non-cortical anatomical structures, (2) calculate associated volumetrics and morphometrics, and (3) determine patient-specific connectivity profiles to generate subject-level and population-level connectograms. The scalability of our approach is demonstrated for a population of 50 adults. Two essential advantages of the connectogram are (1) the enormous potential for mapping and analyzing the human connectome, and (2) the unconstrained ability to expand and extend this analysis framework to the investigation of clinical populations and animal models.

Introduction

The ability to collect enormous amounts of structural and functional connectivity data from human populations has grown so impressively that it has by far surpassed the rate at which methods for the analysis, visualization and interpretation of such data are made available. Due to the high dimensionality and high information complexity of data acquired using magnetic resonance imaging (MRI), functional MRI (fMRI) and diffusion tensor imaging (DTI), novel perspectives upon their optimal utilization often require the innovation of ingenuous ways to capture, condense and systematize complex architectural and functional relationships between cortical units. In the past, cortical network architecture as inferred from neuroimaging has preponderantly been visualized using the obvious symbols of graph theory. Although precise and minimalistic, such representations are not always adequate, however, in the context of the emerging field of connectomics because typical approaches to vertex segregation and edge ordering do not always lead to visual representations that are optimally revealing of essential functional and structural relationships in the brain. Thus, although such representations have been variously adapted to the exploration of cortical structure, function or information-theoretic content, cortical networks remain difficult to understand due to the overwhelming number of complex relationships whose overarching implications can easily be lost during their visual exploration. Consequently, interpretation and analysis of connectivity have traditionally required a disappointing amount of simplification and dimensionality reduction, frequently to the detriment of conveying essential aspects of neural architecture. For these very reasons, historically, the introduction of inventive and illuminating methods for complex data visualization has greatly improved the effectiveness of scientific analysis and dissemination, as in Darwin's introduction of directed graphs to depict phylogenetic information (Darwin, 1859) or Sneath's use of heat maps to understand array and expression data (Sneath, 1957).

The term ‘connectome’ was suggested independently and simultaneously in 2005 bySporns et al. (2005) and by Hagman (2005) to refer to a comprehensive map of neural connections in the brain. The generation and study of connectomes are known as ‘connectomics’. In this paper, a novel methodology for the conceptual mapping and visualization of human connectomics is introduced through the use of an intuitive circular representation which is tailored in a germane fashion to the depiction of brain architecture. It is demonstrated how this simple and elegant conceptual framework is equipped with the ability to organize, inspect and classify brain connections in a visually-insightful and content-rich manner, and with the clear advantage of a high data-to-ink ratio. We name this representation a ‘connectogram’. Using joint MRI/DTI data acquisition and automatic image segmentation, a protocol is illustrated for the extraction of 148 cortical and 17 non-cortical anatomical parcellations using standard nomenclature, followed by the calculation of structural anatomy metrics (volume, area, cortical thickness, curvature) for cortical regions. For some given human subject, these structural data are subsequently combined with the connectivity profile extracted from DTI to generate the connectogram of that subject. To demonstrate the scalability potential of this approach, the generation of a statistically-informed, population-level connectogram is illustrated for a population of 50 adult male subjects. Intrinsic merits of the present approach include significant potential for connectome mapping and analysis across the human species, as well as an essentially unlimited capability of extending this approach to the study, representation, and comparison of diseased populations.

Materials and methods

Subjects

50 healthy adult males with ages between 25 and 35 were included in the study. All subjects were screened to exclude cases of pathology known to affect brain structure, a history of significant head injury, a neurological or psychiatric illness, substance abuse or dependence, or a psychiatric disorder in any first-degree relative.

Neuroimaging, segmentation and parcellation

T₁-weighted neuroimaging data were selected from the LONI Integrated Data Archive (IDA; http://ida.loni.ucla.edu). Segmentation and regional parcellation were performed using FreeSurfer (Dale et al., 1999; Fischl et al., 1999; Fischl et al., 2002) following the nomenclature described inDestrieux et al. (2010). For each hemisphere, a total of 74 cortical structures were identified in addition to 7 subcortical structures and to the cerebellum. Segmentation results from a sample subject are shown in Fig. 1(A). One midline structure (the brain stem) was also included, for a total of 165 parcellations for the entire brain. The cortex was divided into 7 lobes, with the number of parcellations in each being equal to 21 (frontal, Fro), 8 (insula, Ins), 8 (limbic, Lim), 11 (temporal, Tem), 11 (parietal, Par), and 15 (occipital, Occ). Five representative statistics were computed for each parcellation: gray matter (GM) volume, surface area, mean cortical thickness, mean curvature, and white matter (WM) fiber count per unit GM volume (‘degree of connectivity’). Diffusion tensors were computed from DWI images and rotationally re-oriented at each voxel. Tensor-valued imageswere linearly realigned based on trilinear interpolation of log-transformed tensors as described inChiang et al. (2011) and resampled to isotropic voxel resolution (1.7×1.7×1.7 mm³). Diffusion gradient data were processed in native space using TrackVis (trackvis.org) to reconstruct fiber tracts. Data processing workflows were created using the LONI Pipeline (pipeline.loni.ucla.edu). The results of DTI tractography analysis for a sample subject are shown in Fig. 1(B).

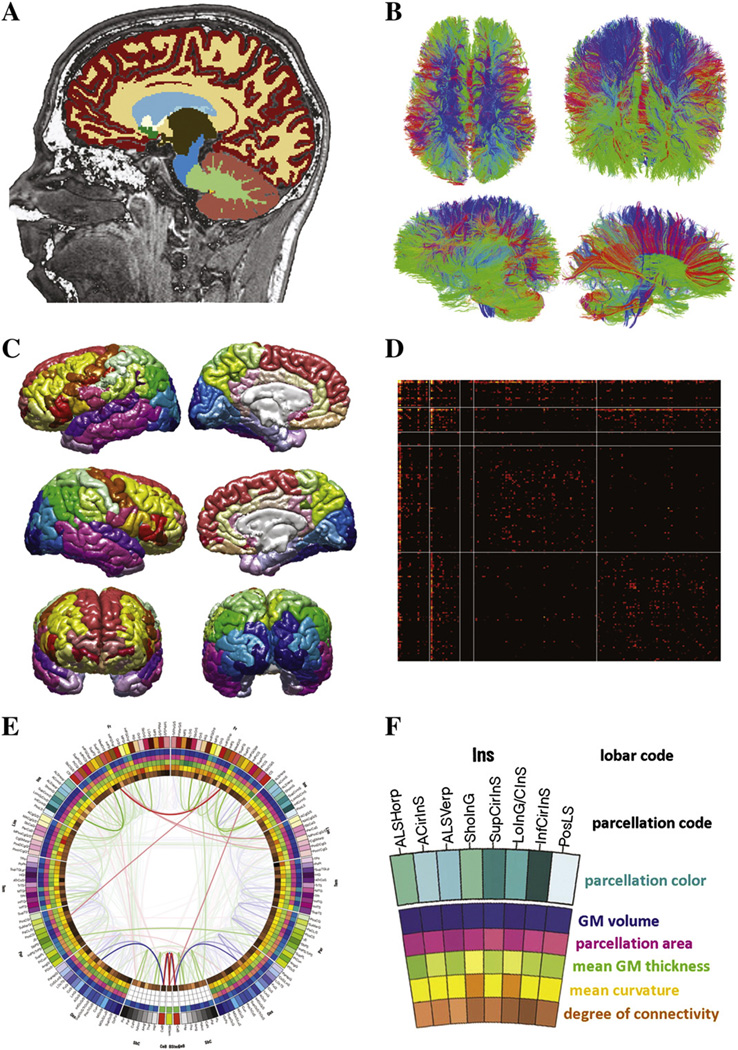
Fig. 1.

(A) Segmentation results from a sample subject selected from the LONI IDA and included in the present study. Segmentation and regional parcellation were performed using FreeSurfer (Dale et al., 1999; Fischl et al., 1999; Fischl et al., 2002) following the nomenclature described inDestrieux et al. (2010). (B) Results of DTI tractography analysis for a sample subject. Diffusion tensors were computed from DWI images and rotationally re-oriented at each voxel. Diffusion gradient data were processed in native space using TrackVis (trackvis.org) to reconstruct fiber tracts. (C) Representation of the reconstructed pial surface for a sample subject. Each cortical lobe was assigned a unique color scheme, as explained in the Materials and methods section. Additionally, every structure was assigned its unique RGB color based on esthetic considerations (see text for details). (D) Example of a connectivity matrix computed for a sample subject. Vertical and horizontal lines are used to delimitate entries in the matrix corresponding to connections within the left and right non-cortical regions (first two squares on the diagonal), within the left and right cortical hemispheres (last two squares on the diagonal), as well as connections between the two hemispheres or between cortex and non-cortical structures (off-diagonal elements). (E) A sample connectogram created a single subject (see Fig. 2 and text for details). (F) Legend of the representation of cortical metrics in the connectogram. Within the circular structure representing the cortical parcellations, five circular heat maps are present, each encoding one of five structural measures associated with the corresponding parcellation. Proceeding inward towards the center of the circle, these measures re: total GM volume, total area of the surface associated with the GM–WM interface (at the base of the cortical ribbon), mean cortical thickness, mean curvature and connectivity per unit volume.

Color coding and abbreviation schemes

Each cortical lobe was assigned a unique color scheme: black to red to yellow (Fro), charlotte to turquoise to forest green (Ins), primrose to lavender rose (Lim), pink to lavender to rosebud cherry (Tem), lime to forest green (Par), and lilac to indigo (Occ). Every structure was assigned its unique RGB color based on esthetic considerations; subcortical structures were colored light gray to black. Color scheme choice and assignment to each lobe were made by taking into account the arrangement and adjacency of lobes on the cortical surface, with the goal of avoiding any two adjacent lobes from having overlapping or similar color schemes. The individual colors of the scheme associated with any particular lobe were assigned to every parcellation within that lobe in such a way as to create an esthetic effect when displayed on cortical surfaces or connectograms. To label each parcellation with a certain name, an abbreviation scheme was created which was both unambiguous and short enough to be displayable outside the connectogram's outermost ring. Table 1 summarizes each parcellation's abbreviation, full description and FreeSurfer code as defined in the original parcellation scheme (Destrieux et al., 2010), as well as the associated RGB code. Table 2 contains the legend to the abbreviations and specifies their unambiguous mapping to corresponding keywords. An illustration of the color coding used for each parcellation as described above is shown in Fig. 1(C). In addition, it should be mentioned that the color labeling convention described above is only one of the numerous coloring schemes which could be employed. However, one advantage that our convention offers is that it minimizes the likelihood that the color maps for two distinct, adjacent lobes are similar, which thus ensures straightforward association of distinct lobes with distinct coloring schemes. Another advantage of our convention is its potential for standardization, such that the color schemes used in the present study can be used again either by ourselves or by other researchers in future studies without the possibility of confusion.

Table 1.

Summary of each parcellation's abbreviation, full description and FreeSurfer code as defined in the original parcellation scheme (Destrieux et al., 2010), as well as the associated RGB code in the connectogram.

Abbreviation	Description	FreeSurfer code	RGB code
Neocortical structures
ACgG/S	Anterior part of the cingulate gyrus and sulcus	G_and_S_cingul-Ant	255	255	180
ACirInS	Anterior segment of the circular sulcus of the insula	S_circular_insula_ant	102	255	255
ALSHorp	Horizontal ramus of the anterior segment of the lateral sulcus (or fissure)	Lat_Fis-ant-Horizont	0	255	204
ALSVerp	Vertical ramus of the anterior segment of the lateral sulcus (or fissure)	Lat_Fis-ant-Vertical	0	255	255
AngG	Angular gyrus	G_pariet_inf-Angular	0	255	0
AOcS	Anterior occipital sulcus and preoccipital notch (temporo-occipital incisure)	S_occipital_ant	51	51	255
ATrCoS	Anterior transverse collateral sulcus	S_collat_transv_ant	153	0	204
CcS	Calcarine sulcus	S_calcarine	102	153	255
CgSMarp	Marginal branch (or part) of the cingulate sulcus	S_cingul-Marginalis	255	192	201
CoS/LinS	Medial occipito-temporal sulcus (collateral sulcus) and lingual sulcus	S_oc-temp_med_and_Lingual	153	204	255
CS	Central sulcus (Rolando's fissure)	S_central	255	51	0
Cun	Cuneus (O6)	G_cuneus	0	153	255
FMarG/S	Fronto-marginal gyrus (of Wernicke) and sulcus	G_and_S_frontomargin	204	0	51
FuG	Lateral occipito-temporal gyrus (fusiform gyrus, O4–T4)	G_oc-temp_lat-fusifor	102	102	255
HG	Heschl's gyrus (anterior transverse temporal gyrus)	G_temp_sup-G_T_transv	102	0	102
InfCirInS	Inferior segment of the circular sulcus of the insula	S_circular_insula_inf	0	102	102
InfFGOpp	Opercular part of the inferior frontal gyrus	G_front_inf-Opercular	255	204	0
InfFGOrp	Orbital part of the inferior frontal gyrus	G_front_inf-Orbital	153	051	0
InfFGTrip	Triangular part of the inferior frontal gyrus	G_front_inf-Triangul	255	0	0
InfFS	Inferior frontal sulcus	S_front_inf	153	102	0
InfOcG/S	Inferior occipital gyrus (O3) and sulcus	G_and_S_occipital_inf	51	153	255
InfPrCS	Inferior part of the precentral sulcus	S_precentral-inf-part	255	153	0
IntPS/TrPS	Intraparietal sulcus (interparietal sulcus) and transverse parietal sulci	S_intrapariet_and_P_trans	51	255	51
InfTG	Inferior temporal gyrus (T3)	G_temporal_inf	255	0	255
InfTS	Inferior temporal sulcus	S_temporal_inf	204	0	153
JS	Sulcus intermedius primus (of Jensen)	S_interm_prim-Jensen	153	204	0
LinG	Lingual gyrus, lingual part of the medial occipito-temporal gyrus (O5)	G_oc-temp_med-Lingual	102	204	255
LOcTS	Lateral occipito-temporal sulcus	S_oc-temp_lat	153	153	255
LoInG/CInS	Long insular gyrus and central insular sulcus	G_Ins_lg_and_S_cent_ins	0	204	204
LOrS	Lateral orbital sulcus	S_orbital_lateral	102	0	0
MACgG/S	Middle–anterior part of the cingulate gyrus and sulcus	G_and_S_cingul-Mid-Ant	255	240	191
MedOrS	Medial orbital sulcus (olfactory sulcus)	S_orbital_med-olfact	255	102	0
MFG	Middle frontal gyrus (F2)	G_front_middle	255	255	051
MFS	Middle frontal sulcus	S_front_middle	255	153	51
MOcG	Middle occipital gyrus (O2, lateral occipital gyrus)	G_occipital_middle	0	204	244
MOcS/LuS	Middle occipital sulcus and lunatus sulcus	S_oc_middle_and_Lunatus	0	51	255
MPosCgG/S	Middle–posterior part of the cingulate gyrus and sulcus	G_and_S_cingul-Mid-Post	255	224	203
MTG	Middle temporal gyrus (T2)	G_temporal_middle	255	102	204
OcPo	Occipital pole	Pole_occipital	0	0	153
OrG	Orbital gyri	G_orbital	255	255	153
OrS	Orbital sulci (H-shaped sulci)	S_orbital-H_Shaped	255	204	204
PaCL/S	Paracentral lobule and sulcus	G_and_S_paracentral	204	255	153
PaHipG	Parahippocampal gyrus, parahippocampal part of the medial occipito-temporal gyrus (T5)	G_oc-temp_med-Parahip	204	204	255
PerCaS	Pericallosal sulcus (S of corpus callosum)	S_pericallosal	255	164	200
POcS	Parieto-occipital sulcus (or fissure)	S_parieto_occipital	204	255	51
PoPl	Polar plane of the superior temporal gyrus	G_temp_sup-Plan_polar	204	153	255
PosCG	Postcentral gyrus	G_postcentral	204	255	204
PosCS	Postcentral sulcus	S_postcentral	153	255	0
PosDCgG	Posterior–dorsal part of the cingulate gyrus	G_cingul-Post-dorsal	255	175	201
PosLS	Posterior ramus (or segment) of the lateral sulcus (or fissure)	Lat_Fis-post	204	255	255
PosTrCoS	Posterior transverse collateral sulcus	S_collat_transv_post	51	102	255
PosVCgG	Posterior–ventral part of the cingulate gyrus (isthmus of the cingulate gyrus)	G_cingul-Post-ventral	255	208	202
PrCG	Precentral gyrus	G_precentral	204	102	0
PrCun	Precuneus (medial part of P1)	G_precuneus	204	255	0
RG	Straight gyrus (gyrus rectus)	G_rectus	255	204	153
SbCaG	Subcallosal area, subcallosal gyrus	G_subcallosal	255	153	200
SbCG/S	Subcentral gyrus (central operculum) and sulci	G_and_S_subcentral	255	102	153
SbOrS	Suborbital sulcus (sulcus rostrales, supraorbital sulcus)	S_suborbital	255	51	102
SbPS	Subparietal sulcus	S_subparietal	102	153	0
ShoInG	Short insular gyri	G_insular_short	51	255	204
SuMarG	Supramarginal gyrus	G_pariet_inf-Supramar	204	255	102
SupCirInS	Superior segment of the circular sulcus of the insula	S_circular_insula_sup	0	153	153
SupFG	Superior frontal gyrus (F1)	G_front_sup	255	102	102
SupFS	Superior frontal sulcus	S_front_sup	204	153	0
SupOcG	Superior occipital gyrus (O1)	G_occipital_sup	0	0	255
SupPrCS	Superior part of the precentral sulcus	S_precentral-sup-part	255	0	102
SupOcS/TrOcS	Superior occipital sulcus and transverse occipital sulcus	S_oc_sup_and_transversal	0	102	255
SupPL	Superior parietal lobule (lateral part of P1)	G_parietal_sup	153	255	153
SupTGLp	Lateral aspect of the superior temporal gyrus	G_temp_sup-Lateral	153	51	255
SupTS	Superior temporal sulcus	S_temporal_sup	204	51	255
TPl	Temporal plane of the superior temporal gyrus	G_temp_sup-Plan_tempo	153	0	153
TPo	Temporal pole	Pole_temporal	255	204	255
TrFPoG/S	Transverse frontopolar gyri and sulci	G_and_S_transv_frontopol	255	153	153
TrTS	Transverse temporal sulcus	S_temporal_transverse	255	153	255
Subcortical structures
Amg	Amygdala	Amygdala	159	159	159
CaN	Caudate nucleus	Caudate	96	96	96
Hip	Hippocampus	Hippocampus	223	223	223
NAcc	Nucleus accumbens	Accumbens-area	128	128	128
Pal	Pallidum	Pallidum	64	64	64
Pu	Putamen	Putamen	32	32	32
Tha	Thalamus	Thalamus-proper	191	191	191
Cerebellar structure
CeB	Cerebellum	Cerebellum–cortex	255	64	0
Midline structure
BStem	Brain stem	Brain-stem	207	255	48

Table 2.

Abbreviations for cortical parcellations used in connectograms. This scheme unambiguously maps the correspondence between each word or prefix and the appropriate keyword (see Table 1 for a list of parcellations).

Abbreviation	Keyword
A	Anterior
Acc	Accumbens
Ang	Angular
B	Brain
C	Central
Ca	Callosal
Cau	Caudate
Cc	Calcarine
CeB	Cerebellum
Cg	Cingulate
Cir	Circular
Cla	Claustrum
Co	Collateral
Cun	Cuneus
D	Dorsal
F	Frontal/fronto-
Fu	Fusiform
G	Gyrus/gyri
H	Heschl
Hip	Hippocampus/hippocampal
Hor	Horizontal
In	Insula/insular
Inf	Inferior
Int	Intra-
J	Jensen
L	Lateral/lobule
Lin	Lingual
Lu	Lunate/lunatus
Lo	Long
M	Middle
Med	Medial
Mar	Marginal
N	Nucleus
Oc	Occipital/occipito-
Op	Opercular
Or	Orbital
P	Parietal
Pa	Para-
Pal	Pallidum
Per	Peri-
Pl	Plane
Po	Pole/polar
Pos	Posterior/post-
Pr	Pre-
Pu	Putamen
p	Part
pl	Plane
R	Rectus
S	Sulcus/sulci
Sb	Sub-
Sho	Short
Su	Supra-
Sup	Superior
T	Temporal
Tha	Thalamus
Tr	Transverse
Tri	Triangular
V	Ventral
ver	Vertical

Connectivity calculation

To compute connectivity between regions for each subject, fiber tractography was performed using the FACT tracking algorithm (Mori et al., 1999) in TrackVis software (http://trackvis.org). Based on the raw FA at each voxel, TrackVis was used to reconstruct each fiber; as the algorithm processed a tract passing along a set of voxels, a drop in FA below the automatic threshold signaled the algorithm to stop and move on to the next tract. The location of each fiber tract extremity was identified via automatic thresholding in TrackVis from within the set of voxels associated with each parcellated region, while the GM volume associated with each parcellation was calculated in FreeSurfer. For those fibers which both originated and ended within any two distinct parcellations of the 165 available, each fiber extremity was associated with the appropriate parcellation. For each tract, the corresponding entry in the connectivity matrix of the subject's brain was appropriately updated to reflect an increment in fiber count (Hagmann et al., 2008; Hagmann et al., 2010). Fibers that both originated and ended within the same parcellation were discarded. Each subject's connectivity matrix was normalized by the total number of fibers within that subject; for population-level analysis, all connectivity matrices were pooled across subjects and averaged to compute probabilistic connection probabilities. A sample connectivity matrix thus obtained is shown in Fig. 1(D).

Connectogram design

Structure and connectivity information were graphically rendered in a circular diagram format using freely available Circos software, which has been described in detail elsewhere (Krzywinski et al., 2009; www.cpan.org/ports). In brief, Circos is a cross-platform Perl application which employs a circular layout to facilitate the display of relationships between pairs of positions by the use of various graphical elements, including links and heat maps. Although traditionally used to visualize genome data, Circos can be effectively applied to the exploration of data sets involving complex relationships between large numbers of factors. In the present case, cortical parcellations were represented as a circular array of 165 radially aligned elements representing the left (quadrants II–III) and right (quadrants I, IV) cerebral hemispheres, each positioned symmetrically with respect to the vertical axis. We name this representation a ‘connectogram’. The brain stem was positioned at the inferior extremity of the Circos ring because of it being the onlymidline structure. In this fashion, Circos' ability to display chromosomeswasmodified for lobar depiction, while its functionality for illustrating cytogenetic bands was used instead to represent cortical parcellations. As previously described, each parcellation was assigned a unique RGB color. A complete list of parcellations, their abbreviations and associated RGB codes are provided in Table 1. Parcellationswere arrangedwithin each lobe in the order of their location along the antero-posterior axis of the cortical surface associated with the published FreeSurfer normal population atlas (Destrieux et al., 2010). To determine this ordering, the center of mass was computed for the GM surface portion associated with each parcellation, and the order of all parcellations was determined based on the locations of these centers of mass as their distance from the frontal pole increased along the antero-posterior coordinate axis. Thus, parcellated regions are displayed on each of the left and right semicircles of the connectogram in antero-posterior order, which makes the arrangement straightforward to interpret.

Connectivity representation

For subject-level connectograms, links were generated between any two parcellations whenever a WM tract existed between them. In population-level analyses, the former was done whenever there was a non-vanishing probability for a WM tract to exist between the two regions. Links were color-coded by the average fractional anisotropy (FA) value associated with the fibers between the two regions connected by the link, as follows. The lowest and highest FA values over all links (FA_min and FA_max, respectively) were first computed. For any given connection i where i=1, …, N (N being the total number of connections), the FA value FA_i associated with that connection was normalized as FA′_i =(FA_i−FA_min)/(FA_max−FA_min), where the prime indicates the FA_i value after normalization. After this normalization, FA′_i values were distributed in the interval [0, 1], where 0 corresponds to FA_min and 1 corresponds to FA_max. The interval [0, 1] was then divided into three subintervals (bins) of equal size, namely [0, 1/3], [1/3, 2/3], and [2/3, 1]. For every i = 1, …, N, link i was color-coded in either blue, green or red, depending on whether its associated FA′_i value belonged to the first, second, or third bin above, respectively. In addition to encoding FA in the link's color as described, fiber count was also encoded as link transparency. Thus, within each of the three FA bins described, the link associated with the highest fiber count within that bin was rendered as perfectly opaque, whereas the link with the lowest fiber count was colored as transparent as possible without rendering it invisible. For example, the link with FA′_i = 1/3 was colored opaque blue, whereas the link with the lowest FA′_i value was colored as faintest (most transparent) blue. Similarly, the link with FA′_i = 2/3 was colored opaque green, and the link with the lowest value of FA′_i greater than 1/3 was colored faintest green. The links associated with the lowest fiber counts were drawn first, and links with progressively larger fiber counts were drawn on top of the former. The process was successively repeated by drawing links with higher fiber counts on top of links with lower fiber counts. Thus, links associated with the largest fiber counts were drawn on top of all other links. A sample connectogram created using the methods above is shown in Fig. 1(E). To represent directionality information, links can be displayed such that they gradually change color from one extremity to the other in order to distinguish incoming from outgoing information. For example, a link transmitting information from region A to region B can be colored such that its extremity at A is red (outgoing information) and its extremity at B is blue (incoming information). The link would thus gradually change color along its length from A to B, indicating directionality from the former to the latter. In addition, the user can additionally select only one or several parcellated regions for which links are displayed.

Representation of cortical metrics

Within the circular structure representing the cortical parcellations, five circular heat mapswere generated, each encoding one of five structural measures associated with the corresponding parcellation. Proceeding inward towards the center of the circle, these measures were: total GM volume, total area of the surface associated with the GM–WM interface (at the base of the cortical ribbon), mean cortical thickness, mean curvature and connectivity per unit volume. For each parcellation, the latter measure was computed as the number of fibers with endings within that parcellation divided by the total GM volume of the parcellation. For the subject-level analysis, these measures were computed over the entire volumetric (or areal, as appropriate) extent of each parcellation; for the population-level analysis, they were additionally averaged over all subjects. Values for each structural measure were encoded as colors, using a color scheme mapping that ranged from the minimum to the maximum of the data set. For example, the cortical thickness t with values ranging from t_min to t_max was normalized as t₁ = (t−t_min)/(t_max−t_min). The latter value was mapped onto a unique color from the color map of choice. Thus, for example, hues at color map extremities correspond to t_min and t_max, as required. For subcortical structures, brain stem and cerebellum, three measures (area, thickness and curvature) were unavailable on a parcellation-by-parcellation basis; their corresponding heat map entries were consequently left blank. A detailed legend that outlines the representation of cortical metrics, as outlined above, is shown in Fig. 1(F).

Network analysis

Because network theory can provide essential insight into the structural properties of cortical connectivity networks in both health and disease (Sporns, 2011), several network metrics of particular significance were computed for each subject, starting with the degree of each node. In our case, nodes were denoted by parcellated regions and edges were represented by fiber tracts. The node degree is the number of edges connected to a node and its calculation has fundamental impact upon many network measures; moreover, node degree distributions are highly informative of network architecture. The entry indexed by i and j in the distance matrix of the graph contains the minimum length of the path connecting vertices i and j and was computed using the algebraic shortest paths algorithm (Rubinov and Sporns, 2010). The node assortativity (Newman, 2002), i.e. the correlation coefficient for the degrees of neighboring nodes, was also computed in addition to the graph diameter, which is the largest entry in the distance matrix. The eccentricity of a node is the greatest geodesic distance between it and any other vertex, and can be thought of as how far a node is from the node most distant from it in the network. A measure related to eccentricity is the graph radius, which is the minimum eccentricity of any vertex. To investigate local network segregation, the clustering coefficient (Fagiolo, 2007), transitivity, the community structure and the modularity (Newman and Leicht, 2007) of the network were computed. Investigating network segregation is important because it can reveal how much information brain regions exchange as well as the extent to which such regions remain structurally segregated from each other. The clustering coefficient is an elementary measure of local segregation and measures the density of connections between a node's neighbors. The transitivity is a collectively normalized variant of the clustering coefficient which circumvents the problem of disproportionate influence by low-degree nodes upon the clustering coefficient value. The community structure (Blondel et al., 2008) yields a subdivision of the network into non-overlapping groups of nodes in a manner that maximizes the number of within-group edges, and minimizes the number of between-group edges. Finally, modularity conveys the balance of density of within-and between-module connections, and represents another useful measure of network segregation. To study network integration, the characteristic path length of the network was computed, which is the average of the entries in the distance matrix. A related and allegedly more robust measure of integration is the global efficiency of the network (Latora and Marchiori, 2001), which is the average of the inverse of the distance matrix. The local efficiency is the global efficiency computed on the neighborhood of the node, and is related to the clustering coefficient. The network density is another useful measure which is equal to the fraction of present connections to possible connections. Finally, to grasp the effects of network influence and centrality, the network participation coefficient (Guimera and Nunes Amaral, 2005) was calculated, which assesses the diversity of between-module connections. In addition, betweenness centrality (Brandes, 2001)was computed, which is the fraction of all shortest paths in the network that contains a given node. Nodes with high values of betweenness centrality participate in a large number of shortest paths. For each of the measures listed above, the mean and standard deviation were computed for each subject. To compare the connectivity profile of a sample subject against that of his/her population, the mean value of each measure over all vertices was standardized using the corresponding mean and standard deviation of the means of that measure of the population, and Z scores were then computed for the sample subject.

Availability

The connectogram generation workflow is being made freely available via the LONI Pipeline environment (pipeline.loni.ucla.edu). Details and a sample pipeline file are provided in the Supplementary material.

Results

Fig. 2 illustrates the connectivity profile of a sample subject drawn from our normal population. To illustrate the capabilities of our methodology, it is useful to discuss specific features of this connectivity profile as obviated by the connectogram. One such feature is the thick red link that connects the left and right superior frontal gyri (SupFG) in the connectogram. The fact that this link is colored in red indicates, as explained in the previous section, that the fiber tracts between these regions have mean FA values that are greater than 67% of all FA values in the entire brain. The complete opacity of the link (i.e. its full red color, compared to other links that are colored using transparent, light hues of red) indicates that, among all regions in the brain that are connected to each other, the right and left gyri are linked to each other by connections that have a very high fiber count compared to counts between any two regions. In other words, other regions are connected by fibers that have lower counts, with the exception of the connection between the brain stem and left and right cerebella, which also have particularly large fiber counts. All these results are to be expected given the large area and spatial extent of the SupFG, which is colored in Fig. 1(C) using the same color as that of the outermost connectogram segment associated with this structure in Fig. 2 (light pink, see Fig. 1(F) for the connectogram legend).

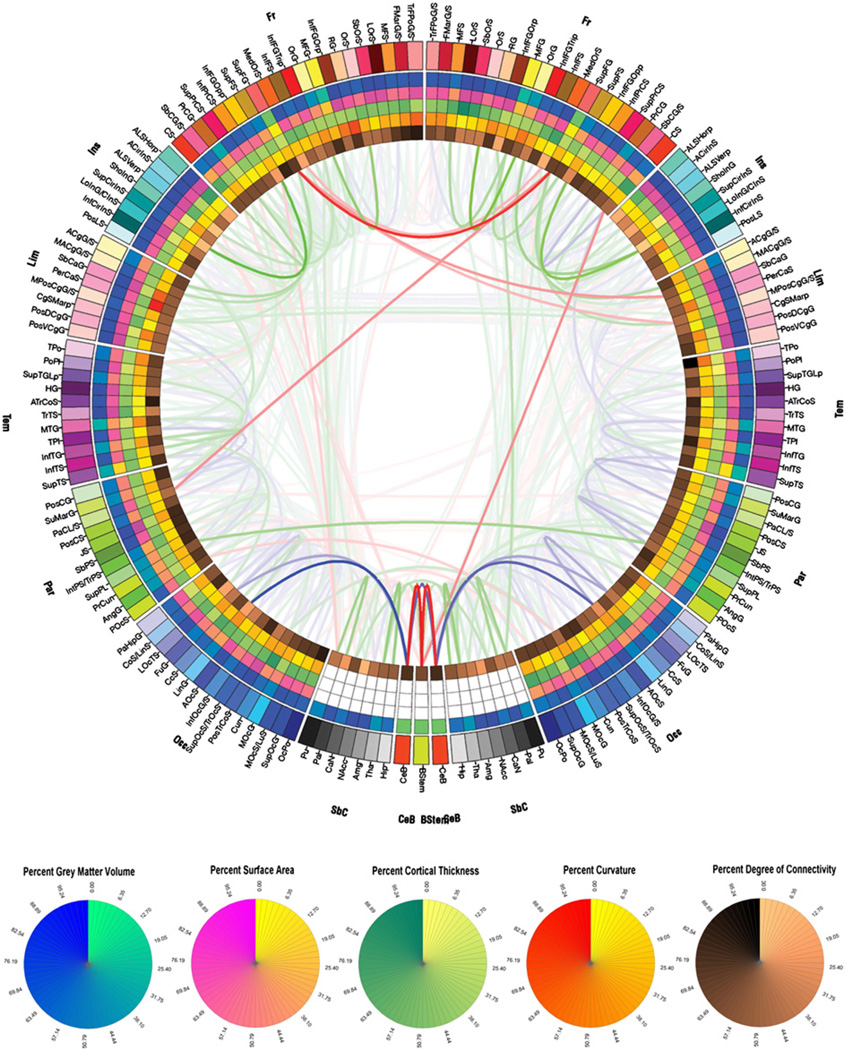
Fig. 2.

Connectogram for a sample subject. The outermost ring shows the various brain regions arranged by lobe (fr — frontal; ins — insula; lim — limbic; tem — temporal; par — parietal; occ — occipital; nc — non-cortical; bs — brain stem; CeB — cerebellum) and further ordered anterior-to-posterior. The color map of each region is lobe-specific and maps to the color of each regional parcellation as shown in Fig. 1(C). The set of five rings (from the outside inward) reflect the measures listed in Fig. 1(F). For non-cortical regions, only average regional volume is shown. The links represent the computed degrees of connectivity between segmented brain regions. Links shaded in blue represent DTI tractography pathways in the lower third of the distribution of FA, green lines the middle third, and red lines the top third (see text for details). Circular color maps detail the scale for each metric.

Proceeding inward towards the center of the circle, the next ring encodes the GM volume of each parcellation. In the case of the SupFG, the bright green displayed for both left and right gyri indicates that the GM volumes of these structures are (among) the largest among those of all parcellations, which is again expectable given the spatial extent of these anatomical structures. The next concentric circle is encoding the total area of the parcellation, and in the case of the superior frontal gyri the associated color is bright yellow which indicates, as expected, that these structures have some of the largest areas among all parcellations. The GM thickness (next concentric circle) of the gyri is encoded by light green, which indicates that their thickness is close to the average parcellation thickness. The mean curvature of the SupFG is revealed to be somewhat larger than average, given that the encoded colors for both left and right gyri are light orange hues. Finally, the degree of connectivity (depicted on the innermost circle of the connectogram) is relatively low. This measure, which represents the total count of fibers with endings in the structure under consideration divided by the total surface area of that structure, indicates that the SupFG has relatively low surface density of fibers for the sample patient considered. Information regarding the GM volume, parcellation area, mean GM thickness, mean curvature and degree of connectivity can be decoded for other regions from the connectogram using the color scaling displayed in Fig. 2, in a manner analogous to that exemplified above for the SupFG. In conclusion, the discussion above highlights the richness of information that can be gathered visually from the connectogram about any cortical regions based on the color coding used.

An interesting feature of the connectogram in Fig. 2 is the asymmetry in the connectivity profile of the left SupFG compared to that of the right SupFG. Specifically, the connections of the left SupFG to the right subcallosal gyrus (SbCaG) and to the right middle posterior cingulated gyrus and sulcus (MPosCgG/S) have higher fiber counts and larger FAs than the connections between the corresponding contralateral structures (i.e. right SupFG to left SbCaG and to left MPosCgG/S). This interesting characteristic associated with the connectivity profile of this subject is very easy to note from the connectogram, and highlights its usefulness in identifying patterns of either symmetry or asymmetry in the brain. Although it is not our purpose here to provide an exhaustive description of all connectivity patterns in the selected subject in Fig. 2, suffice it to note that the connectogram approach is very useful for such type of undertaking, as well as for exploring the connectivity profile of specific regions.

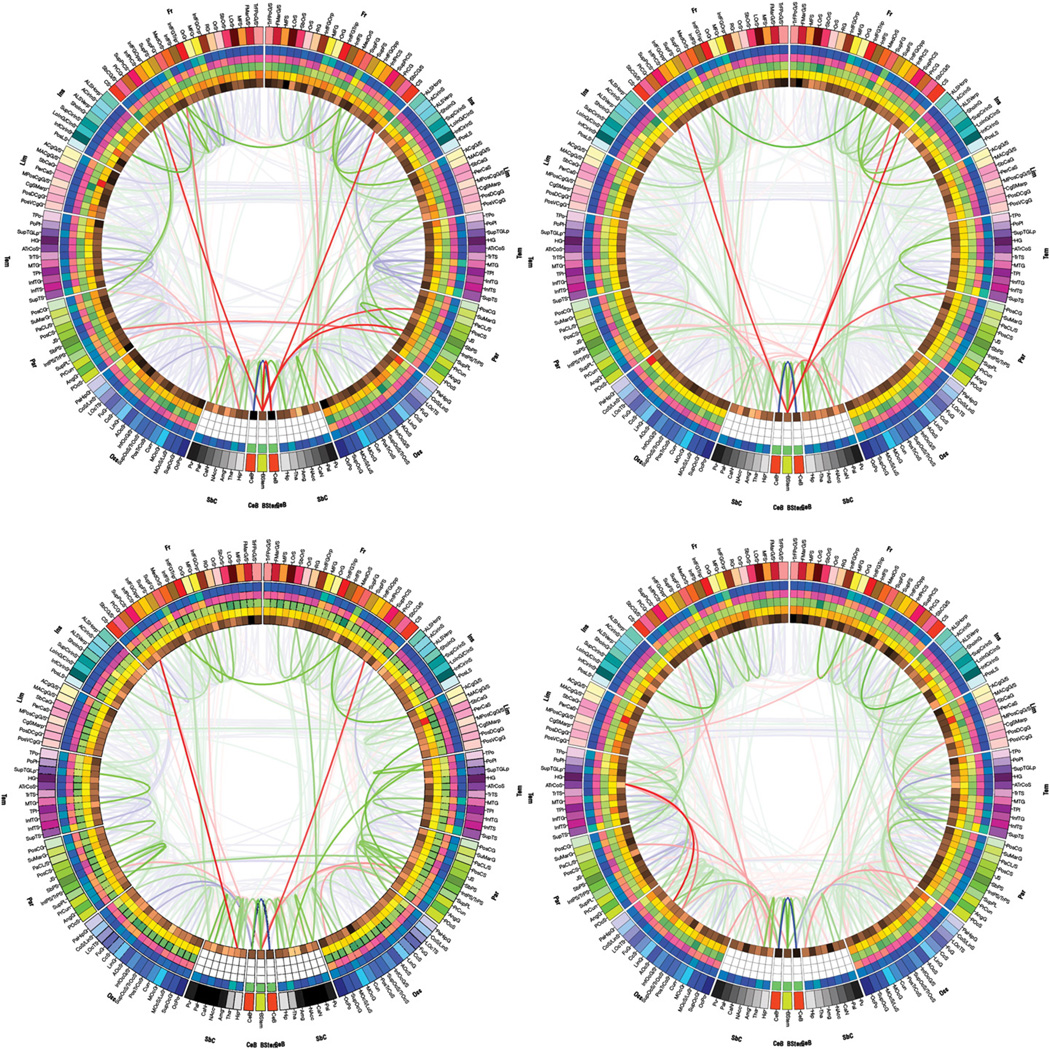
Whereas Fig. 2 displayed the connectivity profile of one sample subject, Fig. 3 illustrates the connectivity profiles of four other subjects selected from our population. The purpose of this figure is to graphically illustrate the degree of similarity as well as the variability between the connectivity profiles of different subjects, which can be easily explored using our connectogram methodology. For all four subjects presented, the left and right cerebella are linked by connections that have large fiber counts and relatively low FA, whereas structures that are part of the dorsolateral prefrontal cortex (e.g. precentral and central gyri or sulci) are consistently linked to subcortical structures, creating a characteristic ‘V-shaped’ pattern in the connectograms. Careful visual investigations of these four connectograms reveal other common patterns as well, but also a great degree of variability between subjects, not only in the fiber counts of various connections between regions but also in the FA values associated with them.

Fig. 3.

Connectograms of four subjects selected from the healthy population. Illustrated are both the degrees of similarity and of variability between the connectivity profiles of different subjects, which can be easily explored using our connectogram methodology.

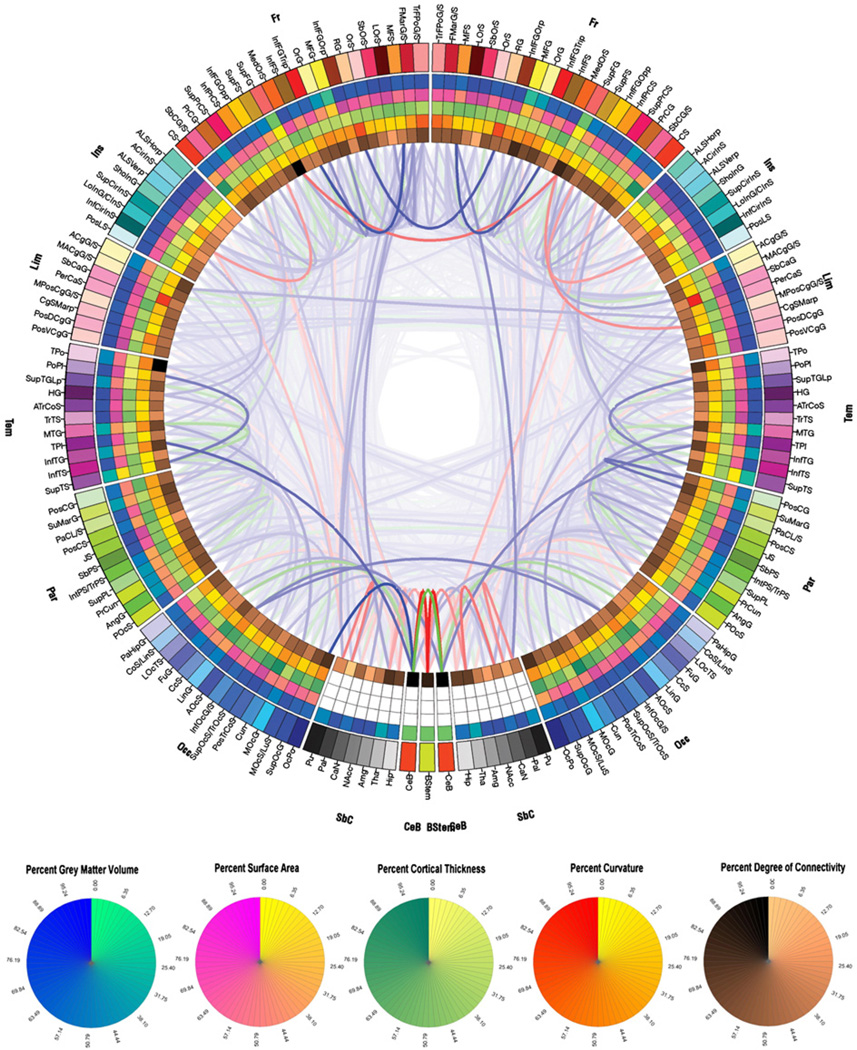
Fig. 4 displays the population-level connectogram pooled over all 50 subjects included in our analysis using the methods already described. As expected given the process of averaging across subjects, this connectogram exhibits a greater degree of bilateral symmetry than all other subject-specific connectograms already examined. Although some left–right asymmetry persists even here, it is reasonable to expect that either (A) some patterns of this type may disappear with the inclusion of additional subjects in the analysis, or (B) some asymmetry patterns may in fact be enhanced with increasing sample size. The latter would then suggest structural laterality differences that are highly consistent over a very large population, and the methods of statistical analysis could then be employed to quantify the significance of such differences. Whereas it is not our purpose here to investigate how our population connectogram might change upon inclusion of additional subjects, it is worthwhile to point out that our methodology is highly amenable to this type of investigation. This is the case not only for healthy populations, but also for clinical populations where connectomic analysis using our approach might allow one to obtain significant insights regarding the structural connectivity profile in disease.

Fig. 4.

As in Fig. 2, for the entire population of 50 subjects.

Although differences between control and target populations are not explored in this study via connectogram design, it is useful to demonstrate our ability to perform statistical analyses using our paradigm by comparing the cortical network properties of the subject in Fig. 2 against the mean connectivity profile of his/her population, which is displayed in Fig. 4. To this end, Table 3 displays, for the sample patient in Fig. 2, the mean values of the network metrics described in the previous section, in addition to the values of the Z score associated with each of these metrics for the sample subject, computed as previously described. Inspection of the Z scores in Table 3 indicates that, for all computed network metrics, the sample subject that was selected for illustration was never farther away than 1.228 standard deviations from the mean of the healthy population from which he/she was selected, indicating that this subject was quite typical of the population from the standpoint of the cortical network measures that were calculated. This simple analysis of cortical measures in which a single subject was compared to an entire population using the standard measures of network theory can be used in conjunction with the analysis of the connectogram of the subject to gain insight into his/her connectivity profile. It is quite possible that this type of investigation can be useful especially when comparing a patient with any of the many clinical conditions that affect structural connectivity (e.g. traumatic brain injury (TBI), parkinsonism, dementia, etc.) to a population of matched healthy subjects or to other diseased subjects. Thus, the methodology outlined in this paper can be applied to a wide variety of case studies and even to the comparison of two different populations, with potential relevance to many areas of neuroscience.

Table 3.

Statistical comparison of the sample subject in Fig. 1 to the healthy population of adults from which he/she was drawn. Listed are (1) the network measures computed, (2) the mean of each network measure over all network nodes for the sample subject and for the population, as well as (3) the Z score for the sample subject. Where measures are designated as binary in parentheses, the cortical network was assumed to be binary (i.e. with an edge weight of 1 if a connection existed between the nodes involved). Where measures are designated as weighted, the weight of each edge in the cortical network was assumed to be equal to the fiber count associated with the connection between nodes

Network measure	Mean		Z score
	Sample subject	Population
Assortativity	0.004	0.027	0.694
Betweenness (binary)	367.673	336.961	0.693
Betweenness (weighted)	645.600	620.600	0.326
Clustering coefficient (binary)	0.458	0.459	−0.051
Clustering coefficient (weighted)	3.371	6.284	−0.861
Community structure	4.630	4.977	−0.523
Degree	8.315	10.477	−1.001
Density	0.051	0.064	−1.001
Diameter	7.000	6.392	0.783
Distance (binary)	3.242	3.056	0.694
Distance (weighted)	7.806	7.473	0.224
Eccentricity	5.673	5.054	1.228
Efficiency (global)	0.360	0.384	−0.794
Efficiency (local)	0.656	0.682	−0.620
Lambda	3.222	3.037	0.694
Modularity	0.692	0.662	1.124
Participation coefficient	0.288	0.303	−0.598
Radius	4.000	3.451	0.642
Transitivity (binary)	0.340	0.360	−0.614
Transitivity (weighted)	2.495	5.001	−0.886

Discussion

Significance and innovation

With the intense interest in the in vivo mapping of human connectomics, as evident in the launching of the Human Connectome Project (HCP, www.humanconnectomeproject.org) by the National Institutes of Mental Health and Aging, considerable effort has arisen into techniques that graphically represent the interconnectedness of neural structures. Along with ongoing efforts to map population level connectomics is an interest for clinical application to the individual subject or patient. Being able to graphically depict and assess deviation from population-level averages is illustrative of damaged or altered connectivity, as in the case of TBI. Such illustration can be essential for localizing compromised regional connectivity and for characterizing network-level changes in network efficiency resulting from cortical insult.

The use of summary graphical depictions has been strongly advocated as a means for clinicians to rapidly and succinctly examine patient case, medication, and treatment histories at a glance (Powsner and Tufte, 1994, 1997). Computations of network-level properties are a valuable means to assess efficiency and the ‘wiring costs’ needed to link spatially disparate brain regions (Bullmore et al., 2009). In addition, calculation of population average network metrics and of their degree of variation permits individualized connectomics comparison. As noted above, this is of potentially great importance in the context of patients having degenerative disease (e.g. dementia, TBI, mental illness, etc.).

In this article, we have introduced a novel technique for the mapping and visualization of population-level and individual human connectomics via an intuitive two-dimensional circular representation. We illustrate, in a population of subjects as well as in an instance drawn from it, how this simple and elegant conceptual framework is well suited toward the organization, representation, and inspection of brain connectivity in a visually-insightful and content-rich manner. Using combined MRI/DTI data acquisition and automatic image segmentation, we have described our approach for the extraction of 148 cortical and 17 non-cortical anatomical parcellations using standardized nomenclature, followed by the calculation of structural anatomy metrics (volume, area, cortical thickness, curvature) for cortical regions. By combining these structural data with the connectivity profile extracted from high-angular resolution DTI, we have been able to generate detailed representations of regional geometry and connectivity for each individual to assess and examine their statistical properties.

The graphical representation presented here differs from three-dimensional approaches which provide excellent renderings of nodes and their linkages in anatomical space (Bullmore and Sporns, 2009), and that when examined along with force-directed graphs illustrate clustering and relatedness (Hagmann et al., 2008). For example, the Connectome Viewer Toolkit (http://www.connectomeviewer.org) is an open source framework to analyze and interactively display connectomes in three dimensions using a variety of visualization options (Gerhard et al., 2011). The 3D nature of such graphs, while essential for the accurate illustration of relative anatomical proximity of network nodes, requires an interactive graphical user interface in which to manipulate, orient, and examine degrees of connectivity within brain networks. These representations are sometimes difficult to include efficiently in journal articles or for examination in print due to their intrinsic three-dimensional nature. Two-dimensional approaches have been explored (Bassett and Gazzaniga, 2011) in the form of wiring diagrams that employ the classical representations of graph theory, and such representations are helpful for understanding network structure. However, many of them do not provide additional insight into nodal neuroanatomy and can often be difficult to interpret or to explore due to frequent, dense clustering of nodes throughout the two-dimensional spatial extent of the connectivity representation, as well as to the large number of graph edges, which can render emerging properties of the system difficult to discern. As expanded in the following section, our representation overcomes many of these drawbacks and provides a useful method for connectomic visualization.

To our knowledge, methods which are suitable for jointly representing inter-regional connectivity in addition to regional anatomical metrics have not been widely examined. Moreover, the present method is among the very few that allows one to explore cortical network connectivity in 2D format without the drawbacks of directly converting 3D graphs into 2D images. Such drawbacks include, for example, the loss of significant information contained in the 3D structure of the representation, such as spatial positioning of nodes either closer or farther away from the user's viewpoint. By contrast, our present technique makes use of its 2D, circular modality of display to eliminate the disadvantages that can be incurred as a 3D graph is converted to two dimensions for printing and inspection without the requirement of using a dedicated software package. In addition, the inclusion of edge transparency and the freedom of its manipulation by the user can be employed to highlight significant connections in their decreasing order of importance without compromising the overall complexity of the graph structure.

Another important advantage of the present approach includes significant potential for connectographic mapping and analysis across human samples, as well as an essentially unbounded capacity for extending this powerful analysis method to the study and comparison of diseased populations and/or animal models, as described for example in (Irimia et al., in press) Our methodology provides an anatomically informed arrangement of (1) nodal cortical and sub-cortical architecture, (2) their geometric properties, and (3) the degree and properties of regional connectivity. Representing such information has not previously been performed within a single summary graphic. However, the information needed to create them is readily available from workflow tools such as LONI Pipeline utilizing FreeSurfer, Track-Vis, etc. Thus, the representation presented here has similar qualities for the ease for depicting and representing a complete set of connectomics information. The color-driven representation of neuroanatomical geometry as well as degree of inter-regional connectedness also have a number of esthetic qualities — not the least of which is a high data-to-ink ratio (Tufte, 2001), e.g. maximizing scientific information content while minimizing superfluous graphical elements. In the following section, the innovative aspects of our circular representation framework are compared in more detail with the features of other methods employing either 2D or 3D representations. The connectogram software presented in this paper is freely available for download as an integrated module within the LONI Pipeline (pipeline.loni.ucla.edu, see also Dinov et al., 2010).

Comparison with other methods

A wide array of methodologies for the visualization of connectivity has been proposed. Most of these representations rely on variations of classical graph theory to (1) create and position network nodes at 3D locations associated with various anatomical landmarks, (2) represent nodes using shapes of various sizes and colors in order to encode properties of interest, and to (3) modulate edge properties (weight, color, thickness, etc.) according to the degree of connectivity between nodes as expressed using some metric of choice. In the remainder of this subsection, these three modalities of visualization are discussed and analyzed from the perspective of existing methodologies and then compared to our own approach to emphasize the advantages and disadvantages of each framework.

The first task involved in connectomics visualization is that of node creating and positioning. One method of representation which is very popular in this respect is illustrated in numerous publications (Bassett et al., 2011; Gerhard et al., 2011; Yan et al., 2011), where nodes are positioned at the 3D anatomical coordinates of anatomical brain regions, and connection strengths are represented by edge thickness. This modality of representing brain connectivity has the advantage that, when viewed in three dimensions, it allows one to associate underlying neuroanatomy with precisely the locations of the regions of interest involved in the connectivity representation. An important disadvantage of this method is that it can sometimes make emergent network structure very difficult to grasp (Sanz-Arigita et al., 2010). By comparison, our proposed visualization paradigm arranges nodes in their order along the antero-posterior axis (which preserves the logical spatial ordering of the parcellated regions), although it omits their precise 3D coordinates. However, even in doing so, our method provides the capability of making all nodes equally visible to the viewer when the connectogram is inspected on the printed page or outside any software environment that involves the manipulation of perspective in three dimensions for the purpose of detailed inspection. In fairness, it should be noted that 2D visualization of brain networks where node positioning follows exact anatomical positioning is in fact possible if the cortical surface is spread out as a 2D sheet, as for example in (Palva et al., 2010) or using certain parameter options of the Connectome Viewer software (Gerhard et al., 2011). However, such representations remain at least partially problematic because of the difficulty to associate arbitrary locations on 2D flattened maps of the cortex to the familiar 3D topology of the brain. By contrast, our circular scheme follows the conventional antero-posterior positioning of nodes, thus creating a more intuitive 2D visualization of network structure.

The second challenge which must be addressed to visualize a connectome diagrammatically is that of depicting nodes using visual symbols that are representative of their properties. For example, in (Chen et al., 2011; Dosenbach et al., 2007; Ginestet and Simmons, 2011; Spoormaker et al., 2010) and many other publications, nodes are depicted as circles or spheres that are colored differently to encode various properties. One advantage of this modality of visualization is that it allows one to easily grasp common edge properties, as well as to visually classify nodes into classes according to their coloring. Disadvantages of this method include the fact that nodes that are very close to each other may visually overlap edges or each other, thus making graph structure more difficult to decipher and interpret. This problem may be partially addressed by modifying node transparency (Ginestet and Simmons, 2011), although this does not entirely remove the difficulty of depicting cortical networks with high densities of nodes or edges. By contrast to these methods, ours ensures that all nodes are simultaneously visible. In addition, our connectogram approach allows one to display an arbitrary number of node properties at a time through the use of color-coded rings that are concentric to the outermost circle.

The third difficulty involved in depicting connectomics relationships schematically involves the modulation of edge properties (weight, color, thickness, etc.) according to the degree of connectivity between nodes as expressed using some metric of choice. In many applications, edges are modulated by color (Cao and Slobounov, 2010; van den Heuvel and Pol, 2010) or by thickness (He and Evans, 2010; He et al., 2010). In one widely-disseminated approach similar to ours in its use of a circular diagram (Holten, 2006; Modha and Singh, 2010), concentric circles are used to represent the hierarchical subdivision of the central nervous system in a top–down approach (e.g. brain to cortex to lobes to gyral/sulcal structures, etc.). In such representations, edges radiate from the center of a circle (the top structure) to the circumference (the lowest-level structures) and edge position in the hierarchy is consequently important. In this last approach as well as in ours, the circular shape of the connectivity graph is appealing and useful for the 2D representation of relationships between different areas of the brain. One challenge that the circular approach to connectome viewing addresses is that of complexity and dimensionality reduction. In the hierarchical approach (Holten, 2006; Modha and Singh, 2010), this is addressed via the top–down organization of connections; in ours, it can be controlled by displaying connections emanating only from one hemisphere, one lobe, or from a single brain structure, thus allowing the user great leeway in the ability to modify the level of complexity being displayed in the connectogram.

Conclusion

Circle-based arrangements for connectome visualization are increasingly gaining acceptance in neuroimaging and computational neuroscience circles (Modha and Singh, 2010). While many examples of connectomic and network-level layouts have been proposed, the approach described here for the joint 2D graphical representation of regional geometric attributes and inter-regional connectivity is a novel, informative, and attractive means for depicting whole brain connectivity from neuroimaging data. It allows for single subject as well as population-level rendering and is complimentary to computations of network architecture. The manner in which we envision the potential contribution of our proposed method to existing visualization tools for connectomics is by complementing existing software methodologies for mapping the highly complex networks of the cortex, such as the Connectome Viewer. In introducing the present visualization method, our purpose is to acknowledge the strengths and weaknesses of various other methods for depicting connectomics, and consequently to complement them in a constructive manner that is beneficial to members of the community who use such tools. In conclusion, our depiction of structural and connectivity data highlights the detailed richness of connectome-related information, which is often challenging to visualize and interpret. Consequently, we expect our representation to have appreciable applicability to the study of both population- and patient-level connectivity.

Supplementary materials related to this article can be found online at doi:10.1016/j.neuroimage.2012.01.107.

Abbreviations

DTI

diffusion tensor imaging

fMRI

functionalmagnetic resonance imaging

FA

fractional anisotropy

Fro

frontal

GM

gray matter

HCP

Human Connectome Project

Ins

insula

IDA

integrated data archive

Lim

limbic

LONI

Laboratory of Neuro Imaging

MPosCgG/S

medial posterior cingulate gyrus and sulcus

MRI

magnetic resonance imaging

NA-MIC

National Alliance for Medical Image Computing

NIH

National Institutes of Health

Occ

occipital

Par

parietal

SbCaG

subcallosal gyrus

SupFG

superior frontal gyrus

TBI

traumatic brain injury

Tem

temporal

WM

white matter

3D

threedimensional