Acute and fractionated irradiation differentially modulate glioma stem cell division kinetics

Abstract

Glioblastoma multiforme (GBM) is one of the most aggressive human malignancies with a poor patient prognosis. Ionizing radiation (IR) either alone or adjuvant after surgery is part of standard treatment for GBM but remains primarily non-curative. The mechanisms underlying tumor radioresistance are manifold and, in part, accredited to a special subpopulation of tumorigenic cells. The so-called glioma stem cells (GSCs) are bestowed with the exclusive ability to self-renew and repopulate the tumor, and have been reported to be less sensitive to radiation-induced damage through preferential activation of DNA damage checkpoint responses and increased capacity for DNA damage repair. During each fraction of radiation, non-stem cancer cells (CCs) die and GSCs become enriched and potentially increase in number, which may lead to accelerated repopulation. We propose a cellular Potts model (CPM) that simulates the kinetics of GSCs and CCs in glioblastoma growth and radiation response. We parameterize and validate this model with experimental data of the U87-MG human glioblastoma cell line. Simulations are performed to estimate GSC symmetric and asymmetric division rates and explore potential mechanisms for increased GSC fractions after irradiation. Simulations reveal that, in addition to their higher radioresistance, a shift from asymmetric to symmetric division or a fast cycle of GSCs following fractionated radiation treatment is required to yield results that match experimental observations. We hypothesize a constitutive activation of stem cell division kinetics signaling pathways during fractionated treatment, which contributes to the frequently observed accelerated repopulation after therapeutic irradiation.

Major findings

The calibrated Cellular Potts model reproduces experimentally observed in vitro and in vivo ratios of Glioma Stem Cells (GSCs) in the U87-MG cell line when the frequency of GSC symmetric division events is 35%. The model verifies acute and fractionated irradiation yield enrichment in GSCs due to their reduced radiosensitivity. GSC radioresistance alone, however, while reproducing the 4-fold enrichment in GSCs after acute irradiation, is insufficient to yield the 6-fold enrichment after fractionated irradiation with equal total dose. An additional prolonged increase in GSC symmetric division events or a significantly shortened GSC cell cycle after repeated exposure is required to reproduce experimentally observed GSC ratios after fractionated irradiation.

Quick guide to equations and assumptions

We use a Cellular Potts model (CPM) (1,2) to simulate tumor development and response to irradiation. Cells behavior is determined by intrinsic parameters and interaction with adjacent cells, dependent on population-level changes in effective energy E (i.e. Hamiltonian function), which determines cell structure, motility, adhesion and response to extrinsic signals:

$$\begin{array}{l}E=\stackrel{\text{boundary}\text{energy}}{\overbrace{\sum _{\overrightarrow{i},\overrightarrow{j}\mathit{neighbor}}J\left(\tau \left(\sigma \left(\overrightarrow{i}\right)\right),\tau \left(\sigma \left(\overrightarrow{j}\right)\right)\right)\left(1-\delta \left(\sigma \left(\overrightarrow{i}\right),\sigma \left(\overrightarrow{j}\right)\right)\right)}}\\ +\stackrel{\text{volume}\text{constraint}\text{energy}}{\overbrace{\sum _{\sigma }{\lambda }_{\text{surface}}\left(\sigma \right){\left(\nu \left(\sigma \right)-V_{\text{target}}\left(\sigma \right)\right)}^2}}\\ +\stackrel{\text{surface}\text{area}\text{constraint}\text{energy}}{\overbrace{\sum _{\sigma }{\lambda }_{\text{surface}}\left(\sigma \right){\left(s\left(\sigma \right)-S_{\text{target}}\left(\sigma \right)\right)}^2}}\end{array}$$ (1)

where i⃗ =(x_i,y_i) and j⃗ = (x_j,y_j) denote neighboring lattice sites, σ(i⃗) denotes the cell at lattice site i⃗, and J(τ(σ(i⃗)), τ(σ(j⃗))) denotes the contact energy per unit area between cells at neighboring lattice sites. v(σ) and s(σ) are the volume (total number of pixels in the cell) and surface area which are constrained close to the target volume V_target and surface area S_target respectively; λ_volume (σ) and λ_surface (σ) denote the inverse volume compressibility and inverse membrane compressibility of the cell; and δ is the Kronecker delta with $\delta \left(\sigma \left(\overrightarrow{i}\right),\sigma \left(\overrightarrow{j}\right)\right)=\{\begin{array}{cc}0,& \text{if}\sigma \left(\overrightarrow{i}\right)\ne \sigma \left(\overrightarrow{j}\right)\\ 1,& \text{if}\sigma \left(\overrightarrow{i}\right)=\sigma \left(\overrightarrow{j}\right)\end{array}$.

The cell lattice evolves through attempts by cells to extend their boundaries into neighboring cells’ lattice sites, displacing the neighboring cells that currently occupy those sites. For each index-copy attempt, we randomly select a cell boundary pixel (source) and attempt to displace a randomly chosen neighboring cell pixel (target). The effective energy change, ΔE, is calculated by assuming the source cell displaces the target cell at that pixel. If ΔE is negative (i.e., the change is energetically favorable), the index-copy attempt is accepted. If ΔE is positive, the index-copy attempt is accepted with probability (i.e. Boltzmann acceptance function):

$$P=e^{-\mathrm{\Delta }E/T_m}$$ (2)

where T_m determines the amplitude of cell membrane fluctuations (equivalent to effective cell motility). These cell rearrangement dynamics involve utilizing relaxational Monte-Carlo-Boltzmann-Metropolis dynamics (3,4). On an N sites lattice, N displacement attempts are made in each Monte Carlo Step (MCS). The translation of experimental time into MCS depends on the average ratio of ΔE/T_m (2). Simulations are performed in the open-source CompuCell3D simulation environment (2) on a 4000×4000 square lattice with periodic boundary conditions and T_m=50 (c.f., Eq. 2).

Assumptions

Glioblastoma are heterogeneous with subpopulations of glioma stem cells (GSCs) and non-stem cancer cells (CC). The kinetics and interactions of both populations dictate dynamics of the population as a whole.

Basic cell kinetics

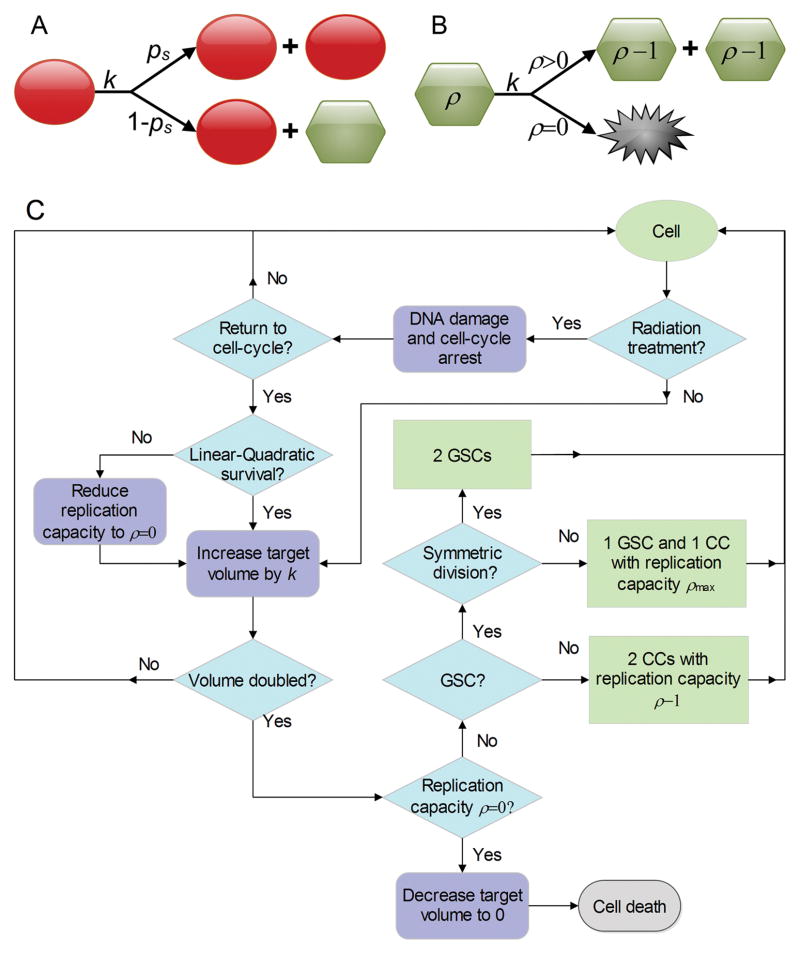
Cells are considered individual entities with a cell cycle (with length T_c) and a limited proliferation capacity ρ=[0, ρ_max]. For GSCs, ρ_max=∞. At each cell division, GSCs undergo symmetric division with probability p_s to produce two GSCs with identical features, or with probability 1−p_s asymmetric division to produce a GSC and a CC with limited proliferation capacity ρ_max. The proliferation capacity ρ is decremented at each CC division and inherited by both daughter CCs. CCs die when a proliferation attempt yields ρ<0 (Figure 1). To model proliferation, cell target volume V_target (σ) is increased with growth rate k until the actual cell volume v(σ) is doubled. If the local environment is not favorable for cell growth and cells cannot reach their target volume (that is, the effective energy change, ΔE for a cell to increase in size is so large that the Boltzmann acceptance probability P (c.f., Eq. 2) becomes infinitesimal), cells are considered growth arrested, or quiescent.

Figure 1.

Schematic of cell division fate model. (A) Glioma stem cells (GSC, red circle) divide with rate k, either symmetrically with probability p_s or asymmetrically with probability 1−p_s, where one daughter cell is a non-stem cancer cell (CC, green hexagon) with proliferation potential ρ_max. (B) Non-stem cancer cells (CC, green hexagon) grow with rate k, and produce two CCs with decremented proliferation potential ρ−1 if ρ>0, or die if proliferation potential is exhausted (ρ=0). (C) Flowchart of simulation process.

Radiation response model

After exposure to irradiation cells become arrested in the cell cycle and attempt to repair radiation-induced DNA damage (5). The probability of successful repair and thus cell survival after application of dose d is modeled using the established linear-quadratic (LQ) model:

$$S=e^{-\xi \lambda \left(\alpha d+\beta d^2\right)}$$ (3)

where αd describes cell killing due to a single event, and βd² describes cell killing after combination of two independent, potentially repairable events, with α and β being cell-specific radiosensitivity parameters (6). We introduce ξ and λ as radiation protection factors for quiescent cells and GSCs, respectively. The basic LQ model has been extended to take into account the effects of inter-fraction tumor repopulation (6). Alternatively, the LQ model can be applied repeatedly as independent events at discrete time intervals if inter-fraction population dynamics are simulated by a tumor growth model (7,8). We assume the cells that are fated to die undergo cell death at the next division attempt, which is achieved by setting the proliferation capacity of a hit cell to ρ=0.

Introduction

GBM are among the most lethal primary human malignancies, possessing rapid growth, high invasiveness and treatment resistance. Standard treatment for GBM comprises surgical resection of the gross tumor mass followed by radiotherapy of 60 Gy in 30–33 fractions of 1.8–2 Gy (9). The prognosis for patients with GBM remains poor because of refractory response to radiation and other treatments (10,11). Therapeutic failure is due, in part, to tumor cell heterogeneity derived from both genetic and epigenetic sources (12). GBM frequently recur after treatment with ionizing irradiation (IR) (13), indicating survival of tumorigenic cells. It has been shown that only a subpopulation of cells – the so-called glioma stem cells (GSCs) – are able to initiate brain tumors in a mouse model (14–16). Studies from our group and other laboratories have demonstrated that the number of cancer colonies correlates with the frequency of cancer stem cells (17,18). The population of GSCs has been shown to be highly resistant to IR due to more efficient DNA damage response mechanisms and environmental survival cues (11,19–21). By detecting the expression of CD133 (Prominin-1), a pivotal marker of putative GSC, the percentage of GSCs as well as their population size was found to be increased after radiation exposure (11,21,22). Importantly, irradiation did not induce CD133 expression in CD133⁻ cells, confirming that increase in CD133⁺ cells is due to proliferation of the original CD133⁺ subpopulation. Surviving GSCs are able to initiate secondary tumors with enhanced aggressiveness and decreased latencies relative to untreated tumors (11,23). The survival and increase of the GSC population during radiation therapy may be a leading cause of accelerated and more aggressive GBM recurrence after radiation therapy.

In the present study, we found that resistance of GSCs to IR alone is insufficient to explain the experimentally observed increased GSC ratios after fractionated radiation treatment. We show that an additional radiation-induced shift in GSC division in favor of symmetric division or a faster cycling time reproduces the reported in vitro and in vivo enrichment of GSCs (22). Based on our previous studies (8,17,24,25), we develop a cellular Potts model (CPM) that simulates cancer stem cell-driven GBM growth and radiation response. In particular, this model estimates symmetric and asymmetric GSC division rates before and after irradiation, and simulates the growth dynamics of the irradiated GBM population with and without irradiation-induced constitutive changes in GSC division dynamics.

Materials and Methods

Cell Culture

The U87-MG cell line was obtained from American Type Culture Collection (ATCC, Bethesda, MD, USA) where cell line authentication and species identification was performed. Cells were grown in Minimum Essential Medium (MEM, Invitrogen Life Technologies, Grand Island, NY) supplemented with 10% fetal bovine serum (FBS, Lonza, Hopkinton, MA) and maintained at 37°C with 5% CO₂ in humidified air. Time-lapse video microscopy was used to monitor cell behavior. Images were taken every 15 minutes, by using a digital camera (Photometric Coolsnap HQ2 CCD) coupled to an inverted microscope. We used CellTrack (26), an open source software, for cell tracking and motility analysis to estimate cell proliferation and migration rates.

For clonogenic survival assays, single cell suspensions were irradiated with the Gammacell 40 irradiator (MDS Nordion, Inc., Ottawa, ON, Canada) with doses ranging from 0–16 Gy at 0.48 Gy per minute. Irradiated cells were plated in 10 cm dishes at low density. Cells were fixed with 70% ethanol, stained with 0.2% crystal violet 14 days after irradiation. Cell colonies of 50 cells or more were scored.

Simulation Process

Cellular kinetics are simulated through the following steps (Figure 1):

1. Increase the target volume of cell σ with fixed rate k.

2. If the volume of cell σ is doubled (v(σ) ≥ 2v₀) cell division is attempted.

   1. If cell σ is a GSC, it divides symmetrically with probability p_s to produce two GSCs, or asymmetrically with probability 1−p_s to produce a GSC and a CC with limited proliferation potential ρ_max (see next section).

   2. If cell σ is a CC, both daughter CCs inherit a decremented proliferation capacity ρ−1.

3. If the proliferation capacity of cell σ is exhausted (ρ=0), the death of cell σ is invoked by setting V_target (σ)=0.

4. Cell σ is labeled as currently quiescent when no increase in cell volume v(σ) has occurred for consecutive simulated t=6 hrs (180 MCS).

5. If a cell σ is irradiated, the cell gets arrested in its cell cycle for a period of time T_a.

6. If a cell σ is unrepaired when re-entering the cycle (calculated by Eq. (3)), cell death is evoked by setting proliferation capacity ρ=0.

Parameterization

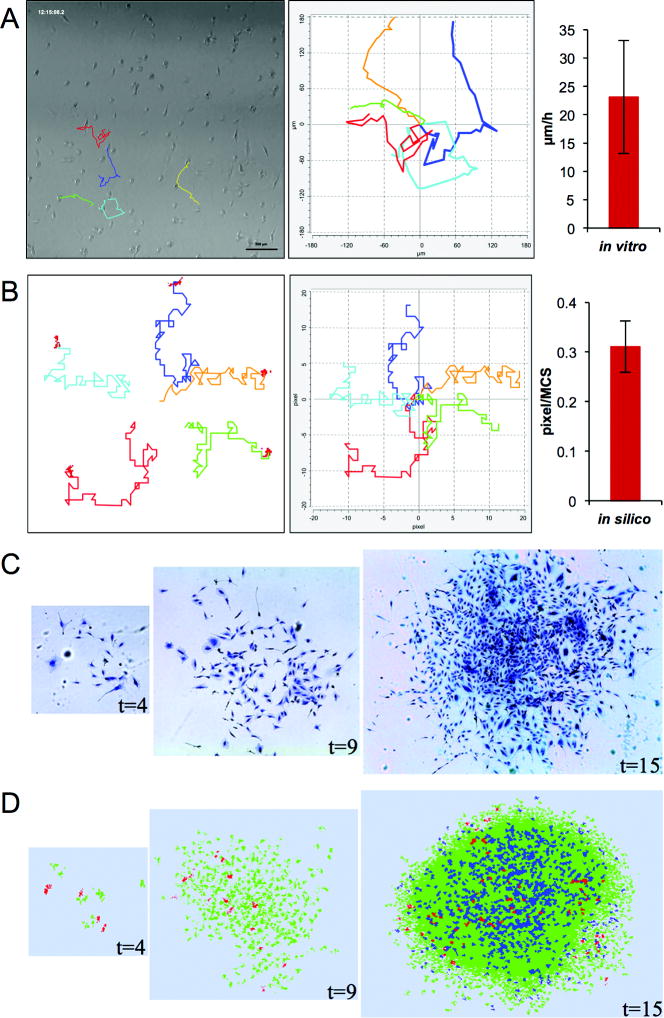
We set the initial size of a cancer cell in the cellular Potts model (CPM) to v₀=4×4 pixels. We estimated the average diameter of U87-MG cell, r, in vitro at approximately 10 μm (n=20). Using these measurements, 1 pixel equals 2.5 μm×2.5 μm. The average migration speed of U87-MG cells, v, in vitro is 23.4 μm hr⁻¹ (n=24, Figure 2A), which is in good agreement with the literature (27,28). The average replacement of cells in CPM is approximately 0.31 pixels MCS⁻¹ (Figure 2B). Equating experimental and simulated cell migration speeds implies that 30 MCS approximate 1 hr. By tracking two consecutive mitotic events of individual U87-MG cells we obtained the cell cycle length to be T_c=25 hrs (n=22). Therefore, the growth rate of in silico cells is k = (V_target − v₀)/T_c =0.0213 pixel MCS⁻¹, where V_target =2v₀ represents the doubling volume of cancer cells. The proliferation potential of CC is set to ρ_max = 10 which has previously been shown to enable fast tumor growth (17).

Figure 2.

Model parameterization. (A) Tracking of migrating U87-MG cells in vitro and re-plotted with a common origin (left panel). Average migration distance (right panel; mean ± s.d., n=24). (B) Tracking of migrating generalized cells in silico and re-plotted with a common origin (left panel). Average displacement distance (mean ± s.d., n=30). (C) In vitro growth of a U87-MG cell population at t=4, 9 and 15 days. (D) In silico growth of a parameterized cell population at t=4, 9 and 15 days. Color-coded are GSC (red), proliferating CC (green) and quiescent CC (blue). (E) Population expansion via self-metastases at t=15, 75 and 120 days. Circles are added to visualize separate population clusters. Arrows indicate the locations of GSCs. Parameters used in the present simulation include p_s=0.02, ρ_max=10. Figures in (D) and (E) labeled with star mark (*) are identical.

Radiation-induced cell cycle arrest of U87-MG cells is observable through a decreased mitotic index immediately after irradiation that returns to control levels after 16 hrs (5). We assign a cell cycle arrest time 0 ≤ T_a ≤ 16 hrs for each cell from a uniform distribution. Using clonogenic assays for long-term cell survival of U87-MG cells after single doses of radiation ranging from 0–16 Gy, we derived for sensitivity parameters in the LQ model (Eq. 3) the unconstrained best-fit values of α=0.3859 and β=0.01148 (Figure 3). Radioresistance of quiescent cells is a major determinant for treatment success (29), and the spatial distribution of proliferating cells and their killing by radiation plays a crucial role in the redistribution of quiescent cells into the cell cycle (8). For radiosensitive proliferating cells we assume ξ=1, and a reduced sensitivity of ξ=0.5 is assumed for non-cycling quiescent cells (30,31).

Figure 3.

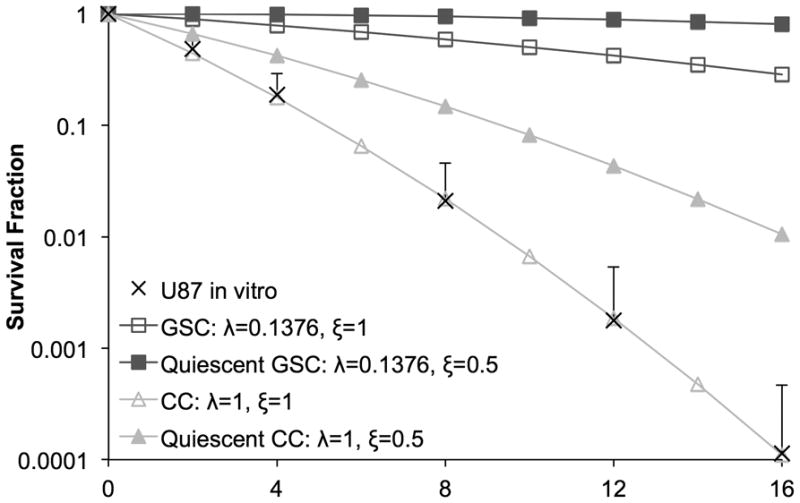
Clonogenic survival fraction of U87-MG in vitro after single-doses of irradiation (mean + s.d., n=3) and unconstrained best-fit curve with α=0.3859 and β=0.01148. Survival curves plotted for estimated radioprotection factors of GSC (λ=0.1376) and quiescent CC/GSC (ξ=0.5).

To match the reported increase in GSC fraction after different doses of irradiation (22), survival probabilities above 100% are required, which implies that different α and β values for GSC alone are insufficient to explain the reported data. Nevertheless, GSC radiation response parameters need to be reliably identified in the future. From the dose response survival curves (Figure 3) we estimate the GSC radiation protection factor λ_GSC=0.1376 by applying 4.5-fold lower apoptosis rate than CCs (λ_CC =1) at 3 Gy radiation as reported (11). Model parameters with their values are listed in Table 1.

Table 1.

Model parameters and values.

Parameter	Meaning	Value	Reference
r	Cell diameter	10 μm	in vitro U87-MG cell line
v	Cell migration speed	23.4 μm hr−1	in vitro U87-MG cell line
Tc	Cell cycle time	25 hrs	in vitro U87-MG cell line
k	Cell growth rate	0.0213 pixel MCS−1	in vitro U87-MG cell line
ρmax	Non-stem cell proliferation capacity	10	assumed from (17)
ps	GSC symmetric division rate	0.35	estimated using data from (22)
Ta	Cell cycle arrest time post IR	random in 0–16 hrs	in vitro U87-MG cell line (5)
α	Radiosensitivity of single-hit killing	0.3859	in vitro U87-MG cell line
β	Radiosensitivity of double-hit killing	0.01148	in vitro U87-MG cell line
λGSC	Radioprotection of GSCs	0.1376	estimated from in vitro U87-MG cell line and (11)
ξ	Radioprotection of non-cycling cells	0.5	(30,31)

Results

Tumor population growth

To compare in silico tumor population formation with observed in vitro morphologies we place a GSC in the center of the computational lattice and monitor tumor growth for 15 days. The seeded cell performs a random walk and gives rise to two daughter cells that subsequently repeat the aforementioned dynamics. An initially sparse collection of cells forms an in silico tumor population (Figure 2D) comparable to in vitro U87-MG growth (Figure 2C).

Estimation of GSCs symmetric division rate

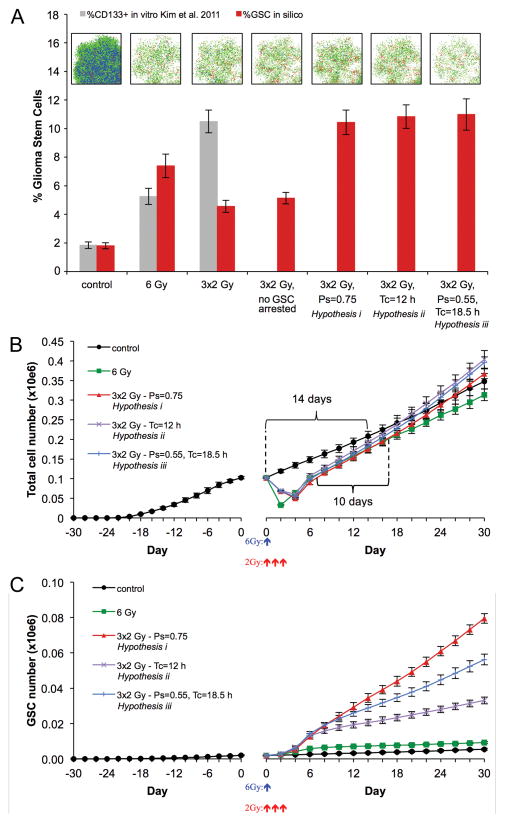
The fraction of U87 CD133⁺ cells in vitro and in vivo has recently been estimated to be 1.8–3.0% (33), which is comparable to 2.51 ± 2.12% GSCs reported in primary GBM specimens. The frequency of GSCs depends pivotally on the frequency of symmetric GSC division events (p_s in our model) to expand the stem cell pool. To estimate the symmetric division rate of GSCs we simulate tumor growth with varying p_s values. By comparing the frequency of GSCs in in silico tumors of 10⁵ cells with the reported fraction of CD133⁺ cells we estimated the symmetric division rate to be 35–45% (p_s=0.35–0.45) for the U87-MG glioblastoma cell line (Figure S1). Taking the lower boundary, i.e. p_s=0.35, we simulate the growth of five tumors from one GSC to a population of ~10⁵ cells with average 1.81% GSCs (n=5) (Figure 4).

Figure 4.

(A) Enrichment of CD133⁺ fraction in vitro (gray; means ± s.d., n=3) (22) and enrichment of GSC fraction in silico after irradiation for different GSC kinetics hypotheses (red; means ± s.d., n=5; see text for details). Representative in silico simulation snapshots are shown. Color-coded are GSC (red), proliferating CC (green) and quiescent CC (blue). Cell counts and simulation snapshots 48 hrs after irradiation. (B) Pre- and post-treatment total cell number evolution for different GSC kinetics hypotheses (means ± s.d., n=5). Treatment initiated at day 0. Curly brackets represent tumor population doubling times for control and irradiated tumors. (C) Pre- and post-treatment GSC number evolution for different GSC kinetics hypotheses (means ± s.d., n=5). Treatment initiated at day 0.

Enrichment of GSCs

We simulate continuing tumor growth either without (control) or with exposure to IR, and compare GSC fractions and tumor progression rates. Utilizing available data in the literature we simulate single-dose irradiation with 6 Gy. At 48 hrs after irradiation, the simulated percentage of GSCs is 7.4%, approximately 4.1-fold enrichment relative to the untreated control (1.81%, c.f. Figure 4A), reproducing the increased ratios of GSCs reported in the literature (3–5 fold) (11,22). The observed enrichment is due to (i) a larger fraction CCs being killed by IR, and (ii) GSCs re-entering the proliferation cycle.

Surprisingly, GSC enrichment to 10.33% after fractionated radiation of 3×2 Gy as reported experimentally (22) was not observed in the CPM, even if increased damage repair in GSCs (11) yields no GSC cell cycle arrest and immediate advancement in the cell cycle (Figure 4A). This disparity indicates that the increase in the proportion of GSCs was not only caused by selection of a radioresistant subpopulation but also an increase in GSC population. Therefore, we hypothesize that repeated exposure to radiation might alter the division kinetics of GSCs. The underlying mechanisms might be comparable to activated signaling pathways such as Sonic Hedgehog (SHh), Notch, Wnt and epidermal growth factor receptor (EGFR), that enable the expansion of the somatic stem cell pool through increased symmetric division during normal development and wound healing (34). Radiation has furthermore been shown to activate the AKT/cyclin D1/Cdk4 pathway in human glioblastoma cells (35), which yields a significantly shorter cell cycle time of 15–16 hrs in human embryonic stem cells compared to somatic cells due to an abbreviated G1 phase (36). As single dose IR of 2 Gy did not cause a significant change in the population of CD133⁺ cells in vivo (22), it is conceivable that either symmetric division probability p_s or GSC growth rate k increases during repeated exposure to IR or, as considered herein, constitutively after the second fraction of radiation. Applying a constitutive (i) increase of p_s=0.75 or (ii) decrease of T_c=12 hrs (and therefore an increase in growth rate k per time unit) yields GSC fractions after 48 hrs in best agreement with the experimental observation (22) (Figure 4A). A similarly good fit was observed for (iii) the combination of partial modulation of both mechanisms (p_s=0.55, T_c=18.5 hrs; both mechanisms modulated by half of the estimated difference when altered individually) (Figure 4A).

Accelerated Tumor Repopulation

Simulated tumors of 10⁵ cells treated with fractionated 3×2 Gy IR reach pre-treatment size 6 days after treatment start (3 days after final dose) (Figure 4B), and 3 weeks after treatment start the average mass of irradiated tumors exceeds that of untreated control tumors. While control tumors took 14 days to double their cell number (to 2×10⁵ cells), tumors treated with fractionated IR doubled in 10 days. The overall tumor population growth rates (not to be confused with cell growth rate k) after treatment with fractionated IR for all hypotheses (i-iii) are unanimously greater than 0.05 (Table 2), while untreated control tumors grow at a rate of 0.0389, which is in excellent agreement with previous untreated glioblastoma growth rate estimations (37,38). Tumor composition 30 days after treatment began, however, is remarkably different for tumors after fractionated irradiation following the different hypotheses discussed above. While tumors with a shortened T_c=12 hrs (hypothesis (ii)) have the fewest stem cells, their total cell number is the highest due to frequent production of CCs. Tumors formed by GSCs with largest p_s=0.75 (hypothsis (i)) contain the largest number of GSCs, but the least overall total number of cells due to the longer cell cycle compared hypotheses (ii) and (iii) (Figure 4B,C).

Table 2.

Comparison of tumor composition and growth rates after simulated IR schedules (means ± s.d., n=5).

	# of GSCs 48 hrs after IR at 105 cells	% of GSCs 48 hrs after IR at 105 cells	Post-IR population growth rate	# of total tumor cells 30 days after IR begins
Control	2137 ± 311	1.81% ± 0.21	0.0389	347,973 ± 19,788
6 Gy	2411 ± 318	7.4% ± 0.83	0.0445	313,866 ± 15,043
3×2 Gy, ps=0.75 hypothesis (i)	5291 ± 707	10.44% ± 0.85	0.0527	367,254 ± 12,540
3×2 Gy, Tc=12 hrs hypothesis (ii)	6591 ± 801	10.84 %± 0.82	0.0535	403,629 ± 22,444
3×2 Gy, ps=0.55, Tc=18.5 hrs hypothesis (iii)	5908 ± 851	10.99% ± 1.1	0.0539	395,517 ± 14,605

Exposure to single 6 Gy IR also yields tumors of pre-treatment size within 7 days (Figure 4B,C) but the modest increase in GSC numbers does not yield an apparent accelerated growth in the short time frame observed. The tumor population growth rate of 0.0445, however, is slightly larger than that of the untreated control, and the thus treated tumor is expected to outgrow the untreated tumor 49 days after treatment. The simulation statistics are summarized in Table 2.

Discussion

We have presented a CPM of GSC and CC kinetics in glioblastoma growth and response to IR. The study aimed to identify cancer stem cell division modes that generate observed frequencies of cancer stem cells in GBM, as well as the role of GSCs in glioblastoma response to IR and subsequent accelerated repopulation. The key cell kinetics parameters in the model were calibrated using experimental data obtained in our laboratory as well as from the literature, yielding simulations of population growth that are in good agreement with experimental results. We obtained the best agreement with reported fractions of GSCs if symmetric division occurs in 35–45% of mitotic GSC events. Whilst these division probabilities reproduce experimentally observed enrichment ratios after single-dose irradiation, our simulations reveal that such frequencies are insufficient to reproduce the 6-fold enrichment observed after exposure to identical dose delivered in smaller fractions.

We hypothesized that fractionated radiation increases activation of GSC signaling pathways such as AKT/cyclin D1/Cdk4, SHh, Notch, Wnt and EGFR, which have been shown to orchestrate stem cell survival, self-renewal, proliferation, and differentiation during normal tissue development and repair (34) (Figure 5). While these pathways that are tightly regulated in normal tissue, it is conceivable that their regulation is aberrant in tumors (Figure 5). Recently, Lathia and colleagues showed that GSC division mode is regulated by growth factors including epidermal growth factor (EGF) and fibroblast growth factor (FGF) (39). EGF-mediated signaling pathways have been shown to contribute to increased migration, survival, proliferation and self-renewal capacity (40), and to maintain the stemness of GSCs with enhanced malignant phenotypes (41). SHh-Gli signaling is required for self-renewal and tumorigenic potential of GSCs, and its inhibition is able to prevent GSCs proliferation (42). Notch signaling is highly involved in regulating self-renewal and expansion of many different types of normal and cancer stem cells (43). Inhibition of Notch signaling in GSCs (e.g., by γ-secretase inhibitor) attenuates the formation of neurosphere-like colonies, increases neuronal differentiation, reduces CD133⁺ cell fraction in vitro, and decreases tumorigenicity in vivo (44), whilst its overexpression has been linked to GSC radioresistance (45) much like Wnt signaling (46–48). Particularly, Notch2 was markedly upregulated in glioma cells treated with fractionated radiation comparing to single-dose radiation (22) lending further support to our hypothesis. Increased activation of Notch-1 following fractionated radiation was also found in breast cancer stem cells conceiving a possible mechanism for the accelerated repopulation of breast tumors following radiotherapy (49).

Figure 5.

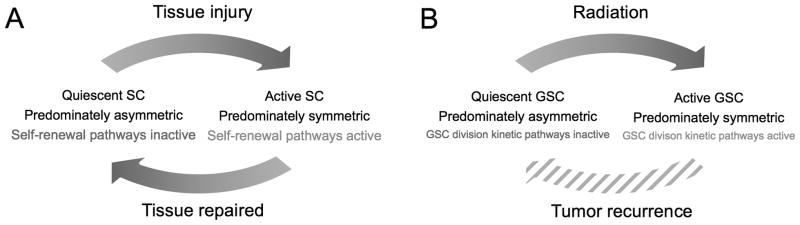
(A) Normal stem cell (SC) response to tissue injury adapted from (34). (B) Proposed GSC response to fractionated irradiation exposure.

Model simulations show that either an increased symmetric division rate or a faster cell cycle of GSCs after repeated exposure to radiation is sufficient to reproduce the elevated enrichment observed experimentally. Frequencies of symmetric GSC division even larger than the herein estimated 75% have been reported recently if exposed to the right milieu of growth factors (39), and aforementioned literature suggests that fractionated irradiation is capable of creating such environment. Observations or references to the alternative hypothesis of a post-irradiation cell cycle in glioma cells as short as 12 hrs, however, are unbeknownst to the authors. It is, nevertheless, conceivable that the increased activation of stem cell division kinetics signaling pathways as discussed above partially modulates both cell cycle progression as well as symmetric division of GSCs. The simulated example with p_s=55% and T_c=18.5 hrs (both mechanisms modulated by half of the estimated difference when altered individually) reproduces the experimental data similarly well with biologically relevant parameter values. Increase in GSC symmetric division rate appears to be the dominant mechanism for increasing the GSC pool, which is in line with previous calculations that regulation of self-renewal is essential for efficient repopulation in the healthy hematopoietic system (50). Future experiments will need to identify which of the discussed hypotheses is prevalent after fractionated irradiation of glioblastoma cells.

Taken together, the presented study reveals that sub-lethal perturbation of a primary GBM selects for and increases the more aggressive subpopulation of GSCs, yielding accelerated repopulation, fast recurrence and worsens prognosis, as previously hypothesized (11,23). If GSCs survive irradiation, recurring tumors show increased population growth rates. Consequently, pre-treatment tumor sizes will be acquired relatively shortly after irradiation with inadequate dose, and inevitably such treated tumors will outgrow untreated control. Whilst the diffusive nature of GBM is the major cause for tumor recurrence, fractionated irradiation-induced increase in GSC self-renewal capacity and/or accelerated cell cycle progression are conceivable as general mechanisms contributing to tumor resistance and accelerated repopulation after apparently adequate radiation treatment.

For computational convenience we focused in our study on early microscopic tumors. Tumors smaller than diffusion-limited size (approximately 1 mm in diameter, 10⁶ cells) are fully oxygenated (51), and therefore hypoxia can be ignored in the presented model. It is of note, however, that self-metastatic tumor growth is self-similar and population composition at smaller sizes is representative for later tumors (17,52). For the applicability of the treatment model we might argue that such microscopic tumors exist in the target area of radiation. GBM are highly infiltrative, and while surgery removes the bulk of the tumor, an appreciable number of cancer cells and microscopic foci have diffused beyond surgical margin throughout the brain (53).

We used in vitro data to parameterize radiosensitivity parameters of the linear-quadratic model (Eq. 3). The obtained α and β values are an order of magnitude larger than estimated by Rockne and colleagues (54) to match clinical response of primary GBM. By scaling the radiosensitivity of quiescent cells (ξ) as well as GSCs (λ), however, the linear sensitivity parameter α of the overall population matches their estimated parameters from clinical response data (54).

The only parameter in the presented model that we are unable to estimate (and to our knowledge has not been reported in the literature) is the proliferation capacity ρ_max of CC. We assumed ρ_max=10 based on previous simulation results that revealed aggressive tumor progression for this parameter value (17). This parameter, however, plays a pivotal role in modulating the frequency of cancer stem cells in solid tumors (52). Therefore, the estimated GSC symmetric division rate of 35–45% to yield 1.8–3.0% of GSC in the total tumor population is only an estimate that is closely linked to the chosen CC proliferation capacity. Further experimental work into identifying the proliferation capacity of CC is required to confidently derive GSC division modes pre- and post therapeutic intervention. Furthermore, our studies were carried out on the U87-MG glioblastoma cell line that was reported in the literature (22). This cell line has limited capability to recapitulate the in vivo biology of human glioblastoma, and further validation on primary GSCs are required before profound conclusions for treatment planning can be drawn.