Variation of Cats under Domestication: Genetic Assignment of Domestic Cats to Breeds and Worldwide Random Bred Populations

Summary

Both cat breeders and the lay public have interests in the origins of their pets, not only in the genetic identity of the purebred individuals, but also the historical origins of common household cats. The cat fancy is a relatively new institution with over 85% of its 40–50 breeds arising only in the past 75 years, primarily through selection on single-gene aesthetic traits. The short, yet intense cat breed history poses a significant challenge to the development of a genetic marker-based breed identification strategy. Using different breed assignment strategies and methods, 477 cats representing 29 fancy breeds were analysed with 38 short tandem repeats, 148 intergenic and five phenotypic single nucleotide polymorphisms. Results suggest the frequentist method of Paetkau (accuracy single nucleotide polymorphisms = 0.78, short tandem repeats = 0.88) surpasses the Bayesian method of Rannala and Mountain (single nucleotide polymorphisms = 0.56, short tandem repeats = 0.83) for accurate assignment of individuals to the correct breed. Additionally, a post-assignment verification step with the five phenotypic single nucleotide polymorphisms accurately identified between 0.31 and 0.58 of the mis-assigned individuals raising the sensitivity of assignment with the frequentist method to 0.89 and 0.92 single nucleotide polymorphisms and short tandem repeats respectively. This study provides a novel multi-step assignment strategy and suggests that, despite their short breed history and breed family groupings, a majority of cats can be assigned to their proper breed or population of origin, i.e. race.

Introduction

Over the past 140 years, a plethora of pedigreed cat varieties have developed due to mankind’s imposed artificial selection on the process of cat domestication. Since the first cat show in London in 1871, which showcased only five breeds, the development of pedigreed cats has increased in popularity (Penny Illustrated Paper 1871). In the USA, the Cat Fanciers’ Association (CFA, http://www.cfa.org/) currently recognizes 41 breeds for competition, and The International Cat Association (TICA, http://www.tica.org/) accepts 57 breeds. A majority of the breeds acknowledged by these two large registries are also typical breeds around the world; however, each breed registry has specific nuances for breed standards and breeding practices. Furthermore, cat breed standards are defined by phenotypic characteristics. Many of these phenotypes, such as hair length, coat patterning and colours, are single gene traits found at low to moderate levels in the general non-pedigreed cat population. Several commercial laboratories are marketing genetic tests to elucidate the breed ancestry of dogs, “your best friend” (Wisdom Panel, http://www.wisdompanel.com/; Canine Heritage Breed Test, http://www.canineheritage.com/), prompting cat owners to wonder about the ancestral origins of their own feline companions.

Because random bred house cats have a different history compared to dogs, genetic testing for breed and population assignments requires a slightly different approach. Whereas the average canine found in the streets of most developed countries is more likely a cross-bred individual from multiple purebred lines, the average random-bred cat is not a descendant of its pedigreed counterparts. For cats, the opposite scenario is more likely – pedigreed feline stocks are the descendants of common street cats from discrete parts of the world that have been selected for one or more distinct traits (Table 1). Random bred cats are the original populations from which the breeds developed, not a population of pedigreed cats gone feral. Also converse to most dog registries, to improve population health and reduce the effects of inbreeding depression, cat breeding associations often seek to diversify their breed populations with random bred cats from the breed’s presumed ancestral origin. For this reason, most cat registries use the term “pedigreed” and not “purebred”.

Table 1.

Traditional cat breed origins.

Breed	Fixed or Hallmark† Phenotype‡	Origin	Date of Establishment	Derived Breeds
Abyssinian	Shorthair, ticked, agouti	India, Africa	1868	Somali*
American Bobtail†	Bobtail	Mutation-USA	1960
American Curl†	Rostral curl to pinnea	Mutation-USA	1981
American Shorthair		USA	1966
American Wirehair	Wired hair	Mutation-USA	1966
Australian Mist		Mix-Australia	1990’s	Several breeds
Birman	Siamese points, gloves, longhair	Burma	<1868	Snowshoe*
British Shorthair		England	1870s
Burmese	Non-agouti, Burmese points	Burma	1350–1767	Asian, Bombay, Tiffanie*, Malayan, Burmilla
Chartreux	Dilute, non-agouti	France	XIV century
Cornish Rex	Curly coat	Mutation-UK	1950
Devon Rex†	Curly coat	Mutation-UK	1960	Sphynx (1966)
Egyptian Mau	Shorthair	Egypt	1953
European Shorthair		Europe
Japanese Bobtail	Bobtail	Japan	VI–XII century
Korat	Dilute, non-agouti	Thailand	1350–1767
LaPerm†	Curly coat	Mutation-USA	1986
Maine Coon	Longhair	USA	1860s
Manx†	No tail	Isle of Man	<1868	Cymric*
Munchkin†	Short legs	USA	1990’s
Norwegian Forest	Longhair	Norway	<1868
Ocicat	Spots	Crossbred	1964	Siamese × Abyssinian
Ojos Azules	Blue eyes	Mutation-USA	1980s
Persian	Longhair	Persia	<1868	Exotic*, Kashmir, Himalayan, Peke-faced, Burmilla
Ragdoll	Longhair	USA	1960s	Ragamuffin
Russian Blue	Dilute, non-agouti	Russia	<1868	Nebelung*
Scottish Fold†	Ventral fold to pinnea	Mutation	1961	Highland Fold* (Coupari)
Selkirk Rex†	Curly coat	Mutation-USA	1980’s
Siamese	Siamese Points, Shorthair, Non-agouti	Thailand	1350–1767	Colorpoint*, Javanese*, Balinese*, Oriental*, Havana Brown, Don Sphynx, Peterbald
Siberian	Longhair	Russia	<1868
Sokoke		Africa
Sphynx	Hairless	Canada	1960s	Devon Rex
Tonkinese†	Shorthair, heterozygous Burmese and Siamese points	Crossbred	1950s	Siamese × Burmese
Turkish Angora	Longhair	Ankara, Turkey	XV century
Turkish Van	Longhair	Van Lake, Turkey	<1868

Origins are according to: Gebhardt (1991), The Royal Canin Encyclopedia (2000), The International Cat Association (http://tica.org/), and Australian Mist Breed Council (http://www.australianmist.info/Home.html).

^†Some breeds allow variants that do not have the hallmark trait, such as straight-eared American Curls or straight-coated Selkirk Rex. The Tonkinese has colour variants that produce Siamese and Burmese colourations. These variants are available for breeding but not for competition.

^‡Many breeds have limited colourations and patterns that vary between registries. Only the most definitive colourations and patterns across most registries are presented.

^*Many derived breeds are long- or shorthaired varieties of the foundation breed but have different breed names; others are delineated by longhair or shorthair in the breed name. Several additional rex-coated cat populations have not developed into viable populations or are extinct.

Two studies have evaluated the genetic distinction of cat breeds. Lipinski et al. (2008) defined the connections between the random bred cat populations and their descendant pedigreed lines using a DNA marker panel containing two tetranucleotide and 36 dinucleotide microsatellites [a.k.a. short tandem repeat (STR)] markers. Five hundred fifty-five individuals were demarcated into 20 breeds. Four breeds remained unresolved as the selected markers lacked sufficient power for demarcation, suggesting the grouping of same cat breeds into breed families. Furthermore, the breeds sampled by Lipinski et al. were shown to be similar to the populations of street cats found in Europe, the Eastern Mediterranean and Southeast Asia. Menotti-Raymond et al. (2008) used a panel of 11 tetranucleotide STR markers to characterize the delineation of cat breeds. Using only the STR markers, 1040 individuals were demarcated into eight individual breeds and nine additional breed groups. Twenty breeds could not be resolved at the breed level. These studies indicate that distinct populations and breeds of cats can be defined genetically, that breeds do have different worldwide origins, tetranucleotide STRs do not perform as well as dinucleotide markers defining cat breeds, and some breeds are so closely related that they cannot be distinguished with even the rapidly evolving dinucleotide STRs.

The 38 highly polymorphic markers of Lipinski et al. (2008) and a recently developed panel of 148 intergenic autosomal single nucleotide polymorphisms (SNPs) were recently applied to an extensive sample of random bred street cats collected throughout the world (Kurushima, 2011). Nine hundred forty-four samples were collected from 37 locations spread throughout North and South America, Europe, Africa, and Asia. The study found both marker sets to be efficient at distinguishing five long-established races, however, a few geographically close populations were better delineated with either SNPs or STRs, most likely due to varying mutation rates between the markers.

Many methods of assignment testing have been developed using a variety of both genetic markers and statistical methods (Paetkau et al. 1995; Rannala & Mountain 1997; Pritchard et al. 2000; Baudouin & Lebrun 2001). These techniques have been applied to various breeding populations including pigs, cattle and dogs (Schelling et al. 2005; Negrini et al. 2009; Boitard et al. 2010). In cattle, Negrini et al. (2009) used 90 SNPs to both allocate and then assign 24 breeds under both the Bayesian methods of Pritchard et al. (2000), Rannala & Mountain (1997) and Baudouin & Lebrun (2001), and the likelihood method of Paetkau et al. (1995). Negrini et al. (2009) concluded that the Bayesian and frequentist methods, implemented respectively through Rannala & Mountain (1997; Bayesian) and Petkau et al. (1995; frequentist), worked best when attempting to assign unknown individuals to a known database of representative samples from each breed.

This paper assesses the ability of a panel of 148 evenly dispersed genome-wide SNPs for population assignment of domestic cats. Different assignment techniques are examined in a species exhibiting many recent and extreme population bottlenecks in addition to large numbers of population migrants, also comparing the power and efficiency of this 148 SNP panel to four-fold fewer STRs. The strength of phenotypic DNA variants is tested for sensitivity and specificity to support individual assignment, in particular for closely related cat breeds that are demarcated by these single gene traits.

Materials and Methods

Sample Collection and Genotyping

Twenty-nine breeds were represented by 477 cats. This study included 354 cats from the work of Lipinski et al. (2008) that analysed 22 breeds. The 123 newly collected samples represented seven additional breeds, including Scottish Fold, Cornish Rex, Ragdoll, Manx, Bengal, Ocicat, and Australian Mist. All cats were representatives of their breed as found within the USA, except for the Australian Mist cats and a few Turkish Angora and Turkish Van samples from international submissions. Additionally, all cats were pedigreed and verified to be unrelated to the grandparent level. Worldwide random bred data (n = 944) was included from the previous study of Kurushima (2011) to assess the origins of each of the breed populations. New samples were collected via a buccal (cheek) swab and extracted using the Qiagen DNeasy Blood and Tissue kit following the manufacturer’s protocol.

Thirty-eight STRs were genotyped in the 123 newly acquired cats following the PCR and analysis procedures of Lipinski et al. (2008). Unlinked non-coding autosomal SNPs (n = 169) were selected to evenly represent all autosomes from the 1.9× coverage cat genomic sequence, which was defined by one Abyssinian cat as re-sequencing data was not available at the time of selection (Pontius et al. 2007). Primers were designed with the VeraCode Assay Designer software (Illumina, Inc.). Only SNPs that received a design score of 0.75 or higher (with a mean design score of 0.95) (n = 162) were included in the analysis (Table S1). Five additional phenotypic SNPs were also evaluated in all cats. The phenotypic SNPs consisted of a causative mutation for the most common form of longhair in cats [AANG02027250.1(FGF5):g.18442A>C] (Kehler et al. 2007), Burmese and Siamese colour points [AANG02171092.1(TYR):g.11026G>T and AANG02171093.1(TYR):g.1802G>A respectively] (Lyons et al. 2005b) and the mutations for the colour variants chocolate and cinnamon [AY804234S6(TYRP1):g.593G>A and AANG02185848.1(TYRP1):g.10736C>T] (Lyons et al. 2005a).

Golden Gate Assay amplification and BeadXpress reads were performed per the manufacturer’s protocol (Illumina, Inc.) on 50–500 ng of DNA or whole genome amplified product. beadstudio software v. 3.1.3.0 with the Genotyping module v. 3.2.23 (Illumina, Inc.) was used to analyze the data. Samples with a call rate less than 0.80 (n = 21) were removed from further clustering analysis. Additionally, only SNPs with a GenTrain Score greater than 0.55 (n = 148) were included in the analysis (Table S1). Each run of the SNP assay contained both an internal positive and negative control in order to validate repeatability and detect contamination.

Population Statistics

Hardy-Weinberg equilibrium (HWE) with associated chi-squared tests, as well as observed and expected heterozygosites, were calculated by breed with genalex v.6.3 (Peakall & Smouse 2006). Inbreeding coefficients (F_IS) within each breed and between population variation values (F_ST) were calculated with fstat v. 2.9.3.2 (Goudet 1995). Because of the predicted recent separation (co-ancestry) and small population sizes of the breeds under consideration, Reynold’s genetic distance was calculated between all pairs of breeds with the SNP dataset (Reynolds et al. 1983). Nei’s genetic distance was used with the STR dataset to accommodate the rapid mutation rate characteristic of STRs (Nei 1972). Both distances were implemented through the software package phylip v. 3.69 (Felsenstein 1989).

Population Structuring

Bayesian Clustering

Datasets were analysed with the Bayesian clustering program structure v.2.3.1 (Pritchard et al. 2000) under the admixture model with correlated allele frequencies and a burn in of 100,000 with 100,000 additional iterations. Values of Q were calculated from K = 1 to K = 33; each run was replicated 10 times. Posterior log likelihoods were used to calculate ΔK to best estimate the number of ancestral populations through the program harvester v.0.56.4 (Evanno et al. 2005). All 10 iterations were then combined through the program clumpp v.1.1.2 (Jakobsson & Rosenberg 2007) to create a consensus clustering. To assess the effects of varying marker types on the final results, analysis using structure was conducted with the two different datasets, SNPs and STRs.

Principal Coordinate Analysis

Principal coordinate analyses were conducted on the Reynold’s (SNPs) and Nei’s (STRs) genetic distance matrices using the software genalex v.6.3 (Peakall & Smouse 2006). For the PCA plots, both the data in the present manuscript and data from the worldwide random bred populations (Kurushima, 2011) were considered to show the relationship of the cat breeds and their random bred population origins.

Breed Race Assignment

Cat breed populations were assigned to the eight ancestral races of random bred worldwide populations of cats (Europe, Mediterranean, Egypt, Iraq/Iran, Arabian Sea, India, Southeast Asia and East Asia) identified in the previous study by Kurushima (2011) by calculating −log(likelihood) values using the Bayesian population assignment methods available in the software geneclass2 v.2.0.h (Piry et al. 2004). Breeds were assigned to the race that produced the highest −log(likelihood) value.

Assignment Testing

Ten sets of 50 individuals were selected randomly from the sample set and assigned to a population of origin using the remaining samples as the reference populations using geneclass2 v.2.0.h (Piry et al. 2004). The Bayesian method of Rannala and Mountain (1997) and the frequentist method suggested by Paetkau et al. (1995) were compared, as these methods performed best in the previous assignment study of Negrini et al. (2009) when compared to the Pritchard et al. (2000) and the Baudoulin & Lebrun methods (2001). Average probabilities were computed using the Paetkau et al. (2004) Monte Carlo resampling method through a simulation of 1000 individuals and a type I error rate (α) of 0.01. Additionally, the assignment tests were performed in three iterations: intergenic SNPs, intergenic and phenotypic SNPs combined, and STRs. Tallies of type I error (an individual not reassigned to its population of origin) and type II error (an individual assigned to the wrong population) were used to calculate the sensitivity and specificity of the assignment method (Negrini et al. 2009).

The differences of the STR and SNP assignments also were compared, post-assignment, with and without the use of phenotypic SNPs. Cats were considered mis-assigned if they had genotypes exclusionary for the breed; for example, an individual assigned to the Exotic Shorthair breed was identified as mis-assigned if it was homozygous for longhair, a recessive trait in cats not found in that breed (see Table 1 for phenotypic diagnostic to breeds).

Results

Summary Statistics

Pedigreed cats (n = 477), representing 29 recognized breeds were included in this study (Table 2). Analysis of all cats from the previous Lipinski (2007) study was attempted, however DNA quality and quantity caused some sample loss, as did available SNP analysis resources. The number of cats per breed ranged from seven to 25 with an average of 16.4 individuals per breed. STRs had an average call rate of 88.2% and SNPs had a 94.0% average call rate. Although the chi-squared goodness-of-fit test indicated that 126 of the 148 SNPs and 36 of the 38 STRs were not in HWE in at least one breed group, only one SNP marker (AANG02147808.1:g.9376T>C) was not in HWE in more than 50% of the breeds (Table S2). Twenty-seven breeds have 10–25 loci not in HWE; however, the Russian Blue and Turkish Van breeds have 31 and 33 of the 186 genetic markers not in HWE respectively. The frequency of the genotypes and alleles for the phenotypic SNPs are indicated in Table 3. The FGF5 mutation AANG02027250.1:g.18442A>C causing longhaired cats in the homozygous state was by far the most prevalent of the phenotypic SNPs, which was found in all but eight of the breeds. In contrast, coat color cinnamon, caused by AANG02185848.1(TYRP1):g.10736C>T, was observed in only five breeds, two breeds having a frequency lower than 0.1.

Table 2.

Population statistics of cat breeds.

		Total	Total	PAB	PAW	Na	Na	Ho	Ho	FIS	FIS
Breed	n	Alleles(SNP)	Alleles(STR)	(str)	(str)	(snp)	(str)	(snp)	(str)	(snp)	(str)
Abyssinian	15	277	130	1	1	1.87	3.42	0.29	0.42	0.02	0.11
American SH	13	269	168	0	0	1.82	4.42	0.28	0.55	−0.02	0.04
Australian Mist	15	273	156	4	0	1.85	4.11	0.27	0.57	−0.01	−0.05
Bengal	18	274	192	10	2	1.85	5.05	0.24	0.58	0.07	0.03
Birman	20	247	133	3	0	1.67	3.50	0.17	0.44	0.13	0.03
British SH	18	276	192	2	0	1.87	5.05	0.24	0.55	0.10	0.06
Burmese	19	262	158	2	1	1.77	4.16	0.20	0.42	0.08	0.16
Chartreux	13	264	151	0	0	1.78	3.97	0.24	0.56	0.10	0.04
Cornish Rex	15	262	163	2	0	1.77	4.29	0.24	0.56	0.05	0.03
Egyptian Mau	14	268	160	1	0	1.81	4.21	0.25	0.50	0.03	0.11
Exotic SH	19	279	178	1	1	1.89	4.68	0.25	0.53	0.07	0.07
Havana Brown	14	245	113	1	0	1.66	2.97	0.17	0.42	0.12	−0.02
Japanese Bobtail	19	267	191	4	0	1.80	5.03	0.22	0.58	0.15	0.08
Korat	25	246	150	2	0	1.66	3.95	0.17	0.52	0.08	0.03
Maine Coon	19	282	210	2	1	1.91	5.53	0.26	0.60	0.11	0.04
Manx	17	282	233	6	2	1.91	6.13	0.30	0.70	0.00	−0.02
Norwegian Forest	16	284	248	8	0	1.92	6.45	0.28	0.67	0.06	0.02
Ocicat	10	264	142	3	2	1.78	3.74	0.24	0.50	0.04	0.05
Persian	15	276	181	1	0	1.87	4.76	0.29	0.50	−0.02	0.15
Ragdoll	15	265	178	4	0	1.79	4.68	0.29	0.62	−0.06	0.00
Russian Blue	17	259	146	2	1	1.75	3.84	0.19	0.45	0.16	0.06
Scottish Fold	17	269	180	2	1	1.82	4.74	0.26	0.57	0.00	0.05
Siamese	15	242	133	2	1	1.64	3.50	0.20	0.47	0.00	0.02
Siberian	17	275	227	4	2	1.86	5.97	0.26	0.71	0.09	−0.06
Singapura	17	232	94	1	0	1.57	2.47	0.18	0.34	0.06	0.02
Sokoke	7	222	92	0	0	1.50	2.42	0.17	0.37	0.00	0.00
Sphynx	17	277	178	2	0	1.87	4.68	0.27	0.55	0.05	0.05
Turkish Angora	21	284	275	10	1	1.92	7.24	0.25	0.67	0.11	0.06
Turkish Van	20	277	259	6	0	1.87	6.82	0.24	0.60	0.12	0.12
Total	477	296	490			1.79	4.54	0.24	0.53	0.06	0.04

n, number of samples; PA_B, private alleles within breeds; PA_W, private alleles within breeds and worldwide random bred populations; Na, average effective number of alleles; Ho, observed heterozygosity; F_IS, inbreeding coefficient. SNP statistics were calculated using intergenic SNPs only.

Table 3.

Phenotypic SNP frequencies.

		Long Hair FGF5 475A>C					Burmese Points TYR 715G>T					Siamese Points TYR 940G>A					Chocolate TYRP1 1373+5G>A					Cinnamon TYRP1 298C>T
Breed	n*	AA	AC	CC	Freq. C	n*	GG	GT	TT	Freq. T	n*	GG	GA	AA	Freq. A	N*	GG	GA	AA	Freq. A	n*	CC	CT	TT	Freq. T
Abyssinian	15	15	0	0	0	15	15	0	0	0	15	15	0	0	0	15	12	3	0	0.10	15	4	6	5	0.53
American SH	13	10	2	1	0.15	13	11	2	0	0.08	13	13	0	0	0	13	12	0	1	0.08	13	13	0	0	0
Australian Mist	13	11	2	0	0.08	15	2	0	13	0.87	12	10	1	1	0.13	15	6	6	3	0.40	15	7	7	1	0.30
Bengal	16	15	1	0	0.03	18	16	2	0	0.06	14	9	4	1	0.21	18	16	2	0	0.06	17	17	0	0	0
Birman	19	0	0	19	1.00	20	20	0	0	0	16	0	0	16	1.00	20	12	5	3	0.28	20	20	0	0	0
British SH	18	16	2	0	0.06	18	18	0	0	0	17	13	0	4	0.24	18	11	2	5	0.33	18	15	3	0	0.08
Burmese	19	19	0	0	0	19	0	1	18	0.97	16	16	0	0	0	19	9	4	6	0.42	19	18	0	1	0.05
Chartreux	10	5	5	0	0.25	13	13	0	0	0	11	11	0	0	0	13	13	0	0	0	13	13	0	0	0
Cornish Rex	15	14	1	0	0.03	15	15	0	0	0	14	3	4	1	0.21	14	13	1	0	0.04	15	15	0	0	0
Egyptian Mau	12	12	0	0	0	14	14	0	0	0	12	12	0	0	0	14	14	0	0	0	14	14	0	0	0
Exotic SH	17	5	10	2	0.41	19	19	0	0	0	17	14	2	1	0.12	19	15	3	1	0.13	19	19	0	0	0
Havana Brown	11	11	0	0	0	14	14	0	0	0	12	10	1	1	0.13	14	0	1	13	0.96	14	14	0	0	0
Japanese Bobtail	14	8	2	4	0.36	18	18	0	0	0	15	13	2	0	0.07	19	19	0	0	0	19	19	0	0	0
Korat	23	22	1	0	0.02	25	25	0	0	0	21	20	1	0	0.02	25	1	2	22	0.92	25	25	0	0	0
Maine Coon	14	0	0	14	1.00	18	18	0	0	0	17	17	0	0	0	19	16	2	1	0.11	19	19	0	0	0
Manx	15	8	6	1	0.27	17	17	0	0	0	16	16	0	0	0	17	16	1	0	0.03	17	17	0	0	0
Norwegian Forest	13	8	3	2	0.27	16	16	0	0	0	15	15	0	0	0	16	15	0	1	0.06	16	16	0	0	0
Ocicat	8	8	0	0	0	10	10	0	0	0	9	9	0	0	0	10	4	1	5	0.55	10	6	3	1	0.25
Persian	15	0	1	14	0.97	15	15	0	0	0	15	5	4	6	0.53	15	12	2	1	0.13	15	15	0	0	0
Ragdoll	15	4	3	8	0.63	15	15	0	0	0	15	0	0	15	1.00	15	13	2	0	0.07	15	15	0	0	0
Russian Blue	15	14	0	1	0.07	17	16	1	0	0.03	15	11	3	1	0.17	17	17	0	0	0	17	17	0	0	0
Scottish Fold	16	13	3	0	0.09	17	17	0	0	0	15	14	1	0	0.03	17	13	4	0	0.12	17	17	0	0	0
Siamese	15	15	0	0	0	15	15	0	0	0	13	0	0	13	1.00	15	2	6	7	0.67	15	15	0	0	0
Siberian	14	1	3	10	0.82	16	16	0	0	0	15	8	6	1	0.27	17	16	1	0	0.03	17	17	0	0	0
Singapura	16	16	0	0	0	15	0	0	15	1.00	14	14	0	0	0	17	17	0	0	0	17	17	0	0	0
Sokoke	6	6	0	0	0	7	7	0	0	0	4	3	0	1	0.25	6	5	1	0	0.08	7	7	0	0	0
Sphynx	16	9	1	6	0.41	16	6	6	4	0.44	12	9	1	2	0.21	17	8	5	4	0.38	17	17	0	0	0
Turkish Angora	20	0	0	20	1.00	21	21	0	0	0	20	17	1	2	0.13	20	15	5	0	0.13	21	21	0	0	0
Turkish Van	18	0	0	18	1.00	19	19	0	0	0	20	19	1	0	0.03	19	14	2	3	0.21	20	20	0	0	0

^*All individuals were attempted for all phenotypic SNPs; differing sample sizes are due to assay drop out.

Genetic Diversity

The population’s genetic data are presented in Table 2. Effective SNP alleles ranged from 1.50–1.92 with an across breed average of 1.79. The average effective number of STR alleles observed was 4.54 across breeds, ranging from 2.42–7.23. Private STR alleles within breeds ranged from 0–10. However, when compared to worldwide random bred populations, private alleles within breeds dropped to between 0–2 per breed (Table 2). No SNPs had private alleles in a breed, although breeds had anywhere from 12 to 74 SNP alleles fixed within their population (Turkish Angora and Sokoke respectively), and the minor allele frequency averaged across all loci ranged from 0.22 in Bengal to 0.32 in Abyssinian with a mean of 0.25 (data not shown).

The average SNP-based observed heterozygosity was 0.24, ranging from 0.17–0.30, whereas the average STR-based observed heterozygosity was 0.53, ranging from 0.34–0.71 (Table 2, Fig. S1). F_IS were lowest in the Ragdoll (−0.06) and Siberian (−0.06) with SNPs and STRs respectively and highest within the Australian Mist Cats (0.16) and Burmese (0.16). Between population variation F_ST values were 0.24 ± 0.01 with SNPs and 0.27 ± 0.02 with STRs (data not shown).

Breed Clustering

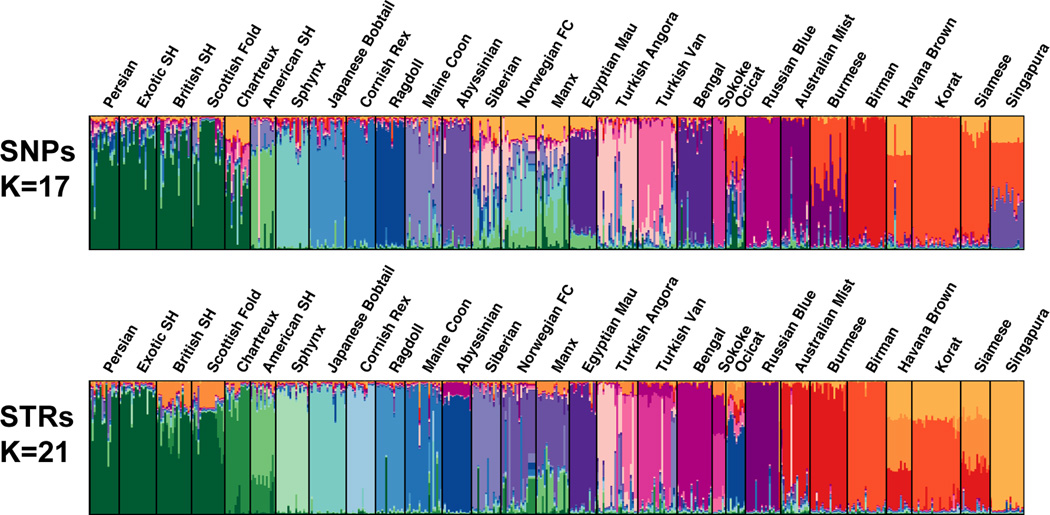
The most likely value of K, the number of structured groupings, could not be decisively determined. A significant difference between the log likelihoods was not evident for either marker type between K = 17–33 (Fig. S2), however a plateau was suggested near K = 21 for STRs and near K = 17 for SNPs; the structure plots are presented in Fig. 1. As a result, a combination of the ΔK plots and common sense directed selection of the most likely number of populations. For STRs, at K > 24 (Fig. S3a), different lineages (breed lines) within specific breeds, such as Norwegian Forest Cat and Turkish Angora, became apparent before five other breed groups would delineate: Persian/Exotic SH, British SH/Scottish Fold, Australian Mist/Burmese, Birman/Korat and Siamese/Havana Brown. Similar results were found for the SNP-based analyses; however the associations of the Asian based breeds varied (Fig. S3b). SNPs appear to resolve the Birman and Singapura breeds from the other Asian breeds more readily. Considering both SNPs and STRs, Persians appear to have influenced several breeds: Exotic Shorthair, Scottish Fold, British Shorthair and, to a lesser extent, Chartreux (Fig. 1). Within breeds of Asian heritage, Siamese have a strong influence on the Havana Brown, Korat and, to a lesser extent, Birman and Singapura (Fig. 1).

Figure 1.

Bayesian clustering of cat breeds. Clustering of breeds at K=17 and K=21 as calculated with SNPs and STRs respectively. Each column represents an individual cat. The y-axis represents Q, or the proportional estimate of genetic membership to the given cluster (K). Each K cluster is indicated by a unique color.

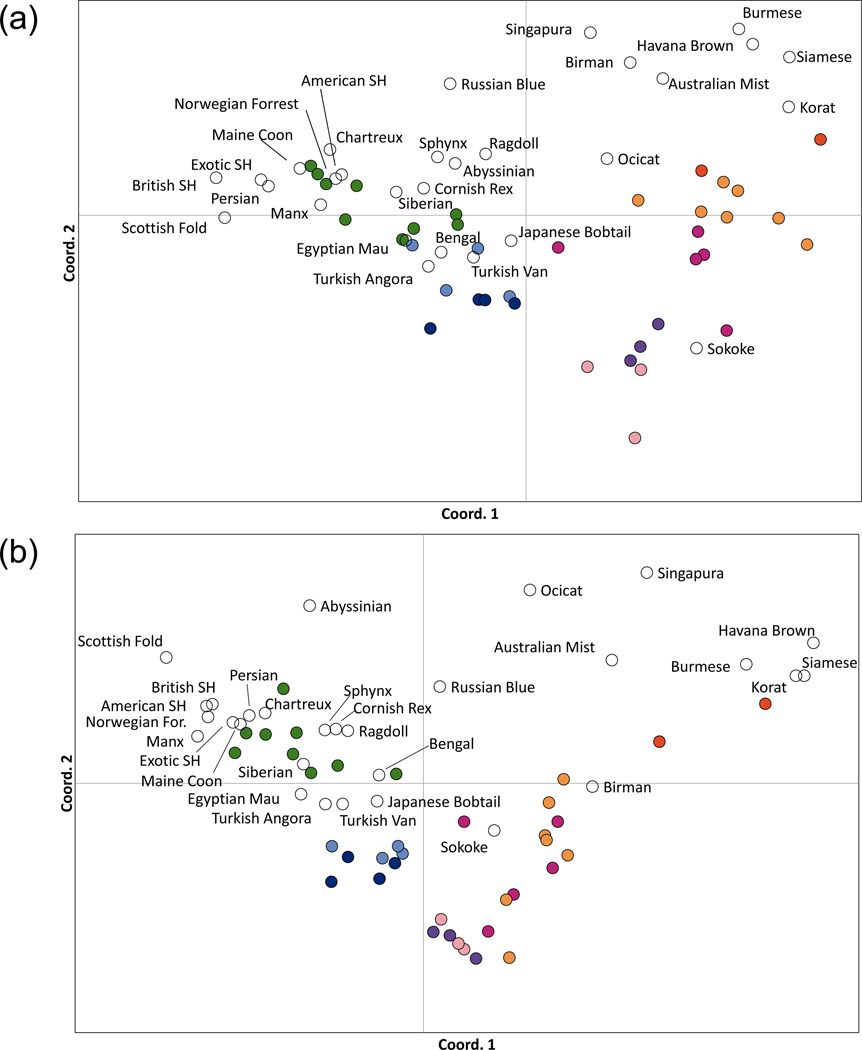
The principal coordinate analyses indicated the relationship of the breeds and their likely closest random bred origins, i.e. race (Fig. 2). The breeds that originated solely from European and American random bred cats clustered with the random bred populations of Europe and America. Likewise, breeds with Asian descent grouped with South Asian populations of random bred cats. The breeds that do not share similar coordinates with a random bred population, such as Russian Blue, Ocicat, Singapura, Australian Mist and Birman, have a strong influence from both Europe and Asia.

Figure 2.

Principal coordinate analysis of cat breeds and worldwide random bred cat populations. Colour shades indicate the population membership of the respective random bred populations as determined by Kurushima (2011). Green, European or European-derived; light blue, Eastern Mediterranean; dark blue, Egypt; purple, Iraq/Iran; light pink, Arabian Sea; dark pink, India; light orange, Southeast Asia; dark orange, East Asia; white, pedigreed breed groups. a) SNPs as calculated by Reynold’s genetic distance (Reynolds et al. 1983); b) STRs as calculated by Nei’s genetic distance.

Using Bayesian clustering, the breeds were then assigned back to the eight random bred races of Kurushima (2011) (Table S3a and S3b). Four regional areas seem to have contributed to the development of the considered cat breeds. Asian breeds, such as Birman, Burmese and Siamese, grouped with Southern Asian cats; Western breeds, such as Persian, Norwegian Forest Cat and Maine Coon, grouped with the Western European random bred cats; Turkish Angora and Turkish Van assigned to the Eastern Mediterranean cats and the Sokoke to the India/Arabian Sea region. Three breeds showed regional variation depending on the marker type used for assignment. When analysed with data from SNPs and STRs, the Turkish Angora was assigned to Europe or to the Eastern Mediterranean, Bengal was assigned to Europe or to the Arabian Sea, and Ocicat was assigned to South Asia or Europe.

Assignment Testing

The accuracy of assignment testing varied depending upon not only the assignment method but also the marker type used to differentiate the cat breeds. For example, when comparing the Bayesian method of Rannala & Mountain (1997) versus the frequentist method of Paetkau et al. (1995), the average sensitivity of assignment for the 148 non-phenotypic SNPs was 0.56 and 0.78 respectively (Table 4a,b). When the five phenotypic SNPs were included with the random SNPs, the average assignment sensitivity was 0.54 ± 1.4 and 0.83 ± 0.09 respectively. Overall, the STRs had higher average sensitivities of 0.83 ± 0.05 and 0.88 ± 0.04 respectively. In six breeds, adding phenotypic SNPs into the frequentist assignment of individuals reduced the sensitivity of the test, and in six breeds, specificity was reduced.

Table 4.

a Assignment accuracy of cats to breeds using the Bayesian method.
		Intergenic SNPs					Intergenic and phenotypic SNPs					STRs
Breed	n	EI	EII	Sens.	Spec.	Ave. Prob.	EI	EII	Sens.	Spec.	Ave. Prob.	EI	EII	Sens.	Spec.	Ave. Prob.
Abyssinian	11	4	0	0.64	1.00	0.98	4	0	0.64	1.00	0.98	2	0	0.82	1.00	0.54
American SH	17	8	0	0.53	1.00	0.99	11	0	0.35	1.00	1.00	4	0	0.76	1.00	0.54
Australian Mist	20	0	1	1.00	0.95	1.00	0	2	1.00	0.91	1.00	2	15	0.90	0.55	0.92
Bengal	23	7	0	0.70	1.00	1.00	2	0	0.91	1.00	0.99	0	0	1.00	1.00	0.79
Birman	22	4	0	0.82	1.00	0.96	6	0	0.73	1.00	0.99	1	0	0.95	1.00	0.72
British SH	17	17	10	0	0	1.00	13	5	0.24	0.44	0.99	7	1	0.59	0.91	0.24
Burmese	16	4	1	0.75	0.92	1.00	2	0	0.88	1.00	1.00	4	1	0.75	0.92	0.86
Chartreux	11	1	13	0.91	0.43	1.00	1	7	0.91	0.59	1.00	1	1	0.91	0.91	0.61
Cornish Rex	23	12	0	0.48	1.00	0.97	14	0	0.39	1.00	0.98	5	0	0.78	1.00	0.58
Egyptian Mau	14	3	0	0.79	1.00	1.00	4	0	0.71	1.00	1.00	1	0	0.93	1.00	0.59
Exotic SH	22	16	8	0.27	0.43	1.00	17	6	0.23	0.45	1.00	6	1	0.73	0.94	0.69
Havana Brown	15	2	2	0.87	0.87	1.00	2	1	0.87	0.93	1.00	0	0	1.00	1.00	0.93
Japanese Bobtail	18	2	33	0.89	0.33	1.00	7	34	0.61	0.24	1.00	1	0	0.94	1.00	0.55
Korat	24	0	15	1.00	0.62	1.00	0	17	1.00	0.59	1.00	2	0	0.92	1.00	0.55
Maine Coon	27	3	21	0.89	0.53	1.00	10	32	0.63	0.35	1.00	6	1	0.78	0.95	0.61
Manx	22	20	1	0.09	0.67	1.00	21	1	0.05	0.50	1.00	4	16	0.82	0.53	0.48
Norwegian Forest	16	8	4	0.50	0.67	1.00	5	25	0.69	0.31	1.00	2	25	0.88	0.36	0.41
Ocicat	7	4	0	0.43	1.00	0.99	3	1	0.57	0.80	0.99	1	0	0.86	1.00	0.63
Persian	12	12	0	0	*	*	10	0	0.17	1.00	*	2	13	0.83	0.43	0.57
Ragdoll	16	16	0	0	*	*	16	0	0	*	*	5	0	0.69	1.00	0.6
Russian Blue	19	0	0	1	1.00	1.00	4	0	0.79	1.00	1.00	3	0	0.84	1.00	0.93
Scottish Fold	19	18	0	0.05	1.00	1.00	16	0	0.16	1.00	1.00	6	0	0.68	1.00	0.67
Siamese	19	19	0	0	*	*	19	0	0	*	*	1	0	0.95	1.00	0.63
Siberian	9	9	0	0	*	*	6	23	0.33	0.12	1.00	1	9	0.89	0.47	0.27
Singapura	19	1	0	0.95	1.00	1.00	0	0	1.00	1.00	1.00	2	0	0.89	1.00	0.86
Sokoke	5	0	0	1.00	1.00	1.00	0	0	1.00	1.00	1.00	0	0	1.00	1.00	0.81
Sphynx	25	16	0	0.36	1.00	0.99	14	0	0.44	1.00	0.99	3	0	0.88	1.00	0.34
Turkish Angora	18	5	125	0.72	0.09	1.00	11	134	0.39	0.05	1.00	11	2	0.39	0.78	0.46
Turkish Van	14	10	3	0.29	0.57	0.98	13	3	0.07	0.25	0.99	3	3	0.79	0.79	0.69
All Breeds	500	221	237	0.56	0.54	0.99	231	291	0.54	0.48	1.00	86	88	0.83	0.82	0.63
95% confidence interval				0.14	0.12				0.13	0.13				0.05	0.08

b Assignment accuracy of cats to breeds using the frequentist method.
		Intergenic SNPs					Intergenic and phenotypic SNPs					STRs
Breed	n	EI	EII	Sens.	Spec.	Ave. Prob.	EI	EII	Sens.	Spec.	Ave. Prob.	EI	EII	Sens.	Spec.	Ave. Prob.
Abyssinian	11	0	0	1.00	1.00	0.32	0	0	1.00	1.00	0.32	2	0	0.82	1.00	0.33
American SH	17	1	0	0.94	1.00	0.53	4	0	0.76	1.00	0.60	2	0	0.88	1.00	0.27
Australian Mist	20	0	2	1.00	0.91	0.57	0	3	1.00	0.87	0.58	2	1	0.90	0.95	0.27
Bengal	23	2	0	0.91	1.00	0.43	2	0	0.91	1.00	0.43	0	0	1.00	1.00	0.21
Birman	22	1	0	0.95	1.00	0.39	1	0	0.95	1.00	0.38	1	0	0.95	1.00	0.34
British SH	17	10	6	0.41	0.54	0.45	5	4	0.71	0.75	0.33	5	3	0.71	0.80	0.16
Burmese	16	2	2	0.88	0.88	0.51	3	0	0.81	1.00	0.51	0	2	1.00	0.89	0.26
Chartreux	11	2	0	0.82	1.00	0.31	2	0	0.82	1.00	0.31	0	0	1.00	1.00	0.15
Cornish Rex	23	5	0	0.78	1.00	0.29	4	1	0.83	0.95	0.30	2	0	0.91	1.00	0.25
Egyptian Mau	14	1	0	0.93	1.00	0.29	2	0	0.86	1.00	0.32	3	0	0.79	1.00	0.18
Exotic SH	22	19	7	0.14	0.3	0.43	10	5	0.55	0.71	0.37	4	1	0.82	0.95	0.39
Havana Brown	15	1	0	0.93	1.00	0.48	2	1	0.87	0.93	0.49	0	0	1.00	1.00	0.37
Japanese Bobtail	18	4	0	0.78	1.00	0.29	3	0	0.83	1.00	0.26	1	0	0.94	1.00	0.29
Korat	24	1	0	0.96	1.00	0.41	0	0	1.00	1.00	0.42	0	0	1.00	1.00	0.45
Maine Coon	27	5	8	0.81	0.73	0.44	1	13	0.96	0.67	0.44	6	5	0.78	0.81	0.35
Manx	22	8	11	0.64	0.56	0.33	5	9	0.77	0.65	0.40	4	12	0.82	0.60	0.14
Norwegian Forest	16	1	46	0.94	0.25	0.33	3	20	0.81	0.39	0.37	1	3	0.94	0.83	0.06
Ocicat	7	0	1	1.00	0.88	0.27	0	2	1.00	0.78	0.30	1	1	0.86	0.86	0.10
Persian	12	9	19	0.25	0.14	0.39	6	10	0.50	0.38	0.45	1	6	0.92	0.65	0.26
Ragdoll	16	3	0	0.81	1.00	0.26	2	0	0.88	1.00	0.26	4	0	0.75	1.00	0.32
Russian Blue	19	0	0	1.00	1.00	0.31	1	0	0.95	1.00	0.32	3	0	0.84	1.00	0.39
Scottish Fold	19	10	0	0.47	1.00	0.84	10	0	0.47	1.00	0.85	2	0	0.89	1.00	0.45
Siamese	19	1	0	0.95	1.00	0.33	0	0	1.00	1.00	0.32	0	0	1.00	1.00	0.17
Siberian	9	5	3	0.44	0.57	0.19	4	3	0.56	0.63	0.22	0	18	1.00	0.33	0.11
Singapura	19	1	0	0.95	1.00	0.45	0	0	1.00	1.00	0.44	3	0	0.84	1.00	0.32
Sokoke	5	0	0	1.00	1.00	0.41	0	0	1.00	1.00	0.42	0	0	1.00	1.00	0.46
Sphynx	25	3	2	0.88	0.92	0.32	3	2	0.88	0.92	0.31	1	0	0.96	1.00	0.25
Turkish Angora	18	10	1	0.44	0.89	0.23	6	8	0.67	0.60	0.37	9	7	0.50	0.56	0.21
Turkish Van	14	5	3	0.64	0.75	0.27	4	2	0.71	0.83	0.37	2	3	0.86	0.80	0.18
All Breeds	500	110	111	0.78	0.78	0.39	83	83	0.83	0.83	0.39	59	62	0.88	0.88	0.27
95% confidence interval				0.09	0.10				0.06	0.07				0.04	0.06

Bayesian method of Rannala & Mountain (1997).

^*Essentially zero due to lack of sensitivity; n, number of samples from this breed tested over ten iterations; E_I, members of a breed that were incorrectly assigned to another breed; E_II, members of a different breed that were incorrectly assigned to the breed in question; Sens., sensitivity; Spec., specificity; Ave. Prob., average probability of assignment as calculated by the Paetkau et al. (2004) Monte-Carlo resampling method.

Frequentist method of Paetkau et al. (1995).

^*Essentially zero due to lack of sensitivity; n, number of samples from this breed tested over ten iterations; E_I, members of a breed that were incorrectly assigned to another breed; E_II, members of a different breed that were incorrectly assigned to the breed in question; Sens., sensitivity; Spec., specificity; Ave. Prob., average probability of assignment as calculated by the Paetkau et al. (2004) Monte-Carlo resampling method.

The post-assignment allocation using the five phenotypic SNPs was able to correctly classify 57.5% of the 221 animals originally mis-assigned by the Bayesian method with the intergenic SNPs and 50% of the 110 individuals originally mis-allocated by the frequentist method (Table 5). The phenotypic-based corrections increased the sensitivity and specificity of the Bayesian method to 0.75 and 0.77 respectively, and the frequentist to 0.89 (both sensitivity and specificity), and resulted in better resolution than did the use of intergenic SNPs alone (data not shown). The effect of using phenotypic SNPs post-assignment was less effective in the STR assignments (identifying 27% and 32% of the Bayesian and frequentist mis-assignments respectively). The influence of recent breed development on the mis-assignment of individuals may be further visualized by plotting the crossed assignment rate as a function of the genetic distance between breeds (Fig. S4a,b). The crossed assignment rate increased as the genetic distance between breeds decreased.

Table 5.

Total mis-assigned individuals identified post-assignment by phenotypic SNPs.

	Assigned by SNPs				Assigned by STRs
	Bayesian		Frequentist		Bayesian		Frequentist
	Total	Freq.	Total	Freq.	Total	Freq.	Total	Freq.
Long Hair	105	0.49	37	0.34	11	0.13	11	0.18
Burmese Points	15	0.07	3	0.03	1	0.02	2	0.03
Siamese Points	15	0.07	16	0.15	6	0.07	3	0.05
Chocolate	8	0.04	0	0	2	0.02	0	0
Cinnamon	14	0.07	5	0.05	4	0.05	4	0.07
Total*	127	0.58	55	0.50	22	0.26	19	0.32

Frequency (SNPs: Bayesian = 221, Frequentist = 110 STRs: Bayesian = 86, Frequentist = 59)

^*A few individuals were identified as mis-assigned with multiple phenotypic SNPs.

Discussion

The artificial selection and population dynamics of domestic cats and their associated fancy breeds are unique amongst domesticated species. Cats are one of the more recent mammalian domesticates, arguably existing in a unique quasi-domesticated state. Although domestication is an ongoing process, the earliest instance of cat taming is credited to a Neolithic burial site on Cyprus dated to 9500–9200 years ago (Vigne et al. 2004). Unlike other agricultural species and the domestic dog, until recently cats have had minimal artificial selection pressures on their form and function as they have naturally performed their required task of vermin control. Barriers to gene flow are mitigated as cats are transported between countries via both purposeful and accidental human-mediated travel, although recently rabies control legislation has reduced the migration of cats between some countries. Overlapping niches between the wildcat progenitors, random bred feral cats, random bred house cats, and fancy breeds likely produces continual, however limited, horizontal gene flow throughout the domestic cat world.

The overall selection on the cat genome may be predicted to be less intense than in other domesticated species. The cat fancy is less than 150 years old, and a majority of cat breeds were developed in the past 50–75 years. Human selection in cats has focused on aesthetic qualities, such as coat colours and fur types, as opposed to complex behaviours and qualities, such as hunting skills and meat or milk production in dog or in other livestock species. Many of the cat’s phenotypic attributes, even those that affect body and appendage morphologies, are traits with basic Mendelian inheritance patterns. One simple genetic change, such as the longhair of the Persian versus the shorthair of Exotic Shorthairs, is the defining characteristic between these two breeds. Burmese and Siamese points are found in a large metafamily of breeds that includes Burmese, Siamese, Javanese, Tonkinese and Birman, to name a few (Table 1). Brown colorations are diagnostic in breeds such as the Havana Brown and Korat (chocolate) and the Abyssinian (cinnamon). These selective pressures are reflected in the causative SNP frequencies in (Table 3).

Cat registries have recognized that some breeds are “natural”, such as the Korat and Turkish Van. These breeds are specific population isolates and random bred cats of similar origins can be used to augment their gene pools. Other breeds are recognized as “hybrids”, developed from purposeful cross-breeding of either different breeds or species. One such example is the Ocicat, an intentional Abyssinian and Siamese cross. The Bengal is a unique breed that is an interspecies hybrid between an Asian leopard cat and various domestic breeds (Johnson-Ory 1991). As a result, some cat breeds may be a concoction of various genetic backgrounds, including cats of different breeds but having the same racial origins, cats of different breeds from different racial origins and even different species.

The 29 breeds were selected to represent the major breeds of the cat fancy. Some breeds may have developed from natural populations, while most cat breeds developed in the past 50 years. Several breeds that had clearly derived from another breed, such as Persians and Exotic Shorthairs, were purposely chosen, whereas others were selected because they were recently developed hybrid breeds, such as the Ocicat, Bengal and the Australian Mist. Thus, STRs may be better for breaking up breed families, whereas intergenic SNPs may give us more insight into the natural populations. More slowly evolving SNPs and relatively quickly evolving STRs were examined to assess their power to resolve cat breeds that have different patterns, origins and ages of ancestry.

Significant genetic variation is present in many cat breeds and cannot be predicted entirely by effective population size (popularity among cat breeders) or breeding practices alone. The Turkish Angora, originating from Turkey, an area near the seat of cat domestication (Driscoll et al., 2007, Lipinski et al., 2008), had the highest effective number of alleles for both SNPs and STRs. A wide distribution of heterozygosity levels and inbreeding values was found throughout the remainder of the cat breeds. However, the SNPs and STRs were not always concordant (as can be seen in Fig. S1). A previous study found STRs often underestimate F_ST compared to SNPs, most likely due to a rapid STR mutation rate, often leading to convergence (Sacks & Louie 2008). An alternative hypothesis is that long isolated breeds of a large population size have had sufficient time and opportunity to increase STR heteorzygosity through mutation, but not so for SNPs. Regardless, SNPs and STRs have differing relative observed heterozygosity values for some of the breeds (namely Abyssinians, Persians and Japanese bobtails) and is reflected in their F_IS values.

Two of the most prevalent breeds are Persians and Bengals (http://www.tica.org/). Persians were one of the first breeds to be recognized, and Bengals, although only introduced in the past 40 years, have risen to worldwide fame. Both breeds had moderate levels of heterozygosity and inbreeding. Several less popular breeds, such as the Cornish Rex, contained fairly high levels of variation and low inbreeding, whereas two recently developed breeds, the Siberian and Ragdoll, revealed high variation, perhaps a reflection of their recent development from random bred populations. Thus, levels of variation and inbreeding cannot entirely be predicted based on breed popularity and breed age, implying management by the cat breeders may be the most significant dynamic for breed genetic population health.

The Bayesian cluster analysis supported the breed demarcations from previous studies, especially the STR analyses of Lipinski et al. (2007). Previously, 22 breeds, which included 15 of 16 “foundation” cat breeds designated by the Cat Fanciers’ Association, delineated as 17–18 separate populations. This study added seven additional breeds, including the missing 16^th “foundation” breed, the Manx. However, the most likely value of K (number of structured groupings) could not be decisively determined by methods developed for wild populations. As structure creates a probability distribution of the breed populations by inferring the previous generation’s genotypic frequencies through the principles of HWE, several practices in cat breeding result in genetic populations that do not always align with the inferences of structure. Cat breeds have variation in age of establishment and significantly different genetic population origins, and the dissimilarity in breeding practices can create distinct lines within a single breed that may be as unique as one of the more recently established breeds. Additionally, many breeds were created through the crossing of two, often highly divergent, populations of cats resulting in a hybrid of sorts, whereas other breeds still allow the introduction of cats from random bred populations. These instances confounded the log-likelihood calculations, making an empirical determination difficult.

As in previous studies, the breeds that were not deemed genetically distinct can be explained by the breed history (Lipinski et al. 2008; Menotti-Raymond et al. 2008). The two large breed families of Siamese and Persian-types were re-identified, and the Persian family expanded with Scottish Folds. The Australian Mist was added to the previously recognized grouping of the Siamese/Havana Brown/Burmese, as this breed was created by cross-breeding with Burmese. More recent breeds, such as the Ragdoll and Bengal, are resolved as separate breed populations, suggesting STRs alone can differentiate about 24 of 29 breeds, in addition to Turkish- versus USA-originating Turkish Angoras. At K = 17, SNPs could separate Birman from other Asiatic breeds but not the Singapura. Thus, both sets of markers provide valuable insight to the relationship of the breeds. Because the breeds within the larger family groups are generally different by only a single gene trait, an actual breed designation may not be appropriate and perhaps should be consider varieties within a breed. The cat fancy has precedence for this concept, the pointed Persian, a Himalayan, is considered a variety in the CFA but a breed by TICA.

Regardless of the marker assayed, the principal coordinate and Bayesian assignment analyses clustered the majority of breeds with the random bred population that was most influential to its creation, as suggested by popular breed histories. Sixteen breeds originated from European populations, six breeds from South Asian populations, two breeds from the Eastern Mediterranean, and the Sokoke from the India or Arabian Sea region. However, some marker specific differences were noted. When SNP and STR results were compared through Bayesian assignment, the Turkish Angora was assigned to Europe or the Eastern Mediterranean, respectively, Bengal was assigned to Europe or the Arabian Sea respectively and the Ocicat was assigned to South Asia or Europe respectively. These dissimilarities were not reflected in the PCA results that were remarkably similar in both SNPs and STRs. This was most likely due to offsetting the mutation rate differences with distance matrices that accommodate these attributes.

Nonetheless, the aforementioned breeds have unique histories that may explain the marker discrepancies with Bayesian assignment to random bred populations. The Turkish Angora breed was reconstituted from the Persian (European) pedigree post World Wars, and their genetic diversity has recently been supplemented via outcrossing to Turkish random bred cats. The identified subpopulations within the breed may reflect the latest influx of random bred cats. The Bengal and the Ocicat clustering could be a result of the contribution of breeds from very different regional origins such as Abyssinian, Egyptian Mau and the Siamese.

Overall, the frequentist method of Paetkau et al. (1995) outperformed the Bayesian method of Rannala and Mountain (1997) in assigning unknown individuals to their breed of origin. Both methods rely on a frequency distribution to estimate the probability that an unknown arose in a given population. The differences lie in how that frequency distribution is established. Paetkau’s frequentist method generates the frequency distribution based on the observed alleles in each population, whereas the Bayesian method begins with an initial distribution in which every population in the dataset has an equal allele density and then calculates a posterior probability distribution based on the initial assumption given the observed data. Both methods assume the populations are in HWE, however the frequentist method is able to accommodate populations with drastically different allele frequencies – populations such as those seen as a result of the cat fancy. Directed breeding, such as that used in the development of pedigreed cats inherently violates the assumptions of HWE. Therefore, a frequentist method that identifies an individual’s origin based on the frequency of the genotypes in each potential population should excel in assignment accuracy for inbred populations.

Many breeds are defined by one genetic trait in the cat fancy. Although many breeds can share a trait, such as long hair, this same trait can exclude a breed (Table 3). Thus, phenotypic traits were tested post-assignment, as many are not highly breed selective pre-assignment. Although the 38 highly polymorphic STRs consistently outperformed the SNPs, the addition of phenotypic SNPs as post-assignment verification significantly improved the assignment rates. The reduction in sensitivity and specificity when combing the phenotypic SNPs in the assignment may be due to the strength of selection imposed on these markers. In general, breeds that were more inbred, not open to outcrosses and not developed through the crossing of pre-existing breeds had a higher accuracy in reassignment; the Russian Blue, Sokoke and Abyssinian are examples. In contrast, breeds where outcrossing is common, either with other breeds or random bred populations, tended to confuse the assignment algorithm and had a high probability of both Type I and II error, such as the Persians, Turkish Angoras and Ragdoll. The most common error in assignment by far was cross assignment between Exotic Shorthairs and Persians within this breed family, a problem easily remedied by exploiting the FGF5 SNP causing longhair in Persians.

Initially, cats could be localized to a regional population and breed family by STRs and/or SNPs. Secondary differentiation within the breed family could be determined by genotyping mutations for phenotypic traits, especially traits that are specific to or fixed within a breed. Some traits are required for breed membership; a Birman or Siamese must be pointed, implying homozygosity for the AANG02171093.1(TYR):g.1802G>A variant. Some traits are grounds for exclusion: all Korats are solid blue, and no other colours or patterns are acceptable. Therefore, a trait such as the longhair AANG02027250.1(FGF5):g.18442A>C variant could be used as a means for identifying members of the Persian, Maine Coon, Turkish Angora, Turkish Van and Birman breeds and, likewise, a means for discrimination as an exclusion marker for breeds such as the Abyssinian, Egyptian Mau, Sokoke and Ocicat. Other single gene traits may be used to identify members of a small family of cat breeds as well, such as the Burmese points, AANG02171092.1(TYR):g.11026G>T, are a prerequisite for membership to the Burmese and Singapura breeds. The cinnamon mutation, AANG02185848.1(TYRP1):g.10736C>T, is very rare in the general cat population, yet is a defining characteristic of the red Abyssinian.

Cat fancy registries may not agree with assignments due to variations in breeding practices between the registries for a given breed. The Tonkinese, which is genetically a compound heterozygote for the AANG02171092.1(TYR):g.11026G>T and the AANG02171093.1(TYR):g.1802G>A variants, can produce both pointed and sepia cats; thus Tonkinese can genetically resemble a Siamese or Burmese at the TYR locus respectively. However, in some cases registration restrictions do not allow these Tonkinese variants to be registered as Siamese or Burmese. In addition, some breed registries allow colour and hair variants that may not be permitted in another, confusing possible breed assignments. Thus, the cats assigned in this study are more likely specific to the cat fancy of the United States, and tests for other breed populations that are registry or regional specific may need to be developed. Since the development of this SNP panel, additional phenotypic SNPs have been discovered in cats including the Norwegian Forest Cat colour variant amber (Peterschmitt et al. 2009), three additional long-haired mutations (Kehler et al. 2007) and the mutations responsible for hairlessness in Sphynx and rexing of the Devon Rex (Gandolfi et al. 2010). These additional mutations, as well as disease mutations, could further delineate cat breeds.

Aside from the public interest in knowing if their prized family pet is descended from a celebrated pedigree, breed assignment is a vital tool in tracing the spread of genetically inherited diseases throughout the cat world. Much like humans and dogs, certain populations of cats are known to be at higher risk for particular diseases, such as heart disease in the Maine Coon and Ragdoll (Meurs et al. 2005; Meurs et al. 2007), polycystic kidney disease in the Persian (Lyons et al. 2004) and progressive retinal atrophy in the Abyssinian (Menotti-Raymond et al. 2007). Knowing if a particular feline descended from one of these at-risk populations may influence treatments in a clinical setting and help to better care for our animal companions. In addition, understanding the population structuring of the cat breeds can be of assistance to case–control studies for genome-wide association studies. The current study defined 24 of 29 cat breeds and an additional three breeds using phenotypic SNPs. With additional phenotypic and perhaps disease-causing SNPs, the power of this STR/SNP panel to accurately assign individuals to specific cat breeds, in particular those breeds that are defined expressively by single-gene traits, would be greatly increased.