RIGHT AND LEFT VENTRICULAR DIASTOLIC PRESSURE–VOLUME RELATIONS: A COMPREHENSIVE REVIEW

Abstract

Ventricular compliance alterations can affect cardiac performance and adaptations. Moreover, diastolic mechanics are important in assessing both diastolic and systolic function, since any filling impairment can compromise systolic function. A sigmoidal passive filling pressure-volume relationship, developed using chronically instrumented, awake-animal disease models, is clinically adaptable to evaluating diastolic dynamics using subject-specific micromanometric and volumetric data from the entire filling period of any heartbeat(s). This innovative relationship is the global, integrated expression of chamber geometry, wall thickness, and passive myocardial wall properties. Chamber and myocardial compliance curves of both ventricles can be computed by the sigmoidal methodology over the entire filling period and plotted over appropriate filling pressure ranges. Important characteristics of the compliance curves can be examined and compared between the right and the left ventricle, and for different physiological and pathological conditions. The sigmoidal paradigm is more accurate and, therefore, a better alternative to the conventional exponential pressure-volume approximation.

Introduction

Diastolic dysfunction has in the past taken a back seat to systolic, in part because systolic abnormalities are easier to recognize, whereas heart failure due to diastolic dysfunction is not easily distinguished by clinical examination, so that a number of patients may go unrecognized. However, recognition of diastolic heart failure is important in planning an effective therapy. Moreover, abnormalities of ventricular diastolic function, such as reduced myocardial and chamber compliance, can also have a significant influence upon systolic function by limiting diastolic filling, stroke volume and cardiac output, and upon epigenetic adaptations by hindering stretch-activated signaling mechanisms [1] and mechanotransduction. Epidemiological, clinical and experimental studies have documented both the rising burden of diastolic heart failure and several mechanisms that distinguish it from systolic failure [2–7].

Nowadays, thanks to major strides in the evaluation of diastolic performance, diastolic dysfunction as a component of heart failure is sufficiently recognized as to be a part of heart failure coding in the International Classification of Diseases (ICD-10, codes I50.30–33). Additionally, the material properties of the myocardium during diastolic filling influence both diastolic and systolic function [8]. It is now widely appreciated that enhancing diastolic filling has clinical merit and that the significance of left ventricular diastolic dysfunction can be far reaching [9]. For instance, through the passive transmission of elevated end-diastolic pressures, left ventricular diastolic dysfunction may induce pulmonary hypertension, reactive pulmonary vasoconstriction, and vascular remodeling; in time, right ventricular failure can develop, which can further exacerbate the left ventricular failure because of their close mechanical and cellular integration [10].

Alterations in the compliance of either ventricular chamber may play an integral role in cardiac performance and adaptations. Accordingly, quantification by sensitive methods of the diastolic global behavior of both ventricles and of the mechanical properties of the right and left ventricular myocardium is necessary to properly assess the functional state of the heart and epigenetic alterations in health and disease.

Diastolic RV/LV filling dynamics fundamentals

The definition and temporal limits of diastole can be described in both cellular and hemodynamic terms [2,7]. Operationally, we can define right and left ventricular diastole as the period from semilunar valve closure to atrioventricular (AV) valve closure; it encompasses two main features determining dynamics: relaxation, and compliance [11,12]. There are many individual determinants that influence diastolic performance, including systolic function, heart rate, preload, and afterload. For instance, left ventricular systolic failure compels LV end-systolic volume to rise and forces the left ventricle to operate on a steeper portion of its diastolic pressure–volume relation, contributing to low LV preload reserve and exercise intolerance [13]. Ipsilateral atrial function, contralateral ventricular function, and pericardial restraint also impact ventricular diastolic function, while both rhythm and PR interval can affect diastolic filling patterns [2,14,15]. Early diastolic filling is normally dominant (E-wave), with a supplementary increment associated with atrial contraction (A-wave). The main influences on the early inflow rate and volume pertain to myocardial relaxation dynamics and are different from those affecting late filling that commonly relate to passive ventricular and myocardial compliance. Relaxation and compliance will next be considered separately.

Relaxation

Cardiomyocyte contraction is initiated by the influx of Ca⁺⁺ through L-type calcium channels in the cell membrane [16,17]. The rise in intracellular calcium triggers a further Ca⁺⁺ release by the ryanodine receptors in the membrane of the sarcoplasmic reticulum which transport Ca⁺⁺ out into the cytosol in a positive feedback response, raising the free intracellular [Ca⁺⁺] approximately tenfold [18]. Ca⁺⁺ then associates with troponin C in the sarcomere and induces contraction. Release of Ca⁺⁺ from the sarcomere causes relaxation and Ca⁺⁺ reuptake into the sarcoplasmic reticulum by the sarco/endoplasmic reticulum Ca⁺⁺-ATPase (SERCA); this is an energy-dependent [17] process (lusitropy). The ability of SERCA to pump calcium back into the sarcoplasmic reticulum is governed by its interaction with phospholamban, a small modulatory protein within the membrane of the sarcoplasmic reticulum [19].

Thus, the molecular basis for ventricular relaxation is a decline in actin-myosin cross-bridge formation, and the reuptake of cytosolic Ca⁺⁺ into the sarcoplasmic reticulum. These two processes become manifest as ventricular pressure starts to decline, after peak systole. Since relaxation is an ATP-requiring, energy consuming process, it is delayed in energy-deficient states, such as ischemia [20]. Once LV/RV pressure falls below aortic/pulmonic root pressure, the isovolumic relaxation period ensues, when both AV and semilunar valves are closed. As soon as declining ventricular pressures cross-over below the atrial, the AV valves open and early rapid filling ensues. Relaxation rather than passive compliance is normally more important in early diastole. Accordingly, relaxation modifications strongly influence diastolic performance in normal individuals, as, e.g., relaxation may be enhanced with increased sympathetic tone by autonomic reflexes to yield a more rapid pressure descent and a shorter isovolumic relaxation period [2].

Relaxation may be impaired with ischemia, ventricular hypertrophy, and many cardiac diseases, so that it may be inadequate in early diastole; when seriously impaired, it can remain incomplete even at end-diastole [2,21]. Delayed relaxation generally brings about a shift in ventricular filling later in diastole (with the “atrial kick”), instead of the normal situation where most inflow occurs during the E-wave in the early rapid filling phase [2,12,22]. Hypertrophy and impaired relaxation often coexist in patients with hypertrophic cardiomyopathy (HCM) or calcific valvular aortic stenosis, leading to holodiastolic dysfunction [4,12,21].

Compliance

Right and left ventricular distensibility pertains to the ratio (dV/dP) of the incremental rise in chamber volume for a given small increase in distending pressure and refers to the compliance of the ventricle as a hollow structure—see below. More compliant ventricles expand more readily with rising distending pressure. Preload dependent changes in compliance occur with any acute alteration in volume. The effective chamber distensibility decreases as the chamber progressively fills; fuller ventricles distend less easily (are stiffer) than less full ones. This implies that compliance rather than relaxation considerations are usually more influential in late diastole [12].

Chamber geometry influences distensibility, as thicker than normal ventricular walls are harder to distend, giving rise to a leftward shift of the diastolic pressure–volume curve [4,12,23,24]. At a given diastolic pressure, right and left ventricular passive global distensibility is determined mainly by the relative values for chamber volume and ventricular muscle mass and the effective stiffness of a unit of myocardium [4,25]. Chamber compliance is affected by myocardial tissue characteristics, with interstitial fibrosis having an adverse effect on distensibility [7,12,24,26]. Several other factors also contribute to ventricular stiffness, including coronary turgor or “erectile effect” and pathologic alterations of chamber shape [25,27].

Myocardial hypertrophy also increases extracellular connective tissue [4,12,24] and myocardial intracellular cytoskeletal components [21], thus raising the intrinsic myocardial stiffness. Similarly, following chronic ischemia and infarction, there ensue subcellular remodeling and an inappropriate accumulation of extracellular matrix (ECM) proteins, causing myocardial stiffness to rise [8,28]. The operating volume modifies chamber stiffness, since a ventricle becomes harder to fill with progressive distension, even without any change in muscle mass or myocardial tissue characteristics. Incomplete relaxation may under pathologic conditions persist in late diastole, contributing to a less compliant chamber [4,7,29].

Other factors

Pressure–volume relationships and ventricular compliance are determined primarily by complex interactions between myocardial properties, size and configuration of the right and left ventricular cavity, transmural pressure, and wall thickness. Heart rate elevations have a significant effect on diastolic filling because narrowed diastolic periods may result in one merged wave, rather than an early E-wave and a late A-wave of diastolic filling. Rhythm disturbances may also have a profound impact, such as the loss of the atrial contraction A-wave in atrial fibrillation. Atrial hemodynamic factors are likewise important: increased atrial pressures tend to amplify the early diastolic E-wave, which can mask (“pseudonormalization”) delayed relaxation dynamics [2]. Impaired atrial contraction obviously diminishes the contribution of the A-wave to filling.

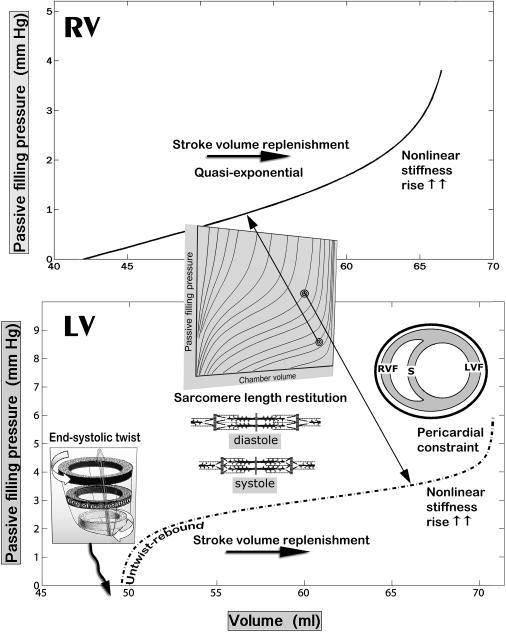
Elevated intrathoracic pressures and pericardial restraint [2,14], diminished venous return to the right ventricle during a sustained Mueller maneuver in humans resulting from a collapse of the great systemic venous trunks at the thoracic inlets [30], and other factors can also impair diastolic filling. The systemic venous collapse at the superior and the inferior thoracic apertures through application of downstream suction—negative intrathoracic pressure during the Mueller maneuver—is akin to the collapse of a wet straw when trying to drink through it [2]. Impaired diastolic ventricular filling can also reflect the direct mechanical effects of contralateral ventricular distention, since the ventricles share a common septum and, therefore, the filling of one influences the distensibility of the other, a phenomenon known as direct diastolic ventricular interaction [4,31,32]. Diastolic ventricular interaction can be exaggerated in atrial or ventricular septal defects [33]. This sort of interaction is markedly increased when the restriction exerted by the surrounding pericardium is raised (see insert in Figure 2, bottom). Growth of the pericardium and its volumetric capacity can be a compensatory epigenetic adaptation mitigating pericardial constraint in chronic cardiac enlargement [14].

Fig. 2.

Representative RV and LV P_f–V relationships. The lower panel shows a distinctly sigmoidal LV P_f–V relationship. The top panel shows an RV P_f–V relationship that could also be fitted with an exponential model; its shape, however, can also be viewed as corresponding to the upper, convex to the abscissa, portion of an overall sigmoidal curve (See Fig. 1). Such curves belong to the ensemble of sigmoidal diastolic P_f–V trajectories in Fig. 1 b

Assessment of passive filling pressure

The processes occurring during the early diastolic filling period are generally neither purely passive nor purely active [11,12,20,34–37]. Measured pressures and myocardial stresses have been found to continue to decline well into the filling phase as relaxation is not generally complete at AV valve opening. Depending on applying normal or abnormal lusitropic states, relaxation of the myocardium has been shown to influence filling dynamics through variable portions of the diastolic filling phase.

Pasipoularides' diastolic relaxation–passive filling pressure (RPF) model for the left and right ventricles [11,12,20,37] separates the total measured ventricular diastolic pressure into components of a decaying active relaxation pressure, P_r, and a rising passive filling pressure, P_f, independent of active myocardial stresses and the factors that influence them. This model of additive passive and active components is in agreement with classic muscle mechanics concepts [38–40] encompassing a passive elastic element (PE) in parallel with the active contractile element (CE). Strain rate-dependent viscous effects are not included in this model because strain rate-dependent myocardial resistance to stretch is minimal or absent ordinarily and is overshadowed by relaxation processes [12,41].

Mitral occlusion experiments in dogs and humans undergoing mitral valvuloplasty have shown that measured diastolic pressure decays more slowly in filling beats than in non-filling beats [12,41]. This is to be expected in the context of the RPF model and reflects the development (in the filling beats) of the passive filling pressure. It has been shown that a load dependence of relaxation is manifested only when elongation of heart muscle occurs at or soon after the peak of the contraction, when the applying rates of active tension decay are high, and is negligible when the rates of decay are low [42–44]. A load independent relaxation after mitral valve opening, postulated in the RPF model, is associated with the then applying low rates of decline of the relaxation pressure since the instantaneous rates of decay of an exponential are proportional to its applying decaying values [12,22].

Although many different methods had been used to gauge diastolic function and ventricular compliance before its introduction, the RPF model is the only method able to characterize RV and LV pressure–volume relations and compliances over the entire diastolic filling period. Confirmation of its validity was provided independently by the elegant clinical investigations of Paulus and his coworkers [41]. Prior to it, simple indices such as end-diastolic pressure and volume were commonly used to appraise diastolic function and its abnormalities. However, such indices at best carry only limited information because they pertain to only one or a few points during diastole. Moreover, in order to ostensibly exclude contractile decaying forces, only the latter part of diastole was considered; consequently, important factors in early filling were completely ignored. This remains an area of some controversy [45]. Conversely, diastolic passive filling pressure–volume relations obtained by Pasipoularides' RPF model [11,12] exemplify passive diastolic properties of the right and left ventricular chambers and ventricular myocardium throughout the entire filling period. This has allowed evaluation of the roles of interacting active-and-passive dynamic factors affecting diastolic dynamics in numerous studies, extending to the present [2–4,6,20,21,26,34–37,41,45–49].

Sigmoidal model for ventricular passive filling pressure vs. volume relationships

The passive filling pressure–volume relationship can be approximated by conventional exponential or innovative sigmoidal curve-fit functions. In both the RPF–exponential and the RPF–sigmoidal approaches, the passive filling pressure vs. volume plots are obtained using not the measured (total) diastolic ventricular pressure but, rather, the passive filling (P_f) pressure. Accordingly, the external (pericardial/intrathoracic) pressure becomes irrelevant; it drops off when subtracting the relaxation (P_r) pressure from the measured total pressure to get the needed passive filling, P_f, pressure; details are to be found in previous publications [4,29].

Following assessment of the passive filling pressure by the RPF model, diastolic cardiodynamic measurements can be analyzed by the companion sigmoidal pressure–volume model (SPV) for the passive filling pressure vs. volume relationship (Eq. 1) and the consequent myocardial compliance formulations [2,37,50].

$${\mathrm{P}}_{\mathrm{f}}=-\mathrm{B}+\sqrt{\frac{\mathrm{A}}{\mathrm{C}}-\frac{1}{\mathrm{C}}\ln [\frac{{\mathrm{K}}_2}{{\mathrm{V}-\mathrm{K}}_1}-1]}$$ (Eq.1)

The 3 panels in part a of Figure 1 demonstrate graphically how the shape of the sigmoidal P_f–V curve-fit at small chamber volumes corresponds to the shape of an increasing but concave to the volume axis exponential and at higher operating volumes and pressures to the shape of an increasing but convex to the volume axis exponential (left panels). Concave connotes that the increase in distending pressure required by a one-unit increase in chamber volume becomes progressively smaller with increasing volumes. Convex means that the increase in distending pressure required by a one-unit increase in chamber volume becomes progressively larger as volume approaches its “ceiling.” This sequential juxtaposition emphasizes that different dynamic mechanisms apply over the successive operating volume ranges during the diastolic filling process. Obviously, the sigmoidal curve-fit function (right top panel) encompasses the entire diastolic P_f–V range. Equally remarkable is that, as shown in part b. of Figure 1 (right bottom panel), the sigmoidal curve-fit can encompass a wide ensemble of P_f–V curve shapes by appropriate adjustment of the estimates of its parameters displayed in Eq. 1: A, B, C, K₁ and K₂.

Fig. 1.

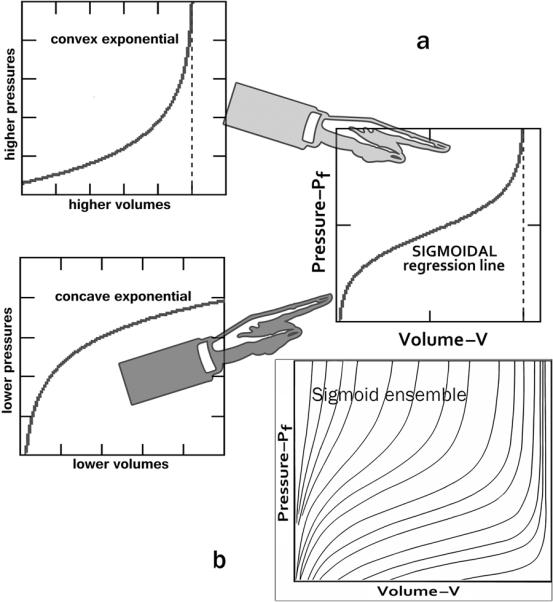
a The shape of the sigmoidal curve at lower chamber volumes and pressures corresponds to the shape of an increasing but concave to the volume axis exponential function and at higher operating volumes and pressures to the shape of an increasing but convex to the volume axis exponential function (left panels). Concave means that the increase in distending pressure required by a one-unit increase in chamber volume becomes progressively smaller with increasing volumes. Convex means that the increase in distending pressure required by a one-unit increase in chamber volume becomes progressively larger. This sequential juxtaposition emphasizes different dynamic mechanisms applying over the successive operating volume ranges. The sigmoidal curve-fit function (right panel) encompasses the entire P_f–V range. b Representative ensemble of sigmoidal diastolic P_f–V trajectories

Notably, sigmoidal curve-fitting has found wide applicability in many areas of medical research, from cardiomyocyte force–sarcomere length relationships at different free [Ca⁺⁺], to pulmonary P–V curves and lung compliance. As regards the sigmoidal curve-fit shapes (see ensemble in part b. of Figure 1), there are many different mathematical functions available to produce them; thus, in an insightful paper in Circulation, Stefanadis et al. [51] applied a polynomial regression line to curve-fit clinical aortic pressure–diameter data, which they also label a sigmoidal relation. The substantive point is that it is the sigmoidality (versus exponentiality) in P_f–V data that matters and should be “captured” by the curve-fit parameters, rather than the particular function utilized. An appropriate sigmoidal function conveniently encapsulates details of the information provided by observations on a subject or experimental animal into a small set of estimated curve-fit parameters, which can be interpreted physiologically and used to derive underlying relevant physiological mechanisms or attributes.

The integrated RPF-SPV paradigm allows the evaluation of chamber and myocardial passive properties using data from the entire filling period of any single heartbeat of interest, just as the earlier exponential and biexponential (bilinear passive stiffness–stress plots) approaches [11,12]. However, the sigmoidal model provides a more accurate fit to the data and is more sensitive [37] to changes in the pressure-volume curve than the exponential. The parameters K₁ and K₂ determine the upper (V_upper) and lower (V_lower) volume limits of the entire sigmoidal curve (see Figure 1, right). V_upper corroborates the strong recruitment at high distending pressure levels of very stiff fibrocollagenous composite wall elements, including overextended intracellular cytoskeletal structural proteins [21], and the pericardial constraint referred to earlier (see insert in Figure 2, bottom). Parameters A and C (in Eq. 1) adjust the curvature, as indicated in Figure 3. Most importantly, the parameter B vertically shifts the sigmoidal curve and determines what portion of the curve and how much of its true sigmoidal overall shape is manifest above the abscissa (zero-P_f level); i.e., a high value of B shifts the whole curve downward, so that only its quasi-exponential upper portion is seen, as is indicated in Figure 4 [37,50]. Furthermore, as is indicated in Figures 1 & 2, at lower operating endsystolic volumes along any given LV P_f–V trajectory, the dynamic relationship assumes an all the more sigmoidal, rather than exponential, appearance.

Fig. 3.

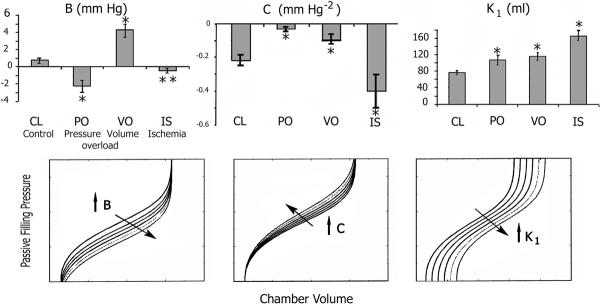
Top: Experimental RV disease modalities induce significant changes in parameters B, C, and K₁ of the sigmoidal model. Bottom: the impact of individual parameter changes on the overall shape of the sigmoidal curve. Left: an increase in B results in a submersion of the lower portion of the curve; the portion of the sigmoidal curve remaining above the abscissa may then resemble an exponential. Middle: an increase in C results in a rise with leftward rotation of the middle portion of the curve without altering the position of the asymptotes; the slope dP_f/dV undergoes changes along the curve, implying alterations in compliance. Right: an increase in K₁ results in a horizontal, rightward displacement of the entire curve to higher operating volumes [Adapted from Pasipoularides et al. [37], with permission of the American Physiological Society]

Fig. 4.

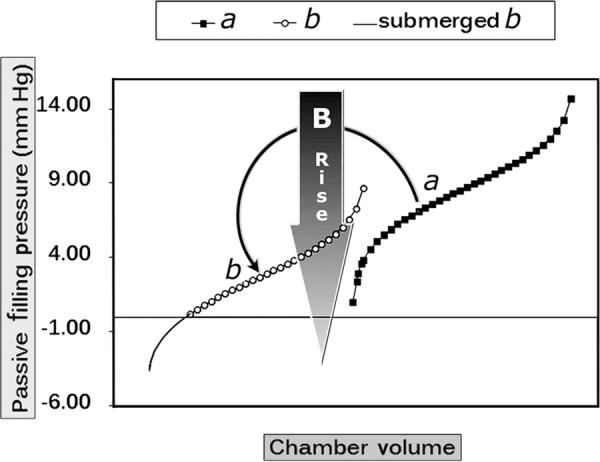
RV and LV diastolic pressure–volume relations: more than meets the eye! A rise in parameter B of a sigmoidal curve can displace it downward as is shown, from a to b; the portion of the overall sigmoidal P_f–V relation that emerges above the abscissa and is actually manifested may then appear to be quasi-exponential

Ventricular chamber and myocardial compliance concepts

Instantaneous diastolic compliance values are not amenable to direct experimental compilation during the filling process. A compliance index (dV/dP_f) can be derived from the sigmoidal equation for P as a function of chamber volume (Eq. 1) by first recasting it in terms of its inverse sigmoidal equation for chamber volume V as a function of P_f, and by then taking the derivative of V with respect to P_f [37,50]:

$$\frac{\mathrm{dV}}{{\mathrm{dP}}_{\mathrm{f}}}=\frac{2\cdot {\mathrm{K}}_2\cdot \mathrm{C}\cdot ({\mathrm{P}}_{\mathrm{f}}+\mathrm{B})\cdot {\mathrm{e}}^{\mathrm{A}-\mathrm{C}{({\mathrm{P}}_{\mathrm{f}}+\mathrm{B})}^2}}{{\left(1+{\mathrm{e}}^{\mathrm{A}-\mathrm{C}{({\mathrm{P}}_{\mathrm{f}}+\mathrm{B})}^2}\right)}^2}.$$ (Eq.2)

As a general rule, the derivative of any sigmoidal function will be bell- or bump-shaped, rising and falling very slowly at the start and end of the process to which it pertains and exhibiting higher values and a maximum in-between. Conversely, the integral of any smooth, positive, bump-shaped function will be a sigmoidal curve. The maximum of the derivative (Eq. 2) corresponds to the inflection point of the sigmoidal P_f–V curve.

From Eq. 2, we can next obtain the RV and LV chamber compliance, CC=dV/(V_wdP_f), by dividing dV/dP_f by the wall (myocardial) volume, V_w [37]. CC is a mechanical attribute of the chamber as a hollow expandable structure, and can be employed to accurately compare the distensibility of different ventricles over comparable filling pressure ranges. Similarly, the myocardial compliance, MC=dV/(VdP_f), which is an index characterizing myocardial (wall-tissue) extensibility, is estimated by dividing dV/dP_f (Eq. 2) by the chamber volume, V [37]. MC can be utilized to accurately compare the passive extensibility of the myocardium (wall tissue) of different ventricles over any applying filling pressure range of interest. The need to plot MC versus the applying filling pressure, P_f, in order to properly compare different myocardial wall extensibilities, arises because of its strong dependence on operative pressure (preload) levels, as was indicated in introducing the compliance concept.

The preceding operational approach to ventricular and myocardial compliance formulations and its rationale have been previously established [4,37,50]. Only micromanometric RV and LV diastolic pressure and angiocardiographic, 3D-echocardiographic, or multimodal imaging dynamic geometric measurements are needed [2,52,53]. In the clinical setting, such a simplified approach is far more expedient than application of stress–strain relationships, which require extremely sophisticated geometric measurements and mathematical models, especially in the right ventricle or with complicated, abnormal LV geometries [4,23,24,54].

RV and LV P_f–V relationships

Even though, excluding the early filling segment, diastolic pressure-volume curves may appear exponential, it does not follow that the entire diastolic pressure–volume relationship (including early filling) must be exponential (cf. Figure 1). In fact, the a priori imposition of an exponential model, as commonly practiced, causes important shifts and shape changes of the diastolic P_f–V curve to be missed. On the contrary, such changes are captured in corresponding alterations of the sigmoidal curve parameters (Eq. 1). As is shown in Figure 2, bottom, when P_f is plotted against V throughout the diastolic filling period, a sigmoidal relation is observed for the left ventricle. At its mid-to-upper pressure and volume ranges, the P_f–V relation appears somewhat exponential, as it is commonly assumed to be. However, at the lower volume range of the early filling stage the curve is concave toward the abscissa [37,50]. The phenomenon could be related to the inflation of a thick-walled balloon, in which sufficient pressure must be built-up before the walls begin to distend. This sigmoidal shape is not surprising in light of discovering of similarly shaped pressure-volume relations for the aorta of humans in an intensive care unit (ICU) setting by Heerman and his collaborators [55], who emphasized the similarity of their findings to those of Pasipoularides et al. in animal models of cardiac disease [37].

Advantages of the sigmoidal over exponential curve-fit parameters

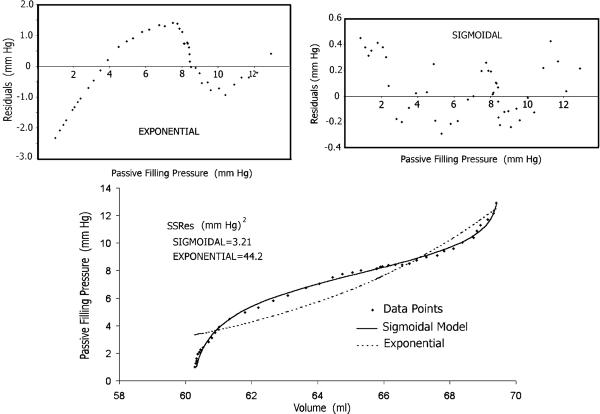
As is shown in Figure 2, top, and expounded in Figure 4, the right ventricular P_f–V relationship appears to be more exponential in shape, but the operating range of the RV data actually corresponds to the upper portion of a comprehensive sigmoidal curve-fit. This observation can be confirmed by comparing the curve-fit of the P_f–V data using an exponential with the curve-fit using the sigmoidal equation; the accuracy is significantly better for the sigmoidal curve-fit, based on the residuals and standard deviations of the residuals of the sigmoidal or exponential curve-fits [37,50].

Residuals are the deviations of the data points from the fitted curve; the residuals plots provide insight into the quality of the fitted curve. As revealed by inspecting the corresponding plots in Figure 5, the residuals of the exponential (but not of the sigmoidal) curve-fit are characterized by a strong correlation of sequential observations, implying a nonrandom distribution of the residuals; note the different scales of the ordinates in these plots. This correlation indicates that a systematic effect is neglected by the exponential model but not by the sigmoidal. Generally, if the model curve fits the data well, one expects the data-point deviations to be randomly distributed around the fitted curve, as is the case with the sigmoidal curve-fit. On the contrary, the exponential model needs improvement. In considering residuals amounting to a few mm Hg, it is important to bear in mind two pertinent considerations: in tricuspid stenosis we recognize that a pressure gradient of 5 mm Hg is associated with systemic venous congestion, and the diagnosis of tricuspid stenosis is done on the basis of an atrioventricular mean gradient of only 2 mm Hg [2].

Fig. 5.

Bottom: there is an extraordinarily closer agreement between the P_f–V data points' scattergram and the least-squares fitted curve when the sigmoidal model is used, than with the exponential. The residual sum of squares (SSRes) for the former is smaller by one order of magnitude than for the latter. Top: the residuals of the exponential, but not of the sigmoidal, curve-fit are characterized by a strong correlation of sequential observations; note the different scales of the ordinates in the residual plots. This correlation indicates that a systematic effect is neglected by the exponential curve fit but not by the sigmoidal [Reproduced from Pasipoularides et al. [37], with permission of the American Physiological Society]

Further statistical analysis showed that, in contradistinction to the sigmoidal the simple exponential model was not sensitive enough to detect the important P_f–V alterations arising in experimental animal disease models: these included changes sigmoidality and in relative elevation or depression of the P_f–V data in the midrange operating volumes, leftward rotation, and changes in the derived compliance values [37]. Whereas significant compliance changes from control were detected and quantified in all three RV disease states by the sigmoidal, none was detected by the exponential model [37]. Accordingly, it is preferable to use the sigmoidal model evaluate and compare the passive filling properties of the right and left ventricles.

Quantitative comparison of RV and LV P_f–V curves

A less pronounced sigmoidality of the ventricular P_f–V curves is associated with lower values of wall mass-to-chamber volume (relative wall thickness). The visual differences between right and left ventricular P_f–V relationships are confirmed quantitatively by the parameters that describe the sigmoidal P_f–V curve [37,50,56], which are summarized in Table 1. Comparisons of the sigmoidal parameters, which were identified above in conjunction with Eq. 1 and the associated analysis, reveal significant differences in operating vertical pressure-shift, curvature and shape between the right and left ventricles. In particular, the average value of the pressure-shift parameter B is statistically (P<0.002) substantially greater for the right ventricle, indicating that the RV operating passive filling pressure range corresponds solely to the mid-to-upper portion of an overall sigmoidal curve, whereas the operating range of the left ventricle encompasses most or all of the sigmoidal shape—see Figures 1, 2, and 4.

TABLE 1.

Siamoidal Curve Fit Parameters. [50, 56]

	K1 (ml)	K2 (ml)	A	B (mm Hg)	c (mm Hg−2)
LV	49.3±9.0	21.4±2.2	5.13±1.28	1.64±0.43	0.24±0.07
RV	−12.5±12.6	51.9±12.7	3.23±0.62	9.59±2.11	0.08±0.03
P value	< 0.001	< 0.031	NS	< 0.002	0.043

K₁ and K₂ determine the upper and lower volume limits of the entire sigmoidal curve; A and C determine the curvature; B vertically shifts the curve.

Exaggerated sigmoidality of left ventricular P_f–V relations, in addition to recognizably sigmoidal RV P_f–V relations, as illustrated for a hypovolemic state in Figure 6, panel c, accompany any increase in ventricular end-systolic relative wall thickness. Such P_f–V relations prevail in pressure overload induced concentric hypertrophy and in LV or RV hypertrophic cardiomyopathy [21,57], and also in certain circulatory states characterized by low venous return with hyperdynamic ventricular contraction and greatly diminished end-systolic volumes [21,58]. These states are clinically typified by powerful activation of the sympathoadrenal system with reduced end-systolic chamber dimensions, in a reflex compensatory response to severe hypovolemia [59] accruing from hemorrhage, burns, dehydration from gastrointestinal losses, diabetic ketoacidosis, or excessive sweating, etc.

Fig. 6.

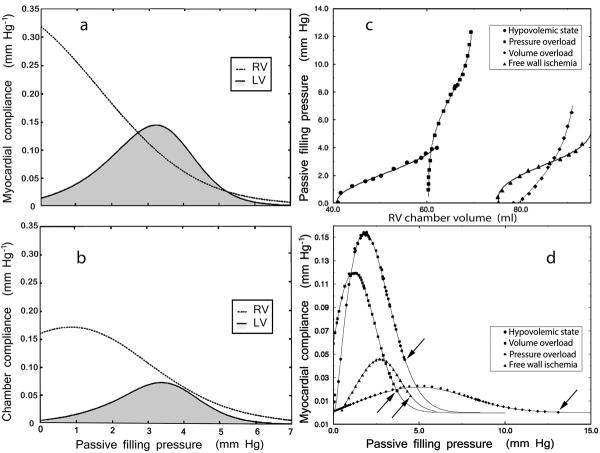
Left panels: myocardial (panel a) and chamber (panel b) normal compliance curves of chronically instrumented pigs plotted against the ventricular passive filling pressure for both the right (dotted line) and the left (solid line, shaded) ventricle. Right panels: characteristic shapes of RV P_f–V relationships (panel c) and corresponding global curves of RV myocardial compliance (panel d) under hypovolemic conditions, and during surgically created subacute (2–5 wk) states of pressure overload, volume overload and RV free wall ischemia in chronically instrumented dogs; arrows identify the end-diastolic data points.

It is a key quantitative feature of the sigmoidal model that lowered RV end-systolic chamber dimensions with increased relative wall thickness bring about a statistically substantial decrease from control in the pressure-shift parameter B, along lines typified by an experimentally induced RV pressure overload (PO). This is associated with a shift from quasi-exponential to a distinctly sigmoidal P_f–V curve-shape, as the RV P_f–V curve becomes less submerged than normal below the abscissa (see Figure 4) [37]. Effectively, the RV P_f–V curve becomes more like the LV P_f–V curve, as is illustrated in the RV PO example in Figure 6, panel c. Conversely, in the eccentric hypertrophy of an LV volume overload (VO), a change in the P_f–V relation accrues from the increased operating chamber volume, which causes a reduction in relative LV wall thickness. This reduction makes the left ventricle more compliant during early diastole as is exemplified in Figure 4 in the submersion of the overall P_f–V curve below the abscissa. In RV free wall ischemia (IS) there is, on one hand, an increase in the operating volumes (i.e., reduction in end-systolic relative wall thickness), resulting in a submersion of the P_f–V relation. On the other, previous studies [4,34] have shown that regional hypertrophy eventually ensues under ischemia, as nonischemic muscle compensates for pumping capability lost due to ischemic wall regions. On balance, in our disease model of IS there was a statistically significant elevation of the P_f–V relation with reduced sigmoidal parameter B [37].

Evidently, the configuration and placement of the diastolic P_f–V curves on the coordinate plane are important in determining the filling properties of the right and left ventricular chambers [4]. As discussed above, one important advantage of using the sigmoidal equation to model the P_f–V relationship is the inclusion of the pressure-shift parameter B, which determines the vertical position of the overall curve. An upward shift (decreased B), indicates that a higher atrial pressure is required to fill the ventricle, regardless of applying chamber compliance or myocardial effective distensibility.

The parameter B may be used in future applications to quantify vertical parallel shifts of the P_f–V curve associated with intrathoracic blood volume swings, pathologic conditions (e.g., COPD, bronchial asthma) affecting intrathoracic pressures, or augmented diastolic pericardial–ventricular interaction. In addition, the sigmoidal model parameter K₁ can allow for horizontal shifts of the P_f–V curve—taken as a whole—along the volume axis, while maintaining more or less unaffected its overall shape and the values of its other physiologically significant parameters, including B (see Figure 3). An increase in K₁ indicates that the right or left ventricle has increased its preload in an effort to maintain pumping, a manifestation of the Frank-Starling mechanism. Under RV PO and VO, the sigmoidal model parameter C increased. This indicates a counterclockwise rotation of the P_f–V curves in the midrange of operating volume (Figure 3). In IS, C decreased, indicating a clockwise rotation of the P_f–V relation over the same range. It should be noted at this juncture that the precise impact of any individual sigmoidal parameter on the global shape of the P_f–V curve actually depends not only on its own value, but also on the values taken by the other sigmoidal model parameters; this is generally the case with nonlinear systems and equations, such as Eq. 1, and has been previously discussed in depth [37].

Assessment of ventricular chamber and myocardial compliances

As explained in the section on Ventricular chamber and myocardial compliance concepts, ventricular chamber compliance is different from myocardial compliance. Chamber compliance is a measure of the capacity of the ventricle to distend under pressure and is dependent not only on myocardial compliance but also on ventricular size and geometry. Conversely, myocardial compliance specifies only the susceptibility of the myocardium to stretch when it is subjected to physiological distending wall stresses and is a material property of RV and LV muscle.

Since the evaluation of compliance at a single pressure and volume point cannot adequately describe either ventricular or muscle compliance, which depend strongly on the applying chamber pressure and volume levels, examination of the compliance curves over the entire pertinent diastolic pressure and volume ranges is required [4,12,22–24,37,50]. The need to evaluate and compare compliance curves (and not single numerical values) over the entire applicable diastolic pressure and volume range arises because filling is a process that has much greater temporal duration than any single point along its progression, regardless of how it is chosen. As shown in Figure 6, panels a, b and d, throughout the diastolic filling process there are gradual but substantial, nonlinear changes in compliance characteristics, which cannot be captured adequately by considering in isolation just 1 or a few points—“cinematographic frames”—sliced-out from the overall trajectory of the process unfolding under the applying physiologic or pathologic conditions.

Since compliance is a purely passive property, prior to the introduction of Pasipoularides' RPF model [11,12] methods for estimating ventricular compliance from pressure–volume relations had ignored early diastolic properties, because the processes going on during this early diastolic period are neither purely passive nor purely active. Furthermore, they had relied on the, at times problematic, assumption that myocardial contractile forces have invariably decayed to negligible levels in the latter part of diastole. However, when the RPF model is used to calculate the passive filling pressure and the RV or LV P_f–V curves, myocardial and chamber compliance lines (with the exponential P_f–V model) or curves (with the sigmoidal P_f–V model) can be evaluated in the beating ventricle over the entire applying diastolic filling period and for the overall filling process. As is shown in Figure 6, panels a and b, quantitative comparison of the representative right and left ventricular compliance curves reveals that both myocardial and chamber RV compliances at the onset of filling are significantly higher than their LV counterparts. This indicates that the right ventricle can begin to expand with just a small incipient rise in its filling pressure, P_f. In contrast, at small end-systolic chamber volumes, the left ventricle requires a higher P_f buildup to generate sufficient tensile stresses in its walls before it can begin to enlarge.

Molar (large-scale) wall twist-untwist and micro-and-submicroscopic (small-scale) cardiomyocyte and ECM deformation-and-rebound processes

Swift restitution of the “released configuration” of twisted/deformed myocardial wall elements from their end-systolic arrangement ensues with the ongoing active relaxation of the right and left ventricular myocardium, and the rise of ventricular P_f with forward AV valve leaflet displacement, initially, and valve opening, subsequently. These events underlie the initial phase of increasing LV chamber and myocardial compliances up to their maxima, depicted in Figure 6, panels a and b. The organized larger-scale twist-untwist process and smaller-scale strain-energy storing-and-release mechanisms, which have been recently described elsewhere [21], are factors abetting initiation and development of early-diastolic LV filling. Essentially, the preceding active systolic contraction deforms the myocardial wall to some end-systolic high-energy conformation. Removal of the contractile wall-stresses is then equivalent to specifying a different target-metric for the low-energy configuration sought by the rebounding LV wall [21,37].

The behavior evident in the initial (lower-volume) portion of the sigmoidal LV P_f–V curve may also be interpreted, in part, as a manifestation of LV wall untwisting [21] and viscoelastic creep [2,37]; both of these factors abet early-diastolic filling by increasing LV compliance.

Normal right and left ventricular compliance comparisons

The initial phase of wall rebound and swiftly increasing LV myocardial and chamber compliances is followed by gradual wall-stiffening and decreasing left ventricular CC and MC with progressive distention, as is shown in Figure 6, panels a and b. These panels illustrate representative compliance curves for both the right and the left ventricles, plotted over the appropriate filling pressure range for comparison of pertinent dynamic characteristics [4,12,22,24,37,50]. The RV CC is normally near its maximum at P_f 0 and, after a transient small rise attributable to untwist/rebound processes, akin to albeit much milder than their left-sided counterparts, decreases monotonically but nonlinearly with increasing P_f [37]. This is to be expected because, in absence of concentric hypertrophy, RV P_f–V relationships typically correspond only to the portion of the sigmoidal curve which lies above the concave to the abscissa early-diastolic portion—see Figures 1, 2, and 4.

Table 2 complements panels a and b of Figure 6, and presents quantitative comparisons of RV and LV compliance curve characteristics [37,50,56]. At P_f 0, both MC and CC are substantially greater for the right than the left ventricle. Normally, maximum chamber compliance is substantially higher for the right ventricle because it is thin-walled; since for a given chamber volume a lower filling pressure is required than for the LV, P_f at maximum CC is considerably lower in the right than the left ventricle. On the other hand, there is no statistically significant difference between the maximum myocardial compliances because the muscle material properties are comparable in the two ventricles. Similarly, no statistically significant difference is found in the end-diastolic MC and CC in the left and right ventricles, because at end-diastole the myocardium is stretched to near its limit, while its compliance and that of the chamber are both approaching zero in both sides of the heart.

TABLE 2.

Compliance Curve Characteristics. [50, 56]

	MC0	CC0	MCmax	CCmax	Pf | Cmax	MCed	CCed
LV	0.006±0.002	0.003±0.001	0.218±0.060	0.121±0.028	3.78±0.65	0.008±0.003	0.047±0.025
RV	0.313±0.084	0.217±0.046	0.343±0.074	0.259±0.030	0.64±0.29	0.008±0.002	0.012±0.003
P value	< 0.002	< 0.001	NS	< 0.004	0.001	NS	NS

MC₀, myocardial compliance at P_f = 0; CC₀, chamber compliance at P_f = 0; MC_max, maximum myocardial compliance; CC_max, maximum chamber compliance; P_f | _Cmax passive filling pressure (mm Hg) at maximum compliance; MC_ed end-diastolic myocardial compliance; CC_ed, end-diastolic chamber compliance; all compliances are in (mm Hg)⁻¹.

Clinical implications of myocardial compliance changes

Studies on chronically instrumented awake dogs, utilizing the sigmoidal paradigm [20,37] in subacute (2–5 wk), surgically induced RV disease, showed that the passive compliance of RV muscle changed significantly as a result of PO, VO, and IS. As explained in the section on Advantages of the sigmoidal over exponential curve-fit parameters, whereas significant changes from control were detected and quantified in all three RV disease states by the sigmoidal, none was detected by the conventional exponential model [37]. In VO, a significant increase in operating end-diastolic compliance was observed, while the level of end-diastolic pressure remained unchanged. This is consistent with the increase in parameter C observed in the P_f–V relations, which causes a counterclockwise rotation of the sigmoidal curves in the midrange of operating volume, as was described above (Figure 3); it is accompanied by a reduction in the slope of the final segment of the P_f–V curve and an ensuing higher end-diastolic compliance (see Figure 6, panel d). Because of this compliance augmentation in VO, there may be less of a tendency to elevate central venous pressure levels than in PO or IS. In contrast to control conditions, for which the signs of the sigmoidal parameter B in individual animals were mixed, individual values for B in VO were uniformly positive (depression of the overall P_f–V curve); this finding is in even sharper contrast to PO, in which B was uniformly negative (upward shift of the P_f–V data). In VO due to tricuspid regurgitation it may be the regurgitant tricuspid flow (v-wave) itself that can directly elevate central venous pressure and impair forward stroke volume.

PO and IS resulted in decreased maximum myocardial compliance. Decreased maximum RV myocardial compliance in early diastole will have the direct clinical consequence of increasing central venous pressure and, in turn, decreasing cardiac output. Both of these effects will be exacerbated with tachycardia. Since the P_f–V relations were shifted upward in PO, the pressure levels applying at maximum myocardial compliance and at end diastole were both significantly increased, again tending to elevate central venous pressure.

As noted in the introductory section on Compliance, the depression of myocardial compliance in pressure overload is associated, in part, with fibrosis involving the ECM, especially in the subendocardial regions [4,12,21,24,34]; comparable regional fibrotic changes accompany wall ischemia [8]. The striking drop of myocardial compliance throughout diastolic filling in pressure overload, exemplified in Figure 6, panel d, is striking and likely to have multifaceted subtle and heretofore incompletely characterized consequences. When the ECM stiffens, its biomechanical and supplementary physical properties change and affect cardiomyocyte and other myocardial cells' functions, through cytoskeleton-based rigidity-sensing mechanisms [21,60]. Likewise, stretch-activated cell membrane ion channels (SACs) serve as myocardial mechanotransducers coupled to signaling cascades and thereby initiate the complex short- and longer-term adaptive responses of cardiomyocytes and the heart to stretch. Consequently, details of ECM alterations reflected in changes in sigmoidal model myocardial compliance parameters can be significant in modern therapeutics: they could have intriguing modulatory effects on patterns of gene expression and on stem cell proliferation rate and fate [61,62].

Conclusions

The integrated RPF–sigmoidal paradigm allows the evaluation of chamber and myocardial passive properties using subject-specific right and left ventricular micromanometric and volumetric data from the entire filling trajectory corresponding to any heartbeat(s) of interest, just as its predecessor, the RPF–exponential approach. The RPF–sigmoidal methodology can characterize dynamic RV and LV passive filling pressure–volume relations using a sigmoidal function. The chamber and myocardial compliance curves of both right and left ventricles can be computed by the sigmoidal methodology over the entire filling period and plotted over the appropriate filling pressure ranges. Important characteristics of the compliance curves can be examined and compared between the right and the left ventricle and for different physiological and pathological conditions, to assess right and left ventricular function and the effects of therapeutic interventions. The sigmoidal curve-fit parameters and derived compliance characteristics allow more accurate quantitative assessment of RV and LV diastolic properties and filling dynamics under different pathophysiologic conditions than the predecessor RPF–exponential approach. The sigmoidal paradigm is, therefore, a superior alternative to the exponential approximation.