Micro and nano MgO particles for the improvement of fracture toughness of bone-cement interfaces

Abstract

The objective of this study was to determine whether inclusion of magnesium oxide (MgO) in micro and nanoparticulate forms in poly Methyl MethAcrylate (PMMA) cement has any influence on the fracture toughness of bone-cement interfaces. An interfacial fracture mechanics technique was used to compare the values of fracture toughness (K_IC) among bone-PMMA, bone-PMMA with micro MgO particles and bone-PMMA with nano MgO particles interfaces. This study found that the values of K_IC of bone-PMMA with micro MgO particles and bone–PMMA with nano MgO particles interfaces were significantly higher when compared to the values of K_IC of the bone-PMMA interface (p<0.0001). Results indicated that the addition of the micro and nano MgO particles to PMMA improved the quality of bone-cement union.

1. Introduction

The fracture mechanics at the bone-cement interface is a critical issue for the cemented implant fixation. Several research groups reported improvements of PMMA cement strength, osteoblast cell growth, and surface roughness properties by incorporating additives such as MgO, hydroxyapatite, chitosan to PMMA (Heo et al., 2007; Lewis, 2008; Liu and Webster, 2007). The effects of these additives to PMMA on the mechanical strength of bone-PMMA interfaces are unknown. Our study found that MgO is one of the most suitable additives to PMMA, since osteoblast cell adhesion to the MgO included PMMA specimens was significantly higher than the cell adhesion to PMMA cement only specimens (P<0.001) and no significant change of mechanical strength was observed due to the addition of MgO to PMMA (Khandaker et al., 2011a). Ricker et al. (Ricker et al., 2008) demonstrated that compared to micro particles, PMMA with nanoparticles of MgO reduced harmful exothermic reactions of PMMA during solidification and increased radiopacity. The suitability of incorporating micro and nanoparticles of MgO additives to PMMA for orthopedic applications necessitates estimating the K_IC of the respective bone-cement interfaces. The scope of work for this study was to quantify elastic properties (Young’s modulus, E and Poisson’s ratio, υ) of PMMA, PMMA with micro MgO particles and PMMA with nano MgO particles cements, and to determine the fracture toughness, K_IC, of bone-PMMA, bone-PMMA with micro MgO particles and bone-PMMA with nano MgO particles interfaces. Several researchers investigated the nominal strength of bone-PMMA interfaces where no defects were introduced in the test specimen (Mann et al., 2001; Wood et al., 2000). This study used a fracture mechanics technique developed by Wang and Agrawal (Wang and Agrawal, 2000), since it is a more fundamental and meaningful estimation of interface fracture toughness of bone-cement than nominal strength measurement technique used by the previous authors. Cortical bone was used in place of trabecular bone (Graham et al., 2003) in the test specimen to reduce variability of test results due to bone porosity.

2. Materials and Methods

2.1. Sample preparation

Cobalt^™ HV bone cement (CBC) (Biomet Inc., Warsaw, IN) was used as the PMMA cement. Micron MgO (Sial) and nanometer MgO (Aldrich) particles were purchased from Sigma-Aldrich. Their particle size distributions were measured by Microtrac Inc. (Montgomeryville, PA) Nanotrac S3500 and Ultra instruments, respectively. According to manufacturer recommendations, CBC specimens were prepared by hand mixing 2.2 grams of PMMA powder with 1.1 ml of methyl methacrylate (MMA) monomer using powder: monomer ratio of 2:1. Ten wt% (0.22 gram) of micro and nano MgO particles were mixed with 1.98 grams of PMMA beads to prepare PMMA with micro MgO particles (mCBC) and PMMA with nano MgO particles (nCBC) cements, respectively. The mixers were added with 1.1 ml of MMA monomers maintaining the same powder: monomer ratio of 2:1 for the preparation of mCBC and nCBC samples. All samples were cured in a custom made mold (Figure 1) under 60 KPa pressure (clinically applied pressure during orthopedic surgeries (Ries et al., 1998)) to a block of size (22×12×4) mm. Each block was milled to a flat dumbbell-shaped specimen (Figure 2(a)) according to ASTM E855-90 standards (ASTM, 1994). This standard is suitable for the tensile test of a small size biological sample (Athanasiou et al., 2000). Specially, the length to width ratio at the gage section of the specimen is suitable for the tensile stage (accommodation for maximum 24 mm long sample) and the microscope used in this study.

Figure 1.

Fabricated mold used for the preparation of cement and bone-cement specimens. The base plate contains (22×12×25) mm curing chamber, which has front, back and top openings. Two ABS plastic blocks were used to cover the front and back sides of the chamber. A custom made clamp was used to restrict the side blocks movement. The top plate can slide freely to the curing chambers using 4 round rods. The top plate has (22×12×23) mm extruded block at the center that can close the top side of the curing chamber and apply pressure during curing. A set of weights were placed at the top plate to provide 60 KPa pressure (Ries et al., 1998). Variable thickness of cement blocks (22×12×2~10 mm) were successfully cured using the mold.

Figure 2.

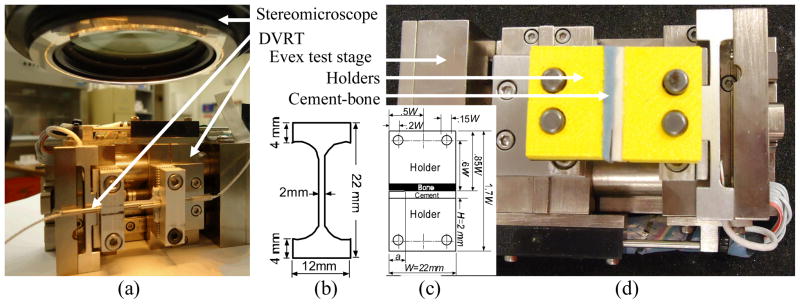
(a) Tension test on a flat dumbbell-shaped cement specimen to measure the Young’s modulus and Poisson’s ratio of the cement specimen. Evex tensile stage, microstrain Inc. displacement variable reluctant transducer, and Nikon stereo microscope was used to record load, longitudinal displacement and transverse displacement during the experiment, (b) the schematic diagram and dimension of the flat dumbbell-shape specimen. The depth of the specimen is 4 mm, (c) the schematic diagram and dimension of the single edge sandwiched bone-cement specimen. The depth of the holder and specimen is 12 mm, and (d) tension test setup for the measurement of the interface fracture toughness of bone-cement specimen.

To prepare the bimaterial specimen (Figure 2(b)), a fresh bovine femur of unknown age and post mortem period was used. Cortical bone coupon was extracted from the mid-diaphysis of the femur. The coupon was milled to bars of size (22×12×2) mm using a constant cutting speed (1000 rev/min) and feed rate (50 mm/min) to ensure consistent bone surface roughness. The longitudinal axis of the bars was parallel to the longitudinal axis of the bone. The cement was packed and pressurized (60 KPa) on the bone bar in the mold (Figure 1), which was covered (12×6) mm at one of the side edges by a thin plastic sheet. The plastic sheet was accessed through the side blocks in the mold. The plastic sheet was removed manually after curing. Bone-cement samples were carefully glued with two ABS plastic holders (made using Dimension 3D printer) by cyanoacrylate adhesive. The bone bars were maintained wet in saline during sample preparation.

2.2. Experiments and analysis

Tension tests were conducted on the flat dumbbell-shaped and wet bimaterial samples at room temperature and loading rate 0.01 mm/sec using Evex tensile stage (Evex Analytical Instruments Inc., Princeton, NJ) as shown in Figure 2(a) and Figure 2(b), respectively. Young’s modulus, E and Poisson’s ratios, υ, were calculated from three of each CBC, mCBC, and nCBC samples. Load was applied to the cement specimen below elastic limit to measure E and υ values of cements. A displacement variable reluctant transducer (DVRT) (MicroStrain, Inc, Williston, VT) was secured along the gauge length (8~10 mm) to measure longitudinal displacement. A Nikon SMZ stereomicroscope (10x magnification) was used to sequentially capture images at 10 sec intervals to measure transverse displacement at the center of the gauge section. The load from Evex tensile stage, longitudinal displacement from DVRT, and transverse displacement were continuously recorded using Evex nanoanalysis, National Instrument LabView 10.0, and Nikon NIS BR softwares, respectively. The slopes of longitudinal stress-longitudinal strain curves were used to calculate E. The transverse strain was calculated directly by dividing the transverse displacement by the initial width of the specimen. The transverse strains were calculated at 30 and 60 sec test times. Two values of υ were calculated from the ratio of the transverse strains and longitudinal strains for the corresponding test times.

The load and displacement were continuously recorded until the failure of the bimaterial specimens. The K_IC values of bone-cement samples were calculated according to Wang and Agrawal (Wang and Agrawal, 2000) for a 0° loading angle using:

$$K_{IC}=\frac{P_C{\lambda }^{\psi }Y\sqrt{\pi a}}{BW},$$ (1)

where K_IC is the mode I fracture toughness, P_C is the critical load that breaks the interface, and λ is a scale factor determined using:

$$\lambda =\sqrt{\frac{1-\alpha }{1-{\beta }^2}}.$$ (2)

The values of α and β are Dundurs parameters, which estimate the elastic mismatch across the bi-materials interface (Dundurs, 1969), given by:

$$\begin{array}{l}\alpha =\frac{E_1\left(1-{\nu }_2^2\right)-E_2\left(1-{\nu }_1^2\right)}{E_1\left(1-{\nu }_2^2\right)+E_2\left(1-{\nu }_1^2\right)}\\ \beta =\frac{E_1\left(1-{\nu }_2-2{\nu }_2^2\right)-E_2\left(1-{\nu }_1-2{\nu }_1^2\right)}{2E_1\left(1-{\nu }_2^2\right)+2E_2\left(1-{\nu }_1^2\right)}\end{array}$$ (3)

where E₁, E₂, and ν₁, ν₂ are elastic moduli and Poisson’s ratios of the cement and bone, respectively. In Eq.(1), ψ is a correction factor determined using (Wang and Agrawal, 2000):

$$\psi =e^{5.056{(h/W)}^{0.777}},$$ (4)

and Y is a shape function determined using (Wang and Agrawal, 2000):

$$Y=\frac{1}{1-\rho }\sqrt{\frac{0.26+2.65\frac{\rho }{1-\rho }}{1+0.55\frac{\rho }{1-\rho }-0.08{\left(\frac{\rho }{1-\rho }\right)}^2}}$$ (5)

where ρ=a/W. Initial crack length, thickness and width of the specimen are given by a, B, and W, respectively.

The data was analyzed using SAS version 9.1 (SAS Institute, Inc., Cary, NC). The statistical analyses (1-way ANOVA) were performed on the means of the 3 groups for the p-values calculations of experimental parameters (E, υ, and K_IC). The groups were CBC, mCBC, and nCBC for E and v, whereas the groups were bone-CBC, bone-mCBC, and bone-nCBC for K_IC. The average values of E and υ of cements, dimensions and fracture forces of bone-cement specimen were used for the calculation of K_IC. The values of E and υ for longitudinal bovine cortical bone were considered to be 20.4 GPa (Cowin, 2001) and 0.33 (Lasaygues and Pithioux, 2002), respectively. For all statistical analysis, P<0.05 was considered statistically significant.

3. Results and Discussion

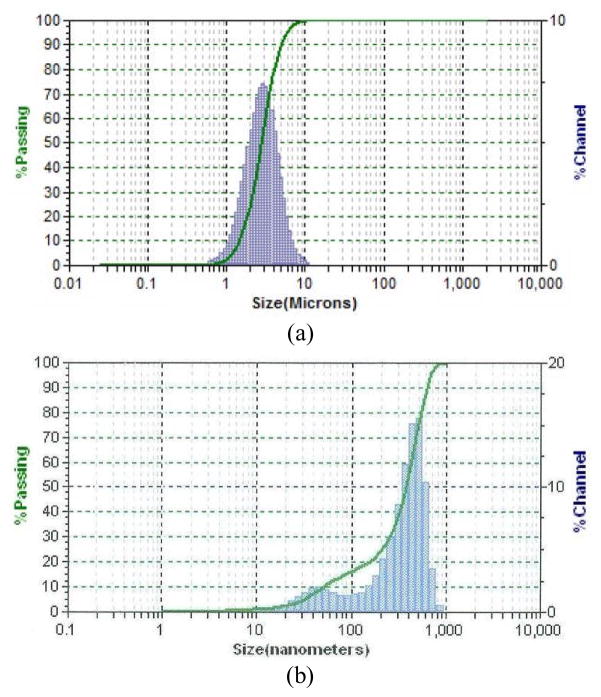
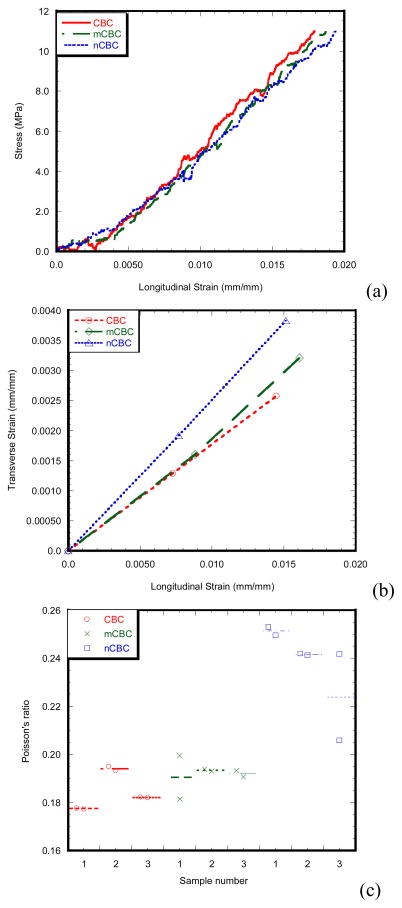
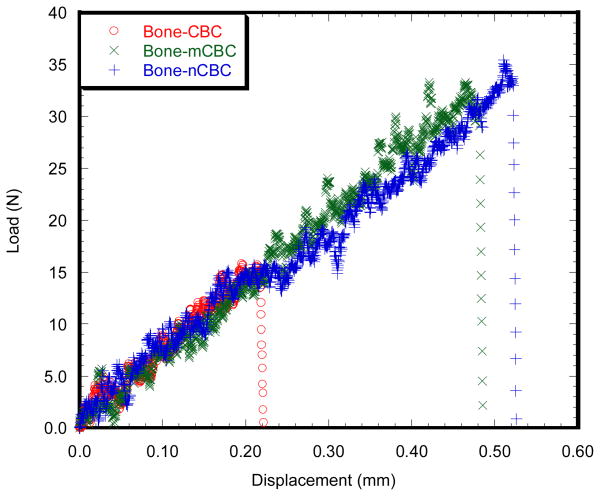
Figure 3 and Table 1 show the particle size distributions and parameters of the micro and nano MgO particles, respectively. It is clear that the sizes of MgO particles are in the ranges of micron and nanometers, respectively. Figure 4(a) and (b) shows the linearity of longitudinal stress-longitudinal strain and transverse strain-longitudinal strain curves of a CBC, mCBC and nCBC specimen, respectively. Figure 4(c) shows the variation of υ values of all tested cement samples. Table 2 reports the E and υ of cement samples. Results show that the variation of E is opposite to the variation of υ due to the incorporation of MgO particles to CBC. Decrease of E values and increase of υ was observed due to the addition of MgO particles to CBC. Figure 5 compares the load-displacement curves of various bone-cement specimens. The load-displacement response of bone-CBC specimens is characterized as elastic response and then sudden failure of the specimen without noticeable inelastic region. Table 3 presents statistics for K_IC of bone-cement specimens. Results show the K_IC (KPa.m^1/2) of bone-mCBC (25.05 ± 5.00) and bone–nCBC (27.24 ± 5.25) interfaces are significantly higher (p<0.0001) when compared to the K_IC of the bone-CBC (9.71 ± 2.23) interface.

Figure 3.

Particle-size distribution of the two MgO powders: (a) (micro size) and (b) (nano size).

Table 1.

Some particle-size parameters and specific surface of the two MgO powders used

Types	D (10)a	Median size, D (50)	D (90)b	Particle size volume average	Particle size number average	Particle size diameter average	Specific surface area (m2/cc)
Micro	1.458 (μm)	2.778 (μm)	4.92 (μm)	3.04 (μm)	1.481 (μm)	2.417 (μm)	2.483
Nano	50 (nm)	382 (nm)	614 (nm)	362 (nm)	4.07 (nm)	116.2 (nm)	51.62

^aD(10) means 10% of the powder particles are smaller than this value.

^bD(90) means 90% of the powder particles are smaller than this value.

Figure 4.

(a) Longitudinal stress vs. longitudinal strain plots of a CBC, mCBC and nCBC specimen. (b) Transverse strain vs. longitudinal strain plots of a CBC, mCBC and nCBC specimen calculated at 30 sec and 60 sec test time. (c) Dot plots of the Poisson’s ratios of three CBC, mCBC and nCBC samples. Plots show the two Poisson’s ratio measurements for each sample at 30 sec and 60 sec test times.

Table 2.

Experimental parameters determined for the tensile test on the flat dumbbell-shaped cement CBC (n=3), mCBC (n=3) and nCBC (n=3) specimen. Results of the 1-way ANOVA indicate a significant difference for the experimental parameters (E and υ).

Experimental parameters	Specimen types			Significance test
	CBC	mCBC	nCBC
Young’s modulus, E1 (Mpa)	740.41 ± 16.41	696.93 ± 16.83	662.02 ± 19.37	P = 0.0124
Poisson’s ratio, v1	0.183 ± 0.002	0.196 ± 0.006	0.239 ± 0.01	P<0.0001

Figure 5.

Load versus displacement graphs of (a) bone-CBC, (b) bone-mCBC and (c) bone-nCBC specimens. The maximum loads for the fracture of the bone-cement specimen were recorded for the calculation of the fracture toughness of bone-cement specimen.

Table 3.

Descriptive statistics of the experimental single edge sandwiched bone-cement specimen data.

Specimen type	No of specimen	Demension of the test specimen				Interface fracture toughness (KPa.m1/2)
		Width, W (mm)	Height, H (mm)	Thickness, B (mm)	Pre-crack length, a (mm)	average	St. dev.	Max.	Min.
Bone-CBC	6	21.48 ± 0.04	1.77 ± 0.16	11.94 ± 0.03	5.38 ± 0.15	9.71	2.23	12.85	6.87
Bone-mCBC	6	21.65 ± 0.29	1.67 ± 0.15	11.95 ± 0.04	5.33 ± 0.18	25.05	5.00	30.04	16.18
Bone-nCBC	6	21.59± 0.13	1.69 ± 0.10	11.98 ± 0.07	5.27 ± 0.15	27.24	5.25	35.24	20.71

This observed result is due to the differences in surface roughness, modulus, and residual stress at the interfaces of bone-cement with MgO in cement compared to that without MgO. Our separate study found that PMMA that contained micro or nano MgO particles possessed greater interface surface roughness as compared to those without MgO (Khandaker et al., 2011b). Increase of surface roughness led to a decrease of micro movement of cracks at the interface of bone-cement, thus increased the load and elongation at the fracture (Figure 5). This behavior is consistent with published research (Ramaniraka et al., 2000; Wang and Tong, 2008; Zelle et al., 2011), where it was found that increased surface roughness helped strengthen the interfacial mechanical properties of bone-cement or implant-cement joints. Cements with micro or nano MgO particles exhibited lower elastic modulus (Table 2) and higher exothermic temperatures while curing (Ricker et al., 2008) compared to those without MgO. The lower modulus cement can diminish local contact stresses at the bone-cement interface (Funk and Litsky, 1998). The residual stresses, caused by the exothermic temperature difference, can influence the fracture energies at the bone-cement interface (Zor et al., 2002). The accumulation of stresses due to modulus and temperature differences at the interface of bone-cement with MgO can be lower than without MgO, which resulted in higher K_IC for bone-cement with MgO than without MgO.

There are no publication on E and υ of CBC or K_IC of bone-CBC interface to compare this study results. However, the value of E of CBC (740.41 ± 16.41 MPa) in this study is in close agreement with E of PMMA (674 MPa) found by Gillani et al. (Gillani et al., 2010). The value of K_IC of bone - CBC interface in this study was lower than that of Wang and Agrawal (Wang and Agrawal, 2000) (about 0.4 MPa.m^1/2)between bovine cortical bone and Great Lakes Orthodontic’s Splint dental cement (E=2.5 GPa, υ=0.25). This difference was reasonable since the cement used in this study is different from the test specimen used by Wang and Agrawal.

4. Conclusion

This study has demonstrated that the incorporation of micro and nanoparticles of MgO to PMMA enhanced the fracture toughness of bone-PMMA interfaces. This finding suggests that adding MgO particles to PMMA should be further investigated with respect to applications in total joint arthroplasty (TJA). The results of the mechanical properties (E, υ, K_IC) obtained from this study can be used in the finite element modeling of TJA. The optimal concentration of MgO particles to PMMA to enhance mechanical and biological performances is currently under investigation.