Abstract
Social expectations play a critical role in everyday decision-making. However, their precise neuro-computational role in the decision process remains unknown. Here we adopt a decision neuroscience framework by combining methods and theories from psychology, economics and neuroscience to outline a novel, expectation-based, computational model of social preferences. Results demonstrate that this model outperforms the standard inequity-aversion model in explaining decision behavior in a social interactive bargaining task. This is supported by fMRI findings showing that the tracking of social expectation violations is processed by anterior cingulate cortex, extending previous computational conceptualizations of this region to the social domain. This study demonstrates the usefulness of this interdisciplinary approach in better characterizing the psychological processes that underlie social interactive decision-making.
Keywords: decision neuroscience, expectations, social cognition, social norm, inequity aversion, neuroeconomics
INTRODUCTION
Behaving socially appropriately routinely requires the ability to accurately infer what others expect of us. For example, imagine you are patiently waiting in line and a stranger cuts in front of you. What are the social norms that inform behavior in this situation? Perhaps you felt uncomfortable because this person violated an unspoken rule that everyone will wait their turn, and contemplated whether or not to inform them of their transgression. An important, though understudied, question is how beliefs about social norms influence these types of everyday social decisions.
To date, there have been several theoretical accounts that endeavor to explain how we make choices in these social contexts. One prominent model of social preferences argues that people value equality and prefer situations when all participants receive the same amount, even if this is nothing (Fehr and Schmidt, 1999; Bolton and Ockenfels, 2000). Indeed, a recent study has suggested that brain areas associated with valuation and reward processing could underlie this preference (Tricomi et al., 2010).
However, despite its popularity and intuitive appeal, there is increasing evidence that inequity aversion is not a complete account of social decision-making. For example, unfair and unequal offers in a commonly used task examining social preferences, the Ultimatum Game (UG), will be accepted if there is evidence that the proposer's intentions were ‘noble’ (Falk et al., 2003). In this study, responders were more likely to accept an unfair $2 offer if they believed this was chosen over an alternative $0 offer compared to when they believed the alternative choice was a $5 offer. In addition, responders will still reject unfair offers even when knowing that this behavior will not impact the proposers payoff (Yamagishi et al., 2009). In this study, the authors compared rejection rates to offers in the standard UG to an impunity game, in which rejecting an offer only affects the responder's payoff, not the proposers, which actually increases the inequity in payoffs between the two players.
An alternative approach to understanding social decision behavior is to focus on the expectations people have regarding a social interaction. These expectations may reflect a social norm about what a majority of people would do in a given situation. Using this framework, we propose that people develop context-specific expectations of social scenarios, which are subsequently used as behavioral reference points. For example, rejection rates in the UG increase when participants are provided with information about how other players have responded (Bohnet and Zeckhauser, 2004), and decrease when they believe that an unfair offer is ‘typical’ (Sanfey, 2009). These results suggest that expectations about context appropriate behavior, rather than pure payoff equity per se, may provide a better account of motivation in bargaining behavior. Here, we compared a novel model of expectations to a prominent inequity aversion model in an effort to understand the motivations underlying social interactive decision-making. In addition, we used this model in conjunction with fMRI to identify brain networks involved in the computational process of tracking violations of social expectations.
METHODS
Participants
Eighteen participants (mean age = 19.9, female = 56%) were recruited via advertisements posted on the campus of the University of Arizona. All participants were screened for any significant health-related or neuropsychiatric disorders, and none was currently taking psychoactive medication. One participant was excluded from the analysis for technical reasons (data not shown). All participants gave informed consent according to procedures approved by the University of Arizona's Institutional Review Board.
Procedure
Participants completed two separate sessions. During the first behavioral session, participants met in small groups and learned the rules of the UG. Participants then played in the role of proposer and made offers to 20 other people. They were informed that these were other participants in the experiment. Participants then had their picture taken and were told that other experimental participants would make proposals to them after viewing their picture, and that they would decide whether to accept or reject these offers while being scanned in a subsequent session (Session 2). This two-stage procedure was designed to increase the plausibility that participants were interacting with real people. The average delay between Sessions 1 and 2 was 6.39 days (s.d. = 2.59).
Expectations
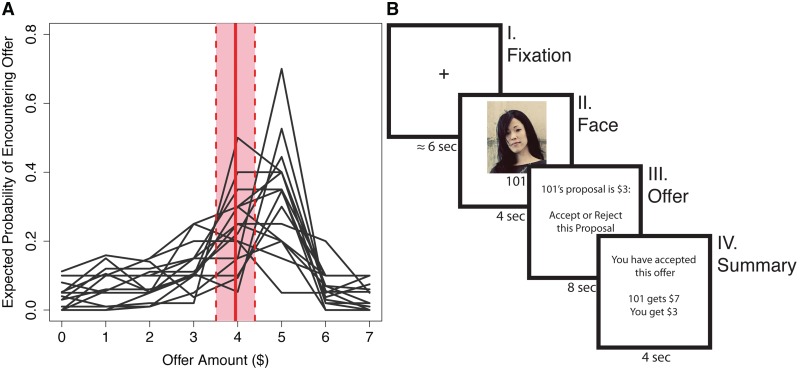
Prior to being scanned, we elicited participants’ beliefs about the kinds of offers they expected to encounter, with participants being asked the number of people out of 100 that they believed would make an offer between [0,7] dollars. These elicited expectations were used to create a distribution of the frequency of offers that they expected to encounter (Figure 1A). The weighted mean of this distribution was used to represent each participant's initial expectation (Sanfey, 2009). Formally, the weighted mean  of the set of offers x = [0,7] with the accompanying set of belief weights b is the quantity
of the set of offers x = [0,7] with the accompanying set of belief weights b is the quantity
| (1) |
where n is the number of offers in x.
Fig. 1.
Ultimatum game. (A) Participant's expectations about the Ultimatum game. Solid red line reflects average weighted mean. Dotted lines reflect ±1 s.d. (B) A trial timeline. (I) Fixation cross. (II) Picture of their partner for the round. (III) Offer revealed and participant decision (accept or reject offer). (IV) Summary of earnings for the round.
Ultimatum game
Participants played a standard single-shot UG in the role of responder with 48 different proposer partners while undergoing fMRI (Figure 1B). In this game, a proposer is charged with splitting a sum of money with a partner. The responder then decides either to accept or reject this proposed offer. If accepted, the money is split as suggested, but if rejected then neither player receives anything (Guth et al., 1982). Twenty-four of the partners used were human, 12 were computers, and 12 were non-intentional humans (i.e. humans whose responses were randomly generated). Each offer was preceded by a picture of their partner for that round. Though participants were told that the human-intentional offers would be made by other players, in actual fact all offers were controlled by the experimenter, and all participants saw the same set of offers. This set consisted of equal numbers (12 each) of {1,3,5} dollar offers, all of which were made from a $10 pot. For each participant, partner pictures were randomly paired to an offer amount, ensuring that there was no potential picture by offer amount interaction. Only the human intentional offers were included in the modeling analyses. Participants were paid $20 for participating with an additional $5 bonus, which they believed was based on their performance in the game. While participants were not specifically queried about the extent to which they believed they were playing with real people, no participant questioned the cover story, and our behavioral results are consistent with studies that did not employ deception (Camerer, 2003).
Data analyses
All behavioral statistics were computed using the R statistical package (R Development Core Team, 2008). A mixed logit model (Jaeger, 2008) with the amount of money offered, and participant's initial expectation was used to predict participant's decisions to accept or reject. We allowed the slopes for the offer parameter to randomly vary by subject, but did not estimate a parameter for the intercept because of the linear dependence on participant's expectations.
Modeling
To demonstrate the importance of considering expectations in the UG, we compared a novel expectation model, which incorporates expectations to the standard inequity-aversion model, which posits that people are motivated to minimize the difference between their payoffs.
Expectation model
The expectation model (Smith, 2009) was developed in the context of Psychological Game Theory (Geanakoplos et al., 1989; Battigalli and Dufwenberg, 2009) which describes a mathematical framework in which beliefs can be modeled in the utility function. Similar to other models of emotion (Dufwenberg and Gneezy, 2000; Battigalli and Dufwenberg, 2007), this model operationalizes anger as a belief dependent emotion and predicts that people experience anger when their beliefs about behavioral norms in a given context are violated. In the UG, offers that are lower than participants’ expectations should bias participants to reject the offer. Formally, Player 2's utility U of a given action i can be defined as
| (2) |
In this model, Player 2 is interested in both maximizing the amount of money they will make (M2) and minimizing their anger, which is defined as the non-negative difference between the amount of money that they expect Player 1 to offer (E2S1) and the amount of money that Player 1 actually offers (S1). The anger term is scaled by a free parameter which is constrained 0 < θ < 1 and is modulated by the size of the offer.
Inequity-aversion model
This popular model of social preferences (Fehr and Schmidt, 1999; Bolton and Ockenfels, 2000) predicts that people value fairness and will be biased to reject offers as inequity increases (Fehr and Camerer, 2007; Tricomi et al., 2010). Formally, Player 2's utility for a given action i can be defined as
| (3) |
where M1 is the amount of money that Player 1 will receive and M2 is the amount of money that Player 2 will receive.1 The superscript + indicates that these differences must be non-negative. The inequality term is scaled by a free parameter which is constrained 0 < θ < 1.
Choice rule
The probability P of taking an action i (i.e. accept or reject) was computed by placing the utility values for each decision into a softmax function.
| (4) |
Parameter estimation
Best fitting parameters were derived using the MATLAB fmincon function (Nelder and Mead, 1965) by maximizing the log likelihood of the data under each model on a trial-to-trial basis. Multiple start locations were used to reduce the likelihood of the optimization algorithm getting stuck in local minima. LLEs were calculated separately for each participant as
| (5) |
where i denotes the participant's choice for a given trial t.
To evaluate the model fits we calculated the Bayesian Information Criteria (BIC) (Schwarz, 1978), which is a metric of model fit that rewards the most parsimonious model by adding a penalty for additional free parameters.
| (6) |
where L is the maximized value of the likelihood function for the model, k is the number of free parameters estimated, and n is the number of observations.
We also computed a Pseudo R2 measure, which compares the improvement in LLE gained by the model compared to a model that chose randomly (i.e. probability = 0.5 for each trial).
| (7) |
where r is the LLE for the random model.
Model simulation
The behavioral predictions for the models were computed by using a theta value of 0.3 (the approximate value estimated in the model fitting procedure) and then calculating the probability of accepting each offer from the set [0,5] using equations (2), (3), and (4). For the expectation model, we varied expectations between [3,5], which was the range we encountered in our behavioral sample (See Figure 1A).
Neuroimaging analyses
Data acquisition
Each scanning session included a T1-weighted MPRAGE structural scan (TR = 11 ms, TE = 4 ms, matrix = 256 X 256, slice thickness = 1 mm, gap = 0 mm), followed by five functional runs. The first three functional runs contained the UG trials and the last two contained the memory trials (see (Chang and Sanfey, 2009) for more details about the memory study). Functional scans used a three-shot multiple echo planar imaging (MEPI) GRAPPA sequence using parameters selected to maximize signal in regions associated with high susceptibility artifact, such as orbitofrontal cortex and medial temporal lobe (Chang et al., 2011) (TR = 2000 ms, TE = 256 ms, matrix = 96 X 96, FOV = 192 mm, slice thickness = 3.0 mm, 42 axial slices, voxel size 2 X 2 X 3).
Data pre-processing
Functional imaging data were preprocessed and analyzed using the FSL Software package 4.1.4 (FMRIB, Oxford, UK). The first three volumes of each functional run were discarded to account for T1 equilibrium effects. Images were corrected for slice scan time using an ascending interleaved procedure. Head motion was corrected using MCFLIRT using a six-parameter rigid-body transformation. Images were spatially smoothed using a 5-mm full width at half maximum Gaussian kernel. A high-pass filter was used to cut off temporal periods longer than 66 seconds. All images were initially co-registered to the participant's high resolution structural scan and were then co-registered to the MNI 152 person 2-mm template using a 12-parameter affine transformation. Scanner artifacts, physiological artifacts (i.e. cardiac and respiration) and head movement related artifacts were removed from the data using independent components analysis (Beckmann and Smith, 2004; Tom et al., 2007). All functional analyses are overlaid on the participants’ average high-resolution structural scan in MNI space.
General analysis methods
A three-level mixed effects general linear model (GLM) was used to analyze the imaging data. A first-level GLM was defined for each participant's functional run that included a boxcar regressor for each epoch of interest (e.g. decision phase) convolved with a canonical double-gamma hemodynamic response function (HRF). The duration of epochs in which participants submitted a response were modeled using the participant's reaction time (Grinband et al., 2008). To account for residual variance, we also included the temporal derivatives of each regressor of interest, the six estimated head movement parameters, and any missed trials (i.e. trials in which participants failed to respond, n = 6) as covariates of no interest. The resulting general linear model was corrected for temporal autocorrelations using a first-order autoregressive model. A second-level fixed effects model was fit for each subject to account for intra-run variability. For each participant, contrasts were calculated between parameter estimates for different regressors of interest at every voxel in the brain. A third-level mixed effects model using FEAT with full Bayesian inference (Woolrich et al., 2004) was used to summarize group effects for every specified contrast. Statistical maps were corrected for multiple comparisons using whole brain cluster correction based on Gaussian random field theory with an initial cluster threshold of Z > 2.3 and a Family Wise Error corrected threshold of P < 0.05 (Worsley et al., 1992).
Imaging analysis 1: trial analysis
To examine the neural responses to linear deviations in expectation violation, we subtracted the amount of money offered at each trial from the participants’ initial expectations and coded them as 0, 1, 2 or 3+. Thus, this model consisted of the four expectation violation predictors, two additional predictors for the other phases of the task (i.e. face phase, summary phase and computer and non-intentional human control trials), a regressor indicating missed trials, the temporal derivatives of these nine regressors and the six motion parameters, which resulted in a GLM with a total of 24 predictors. We then used a within subject linear contrast of the expectation deviations (i.e. −2 −1 1 2) to examine the neural signals that parametrically tracked these deviations.
Imaging analysis 2: model prediction
While Analysis 1 reveals neural responses associated with trial-to-trial deviations of expectation, these violations are necessarily correlated with the amount of money offered (i.e., smaller offers are always associated with larger expectation violations). To examine the independent effect of expectations, we restricted our analysis to the intermediate $3 offers and examined neural responses that linearly tracked with participants’ initial expectations. We selected the $3 offers for this analysis because the model simulation revealed that these offers should be most susceptible to expectation effects (Figure 2A). Thus, this model included the following regressors: face phase, human $1 offers, human $2 offers, human $3 offers, human $5 offers, non-intentional human control trials, computer trials, summary phase trials, missing trials and head motion parameters. Together with the temporal derivatives, this produced a model with a total of 24 regressors. For this analysis, we used a linear contrast of expectations [i.e. expectations that were between 2.5–3.4 (n = 3), 3.5–4.4 (n = 11) and 4.5–5.4 (n = 3)] to examine neural responses that linearly tracked with expectations for the intermediate $3 offers across participants. Importantly, our randomization procedure ensured that there were no other systematic differences across the $3 trials such as the face of the partner, which was confirmed using a Fisher's Exact test using Monte Carlo Simulation with 10 000 samples, P = 0.93.
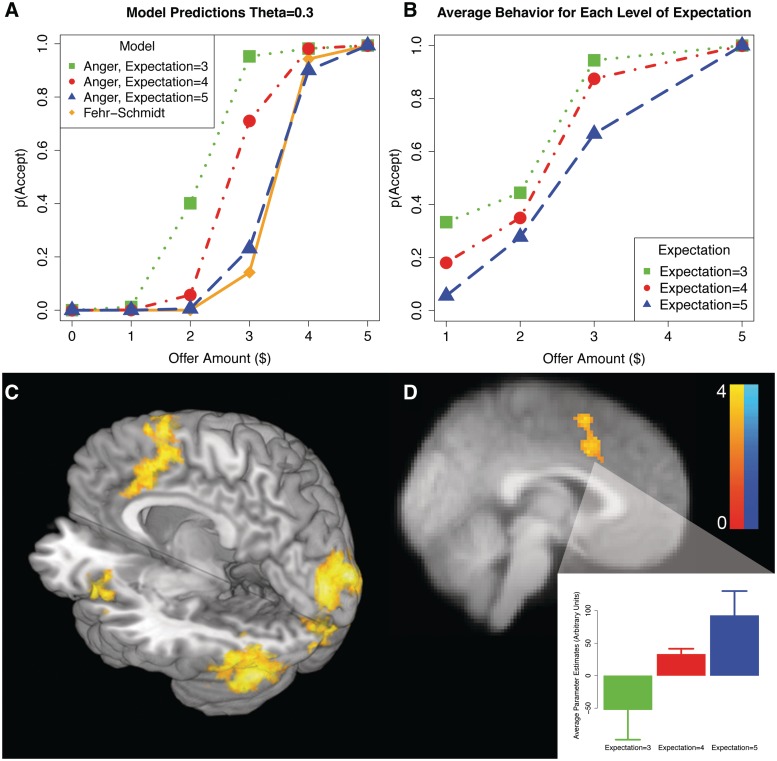
Fig. 2.
Ultimatum game results. (A) Results of the model simulations for θ = 0.3. Participants are more likely to accept unfair offers as a function of their initial expectations. (B) Average acceptance rates for each offer amount for varying expectations. Importantly, the acceptance rates closely follow the pattern predicted by the Expectation model. (C) Neuroimaging results of a linear contrast of deviations from expectation, revealing linearly increasing activity in left anterior insula, anterior cingulate cortex and supplementary motor area. (D) Neuroimaging results for the linear contrast of expectation across subjects for $3 offers. Activity in the ACC/preSMA increases as a function of expectations. The color bar reflects Z-statistics. Imaging analyses are corrected for multiple comparisons using cluster correction, Z > 2.3, P < 0.05.
RESULTS
Behavioral
As expected (Sanfey et al., 2003), participants were more likely to reject offers as they became less equitable (parameter estimate = −6.90, s.e. = 1.24, odds ratio = 0.001, z = −5.56, P < 0.001). Importantly, however, after controlling for offer amount, participants were more likely to reject offers when they had higher initial expectations, parameter estimate = 2.98, s.e. = 0.39, odds ratio = 19.60, z = 7.71, P < 0.001. These results (Figure 2B), suggest that participants' prior beliefs about the social norm are important in determining whether or not an offer will be accepted.
Modeling
To better understand the computational mechanism underlying this result, we compared the ability of the two competing models to explain the behavioral data. The results, summarized in Table 1, revealed that the expectation model was a better account of the data than the inequity-aversion model as evidenced by differences in participants’ BIC scores for each model, t(16) = −2.08, P < 0.05.2 Simulations of the models (Figure 2A) illustrate that they both make identical predictions when participants believe that the social norm is $5 (50% of a $10 pot). However, the models make divergent predictions for behavior as expectations decrease, with the largest difference being for the intermediate $3 offers.
Table 1.
Modeling results
| Model | LLE (s.d.) | BIC (s.d.) | Pseudo-R2 (s.d.) | Theta (s.d.) |
|---|---|---|---|---|
| Anger | −3.84 (2.36) | 10.86 (4.71) | 0.77 (0.14) | 0.28 (0.26) |
| Fehr–Schmidt | −4.45 (1.75) | 12.07 (3.49) | 0.73 (0.11) | 0.26 (0.23) |
Notes: Values given for the subject average log likelihood estimate (LLE), Bayesian information criteria (BIC), pseudo-r2 and the estimated theta parameter for each model.
Trial analysis
Using a parametric contrast of deviation from expectations on a trial-by-trial level, we find increasing activity in left insula, ACC and pre-supplementary motor areas as offers increasingly violated individual participants’ expectations (Figure 2C, and Table 2). We did not observe any significant results associated with positive violations of expectation, even at a lower threshold (P < 0.005 uncorrected).
Table 2.
Imaging results
| Analysis | Direction | Hemisphere | Region | BA | Z-value | X | Y | Z |
|---|---|---|---|---|---|---|---|---|
| Trial analysis | ||||||||
| Positive | ||||||||
| L | Frontoinsular cortex | NA | 3.76 | −38 | 18 | −14 | ||
| L | Insula | 48 | 3.09 | −30 | 18 | −10 | ||
| L | LOC, Inferior division | 19 | 3.89 | −38 | −84 | −20 | ||
| L | LOC, Superior division | 3.54 | −26 | −62 | 38 | |||
| L | Occipital pole | 17 | 3.94 | −14 | −102 | 8 | ||
| R | ACC | 24 | 3.22 | 2 | 22 | 36 | ||
| R | LOC, Inferior division | 19 | 4.01 | 42 | −84 | −18 | ||
| R | LOC, Superior division | 19 | 3.5 | 26 | −68 | 34 | ||
| R | Occipital pole | 17 | 4.21 | 6 | −94 | 6 | ||
| R | Superior frontal gyrus | 8 | 3.26 | 14 | 18 | 56 | ||
| R | SMA | 6 | 3.16 | 4 | 8 | 66 | ||
| Negative | ||||||||
| No suprathreshold clusters | ||||||||
| Model prediction | ||||||||
| Positive | ||||||||
| L | ACC | 24 | 3.57 | −4 | 10 | 40 | ||
| L | SMA | 6 | 3.69 | −4 | 8 | 56 | ||
| R | IFG, Pars opercularis | 48 | 3.96 | 36 | 12 | 24 | ||
| R | Precentral gyrus | 44 | 3.37 | 42 | 4 | 34 | ||
| Negative | ||||||||
| No suprathreshold clusters |
Notes: This table reflects the results of the two imaging analyses and shows the local maxima of clusters surviving cluster correction Z > 2.3, P < 0.05 in MNI space. Cortical and subcortical regions were identified using the Harvard-Oxford Probabilistic Anatomical Atlas. Abbreviations: LOC = lateral occipital cortex, SMA = supplementary motor area, ACC = anterior cingulate cortex.
Model prediction
We then used the model's predictions to highlight neural processes specifically associated with the tracking of expectation violations, which are computationally distinct from tracking inequity. A whole brain analysis for regions that linearly track with the model's predictions for the $3 offers reveals that only the ACC, SMA and precentral gyrus underlies this process (Figure 2D, and Table 2). Participants with higher expectations demonstrated increased activity in ACC when deciding about the intermediate $3 offers.
DISCUSSION
In this study we were interested in examining the role of expectations in social decision-making, and in particular how social norms impact perceptions of fairness. We used a simple behavioral economic bargaining game to examine a financially consequential social decision. Replicating a previous behavioral study (Sanfey, 2009), responder's expectations about how they believed proposers would play the UG appeared to impact their decisions regarding unfair offers. Specifically, we found that responders who expected proposers to make lower offers were more likely to accept these offers. This effect cannot be explained by the popular notion that people merely prefer to minimize inequity in payoffs (Fehr and Schmidt, 1999; Bolton and Ockenfels, 2000). Instead, we find that our formal model of expectations (Smith, 2009) provides a better account of participants’ behavior than the competing inequity-aversion model. This suggests that people have context-specific beliefs about what to expect and are more likely to reject offers that violate these expectations.
We were further interested in examining the neural systems that play a computational role in this process. Violations of expectation at the single trial level were associated with the insula, ACC and DLPFC, which is highly consistent with what has previously been associated with inequity in previous experiments using the Ultimatum Game (Sanfey et al., 2003; Tabibnia et al., 2008; Guroglu et al., 2010; Kirk et al., 2011).3 In fact, because negative expectation violations were necessarily correlated with inequity by our design, it is possible that these results can also be explained by inequity aversion. However, we were able to examine processes specific to expectation violations by restricting our analysis to the intermediate $3 offers, which were demonstrated to be the most susceptible to variations in individual expectations by our model simulation. A whole brain search revealed that the ACC was integral in tracking the predictions of our formal model with participants with higher expectations demonstrating increased activity in the ACC when receiving the $3 offers. The ACC has previously been associated with many other expectation-based effects such as anticipating aversive events (Ploghaus et al., 1999), detecting novel events (Downar et al., 2000), placebo effects (Wager, et al., 2004), weighting social prediction errors (Behrens et al., 2008) and conforming to others’ expectations (Klucharev et al., 2009). A previous study found that while this region was associated with increasingly unfair offers, it did not underlie decisions to reject (Sanfey et al., 2003). This suggests that a neural signal, perhaps akin to a prediction error signal in basic reinforcement learning (Cavanagh et al., 2010), may be leveraged to calculate conflict between individual preferences and social norms (Klucharev et al., 2009) and thereby bias decision-making. This interpretation is highly consistent with a recent proposal that this region is involved in processing both negative affect and cognitive control (Shackman et al., 2011).
This result also fits with broader ideas of how expectations are important in social decision-making. We have previously demonstrated that people are motivated by guilt to cooperate in order to avoid disappointing a relationship partner's expectations, a process mediated by the insula, ACC and SMA (Chang et al., 2011). In the present study, we find that people generate a similar neural signal when others violate their expectations, which may serve as an emotional signal to bias behavior to enforce a social norm. Together, these two studies demonstrate that a coherent network in the brain associated with both conflict and emotion underlies decisions to behave consistently with a social norm. This provides a plausible unitary neurobiological mechanism to explain observations that violations of a norm by others leads to feelings of anger, while violations of the norm by oneself lead to feelings of guilt (Haidt, 2003; Giner-Sorolla and Espinosa, 2011).
In summary, these results provide compelling evidence for the role of expectations in social decision-making behavior. Our model provides not only a better account of the behavioral data than an inequity aversion model, but reveals that the process of detecting expectation violations underlying decisions to reject is associated with the same neural network that has previously been demonstrated to underlie other, more basic, expectation-based effects. Overall, these results demonstrate that people do not use simple heuristics such as equal splits in considering their responses to financial proposals, but rather rely on their context-specific beliefs about the social norm to make their decisions.
Acknowledgments
The authors wish to thank Mascha van't Wout and Katia Harle for their assistance in data collection and Alec Smith and Michael Frank for their helpful comments. This work was supported by awards from the National Institute of Aging (R21AG030768 to A.G.S.) and the National Institute of Mental Health (F31MH085465 to L.J.C.).
Footnotes
1It is important to note that because we only have one data point for expectations per participant the two models could in principle converge on identical predictions regarding the set of offers examined here if an intercept was included in the inequity aversion model. However, we do not believe there to be a principled psychological reason to estimate such a parameter in the model, as it would allow for flexibility in the fairness reference point and extend the model beyond strict inequity. Useful future work could directly manipulate expectations and/or include offers greater than 50% of the endowment to fully test the divergent predictions of the two models. Here, we have attempted to limit the potential for over fitting and opted to compare the purest conceptual implementations of the two models, allowing only one free parameter in each.
2A significant difference between the two models was also found for the pseudo-r2 measure.
3It is important to note that we also replicate these extant results in the current study using a linear contrast of inequity at 0.005 uncorrected.
References
- Battigalli P, Dufwenberg M. Guilt in games. American Economic Review. 2007;97(2):170–6. [Google Scholar]
- Battigalli P, Dufwenberg M. Dynamic psychological games. Journal of Economic Theory. 2009;144(1):1–35. [Google Scholar]
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Transactions in Medical Imaging. 2004;23(2):137–52. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Behrens TE, Hunt LT, Woolrich MW, Rushworth MF. Associative learning of social value. Nature. 2008;456(7219):245–9. doi: 10.1038/nature07538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohnet I, Zeckhauser R. Social comparisons in ultimatum bargaining. Scandinavian Journal of Economics. 2004;106(3):495–510. [Google Scholar]
- Bolton GE, Ockenfels A. ERC: a theory of equity, reciprocity, and competition. American Economic Review. 2000;90(1):166–93. [Google Scholar]
- Camerer CF. Behavioral Game Theory. New York: Russell Sage Foundation; 2003. [Google Scholar]
- Cavanagh JF, Frank MJ, Klein TJ, Allen JJ. Frontal theta links prediction errors to behavioral adaptation in reinforcement learning. Neuroimage. 2010;49(4):3198–209. doi: 10.1016/j.neuroimage.2009.11.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang LJ, Sanfey AG. Unforgettable ultimatums? Expectation violations promote enhanced social memory following economic bargaining. Frontiers in Behavioral Neuroscience. 2009;3:36. doi: 10.3389/neuro.08.036.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang LJ, Smith A, Dufwenberg M, Sanfey AG. Triangulating the neural, psychological, and economic bases of guilt aversion. Neuron. 2011;70(3):560–72. doi: 10.1016/j.neuron.2011.02.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downar J, Crawley AP, Mikulis DJ, Davis KD. A multimodal cortical network for the detection of changes in the sensory environment. Nature Neuroscience. 2000;3(3):277–83. doi: 10.1038/72991. [DOI] [PubMed] [Google Scholar]
- Dufwenberg M, Gneezy U. Measuring beliefs in an experimental lost wallet game. Games Economic Behaviour. 2000;30(2):163–82. [Google Scholar]
- Falk A, Fehr E, Fischbacher U. On the nature of fair behavior. Economic Inquiry. 2003;41(1):20–6. [Google Scholar]
- Fehr E, Camerer CF. Social neuroeconomics: the neural circuitry of social preferences. Trends in Cognitive Science. 2007;11(10):419–27. doi: 10.1016/j.tics.2007.09.002. [DOI] [PubMed] [Google Scholar]
- Fehr E, Schmidt KM. A theory of fairness, competition, and cooperation. Quarterly Journal of Economics. 1999;114(3):817–68. [Google Scholar]
- Geanakoplos J, Pearce D, Stacchetti E. Psychological games and sequential rationality. Games and Economic Behavior. 1989;1(1):60–79. [Google Scholar]
- Giner-Sorolla R, Espinosa P. Social cuing of guilt by anger and of shame by disgust. Psychological Science. 2011;22(1):49–53. doi: 10.1177/0956797610392925. [DOI] [PubMed] [Google Scholar]
- Grinband J, Wager TD, Lindquist M, Ferrera VP, Hirsch J. Detection of time-varying signals in event-related fMRI designs. Neuroimage. 2008;43(3):509–20. doi: 10.1016/j.neuroimage.2008.07.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guroglu B, van den Bos W, Rombouts SA, Crone EA. Unfair? It depends: neural correlates of fairness in social context. [Research Support, Non-U.S. Gov't] Social Cognitive and Affective Neuroscience. 2010;5(4):414–23. doi: 10.1093/scan/nsq013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guth W, Schmittberger R, Schwarze B. An experimental analysis of ultimatum bargaining. Journal of Economic Behavior and Organization. 1982;3:367. [Google Scholar]
- Haidt J. The moral emotions. In: Davidson RJ, Scherer KR, Goldsmith HH, editors. Handbook of Affective Sciences. Oxford: Oxford University Press; 2003. pp. 852–70. [Google Scholar]
- Jaeger TF. Categorical data analysis: away from ANOVAs (trsnformation or not) and towards logit mixed models. Journal of Memory and Language. 2008;59(4):434–46. doi: 10.1016/j.jml.2007.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirk U, Downar J, Montague PR. Interoception drives increased rational decision-making in meditators playing the ultimatum game. Frontiers in Neuroscience. 2011;5:49. doi: 10.3389/fnins.2011.00049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klucharev V, Hytonen K, Rijpkema M, Smidts A, Fernandez G. Reinforcement learning signal predicts social conformity. Neuron. 2009;61(1):140–51. doi: 10.1016/j.neuron.2008.11.027. [DOI] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. The Computer Journal. 1965;7(4):308–13. [Google Scholar]
- Ploghaus A, Tracey I, Gati JS, Clare S, Menon RS, Matthews PM, et al. Dissociating pain from its anticipation in the human brain. Science. 1999;284(5422):1979–81. doi: 10.1126/science.284.5422.1979. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. Austria: Vienna; 2008. R: A language and environment for statistical computing. [Google Scholar]
- Sanfey AG. Expectations and social decision-making: biasing effects of prior knowledge on Ultimatum responses. Mind & Society. 2009;8(1):93–107. [Google Scholar]
- Sanfey AG, Rilling JK, Aronson JA, Nystrom LE, Cohen JD. The neural basis of economic decision-making in the Ultimatum game. Science. 2003;300(5626):1755–8. doi: 10.1126/science.1082976. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6(2):461–4. [Google Scholar]
- Shackman AJ, Salomons TV, Slagter HA, Fox AS, Winter JJ, Davidson RJ. The integration of negative affect, pain and cognitive control in the cingulate cortex. Nature reviews Neuroscience. 2011;12:154–67. doi: 10.1038/nrn2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith AC. Beliefs and emotions in games and decisions. Doctoral Dissertation, University of Arizona, Tucson, AZ. Retrieved August 15, 2011, from ProQuest Dissertations and Theses. (Publication no. AAT 3359780); 2009. [Google Scholar]
- Tabibnia G, Satpute AB, Lieberman MD. The sunny side of fairness: preference for fairness activates reward circuitry (and disregarding unfairness activates self-control circuitry) Psychological Science. 2008;19:339–47. doi: 10.1111/j.1467-9280.2008.02091.x. [DOI] [PubMed] [Google Scholar]
- Tom SM, Fox CR, Trepel C, Poldrack RA. The neural basis of loss aversion in decision-making under risk. Science. 2007;315(5811):515–8. doi: 10.1126/science.1134239. [DOI] [PubMed] [Google Scholar]
- Tricomi E, Rangel A, Camerer CF, O'Doherty JP. Neural evidence for inequality-averse social preferences. Nature. 2010;463(7284):1089–91. doi: 10.1038/nature08785. [DOI] [PubMed] [Google Scholar]
- Wager TD, Rilling JK, Smith EE, Sokolik A, Casey KL, Davidson RJ, et al. Placebo-induced changes in FMRI in the anticipation and experience of pain. Science. 2004;303(5661):1162–7. doi: 10.1126/science.1093065. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Behrens TE, Beckmann CF, Jenkinson M, Smith SM. Multilevel linear modelling for FMRI group analysis using Bayesian inference. Neuroimage. 2004;21(4):1732–47. doi: 10.1016/j.neuroimage.2003.12.023. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Evans AC, Marrett S, Neelin P. A three-dimensional statistical analysis for CBF activation studies in human brain. Journal of Cerebral Blood Flow and Metabolism. 1992;12(6):900–18. doi: 10.1038/jcbfm.1992.127. [DOI] [PubMed] [Google Scholar]
- Yamagishi T, Horita Y, Takagishi H, Shinada M, Tanida S, Cook KS. The private rejection of unfair offers and emotional commitment. Proceedings of the National Academy of Science USA. 2009;106(28):11520–3. doi: 10.1073/pnas.0900636106. [DOI] [PMC free article] [PubMed] [Google Scholar]