Abstract
A Traditional Chinese Medicine (TCM) formula is a collection of several herbs. TCM formulae have been used to treat various diseases for several thousand years. However, wide usage of TCM formulae has results in rapid decline of some rare herbs. So it is urgent to find common available replacements for those rare herbs with the similar effects. In addition, a formula can be simplified by reducing herbs with unchanged effects. Based on this consideration, we propose a method, called “formula pair,” to replace the rare herbs and simplify TCM formulae. We show its reasonableness from a perspective of pathway enrichment analysis. Both the replacements of rare herbs and simplifications of formulae provide new approaches for a new formula discovery. We demonstrate our approach by replacing a rare herb “Forsythia suspensa” in the formula “the seventh of Sang Ju Yin plus/minus herbs (SSJY)” with a common herb “Thunberg Fritillary Bulb” and simplifying two formulae, “the fifth of Du Huo Ji Sheng Tang plus/minus herbs (FDHJST)” and “Fang Feng Tang” (FFT) to a new formula “Fang Feng Du Huo Tang” (FFDHT).
1. Introduction
Traditional Chinese Medicine is an ancient system used in disease treatments for several thousand years already [1, 2]. Currently, TCM is popular only in Asia, but also in United States, Europe, and other countries as a complementary or alternative medicine [3, 4]. Nearly 100,000 TCM formulae have been recovered [5, 6], each of which normally contains several herbs. Here, “herbs” refer to not only plants, but also animals and minerals with effects of treatments [7].
An herb normally has five attributes: they have nature, taste, channel tropism, functions, and indications [8–10]. Nature refers to a basic characteristic based on the patient's reaction to an herb, and it has four properties: cold, cool, warm, and hot; taste indicates the actions an herb has on human body and it includes five characters: spicy, sour, sweet, bitter, and salty; channel tropism denotes an herb's selective therapeutic effects on a certain part of the body, and it includes twelve different organs: heart, liver, spleen, lung, kidney, stomach, large intestine, small intestine, bladder, gallbladder, pericardium, three warmers; functions signify the mechanisms of an herb's therapeutic effects. For example, a common herb and “Chinese angelica,” has the functions of “harmonizing the blood,” “regulating menses,” and “moistening intestines”; indications describe the diseases or symptoms treated by an herb. Several herbs compose a formula in the order of Master, Adviser, Soldier, and Guild [11], while a later order indicates less importance [12].
A formula usually contains many active compounds. These compounds target many molecules in the cell and work together to increase therapeutic efficacy and reduce adverse effects [6, 11]. Although great efforts have been made, the mechanisms of most formulae are still unknown [6, 13]. Recently, systems biology approaches [14] and TCM informatics [15] have been applied to explore the mechanisms for different formulae, but with a little significant progress. In this study, we explore the pharmacological effects of formulae from a perspective of pathway enrichment analysis.
The availability of some herbs has a rapid decline with their wide usage [16]; for example “Shi-He Ming Yan Wan” [17], a powerful formula, has been used to treat many different diseases. It has been believed that the treatment power of the formula partially comes from a rare herb “rhinoceros horn,” which is widely used in many TCM formulae. Due to poaching and illegal trade, the number of black rhinos has shrunk by 96% since 1970 in Africa. The same situation has happened for “Pholidota,” “Forsythia suspensce,” “Cordyceps sinensis,” and so forth. So to continually use those formulae to treat the diseases, it is urgent to find the common available replacements for those rare herbs with the same effects [18].
Herb switches and simplification in a formula have been tested. For example, “Liu-wei-di-huang” (LWDH) [12], a famous formula with six herbs, was simplified from “Ba-wei-di-huang” (BWDH) by discarding two herbs based on herbs' attributes. In our study, we adopted the similar concept and simplified TCM formula with a “formula pair” method based on large-scale computation. We then showed the reasonableness of our approach with a perspective of pathway enrichment analysis, same as to the replacements of rare herbs.
2. Materials and Methods
2.1. Data Sources
We collected 4,343 formulae and 6,171 herbs from SIRC/TCM database (http://www.tcm120.com/1w2k/q_pres.asp). If several formulae have a same name but different herbs, we took the classical one (e.g., formula A) as a leader and named others as “the nth of formula A plus/minus herbs” (n = 1, 2,3…). Disease ontology identities (DOIDs) of diseases treated by formulae were obtained from human disease ontology.
2.2. Score System of Combinational Degree (CD) for Formula Pairs
Combinational degree refers to the similarity between two formulae. The CD was calculated to evaluate combinational degree between two formulae based on the herbs they share and the weights of shared herbs. Assuming there are two formulae F 1 and F 2. L 1 and L 2 are the number of herbs in F 1 and F 2, respectively, n is the number of shared herbs, herb i indicates one of the shared herbs, and m 1i and m 2i signify the sequential numbers of herb i's positions in F 1 and F 2. The weights of herb i in F 1 and F 2, named W 1i and W 2i, are calculated as
| (1) |
The CD of F 1 and F 2 is calculated as
| (2) |
An example is shown in Table 1.
Table 1.
Weight of each herb in F 1 and F 2.
| Formula | herb 1 | herb 2 | herb 3 | herb 4 | herb 5 | herb 6 | herb 7 |
|---|---|---|---|---|---|---|---|
| F 1 | 1 | 0.8 | 0.6 | 0.4 | 0.2 | ||
| F 2 | 1 | 0.75 | 0.5 | 0.25 |
*Assuming F 1 includes 5 herbs: herb 1, herb 2, herb 3, herb 4, and herb 5, while F 2 includes 4 herbs: herb 2, herb 4, herb 6, and herb 7. Herb 2 and herb 4 are assumed as shared herbs of F 1 and F 2. Weight of each herb is shown in this table. So CD of F 1 and F 2 is calculated as CD(F1,F2) = (0.8 + 1)/2 + (0.4 + 0.75)/2 = 1.475. Then CD(F1,F2) was divided by 7.5 to 0.197 for normalization.
We calculated all formula pairs of 4,343 formulae. The generated values for those CDs are from 0 to 7.5; we then normalized them to [0, 1] for convenient purpose. Combinational degree was used as an evaluation index of the similarity between two formulae. For a pair of formulae with a CD value of 0, we considered these two formulae without combination, which also means that they have no shared herbs. CD ∈ (0, 0.3] indicates the two formulae as low combination, while CD ∈ (0.3,0.7] as middle combination, and CD ∈ (0.7,1] as high combination based on the number of shared herbs in two formulae and the position of each herb in the formulae.
2.3. Disease Similarity Calculation for Each Formula Pair
DOSim [19] is an R package used to calculate the similarity between diseases using DOID based on disease ontology. For 4,343 formulae-treated diseases, only l,769 formulae-treated diseases can be mapped to DOIDs. Assuming that p and q represent the number of diseases treated by formulae F 1 and F 2, respectively, DOSim will generate p∗q similarity values for this formula pair. Each similarity value can be denoted as K i(i = 1, 2,…, p∗q). The similarity of treated diseases between F 1 and F 2, named as Sim, can be calculated as follows:
| (3) |
For a pair of formulae with a Sim ∈ [0,0.3], we consider that those diseases the two formulae treat have no similarity, and a Sim ∈ (0.3,0.7] indicates those diseases with significant similarity for a formula pair, a Sim ∈ (0.7,1] with high similarity.
2.4. Score System of Attribute Similarities (AS) for Herb Pairs
To evaluate whether the attributes of two herbs are similar or not, a sore system was constructed for the purpose. For the five attributes in a formula, we define each one with a weight of 1. Based on a previous study, the detailed algorithms are as follows.
(1) The four natures of an herb are represented as X 1, X 2, X 3, and X 4, respectively. Different herbs have different natures. If an herb has only one nature, we reward this nature a value of 1 and other natures as 0. If the nature of an herb is “ping,” which means neutral, a value of 0.25 will be assigned to each of the four natures. A slight nature, for example, “slight cold,” will get a value of 0.8; for a severe nature, such as “severe cold,” we assign it a value of 1.2. For two herbs i and j, the similarity of their natures, named A i,j, is calculated as
| (4) |
An example is shown in Table 2.
Table 2.
Values of natures for herb i and herb j.
| Cold | Cool | Warm | Hot | |
|---|---|---|---|---|
| Herb i | 0.25 | 0.25 | 0.25 | 0.25 |
| Herb j | 0.8 | 0 | 0 | 0 |
*Assuming herb i has a nature of “ping” and herb j has a nature of “slight cold.” Values of natures are showed in this table. So A i,j is calculated as A i,j = 0.25/(0.8 + 0.25 + 0.25 + 0.25) ≈ 0.16.
(2) The five tastes are represented as Y 1, Y 2,…, Y 5, respectively. According to the similar principal, if an herb has several tastes, we reward each of those tastes a value of 1 and 0 to other unidentified tastes. For a slight taste, such as “slight sour,” a value of 0.8 will be assigned. If the taste of an herb is described as “tasteless,” the value of “sweet” will be added 0.5. If the taste of an herb is depicted as “pucker,” the value of “sour” will get 0.5 bonus. For the two herbs i and j, the similarity of tastes, named B i,j, is calculated as
| (5) |
(3) The twelve channel tropisms are represented as Z 1, Z 2,…, Z 12, respectively. According to the similar principal, if an herb has several channel tropisms, we reward each of those channel tropisms a value of 1 and 0 to other unidentified channel tropisms. For the two herbs i and j, their similarity of tastes, named C i,j, is calculated as
| (6) |
(4) The numbers of functions for herbs i and j are named as FTi and FTj. FTi,j is the number of shared functions between two herbs. The similarity of the functions between two herbs, named D i,j, is calculated as
| (7) |
An example is shown in Table 3.
Table 3.
Functions and D i,j of herb i and herb j.
| Herb i | Function 1 | Function 2 | Function 3 | Function 4 | Function 5 |
|---|---|---|---|---|---|
| Herb j | Function 2 | Function 4 | Function 6 | Function 7 |
*Assuming herb i has 5 functions and herb j has 4 functions. Function 2 and Function 4 are shared functions. So D i,j is calculated as D i,j = (2∗2)/(5 + 4) ≈ 0.44.
(5) The numbers of indications for herbs i and j are named as ICi and ICj. ICi,j is the number of shared indications between two herbs. The similarity of the indications between two herbs, named E i,j, is calculated as
| (8) |
So, attribute similarity (AS) of herb i and herb j is calculated as
| (9) |
If herbs i and j have an AS value greater than 3, they are considered to have high attributes' similarity.
3. Results
It has been a long history to use herbs to treat diseases. Herbs usually are any part of plants or certain animals with their medicinal effects. Since rare herbs decline rapidly with their wide usage, they face great threat of extinction. To protect those invaluable plants or animals, it is urgent to find the replacement for the formulae with rare herbs. Meanwhile, formulae are not changeless and can be simplified for the cost efficiency and availability. However, the prerequisites for replacements of rare herbs and simplifications of existed formulae are that the new formulae should not change the medical effects compared to original ones. According to this concept, we designed related strategy and used it to computationally detect the possibility of the replacement for all of the formulae we collected.
3.1. Replacements of Rare Herbs
Combinational degree refers to the similarity of two formulae; the smaller the degree, the less similarity between two formulae. Accordingly, the formula pairs with CDs ∈ (0,0.3] were used for herb replacement. With this criterion, two formulae in the pair share few herbs, thus, avoiding rare herbs shared by the two formulae, since if a rare herb is the shared herb for a formula pair, the herb used to replace the rare herb may be the rare herb itself according to our method. Assuming herb i is a rare herb in formulae F 1 and herb j is a common one in F 2, to replace herb i with herb j, we built a strict model as follows:
Sim1,2 ∈ (0.7,1],
ASi,j > 3,
min(W 1i, W 2j)/max(W 1i, W 2j) > 0.8.
The replacement of herb i with j should meet all of the three conditions above. Condition (1) guarantees that herbs i and j contribute highly similar effects. Condition (3) assures that herbs i and j have similar weights. Under such circumstance, when herb j replaces herb i in F 1, the order of Master, Adviser, Soldier, and Guild in F 1 can be kept, and the impact of the replacement will be minimized and can be ignored.
Forsythia suspensa is a rare herb protected by law due to its severe decline. According to our model, we replaced it in the formula “the seventh of Sang Ju Yin plus/minus herbs” (SSJY) with a common herb “Thunberg Fritillary Bulb,” which is a component (herb) in another formula “Sang Ke Tang” (SKT). Both SSJY and SKT can treat chronic bronchitis. Herbs in SSJY and SKT are shown in Table 4.
Table 4.
Herbs in SSJY, SKT, and SJZBY.
| Formula | Herbs | |||
|---|---|---|---|---|
| SJYJJS | Mulberry leaf | Chrysanthemum | Forsythia suspense | Reed rhizome |
| Common hogfennel root | Bitter apricot kernel | Platycodon root | Liquorice | |
| SKT | Mulberry leaf | Fermented soybean | Thunberg fritillary bulb | Radix adenophorae |
| White mulberry root-bark | Cape jasmine fruit | Bitter apricot kernel | Liquorice | |
| SJZBY | Mulberry leaf | Chrysanthemum | Thunberg fritillary bulb | Reed rhizome |
| Common hogfennel root | Bitter apricot kernel | Platycodon root | Liquorice |
SSJY and SKT, meet the requirements in the replacement model based on the following results:
CD(SSJY,SKT) = 0.162;
Sim = 0.999;
in SSJY, W Forsythia suspensa = 0.75; in SKT, W Thunberg fritillary bulb = 0.75; W Forsythia suspensa/W Thunberg fritillary bulb = 1;
AS(Forsythia suspensa,Thunberg fritillary bulb) = 3.44.
So, we replaced “Forsythia suspensa” in SSJY with “Thunberg Fritillary Bulb” in SKT. The replacement resulted in a new formula and we named it as “Sang Ju Zhe Bei Yin” (SJZBY, Table 4).
3.2. Formulae Simplifications
To simplify a formula, we also built a model. For a formula pair with CD ∈ (0.3,0.7] and Sim ∈ (0.7,1], both of them can treat the same or highly similar diseases, we believe that the high similarity of the two formulae is caused by the shared herbs and the rest herbs with AS > 3. Under such assumption, two formulae can be simplified to a new formula which only consists of shared herbs and herbs with high attributes' similarity.
Assuming formulae F 1 and F 2 are a formula pair with CD ∈ (0.3,0.7] and Sim ∈ (0.7,1], F 1 has N herbs, and F 2 has M herbs; the number of shared herbs is K. For other (N − K) herbs in F 1 and (M − K) herbs in F 2, we calculate AS for each herb pair, and totally there are (N − K)∗(M − K) pairs. As a result, we then find out those pairs of herbs with their ASs > 3. If there are (P + Q) herbs in those formula pairs with ASs > 3 and there are P herbs in F 1 and Q herbs in F 2, the new formula can be generated as follows:
if (P > Q), new formula will consist of K shared herbs and Q herbs according to the principle of “least herbs.” This formula is named as “new F 2”;
if (P < Q), new formula will consist of K shared herbs and P herbs. This formula is named as “new F 1”;
-
if (P = Q), assuming ∑W p is the total weights of P herbs in F 1 and ∑W q is the total weights of Q herbs in F 2,
- if (∑W p > ∑W q), new formula will be a “new F 1” according to “higher weights, more importance” concept, the “new F 1” formula will consist of K shared herbs plus P herbs;
- if (∑W p < ∑W q), new formula will be a “new F 2”;
- if (∑W p = ∑W q), both “new F 1” and “new F 2” will be new formulae after discarding those unshared herbs with their ASs≦3. The workflow is shown in Figure 1.
Figure 1.
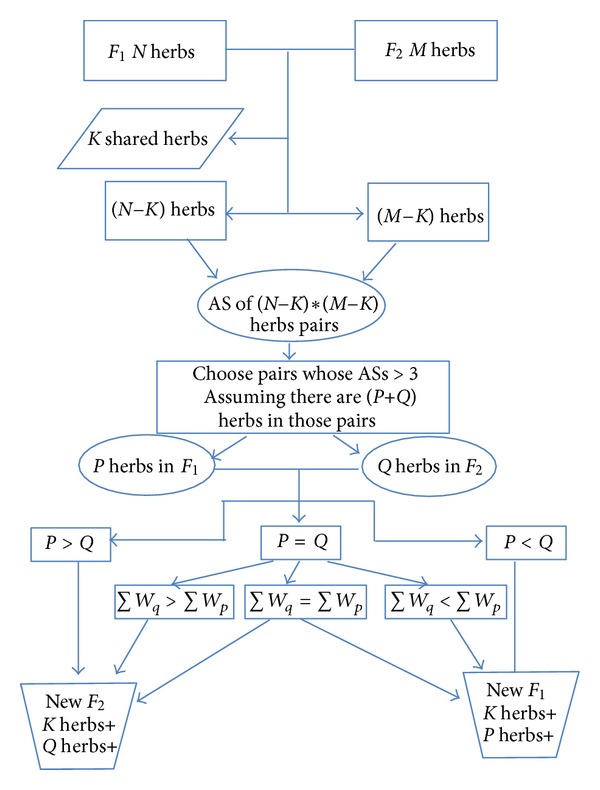
Workflow of simplification.
For example, both formulae “the fifth of Du Huo Ji Sheng Tang plus/minus herbs” (FDHJST) and “Fang Feng Tang” (FFT) can treat rheumatoid arthritis (RA). FDHJST includes 15 herbs (Table 5) and FFT has 8 herbs (Table 5). They have 5 shared herbs: “Radix saposhnikoviae,” “Chinese angelica,” “Radix gentianae macrophyllae,” “Tuckahoe,” “Liquorice”. We calculated AS scores of herb-pairs for the rest unshared herbs and found that AS(Root of doubleteeth pubescent angelica, Notopterygium root) was 3.44 and greater than 3. In FDHJST, W Root of doubleteeth pubescent angelica = 1; in FFT, W Notopterygium root = 0.375. Since the weight of “root of doubleteeth pubescent angelica” in F 1 is greater than the weight (0.375) of notopterygium root in F 2, the new formula, named as “Fang Feng Du Huo Tang (FFDHT)”, will contain 5 shared herbs and “Root of doubleteeth pubescent angelica” (Table 5).
Table 5.
Herbs in FDHJST, FFT, and FFDHT.
| Formula | Herbs | ||
|---|---|---|---|
| DHJSTJJF | Root of doubleteeth pubescent angelica | Mistletoe | Radix gentianae macrophyllae |
| Radix saposhnikoviae | Manchurian wildginger | Chinese angelica | |
| Szechwan lovage rhizome | Chinese herbaceous peony | Drying rehmannia root | |
| Bark of eucommia | Radix achyranthis bidentatae | Ginseng root | |
| Tuckahoe | Cassia bark | Liquorice | |
| FFT | Radix saposhnikoviae | Chinese angelica | Radix gentianae macrophyllae |
| Cassia twig | Notopterygium root | Bitter apricot kernel | |
| Tuckahoe | Liquorice | ||
| FFDHT | Radix saposhnikoviae | Chinese angelica | Radix gentianae macrophyllae |
| Tuckahoe | Root of doubleteeth pubescent angelica | Liquorice | |
3.3. Pathway Enrichment Analysis for SSJY, SKT, and SJZBY
To further verify that our formula replacement is relevant from biomedical view, we carried out pathway enrichment analysis with those target proteins for each formula. Protein targets of herbs in each formula were obtained from TCMID [10]. For SSJY and SKT, they have 21 shared compounds targeting 78 proteins. We used ClueGO [20] to conduct pathway enrichment analysis for those targets with 0.01 as the threshold of P value. The results showed that those targets were enriched in 39 pathways with P values less than 0.01. We ranked those pathway according to the P value of each enriched pathways in an ascending order and selected top 20 pathways (Table 6) for further mechanism analyses.
Table 6.
Top 20 pathways enriched by shared targets of SSJY and SKT with P values less than 0.01.
| Number | Pathway name | P value |
|---|---|---|
| 1 | Leishmaniasis | 1.19E − 08 |
| 2 | Pathways in cancer | 1.83E − 08 |
| 3 | Pertussis | 2.41E − 07 |
| 4 | HTLV-I infection | 3.18E − 06 |
| 5 | Chagas disease (American trypanosomiasis) | 6.94E − 06 |
| 6 | T-cell receptor signaling pathway | 9.98E − 06 |
| 7 | Cytokines and inflammatory response | 1.81E − 05 |
| 8 | Measles | 8.82E − 05 |
| 9 | Legionellosis | 1.16E − 04 |
| 10 | Amoebiasis | 1.16E − 04 |
| 11 | Free radical-induced apoptosis | 1.31E − 04 |
| 12 | Cytokine network | 1.39E − 04 |
| 13 | African trypanosomiasis | 1.42E − 04 |
| 14 | IL-5 signaling pathway | 2.16E − 04 |
| 15 | Colorectal cancer | 2.66E − 04 |
| 16 | Influence of Ras and Rho proteins on G1 to S transition | 3.69E − 04 |
| 17 | NF-κB activation by nontypeable Haemophilus influenzae | 3.69E − 04 |
| 18 | Rheumatoid arthritis | 3.86E − 04 |
| 19 | Toll-like receptor signaling pathway | 7.75E − 04 |
| 20 | Signal transduction through IL1R | 9.92E − 04 |
Among the top 20 pathways enriched by those 78 shared targets, we found that the pathway of cytokines and inflammatory response ranked 7th and the pathway of free radical-induced apoptosis ranked 11th. Both the two pathways were closely related to chronic bronchitis.
The results showed that there were six targets enriched in the pathway of cytokines and inflammatory response. They are granulocyte-macrophage colony-stimulating factor (GM-CSF), tumor necrosis factor (TNF), interleukin-2 (IL-2), interleukin-4 (IL-4), interleukin-6 (IL-6), and interleukin-10 (IL-10).
Inflammation has been proved to be a central factor to the development and progression of chronic bronchitis [21]. GM-CSF is capable of generating both granulocyte and macrophage colonies from precursor cells, and it has important functions in host responses to external stimuli and in inflammatory conditions [21]. Increased levels of GM-CSF have been found in the epithelium and bronchoalveolar lavage fluid from patients with chronic bronchitis [22]. For other targets, TNF shows statistically significant evidence of association with the susceptibility of chronic obstructive pulmonary disease such as chronic bronchitis [23]. IL-4, IL-6, and IL-10 are cytokines with anti-inflammatory effect [24]. The ingredients of both SSJY and SKT have significant impact on those targets, resulting in effective treatment to chronic bronchitis. Therefore, this pharmacological action of SSJY and SKT could be one of the main mechanisms for chronic bronchitis treatment.
Another pathway closely connected with chronic bronchitis is free radical-induced apoptosis. It has been reported that apoptosis of structural cells in the lung may contribute to the pathogenesis of chronic bronchitis [25, 26]. There is an increase in endothelial and epithelial apoptosis in the lungs of patients with chronic bronchitis which cannot be counterbalanced by an increase in proliferation, resulting in a destruction of lung tissue. Therefore, apoptosis has been proposed to be a therapeutic target [26]. Since targets of SSJY and SKT enrich in this pathway, the two formulae may inhibit the apoptosis in endothelial and epithelial cells by a multitarget effect. This pharmacological action of SSJY and SKT may be another main mechanism for chronic bronchitis treatment. Since those shared targets of SSJY and SKT are enriched in the two pathways, this could be the reason why both SSJY and SKT can treat chronic bronchitis.
The new formula, SJZBY, also includes the same 78 targeted proteins. Therefore, it is reasonable to say that SJZBY should have the similar effect on the treatment of chronic bronchitis. Pathway enrichment analysis for shared targets of those formulae shows the reasonableness of this replacement.
3.4. Pathway Enrichment Analysis for FDHJST, FFT, and FFDHT
Pathway enrichment analysis was also applied to explore the potential mechanism for formula simplification. We collected the potential targets for formulae—FDHJST, FFT, and FFDHTl; they are 182, 133, and 95 proteins, respectively. The results show that targets of FDHJST, FFT, and FFDHT are enriched in 73, 64, and 53 pathways with P values less than 0.01, respectively. Same as the above mentioned method, we ranked those pathways according to the P value of each enriched pathway in an ascending order and selected top 20 pathways (Tables 7, 8, and 9) for further mechanism analyses.
Table 7.
Top 20 pathways enriched by targets of FDHJST with P values less than 0.01.
| Number | Pathway name | P value |
|---|---|---|
| 1 | Pathways in cancer | 4.17E − 21 |
| 2 | Cytokines and inflammatory response | 7.15E − 13 |
| 3 | Colorectal cancer | 5.71E − 12 |
| 4 | Cytokine network | 2.60E − 11 |
| 5 | Malaria | 4.64E − 11 |
| 6 | Chagas disease (American trypanosomiasis) | 4.63E − 10 |
| 7 | Pancreatic cancer | 7.47E − 10 |
| 8 | Amoebiasis | 9.38E − 10 |
| 9 | Bladder cancer | 1.27E − 09 |
| 10 | Leishmaniasis | 1.87E − 09 |
| 11 | Pertussis | 2.31E − 08 |
| 12 | Tuberculosis | 3.50E − 08 |
| 13 | Legionellosis | 5.52E − 08 |
| 14 | Rheumatoid arthritis | 7.19E − 08 |
| 15 | Small cell lung cancer | 1.53E − 07 |
| 16 | Chronic myeloid leukemia | 2.16E − 07 |
| 17 | Prostate cancer | 3.56E − 07 |
| 18 | HTLV-I infection | 3.64E − 07 |
| 19 | Influenza A | 6.90E − 07 |
| 20 | African trypanosomiasis | 1.26E − 06 |
Table 8.
Top 20 pathways enriched by targets of FFT with P values less than 0.01.
| Number | Pathway name | P value |
|---|---|---|
| 1 | Pathways in cancer | 3.87E − 17 |
| 2 | Colorectal cancer | 1.17E − 11 |
| 3 | Cytokines and inflammatory response | 1.18E − 09 |
| 4 | Cytokine network | 2.52E − 09 |
| 5 | Prostate cancer | 3.27E − 09 |
| 6 | Amoebiasis | 5.10E − 09 |
| 7 | Pancreatic cancer | 2.22E − 08 |
| 8 | Chagas disease (American trypanosomiasis) | 3.30E − 08 |
| 9 | Chronic myeloid leukemia | 3.86E − 08 |
| 10 | Pertussis | 4.62E − 08 |
| 11 | Leishmaniasis | 4.62E − 08 |
| 12 | Apoptotic signaling in response to DNA damage | 1.85E − 07 |
| 13 | Tuberculosis | 2.32E − 07 |
| 14 | Small cell lung cancer | 2.39E − 07 |
| 15 | Influence of Ras and Rho proteins on G1 to S Transition | 6.39E − 07 |
| 16 | p53 signaling pathway | 6.79E − 07 |
| 17 | Toxoplasmosis | 1.23E − 06 |
| 18 | Measles | 1.51E − 06 |
| 19 | Malaria | 1.61E − 06 |
| 20 | HTLV-I infection | 2.85E − 06 |
Table 9.
Pathways enriched by targets of FFDHT with P values less than 0.01.
| Number | Pathway name | P value |
|---|---|---|
| 1 | Pathways in cancer | 4.96E − 16 |
| 2 | Colorectal cancer | 4.32E − 11 |
| 3 | Prostate cancer | 3.23E − 10 |
| 4 | p53 signaling pathway | 5.15E − 08 |
| 5 | Pertussis | 1.66E − 07 |
| 6 | Small cell lung cancer | 6.70E − 07 |
| 7 | Influence of Ras and Rho proteins on G1 to S transition | 1.44E − 06 |
| 8 | Endometrial cancer | 1.49E − 06 |
| 9 | Pancreatic cancer | 1.49E − 06 |
| 10 | Amyotrophic lateral sclerosis (ALS) | 1.78E − 06 |
| 11 | Cytokines and inflammatory response | 2.68E − 06 |
| 12 | Bladder cancer | 4.68E − 06 |
| 13 | Tuberculosis | 4.79E − 06 |
| 14 | Amoebiasis | 9.81E − 06 |
| 15 | Apoptosis | 1.27E − 05 |
| 16 | HTLV-I infection | 1.35E − 05 |
| 17 | Cytokine network | 1.45E − 05 |
| 18 | RB tumor suppressor/checkpoint signaling in response to DNA damage | 1.61E − 05 |
| 19 | Apoptotic signaling in response to DNA damage | 2.01E − 05 |
| 20 | Chronic myeloid leukemia | 3.19E − 05 |
In those top 20 pathways enriched by targets of FDHJST, we found that the pathway of cytokines and inflammatory response were closely connected with RA. The result showed that the P value of this pathway ranked second in the top 20 pathways. Further research showed that there were thirteen targets of FDHJST enriched in this pathway. They are GM-CSF, interferon beta (IFNB), interferon-gamma (IFNG), transforming growth factor beta-1 (TGFB1), TNF, interleukin-1 alpha (IL-1A), IL-2, IL-4, IL-5, IL-6, IL-8, IL-10, IL-13.
A previous report has confirmed that antagonism of GM-CSF represents a novel therapeutic approach for a variety of autoimmune-mediated inflammatory diseases, including RA [27]. IFNG can stimulate the production of chemokines and is a powerful activator of mononuclear phagocytes; IFNG has also been tried in immune-mediated diseases such as RA [28]. IFNB has shown antirheumatic potential [28]. TNF is proven to be expressed at high levels in rheumatoid joint tissue, where they contribute significantly to inflammation and articular destruction. TNF is the first cytokine to be fully validated as a therapeutic target for RA [29]. TGFB1 is highly expressed in joints in RA and is considered to be a regulator of anti-inflammation in RA [30]. Enhanced expression of TGFB1 protein has been detected in RA synovia and it may be related to the active pathological changes in RA synovia including synoviocyte hyperplasia, inflammatory cell infiltration, sublining angiogenesis, and granuloma formation [31].
For those interleukins, IL-6 and IL-8 can be found in RA pathway in KEGG pathway annotation [32]. IL-10, also known as human cytokine synthesis inhibitory factor, is an anti-inflammatory cytokine and has been proposed to treat RA in clinical practice because of its capacity to inhibit cellular immunity and deactivate macrophages [33]. In summary, considering the proteins of compounds from FDHJST target, the pathway enrichment analysis demonstrates the potential mechanisms of the formula on RA treatment.
Among those top 20 enriched pathways by targets of FFT, the pathway of cytokines and inflammatory response was closely connected with RA. The result showed that this pathway ranked third among the top 20 pathways according the P value. There were ten targets of FFT enriched in this pathway. They are GM-CSF, IFNB, TNF, IL-2, IL-4, IL-5, IL-6, IL-8, IL-10, IL-13, all of which are the same targets of FDHJST. This result indicates that the potential mechanism of FFT to treat RA is highly similar to that of FDHJST.
After simplification, the resulting new formula, FFDHT, was also enriched in the pathway of cytokines and inflammatory response with the P value ranked 11th among the top 20 pathways. Seven targets were enriched in this pathway. They are GM-CSF, TNF, IL-2, IL-4, IL-6, IL-8, IL-10, all of which are also the targets of FDHJST or FFT. Accordingly, it is reasonable to state that FFDHT inherits the pharmacological effects of original ones and has a highly potential effect the treatment of RA, which shows the reasonableness of this simplification.
4. Discussion
Many herbs used in Traditional Chinese Medicine are endangered, such as tiger bone used to treat rheumatism. Its widely usage results in the rapid decline of tigers with the poaching and illegal trade, which push tigers to extinction [17]. Another example is Cordyceps sinensis; the huge commercial demand of Cordyceps sinensis for its powerful tonic function has led to the excessive harvest and its dramatic decline [34]. Therefore, those invaluable herbs are hard to be obtained currently, and the practices in TCM face a great challenge to use those related formulae to treat the diseases. Finding the common replacements for those invaluable rare herbs is in high demand. In this study, we proposed a method to replace rare herbs with common available ones and showed its reasonableness from a perspective of pathway enrichment. The case study suggests the applicability for the replacement of rare herbs, which opens the gate for wide implementation in the field and could have the profound impact on this field.
Moreover, we also proposed a method to simplify formulae based on the similar rationale. A new formula can be formulated with “less herbs but same effect” concept to the original one. Pathway enrichment analysis also shows the reasonableness of the simplification. Our approaches provide an alternative way to reformulate those traditional prescriptions.
Although herbs have been widely used for thousands of years, most of their targets are still unclear and the mechanisms underling their effects remain unknown. And that has strongly prevented the modernization of traditional Chinese Medicine. For example, in the method of score system of attributes' similarities for herb pairs, we found that “rhinoceros horn” and “Buffalo Horn” have high attributes' similarity (AS = 3.5). Replacement of “rhinoceros horn” with “Buffalo Horn” had been used in clinic, we would like to explore the rationale from a perspective of pathway enrichment. However, no targets of the two herbs have been inferred. And similar situation between “walnut kernel” and “Cordyceps sinensis,” we also found that “walnut kernel” has a potential to replace “Cordyceps sinensis” since the AS between them is 3.2. However, no targets have been identified yet. With the progress of pharmacological research on herbs, it can be anticipated that more and more targets will be identified; we believe that more replacements can be carried out based on our approaches and the potential mechanisms behind those replacements can be explored from a perspective of pathway enrichment.
In this work, both replacement of rare herbs and simplification of formulae were computationally tested; our approaches provide an alternative way for new TCM formulation and mechanism inference. To fully verify our method and test the effects of those new formulae, more preclinical experiments need to be conducted. By the combination of in silico and web lab approaches, we expect that the modernization of Traditional Chinese Medicine will be speeded up; thus, people will benefit from this progress.
Acknowledgment
The authors are grateful to Ms. Bingxing Lu for her help in paper preparation. This work was supported by the National 973 Key Basic Research Program (Grant no. 2010CB945401 and 2012CB910400), the National Natural Science Foundation of China (Grant no. 31171264, 31071162, 31000590, and 81171272), and the Science and Technology Commission of Shanghai Municipality (11DZ2260300).
References
- 1.Zhao J, Jiang P, Zhang WD. Molecular networks for the study of TCM pharmacology. Briefings in Bioinformatics. 2009;11(4):417–430. doi: 10.1093/bib/bbp063. [DOI] [PubMed] [Google Scholar]
- 2.Li S, Zhang ZQ, Wu LJ, Zhang XG, Li YD, Wang YY. Understanding ZHENG in traditional Chinese medicine in the context of neuro-endocrine-immune network. IET Systems Biology. 2007;1(1):51–60. doi: 10.1049/iet-syb:20060032. [DOI] [PubMed] [Google Scholar]
- 3.Chan E, Tan M, Xin JN, Sudarsanam S, Johnson DE. Interactions between traditional Chinese medicines and Western therapeutics. Current Opinion in Drug Discovery and Development. 2010;13(1):50–65. [PubMed] [Google Scholar]
- 4.Cheung F. TCM: made in China. Nature. 2011;480(7378):S82–S83. doi: 10.1038/480S82a. [DOI] [PubMed] [Google Scholar]
- 5.Wang L, Zhou GB, Liu P, et al. Dissection of mechanisms of Chinese medicinal formula Realgar-Indigo naturalis as an effective treatment for promyelocytic leukemia. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(12):4826–4831. doi: 10.1073/pnas.0712365105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wen ZN, Wang ZJ, Wang S, et al. Discovery of molecular mechanisms of traditional Chinese medicinal formula Si-Wu-Tang using gene expression microarray and connectivity map. PLoS ONE. 2011;6(3) doi: 10.1371/journal.pone.0018278.e18278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shi J, Liu Y-L, Fang Y-X, Xu G-Z, Zhai H-F, Lu L. Traditional Chinese medicine in treatment of opiate addiction. Acta Pharmacologica Sinica. 2006;27(10):1303–1308. doi: 10.1111/j.1745-7254.2006.00431.x. [DOI] [PubMed] [Google Scholar]
- 8.Xiao B, Tao O, Luo J, Wang Y. Relationships between properties and functional targets of Chinese herbs. Journal of Chinese Integrative Medicine. 2011;9(7):789–793. doi: 10.3736/jcim20110714. [DOI] [PubMed] [Google Scholar]
- 9.Lukman S, He Y, Hui SC. Computational methods for traditional chinese medicine: a survey. Computer Methods and Programs in Biomedicine. 2007;88(3):283–294. doi: 10.1016/j.cmpb.2007.09.008. [DOI] [PubMed] [Google Scholar]
- 10.Xue RC, Fang Z, Zhang MX, et al. TCMID: traditional Chinese medicine integrative database for herb molecular mechanism analysis. Nucleic Acids Research. 2012;41(1):D1089–D1095. doi: 10.1093/nar/gks1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yan SK, Zhao J, Dou SS, et al. Methodology of modernization research in traditional Chinese medicine based on systems biology and network biology. Chinese Journal of Natural Medicines. 2009;7(4):249–259. [Google Scholar]
- 12.Li S, Zhang B, Jiang D, Wei Y, Zhang N. Herb network construction and co-module analysis for uncovering the combination rule of traditional Chinese herbal formulae. BMC Bioinformatics. 2010;11(11, article S6) doi: 10.1186/1471-2105-11-S11-S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tian P. Convergence: where west meets east. Nature. 2011;480(7378):S84–S86. doi: 10.1038/480S84a. [DOI] [PubMed] [Google Scholar]
- 14.Kitano H. Systems biology: a brief overview. Science. 2002;295(5560):1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]
- 15.Rui F. Progress in TCM Informatics. Chinese Journal of Information on TCM. 2009;16(1):2–7. [Google Scholar]
- 16.Li JD. System study of endangerment medicinal animals in China. journal of Chinese Materia Medica. 2001;26(11):728–730. [PubMed] [Google Scholar]
- 17.Graham-Rowe D. Biodiversity: endangered and in demand. Nature. 2011;480(7378):S101–S103. doi: 10.1038/480S101a. [DOI] [PubMed] [Google Scholar]
- 18.Ang-Lee MK, Moss J, Yuan C-S. Herbal medicines and perioperative care. Journal of the American Medical Association. 2001;286(2):208–216. doi: 10.1001/jama.286.2.208. [DOI] [PubMed] [Google Scholar]
- 19.Li J, Gong BS, Chen X, et al. DOSim: an R package for similarity between diseases based on disease ontology. BMC Bioinformatics. 2011;12(1, article 266) doi: 10.1186/1471-2105-12-266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bindea G, Mlecnik B, Hackl H, et al. ClueGO: a cytoscape plug-in to decipher functionally grouped gene ontology and pathway annotation networks. Bioinformatics. 2009;25(8):1091–1093. doi: 10.1093/bioinformatics/btp101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shen M, Vermeulen R, Chapman RS, et al. A report of cytokine polymorphisms and COPD risk in Xuan Wei, China. International Journal of Hygiene and Environmental Health. 2008;211(3-4):352–356. doi: 10.1016/j.ijheh.2007.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Balbi B, Bason C, Balleari E, et al. Increased bronchoalveolar granulocytes and granulocyte/macrophage colony-stimulating factor during exacerbations of chronic bronchitis. European Respiratory Journal. 1997;10(4):846–850. [PubMed] [Google Scholar]
- 23.Castaldi PJ, Cho MH, Cohn M, et al. The COPD genetic association compendium: a comprehensive online database of COPD genetic associations. Human Molecular Genetics. 2010;19(3):526–534. doi: 10.1093/hmg/ddp519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Opal SM, DePalo VA. Anti-inflammatory cytokines. Chest. 2000;117(4):1162–1172. doi: 10.1378/chest.117.4.1162. [DOI] [PubMed] [Google Scholar]
- 25.Segura-Valdez L, Pardo A, Gaxiola M, Uhal BD, Becerril C, Selman M. Upregulation of gelatinases A and B, collagenases 1 and 2, and increased parenchymal cell death in COPD. Chest. 2000;117(3):684–694. doi: 10.1378/chest.117.3.684. [DOI] [PubMed] [Google Scholar]
- 26.Demedts IK, Demoor T, Bracke KR, Joos GF, Brusselle GG. Role of apoptosis in the pathogenesis of COPD and pulmonary emphysema. Respiratory Research. 2006;7(1, article 53) doi: 10.1186/1465-9921-7-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cornish AL, Campbell IK, McKenzie BS, Chatfield S, Wicks IP. G-CSF and GM-CSF as therapeutic targets in rheumatoid arthritis. Nature Reviews Rheumatology. 2009;5(10):554–559. doi: 10.1038/nrrheum.2009.178. [DOI] [PubMed] [Google Scholar]
- 28.Van Holten J, Plater-Zyberk C, Tak PP. Interferon-β for treatment of rheumatoid arthritis? Arthritis Research. 2002;4(6):346–352. doi: 10.1186/ar598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Taylor PC, Feldmann M. Anti-TNF biologic agents: still the therapy of choice for rheumatoid arthritis. Nature Reviews Rheumatology. 2009;5(10):578–582. doi: 10.1038/nrrheum.2009.181. [DOI] [PubMed] [Google Scholar]
- 30.Sugiura Y, Niimi T, Sato S, et al. Transforming growth factor beta-1 gene polymorphism in rheumatoid arthritis. Annals of the Rheumatic Diseases. 2002;61(9):826–828. doi: 10.1136/ard.61.9.826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dai L, Ye ZQ, Tang MA, Yin PD. Expression of TGFB1 in rheumatoid synovia and its relationship with synovial pathological changes. Chinese Journal of Rheumatology. 2000;4(6):357–360. [Google Scholar]
- 32.Ogata H, Goto S, Sato K, Fujibuchi W, Bono H, Kanehisa M. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Research. 1999;27(1):29–34. doi: 10.1093/nar/27.1.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.St Clair EW. Interleukin 10 treatment for rheumatoid arthritis. Annals of the Rheumatic Diseases. 1999;58(1):I99–I102. doi: 10.1136/ard.58.2008.i99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yang DR. Regional and ecological distribution of Cordyceps sinensis . Journal of Anhui Agricultral University. 1999;26:143–148. [Google Scholar]


